The Energy Cost of Sprint Running and the Energy Balance of Current World Records from 100 to 5000 m

Abstract

The time course of metabolic power during 100–400 m top running performances in world class athletes was estimated assuming that accelerated running on flat terrain is biomechanically equivalent to uphill running at constant speed, the slope being dictated by the forward acceleration. Hence, since the energy cost of running uphill is known, energy cost and metabolic power of accelerated running can be obtained, provided that the time course of the speed is determined. Peak metabolic power during the 100 and 200 m current world records (9.58 and 19.19 s) and during a 400 m top performance (44.06 s) amounted to 163, 99 and 75 W kg⁻¹, respectively. Average metabolic power and overall energy expenditure during 100–5000 m current world records in running were also estimated as follows. The energy spent in the acceleration phase, as calculated from mechanical kinetic energy (obtained from average speed) and assuming 25% efficiency for the transformation of metabolic into mechanical energy, was added to the energy spent for constant speed running (air resistance included). In turn, this was estimated as: (3.8 + k′ v²) · d, where 3.8 J kg⁻¹ m⁻¹ is the energy cost of treadmill running, k′ = 0.01 J s² kg⁻¹ m⁻³, v is the average speed (m s⁻¹) and d (m) the overall distance. Average metabolic power decreased from 73.8 to 28.1 W kg⁻¹ with increasing distance from 100 to 5000 m. For the three shorter distances (100, 200 and 400 m), this approach yielded results rather close to mean metabolic power values obtained from the more refined analysis described above. For distances between 1000 and 5000 m the overall energy expenditure increases linearly with the corresponding world record time. The slope and intercept of the regression are assumed to yield maximal aerobic power and maximal amount of energy derived from anaerobic stores in current world records holders; they amount to 27 W kg⁻¹ (corresponding to a maximal O₂ consumption of 77.5 ml O₂ kg⁻¹ min⁻¹ above resting) and 1.6 kJ kg⁻¹ (76.5 ml O₂ kg⁻¹). This last value is on the same order of the maximal amount of energy that can be derived from complete utilisation of phosphocreatine in the active muscle mass and from maximal tolerable blood lactate accumulation. The anaerobic energy yield has also been estimated, throughout the overall set of distances (100–5000 m), assuming that, at work onset, the rate of O₂ consumption increases with a time constant of 20 s tending to the appropriate metabolic power, but stops increasing once the maximal O₂ consumption is attained. Hence the overall energy expenditure can be partitioned into its aerobic and anaerobic components. This last increases from about 0.6 kJ kg⁻¹ for the shortest distance (100 m) to a maximum close to that estimated above (1.6 kJ kg⁻¹) for distances of 1500 m or longer.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Since the beginning of the last century, the analysis of world records has fascinated scientists dealing with muscle and exercise physiology (e.g. Hill 1925) because, on one side, world records represent the best possible performances in any given sport event in any specific point in time; on the other, the assessment of world record times and speeds is by several order of magnitude more accurate than any possible laboratory measurement. Following this time honoured tradition, we will here present an energetic analysis of the current world records in running from 100 to 5000 m. Necessary prerequisite of the matter at stake will be the discussion of a recently developed approach to estimate the energy cost of sprint running, an obviously crucial requirement when dealing with the shorter distances.

Hence, the present chapter is organised as follows.

We will first describe a model proposed by di Prampero et al. (2005) wherein accelerated/decelerated running on flat terrain is considered biomechanically equivalent to uphill/downhill running at constant speed, the slope being dictated by the forward acceleration. If this is so, since the energy cost of uphill/downhill running at constant speed is fairly well know, it is a rather straightforward matter to estimate the energy cost of accelerated/decelerated running, once the acceleration is determined. This will allow us to estimate peak metabolic power and overall energy expenditure during top running performances over 100–400 m distances.

We will then discuss a model to estimate the overall energy spent over 100–5000 m covered at current world record speed, based on a simplified assessment of the energy spent to accelerate the runner’s body in the initial part of the race. We will show that, for the three shorter distances (100, 200 and 400 m), wherein, thanks to the availability of the time course of the speed throughout the race, the more refined analysis described above can be applied, the two approaches yield rather close estimates of overall energy expenditure and mean metabolic power.

The so obtained overall energy expenditure over distances between 100 and 5000 m will then be plotted as a function of the corresponding world record time. The slope and intercept of the resulting straight line regression, as obtained for the five longer distances (1000–5000 m) will be interpreted to yield an estimate of the maximal aerobic power and of the maximal amount of energy derived from anaerobic stores in the current world records holders over these distances. The resulting values turn out to be 27 W kg⁻¹ (corresponding to a maximal O₂ consumption of 77.5 ml O₂ kg⁻¹ min⁻¹ above resting) and to 1.6 kJ kg⁻¹ (76.5 ml O₂ kg⁻¹). It is fair to point out here that this approach is conceptually similar to that proposed by B. B. Lloyd in 1966 for assessing the maximal aerobic speed and the maximal distance covered at the expense of anaerobic energy.

The anaerobic energy yield will also be estimated, throughout the overall set of investigated distances (100–5000 m), assuming that, at work onset, the rate of O₂ consumption increases with a time constant of 20 s tending to the appropriate metabolic power, but stops increasing once the maximal O₂ consumption is attained. This will allow us to estimate the overall amount of energy derived from aerobic sources wherefrom, since the overall energy spent over the corresponding distance is known, the energy yield from the anaerobic sources is easily obtained; it increases from about 0.6 kJ kg⁻¹ for the shortest distance (100 m) to attain a maximal value close to that estimated above (1.6 kJ kg⁻¹) for distances of 1500 m or longer (1 mile, 2000, 3000 and 5000 m).

It can therefore be concluded that the maximal capacity of the anaerobic stores in world class athletes is on the order of 1.6 kJ kg⁻¹. This is compatible with the maximal amount of energy that can be derived from complete utilisation of phosphocreatine in the active muscle mass and from maximal tolerable blood lactate accumulation.

2 The Energy Cost of Sprint Running

Direct measurements of energy expenditure during sprint running are rather problematic because of the massive utilization of anaerobic sources and because of the resulting short duration of any such events that prevents the attainment of a steady state. Indeed, so far the energetics of sprint running has mainly been estimated indirectly from biomechanical analyses, on the bases of assumed overall efficiencies of metabolic to mechanical energy transformation (Cavagna et al. 1971; Fenn 1930a, b; Kersting 1998; Mero et al. 1992; Murase et al. 1976; Plamondon and Roy 1984), or else assessed by means of rather indirect procedures (Arsac 2002; Arsac and Locatelli 2002; di Prampero et al. 1993; Summers 1997; van Ingen Schenau et al. 1991, 1994; Ward-Smith and Radford 2000).

An alternative approach is to assume that sprint running on flat terrain, during the acceleration phase is biomechanically equivalent to uphill running at constant speed, the slope being dictated by the forward acceleration and that, conversely, during the deceleration phase it is biomechanically equivalent to running downhill. If this is so, since the energy cost of uphill (downhill) running at constant speed is rather well know over a fairly large range of inclines, it is a rather straightforward matter to estimate the energy cost of accelerated (decelerated) running, once the acceleration (deceleration) is known.

3 Theory

The theory underlying the analogy mentioned above is summarised graphically in Fig. 12.1, as from the original paper by di Prampero et al. (2005); it has been recently reviewed by di Prampero et al. (2015) and is briefly sketched below, the interested reader being referred to the original papers.

Fig. 12.1

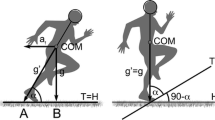
The subject is accelerating forward while running on flat terrain (left) or running uphill at constant speed (right). COM, subject’s centre of mass; a_f, forward acceleration; g, acceleration of gravity; ${\text{g}}^{{\prime }} = \surd ({\text{a}}_{\text{f}}^{2} + {\text{g}}^{2} )$, vectorial sum of a_f plus g; T, terrain; H, horizontal; $\upalpha$, angle between the runner’s mean body axis throughout the stride and T; $90 -\upalpha$, angle between T and H. See text for details

Figure 12.1 (left panel) shows that a runner accelerating on flat terrain must lean forward in such a way that the angle $\upalpha$ between his/her mean body axis and the terrain is smaller the greater the forward acceleration (a_f). This state of affairs is analogous to running uphill at constant speed, provided that the angle $\upalpha$ between mean body axis and terrain is unchanged (Fig. 12.1, right panel). It necessarily follows that the complement of $\upalpha$, i.e. the angle between the terrain and the horizontal (${90 - \alpha }$), increases with a_f.

The incline of the terrain is generally expressed by the tangent of the angle between the terrain and the horizontal (${90 - \alpha }$). As shown in Fig. 12.1 (left panel), this is the ratio of the segment AB to the acceleration of gravity (g):

$$\tan (90{-}\alpha ) = AB/g$$

(12.1)

In turn since the length of the segment AB is equal to a_f, Eq. (12.1) can be rewritten as:

$$\tan (90{-}\alpha ) = a_{f} /g = ES$$

(12.2)

where ES is the tangent of the angle which makes accelerated running (Fig. 12.1, left panel) biomechanically equivalent to running at constant speed up a corresponding slope (Fig. 12.1, right panel), hence the definition Equivalent Slope (ES).

Inspection of Fig. 12.1 also shows that, in addition to being equivalent to running uphill, accelerated running is characterised by yet another difference, as compared to constant speed running. Indeed, the force that the runner must develop (average throughout a whole stride), as given by the product of the body mass and the acceleration, is greater in the former case (= M · g′) as compared to the latter one (= M · g), because g′ > g (Fig. 12.1, left panel). Thus, accelerated running is equivalent to uphill running wherein, however, the body mass is increased in direct proportion to the ratio g′/g. Since ${\text{g}}^{{\prime }} = \surd ({\text{a}}_{\text{f}}^{2} + {\text{g}}^{2} )$, this ratio, which will here be defined “equivalent body mass” (EM) is described by:

$$EM = M \cdot g^{{\prime }} /M \cdot g = \surd (a_{f}^{2} + g^{2} )/g = \surd [(a_{f}^{2} /g^{2} ) + 1]$$

(12.3)

Substituting Eq. (12.2) into Eq. (12.3), one obtains:

$$EM = \surd [(a_{f}^{2} /g^{2} ) + 1] = \surd (ES^{2} + 1)$$

(12.4)

It must also be pointed out that during decelerated running, which is equivalent to downhill running, and in which case the equivalent slope (ES) is negative, EM will nevertheless assume a positive value because ES in Eq. (12.4) is raised to the power of 2. It can be concluded that, if the time course of the velocity during accelerated/decelerated running is determined, and the corresponding instantaneous accelerations/decelerations calculated, Eqs. (12.2) and (12.4) allow one to obtain the appropriate ES and EM values, thus converting accelerated/decelerated running into the equivalent constant speed uphill/downhill running. Hence, if the energy cost of this last is also known, the corresponding energy cost of accelerated/decelerated running can be easily obtained.

The energetics of running at constant speed, on the level, uphill or downhill, has been extensively investigated since the second half of the XIX century (for references see Margaria 1938; di Prampero 1986). Minetti et al. (2002) determined the energy cost of running at constant speed over the widest range of inclines studied so far (at least to our knowledge): from −0.45 to +0.45 and showed that throughout this whole range of inclines the energy cost of running per unit body mass and distance (C_r) is independent of the speed and is described by the polynomial equation that follows (Fig. 12.2):

Fig. 12.2

Energy cost of running at constant speed, C_r (J kg⁻¹ m⁻¹), as a function of the incline (i) of the terrain. The function interpolating the full dots is described by Eq. (12.5). Straight lines irradiating from the origin indicate net efficiency of work against gravity, the values of which are indicated in the inset. Open dots and diamonds are data from previous studies (from Minetti et al. 2002)

$$C_{r} = 155.4 \cdot i^{5} {-}30.4 \cdot i^{4} {-}43.3 \cdot i^{3} + 46.3 \cdot i^{2} + 19.5 \cdot i + 3.6$$

(12.5)

where C_r is expressed in J kg⁻¹ m⁻¹, i is the incline of the terrain, i.e. the tangent of the angle between the terrain and the horizontal, and the last term (3.6 J kg⁻¹ m⁻¹) is the energy cost of constant speed running on compact flat terrain. Thus, substituting i with the equivalent slope (ES), denoting C₀ the energy cost of constant speed level running, and multiplying by the equivalent body mass (EM), Eq. (12.5) can be rewritten as:

$$C_{r} = (155.4 \cdot ES^{5} {-}30.4 \cdot ES^{4} {-}43.3 \cdot ES^{3} + 46.3 \cdot ES^{2} + 19.5 \cdot ES + C_{0} ) \cdot EM$$

(12.6)

Equation (12.6) allows one to estimate the energy cost of accelerated running provided that the instantaneous velocity, the corresponding acceleration values, and hence ES and EM, are known. Strictly speaking the individual value of C₀ should also be known; however, in view of its relatively minor interindividual variation (Lacour and Bourdin 2015), it is often convenient to utilise an average value from the literature, a fact that it is not likely to greatly affect the final outcome.

This approach was originally proposed by di Prampero et al. (2005) and applied to 12 medium level sprinters [best performance time over 100 m: 11.30 s (±0.35, SD)]. It was then utilised by Osgnach et al. (2010) to determine metabolic power and energy expenditure in elite soccer players during official games and it was recently extended to evaluate Usain Bolt’s 100 m world record performance (9.58 s, Berlin, 2009) (di Prampero et al. 2015). Throughout these studies, the energy cost of running was obtained by means of Eq. (12.6), wherefrom the metabolic power, as given by the product of C_r and speed, was obtained.

However, it should be noted that Eq. (12.6) applies only within the range of inclines actually studied by Minetti et al. (2002). Indeed, whenever the calculated ES is far from the maximal (+0.45) or minimal (−0.45) inclines on which the equation was based the obtained values of C_r become unreasonably high, or even negative (in the case of large down-slopes). This state of affairs is not likely to affect greatly the data obtained on medium level sprinters or in soccer players in which cases the maximal values of ES very rarely exceed 0.50 and even when they do the corresponding duration is substantially less than 1 s. In the case of Bolt’s 100 m record, however, the maximal value of ES attained at the very beginning of the race was on the order of 0.85 and, even if it reached the canonical values within the first second (di Prampero et al. 2015), as pointed out in the paper, it led to an astonishingly high value of C_r and of maximal metabolic power.

In view of these considerations, the aim of the section that follows is to recalculate the values of C_r and of metabolic power throughout a 100 m dash on medium level sprinter and on Usain Bolt, utilising a more conservative approach, but still based on the data obtained by Minetti et al. (2002) during uphill running at constant speed. Specifically, Eq. (12.6), will be used to estimate C_r whenever the calculated ES lies within the range of inclines on which the equation was based (−0.45 ≥ ES ≤ +0.45); for ES > 0.45 C_r will be estimated on the basis of the equation that follow:

$$C_{r} = (55.65 \cdot ES{-}5.61) \cdot EM$$

(12.7)

In turn this equation describes the tangent to the C_r versus incline data reported in Fig. 12.2 for i = +0.45.

This same approach will also be applied to calculate the time course of the metabolic power for the 200 m world record of Usain Bolt (19.19 s, Berlin, 2009) and of the top 400 m performance of L. S. Merritt (44.06 s) at the 2009 IAAF World Championship in Berlin.

4 Methods

In all cases, the velocity was assumed to increase exponentially during the acceleration phase, as described by:

$$v(t) = v(f) \cdot (1{-}{\text{e}}^{ - t/\tau } )$$

(12.8)

where v(t) is velocity at time t, v(f) the peak velocity, and $\uptau$ the appropriate time constant, the values of which are reported in Table 12.1, together with the corresponding v(f).

Table 12.1 Peak velocity (v(f), m s⁻¹) over the indicated distances (m), together with the corresponding time constants ($\uptau$) are reported for U. Bolt’s 100 and 200 m current world records, L. S. Merritt’s 400 m top performance (44.04 s, Berlin, 2009) and for 12 medium level sprinters (MLS) (best time over 100 m = 11.30 s ± 0.30)

In turn the values of $\uptau$ reported in Table 12.1 for the 100 m (MLS and U. Bolt) were calculated interpolating the velocity data obtained by a radar system, (di Prampero et al. 2005; Hernandez Gomez et al. 2013). For the 200 and 400 m (U. Bolt and L. S. Merritt) the velocity values utilised for estimating $\uptau$ were those reported over 50 m intervals by Graubner and Nixdorf (2011), up to the attainment of the highest speed. The speed values, as calculated from Eq. (12.8) and Table 12.1, are reported in Fig. 12.3 for Bolt’s and Merritt’s performances, together with the actually measured ones.

Fig. 12.3

Time course of the speed during the 100 and 200 m world records by U. Bolt (panels A and B) and the 400 m top performance by L. S. Merritt (panel C) (Berlin, 2009), as calculated with the aid of Eq. (12.8) from the $\uptau$ and v(f) values reported in Table 12.1 (continuous line). Full dots: actually measured speed. After the attainment of v(f) actual speed data were linearly interpolated. See text for details and references

The time course of the acceleration was then obtained from the first derivative of Eq. (12.8):

$$a(t) = (v(f) - v(t))/\tau = [v(f){-}v(f) \cdot (1{-}{\text{e}}^{ - t/\tau } )]/\tau$$

(12.9)

where a(t) is the acceleration at time t and all other terms have been defined above.

Equations (12.8) and (12.9) allowed us to estimate energy cost of running [as from Eqs. (12.6) and (12.7)], and hence the instantaneous metabolic power (as given by the product of energy cost and speed) during the acceleration phase. In the case of the 200 and 400 m performances, for times greater than that corresponding to peak speed, the energy cost of running was assumed to be equal to C₀, that, in this latter case as well as in Eq. (12.6), was assumed to be 3.8 J kg⁻¹ m⁻¹. In all cases the so obtained values of C_r were corrected for the energy spent against the air resistance (per unit body mass and distance, J kg⁻¹ m⁻¹), as given by: 0.01 · v(t)², where v(t) is expressed in m s⁻¹ (Pugh 1970; di Prampero 1986).

5 Metabolic Power and Overall Energy Expenditure

The time course of the metabolic power is reported in Fig. 12.4 for Bolt’s (100 and 200 m) current world records and Merritt’s 400 m top performance, together with the average for Medium Level Sprinters (MLS) over 100 m, as estimated from the data by di Prampero et al. (2005). The time integral of the so obtained metabolic power reported in Fig. 12.4 allowed us to estimate the overall energy expenditure (air resistance included) to cover the distances in question as well as the corresponding average power; they are reported in Table 12.2, together with peak power values.

Fig. 12.4

Time course of metabolic power during the 100 and 200 m world records by U. Bolt (panels a and b) and the 400 m top performance by L. S. Merritt (panel c). The lower curve in Panel a is the average time course of metabolic power during the first 6 s of a 100 m dash in 12 medium level sprinters. See text for details and references

Table 12.2 Overall energy expenditure (E_tot*, kJ kg⁻¹), peak and average metabolic power (P_met, W kg⁻¹ or ml O₂ kg⁻¹ min⁻¹ over the indicated distances covered at (or close to) world record speed, as obtained from the time integral of the metabolic power curves reported in Fig. 12.4)

The peak metabolic power reported in Table 12.2 for U. Bolt 100 m world record is essentially equal to the calculated for Bolt himself by Beneke and Taylor (2010) and by di Prampero et al. (2005) for C. Lewis, winner of the gold medal over same distance, with 9.92 s, at the 1988 Olympic Games in Seoul. It is, however, substantially less than that estimated in a previous study by di Prampero et al. (2015) which amounted to 197 W kg⁻¹. Indeed, this last value was obtained on the basis of Minetti et al.’s polynomial Eq. (12.6) which, as mentioned in the paper itself and briefly discussed above, overestimates the energy cost of accelerated running for equivalent slopes (ES) greater than 0.5, whereas in this study, for ES > 0.45 the energy cost of running was obtained by means of Eq. (12.7). It is also interesting to note that the peak power of medium level sprinters at the onset of a 100 m dash is about 50% of Bolt’s value (see Fig. 12.4) for an average performance time over the same distance of 11.3 s, corresponding to an average speed only about 15% slower than Bolt’s record. This highlights the fact that top performances over short distances require large accelerations in the initial phase of the run, a prerequisite for achieving this feat, in addition to the appropriate anthropometric and biomechanical characteristics (Charles and Bejan 2009; Maćkała and Mero 2013; Taylor and Beneke 2012), being the capability to develop very large metabolic power outputs in the shortest possible time.

The procedure to estimate total energy expenditure and average metabolic power values reported in Table 12.2 requires knowledge of the time course of the speed and hence of the acceleration. These data are not always available, nor are they easy to obtain. The paragraphs that follow are therefore devoted to utilise an alternative approach based on the average speed only, as originally proposed by di Prampero et al. (1993) (see also Hautier et al. 2010; Rittweger et al. 2009). It will be shown that this approach yields total energy expenditure and average metabolic power values rather close to those estimated (for the 100–400 m distances) on the basis of the more rigorous procedure described above.

It will be assumed that the additional energy spent in the acceleration phase (E_acc), over and above that for constant speed running, is described by:

$$E_{acc} = M\,v_{mean}^{2} /(2 \cdot \eta )$$

(12.10)

where M is the subject’s body mass, v_mean the average speed and $\upeta$ the efficiency of converting metabolic into mechanical energy. Thus, expressing E_acc per unit body mass and assuming $\upeta = 0.25$ (Cavagna and Kaneko 1977; Cavagna et al. 1971), Eq. (12.10) can be rewritten as:

$$E_{acc} /M = v_{mean}^{2} /0.5 = E_{acc} sp$$

(12.11)

If this is so, the overall energy spent to cover any given distance (d) from a still start, per unit body mass, is given by:

$$E_{tot} = (C_{0} + k^{{\prime }} v_{mean}^{2} ) \cdot d + E_{acc} sp = (C_{0} + k^{{\prime }} v_{mean}^{2} ) \cdot d + v_{mean}^{2} /0.5$$

(12.12)

The so obtained values (above resting), for C₀ = 3.8 (J kg⁻¹ m⁻¹) and k′ = 0.01 (J s² kg⁻¹ m⁻³), are shown in Table 12.3, where the last column reports the E_tot values obtained replacing, in the last term of Eq. (12.12), average with peak speed (v_peak):

Table 12.3 Overall energy expenditure (E_tot, kJ kg⁻¹) over the indicated distances covered at (or close to) current world record velocity in running as from Table 12.2 (E_tot*) is indicated together with the corresponding values obtained via the simplified procedure described in the text [E_tot°, as from Eq. (12.12); E_tot^, as from Eq. (12.12′)]

$$E_{tot} = (C_{0} + k^{{\prime }} v_{mean}^{2} ) \cdot d + E_{acc} sp = (C_{0} + k^{{\prime }} v_{mean}^{2} ) \cdot d + v_{peak}^{2} /0.5$$

(12.12′)

Table 12.3 shows that the ratio between the E_tot values obtained from the time integral of the metabolic power curve and those estimated from the simplified procedures described above for the 100–400 m range from 1.07 to 0.93 if E_tot is calculated from the mean speed (Eq. 12.12) or from 0.89 to 0.99 if it is calculated from the peak speed (Eq. 12.12′). In view of the fact that the mean speed is easily available, whereas this is not always the case for peak speed, we will use the simplified procedure described by Eq. (12.12) to estimate the overall energy spent, as well as the mean metabolic power requirement, for the current world records over distances from 100 to 5000 m; they are reported in Table 12.4.

Table 12.4 Overall energy expenditure (E_tot, kJ kg⁻¹), as obtained according to the simplified procedure (Eq. 12.12) for the indicated distances covered in current world record (WR) times (s) are reported together with corresponding mean metabolic power (P_met, W kg⁻¹)

6 Aerobic Versus Anaerobic Energy Expenditure

The last two columns of Table 12.4 report the mean ${\dot{\text{V}}}{\text{O}_2}$ throughout the entire competition calculated as described in detail elsewhere (di Prampero et al. 2015). Suffice it here to say that ${\dot{\text{V}}}{\text{O}_2}$ at the start of the race was assumed to increase exponentially with a time constant of 20 s, tending to the average power requirement, without increasing any further once ${\dot{\text{V}}}{\text{O}_2}$max had been attained (Margaria et al. 1965). This procedure allowed us to estimate the average ${\dot{\text{V}}}{\text{O}_2}$ throughout the race for any given ${\dot{\text{V}}}{\text{O}_2}$max value (see Table 12.4 and Fig. 12.5). The difference between the average values of metabolic power and of ${\dot{\text{V}}}{\text{O}_2}$ must be fulfilled by the anaerobic stores, the overall energetic contribution of which can therefore be easily obtained from the product of this difference and the time of the race; it is reported in Fig. 12.6 for the two selected ${\dot{\text{V}}}{\text{O}_2}$max values of 22 and 27 W kg⁻¹.

Fig. 12.5

Average metabolic power (mean power, W kg⁻¹) as a function of the current world record time (s) over 100–5000 m distance (blue line and dots). Diamonds and red line, triangles and green line are mean ${\dot{\text{V}}}{\text{O}_2}$ calculated as described in the text, for ${\dot{\text{V}}}{\text{O}_2}$ max of 27 (red line and diamonds) or 22 (green line and triangles) W kg⁻¹. See also Table 12.4 (Color figure online)

Fig. 12.6

Anaerobic contribution to overall energy requirement (AnS, kJ kg⁻¹) as a function of the current world record time (s) over 100–5000 m distance, calculated as described in the text for the indicated values of ${\dot{\text{V}}}{\text{O}_2}$max

The average ${\dot{\text{V}}}{\text{O}_2}$ throughout the 100–400 m world records has also been calculated as described above, but replacing the average metabolic power with its actual time course, as reported in Fig. 12.4. For these three distances, therefore, the contribution of the anaerobic stores to the overall energy requirement could also be calculated from the difference between the time integrals of the metabolic power and the estimated ${\dot{\text{V}}}{\text{O}_2}$ curves; they are not substantially different than those obtained by the simplified procedure described in the preceding paragraphs.

Figure 12.6 shows that the anaerobic contribution to the overall energy requirement, for ${\dot{\text{V}}}{\text{O}_2}$max on the order of 26–27 W kg⁻¹ (74.6–77.5 ml O₂ kg⁻¹ min⁻¹ above resting) tends to a plateau of about 1.6 kJ kg⁻¹, whereas for smaller ${\dot{\text{V}}}{\text{O}_2}$max values it keeps increasing without reaching an asymptote. This suggests that the maximal capacity of the anaerobic stores in world class male runners competing over distances between 100 and 5000 m is on the order of 1.6 kJ kg⁻¹ (76.5 ml O₂ kg⁻¹).

The maximal capacity of the anaerobic stores (AnSmax) can also be assessed from a different approach, essentially equal to that proposed by Lloyd (1966) for estimating “maximal aerobic speed” and “anaerobic distance” for the running world records. Indeed, Lloyd proposed to plot the distance covered as a function of the world record time and showed that, for distances greater than 1000 m the regression becomes a straight line with a positive intercept on the y axis (Fig. 12.7, left panel). He therefore suggested that the slope of the so obtained straight line yields the aerobic speed, i.e. the speed sustained solely on the basis of ${\dot{\text{V}}}{\text{O}_2}$max, whereas the y intercept of the regression represents the distance covered at the expense of the anaerobic stores. It should be pointed out that Lloyd’s interpretation is correct only if the slope of the straight line is calculated within the range of distances allowing ${\dot{\text{V}}}{\text{O}_2}$max to be attained and maintained at the 100% level throughout the competition, i.e., for world class athletes between 1000 and 5000 m (131.96–757.35 s).

Fig. 12.7

Distance (km, left panel) and overall energy expenditure (kJ kg⁻¹, right panel) as a function of the corresponding world record time (s) in running (100–5000 m). The regressions, as calculated from 1000 to 5000 m and reported in the figures, show that, for world class athletes: a the maximal aerobic speed amounts to 6.4 m s⁻¹ (23.04 km h⁻¹); and b the maximal aerobic power to 27 W kg⁻¹ (77.5 ml O₂ kg⁻¹ min⁻¹) above resting. The intercept on the y axis of the regression of the lower panel (1.06 kJ kg⁻¹) allows one to estimate the maximal anaerobic capacity in these athletes. See text for details

Lloyd’s approach can be applied to the overall energy expenditure, as calculated above (see Table 12.4) rather that to the distance covered. Also in this case, for distances between 1000 and 5000 m, the regression becomes a straight line with a positive intercept on the y axis (Fig. 12.7, right panel), as described by:

$$E_{tot} = 1.06 + 0.027 \cdot t$$

(12.13)

for E_tot in kJ kg⁻¹ and t in s. Along the lines propose by Lloyd, the slope of this regression can be interpreted as the average ${\dot{\text{V}}}{\text{O}_2}$max of the athletes competing in these events, that amounts then to 27 W kg⁻¹, whereas its y intercept is an index for the anaerobic stores capacity, as discussed in some detail below.

The overall energy (E_tot) spent during a supramaximal effort to exhaustion is the sum of the energy derived from aerobic and anaerobic stores, as described by:

$$E_{tot} = AnS + \dot{V} O_{2} max \cdot t_{e} {-} \dot{V} O_{2} max \cdot (1 - {\text{e}}^{{ - t_{e} /\tau }} ) \cdot \tau$$

(12.14)

where t_e is the time to exhaustion and $\uptau$ is the time constant of the ${\dot{\text{V}}}{\text{O}_2}$ kinetics at work onset (Scherrer and Monod 1960; Wilkie 1980). The third term of Eq. (12.14) takes into account the fact that ${\dot{\text{V}}}{\text{O}_2}$max is not attained at the very onset of the exercise, but it is reached following an exponential function with the time constant $\uptau$. As such, to yield the correct amount of aerobic energy, the quantity ${\dot{\text{V}}}{\text{O}_2}$max · t_e must be reduced accordingly.

This equation becomes particularly useful if the effort duration to exhaustion is comprised between the minimum necessary for complete utilisation of the anaerobic stores (high energy phosphate breakdown and lactate accumulation) and the maximum allowing for ${\dot{\text{V}}}{\text{O}_2}$max to be maintained at the 100% level throughout the effort duration (50 s ≤ t_e ≤ 15 min) (Wilkie 1980; di Prampero et al. 1993; di Prampero 2003). If this is indeed the case, both AnS and ${\dot{\text{V}}}{\text{O}_2}$max can be safely assumed to be constant and maximal. Furthermore, since $\uptau \approx 20\;{\text{s}}$ (di Prampero et al. 1993; di Prampero 2003), if t_e is greater than about 100 s the quantity ${\text{e}}^{{ - {\text{t}}_{\text{e}} /\uptau}}$ becomes vanishingly small; therefore, under these conditions, also the third term of Eq. (12.14) becomes constant $( \approx \dot{V}O_{2}\max \cdot\uptau)$. Thus, rearranging Eq. (12.14):

$$E_{tot} = [AnSmax{-}\dot{V} O_{2} max \cdot \tau ] + \dot{V} O_{2} \hbox{max} \cdot t_{e} = {\text{Constant}} + \dot{V} O_{2} \hbox{max} \cdot t_{e}$$

(12.15)

The regression of Fig. 12.7, right panel, was calculated for world record times over distances between 1000 and 5000 m, i.e. within the above mentioned time range (131.96–757.35 s). If the additional simplifying assumptions are also made that: (1) world class athletes competing over these distances are characterised by an equal ${\dot{\text{V}}}{\text{O}_2}$max and (2) world record times can be identified with t_e, from Eqs. (12.13) to (12.15):

$$[AnSmax{-}\dot{V} O_{2} max \cdot \tau ] = 1.06$$

(12.16)

Thus, setting ${\dot{\text{V}}}{\text{O}_2}$max = 0.027 (kW kg⁻¹) and $\uptau = 20\;\text{s}$, one obtains:

$$AnSmax = 1.06 + 0.027 \cdot 20 = 1.6({\text{kJ}}\;{\text{kg}}^{ - 1} )$$

(12.17)

a value astonishingly close to that estimated from Fig. 12.6 for ${\dot{\text{V}}}{\text{O}_2}$max of 26–27 W kg⁻¹.¹

These considerations can not be applied to shorter distances because: (i) the corresponding points in Fig. 12.7 (right panel) tend to fall below the regression calculated between 1000 and 5000 m, and (ii) it can not be reasonably assumed that ${\dot{\text{V}}}{\text{O}_2}$max in these athletes is equal to that of the athletes competing over the longer distances. Nor can they be applied to longer distances, in which case it cannot be safely assumed that ${\dot{\text{V}}}{\text{O}_2}$max is maintained to the 100% level throughout the entire duration of the race. Indeed, the slope of the regression between distance and record time, as calculated between 5000 and 10,000 m decreases to 6.09 m s⁻¹, and to 5.61 m s⁻¹ for distances between 10,000 m and the marathon. The corresponding ${\dot{\text{V}}}{\text{O}_2}$ values (for C₀ = 3.8 J kg⁻¹ m⁻¹) and k′ = 0.01 (J s² kg⁻¹ m⁻³) become then 25.4 and 23.1 W kg⁻¹, to be compared to a “maximal aerobic speed” of 6.34 m s⁻¹ and a ${\dot{\text{V}}}{\text{O}_2}$ of 27 W kg⁻¹ (assumed to yield ${\dot{\text{V}}}{\text{O}_2}$max) for distances between 1000 and 5000 m, Fig. 12.7.

The fraction of the overall energy expenditure (E_tot, see Table 12.4) derived from anaerobic sources (FAnS) has been estimated over all distances between 100 and 5000 m for the current world record times for two ${\dot{\text{V}}}{\text{O}_2}$max values (22 and 27 W kg⁻¹). As mentioned above, in all cases it was assumed that, at the start of the race, ${\dot{\text{V}}}{\text{O}_2}$ increases with a time constant of 20 s tending to the appropriate mean power requirement (see Table 12.4), but stops increasing once ${\dot{\text{V}}}{\text{O}_2}$max is attained. FAnS is reported in Table 12.5, together with the time to reach ${\dot{\text{V}}}{\text{O}_2}$max. As shown in this Table, this is shorter the higher the metabolic power requirement, and, for a given metabolic power, is longer the higher ${\dot{\text{V}}}{\text{O}_2}$max. It should be pointed out that, whereas for distances ≥1000 m it can be reasonably assumed that ${\dot{\text{V}}}{\text{O}_2}$max amounts to 27 W kg⁻¹, for the shorter distances the FAnS values estimated for the two smaller ${\dot{\text{V}}}{\text{O}_2}$max values (22 W kg⁻¹) are probably closer to the “truth”.

Table 12.5 Fraction of the overall energy derived from anaerobic sources (FAnS) for distances of 100–5000 m covered in current world record times (s) for the two indicated ${\dot{\text{V}}}{\text{O}_2}$max values

7 Discussion

The preceding sections of this chapter were devoted to an analysis of the energetics of current world records in running over distances from 100 to 5000 m. This was carried out along two different lines, as follows.

For the three shorter distances (100, 200 and 400 m) the time course of the metabolic power was estimated according to the model proposed by di Prampero et al. (2005) wherein accelerated running on flat terrain is considered analogous to uphill running at constant speed, the incline of the terrain being dictated by the forward acceleration. The time integral of the so obtained metabolic power curves allowed us to assess the overall energy spent to cover the distances in question. This approach can be performed only if the time course of the speed throughout the run is known, as such it could not be applied for distances longer that 400 m, in which case these data are not available. Indeed, even in the case of the 400 m, speed data were available only over discrete 50 m intervals, thus weakening the time resolution of the metabolic power curve.

Therefore, for the longer distances (800–5000 m), a different approach was followed, [see Sect. 12.5 and Eqs. (12.12), and (12.12′)]. This, while taking care of the overall energy spent in the acceleration phase, did not allow us to estimate the time course of the metabolic power throughout the race, but only its average values. Even so, when applying this simplified procedure to the 100–400 m distances, the resulting overall energy expenditure turned out fairly close (at least for the 200 and 400 m distances) to that estimated from the time integral of the metabolic power time course (see Table 12.3).

The anaerobic contribution to the overall energy expenditure was then estimated as follows. As described in detail elsewhere (di Prampero et al. 2015), it was assumed that the rate of O₂ consumption at the onset of the run increases exponentially with a time constant of 20 s, tending to the metabolic power requirement, but stops abruptly once ${\dot{\text{V}}}{\text{O}_2}$max is attained (Margaria et al. 1965). In turn, for the distances between 1000 and 5000 m, this was assumed to be 27 W kg⁻¹ above resting (see Fig. 12.7). For the shorter distances, however, this assumption does not seem reasonable; as a consequence the rate of ${\dot{\text{V}}}{\text{O}_2}$ at work onset was estimated also for a smaller ${\dot{\text{V}}}{\text{O}_2}$max value (22 W kg⁻¹).

The time integral of the so obtained ${\dot{\text{V}}}{\text{O}_2}$ kinetics was then subtracted from the total energy expenditure to estimate the overall anaerobic yield over the distances in question, for the appropriate metabolic power and ${\dot{\text{V}}}{\text{O}_2}$max values. It is reported in Table 12.5 for the investigated world records as a fraction of the overall energy expenditure.

As shown in Fig. 12.6, the maximal capacity of the anaerobic stores for world class athletes competing over distances between 1000 and 5000 m and assumed to be characterised by a ${\dot{\text{V}}}{\text{O}_2}$max of 26–27 W kg⁻¹ turned out to be on the order of 1.6 kJ kg⁻¹.

The maximal capacity of the anaerobic stores was also assessed according to a different approach, essentially equal to that proposed by Lloyd (1966) for estimating “maximal aerobic speed” and “anaerobic distance” for the running world records. Briefly, the overall energy expenditure over distances between 100 and 5000 m has been plotted as a function of the current world record time (see Table 12.4). The resulting regression, for distances between 1000 and 5000 m turns out to be linear (Fig. 12.7), its slope yielding the mean maximal aerobic power of the current world record holders over these distances, which amounted to 27 W kg⁻¹ (77.5 ml O₂ kg⁻¹ min⁻¹) above resting. In turn, the y intercept of this same regression allowed us to estimate the maximal capacity of the anaerobic stores that, for a ${\dot{\text{V}}}{\text{O}_2}$max of 27 W kg⁻¹, turned out to be 1.6 kJ kg⁻¹, essentially equal to that estimated from the data of Fig. 12.6 for athletes whose ${\dot{\text{V}}}{\text{O}_2}$max is on the order of 26–27 W kg⁻¹.

It can therefore be concluded that, for high calibre world class athletes, the maximal capacity of the anaerobic stores is indeed on the order of 1.6 kJ kg⁻¹ (76.5 ml O₂ kg⁻¹).

This is consistent with the considerations that follow. (i) The capacity of the anaerobic stores is the sum of the maximal amount of energy that can be obtained from high energy phosphates (ATP + phosphocreatine (PCr)) splitting and from lactate (La) accumulation. (ii) When competing over the distances in question at world record speed, the maximally exercising muscles in world class athletes constitute 20–25% of the body mass. (iii) In resting muscles the ATP and PCr concentrations amount to about 6 and 20 m-mol kg⁻¹ fresh tissue, respectively (e.g. see Francescato et al. 2003, 2008), and since (iv) ATP can not decrease substantially without greatly compromising muscle power production (di Prampero and Piiper 2003), only about 20 m-mol kg⁻¹ of PCr can be utilised from rest to exhaustion, i.e. 4–5 m-mol PCr kg⁻¹ body mass (see point ii above). (v) Hence, assuming a P/O₂ ratio of 6 (mol/mol), the amount of O₂ “spared” thanks to the splitting of PCr in the transition from rest to exhaustion corresponds to 0.67–0.83 m-mol O₂ kg⁻¹ body mass. (vi) Assuming further an energy equivalent of 20.9 J ml⁻¹ O₂, and since 1 m-mol O₂ = 22.4 ml, the maximal amount of energy derived from PCr splitting can be estimated in the range 0.31–0.39 kJ kg⁻¹ body mass. (vii) The maximal blood La concentration attained at the end of competitions at maximal speed over the distances ≥400 m is on the order of 15–20 mM above resting (Arcelli et al. 2014; Hanon et al. 1994; Hautier et al. 2010); and since (viii) the accumulation of 1 mM La yields an amount of energy equal to the consumption of about 3 ml O₂ kg⁻¹ body mass (di Prampero 1981; di Prampero and Ferretti 1999), on the basis of an energetic equivalent of O₂ of 20.9 J ml⁻¹, this corresponds to a maximal energy release from La accumulation of 0.94–1.25 kJ kg⁻¹.

Hence the maximal capacity of the anaerobic stores, as given by the maximal amount of energy that can be obtained from PCr splitting and from La accumulation can be estimated in the range of 1.25 (0.31 + 0.94) to 1.64 (0.39 + 1.25) kJ kg⁻¹ body mass, a value rather close to that calculated as described above (see Figs. 12.6 and 12.7).

8 Critique of Methods

The two procedures underlying the energetic analysis of the world records described above are based on several simplifying assumptions that have been discussed elsewhere (di Prampero et al. 1993, 2005, 2015 and by Rittweger et al., 2009) and that are briefly summarised below, the interested reader being referred to the original papers.

The assessment of the time course of the metabolic power in the three shorter distances, as based on the analogy between accelerated running on flat terrain and uphill running at constant speed (see Fig. 12.1), entails what follows.

• (i) The overall mass of the runner is condensed in his/her centre of mass. This necessarily implies that the stride frequency, and hence the energy expenditure due to internal work performance (for moving the upper and lower limbs in respect to the centre of mass) is the same during accelerated running and during uphill running at constant speed up the same equivalent slope (ES).

• (ii) For any given ES, the efficiency of metabolic to mechanical energy transformation during accelerated running is equal to that of constant speed running over the corresponding incline. This also implies that the biomechanics of running, in terms of joint angles and torques, is the same in the two conditions.

• (iii) The highest ES values attained at the onset of the 100 and 200 m runs are substantially larger than the highest inclines actually studied by Minetti et al. (2002); hence the implicit assumption is also made that for ES > 0.45, the relationship between C_r and the incline is as described by Eq. (12.7). However, even for Bolt’s 100 m world record, after about 6 m the actual ES values become <0.45, so that the assumption on which Eq. (12.7) was constructed is not likely to greatly affect the overall estimate of the energy expenditure, even if it may indeed affect the corresponding time course in the very initial phase of the run.

• (iv) The calculated ES values are assumed to be in excess of those observed during constant speed running on flat terrain in which case the runner is lining slightly forward. This, however, cannot be expected to introduce large errors, since our reference value was the measured energy cost of constant speed running on flat terrain (C₀).

As concerns the simplified approach to estimate the average metabolic power, the energy spent in the acceleration phase over and above that for constant speed running was calculated as summarised below.

• (v) The metabolic energy spent (per kg body mass) to accelerate the runner’s body from zero to the mean (or peak speed) was estimated from the mechanical kinetic energy (0.5 · v², where v is the mean, or peak, speed), assuming that the efficiency of converting metabolic into mechanical energy $(\upeta)$ amounts to 0.25 (Eqs. 12.10–12.12). This is consistent with the analogy between accelerated running on flat terrain and uphill running at constant speed, since in the latter case, for inclines between 20 and 40% $\upeta$ is on the order of 0.22–0.26 (see Fig. 12.2).

In addition, for all distances, the following two assumptions were also made, independently of the model utilised.

• (vi) The energy expenditure against the air resistance, per unit body mass and distance, was assumed to be described by: k′ · v², where v (m s⁻¹) is the air velocity, the constant k′ (J s² kg⁻¹ m⁻³) assumed throughout this study amounting to 0.01 (Pugh 1970; di Prampero 1986), a value lower than that which can be calculated from Arsac and Locatelli (2002) biomechanical data, and than that reported by Tam et al. (2012) which amount to 0.017 and 0.019, respectively.

• (vii) The energy cost, per unit body mass and distance, for constant speed running on flat compact terrain neglecting the air resistance (C₀) was assumed to be =3.8 J kg⁻¹ m⁻¹. The corresponding values reported in the literature range from 3.6 as determined on the treadmill by Minetti et al. (2002), to 4.32 ± 0.42 on the treadmill and to 4.18 ± 0.34 on the terrain, as determined more recently by Minetti et al. (2012) at 11 km h⁻¹, to 4.39 ± 0.43 (n = 65), as determined by Buglione and di Prampero (2013) during treadmill running at 10 km h⁻¹, the great majority of data clustering around a value of 4 J kg⁻¹ m⁻¹ (Lacour and Bourdin 2015). Thus, whereas on the one side it would be ideal to know the individual C₀ of each athlete, a rather unrealistic possibility when dealing with world records holders, on the other, the assumption of a common value of 3.8 J kg⁻¹ m⁻¹ does not seem to greatly bias the obtained results.

Finally the overall metabolic energy expenditure was partitioned into its aerobic and anaerobic fractions as follows.

• (viii) The kinetics of O₂ consumption at work onset was calculated as described above, thus allowing us to estimate the mean ${\dot{\text{V}}}{\text{O}_2}$ throughout the run and hence the aerobic and anaerobic fractions of the total energy expenditure. This approach is supported by a recent series of experiments (di Prampero et al. 2015) in which the actual O₂ consumption was determined by means of a portable metabolic cart in 8 subjects during a series of shuttle runs over 25 m, each bout being performed in 5 s. The speed was continuously assessed by means of a radar system, thus allowing us to estimate the instantaneous energy cost and hence the metabolic power, as given by the product of this last and the speed. The actual O₂ consumption was then compared to that estimated as described above from the metabolic power curve and the subjects’ ${\dot{\text{V}}}{\text{O}_2}$max. The two sets of data turned out to be rather close, thus supporting the approach used in this study to estimate the anaerobic and aerobic contribution to the overall energy expenditure.

9 Conclusions and Practical Remarks

Mathematical modelling of training and performance is becoming increasingly important in a number of professions ranging from health and physical training to rehabilitation from disease or injury, not to mention athletic performance (Clarke and Skiba 2013). Therefore, we deemed it important to condense the preceding analyses into a simple set of rules to estimate: (1) the overall energy expenditure, and (2) the aerobic and anaerobic contributions thereof, in running at speeds greater than the maximal aerobic one, provided that the subject’s ${\dot{\text{V}}}{\text{O}_2}$max, the distance covered (d) and the running time (t_e) are known.

Equation (12.12) shows that the overall energy expenditure (E_tot) can be estimated with reasonable accuracy, if the energy cost of constant speed running (C₀), the constant relating the energy expenditure against the wind to the square of the speed (k′) and the efficiency of metabolic to mechanical energy transformation in the acceleration phase $(\upeta)$ are known. Thus, replacing v_mean with the quantity d/t_e (where t_e is the performance time), Eq. (12.12) can be rewritten as:

$$E_{tot} = [C_{0} + k^{{\prime }} \cdot (d/t_{e} )^{2} ] \cdot d + (d/t_{e} )^{2} (2\eta)^{-1} $$

(12.18)

In turn, the ratio of Eq. (12.18) to the performance time yields the average metabolic power (${\dot{\text{E}}}$) throughout the distance in question:

$$\dot{E} = E_{tot} /t_{e} = [C_{0} + k^{{\prime }} \cdot (d/t_{e} )^{2} ] \cdot d/t_{e} + [(d/t_{e} )^{2} (2\eta)^{-1} ]/t_{e}$$

(12.19)

wherefrom the corresponding anaerobic energy yield (AnS) can be obtained thanks to Eq. (12.20), as derived from first principles in the Appendix:

$$AnS = (\dot{E} - \dot{V}O_{2} max) \cdot t_{e} + \dot{V}O_{2} max \cdot \tau {-}[ - \ln (1{-}\dot{V}O_{2} max/\dot{E}) \cdot \tau \cdot (\dot{E} - \dot{V}O_{2} max)]$$

(12.20)

Thus, if ${\dot{\text{V}}}{\text{O}_2}$max and $\uptau$ are known, it is an easy task to estimate both the aerobic and anaerobic components of E_tot.

As concerns the present study, the relevant quantities utilised in the calculations were as follows: C₀ = 3.8 J kg⁻¹ m⁻¹, k′ = 0.01 J s² kg⁻¹ m⁻³; $\upeta = 0.25$; $\uptau = 20\;{\text{s}}$; d and t_e were the 100–5000 m running distances and the current world records times, and ${\dot{\text{V}}}{\text{O}_2}$max 22 or 27 W kg⁻¹, as indicated. It goes without saying that the choice of these quantities is somewhat arbitrary and can be replaced by more accurate estimates, if available.

Finally, whereas this simplified approach was constructed for running on the level on smooth terrain in the absence of wind, any other condition can be easily incorporated, assigning the appropriate values to C₀, k′, $\upeta$, etc., provided that, over the considered distance and time these quantities can be assumed to be constant.

In closing, and in spite of the inevitable limits of this brief review on sprint running and on world records, we do hope that the readers may consider it a stimulus and a challenge to further investigate this fascinating field.

Appendix

The equations appearing in this Appendix are numbered (12.21)–(12.33), even if some of them have previously been mentioned in the text.

In a preceding section of this chapter (12.6) it was assumed that the overall energy (E_tot) spent during a supramaximal effort to exhaustion can be described by:

$$E_{tot} = AnS + \dot{V}O_{2} max \cdot t_{e} {-}\dot{V}O_{2} max \cdot (1 - {\text{e}}^{{ - t_{e} /\tau }} ) \cdot \tau$$

(12.21)

where AnS is the amount of energy derived from anaerobic sources, t_e is the time to exhaustion and $\uptau( \approx 20\;\text{s})$ is the time constant of the ${\dot{\text{V}}}{\text{O}_2}$ kinetics at work onset. The third term of this equation takes into account the fact that ${\dot{\text{V}}}{\text{O}_2}$max is not attained at the very onset of the exercise, but it is reached following an exponential function with the time constant $\uptau$ (Wilkie 1980). Thus:

$$AnS = E_{tot} - \dot{V}O_{2} max \cdot t_{e} {+}\dot{V}O_{2} max \cdot (1 - {\text{e}}^{{ - t_{\text{e}} /\tau }} ) \cdot \tau$$

(12.22)

Furthermore, if t_e is sufficiently long (i.e. $\ge 4\uptau$), the quantity $\text{e}^{{ - \text{t}_{\text{e}} /\uptau}}$ becomes vanishingly small and the third term of the equation reduces to ${\dot{\text{V}}}{\text{O}_2}$max · τ. In this range of exhaustion times therefore, AnS can be easily estimates as:

$$AnS = E_{tot} - \dot{V}O_{2} max \cdot t_{e} + \dot{V}O_{2} max \cdot \tau$$

(12.22′)

Equations (12.21) and (12.22) are based on the implicit assumption that the ${\dot{\text{V}}}{\text{O}_2}$ kinetics is a continuous exponential function from the value prevailing at work onset to ${\dot{\text{V}}}{\text{O}_2}$max. However, as discussed in detail elsewhere (di Prampero et al. 2015), at the onset of supramaximal exercise [in which case the metabolic power requirement (Ė) is greater than the subject’s ${\dot{\text{V}}}{\text{O}_2}$max] ${\dot{\text{V}}}{\text{O}_2}$ increases exponentially towards Ė with the same time constant $(\uptau \approx 20\;\text{s})$, but stops abruptly at the very moment (t₁) when ${\dot{\text{V}}}{\text{O}_2}$max is attained (Margaria et al. 1965). This is shown graphically in Fig. 12.8, where Ė (red horizontal line) and ${\dot{\text{V}}}{\text{O}_2}$max (blue horizontal line) are indicated as a function of the exercise time, together with the time course of ${\dot{\text{V}}}{\text{O}_2}$ before the attainment of ${\dot{\text{V}}}{\text{O}_2}$max (blue continuous curve) and with the hypothetical time course of ${\dot{\text{V}}}{\text{O}_2}$ above ${\dot{\text{V}}}{\text{O}_2}$max, were Ė = ${\dot{\text{V}}}{\text{O}_2}$max (green broken curve). Inspection of this figure makes it immediately apparent that, whereas Eq. (12.22) is correct for Ė = ${\dot{\text{V}}}{\text{O}_2}$max, whenever Ė > ${\dot{\text{V}}}{\text{O}_2}$max it leads to an overestimate of AnS, the more so, the greater the difference between Ė and ${\dot{\text{V}}}{\text{O}_2}$max.

Fig. 12.8

Overall metabolic power requirement (red horizontal line, Ė) as a function of time (t) during square wave exercise of constant intensity and duration t_e. Subject’s maximal O₂ consumption (${\dot{\text{V}}}{\text{O}_2}$max) is indicated by blue horizontal line. At work onset, ${\dot{\text{V}}}{\text{O}_2}$ increases exponentially towards Ė, but stops abruptly at t₁, i.e. when ${\dot{\text{V}}}{\text{O}_2}$max is attained. Actual ${\dot{\text{V}}}{\text{O}_2}$ before t₁ is indicated by continuous blue curve, whereas after t₁ ${\dot{\text{V}}}{\text{O}_2}$ = ${\dot{\text{V}}}{\text{O}_2}$max. Green broken curve denotes hypothetical ${\dot{\text{V}}}{\text{O}_2}$ time course, were Ė ≤ ${\dot{\text{V}}}{\text{O}_2}$max. Anaerobic energy yield is given by the sum of areas 1 + 2 + 3 + 3′ (red); aerobic yield by the sum of areas 4 + 5 (blue). See text for details and calculations (Color figure online)

The aim of the paragraphs that follow is to describe an approach yielding a more accurate estimate of the anaerobic energy yield (AnS) in running at supramaximal constant metabolic power (Ė), provided the subject’s ${\dot{\text{V}}}{\text{O}_2}$max, the exercise duration (t_e) and $\uptau$ are known. Indeed, on the one side, this set of data allows one to estimate Ė, as described by Eq. (12.18):

$$\dot{E} = E_{tot} /t_{e} = \{ [C_{0} + k^{{\prime }} \cdot (d/t_{e} )^{2} ] \cdot d + (d/t_{e} )^{2} (2\eta)^{-1} \} /t_{e}$$

(12.23)

where all terms have been previously defined (see Sect. 12.6). On the other, if ${\dot{\text{V}}}{\text{O}_2}$max, $\uptau$ and t_e are also known, Fig. 12.8 allows one to appreciate graphically that the anaerobic contribution to the overall energy expenditure is represented by the area delimited by Ė and the ${\dot{\text{V}}}{\text{O}_2}$ − ${\dot{\text{V}}}{\text{O}_2}$max curve, i.e. by the sum of the areas 1, 2, 3 and 3′, whereas the sum of the two areas 4 and 5, below the ${\dot{\text{V}}}{\text{O}_2}$ − ${\dot{\text{V}}}{\text{O}_2}$max curve, represents the aerobic energy yield.

What follows is devoted to assess quantitatively the anaerobic energy yield as given by the sum of the areas defined above, indicated numerically as in the Fig. 12.8.

The ${\dot{\text{V}}}{\text{O}_2}$ kinetics at work onset is described by:

$$\dot{V}O_{2} (t) = \dot{E} \cdot (1 - {\text{e}}^{ - t/\tau } )$$

(12.24)

However, as shown in Fig. 12.8, ${\dot{\text{V}}}{\text{O}_2}$ stops increasing abruptly at time t₁, i.e. when ${\dot{\text{V}}}{\text{O}_2}$max is attained. Thus at t₁:

$$\dot{V}O_{2} (t) = \dot{E} \cdot (1 - {\text{e}}^{ - t1/\tau } ) = \dot{V}O_{2} max$$

(12.25)

Rearranging Eq. (12.25), one obtains:

$$1{-}\dot{V}O_{2} max/\dot{E} = {\text{e}}^{ - t1/\tau }$$

(12.26)

or:

$$\ln (1{-}\dot{V}O_{2} max/\dot{E}) = - \, t_{1} /\tau$$

(12.27)

where from t₁ can be finally obtained as:

$$t_{1} = - \ln (1{-}\dot{V}O_{2} max/\dot{E}) \cdot \tau$$

(12.28)

It can therefore be concluded that Eq. (12.28) allows one to estimate the time necessary to attain ${\dot{\text{V}}}{\text{O}_2}$max, provided that ${\dot{\text{V}}}{\text{O}_2}$max itself, together with Ė and $\uptau$ are known.

It is now possible to estimate the anaerobic energy yield proceeding as follows. The area of the rectangle $( { {{\boxed{ 2 }}} + {{\boxed{ 3 }}} + {{\boxed{ 3 }}}^{\prime }} )$ in Fig. 12.8 can be easily calculated as:

$${{\boxed{ 2 }}} + {{\boxed{ 3 }}} + {{\boxed{ 3 }}}^{\prime } = ( {\dot{E} - \dot{V}O_{2} max} ) \cdot t_{e}$$

(12.29)

The area corresponding to the O₂ deficit incurred once ${\dot{\text{V}}}{\text{O}_2}$max is attained (1 + 2) can be estimated as:

$${{\boxed{ 1 }}} + {{\boxed{ 2 }}} = \dot{V}O_{2} max \cdot \tau$$

(12.30)

Finally the area of the rectangle 2 is given by the product of the time t₁ (Eq. 12.28) and the vertical distance between Ė and ${\dot{\text{V}}}{\text{O}_2}$max:

$${{\boxed{ 2 }}} = t_{1} \cdot ( {\dot{E} - \dot{V}O_{2} max} ) = - \ln ( {1{-}\dot{V}O_{2} max/\dot{E}} ) \cdot \tau \cdot ( {\dot{E} - \dot{V}O_{2} max} )$$

(12.31)

The overall amount of energy derived from anaerobic stores (AnS) is finally expressed by the algebraic sum of the Eqs. (12.29), (12.30) and (12.31):

$$\begin{aligned} AnS & = {{\boxed{ 2 }}} + {{\boxed{ 3 }}} + {{\boxed{ 3 }}}^{\prime } + {{\boxed{ 1 }}} + {{\boxed{ 2 }}} - {{\boxed{ 2 }}} \\ & = ( {\dot{E} - \dot{V}O_{2} max} ) \cdot t_{e} + \dot{V}O_{2} max \cdot \tau -[ - \ln ( {1{-}\dot{V}O_{2} max/\dot{E}} ) \cdot \tau \cdot ( {\dot{E}{-}\dot{V}O_{2} max} )] \\ \end{aligned}$$

(12.32)

It should finally be pointed out that Eq. (12.32) defines the anaerobic energy yield whenever the exercise duration is greater that that necessary for ${\dot{\text{V}}}{\text{O}_2}$max to be attained (t_e > t₁). Whenever t_e ≤ t₁, things become much simpler, since in this specific case the only energy derived from anaerobic stores (AnS′) corresponds to the O₂ deficit incurred, as given by the product of the ${\dot{\text{V}}}{\text{O}_2}$ attained at the very end of the exercise, $( = {\dot{\text{E}}} \cdot (1 - {\text{e}}^{{ - {\text{t}}_{\text{e}} /\uptau}} ))$, Eq. (12.24) and the time constant of the ${\dot{\text{V}}}{\text{O}_2}$ kinetics ($\uptau$):

$$AnS^{{\prime }} = \dot{E} \cdot (1 - {\text{e}}^{{ - t_{e} /\tau }} ) \cdot \tau$$

(12.33)

It should finally be pointed out that, whenever Ė = ${\dot{\text{V}}}{\text{O}_2}$max, Eqs. (12.32) and (12.33) reduce to Eq. (12.22) or (12.22′) depending whether, or not, t_e is sufficiently long for ${\dot{\text{V}}}{\text{O}_2}$max to be attained.

It can be concluded that the anaerobic energy yield in running at supramaximal constant intensity can be easily estimated (Eqs. 12.32 and 12.33), provided that the metabolic power requirement (Eq. 12.23), together with the subject’s ${{\text{V}}}{\text{O}_2\text{max}}$, the exercise duration (t_e) and the time constant of the ${\dot{\text{V}}}{\text{O}_2}$ kinetics at work onset ($\uptau$) are known.