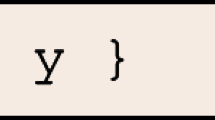Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The idea of verifying that a program meets a given specification for all possible inputs has been studied for a long time. Hoare’s Verifying Compiler Grand Challenge was an attempt to spur new efforts in this area to develop practical tools [1]. A verifying compiler “uses automated mathematical and logical reasoning to check the correctness of the programs that it compiles”. Hoare’s intention was that verifying compilers should fit into the existing development tool chain, “to achieve any desired degree of confidence in the structural soundness of the system and the total correctness of its more critical components”. For example, commonly occurring errors could be automatically eliminated, such as: division-by-zero, integer overflow, buffer overruns and null dereferences.

The first systems that could be reasonably considered as verifying compilers were developed some time ago, and include that of King [2], Deutsch [3], the Gypsy Verification Environment [4] and the Stanford Pascal Verifier [5]. Following on from these, was the Extended Static Checker for Modula-3 [6]. Later, this became the Extended Static Checker for Java (ESC/Java) — a widely acclaimed and influential work in this area [7]. Building on this success was the Java Modeling Language (and its associated tooling) which provided a standard notation for specifying functions in Java [8, 9]. More recently, the Spec# language [10–12] was developed on top of C#, whilst Dafny was developed from scratch to simplify verification [13, 14].

Continuing this line of work, we are developing a verifying compiler for the Whiley programming language [15–18]. Whiley is an imperative language designed to simplify verification and to be suitable for safety-critical systems. For example, Whiley uses unbounded integer and rational arithmetic in place of e.g. IEEE 754 floating point (which is notoriously difficult to reason about [19]). Likewise, pure (i.e. mathematical) functions are distinguished from those which may have side-effects. Our goal is to develop a verifying compiler which can automatically establish a Whiley program as: correct with respect to its declared specifications; and, free from runtime error (e.g. divide-by-zero, array index-out-of-bounds, etc.). More complex properties, such as establishing termination, are not considered (although would be interesting future work). Finally, the Whiley verifying compiler is released under an open source license (BSD), can be downloaded from http://whiley.org and forked at http://github.com/DavePearce/Whiley/. Note that development of the language and compiler is ongoing and should be considered a work-in-progress.

Contribution. The seminal works by Floyd [20], Hoare [21], Dijkstra [22], and others provide a foundation upon which to develop tools for verifying software. However, in developing a verifying compiler for Whiley, we have encountered some gaps between theory and practice. In this paper, we reflect on our experiences using Whiley to verify programs and, in particular, highlight a number of challenges we encountered.

2 Language Overview

We begin by exploring the Whiley language and highlighting some of the choices made in its design. For now, we stick to the basic issues of syntax, semantics and typing and, in the following section, we will focus more specifically on using Whiley for verification. Perhaps one of our most important goals was to make the system as accessible as possible. To that end, the language was designed to superficially resemble modern imperative languages (e.g. Python), and this decision has significantly affected our choices.

Overview. Languages like Java and C# permit arbitrary side-effects within methods and statements. This presents a challenge when such methods may be used within specifications. Systems like JML and Spec# require that methods used in specifications are pure (i.e. side-effect free). An important challenge here is the process of checking that a function is indeed pure. A significant body of research exists on checking functional purity in object-oriented languages (e.g. [23, 24]). Much of this relies on interprocedural analysis, which is too costly for a verifying compiler. To address this, Whiley is a hybrid object-oriented and functional language which divides into a functional core and an imperative outer layer. Everything in the functional core can be modularly checked as being side-effect free.

Value Semantics. The prevalence of pointers — or references — in modern programming languages (e.g. Java, C++, C#) has been a major hindrance in the development of verifying compilers. Indeed, Mycroft recently argued that (unrestricted) pointers should be “considered harmful” in the same way that Dijkstra considered goto harmful [25]. To address this, all compound structures in Whiley (e.g. lists, sets, and records) have value semantics. This means they are passed and returned by-value (as in Pascal, MATLAB or most functional languages). But, unlike functional languages (and like Pascal), values of compound types can be updated in place. Whilst this latter point may seem unimportant, it serves a critical purpose: to give Whiley the appearance of a modern imperative language when, in fact, the functional core of Whiley is pure. This goes towards our goal of making the language as accessible as possible.

Value semantics implies that updates to a variable only affect that variable, and that information can only flow out of a function through its return value. Consider:

figure a

Here, [int] represents a list of ints (i.e. a variable-length array). The semantics of Whiley dictate that, having assigned xs to ys as above, the subsequent update to xs does not affect ys. Arguments are also passed by value, hence xs is updated inside f() and this does not affect f’s caller. That is, xs is not a reference to a list of int; rather, it is a list of ints and assignments to it do not affect state visible outside of f().

Unbounded Arithmetic. Modern languages typically provide fixed-width numeric types, such as 32 bit twos-complement integers, or 64-bit IEEE 754 floating point numbers. Such data types are notoriously difficult for an automated theorem prover to reason about [19]. Systems like JML and Spec# assume (unsoundly) that numeric types do not overflow or suffer from rounding. To address this, Whiley employs unbounded integers and rationals in place of their fixed-width alternatives and, hence, does not suffer the limitations of soundness discussed above.

Flow Typing & Unions. An unusual feature of Whiley is the use of a flow typing system (see e.g. [18, 26, 27]) coupled with union types (see e.g. [28, 29]). This gives Whiley the look-and-feel of a dynamically typed language (e.g. Python). For example, local variables are never explicitly declared; rather, they are declared by assignment. To illustrate, we consider null references. These have been a significant source of error in languages like Java and C#. The issue is that, in such languages, one can treat nullable references as though they are non-null references [30] (Hoare calls this his billion dollar mistake [31]). Although many approaches have been proposed (e.g. [32–36]), Whiley’s type system provides an elegant solution:

figure b

Here, indexOf() returns the first index of a character in the string, or null if there is none. The type int|null is a union type, meaning it is either an int or null. After the assignment “idx = indexOf(str,c)” variable idx has type int|null. The system ensures null is never dereferenced because the type int|null cannot be treated as an int. Instead, one must first check it is an int using e.g. “idx is int” (similar to instanceof in Java). Furthermore, Whiley’s flow type system automatically retypes variables through such conditionals. In the example above, the variable idx is automatically retyped by “idx is int” to have type int on the true branch, and type null on the false branch. This prevents the needs for explicit casts after a type test (as required in e.g. Java).

As another example, we consider unions of the same kind (e.g. a union of record types, or a union of list types). These expose commonality and are called effective unions (e.g. an effective record type). In the case of a union of records, fields common to all records are exposed:

figure c

A Shape is either a Rectangle or a Circle (which are both record types). Any variable of type Shape exposes fields x and y because these are common to all cases. Finally, it’s interesting to note that the notion of an effective record type is similar, in some ways, to that of the common initial sequence found in C [37].

Recursive Data Types. Whiley provides recursive types which are similar to the abstract data types found in functional languages (e.g. Haskell, ML, etc.). For example:

figure d

Here, we again see how flow typing gives an elegant solution. More specifically, on the false branch of the type test “l is null”, variable l is automatically retyped to {int data, LinkedList next} — thus ensuring the subsequent dereference of l.next is safe. No casts are required as would be needed for a conventional imperative language (e.g. Java). Finally, like all compound structures, the semantics of Whiley dictates that recursive data types are passed by value (or, at least, appear to be from the programmer’s perspective).

Performance. Many of our choices (e.g. value semantics and unbounded arithmetic) have a potentially detrimental effect on performance. Whilst this is a trade-off we accept, there are existing techniques which can help. For example, we can use reference counting to minimise unnecessary cloning of compound structures (see e.g. [38]). Furthermore, we can exploit the specifications that are an integral part of Whiley programs. That is, when the compiler can prove an integer will remain within certain bounds, it is free to use a fixed-width type (e.g. a 32 bit int).

3 Verification

A key goal of the Whiley project is to develop an open framework for research in automated software verification. As such, we now explore verification in Whiley.

Example 1 — Preconditions and Postconditions. The following Whiley code defines a function accepting a positive integer and returning a non-negative integer (i.e. natural number):

figure e

Here, the function f() includes a requires and ensures clause which correspond (respectively) to its precondition and postcondition. In this context, $ represents the return value, and must only be used in the ensures clause. The Whiley compiler statically verifies that this function meets its specification.

A slightly more unusual example is the following:

figure f

In this case, we have two alternative (and completely equivalent) definitions for a natural number. We can see that the precondition is equivalent to the postcondition by subtracting $ from both sides. The Whiley compiler is able to reason that these are equivalent and statically verifies that this function is correct.

Example 2 — Conditionals. Variables in Whiley are described by their underlying type and those constraints which are shown to hold. As the automated theorem prover learns more about a variable, it automatically takes this into consideration when checking constraints are satisfied. For example:

figure g

The Whiley compiler statically verifies that this function always returns a non-negative integer. This relies on the compiler to reason correctly about the implicit constraints implied by the conditional. A similar, but slightly more complex example is that for computing the maximum of two integers:

figure h

Again, the Whiley compiler statically verifies this function meets its specification. Here, the body of the function is almost completely determined by the specification — however, in general, this it not the case.

Example 3 — Bounds Checking. An interesting example which tests the automated theorem prover more thoroughly is the following:

figure i

The access str[i] must be shown as within the bounds of the list str. Here, the range constructor X..Y returns a list of consecutive integers from X upto, but not including Y (and, futhermore, if X >= Y then the empty list is returned). Hence, this function cannot cause an out-of-bounds error and the Whiley compiler statically verifies this.

In fact, the specification for indexOf() could be made more precise as follows:

figure j

In this case, we are additionally requiring that, when the return value is an int, then it is a valid index into str. Again, the Whiley compiler statically verifies this is the case.

Example 4 — Loop Invariants. Another example illustrates the use of loop invariants in Whiley:

figure k

Here, a bounded quantifier is used to enforce that sum() accepts a list of natural numbers. Also, an explicit loop invariant has been given through a \(\mathtt{where}\) clause. The key constraint is that summing a list of natural numbers yields a natural number (recall arithmetic is unbounded and does not overflow in Whiley). The Whiley compiler statically verifies that sum() does indeed meet this specification. The loop invariant is necessary to help the compiler generate a sufficiently powerful verification condition to prove the function meets the post condition (more on this later).

Example 5 — Recursive Structures. The Whiley language supports invariants over recursive structures, as the following illustrates:

figure l

This defines something approximating the notion of an unbalanced binary search tree. Unfortunately, the invariant permits e.g. data \(\mathtt{{<}}\) lhs.rhs.data for a given tree node and, thus, is not sufficient to properly characterise binary search trees. Whilst our focus so far has been primarily on array programs and loop invariants, in the future we plan to place more emphasis on handling recursive structures, such as binary search trees.

4 Hoare Logic

We now briefly review Hoare logic [21] and Dijkstra’s predicate transformers [22], before examining in Sect. 5 a number of challenges we encountered putting them into practice. Hoare logic provides some important background to understanding how the Whiley verifying compiler works, and why certain difficulties manifest themselves. Our discussion here is necessarily brief and we refer to Frade and Pinto for an excellent survey [39].

4.1 Overview

The rules of Hoare logic are presented as judgements involving triples of the form: \(\big \{p\big \}\,\ {{{\mathbf {\mathtt{{s}}}}}}\,\ \big \{q\big \}\). Here, \(\mathtt{p}\) is the precondition, \(\mathtt{s}\) the statement to be executed and \(\mathtt{q}\) is the postcondition. Figure 1 presents the rules of Hoare Logic which, following Whiley, we have extended to include explicit loop invariants. To better understand these rules, consider the following example:

$$\begin{aligned} \mathtt{\Big \{x\ge 0\Big \}\;x = x + 1\;\Big \{x>0\Big \}} \end{aligned}$$

Here we see that, if \(\mathtt{x\ge 0}\) holds immediately before the assignment then, as expected, it follows that \(\mathtt{x > 0}\) holds afterwards. However, whilst this is intuitively true, it is not so obvious how this triple satisfies the rules of Fig. 1. For example, as presented it does not immediately satisfy H-Assign. However, rewriting the triple is helpful here:

$$\begin{aligned} \mathtt{\Big \{x+1>0\Big \}\;x = x + 1\;\Big \{x>0\Big \}} \end{aligned}$$

The above triple clearly satisfies H-Assign and, furthermore, we can obtain the original triple from it via H-Consequence (i.e. since \(x+1>0\implies x\ge 0\)). The following illustrates a more complex example:

figure m

Here, we have provided the intermediate assertions which tie the Hoare triples together (note, these are not part of Whiley syntax). These assertions reflect the internal information a verifying compiler might use when establishing this function is correct.

Fig. 1.
figure 1

Hoare logic.

Full size image

4.2 Verification Condition Generation

Automatic program verification is normally done with a verification condition generator [7]. This converts the program source into a series of logical conditions — called verification conditions — to be checked by the automated theorem prover. There are two basic approaches: propagate forward from the precondition; or, propagate backwards from the postcondition. We now briefly examine these in more detail.

Weakest Preconditions. Perhaps the most common way to generated verification conditions is via the weakest precondition transformer [22]. This determines the weakest precondition (written wp(s,q)) that ensures a statement \(\mathtt{s}\) meets a given postcondition \(\mathtt{q}\). Roughly speaking, this corresponds to propagating the postcondition backwards through the statement. For example, consider verifying this triple:

$$\begin{aligned} \mathtt{\Big \{x\ge 0\Big \}\;x = x + 1\;\Big \{x>0\Big \}} \end{aligned}$$

Propagating \(\mathtt{x>0}\) backwards through \(\mathtt{x=x+1}\) gives \(\mathtt{x+1>0}\) via H-Assign. From this, we can generate a verification condition to check that the given precondition implies this calculated weakest precondition (i.e. \(\mathtt{x\ge 0 \implies x+1>0}\)). To understand this process better, let’s consider verifying a Whiley function:

figure n

The implementation of this function does not satisfy its specification. Using weakest preconditions to determine this corresponds to the following chain of reasoning:

$$\begin{aligned} \begin{array}{l} \mathtt{x \ge 0\implies \textit{wp}(\mathtt{x = x - 1},\mathtt{x \ge 0})}\\ \mathtt{\hookrightarrow x \ge 0\implies x - 1 \ge 0}\\ \hookrightarrow \mathtt{false}\\ \end{array} \end{aligned}$$

Here, the generated verification condition is \(\mathtt{x \ge 0\implies \textit{wp}(\mathtt{x = x - 1},\mathtt{x \ge 0})}\). This is then reduced to a contradiction (e.g. by the automated theorem prover) which indicates the original program did not meet its specification.

Strongest Postconditions. By exploiting Floyd’s rule for assignment [20], an alternative formulation of Hoare logic can be developed which propagates in a forward direction and, thus, gives a strongest postcondition transformer [39, 40]. This determines the strong postcondition (written sp(p,s)) that holds after a given statement \(\mathtt{s}\) with pre-condition \(\mathtt{p}\). For example, propagating \(\mathtt{x=0}\) forwards through \(\mathtt{x=x+1}\) yields \(\mathtt{x=1}\). Using strongest postconditions to verify functions is similar to using weakest preconditions, except operating in the opposite direction. Thus, for a triple \(\mathtt{\{p\}\;s\;\{q\}}\), we generate the verification condition \(\mathtt{\textit{sp}(\mathtt{p},\mathtt{s})\implies q}\). For example, consider:

$$\begin{aligned} \mathtt{\Big \{x=0\Big \}\;x=x+1\;\Big \{x>0\Big \}} \end{aligned}$$

In this case, the generated verification condition will be \(\mathtt{x=1\implies x>0}\), which can be trivially established by an automated theorem prover.

5 Experiences

In the previous section, we outlined the process of automatic verification using Hoare logic and Dijkstra’s predicate transformers. This was the starting point for developing our verifying compiler for Whiley. However, whilst Hoare logic provides an excellent foundation for reasoning about programs, there remain a number of hurdles to overcome in developing a practical tool. We now reflect on our experiences in this endeavour using examples based on those we have encountered in practice.

5.1 Loop Invariants

The general problem of automatically determining loop invariants is a hard algorithmic challenge (see e.g. [41–43]). However, we want to cover as many simple cases as possible to reduce programmer burden. We now examine a range of simple cases that, in our experience, appear to occur frequently.

Challenge 1 — Loop Invariant Variables. From the perspective of a practical verification tool, the rule H-While from Fig. 1 presents something of a hurdle. This is because it relies on the programmer to completely specify the loop invariant even in cases where this appears unnecessary. For example, consider the following Whiley program:

figure o

Intuitively, we can see this program satisfies its specification. Unfortunately, this program cannot be shown as correct under the rules of Fig. 1 because the loop invariant is too weak. Unfortunately, rule H-While only considers those facts given in the loop condition and the declared loop invariant — hence, all information about x is discarded. Thus, under H-While, the verifier must assume that x could be negative within the loop body — which may seem surprising because \(\mathtt{x}\) is not modified by the loop!

We refer to x in the example above as a loop invariant variable. To verify this program under rule H-While, the loop invariant must be strengthened as follows:

figure p

Now, one may say the programmer made a mistake here in not specifying the loop invariant well enough; however, our goal in developing a practical tool is to reduce programmer effort as much as possible. Therefore, in the Whiley verifying compiler, loop invariant variables are identified automatically so that the programmer does not need to respecify their invariants.

Challenge 2 — Simple Synthesis. As mentioned above, generating loop invariants in the general case is hard. However, there are situations where loop invariants can easily be determined. The following illustrates an interesting example:

figure q

This function computes the sum of a list of natural numbers, and returns a natural number. The question to consider is: did the programmer specify the loop invariant properly? Unfortunately, the answer again is: no. In fact, the loop invariant needs to be strengthened as follows:

figure r

The need for this is frustrating as, intuitively, it is trivial to see that i >= 0 holds throughout. In the future, we aim to automatically synthesize simple loop invariants such as this.

Observation. The Whiley language also supports the notion of a constrained type as follows:

figure s

Here, the define statement includes a where clause constraining the permissible values for the type ($ represents the variable whose type this will be). Thus, nat defines the type of non-negative integers (i.e. the natural numbers).

An interesting aspect of Whiley’s design is that local variables are not explicitly declared. This gives Whiley the look-and-feel of a dynamically typed language and goes towards our goal of making the language accessible. In fact, permitting variable declarations would provide an alternative solution to the above issue with sum():

figure t

Here, variable declarations are used to restrict the permitted values of variables i and r throughout the function. Unfortunately, Whiley does currently not permit local variable declarations and, hence, the above is invalid. In the future, we plan to support them for this purpose, although care is needed to integrate them with flow typing.

Challenge 3 — Loop Invariant Properties. Whilst our verifying compiler easily handles loop invariant variables, there remain situations when invariants need to be needlessly respecified. Consider the following:

figure u

This example adds two vectors of equal size. Unfortunately, this again does not verify under the rule H-While because the loop invariant is too weak. The key problem is that v1 is modified in the loop and, hence, our above solution for loop invariant variables does not apply. Following rule H-While, the verifying compiler can only reason about what is specified in the loop condition and invariant. Hence, it knows nothing about the size of v1 after the loop. This means, for example, it cannot establish that |v1| == |v2| holds after the loop. Likewise (and more importantly in this case), it cannot establish that the size of v1 is unchanged by the loop (which we refer to as a loop invariant property). Thus, it cannot establish that the size of the returned vector equals that held in v1 on entry, and reports the function does not meet its postcondition.

In fact, it is possible to specify a loop invariant which allows the above function to be verified by our compiler. Since v2 is a loop invariant variable and |v1| == |v2| held on entry, we can use i >= 0 && |v1| == |v2| as the loop invariant.

Observation. The example above presents an interesting challenge that, by coincidence, can be resolved by exploiting a loop invariant variable. However, it raises a more general question: how can we specify that the size of a list is loop invariant? Unfortunately, this is impossible in the Whiley language developed thus far because it requires some notion of a variable’s value before and after the loop body is executed. To illustrate, consider the following hypothetical syntax in Whiley:

figure v

Here, v1‘ represents the value of v1 on the previous iteration. Unfortunately, this syntax is not yet supported in Whiley and, furthermore, its semantics are unclear. For example, on entry to the loop it’s unclear how |v1‘| == |v1| should be interpreted.

Challenge 4 — Overriding Invariants. In most cases, the loop condition and invariant are used independently to increase knowledge. However, in some cases, they need to be used in concert. The following illustrates:

figure w

This example uses the list append operator (i.e. r + [value]) and is surprisingly challenging. An obvious approach is to connect the size of r with i as follows:

figure x

Unfortunately, this is insufficient under the rule H-While from Fig. 1. This is because, after the loop is complete, the rule establishes the invariant and the negated condition. Thus, after the loop, we have \(\mathtt{i\ge count\wedge |r| == i}\), but this is insufficient to establish that \(\mathtt{|r| == count}\). In fact, we can resolve this by using an overriding loop invariant as follows:

figure y

In this case, \(\mathtt{i\ge count\wedge i\le count \wedge |r| == i}\) holds after the loop, and the automated theorem prover will trivially establish that \(\mathtt{|r| == count}\). We say that the loop invariant overrides the loop condition because i \(\mathtt{<= }\) count implies i \(\mathtt{< }\) count.

5.2 Error Reporting

Error reporting is an important practical consideration for any verification tool, as we want error messages which are as meaningful, and precise, as possible. We now consider how the two approaches to verification condition generation affect this.

Weakest Preconditions. An unfortunate side-effect of operating in a backwards direction, as \(\textit{wp}(\mathtt{s},\mathtt{q})\) does, is that reporting useful errors in the source program is more difficult. For example, consider this example which performs an integer division:

figure z

This function contains a bug which can cause a division-by-zero failure (i.e. if x==1 on entry). Using \(\textit{wp}(\mathtt{s},\mathtt{q})\), a single verification condition is generated for this example:

$$\begin{aligned} x > 0\implies (x-1\ne 0\wedge \frac{1}{x-1}>0) \end{aligned}$$
(1)

A modern automated theorem prover (e.g. [44, 45]) will quickly establish this condition does not hold. At this point, the verifying compiler should report a helpful error message. Unfortunately, during the weakest precondition transform, information about where exactly the error arose was lost. To identify where the error occurred, there are two intrinsic questions we need to answer: where exactly in the program code does the error arise? and, which execution path(s) give rise to the error? The \(\textit{wp}(\mathtt{s},\mathtt{q})\) transform fails to answer both because it generates a single verification condition for the entire function which is either shown to hold, or not [46, 47]. One strategy for resolving this issue is to embed attributes in the verification condition identifying where in the original source program particular components originated [7]. Unfortunately, this requires specific support from the automated theorem prover (which is not always available).

Strongest Postconditions. Instead of operating in a backwards direction, our experience suggests it is inherently more practical to generate verification conditions in a forwards direction (and there is anecdotal evidence to support this [39]). Recall that this corresponds to generating strongest postconditions, rather than weakest preconditions. The key advantage is that verification conditions can be emitted at the specific points where failures may occur. In the above example, there are two potential failures: (1) 1/(x-1) should not cause division-by-zero; (2) the postcondition $ > 0 must be met. A forward propagating verification condition generator can generate separate conditions for each potential failure. For example, it can emit the following verification conditions:

$$\begin{aligned}&\mathtt{x > 0\implies x-1\ne 0}\end{aligned}$$
(2)
$$\begin{aligned}&\mathtt{x > 0\implies \frac{1}{x-1}>0} \end{aligned}$$
(3)

Each of these can be associated with the specific program point where it originated and, in the case it cannot be shown, an error can be reported at that point. For example, since the first verification condition above does not hold, an error can be reported for the statement \(\mathtt{x = 1 / (x-1)}\). When generating verification conditions based on \(\textit{wp}(\mathtt{s},\mathtt{q})\), it is hard to report errors at the specific point they arise because, at each point, only the weakest precondition for subsequent statements is known.

6 Related Work

Hoare provided the foundation for formalising work in this area with his seminal paper introducing Hoare Logic [21]. This provides a framework for proving that a sequence of statements meets its postcondition given its precondition. Unfortunately Hoare logic does not tell us how to construct such a proof; rather, it gives a mechanism for checking a proof is correct. Therefore, to actually verify a program is correct, we need to construct proofs which satisfy the rules of Hoare logic.

The most common way to automate the process of verifying a program is with a verification condition generator. As discussed in Sect. 4.2, such algorithms propagate information in either a forwards or backwards direction. However, the rules of Hoare logic lend themselves more naturally to the latter [39]. Perhaps for this reason, many tools choose to use the weakest precondition transformer. For example, the widely acclaimed ESC/Java tool computes weakest preconditions [7], as does the Why platform [48], Spec# [49], LOOP [50], JACK [51] and SnuggleBug [52]. This is surprising given that it leads to fewer verification conditions and, hence, makes it harder to generate useful error messages (recall our discusion from Sect. 4.2). To workaround this, Burdy et al. embed path information in verification conditions to improve error reporting [51]. A similar approach is taken in ESC/Java, but requires support from the underlying automated theorem prover [45]. Denney and Fischer extend Hoare logic to formalise the embedding of information within verification conditions [53]. Again, their objective is to provide useful error messages.

The Dafny language has been developed with similar goals in mind to Whiley [14]. In particular, Dafny was designed to simplify verification and, to this end, makes similar choices to Whiley. For example, all arithmetic is unbounded and a strong division is made between functional and imperative constructs. Here, pure functions are supported for use in specifications and directly as code, whilst methods may have side-effects and can describe pointer-based algorithms. These two aspects are comparable (respectively) to Whiley’s functional core and imperativer outer layer. Finally, Dafny supports explicit pre- and post-conditions for functions and methods which are discharged using Z3 [44].

7 Conclusion

In this paper, we reflected on our experiences using the Whiley verifying compiler. In particular, we identified a number of practical considerations for any verifying compiler which are not immediately obvious from the underlying theoretical foundations.