Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

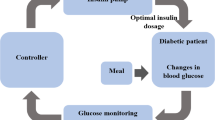
Glucose is a vitally important source of energy for the human body. The skeletal musculature, brain, central nervous system, etc. must always be adequately supplied with glucose. Too high or too low blood sugar levels are harmful and can even cause death. A healthy body regulates the blood sugar levels by itself, thereby the peptide hormone insulin plays a crucial role. It becomes problematic (dangerous for life) when the body has a resistance to insulin or an insulin deficiency, as it is for example the case in diabetic patients. ICU patients suffering from severe, sometimes life-threatening illnesses or injuries often show an impaired insulin sensitivity. Since (strongly) fluctuating blood sugar levels additionally hamper the healing process, these patients need to be strictly observed. Their metabolism of glucose is controlled from outside via the intake/medication of food and insulin yielding an increase or decrease, respectively. To guarantee an adequate control, many frequent blood glucose measurements and tests are manually performed in hospitals, which is obviously associated with large caring effort and hence high costs in terms of time and money. The number of people suffering from diseases of sugar increases steadily worldwide, and health care systems are already overloaded. Therefore, model-based medical decision support using computer simulations for (long-time) predictions and optimizations gains importance.

This work deals with the optimal control of the glucose balance. The basis is the bio-medical model GlucoSafe developed by Pielmeier et al. [1] in 2010. We perform a theoretical (mathematical) analysis of the model and propose an adequate and efficient numerical treatment.

2 Optimal Control Problem

The temporal evolutions of the glucose and insulin concentrations in the body of a patient are determined by a complex interaction where apart from the intake/medication of food and insulin also the activities of liver, kidneys, gut, muscles, central nervous system, brain, etc. play a role. From the bio-medical point of view there are several dependencies and effects that are not fully understood so far, e.g. the impact of the insulin saturation. Moreover, measurements are restricted. However, under simplifying assumptions and closure relations, Pielmeier et al. [1] developed a “grey” model (1) in form of a deterministic nonlinear dynamic system of first-order ordinary differential equations that contains patient-dependent as well as fixed parameters and functions, for details on the bio-medical background see [1–3] and on the mathematical formulation, exact definitions [4]. A graphical illustration of the underlying biological processes that are taken into account is given in Fig. 1.

$$\displaystyle\begin{array}{rcl} \frac{\mathrm{d}G} {\mathrm{d}t} & =& \frac{w} {v_{G}}\left [E((P,G),i_{\boldsymbol{\sigma }}) + d(D) +\pi (t)\right ] \\ \frac{\mathrm{d}D} {\mathrm{d}t} & =& -d(D) +\varepsilon (t) \\ \frac{\mathrm{d}I} {\mathrm{d}t} & =& \frac{c} {v_{I}}(P - I) -\left (r_{L} + r_{K}\right )I + \frac{n +\xi (t)} {v_{I}} \\ \frac{\mathrm{d}P} {\mathrm{d}t} & =& \frac{c} {v_{P}}(I - P) - r_{E}P {}\end{array}$$
(1)

with \(t \in \mathcal{T}\) compact time period and

$$\displaystyle{ E((P,G),i_{\boldsymbol{\sigma }}) = h((P,G),i_{\boldsymbol{\sigma }}) - a_{R}(G) - a_{M}((P,G),i_{\boldsymbol{\sigma }}) - a_{N}(G). }$$
Fig. 1
figure 1

Illustration of the bio-medical model, in the style of Pielmeier et al.

Full size image

The state variables are the glucose concentrations in the blood plasma G (to be controlled) and in the gut content D as well as the insulin concentrations in the blood plasma I and around the cells (the so-called peripheral compartment) P. Between the last two a difference-based diffusion process takes place. The controls are the intakes/medication of parenteral π and enteral nutrition \(\varepsilon\) as well as of exogenous insulin ξ, which we summarize as \(\boldsymbol{u} = {(\pi,\varepsilon,\xi )}^{\top }\). The glucose balance of the liver h as well as the glucose absorption from the gut content d, of the skeletal musculature a M , brain and central nervous system a N are modeled as patient-independent functions, in contrast to the renal glucose excretion a R that depend on the patient data (body weight w, size, age, gender and diabetic status). Further patient-dependent, but temporal constant parameters are the endogenous (post-hepatic) supply of insulin n, the rate of the insulin reduction in liver r L , kidneys r K and in the process of endocytosis r E , the insulin diffusion constant c as well as the volumes of glucose blood plasma v G , insulin blood plasma v I and peripheral compartment v P . The impact of the insulin enters (1) by the quantity \(i_{\boldsymbol{\sigma }}\). Since the understanding of this biological process—involving impact sensitivity and saturation effect—is still rather limited, \(i_{\boldsymbol{\sigma }}\) is expressed in terms of a non-negative parameter tuple \(\boldsymbol{\sigma }\in {\mathbb{R}}^{2}\). This tuple is frequently adapted for each patient using a least-square parameter fit where the deviation of simulation results (1) to earlier measurements is minimized. Note that only the blood sugar G can be measured, but not D, I and P. This makes the initialization of (1) at a certain time t 0 inexact: in combination to a blood sugar measurement G(t 0) = G meas , reference values for D, I, P at t 0 are taken from literature. The initial perturbation decreases over time due to the asymptotic stability of the model (see below). Thus, during the course of a treatment previous simulation results can be used as better initial guesses.

Considering the optimal control of G we solve the following constrained minimization problem,

$$\displaystyle{ \min \limits _{(G,\boldsymbol{u})\in \mathfrak{Z}\times \mathfrak{S}}J(G,\boldsymbol{u}) }$$
(2)

subject to

  • G and \(\boldsymbol{u}\) satisfy the dynamical system (1) with given initial values (not closer specified here)

  • \(\boldsymbol{u} \in U \subseteq \mathfrak{S}\), the set of admissible controls

As cost function we choose thereby

$$\displaystyle{ J(G,\boldsymbol{u}) = \frac{1} {2}\Vert G - {G{}^{{\ast}}\Vert }^{2} + \frac{1} {2}\Vert \mathrm{diag}(\boldsymbol{\kappa }){(\boldsymbol{u} -\boldsymbol{ {u}^{{\ast}}})\Vert }^{2}, }$$

where G ∗ is the target blood sugar level and \(\boldsymbol{{u}^{{\ast}}}\) is the desired control based on bio-medical and economic reasons with weights \(\boldsymbol{\kappa }\in {(\mathbb{R}_{0}^{+})}^{3}\).

3 Analysis and Numerical Treatment

In this section we present a theoretical analysis of the model and propose an adequate numerical treatment.

The initial value problem (1) for the glucose balance is well-posed. For continuous controls it is resolvable in the classical sense. Existence and uniqueness holds according to the Picard-Lindelöf theorem for the sufficiently smooth model functions on the right-hand side of (1). However, bio-medical reasons require also non-continuous controls. Considering \(\boldsymbol{u} \in {L}^{\infty }(\mathcal{T}, {\mathbb{R}}^{3})\) with \(\boldsymbol{u} \geq \boldsymbol{ 0}\), the system (1) has got a unique non-negative solution in the sense of Carathéodory for every choice of non-negative initial values. This stands in accordance with biological demands. In the following, we consider the space of piecewise constant non-negative bounded by a certain upper bound functions as set of admissible controls U. This is reasonable and sufficient for the application. The structure of the dynamical system allows the decoupling into a linear system for I and P, a Riccati equation for D and a non-linear equation for G. The differential equations for I, P and D can be solved explicitly for the chosen U, for closed solution formulas see [4]. Moreover, for each steady state \(\overline{G} > 0\) there exist a constant control \(\boldsymbol{\overline{u}} \geq \boldsymbol{ 0}\) and steady states \(\overline{I},\overline{P},\overline{D} \geq 0\), so that all together satisfy (1). In addition, it can be shown that this solution is asymptotically stable in all medically relevant cases for all possible patient data. So, the controllability of arbitrary stationary states is possible with \(\mathfrak{S}\). The existence of optimal controls in the space \({L}^{2}(\mathcal{T},{(\mathbb{R}_{0}^{+})}^{3})\) can be proven straight forward for (2), following the ideas and procedure prescribed in [5]. Uniqueness is lacked due to the non-linearity of (1); however, this is not necessary from a user point of view.

The ordinary differential system is not stiff such that the numerical computation of solutions can be performed by standard explicit Runge-Kutta methods with adaptive step size control. In particular, we use the method by Dormand/Prince [6]. The computational effort can be thereby reduced by a factor of two when the explicit solution formulas for D, I, P are used for the calculation for G. The optimal control problem (2) can be approached by direct and indirect methods, [5]. Thereby, it is advantageous to consider the associated equivalent reduced problem \(\min _{\boldsymbol{u}}\tilde{J}(\boldsymbol{u})\), \(\tilde{J}(\boldsymbol{u}) = J(G(\boldsymbol{u}),\boldsymbol{u})\). We have compared various direct and indirect methods. For the direct methods, a finite-dimensional optimization problem must be ultimately solved. The SQP method with numerically calculated gradients [7] turned out to be the best one with respect to the run time. As indirect methods, we tested conditional gradient method, gradient projection method and Newton-type methods. Regarding accuracy and computational efficiency, these methods cannot compete with the direct ones for this special problem (2); they are slower by a factor of about 50. The following simulation results are computed by MATLAB, version 7.7. Therefore the SQP method is implemented by MATLAB function fmincon with termination criteria: 10, 000 function evaluations, 500 iterations, tolerance for variable/cost function of 10−12.

4 Results and Discussion

The simulation results show that the model GlucoSafe leads to meaningful and interpretable results as long as we treat patients with a stabilized (non-fluctuating) blood sugar level. Figure 2 illustrates exemplarily the numerical results for G (red curve) in comparison to measured values (black crosses) for an arbitrary patient. From the bio-medical point of view the agreement is very satisfying since the measured values lie much closer than the acceptable area of 20 % deviation (green zone) would demand. In particular, the results for shorter time periods ( ≤ 3.0 h) are much better than for long time periods. The reason for the worsening lies in the insulin effect \(i_{\boldsymbol{\sigma }}\) which is actually a time- and patient-dependent function but modeled here by a simple parameter fit via \(\boldsymbol{\sigma }\). Crucial for a reliable prediction of the long-time behavior is here a frequent adjustment of the parameter tuple \(\boldsymbol{\sigma }\) to measurements. Figure 3 shows the temporal development of G for a forecast period of 3 h. Thereby, the desired blood sugar level is taken to be constant \({G}^{{\ast}} =\mathrm{ 6.0\;\mathrm{m}\mathrm{mol}\mathrm{/}\mathrm{l}}\), [8], and the desired control \(\boldsymbol{{u}^{{\ast}}} =\boldsymbol{ 0}\) with weighting factors \(\boldsymbol{\kappa }= {(\sqrt{10},\sqrt{10},1{0}^{-3})}^{\top }\) in the cost functional J. As admissible controls, we have selected the set of non-negative functions \(\boldsymbol{u}\) that are piecewise constant on the equidistant time grid with step size τ Δ  = 1.0 h and bounded from above by \({(\mathrm{0.041\;\mathrm{m}\mathrm{mol}\mathrm{/}\mathrm{\mathrm{k}\mathrm{g}}},\mathrm{0.026\;\mathrm{m}\mathrm{mol}\mathrm{/}\mathrm{\mathrm{k}\mathrm{g}}},\mathrm{0.334\;U})}^{\top }\mathrm{/}\mathrm{min}\). A statistical validation of our predictions is not possible so far due to our relatively small sample size of data/measurements at hand. For a large clinical study the described methods have been implemented in a software tool by Ulrike Pielmeier and the glucose research group at the Center of Model-based Medical Decision Support, University Aalborg. This is recently applied and tested in hospitals.

Fig. 2
figure 2

Comparison of simulated blood glucose G with measured values for 12 h

Full size image
Fig. 3
figure 3

Predication of the state G for a computed optimal control; desired state G ∗ = 6.0 mmol∕l

Full size image

5 Conclusion and Outlook

This work presented a theoretical analysis and numerical investigation of the bio-medical model GlucoSafe used for the optimal control of the blood glucose via intake/medication of food and insulin. The simulation results are promising for ICU patients with non-fluctuating glucose levels. Improvements of the model lie surely in the concrete definition of the insulin function \(i_{\boldsymbol{\sigma }}\). But also the liver balance h and the endogenous insulin intake n that is assumed to be constant so far pose open research questions to bio-medical experts. A glucose-dependent n would imply a fully coupled dynamical system for all state variables. A interesting challenge from the mathematical point of view is the incorporation of uncertainties coming from the patient data and the measurements. This results in a stochastic control problem for which sensitivity/robustness and controllability have to be investigated.