Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The classical model for flow in a circular cylindrical pipe is described by the Hagen-Poiseuille equation

$$\displaystyle{ u_{\mathit{HP}} = -\frac{p_{z}{R}^{2}} {4\mu } \left (1 - \frac{{r}^{2}} {{R}^{2}}\right ) }$$
(1)

where u HP (r) is the velocity in the z direction, p z is the pressure gradient along the pipe, R is the radius and μ the fluid viscosity. The corresponding flux is given by

$$\displaystyle{ Q_{\mathit{HP}} = 2\pi \int _{0}^{R}ru_{\mathit{ HP}}\,\mathit{dr} = -\frac{\pi {R}^{4}p_{z}} {8\mu } \,. }$$
(2)

In carbon nano-tubes (CNT) it is well documented that the flow is enhanced and the true value of the flux is significantly higher than this classical value.

A popular approach to explain this enhancement is to introduce a slip-length into the mathematical model, that is, the no-slip boundary condition u(R) = 0 is replaced by

$$\displaystyle{ u(R) = -L_{s}\left.\frac{\partial u} {\partial r}\right \vert _{r=R} }$$
(3)

where L s is the slip-length. This leads to modified velocity and flux expressions

$$\displaystyle{ u_{\mathit{slip}} = -\frac{{R}^{2}p_{z}} {4\mu } \left [1 - \frac{{r}^{2}} {{R}^{2}} + \frac{2L_{s}} {R} \right ]\qquad \qquad Q_{\mathit{slip}} = Q_{\mathit{HP}}\left (1 + \frac{4L_{s}} {R} \right )\,, }$$
(4)

hence any magnitude of enhancement can be accounted for by using an appropriate value for L s .

Assuming fluid slip at the wall the value of the velocity at the channel wall is positive: the slip length is defined as the distance the velocity profile must be extrapolated beyond the wall to reach zero [1]. In general the slip length is significantly smaller than the thickness of the bulk flow [2]. For example, Tretheway and Meinhart [3] carry out experiments on water flow in a coated microchannel of width 30 μm and find a slip length of 1 μm. In 1–2 μm channels Choi et al. [4] determine values of the order 30 nm. However, in CNTs Whitby et al. [5] quote lengths of 30–40 nm for experiments in pipes of 20 nm radius. Holt et al. [6] and Majumder et al. [7] quote slip lengths on the order of microns for their experiments with nanometer size pores.

The high values of slip-length in CNT studies have led some authors to question the validity of the slip modified Hagen-Poiseuille model [8, 9]. An alternative explanation to the slip-length is based on the fact that CNTs are hydrophobic [10–12]. The strength of attraction between the water molecules is greater than the attraction between the hydrophobic solid and the water [13, 14]. Indeed it was mainly experiments performed with hydrophobic surfaces that supported early arguments for a slip boundary condition [2]. It has been postulated that hydrophobicity may result in gas gaps, depletion layers or the formation of vapour: experimentally this may be interpreted as “apparent” slippage, see [15].

Obviously any depletion layer must be small. Experiments and simulations have shown that the fluid viscosity is in close agreement with its bulk value down to separations of about ten molecular diameters [2]. For CNTs the fluid properties typically vary within an annular region approximately 0.7 nm from the wall [8, 16, 17].

Consequently, in the following work we will investigate a mathematical model for flow including a region of low viscosity near the tube wall. In light of the results quoted in [14, 18] we will assume the theory is not valid for films below ten molecular diameters thickness. This limit is also imposed through the validity of the continuum assumption, for example the MD simulations of [19] shows results that coincide with a continuum model for a pipe radius of ten molecular diameters.

2 Mathematical Model

Consider a pipe of cross-section R, occupied by two fluids. In the bulk flow region, defined by 0 ≤ r ≤ α, we impose a viscosity μ 1. In the annular region near the wall, defined by α ≤ r ≤ R, we impose a viscosity μ 2 < μ 1. The assumption of two regions with different viscosities leads to what is commonly termed a bi-viscosity model in the non-Newtonian flow literature. In the following analysis there is uncertainty about the values to choose for viscosity and the distance α. If we define the position of the transition \(\alpha = R-\delta\) then, based on previous studies of water in CNTs we will choose δ = 0. 7 nm. However, experiments show that the slip length is a measure of hydrophobicity [4, 20–22] and so for other liquid–solid systems the value of δ may differ.

For unidirectional pressure driven flow through a circular pipe the appropriate mathematical model is

$$\displaystyle{ \frac{\mu _{1}} {r} \frac{\partial } {\partial r}\left (r\frac{\partial u_{1}} {\partial r} \right ) = \frac{\partial p} {\partial z}0 \leq r \leq \alpha \,,\ \frac{\mu _{2}} {r} \frac{\partial } {\partial r}\left (r\frac{\partial u_{2}} {\partial r} \right ) = \frac{\partial p} {\partial z}\alpha \leq r \leq R\,.\quad }$$
(5)

Appropriate boundary conditions are

$$\displaystyle{ \left.\frac{\partial u_{1}} {\partial r} \right \vert _{r=0} = 0\qquad \qquad \,u_{2}(R,z) = 0\,, }$$
(6)

which represent symmetry at the centreline and no-slip at the solid boundary. At the interface between the fluids, r = α, there is continuity of velocity and shear stress

$$\displaystyle{ u_{1} = u_{2}\qquad \qquad \mu _{1}\frac{\partial u_{1}} {\partial r} =\mu _{2}\frac{\partial u_{2}} {\partial r} \,. }$$
(7)

The velocity expressions are then

$$\displaystyle{ u_{1} = \frac{p_{z}} {4\mu _{1}}({r}^{2} {-\alpha }^{2}) -\frac{p_{z}} {4\mu _{2}}({R}^{2} {-\alpha }^{2})\qquad \qquad u_{ 2} = \frac{p_{z}} {4\mu _{2}}({r}^{2} - {R}^{2})\,. }$$
(8)

The flux Q μ is defined as the sum of fluxes in the two regions

$$\displaystyle\begin{array}{rcl} Q_{\mu }& =& -\frac{{\pi \alpha }^{4}p_{z}} {8\mu _{1}} \left [1 -\frac{2\mu _{1}} {\mu _{2}} \left(1 -\frac{{R^2}} {{\alpha}^{2}} \right )\right ] -\frac{{\pi \alpha }^{4}p_{z}} {8\mu _{2}}{ \left (1 -\frac{{R}^{2}} {{\alpha }^{2}} \right )}^{2}{}\end{array}$$
(9)
$$\displaystyle\begin{array}{rcl} & =& Q_{\mathit{HP}} \frac{{\alpha }^{4}} {{R}^{4}}\left[1 + \frac{\mu _{1}} {\mu _{2}}\left(\frac{{R}^{4}} {{\alpha }^{4}} - 1\right)\right]\,.{}\end{array}$$
(10)

The flow rate enhancement is defined as

$$\displaystyle{ \epsilon _{\mu } = \frac{Q_{\mu }} {Q_{\mathit{HP}}} = \frac{{\alpha }^{4}} {{R}^{4}} + \frac{\mu _{1}} {\mu _{2}}\left (1 - \frac{{\alpha }^{4}} {{R}^{4}}\right )\,. }$$
(11)

For the slip model the corresponding enhancement is

$$\displaystyle{ \epsilon _{\mathit{slip}} = 1 + \frac{4L_{s}} {R} \,. }$$
(12)

3 Model Validation

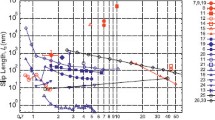
To verify whether this model gives reasonable results we consider the experiments of Whitby et al. [5]. Their flow enhancement indicates a slip length of 30–40 nm for pipes of radius 20 nm. Setting L s  = 35 nm, R = 20 nm determines their enhancement factor as ϵ slip  = 8. Rearranging the expression for ϵ μ gives

$$\displaystyle{ \mu _{2} =\mu _{1}\left [\frac{{R}^{4} {-\alpha }^{4}} {\epsilon _{\mu }{R}^{4} {-\alpha }^{4}}\right ]\,. }$$
(13)

To obtain the same enhancement we set ϵ μ  = 8 and also take \(\alpha = R-\delta = 19.3\) nm to find μ 2 = 0. 018μ 1. So, the current model will provide an enhancement factor of 8 with an average viscosity in the depletion layer approximately 0.02 times that of the bulk flow. It is interesting to note that the viscosity of oxygen is also approximately 0.02 that of water, so this value supports the depletion layer theory. Thomas et al. [23] find \(\epsilon _{\mathit{slip}} \approx 32\) nm when R = 3. 5 nm, taking μ 2 = 0. 018μ 1 Eq. (11) indicates \(\epsilon _{\mu } \approx 33.2\) nm.

To clarify the behaviour of the current model we set \(\alpha = R-\delta\). Since ϵ μ is simply a quartic in α we may expand and rearrange the expression to find

$$\displaystyle{ \epsilon _{\mu } = 1 + \frac{4\delta } {R}\left (\frac{\mu _{1}} {\mu _{2}} - 1\right )\left [1 -\frac{3} {2} \frac{\delta } {R} +{ \left ( \frac{\delta } {R}\right )}^{2} -\frac{1} {4}{\left ( \frac{\delta } {R}\right )}^{3}\right ]\,, }$$
(14)

which is a monotonically decreasing function of R. This is in accordance with the findings of Thomas and McGaughey [8] that the enhancement factor decreases with increasing tube radius. Noting that the reduced viscosity model requires two distinct regions, hence R ≥ δ, the limit to the enhancement predicted by the current theory is determined by setting R = δ, \(\mu _{2}/\mu _{1} = 0.018\) and δ = 0. 7 nm to give ϵ μ  ≈ 50: Whitby et al. [5] predict an enhancement of up to 45 times theoretical predictions.

Equation (15) also allows us to make further inference about the model behaviour and its relation to the slip model. If we compare the above expression with that for ϵ slip we may define the slip length in terms of the thickness of the depletion layer and the viscosity ratio

$$\displaystyle{ L_{s} =\delta \left(\frac{\mu _{1}} {\mu _{2}} - 1\right)\left[1 -\frac{3} {2} \frac{\delta } {R} +{ \left( \frac{\delta } {R}\right)}^{2} -\frac{1} {4}{\left( \frac{\delta } {R}\right)}^{3}\right]\,. }$$
(15)

Further, noting that μ 1∕μ 2 ≫ 1, we can identify three distinct regimes:

  1. 1.

    For sufficiently wide tubes, \((\delta /R)(\mu _{1}/\mu _{2}) \ll 1\), then by Eq. (14) \(\epsilon _{\mu } \approx 1\). There is no noticeable flow enhancement and the no-slip boundary condition will be sufficient.

  2. 2.

    For moderate tubes, \((\delta /R)(\mu _{1}/\mu _{2})\) is order 1 but δ∕R ≪ 1 then

    $$\displaystyle{ \epsilon _{\mu } \approx 1 + \frac{4\delta } {R} \frac{\mu _{1}} {\mu _{2}}\,. }$$
    (16)
  3. 3.

    For very small tubes, δ∕R is order 1, then the full expression for ϵ μ is required.

Note, numerous papers report constant slip-lengths between 20 and 40 nm when R ∈ “some nanometers up to several hundred nanometers”, see [20] for example. Thomas et al. [23] suggest L s varies with R for R ∈ [1. 6, 5] nm.

4 Discussion

The motivation behind this paper was to explain the unrealistically large slip-lengths reported in nanotubes. The mathematical model developed shows that the flow enhancement can be plausibly related to a reduced viscosity model, where the viscosity in the depletion region is always much lower than in the bulk. In pipes with a radius greater than the depletion layer thickness the model indicates that the flow can only be enhanced by an order of magnitude (around 50), not orders as reported in some papers. The term slip-length may be considered misleading, in fact it appears to be a length-scale proportional to the product of the viscosity ratio and the width of the depletion region. This length-scale is a property of the fluid–solid system and remains approximately constant, down to very small radius tubes.

In a wider context the reduced viscosity model provides one possible explanation for the Navier slip boundary condition on a hydrophobic solid surface that is smooth down to the nanoscale (and hence an explanation for flow enhancement). In other systems there may well be different mechanisms to explain the slip boundary condition, for example on rough surfaces one would expect the slip length to be determined by the roughness height-scale.