Keywords

Introduction

Atmospheric phenomena such as reflection, diffraction, and scattering adversely affect the performance of wireless communication systems as they pose severe limitations to wave propagation. As a result, signal transmission may be severely impaired by the existence of various obstacles such as buildings, mountains, or foliage or due to precipitation mechanisms such as rainfall. Moreover, interference can further aggravate signal transmission. In general, the wireless channel characteristics are non-stationary and non-predictable and are subjected to fading normally perceived as signal attenuation.

The various types of fading associated with specific fading mechanisms can be classified into two main categories: large-scale fading and small-scale fading [1]. Large-scale fading is dependent on the distance between transmitter and receiver, whereas small-scale fading is caused by small changes in position (of the order of half wavelength) or by changes in the transmission environment (surrounding objects, moving obstacles crossing the line of sight (LOS) between transmitter and receiver, etc.). Likewise, fading can be classified with regard either to its duration or to where it happens (outdoor or indoor). A high-level overview of the various fading types is given in Fig. 1 [2].

Fig. 1
figure 1

Indicative fading classification

Full size image

To successfully model wireless channels, accurate wave propagation models are required. Such models aim at describing the changes caused to the transmitted waves as they propagate from the transmitter to the receiver and suffer from path loss, interference, noise, and various types of fading. In practical wireless communication systems, the channel state cannot be estimated at the receiver perfectly. Therefore, and regardless of the fading mechanism involved, it is essential to examine the effect of channel estimation errors, on the structure and performance of the receivers by analyzing their performance over correlated fading channels. Indicative examples of fading mechanisms that give rise to correlated microwave terrestrial or satellite transmissions are: (i) fading due to rain attenuation induced on spatially diversified links or (ii) multipath fading. Both the above types of fading are mitigated by well-known diversity combining techniques such as maximal ratio combining and optimal combining. The performance of those diversity techniques deteriorates due to imperfect channel estimation. Hence, to formulate realistic radio channel models, appropriate statistical propagation models are required.

The performance assessment of wireless links in the presence of correlated fading should employ multivariate distributions that represent the joint statistics of different fading mechanisms. In most cases, the relevant distribution is heuristically defined, if possible. The modelling difficulties that arise are related to the nature of the physical phenomena involved and to the algebraic complexity introduced. The commonly adopted performance metrics assessing availability and reliability are the outage probability and the average bit error probability for various transmission rates and quality of service (QoS) levels.

Up to now, various multivariate fading distributions have been employed, such as the Rayleigh, Rice, and Nakagami distributions for short-term fading, caused primarily by multipath propagation, or the lognormal distribution for long-term fading, caused primarily by rain attenuation and shadowing. It should be noted, though, that, in complex propagation environments, more than one type of fadings exist simultaneously [3].

Although correlated fades rarely take large values at the same time, if such an incident happens, it happens in a highly correlated way. The classic linear (Pearson) correlation coefficient fails to appropriately model the interdependence of fading events caused by different mechanisms as their underlying correlation is not linear, particularly as to the tails of the fading distributions. The Rayleigh or the Rice fading models, being stimulated by an inherent Gaussian random process, are basically Gaussian-oriented and do not efficiently model simultaneous deep fades that are affected by an underlying interdependence. Hence, it becomes evident that the benefit expected from diversity in wireless communications, which derives from the assumption that the diversity channels employed should be as de-correlated as possible, must be reconsidered and be modelled via multivariate distributions that can effectively describe the joint statistical behavior between random variables that are not linearly correlated. In this respect, the classic Pearson correlation factor cannot properly represent their underlying interdependence. In particular the n -variate Nakagami distribution describes multipath propagation of relatively large delay time-spread, employing clusters of reflected waves [4]. This distribution incorporates as special cases the Rayleigh distribution and the one-sided Gaussian model distribution, also approximating the Rician fading distribution. Though it performs well for the main part of these distributions, the approximation fails in the tails, which is critical since bit errors or outages occur mainly during deep fades [5].

As for terrestrial or satellite links operating above 10 GHz, where rain attenuation is the primary impairing factor, double site diversity constitutes an effective fade mitigation technique. The basic assumption is that the rain attenuation affecting the (two) diversity links involves two random variables modelled via the bivariate lognormal or, in some cases, the bivariate gamma distribution. The diversity gain determined when deep rain fades occur simultaneously, particularly in tropical zones, does not match the experimental data [6]. Among other reasons, this is attributed to the nonlinear underlying correlation between the two correlated random variables representing the rain attenuation over the two earth-space paths.

Another failure when modelling fading phenomena takes place when short-term fading due to multipath modelled by the Nakagami, Rice, or Rayleigh distribution, coexists with long-term fading due to shadowing modelled by the lognormal distribution [7]. The representation of such complex propagation environments leads to complicated mathematical models inconvenient to accurately evaluate the performance of wireless links. Concluding, the development of alternative mathematical models is necessary to overcome the aforementioned inefficiencies.

Basic Theory of Copulas

One method to model correlated random variables which has recently become quite popular is copula which, in Latin, means “a link, tie or bond.” Copulas introduce a bond between correlated random variables and where first employed in mathematics or statistics by Abe Sklar [8, 9]. Copulas are functions that make feasible to obtain a joint distribution having a particular correlation by combining univariate distributions. Let \(\boldsymbol{X} = (X_{1},X_{2},\ldots,X_{n})\) be a vector of n random variables modelling n correlated fades having marginal cumulative distribution functions (CDFs) F i , i = 1, 2, …, n, respectively. The relevant multivariate CDF is defined by

$$\displaystyle{ \boldsymbol{F}(x_{1},x_{2},\ldots,x_{n}) =\Pr \left \{X_{1} \leq x_{1},\ldots,X_{n} \leq x_{n}\right \} }$$
(1)

and completely determines the correlation of random variables X i , i = 1, 2, …, n. As pointed out in the previous section, the analytic representation of \(\boldsymbol{F}\) might be too complex, making any algebraic evaluations or even numerical estimations practically impossible, thus restricting its practical use. The multivariate Gaussian distribution has become popular because it can easily describe interrelated fades. On the other hand, it has not been proven capable of fitting real data in fading communications channels. The use of copula functions overcomes the issue of estimating multivariate CDFs. This is accomplished by splitting the relevant procedure into two steps:

  1. i.

    Determine the marginal CDFs F i , i = 1, 2, …, n of the particular fading phenomena involved; estimate the parameters of CDFs by fitting the available data using well-established statistical methods;

  2. ii.

    Determine the correlation structure of the random variables X i , i = 1, 2, …, n and select a suitable copula function.

The goal is twofold: to select the most appropriate marginal CDFs in order to fit the real data of each fading mechanism and the copula function that performs better in properly linking the various marginal CDFs and fitting the joint measurements available.

An n-dimensional copula, hereafter denoted by \(\boldsymbol{C}\), is a multivariate CDF with marginals uniformly distributed in [0, 1] that possesses the following properties:

  1. i.

    \(\boldsymbol{C}: {[0,1]}^{n} \rightarrow [0,1]\);

  2. ii.

    As CDFs are always increasing functions, \(\boldsymbol{C}(u_{1},\ldots,u_{n})\) is increasing with respect to any component u i , i = 1, 2, …, n.

  3. iii.

    \(\boldsymbol{C}\) is grounded, that is \(\boldsymbol{C}(u_{1},\ldots,u_{n}) = 0\), if u i  = 0, i = 1, 2, …, n.

  4. iv.

    The marginal with respect to component u i is obtained by \(\boldsymbol{C}(1,\ldots,u_{i},\ldots,1) = u_{i}\), that is, by setting u j  = 1 for any j, j ≠ i, and as it must be uniformly distributed.

From the above properties, it is deduced that, if F 1, …, F n are univariate distribution functions, \(\boldsymbol{C}(F_{1}(x_{1}),\ldots,F_{n}(x_{n}))\) is a multivariate CDF with margins F 1, …, F n , since U i  = F i (x i ), i = 1, …, n, are uniformly distributed random variables. Copulas constitute a useful tool to derive and process multivariate distributions. Based on the definitions, the following relation describes the basic properties of copula functions.

$$\displaystyle\begin{array}{rcl} \boldsymbol{C}(x_{1},x_{2},\ldots,x_{n})& =& \Pr \left \{X_{1} \leq x_{1},\ldots,X_{n} \leq x_{n}\right \} \\ & =& \Pr \left \{F_{1}(X_{1}) \leq F_{1}(x_{1}),\ldots,F_{n}(X_{n}) \leq F_{n}(x_{n})\right \} \\ & =& \Pr \left \{U_{1} \leq u_{1},\ldots,U_{n} \leq u_{n}\right \} =\boldsymbol{ C}(u_{1},\ldots,u_{n}) \\ & =& \boldsymbol{C}(\Pr \left \{X_{1} < x_{1}\right \},\ldots,\Pr \left \{X_{n} < x_{n}\right \}) {}\end{array}$$
(2)

The founding theorem for copulas [8, 9] states that, given a joint multivariate distribution function and the constituent marginal distributions, a copula function exists that relates them. This theorem known as Sklar’s Theorem is very important in explaining copula functions because it provides a way to analyze the correlation structure of multivariate distributions without any requirements for setting any specifications concerning the related marginal distributions such as that they must be or have the same parameters. Also, it defines how multivariate CDFs modelled by copulas are used in many practical applications. According to Sklar’s Theorem, if \(\boldsymbol{F}\) is an n-dimensional CDF with continuous margins F i , i = 1, 2, …, n, then \(\boldsymbol{F}\) has the following unique copula representation (canonical decomposition):

$$\displaystyle{ \boldsymbol{F}(x_{1},x_{2},\ldots,x_{n}) =\boldsymbol{ C}(F_{1}(x_{1}),\ldots,F_{n}(x_{n})) }$$
(3)

From (3) it can readily be deduced that, for continuous multivariate distributions, the univariate margins can be separated from the multivariate correlation. The latter can be represented by a suitable copula function which should be formed based on statistically stable experimental data and efficient regression techniques.

An additional property of copula functions follows:

Let \(\boldsymbol{F}\) be an n-dimensional CDF with continuous margins \(F_{1},\ldots,F_{n}\) and copula \(\boldsymbol{C}\). Then, for any \(\boldsymbol{u} = (u_{1},\ldots,u_{n})\) in [0, 1]n the following relation holds which can be obtained in a straightforward way: 

$$\displaystyle{ \boldsymbol{C}(u_{1},\ldots,u_{n}) =\boldsymbol{ F}(F_{1}^{-1}(u_{ 1}),\ldots,F_{n}^{-1}(u_{ n})) }$$
(4)

where F i −1 is the generalized inverse of F i .

From (4) it is deduced that copulas allow joining together correlated distributions when the constituent marginal distributions are deterministically known. For an n-variate joint distribution \(\boldsymbol{F}\)​, the associated copula is a distribution function \(\boldsymbol{C}\) that satisfies

$$\displaystyle{ \boldsymbol{F}(x_{1},x_{2},\ldots,x_{n}) =\boldsymbol{ C}(F_{1}(x_{1}),\ldots,F_{n}(x_{n});\vartheta ) }$$
(5)

where \(\vartheta\) is the dependence parameter of the copula measuring the correlation depth between the constituent marginal distributions. The above equation can be the starting point of how copulas can be empirically applied to various problems. Although \(\vartheta\) is in general, a vector of parameters, for bivariate applications it is a scalar correlation measure to be specified. Thus, a bivarate distribution is expressed in terms of the constituent marginal distributions and a function \(\boldsymbol{C}\) that binds them together making use of \(\vartheta\). An essential advantage of copula functions is that the various marginal distributions involved may belong to different families. For example, a bivariate distribution might involve the normal distribution representing one random variable and the gamma distribution representing the other. Though in many cases traditional representations of multivariate distributions necessitate that all the random variables involved must have the same marginals, this is not necessary when employing copulas. In this context, the assumption of identically distributed random variables which might be an inefficient simplification in many cases is not necessary when employing copulas.

In general, copulas allow to consider marginal distributions and correlation as two separate though related issues. For many practical applications, the correlation parameter is the main prerequisite for proper estimation. The assumption of linear correlation, which can fully determine elliptic multivariate distributions, must be reconsidered when modelling non-elliptic multivariate distributions. As an example of the weakness of assuming linear correlation, consider two random variables, X which is Gaussian N(0, 1) and X 2. Evidently, the knowledge of X fully determines X 2, that is, the two variables are 100% correlated. However, based on the classic definition of the Pearson correlation coefficient, it is deduced that their covariance is zero, that is

$$\displaystyle{ \mathit{Cov}(X,{X}^{2}) = 0 }$$
(6)

Consequently their correlation coefficient ρ is also zero which means that they are not correlated.

It should be noted that, as copulas are multivariate distributions of uniformly distributed random variables, they may be expressed in terms of marginal probabilities (CDFs). If a copula is a product of two marginals, independence is deduced allowing the separable estimation of each marginal.

How to Use Copulas in Practice

Based on the previous sections, the question arising is how to select the copula appropriate for a specific problem involving multiple correlated random variables. Often, the choice is based on the usual criteria of familiarity, ease of use, and analytical tractability. The estimation of the marginal distribution and its parameters is not affected by the choice of the copula function used for modeling the dependence of the random variables involved. Hence, any statistical distribution that effectively fits the available experimental data could be adopted to describe the one-dimensional phenomenon whereas the parameters of the distribution can be obtained following well-known fitting/regression methods.

However, there might be some cases where the estimation of conditional measures such as the conditional mean \(E(X/Y = y)\) or variance \(V (X/Y = y)\) might be affected by the choice of the copula function used to model the dependence between the random variables X and Y. More precisely if X and Y are continuous random variables with distribution functions F X (x) and F Y (y) respectively, their CDF satisfies the following expression:

$$\displaystyle\begin{array}{rcl} \boldsymbol{F}_{XY }(x,y)& =& \boldsymbol{F}_{XY }\left [F_{X}^{-1}(u),F_{ Y }^{-1}(v)\right ] \\ & =& \Pr \left \{X \leq F_{X}^{-1}(u),Y \leq F_{ Y }^{-1}(v)\right \} =\boldsymbol{ C}(u,v){}\end{array}$$
(7)

Equation (7) shows how the copula function \(\boldsymbol{C}\) bridges the marginal and the joint distribution. The existence of \(\boldsymbol{C}\) is guaranteed by Sklar [8, 9]. The uniqueness of \(\boldsymbol{C}\), once F X , F Y , and \(\boldsymbol{F}_{XY }\) are defined, is ensured as long as the random variables are continuous. In many instances there may be various options for the marginals and little or no idea about the joint distribution function.

Commonly used copulas are:

  1. (i)

    the Gumbel copula for extreme distributions:

    $$\displaystyle{ \boldsymbol{C}_{\vartheta }^{\mathrm{Gu}}(u_{ 1},u_{2}) =\exp \left [-{\left ({\left (-\ln u_{1}\right )}^{\vartheta } +{ \left (-\ln u_{ 2}\right )}^{\vartheta }\right )}^{1/\vartheta }\right ]\text{, }\ \ \ \ \ \vartheta \in [1,\infty ) }$$
    (8)
  2. (ii)

    the Gaussian copula for linear correlation

    $$\displaystyle{ \boldsymbol{C}_{R}^{\mathrm{Ga}}(u) =\boldsymbol{\varPhi }_{ R}^{n}\left({\varPhi }^{-1}(u_{ 1}),\ldots {,\varPhi }^{-1}(u_{ n})\right ) }$$
    (9)
    $$\displaystyle{ \boldsymbol{C}_{R}^{\mathrm{Ga}}(u,v) =\int _{ -\infty }^{{\varPhi }^{-1}(u) }\int _{-\infty }^{{\varPhi }^{-1}(v) } \frac{1} {2\pi \sqrt{1 - R_{12 }^{2}}}\exp \left [\frac{{s}^{2} - 2R_{12}st + {t}^{2}} {2\left (1 - R_{12}^{2}\right )} \right ]dsdt }$$
    (10)

    where R 12 is the standard linear correlation coefficient of the corresponding bivariate normal distribution

  3. (iii)

    the \(\boldsymbol{t}\)-copula for dependence in the tail [10]

    $$\displaystyle\begin{array}{rcl} \boldsymbol{C}_{\nu,R}^{t}(u)=\boldsymbol{t}_{\nu,R}^{n}\left (t_{\nu }^{-1}(u_{ 1}),\ldots,t_{\nu }^{-1}(u_{ n})\right )& & {}\end{array}$$
    (11)
    $$\displaystyle\begin{array}{rcl} \boldsymbol{C}_{\nu,R}^{t}(u,v)=\int _{ -\infty }^{t_{\nu }^{-1}(u) }\int _{-\infty }^{t_{\nu }^{-1}(v) } \frac{1} {2\pi \sqrt{1- R_{12 }^{2}}}{\left [1+\frac{{s}^{2}-2R_{12}st+{t}^{2}} {\nu \left (1-R_{12}^{2}\right )} \right ]}^{-(\nu +2)/2}dsdt& & {}\end{array}$$
    (12)

    where R 12 is simply the usual linear correlation coefficient of the corresponding bivariate \(\boldsymbol{t}_{\nu }\) distribution if ν > 2.

The Gaussian copula derives from the multivariate Gaussian distribution. Other methods of deriving copulas may employ geometry and (4). For example, for two marginal distributions, one following the beta distribution with parameters α and β, and the other following the lognormal distribution with parameters μ and σ, the following copula may be employed

$$\displaystyle{ \boldsymbol{C}_{\vartheta }^{\mathrm{Fr}}(u_{ 1},u_{2}) = -\frac{1} {\vartheta } \ln \left [1 + \frac{\left ({e}^{-\vartheta u_{1}} - 1\right )\left ({e}^{-\vartheta u_{2}} - 1\right )} {{e}^{-\vartheta }- 1} \right ]\text{, }\ \ \ \ \ \vartheta \in \mathbb{R}\setminus \left \{0\right \} }$$
(13)

which is a member of the Frank’s family.

Upon substituting the relevant distribution functions, a new joint distribution comes up. Parameter \(\vartheta\) determines the depth of correlation between the marginals.

A high-level overview of the fading problems encountered in wireless communications suggests that there are experimental data available for various types of fading (random variables) upon which prediction models should be developed and verified by other similar data, if possible. Copulas allow to build new prediction tools avoiding the use of complicated multivariate distribution functions which are rarely available and too complex. In the attempt to determine the copula function that fits real data, various methods must be followed such as minimizing particular cost functions and identifying the parameter \(\vartheta\) affecting the correlation depth. The sensitivity of \(\vartheta\) to the various electric or spatial characteristics of the physical problems involved is examined so that a numerical trend for its determination can be obtained. Consequently, a probabilistic prediction of the fade values is attempted for various engineering configurations of the physical problem as an estimator of the actual system performance.

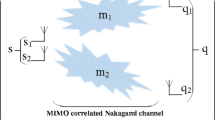
Methodologically the following procedure is proposed. The first step that has to be taken is to formulate the problem each time in hand. As an example assume a MIMO system with two antennas operating over fading channels. A copula function must be formed to determine the relevant outage probability. If SNR i , i = 1, 2 is the signal-to-noise ratio achieved over the i-th channel and the selection combining criterion is adopted, that is the receiver selects the channel exhibiting the maximum SNR, the statistics of system outage are given by:

$$\displaystyle{ P_{\mathit{outage}} =\Pr \left \{SNR_{1}(dB) \leq SNR_{\mathrm{TH}}(dB),SNR_{2}(dB) \leq SNR_{\mathrm{TH}}(dB)\right \} }$$
(14)

where the threshold SNR level appearing in (14) depends on the application, transmission rate, modulation scheme, etc.

If the CDFs of each SNR i , i = 1, 2, are estimated, only the joint statistics must be modelled to determine the outage probability given by (14). To initiate the copula modelling, measurement data are required for the estimation of the CDFs of the individuals SNRs. For this estimation there is no need to derive a closed form distribution function. It must be focused on determining the CDF sample values as accurately as possible. If specific SNR thresholds are employed, the inverse CDFs can correspond to values in [0, 1] related to the uniform random variables U i , i = 1, 2, as in (2). In other words, the one-dimensional datum for each random variable (fade) does not have to be fitted by a closed form statistical distribution since

$$\displaystyle{ \Pr \left \{X_{1} \leq x_{1},\ldots,X_{n} \leq x_{n}\right \} =\boldsymbol{ C}(\Pr \left \{X_{1} < x_{1}\right \},\ldots,\Pr \left \{X_{n} < x_{n}\right \}) }$$
(15)

However, the joint statistical data have to be represented by various copula functions under specific error criteria. The most widely criterion is the least squares one giving rise to following optimization problem.

$$\displaystyle{ \text{minimize}\sum _{\mathit{md}}{\left [P_{\mathit{jom}} -\boldsymbol{ C}\left (P_{\mathit{som\_}1},P_{\mathit{som\_}2};\vartheta \right )\right ]}^{2} }$$
(16)

where

$$\displaystyle\begin{array}{rcl} P_{\mathit{som\_}1} =\Pr \left \{SNR_{1} < SNR_{\mathrm{TH}}\right \}& &{}\end{array}$$
(17)
$$\displaystyle\begin{array}{rcl} P_{\mathit{som\_}2} =\Pr \left \{SNR_{2} < SNR_{\mathrm{TH}}\right \}& &{}\end{array}$$
(18)
$$\displaystyle\begin{array}{rcl} \boldsymbol{C}\left (P_{\mathit{som\_}1},P_{\mathit{som\_}2};\vartheta \right ) = P_{\mathit{jop}}& &{}\end{array}$$
(19)

and the acronyms md, jom, som, and jop stand for measurement data, joint outage measured, single outage measured, and joint outage predicted, respectively.

The copula family that minimizes the cost function expressed in (16) performs better and may be the copula selected to describe the phenomenon under consideration and be adopted for prediction purposes. The nature of the regression is to determine the appropriate value of the dependence factor, \(\vartheta\), for each copula family employed to minimize the cost function given by (16). Hence, after having selected the copula family, the dependence factor \(\vartheta\) is also determined. It should be noted that \(\vartheta\) depends on system parameters such as frequency, polarization, site separation, etc. Therefore, to generalize a copula prediction method, a plethora of measurements are required to generate a statistically stable model for \(\vartheta\), involving the spatial and electromagnetic parameters, allowing the use of the same copulas be employed in similar cases under different operational characteristics.

Conclusions

The copula approach needs to specify the marginal distribution of the random variable involved along with the copula function that correlates them. The copula function can be adjusted to take into account the measurements of the correlated constituent random variables. Employing proper correlation parameters can lead to more efficient representations of joint distributions. The copula method being advantageous in capturing correlation regardless of the marginal type is expected to be very useful when dealing with fading in wireless channels.