Rotational Liquid Film Interacted with Ambient Gaseous Media

Abstract

Annular jets of an incompressible liquid moving in a gas at rest are of interest for applications. The experimental study of annular liquid jets shows existing tulip and bubble jet shapes and also predicts the existence of periodic shape. However, sufficient simplifications of mathematical models of the flow details were made: the effects of the forces of surface tension of the longitudinal motion and the variability of the tangential velocity component of the centrifugal forces in the field were neglected. In this work, the equations described the flow of rotational annular jets of viscous liquid in an undisturbed medium with allowance of the abovementioned effects. The basic model was obtained through the use of quasi-two-dimensional momentum balance equations in the metric space with the co- and contravariant basis vectors suitable for surfaces with complicated shape. The pressure difference outside and within the jet was obtained and analyzed. The results of calculations show the dependence of the jet shape on the relative contributions of the initial rotation rate, viscosity, surface tension, gravity forces, and pressure difference. An exact solution to the problem of the motion of a thin cylindrical shell due to different internal and external pressures is obtained. Analysis of nonlinear instabilities of the Rayleigh–Taylor type in meridional cross section was carried out. It is shown that the instabilities, which appear due to pressure drop, cannot be stabilized by rotation.

1 Introduction

During the first stage of atomization process (atomization is the making of an aerosol, which is a colloid suspension of fine solid particles or liquid droplets in a gas), free rotating films of liquid are formed [11]. As a rule, they take cylindrical or conical forms. For these kinds of films two main mechanisms can be distinguished which disturb the film shape. The first of them is connected to instability and to the growth of flexural perturbations due to the dynamic action of the surrounding gas. The second mechanism of the film distortion of the perfect shape of the film is due to the liquid rotation around the film axis.

In a study [4] special attention is paid to the non-axisymmetric perturbation development due to the film rotation. Due to competition between centrifugal and surface forces, the film acquires a wavy shape even when the flow is stable. Shapes of swirling liquid annular jets were studied in by Epikhin [3]. He accounted for viscosity and friction between air and liquid. These results gave solutions for the effect of these factors on the steady film configuration and its initial velocity profile. The numerical and experimental investigation of stable wavy shapes in free films of ideal liquids was carried out in [5]. But the surface tension effect on the longitudinal motion of the film was neglected. The present work is dedicated to the study of rotating liquid films interacting with the ambient air at different pressures. Asymptotic analysis and numerical simulation were applied. The effect of the liquid viscosity was taken into account.

2 The Main Equations

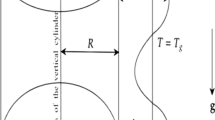
Let us consider a free rotating liquid film following out of an annular nozzle with the assumption that the disintegration of the film takes place fairly far downstream. The motion may naturally be described on the basis of the quasi-two-dimensional equations of thin film dynamics for the momentum balance (Fig. 1); dθ ¹ dθ ² is the element of the film. The overall momentum within the element is expressed as $\rho h\sqrt{a}\mathbf{V}{d\theta }^{1}{d\theta }^{2}$. Entov and Yarin [13] have obtained the quasi-two-dimensional equations in the frame of reference θ ⁱ (i = 1, 2) associated with the middle surface of a film (i.e., the conditional area located in the middle of the film thickness). They considered it as a two-dimensional continuum:

$$\displaystyle{ \begin{array}{l} \partial _{t}\left (g_{1}h\right ) + \partial _{{\theta }^{1}}\left (g_{1}h{W}^{1}\right ) + \partial _{{\theta }^{2}}\left (g_{1}h{W}^{2}\right ) = 0, \\ \partial _{t}\left (\rho \mathbf{V}g_{1}h\right ) + \partial _{{\theta }^{1}}\left (\rho \mathbf{V}{W}^{1}g_{1}h\right ) + \partial _{{\theta }^{2}}\left (\rho \mathbf{V}{W}^{2}g_{1}h\right ) = \partial _{{\theta }^{1}}{\mathbf{N}}^{1} + \partial _{{\theta }^{2}}{\mathbf{N}}^{2} + \mathbf{q}g_{1}, \\ g_{1} = \sqrt{EG - {F}^{2}},\ \ E = \mathbf{a}_{1} \cdot \mathbf{a}_{1},\ \ F = \mathbf{a}_{1} \cdot \mathbf{a}_{2},\ \ G = \mathbf{a}_{2} \cdot \mathbf{a}_{2}.\\ \end{array} }$$

(1.1)

Fig. 1

Element of the film surface with vector components

The following definitions are used: ρ = ρ(θ ¹, θ ²) is the liquid density; V = V(θ ¹, θ ²) is the velocity field; h = h(θ ¹, θ ²) is the film thickness; M is the middle surface, r = r(θ ¹, θ ²) of the film with the parametrization θ ^α being the curvilinear coordinates (Fig. 1); q is the distributed external force per unit area of the film; W is the liquid velocity relative to the frame of reference associated with the median surface of the film (the reference frame velocity is U and W = V −U); ${N}^{\alpha } = {N}^{\alpha \gamma }\mathbf{a}_{\gamma }$ is the internal surface forces per unit length of film cross section along a line θ ^α = const; and N ^{α γ} is the symmetrical contravariant tensor. The corresponding metrics is characterized by the covariant base vectors a _α  = ∂ r∕∂ θ ^α, d r = a _α dθ ^α, and α = 1,  2; a ₃ is the unit normal to the surface M; the contravariant base vectors a ^α and co- and contravariant components of the metric tensor a _{α β} ,  a ^{α β} satisfy the geometric formulas

$$\displaystyle{a_{\alpha \beta } = \mathbf{a}_{\alpha }\mathbf{a}_{\beta },\ \ {a}^{\alpha \beta } ={ \mathbf{a}}^{\alpha }{\mathbf{a}}^{\beta },\ \ {\mathbf{a}}^{\alpha }\mathbf{a}_{\beta } =\delta _{ \beta }^{\alpha },\ \ a_{\alpha \beta }{a}^{\beta \gamma } =\delta _{ \alpha }^{\gamma },\ \ \det a_{\alpha \beta } = a,}$$

where δ _α ^γ is the Kronecker delta function ${g}^{\alpha m}g_{m\beta } =\delta _{ \beta }^{\alpha }$. The components of the tensor N ^{α γ} are given in the form [13]

$$\displaystyle{ {N}^{\alpha \gamma } = \sqrt{g_{1}}\left ({\sigma }^{\alpha \gamma }h + 2\sigma _{{\ast}}{a}^{\alpha \gamma }\right ), }$$

(1.2)

where σ _∗ is the surface tension coefficient and σ ^{α γ} is the contravariant surface stress tensor.

The first equation of (1.1) is continuity, and the second one is the momentum equation. In the case of axisymmetric stable flow (Fig. 2) the motion may be described on the basis of the thin film dynamics (1.1) and (1.2) for quantities averaged over the thickness of the film. For the case of axisymmetric stable flow equations take the following form [13]:

$$\displaystyle\begin{array}{rcl} & & hRV _{\tau } = h_{0}R_{0}V _{\tau 0}, \\ & & \quad \rho \left (hRV _{\tau }\frac{dV _{\tau }} {ds} - V _{\theta }^{2}h\sin \psi \right ) = \frac{d\sigma _{\tau \tau }Rh} {ds} - h\sigma _{\theta \theta }\sin \psi + g\rho Rh\cos \psi, \\ & & \quad \rho \big(hRV _{\tau }^{2} \frac{d\psi } {ds} - V _{\theta }^{2}h\cos \psi \big) =\sigma _{\tau \tau }Rh \frac{d\psi } {ds} - h\sigma _{\theta \theta }\cos \psi \\ & & \qquad + 2\sigma _{{\ast}}\big(R \frac{d\psi } {ds}-\cos \psi \big)\! - g\rho Rh\sin \psi -\left (p_{i}-p_{o}\right )R, \\ & & \quad \rho \big(hRV _{\tau }\frac{dV _{\theta }} {ds} - V _{\theta }V _{\tau }h\sin \psi \big) = \frac{d\sigma _{\theta \tau }Rh} {ds} +\sigma _{\tau \theta }h\sin \psi. {}\end{array}$$

(1.3)

The terms which take into account pressure drop are included additionally by comparison with studies [13]. The first equation of the system (1.1) gives the equation of continuity; the remaining equations are projections of the momentum equation on the directions of the tangent τ and the normal n to the middle surface of the film and on the direction of the variation of the angular (azimuthal) coordinate θ on the middle surface.

Fig. 2

Scheme of a liquid film with motion direction

The following notation is introduced: R is the radius of the middle surface of the film (Fig. 2); h is its thickness; V _τ and V _θ are the longitudinal and rotational components of the fluid velocity vector; the index 0 denotes the values of the quantities at the nozzle exit; ρ is the liquid density; s is the coordinate reckoned along the generator of the middle surface of the film; ψ is the angle between the tangent τ and the axis of symmetry x of the film; p _o and p _i are the outer and inner ambient media static pressures; dψ∕ds is the curvature of the generator of the middle surface of the film; g is the acceleration due to the force of gravity g which is directed along the axis x;  σ _{τ τ} ,  σ _{τ θ} , and σ _{θ θ} are the components of the stress tensor in the coordinate system associated with the middle surface of the film, which are determined for a Newtonian liquid (with allowance for the condition that there are no stresses on the film surfaces) by the relationships

$$\displaystyle\begin{array}{rcl} & & \sigma _{\tau \tau } = 2\mu \Big(2\frac{dV _{\tau }} {ds} + \frac{V _{\tau }\sin \psi } {R}\Big),\ \ \sigma _{\tau \theta } =\mu \Big (\frac{dV _{\theta }} {ds} -\frac{V _{\theta }\sin \psi } {R}\Big), \\ & & \sigma _{\theta \theta } = 2\mu \Big(\frac{dV _{\tau }} {ds} + \frac{2V _{\tau }\sin \psi } {R} \Big), {}\end{array}$$

(1.4)

where μ is the liquid viscosity. Choosing as scales for R and s the radius R ₀, for V _τ and V _θ the velocity V _τ0, for h the thickness h ₀, and for the stresses parameter μ V _τ0∕R ₀, we obtain, using (1.3) and (1.4), the following dimensionless system:

$$\displaystyle\begin{array}{rcl} & & \frac{dV _{\tau }} {ds} = \frac{V _{\theta }^{2}} {V _{\tau }R}\sin \psi +{ \mathit{Re}}^{-1}\left [ \frac{d} {ds}\left ( \frac{\sigma _{\tau \tau }} {V _{\tau }}\right ) - \frac{\sigma _{\theta \theta }} {V _{\tau }R}\sin \psi \right ] +{ \mathit{Fr}}^{-1} \frac{\cos \psi } {V _{\tau }}, \\ & & \,\, \frac{d\psi } {ds} ={ \left (V _{\tau } -{\mathit{We}}^{-1}R -{\mathit{Re}}^{-1} \frac{\sigma _{\tau \tau }} {V _{\tau }}\right )}^{-1}\left [\left ( \frac{V _{\theta }^{2}} {V _{\tau }R} -{\mathit{We}}^{-1} -{\mathit{Re}}^{-1} \frac{\sigma _{\theta \theta }} {V _{\tau }R}\right )\cos \psi \right. \\ & & \qquad \quad \left.-{\mathit{Fr}}^{-1} \frac{\sin \psi } {V _{\tau }} -\frac{\mathit{Eu}} {\,} \mathit{We}R\right ], \\ & & \quad \frac{dV _{\theta }} {ds} + \frac{V _{\theta }} {R}\sin \psi ={ \mathit{Re}}^{-1}\left [ \frac{d} {ds}\left ( \frac{\sigma _{\tau \theta }} {V _{\tau }}\right ) - \frac{\sigma _{\tau \theta }} {V _{\tau }R}\sin \psi \right ], \\ & & \quad \frac{dR} {ds} =\sin \psi,\qquad \frac{dx} {ds} =\cos \psi, {}\end{array}$$

(1.5)

where dimensionless stress tensor components are

$$\displaystyle\begin{array}{rcl} & & \sigma _{\tau \tau } = 2\left (2\frac{dV _{\tau }} {ds} + \frac{V _{\tau }\sin \psi } {R}\right ),\quad \sigma _{\tau \theta } = \frac{dV _{\theta }} {ds} -\frac{V _{\theta }\sin \psi } {R}, \\ & & \sigma _{\theta \theta } = 2\left (\frac{dV _{\tau }} {ds} + \frac{2V _{\tau }\sin \psi } {R} \right ). {}\end{array}$$

(1.6)

The last two equations in (1.5) express obvious geometric relationships. The dimensionless values

$$\displaystyle{\mathit{We} = \frac{\rho h_{0}V _{\tau 0}^{2}} {2\sigma _{{\ast}}},\quad \mathit{Re} = \frac{\rho R_{0}V _{\tau 0}} {\mu },\quad \mathit{Fr} = \frac{V _{\tau 0}^{2}} {gR_{0}},\quad \mathit{Eu} = \frac{\left (p_{i} - p_{o}\right )R_{0}} {2\sigma _{{\ast}}} }$$

are the Weber, Reynolds, Froude, and Euler numbers, correspondingly. The system (1.5) requires formulation of conditions on the near and far ends of the film. On the nozzle exit we have

$$\displaystyle\begin{array}{rcl} \left.x\right \vert _{s=0}& =& 0,\ \ \left.R\right \vert _{s=0} = 1,\ \ \left.V _{\tau }\right \vert _{s=0} = 1,\ \ \left.V _{\theta }\right \vert _{s=0} = \Omega R_{0}/V _{\tau 0} \\ & =& V _{\theta 0}/V _{\tau 0} \equiv V _{\Omega },\ \ \left.\psi \right \vert _{s=0} =\psi _{0}, {}\end{array}$$

(1.7)

where $\Omega$ is the angular velocity (Fig. 2).

The effect of the boundary conditions at the far end of an annular jet with x = L appears to a great extent only in a narrow boundary layer and for fairly high does not propagate upstream. In this context it is enough to solve Cauchy’s problem (1.5)–(1.7).

3 Asymptotic Analysis

We consider the Newtonian liquid films in the equality conditions of the outer and inner static pressures (Eu = 0); gravity effect is neglected (Fr → ∞). It follows from (1.5) and (1.7) that at a definite value of the rotation velocity at the nozzle exit $V _{\Omega } =\,{ \mathit{We}}^{-1/2}$ and with ψ ₀ = 0 for ideal liquid (inverse Reynolds number $\varepsilon ={ \mathit{Re}}^{-1} \rightarrow 0)$, there are no oscillations, and R ≡ 1; consequently, the middle surface of the film has a cylindrical shape (see Appendix).

For the given initial rotation velocity and the film exit angle such that

$$\displaystyle{ V _{\Omega } =\,{ \mathit{We}}^{-1/2} +\beta _{ \Omega },\quad \beta _{\Omega } <<\,{ \mathit{We}}^{-1/2},\quad \psi _{ 0} << 1, }$$

(2.1)

small oscillations in the main parameters of the film must take place along x-axis, and the presence of viscosity cannot alter this picture qualitatively. Consequently, assuming that the inequalities (2.1) are fulfilled, we represent the unknown values in the form

$$\displaystyle{ V _{\tau } = 1 +\alpha (s),\quad V _{\theta } =\,{ \mathit{We}}^{-1/2} +\beta (s),\quad R = 1 +\gamma (s), }$$

(2.2)

where α and γ are small in comparison with unity and β is small in comparison with We ^−1∕2.

The representation (2.2) for R is not subject to doubt when ψ ₀ = 0; in the case 0 < ψ ₀ < < 1 we may also expect a solution oscillating periodically near R = 1 which will be constructed in what follows. In linear approximation s ≈ x and

$$\displaystyle{ \psi \approx \sin \psi \approx \tan \psi = dR/dx = d\gamma /dx << 1. }$$

(2.3)

Substituting (2.2) and (2.3) into (1.5) and (1.6), we obtain after linearization with respect to α,  β, and γ

$$\displaystyle\begin{array}{rcl} & & \frac{d\alpha } {dx} =\,{ \mathit{We}}^{-1} \frac{d\gamma } {dx} +\varepsilon \left (4 \frac{{d}^{2}\alpha } {d{x}^{2}} + 2 \frac{{d}^{2}\gamma } {d{x}^{2}}\right ), \\ & & \!\! \frac{{d}^{2}\gamma } {d{x}^{2}} ={ \left (1 -\,{\mathit{We}}^{-1}\right )}^{-1}\left [\,{\mathit{We}}^{-1}\left (2\beta \,{\mathit{We}}^{1/2} -\gamma -\alpha \right ) -\varepsilon \left (2 \frac{d\alpha } {dx} + 4 \frac{d\gamma } {dx}\right )\right ], \\ & & \frac{d\beta } {dx} = -\,{\mathit{We}}^{-1/2} \frac{d\gamma } {dx} +\varepsilon \left ( \frac{{d}^{2}\beta } {d{x}^{2}} -\,{\mathit{We}}^{-1/2} \frac{{d}^{2}\gamma } {d{x}^{2}}\right ). {}\end{array}$$

(2.4)

Using (2.1) and (2.3) for (1.7), we find that the solutions of the system (2.4) must satisfy the conditions

$$\displaystyle{ \left.\alpha \right \vert _{x=0} = \left.\gamma \right \vert _{x=0} = 0,\quad \left.\beta \right \vert _{x=0} =\beta _{\Omega },\quad d\gamma /dx\,\vert _{\,x=0} =\psi _{0}. }$$

(2.5)

Integrating the first and the third equations of the system (2.4), we obtain

$$\displaystyle\begin{array}{rcl} \alpha & =& C_{1} +\,{ \mathit{We}}^{-1}\gamma +\varepsilon \left (4 \frac{d\alpha } {dx} + 2 \frac{d\gamma } {dx}\right ), \\ \beta & =& D_{1} -\,{\mathit{We}}^{-1}\gamma +\varepsilon \left ( \frac{d\beta } {dx} -\,{\mathit{We}}^{-1} \frac{d\gamma } {dx}\right ),{}\end{array}$$

(2.6)

where C ₁ and D ₁ are indeterminate constants. Substituting (2.6) into the second equation of the system (2.4) and neglecting values $\mathcal{O}\left ({\varepsilon }^{2}\right )$ we get the following equation:

$$\displaystyle{ \frac{{d}^{2}\gamma } {d{x}^{2}} +\gamma \frac{3 +\,{ \mathit{We}}^{-1}} {\,\mathit{We} - 1} = \frac{2\,{\mathit{We}}^{1/2}D_{1} - C_{1}} {\,\mathit{We} - 1} - 4\,\varepsilon \frac{\,\mathit{We} + 1} {\,\mathit{We} - 1} \cdot \frac{d\gamma } {dx}. }$$

(2.7)

Let us find the solution of this equation in the case of low viscosity, Re > > 1, by means of the asymptotic multi-scale method [8, 12]. Note that for typical values of the parameters, $\rho = 1{0}^{3}{\text{kg/m}}^{3},\ R_{0} = 1{0}^{-2}\text{m,}V _{\tau 0} = 1.0\text{m/s}$, the value of $\varepsilon$ is low, due to Re ≈ 10⁴. Since the important effect of viscosity can appear only at far downstream the film exit, we introduce the slow variable $X =\varepsilon x = \mathcal{O}(1)$, which is locally independent from x. Representing the solution in the form of the asymptotic series $\gamma =\gamma _{0} +\varepsilon \gamma _{1}$ and neglecting terms of order higher than Re ⁻¹, we obtain, from (2.7),

$$\displaystyle\begin{array}{rcl} & & \frac{{\partial }^{2}} {\partial {x}^{2}}\left (\gamma _{0} +\varepsilon \gamma _{1}\right ) + 2\varepsilon \frac{{\partial }^{2}\gamma _{0}} {\partial x\partial X} + \frac{3 +\,{ \mathit{We}}^{-1}} {\,\mathit{We} - 1} \left (\gamma _{0} +\varepsilon \gamma _{1}\right ) = \frac{2\,{\mathit{We}}^{1/2}D_{1} - C_{1}} {\,\mathit{We} - 1} \\ & & \quad - 4\varepsilon \frac{{\left (\mathit{We} + 1\right )}^{2}} {\mathit{We}\left (\,\mathit{We}-\right )} \frac{\partial \gamma _{0}} {\partial x}. {}\end{array}$$

(2.8)

Separating out the dominant terms from (2.8), we obtain the equation

$$\displaystyle{ \frac{{\partial }^{2}\gamma _{0}} {\partial {x}^{2}} +\gamma _{0}\frac{3 +\,{ \mathit{We}}^{-1}} {\,\mathit{We} - 1} = \frac{2\,{\mathit{We}}^{1/2}D_{1} - C_{1}} {\,\mathit{We} - 1},}$$

whose solution is

$$\displaystyle\begin{array}{rcl} \gamma _{0}& =& A(X)\,{e}^{imx} + B(X)\,{e}^{-imx} +\gamma _{ r},\quad m =\Big {[ \frac{3\,\mathit{We} + 1} {\,\mathit{We}(\,\mathit{We} - 1)}\Big]}^{1/2}, \\ \gamma _{r}& =& \frac{2\,{\mathit{We}}^{1/2}D_{1}\! - C_{1}} {3 +\,{ \mathit{We}}^{-1}}. {}\end{array}$$

(2.9)

It is assumed that in practice We > 1. In order to determine the unknown functions A and B in (2.9), we will consider the terms of the order $\varepsilon$ in (2.8):

$$\displaystyle{ \frac{{\partial }^{2}\gamma _{1}} {\partial {x}^{2}} + {m}^{2}\gamma _{ 1} = -4\varepsilon \frac{{\left (\mathit{We} + 1\right )}^{2}} {\,\mathit{We}\left (\mathit{We} - 1\right )} \frac{\partial \gamma _{0}} {\partial x} - 2 \frac{{\partial }^{2}\gamma _{0}} {\partial x\partial X}. }$$

(2.10)

Substituting (2.9) in the r.h.s. of (2.10) and requiring absence solutions of type $\gamma _{1} \sim x\exp \left (\pm imx\right )$, which are inadmissible in an asymptotic series, we obtain

$$\displaystyle{ A = A_{0}{e}^{-PX},\quad B = B_{ 0}{e}^{-PX},\quad P = \frac{2{\left (\mathit{We} + 1\right )}^{2}} {\,\mathit{We}\left (\mathit{We} - 1\right )}, }$$

(2.11)

where A ₀ and B ₀ are arbitrary constants.

Cutting off the asymptotic series, we obtain by means of (2.9) and (2.11)

$$\displaystyle{ \gamma _{0} = A_{0}{e}^{-PX+imx} + B_{ 0}\exp {e}^{-PX-imx} +\gamma _{ r}. }$$

(2.12)

In accordance with conditions for γ in (2.5) and (2.12), we obtain

$$\displaystyle{ A_{0} = -\frac{1} {2}\left [i\left (\psi _{0}/m\right ) +\gamma _{r}\right ],\quad B_{0} = \frac{1} {2}\left [i\left (\psi _{0}/m\right ) -\gamma _{r}\right ]. }$$

These latter equations give, with allowance for (2.12),

$$\displaystyle{ \gamma =\gamma _{r}\left [1 - {e}^{-PX}\cos mx\right ] + \frac{\psi _{0}} {m}{e}^{-PX}\sin mx. }$$

(2.13)

Using (2.13) and omitting in (2.6) the important terms of order $\varepsilon$, we obtain

$$\displaystyle{ \begin{array}{l} \alpha = C_{1} +\gamma _{r}\,{\mathit{We}}^{-1}\left [1 - {e}^{-PX}\cos mx\right ] +\,{ \mathit{We}}^{-1} \frac{\psi _{0}} {m}{e}^{-PX}\sin mx, \\ \beta = D_{1} -\gamma _{r}\,{\mathit{We}}^{-1/2}\left [1 - {e}^{-PX}\cos mx\right ] -\,{\mathit{We}}^{-1} \frac{\psi _{0}} {m}{e}^{-PX}\sin mx.\\ \end{array} }$$

(2.14)

By means of the boundary conditions (2.5) for α and β we find from (2.14) that $C_{1} = 0,\ D_{1} =\beta _{\Omega }$. Using Eqs. (2.2), (2.9), (2.11), (2.13), and (2.14), we find

$$\displaystyle{ \begin{array}{l} R = 1 + \frac{2} {3}\beta _{\Omega } \frac{\,{\mathit{We}}^{3/2}} {\,\mathit{We}+\frac{1} {3} } \left (1 - {e}^{-PX}\cos mx\right ) + \frac{\psi _{0}} {m}\,{e}^{-PX}\sin mx, \\ \!\!V _{\tau } = 1 + \frac{2} {3}\beta _{\Omega } \frac{\,{\mathit{We}}^{3/2}} {\,\mathit{We}+\frac{1} {3} } \left (1 - {e}^{-PX}\cos mx\right ) + \frac{\psi _{0}} {m}\,{\mathit{We}}^{-1}\,{e}^{-PX}\sin mx, \\ \!\!V _{\theta } =\,{ \mathit{We}}^{-1/2} + \frac{1} {3}\beta _{\Omega } \frac{\,\mathit{We}+1} {\,\mathit{We}+\frac{1} {3} } + \frac{2} {3}\beta _{\Omega } \frac{\,{\mathit{We}}^{3/2}} {\,\mathit{We}+\frac{1} {3} } \,{e}^{-PX}\cos mx - \frac{\psi _{0}} {m}\,{\mathit{We}}^{-1/2}\,{e}^{-PX}\sin mx, \\ \!\psi = \frac{2} {3}\,\beta _{\Omega } \frac{\,{\mathit{We}}^{3/2}} {\,\mathit{We}+\frac{1} {3} } m\,{e}^{-PX}\sin mx +\psi _{0}\,{e}^{-PX}\cos mx, \\ \!X =\varepsilon x,\quad m =\big {[ \frac{3\,\mathit{We}+1} {\,\mathit{We}\left (\mathit{We}-1\right )}\big]}^{1/2},\quad P = \frac{2{\left (\mathit{We}+1\right )}^{2}} {\,\mathit{We}\left (\mathit{We}-1\right )},\quad \,\mathit{We} > 1.\\ \end{array} }$$

(2.15)

The thickness of the film is calculated by using the continuity equation as h = 1∕RV _τ . We also note that the general solution of the system (2.4) has the form

$$\displaystyle{ \begin{array}{l} \gamma = {e}^{-PX}\left (F_{1}\sin mx + F_{2}\cos mx\right ) +\gamma _{r} + \mathcal{O}\left (\varepsilon \right ), \\ \alpha = C_{2}\,{e}^{-\frac{L-x} {4\,\varepsilon } } +\,{ \mathit{We}}^{-1}\,{e}^{-PX}\left (F_{1}\sin mx + F_{2}\cos mx\right ) +\gamma _{r}\,{\mathit{We}}^{-1} + C_{1} + \mathcal{O}\left (\varepsilon \right ), \\ \beta = D_{2}\,{e}^{-\frac{L-x} {4\,\varepsilon } } -\,{\mathit{We}}^{-1/2}\,{e}^{-PX}\left (F_{1}\sin mx + F_{2}\cos mx\right )-\gamma _{r}{\mathit{We}}^{-1/2}+D_{1}+\mathcal{O}\left (\varepsilon \right ),\\ \end{array} }$$

(2.16)

where the new indeterminate constants $F_{1},\ F_{2},\ C_{2}$, and D ₂ appear. It is easily seen that there is a boundary layer of thickness $\mathcal{O}\left (\varepsilon \right )$ far downstream nozzle exit, x = L, where perturbations of the velocity components α and β are finely adjusted to the boundary conditions $\left.\alpha \right \vert _{x=L} =\alpha _{L},\ \left.\beta \right \vert _{x=L} =\beta _{L}$, where α _L and β _L are prescribed values.

Outside this boundary layer the first terms in the expressions for α and β in (2.16) are unimportant like the terms of order $\mathcal{O}\left (\varepsilon \right )$, and the four constants $F_{1},\ F_{2},\ C_{2}$, and D ₂ are determined by the boundary conditions (2.5). The values C ₁ and D ₁ coincide with those given above, and moreover we have

$$\displaystyle{F_{1} =\psi _{0}/m,\qquad F_{2} = -\frac{2} {3} \frac{\beta _{\Omega }{\mathit{We}}^{3/2}} {\mathit{We} + \frac{1} {3}}.}$$

Correspondingly, (2.16) gives rise to the asymptotic solution (2.15) which holds everywhere outside a narrow layer of thickness $\mathcal{O}(\varepsilon )$ in the vicinity x = L. The boundary conditions at x = L determine the constants C ₂ and D ₂. The solution constructed for the problem (2.15) describes the main effect due to the influence of low viscosity: at a large downstream distance the low viscosity makes a contribution comparable with the oscillation amplitudes of s, which decreases as a result.

It is easy to be satisfied by means (2.15) that in the considered approximation (when the interaction between liquid film and ambient media is assumed to be neglected) the kinetic energy

$$\displaystyle{E = \frac{1} {2}\rho \left (V _{\tau }^{2} + V _{\theta }^{2}\right )}$$

of the liquid (exactly like the momentum projection on the x-axis, ρ R V _θ ) is conserved and only an energy transfer from the rotational to the longitudinal motion takes place, and vice versa, as it happens in the absence of viscous stresses.

It follows from (2.15) that with increase X the oscillations damp, and the film has parameters which differ from those on the nozzle exit. Thus, when $\beta _{\Omega } > 0$, the film expands, and the longitudinal velocity component increases, while the rotational one decreases.

4 Laminar Jet with Different Outer and Inner Pressures of Ambient Media

Laminar flows of rotating annular jets may be described by the Navier–Stokes equations in orthogonal coordinate system $\left \{\mathbf{s},\mathbf{n},\theta \right \}$ attached to the middle surface of the jet as it was shown in Fig. 2. We introduce an additional dimensionless term, χ, considering the pressure drop between outer, “o,” and inner, “i,” media:

$$\displaystyle{\chi = \frac{p_{\,\text{o,st}} - p_{\,\text{i,st}}} {\rho V _{\tau 0}^{2}},}$$

where p _o,st and p _i,st are the outer and inner static pressures, accordingly. We introduce the variable $N = n\varepsilon _{0}^{-1}$ and present the solution in the form of a power series expansion with the parameter $\varepsilon _{0} ={ \mathit{Re}}^{-1/2}$, assuming the normal velocity and thickness of the jet to be small values of first order. In the first approximation, we obtain a system of equations describing the rotating liquid jet flow in the form

$$\displaystyle\begin{array}{rcl} & & \quad \frac{\partial } {\partial s}\left (RV _{\tau }\right ) + \frac{\partial } {\partial N}\left (RV _{n}\right ) = 0, \\ & & \quad V _{\tau }\frac{\partial V _{\tau }} {\partial s} + V _{n}\frac{\partial V _{\tau }} {\partial N} ={ \mathit{Fr}}^{-1}\cos \psi {+\omega }^{2}R\sin \psi + \frac{{\partial }^{2}V _{\tau }} {\partial {N}^{2}} - \frac{V _{\tau }^{2}} {r_{0}(s)} \\ & & = -\frac{\partial p} {\partial N} -{\mathit{Fr}}^{-1}\sin \psi {+\omega }^{2}R\cos \psi, \\ & & \quad V _{\tau } \frac{\partial \omega } {\partial s} + V _{n} \frac{\partial \omega } {\partial N} = -2 \frac{V _{\tau }\omega } {R(s)}\sin \psi + \frac{{\partial }^{2}\omega } {\partial {N}^{2}}. {}\end{array}$$

(3.1)

In the system (3.1), we define r ₀(s) ≡ k ⁻¹(s) as the curvature radius of the jet surface R(s) and ω as the angular velocity. The equations of the middle surface and bounding surfaces of the jet have, respectively, the form

$$\displaystyle\begin{array}{rcl} \frac{dR} {ds} & =& \sin \psi,\quad \frac{dx} {ds} =\cos \psi,\quad N = 0,{}\end{array}$$

(3.2)

$$\displaystyle\begin{array}{rcl} \hspace{-44.0pt}V _{\tau,l } \frac{d\delta _{l } } {ds}& =& 2V _{n,l},\quad N = \frac{1} {2}{\left (-1\right )}^{l+1}\delta (s),\quad l =\bigg\{ \begin{array}{*{20}c} 1,\mathrm{\ for\ outer\ surface\ \textquotedblleft o''}, \\ 2,\mathrm{\ for\ inner\ surface\ \textquotedblleft i''}. \\ \end{array} {}\end{array}$$

(3.3)

The boundary conditions on the interfaces express the absence of tangential stresses and the discontinuity of the normal stresses and, in the considered approximation, have the form

$$\displaystyle\begin{array}{rcl} & & \frac{\partial V _{\tau }} {\partial N} = 0,\ \ p_{l} = p_{l,\,\text{st}} + 2{\left (-1\right )}^{l+1}\sigma _{ s}R_{s}^{-1},\ \ N = \frac{1} {2}{\left (-1\right )}^{l+1}\delta (s),\ \ \frac{2} {R_{s}} \\ & & \qquad = \frac{1} {R(s)}\cos \psi - \frac{d\psi } {ds}. {}\end{array}$$

(3.4)

Here, R _s is the effective curvature radius of the middle surface at the considered point; δ is the liquid film thickness; σ _o and σ _i are the liquid surface tension coefficients at the outer and inner surfaces of the liquid film, $\sigma _{s} = \frac{1} {2}\left (\sigma _{i} +\sigma _{o}\right )$. If the tangential and angular velocity profiles at the nozzle exit, s = 0, are uniform and have minor differences from the profiles for s > 0, V _τ  = V _τ (s),  ω = ω(s), then the first, third, and fourth equations of the system (3.1) have, with allowance for (3.3), the form

$$\displaystyle{ RV _{\tau }\delta = Q_{0} = \text{const},\ \ V _{\tau }\frac{dV _{\tau }} {ds} ={ \mathit{Fr}}^{-1}\cos \psi {+\omega }^{2}R\sin \psi,\ \ V _{\tau } \frac{d\omega } {ds} = -2\frac{\omega V _{\tau }} {R}\sin \psi. }$$

(3.5)

Let us consider the second equation of (3.1). For fixed value of the coordinate s, it is an ordinary equation of the first order in P:

$$\displaystyle{ \frac{dp} {dN} = -{\mathit{Fr}}^{-1}\sin \psi + V _{\tau }^{2}/r_{ 0}(s) {+\omega }^{2}R(s)\cos \psi. }$$

Integrating it across the film and using the boundary conditions (3.4) we find

$$\displaystyle{p_{o} - p_{i} =\big [{\mathit{Fr}}^{-1}\sin \psi - V _{\tau }^{2}/r_{ 0}(s) {-\omega }^{2}R(s)\cos \psi \big]\delta (s).}$$

Expressing by means of the jet shape curvature and using (3.4), we obtain the following equation:

$$\displaystyle\begin{array}{rcl} & & \frac{d\psi } {ds} = \frac{\cos \psi -R\,\mathit{Eu} + \left (\mathit{Fr}_{0}^{-1}\sin \psi -\,\mathit{We}_{0}^{-1}{\omega }^{2}R\cos \psi \right )/V _{\tau }} {R -\,\mathit{We}_{0}^{-1}V _{\tau }}, \\ & & \!\!\mathit{We}_{0}^{-1} = \frac{1} {2}\,Q_{0}\,\mathit{We}_{s},\quad \mathit{Fr}_{0}^{-1} = \frac{1} {2}Q_{0}\,\mathit{We}_{s}{\mathit{Fr}}^{-1},\quad \mathit{Eu} = \frac{1} {2}\,\mathit{We}_{s}\chi,{}\end{array}$$

(3.6)

where $\mathit{We}_{s} = 2\,\mathit{We}_{i}\,\mathit{We}_{o}/\left (\mathit{We}_{i} +\, \mathit{We}_{o}\right )$ is the average Weber at the middle surface of the liquid film. Here, the dimensionless parameters of the problem are replaced by modified dimensionless numbers in accordance with formulas of [2], where Q ₀ = 1 was taken.

Thus, the problem of the flow of incompressible liquid jet in an ideal undisturbed medium reduces to Cauchy’s problem for the system of ODE ( (3.2), (3.5), and (3.6)) with initial conditions

$$\displaystyle{ V _{\tau }(0) = 1,\quad \omega (0) = \Omega,\quad R(0) = 1,\quad \psi (0) =\psi _{0}. }$$

(3.7)

Equations (3.5) in the case Fr ₀ ⁻¹ = 0 can be integrated. With allowance for the initial conditions (3.7), we find

$$\displaystyle{ \omega (s) = \Omega /{R}^{2}(s),\qquad V _{\tau }(s) = \sqrt{1 + {\Omega }^{2 } \left [1 - 1/R(s) \right ]}. }$$

(3.8)

We use the expression (3.8) to calculate the surface radius R ^∗ in the critical section (where the tangential velocity component vanishes) that can take a place in the limit of high initial rotation velocity, $\Omega >> 1$:

$$\displaystyle{ {R}^{{\ast}} = \Omega /\sqrt{1 + {\Omega }^{2}}. }$$

(3.9)

It follows from (3.9) that for strong initial rotation, $\Omega >> 1$, all ${R}^{{\ast}}\left (\Omega \right )$ nears unity, and the critical sections are asymptotically shifted to the start of the flow.

5 Numerical Simulations

Now we study the evolution of rotating annular jet (film) of an ideal liquid. This problem was formulated in Sect. 1 (system (1.5)) for $\varepsilon ={ \mathit{Re}}^{-1} \rightarrow 0$ with initial conditions (1.7). After transformation of this system to a form which is solved for derivatives, Cauchy’s problem indicated is integrated numerically by the Runge–Kutta method. The Runge and Kutta method showed that by combining the results of two additional Euler steps, the error can be reduced to $\mathcal{O}({h}^{5})$.

These algorithms can be extended to arbitrarily large first-order systems of ODE:

$$\displaystyle{ \begin{array}{l} \frac{dy_{i}} {ds} = f_{i}\left (\varepsilon,\ s,\ y_{1}(s),\ldots,y_{M}(s)\right ),\quad i = 1,\ldots,M, \\ y_{i}(s_{0}) = y_{i,0}.\\ \end{array} }$$

(4.1)

The Runge–Kutta fourth-order method for this problem is given by the following equations:

$$\displaystyle{ \begin{array}{l} s_{n+1} = s_{n} + h, \\ \!\!\!y_{i,n+1} = y_{i,n} + \frac{1} {6}\left (k_{i}^{(1)} + 2k_{ i}^{(2)} + 2k_{ i}^{(3)} + k_{ i}^{(4)}\right ),\\ \end{array} }$$

(4.2)

where h = (s _N − s ₀)∕N is the step, n = 0, …, N

$$\displaystyle\begin{array}{rcl} & & k_{i}^{(1)} = hf_{ i}\left (\varepsilon,\ s_{n},\ y_{1,n},\ldots,y_{M,n}\right ), \\ & & k_{i}^{(2)} = hf_{ i}\left (\varepsilon,\ s_{n} + \frac{1} {2}h,\ y_{1,n} + \frac{1} {2}k_{1}^{(1)},\ldots,y_{ M,n} + \frac{1} {2}k_{M}^{(1)}\right ), \\ & & k_{i}^{(3)} = hf_{ i}\left (\varepsilon,\ s_{n} + \frac{1} {2}h,\ y_{1,n} + \frac{1} {2}k_{1}^{(2)},\ldots,y_{ M,n} + \frac{1} {2}k_{M}^{(2)}\right ), \\ & & k_{i}^{(4)} = hf_{ i}\left (\varepsilon,\ s_{n} + h,\ y_{1,n} + k_{1}^{(3)},\ldots,y_{ M,n} + k_{M}^{(3)}\right ). {}\end{array}$$

(4.3)

The calculations for the interval [s _N − s ₀] are considered complete if

$$\displaystyle\begin{array}{rcl} & & \qquad \quad \max \limits _{i\in [1,M]}\bigg\{\big\vert y_{i,N}^{(h/2)} - y_{ i,N}^{(h)}\big\vert /\max \limits _{ i\in [1,M]}\big(\big\vert y_{i,N}^{(h)}\big\vert,\big\vert y_{ i,N}^{(h/2)}\big\vert \big)\bigg\} <\varepsilon _{ 0}, \\ & & y_{i,N}^{(h)} = y_{ i}(s_{N})\big\vert _{h=(s_{N}-s_{0})/N},\qquad y_{i,N}^{(h/2)} = y_{ i}(s_{N})\big\vert _{h/2=(s_{N}-s_{0})/2N},{}\end{array}$$

(4.4)

where $\varepsilon _{0}$ is the calculation error.

To calculate an annular jet of viscous liquid one of the perturbation theory methods may be used, namely, the method of successive approximation in [8, 12]. The first step consists of calculating the velocity distribution in an ideal liquid film, in a gravitational field: Cauchy’s problem (1.5)–(1.7) for $\varepsilon = 0$. In the next step the velocity distributions and the derivatives dV _τ ∕ds,  dV _θ ∕ds,  dψ∕ds,  dR∕ds, and dx∕ds may be found analytically using the solutions $V _{\tau }^{(0)},\,V _{\theta }^{(0)}$, ψ ⁽⁰⁾, R ⁽⁰⁾, and x ⁽⁰⁾ of the system (1.5) obtained for $\varepsilon \rightarrow 0$. Then, using the already obtained data, the stresses $\sigma _{\tau \tau },\ \sigma _{\tau \theta },\ \sigma _{\theta \theta }$ and derivatives d(σ _{τ τ} ∕V _τ )∕ds, d(σ _{τ θ} ∕V _τ )∕ds can be determined to solve the system (1.6), which should be integrated together with (1.5) for the general case $\varepsilon \neq 0$.

The solution to (4.1) will be found using iteration procedure below:

$$\displaystyle{ \begin{array}{l} dy_{i}^{(0)}/ds = f_{i}\left (0,\ s,\ y_{1}(s),\ldots,y_{M}(s)\right ), \\ dy_{i}^{(1)}/ds = f_{i}\big(\varepsilon,\ s,\ y_{1}^{(0)}(s),\ldots,y_{M}^{(0)}(s)\big), \\ dy_{i}^{(2)}/ds = f_{i}\big(\varepsilon,\ s,\ y_{1}^{(1)}(s),\ldots,y_{M}^{(1)}(s)\big),\\ \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \\ dy_{i}^{(q)}/ds = f_{i}\big(\varepsilon,\ s,\ y_{1}^{(q-1)}(s),\ldots,y_{M}^{(q-1)}(s)\big).\\ \end{array} }$$

Follow the estimation

$$\displaystyle{ \begin{array}{l} \big\|y_{i}^{(q)} - y_{i}^{(q-1)}\big\|_{L_{2}[0,S]} \leq \big\| f_{i}\big(\varepsilon,s,y_{1}^{(q-1)}(s),\ldots,y_{M}^{(q-1)}(s)\big) \\ \quad - f_{i}\big(\varepsilon,s,y_{1}^{(q-2)}(s),\ldots,y_{M}^{(q-2)}(s)\big)\big\|_{L_{2}[0,S]} \\ \ \leq \int _{0}^{S}\left \vert f_{i}\big(\varepsilon,\ s,\ y_{1}^{(q-1)}(s),\ldots,y_{M}^{(q-1)}(s)\big) - f_{i}\big(\varepsilon,\ s,\ y_{1}^{(q-2)}(s),\ldots,y_{M}^{(q-2)}(s)\big)\right \vert ds \\ \ \leq {\left \vert \varepsilon \right \vert }^{q}\left \|f_{i}\right \|_{L_{2}[0,S]} \leq \vert \varepsilon {\vert }^{q}K_{i} \mathop{\longrightarrow }\limits _{q\rightarrow \infty } 0\\ \end{array} }$$

for all functions f _i limited on compact $\left [0,S\right ]$. As a rule, for $\varepsilon << 1$, it is enough to limit of only the first iteration, q = 1. The implementation of this method leads to the following ODE system:

$$\displaystyle{ \begin{array}{l} \frac{dV _{\tau }^{(0)}} {ds} = \frac{V _{\theta }^{(0)}V _{\theta }^{(0)}} {V _{\tau }^{(0)}{R}^{(0)}} \sin {\psi }^{(0)} + \frac{{\mathit{Fr}}^{-1}} {V _{\tau }^{(0)}} \cos {\psi }^{(0)}, \\ \frac{{d\psi }^{(0)}} {ds} = \frac{{\cos \psi }^{(0)}} {V _{\tau }^{(0)}-\,{\mathit{We}}^{-1}{R}^{(0)}} \Big(\frac{V _{\theta }^{(0)}V _{\theta }^{(0)}} {V _{\tau }^{(0)}{R}^{(0)}} -\,{\mathit{We}}^{-1} -{\frac{{\mathit{Fr}}^{-1}} {V _{\tau }^{(0)}} \tan \psi }^{(0)} - \frac{\mathit{Eu}} {\,\mathit{We}} \frac{{R}^{(0)}} {{\cos \psi }^{(0)}} \Big), \\ \frac{dV _{\theta }^{(0)}} {ds} = -\frac{V _{\theta }^{(0)}} {{R}^{(0)}} \sin {\psi }^{(0)}.\\ \end{array} }$$

Calculating the terms in (4.1) and multiplying $\varepsilon ={ \mathit{Re}}^{-1}$ by the second derivations ${d}^{2}V _{\tau }^{(0)}/d{s}^{2}$ and ${d}^{2}V _{\theta }^{(0)}/d{s}^{2}$, one obtains

$$\displaystyle{ \begin{array}{l} {\mathit{Re}}^{-1}\big[ \frac{d} {ds}\big( \frac{\sigma _{\tau \tau }} {V _{\tau }}\big) - \frac{\sigma _{\theta \theta }} {V _{\tau }R}\sin \psi \big] \approx \varepsilon \big[ \frac{d} {ds}\big( \frac{\sigma _{\tau \tau }} {V _{\tau }}\big) - \frac{\sigma _{\theta \theta }} {V _{\tau }R}\sin \psi \big]\big\vert _{V _{\tau }=V _{\tau }^{(0)},V _{\theta }=V _{\theta }^{(0)},\,R={R}^{(0)},\psi ={\psi }^{(0)}} \\ \quad =\varepsilon \frac{4} {V _{\tau }^{(0)}} \left [\frac{{d}^{2}V _{\tau }^{(0)}} {d{s}^{2}} -\frac{dV _{\tau }^{(0)}} {ds} \left ( \frac{1} {V _{\tau }^{(0)}} \frac{dV _{\tau }^{(0)}} {ds} +\frac{1} {2} \frac{{\sin \psi }^{(0)}} {{R}^{(0)}} \right )+ \frac{V _{\tau }^{(0)}} {2{R}^{(0)}} \left ({\cos \psi }^{(0)}\frac{{d\psi }^{(0)}} {ds} -\frac{{3\sin {}^{2}\psi }^{(0)}} {{R}^{(0)}} \right )\right ] \\ {\mathit{Re}}^{-1} \frac{\sigma _{\tau \tau }} {V _{\tau }} \approx \frac{\sigma _{\tau \tau }} {V _{\tau }}{\mathit{Re}}^{-1}\big\vert _{ V _{\tau }=V _{\tau }^{(0)},V _{\theta }=V _{\theta }^{(0)},R={R}^{(0)},\psi {=\psi }^{(0)}} = 2\varepsilon \left (2 \frac{1} {V _{\tau }^{(0)}} \frac{dV _{\tau }^{(0)}} {ds} + \frac{{\sin \psi }^{(0)}} {{R}^{(0)}} \right ), \\ {\mathit{Re}}^{-1} \frac{\sigma _{\theta \theta }} {V _{\tau }R} \approx \frac{\sigma _{\theta \theta }} {V _{\tau }R}{\mathit{Re}}^{-1}\big\vert _{ V _{\tau }=V _{\tau }^{(0)},V _{\theta }=V _{\theta }^{(0)},R={R}^{(0)},\psi {=\psi }^{(0)}} = \frac{2\varepsilon } {R}\left ( \frac{1} {V _{\tau }^{(0)}} \frac{dV _{\tau }^{(0)}} {ds} + \frac{{2\sin \psi }^{(0)}} {{R}^{(0)}} \right ),\\ \end{array} }$$

(4.5)

$$\displaystyle{ \begin{array}{l} {\mathit{Re}}^{-1}\big[ \frac{d} {ds}\big( \frac{\sigma _{\tau \theta }} {V _{\tau }}\big) - \frac{\sigma _{\tau \theta }} {V _{\tau }R}\sin \psi \big]\approx \varepsilon \big[ \frac{d} {ds}\big( \frac{\sigma _{\tau \theta }} {V _{\tau }}\big) - \frac{\sigma _{\tau \theta }} {V _{\tau }R}\sin {\psi }^{(0)}\big]\big\vert _{ V _{\tau }=V _{\tau }^{(0)},V _{\theta }=V _{\theta }^{(0)},R={R}^{(0)},\psi {=\psi }^{(0)}} \\ \quad =\varepsilon \! \left [\!\! \frac{1} {V _{\tau }^{(0)}} \frac{{d}^{2}V _{\theta }^{(0)}} {d{s}^{2}} -\frac{V _{\theta }^{(0)}} {V _{\tau }^{(0)}} \frac{{\cos \psi }^{(0)}} {{R}^{(0)}} \frac{{d\psi }^{(0)}} {ds} -\left ( \frac{1} {V _{\tau }^{(0)}} \frac{dV _{\tau }^{(0)}} {ds} + \frac{{2\sin \psi }^{(0)}} {{R}^{(0)}} \right )\!\!\left ( \frac{1} {V _{\tau }^{(0)}} \frac{dV _{\theta }^{(0)}} {ds} -\frac{V _{\theta }^{(0)}} {V _{\tau }^{(0)}} \frac{{\sin \psi }^{(0)}} {{R}^{(0)}} \!\!\right )\!\!\right ]\\ \end{array} }$$

(4.6)

$$\displaystyle{ \begin{array}{ll} \frac{{d}^{2}V _{\tau }^{(0)}} {d{s}^{2}} & = \frac{d} {ds}\left [ \frac{{\left (V _{\theta }^{(0)}\right )}^{2}} {V _{\tau }^{(0)}{R}^{(0)}} \sin {\psi }^{(0)} + \mathit{Fr}{}^{-1} \frac{{\cos \psi }^{(0)}} {V _{\tau }^{(0)}} \right ] \\ \quad & = \frac{V _{\theta }^{(0)}} {V _{\tau }^{(0)}} \left [ \frac{{\sin \psi }^{(0)}} {{R}^{(0)}} \left (2\frac{dV _{\theta }^{(0)}} {ds} -\frac{V _{\theta }^{(0)}} {V _{\tau }^{(0)}} \frac{dV _{\tau }^{(0)}} {ds} -\frac{V _{\theta }^{(0)}} {{R}^{(0)}} \sin {\psi }^{(0)}\right ) - \frac{{\mathit{Fr}}^{-1}} {V _{\tau }^{(0)}V _{\theta }^{(0)}} \frac{dV _{\tau }^{(0)}} {ds} \right. \\ &\qquad \left.+\left (\frac{V _{\theta }^{(0)}} {{R}^{(0)}} \cos {\psi }^{(0)} -\mathit{Fr}{}^{-1} \frac{{\sin \psi }^{(0)}} {V _{\theta }^{(0)}} \right )\frac{{d\psi }^{(0)}} {ds} \right ], \\ \frac{{d}^{2}V _{\theta }^{(0)}} {d{s}^{2}} & = -\frac{d} {ds}\left [\frac{V _{\theta }^{(0)}} {{R}^{(0)}} \sin {\psi }^{(0)}\right ]\!\! = - \frac{{\sin \psi }^{(0)}} {{R}^{(0)}} \left (\frac{dV _{\theta }^{(0)}} {ds} -\frac{V _{\theta }^{(0)}} {{R}^{(0)}} \sin {\psi }^{(0)}\right )\! -\frac{V _{\theta }^{(0)}} {{R}^{(0)}} \cos {\psi }^{(0)}\frac{{d\psi }^{(0)}} {ds}.\\ \end{array} }$$

(4.7)

Substituting the results (4.5) into the base system (1.5)–(1.6), we obtain finally

$$\displaystyle{ \begin{array}{l} \!\frac{dV _{\tau }} {ds} = F_{1}\left (s,V _{\tau },V _{\theta },\psi,R\right ) +\varepsilon G_{1}\left (s,V _{\tau },V _{\theta },\psi,R\right ), \\ \frac{d\psi } {ds} = \left \{\left [ \frac{V _{\theta }^{2}} {V _{\tau }R} -\,{\mathit{We}}^{-1} -\varepsilon \frac{2} {R}\left (\frac{F_{1}\left (.\right )} {V _{\tau }} + \frac{2\sin \psi } {R}\right )\right ]\cos \psi -\frac{{\mathit{Fr}}^{-1}} {V _{\tau }} \sin \psi - \frac{\mathit{Eu}} {\,\mathit{We}}R\right \} \\ \qquad \quad \times {\left [V _{\tau } -\,{\mathit{We}}^{-1}R - 2\varepsilon \left (2\frac{F_{1}\left (.\right )} {V _{\tau }} + \frac{\sin \psi } {R}\right )\right ]}^{-1} \\ \!\frac{dV _{\theta }} {ds} = F_{2}\left (s,V _{\tau },V _{\theta },\psi,R\right ) +\varepsilon G_{2}\left (s,V _{\tau },V _{\theta },\psi,R\right ), \\ \frac{dR} {ds} =\sin \psi,\qquad \frac{dx} {ds} =\cos \psi,\\ \end{array} }$$

(4.8a)

where

$$\displaystyle{ \begin{array}{l} F_{1}(.)\, = \frac{V _{\theta }^{2}} {V _{\tau }} \frac{1} {R}\sin \psi +{ \mathit{Fr}}^{-1} \frac{\cos \psi } {V _{\tau }},\ F_{2}(.) = -\frac{V _{\theta }} {R} \sin \psi, \\ G_{1}(.) = 4 \frac{V _{\theta }} {V _{\tau }^{2}} \left \{ \frac{\sin \psi } {R}\left (2F_{2}(.) -\frac{V _{\theta }} {V _{\tau }}F_{1}(.) -\frac{V _{\theta }} {R} \sin \psi \right ) -\frac{V _{\tau }} {V _{\theta }}F_{1}(.)\left (\frac{F_{1}(.)} {V _{\tau }} + \frac{1} {2} \frac{\sin \psi } {R}\right )\right. \\ \qquad \qquad -\frac{{\mathit{Fr}}^{-1}} {V _{\tau }} \frac{F_{1}(.)} {V _{\theta }} + \frac{{\cos }^{2}\psi } {V _{\tau }-\,{\mathit{We}}^{-1}R}\left (\frac{V _{\theta }^{2}} {V _{\tau }} \frac{1} {R} -\,{\mathit{We}}^{-1} -{\mathit{Fr}}^{-1} \frac{\tan \psi } {V _{\tau }} - \frac{\mathit{Eu}} {\,\mathit{We}} \frac{R} {\cos \psi } \right ) \\ \qquad \qquad \left.\times \left (\frac{V _{\theta }} {R} -{\mathit{Fr}}^{-1} \frac{\tan \psi } {V _{\theta }} + \frac{1} {2R} \frac{V _{\tau }^{2}} {V _{\theta }} \right ) -\frac{3} {2} \frac{V _{\tau }^{2}} {V _{\theta }} \frac{{\sin }^{2}\psi } {{R}^{2}} \right \}, \\ G_{2}(.) = -\left [2 \frac{V _{\theta }} {V _{\tau }R} \frac{{\cos }^{2}\psi } {V _{\tau }-\,{\mathit{We}}^{-1}R}\left (\frac{V _{\theta }^{2}} {V _{\tau }} \frac{1} {R} -\,{\mathit{We}}^{-1} -{\mathit{Fr}}^{-1} \frac{\tan \psi } {V _{\tau }} - \frac{\mathit{Eu}} {\,\mathit{We}} \frac{R} {\cos \psi } \right )\right. \\ \qquad \qquad \left.+ \frac{1} {V _{\tau }} \frac{\sin \psi } {R}\left (F_{2}(.) -\frac{V _{\theta }} {R} \sin \psi \right ) + \left (\frac{F_{1}(.)} {V _{\tau }} + 2 \frac{\sin \psi } {R}\right )\left (\frac{F_{2}(.)} {V _{\tau }} -\frac{V _{\theta }} {V _{\tau }} \frac{\sin \psi } {R}\right )\right ].\\ \end{array} }$$

(4.8b)

Solving the system (4.8a,b) with initial conditions (1.7) numerically using Runge–Kutta algorithm (4.2)–(4.4), one obtains a new velocity distribution V _τ ,  V _θ and the liquid film shape R(x) with allowance for viscosity.

For the case without rotation, when V _θ  |  _s = 0 = 0, the system (4.8a,b) is sufficiently simplified:

$$\displaystyle{ \begin{array}{l} \!\!\!\!\frac{dV _{\tau }} {ds} = F_{1}\left (s,V _{\tau },\psi,R\right ) +\varepsilon G_{1}\left (s,V _{\tau },\psi,R\right ), \\ \frac{d\psi } {ds} = -\left \{\left [\,{\mathit{We}}^{-1} +\varepsilon \frac{2} {R}\left (\frac{F_{1}\left (.\right )} {V _{\tau }} + \frac{2\sin \psi } {R}\right )\right ]\cos \psi +{ \mathit{Fr}}^{-1} \frac{\sin \psi } {V _{\tau }} + \frac{\mathit{Eu}} {\,\mathit{We}}R\right \} \\ \;\;\qquad \times {\left [V _{\tau } -\,{\mathit{We}}^{-1}R - 2\varepsilon \left (2\frac{F_{1}(.)} {V _{\tau }} + \frac{\sin \psi } {R}\right )\right ]}^{-1}, \\ \frac{dR} {ds} =\sin \psi,\quad \frac{dx} {ds} =\cos \psi,\\ \end{array} }$$

where

$$\displaystyle{ \begin{array}{l} F_{1}(.) = \frac{{\mathit{Fr}}^{-1}} {V _{\tau }} \cos \psi, \\ G_{1}(.) = -4\left \{\frac{F_{1}(.)} {V _{\tau }} \left (\frac{F_{1}(.)} {V _{\tau }} + \frac{1} {2} \frac{\sin \psi } {R}\right ) + \frac{{\mathit{Fr}}^{-1}} {V _{\tau }} \frac{F_{1}(.)} {V _{\tau }^{2}} + \frac{3} {2} \frac{{\sin }^{2}\psi } {{R}^{2}} \right. \\ \ \ \qquad \quad \left.+ \frac{{\cos }^{2}\psi } {V _{\tau }-\,{\mathit{We}}^{-1}R}\left ({\mathit{We}}^{-1} +{ \mathit{Fr}}^{-1} \frac{\tan \psi } {V _{\tau }} + \frac{\mathit{Eu}} {\,\mathit{We}} \frac{R} {\cos \psi } \right )\left ( \frac{1} {2R} -{\mathit{Fr}}^{-1} \frac{\tan \psi } {V _{\tau }^{2}} \right )\right \}. \end{array} }$$

The numerical simulations were provided using MAPLE. The main results are present in Fig. 3 for the case with p _o  = p _i  (Eu = 0), We = 13. 74, Fr = 5. 01 × 10⁴ for two different Reynolds numbers, Re = 2,000 (Fig. 3a) and Re = 100 (Fig. 3b).

Fig. 3

Shape of the liquid film for the conditions: We = 13. 74, Fr = 5. 01 × 10⁴; Re = 2, 000 case (a), Re = 100 case (b). Boundary conditions: $x_{\vert s=0} = 0,\,R_{\vert s=0} = 1,\,V _{{\tau }_{\vert s=0}} = 1,\,\psi _{\vert s=0} = 0,\,V _{{\theta }_{\vert s=0}} = 0.001,\,0.01$, 0. 1, 0. 5, 1. 0; the lines correspond to $\left.V _{\theta }\right \vert _{s=0} = (\mathit{a}) \rightarrow 0,\ (\mathit{b}) \rightarrow 0.01,\ (\mathit{c}) \rightarrow 0.1,\ (\mathit{d}) \rightarrow 0.5,\ (\mathit{e}) \rightarrow 1.0$

To show that the values $R\left (x\right )$ are not zero for x > 5 in Fig. 3 (line (a)) we presented their numerical values (see Table 1). It can be seen the value $R\left (x\right ) > 1{0}^{-3}$ even for x > 12.

To show agreement between results obtained from asymptotic analysis to numerical ones, let us consider the ideal liquid film ($\varepsilon = 0)$ for the case $\mathit{We} = 7.14,\ \mathit{Fr} = \infty,\ \left.V _{\tau }\right \vert _{s=0} = 1.0$, $\left.\psi \right \vert _{s=0} = 0$, $\left.V _{\theta }\right \vert _{s=0} = 1.2\,{\mathit{We}}^{-1/2} = 0.44$ on the interval $x \in \left [0,25\right ]$. This case corresponds to situation when the middle surface of the film has to oscillate in a stable flow according to (2.15) obtained in Sect. 2. The results are shown in Fig. 4a.

It can be seen that for the case with ideal liquid we obtain undamped oscillations (Fig. 4a, red line) while accounting for viscosity; $\varepsilon ={ \mathit{Re}}^{-1} = 0.01$ leads to natural damping.

Table 1 Numerical form of the shape R(x)

Let us compare our modeling with numerical results [3] (Fig. 4b) with experiment [9] provided for an annular liquid jet with parameters Re = 100,  We = 110,  Fr = ∞,  Eu = 0 and the initial angular velocities $\left.V _{\theta }\right \vert _{s=0} = 2.0,\ 4.0$. Comparison shows good agreement of our model (solid lines) with experimental data (dash lines).

Our next step is to compare lines a and b with numerical lines a∗ and b∗ obtained for the oil annular rotational jet (for results, see Fig. 5a) with the following parameters and properties: flow rate $\dot{m} = 0.01777\,\mbox{ kg/s}$, initial geometry sizes R ₀ = 0. 002 m, δ ₀ = 1. 524 ⋅ 10⁻⁴ m, fluid density ρ = 765 kg/m³, viscosity μ = 9.2 ⋅ 10⁻⁴ kg/m ⋅ s, and surface tension σ _∗ = 0. 025 N/m [1], for the case when the inner pressure differs from outer one, $\Delta p\neq 0$, and pressure difference between inner and outer pressures is $\Delta p = 21$, 138 kPa. These conditions correspond to the Euler numbers 2. 6 ⋅ 10³,  1. 7 ⋅ 10⁴; We = 347.0, Fr =7586, and Re = 20,000 correspond to the conditions above.

Fig. 4

(a) Shape of the liquid film for the conditions: $\mathit{We} = 7.143,\ \mathit{Fr} = \infty,\ \varepsilon = 0,\ 0.01$; boundary conditions: $\left.x\right \vert _{s=0} = 0,\ \left.R\right \vert _{s=0} = 1,\ \left.V _{\tau }\right \vert _{s=0} = 1,\ \left.V _{\theta }\right \vert _{s=0} = 1.2\,{\mathit{We}}^{-1/2} = 0.44,\,\left.\ \psi \right \vert _{s=0} = 0$; line a corresponds to $\varepsilon ={ \mathit{Re}}^{-1} = 0$, line b—$\varepsilon ={ \mathit{Re}}^{-1} = 0.01$. (b) Shape of the liquid film for the conditions: We = 110,  Fr = ∞,  Re = 100,  Eu = 0, boundary conditions: $\left.x\right \vert _{s=0} = 0,\ \left.R\right \vert _{s=0} = 1,\ \left.V _{\tau }\right \vert _{s=0} = 1,\ \left.V _{\theta }\right \vert _{s=0} = 2.0,4.0,\left.\psi \right \vert _{s=0} = 0$; the lines a and b correspond to $\left.V _{\theta }\right \vert _{s=0} = 2.0$ and 4. 0, accordingly; dash lines for 0 ≤ x ≤ 400—experiment [3, 9]

Fig. 5

(a) Longitudinal velocity V _τ evolution along the axial coordinate x for the conditions: We = 347. 0,  Fr = 7586, Re = 20, 000,Eu = 2. 6 ⋅ 10³,  1. 7 ⋅ 10⁴; boundary conditions: $\left.x\right \vert _{s=0} = 0,\left.\ R\right \vert _{s=0} = 1,\left.\ V _{\tau }\right \vert _{s=0} = 1.5$, $\left.V _{\theta }\right \vert _{s=0} = 0.5,\ \left.\psi \right \vert _{s=0} = 0$; a and $a {\ast}\ \Delta p = 21\text{kPa}$, b and $b {\ast}\ \Delta p = 138\text{kPa}$. (b) Longitudinal velocity on the axial coordinate x for the boundary conditions: $\left.x\right \vert _{s=0} = 0,\ \left.R\right \vert _{s=0} = 1,\ \left.V _{\tau }\right \vert _{s=0} = 1,\ \left.V _{\theta }\right \vert _{s=0} = 0,\ \left.\psi \right \vert _{s=0} = 0$; (a) We = 2. 2,  Fr = 1. 3, V _in = 0. 8m/s, Eu = 0. 00868; (b) We = 8. 8,  Fr = 5. 2,  V _in = 1. 6m/s, Eu = 0. 00868

Comparing our simulations with experiment [10] for a water annular jet without rotation, the nozzle diameter D ₀ = 1. 0 mm and the pressure drop $\Delta p = 2.4\,\text{Pa}$ show good agreement for the two variants of inlet velocities, V _in = 0. 8 and 1.6 m/s (Fig. 5b). Solid lines correspond to our calculations, and symbols ■ and • to experimental data for V _in = 0. 8, 1. 6 m/s, respectively.

6 Analysis of Nonlinear Instability in Meridional Cross Section

Instabilities leading to oscillations in some particular properties of a system are intimately related to pattern formation. Nontrivial patterns form spontaneously as a result of the occurrence and propagation of the fronts of instability. These spontaneous patterns can be turned into functional structures at the corresponding length scale when the pattern-forming processes are properly designed and controlled. In this work, we propose a scenario for mass transfer instability in one-dimensional flow of a one-component fluid near its discontinuous liquid–gas phase transition. Instability leading to density oscillations occurs when the system fails to support steady-state flow due to the absence of mechanically stable uniform state as a consequence of a discontinuous transition. The main hydrodynamic instabilities are the Rayleigh–Taylor and Kelvin–Helmholtz [6, 8]. The instability approaches may be conditionally divided into two parts, linear and nonlinear. The linear approach is well known and simple for study, but it shows only which oscillating modes are stable and which are unstable. Nonlinear approach shows the singularities of the surface between jet and surrounding media that appear as a result of the spatial instability development. In this paragraph we will consider nonlinear approach to study instability in meridional cross section of the jet.

The hydrodynamic instability has 3D character, but for qualitative analysis we limit our research to study the Rayleigh–Taylor instability in meridional plane R, θ assuming the flow to be cylindrically axisymmetric. Then the motion equation may be written as [7]

$$\displaystyle{ \rho \frac{{\partial }^{2}\mathbf{r}} {\partial {t}^{2}} = \Delta p(r,\phi,t)\left (\mathbf{e}_{z} \times \frac{\partial \mathbf{r}} {\partial \phi } \right ), }$$

(5.1)

where ϕ is Lagrange coordinate, i.e., dm = ρ d ϕ, and Δ p = p _i − p _o is assumed to be constant. Substituting $Z = x + iy = r\exp \left (i\phi \right )$ transforms (5.1) to the equation in polar coordinates

$$\displaystyle{ \rho \frac{{\partial }^{2}Z} {\partial {t}^{2}} = i\Delta p\frac{\partial Z} {\partial \phi }. }$$

(5.2)

Fig. 6

(a) k-petal rose: Z(ϕ, t) = exp(iϕ) −λ k ⁻¹exp(ikϕ) with $k = \pm 8,\ \left \vert \lambda \right \vert < 1$. (b) Self-intersecting k-petal rose: Z(ϕ, t) = exp(iϕ) −λ k ⁻¹exp(ikϕ) with $k = \pm 8,\ \left \vert \lambda \right \vert = 1$

Assuming that at the nozzle exit cross section the cylindrical film rotates with angular velocity $\Omega = V _{\theta,0}/R_{0}$ and has zero radial velocity, the initial conditions are given as follows:

$$\displaystyle{ Z\left (\phi,0\right ) =\exp \left (i\phi \right ) - \frac{\lambda _{0}} {k}\exp \left (ik\phi \right ),\qquad \frac{\partial Z\left (\phi,0\right )} {\partial t} = i\Omega \text{Z}\left (\phi,0\right ), }$$

(5.3)

where $\left \vert \lambda _{0}\right \vert < 1$ and k is a wave mode. Note that the second initial condition is sufficiently different from the similar one in [6]. Let us find the solution to the problems (5.2) and (5.3) in the form (Fig. 6a)

$$\displaystyle{ Z(\phi,t) = R(t)\left [\exp (i\phi ) -\lambda (t){k}^{-1}\exp (ik\phi )\right ]. }$$

(5.4)

Note that at $\left \vert \lambda (t)\right \vert \geq 1$ the curve Z(ϕ, τ) becomes self-intersecting (k-petal rose). Fig. 6b illustrates k-petal rose (for λ = 1). It would appear natural to assume that the film lives up to an instant of time t _∗ such that $\left \vert \lambda \left (t_{{\ast}}\right )\right \vert = 1$. Substituting (5.4) into (5.2) gives the system

$$\displaystyle{ \frac{{d}^{2}\lambda } {{d\tau }^{2}} + \frac{2} {R} \frac{dR} {d\tau } \frac{d\lambda } {d\tau } = a\lambda (\tau )(1 - k),\qquad \frac{{d}^{2}R} {{d\tau }^{2}} = -aR(t),\qquad a = \frac{1} {2\pi }\mathit{Eu}/\,\mathit{We} }$$

(5.5)

with initial conditions

$$\displaystyle\begin{array}{rcl} R(0)& =& 1,\quad \frac{dR} {d\tau } \big\vert _{\tau =0} = V _{\theta }\big\vert _{\tau =0} = V _{\Omega },\qquad \lambda (0) =\lambda _{0},\quad \frac{d\lambda } {d\tau }\big\vert _{\tau =0} = 0.{}\end{array}$$

(5.6)

Here τ = t∕t ₀ and $t_{0} = R_{0}/V _{\tau 0}$. Obviously, the system (5.5) splits onto two equations. The second one with its boundary conditions (5.6) accepts analytical solution

$$\displaystyle{ R(\tau ) = \left \{\begin{array}{*{20}c} \cos \sqrt{a}\tau + \frac{V _{\Omega }} {\sqrt{a}} \sin \sqrt{a}\tau, & \Delta p > 0 \\ V _{\Omega }\tau + 1, & \Delta p = 0 \\ \frac{1} {2}\big[\big(1 + (V _{\Omega }/\sqrt{\left \vert a\right \vert })\big)\exp \big(\sqrt{\left \vert a\right \vert }\tau \big) +\big (1 - (V _{\Omega }/\sqrt{\left \vert a\right \vert })\big)\exp \big(-\sqrt{\left \vert a\right \vert }\tau \big)\big],&\Delta p < 0.\\ \end{array} \right. }$$

Substituting (5.4) into the first equation of the system (5.5) gives

$$\displaystyle{ \begin{array}{l} \frac{{d}^{2}\lambda } {{d\tau }^{2}} + F(\tau )\frac{d\lambda } {d\tau } = \text{sign}\left (\Delta p\right )\vert a\vert (1 - k)\lambda (\tau ), \\ F(\tau ) = 2\sqrt{\vert a\vert }\times \left \{\begin{array}{*{20}c} \frac{b-\tan \sqrt{a}\,\tau } {1+b\tan \sqrt{a}\,\tau }, &\Delta p > 0 \\ \frac{b+\tanh \sqrt{\vert a\vert }\,\tau } {1+b\tanh \sqrt{\vert a\vert }\,\tau },&\Delta p < 0, \\ \end{array} \right. \\ \lambda (0) =\lambda _{0},\qquad \frac{d\lambda } {d\tau }\big\vert _{\tau =0} = 0,\\ \end{array} }$$

(5.7)

where $b = V _{\Omega }/\sqrt{\left \vert a\right \vert } = V _{\Omega }\sqrt{2\pi \,\mathit{We } /\mathit{Eu}}$. In the case when pressure drop is absent (5.7) has a trivial solution, λ = λ ₀. In general case the problem (5.7) accepts analytical solution:

$$\displaystyle{ \lambda (\tau ) = \frac{\lambda _{0}} {\sqrt{\vert k\vert }}\left \{\begin{array}{*{20}c} \frac{1} {\cos \sqrt{a}\,\tau +b\sin \sqrt{a}\,\tau }\left \{\begin{array}{*{20}c} \cos \sqrt{ak}\,\tau \big(\sqrt{k} + b\tan \sqrt{ak}\,\tau \big), &k > 0 \\ \cosh \sqrt{a\vert k\vert }\,\tau \big(\sqrt{\vert k\vert } + b\tanh \sqrt{a\vert k\vert }\,\tau \big),&k < 0\\ \end{array} \right. &\Delta p > 0 \\ \sqrt{\vert k\vert }, &\Delta p = 0 \\ \frac{1} {\cosh \sqrt{\vert a\vert }\,\tau +b\sinh \sqrt{\vert a\vert }\,\tau }\left \{\begin{array}{*{20}c} \cosh \sqrt{\vert ak \vert }\,\tau \big(\sqrt{\vert k\vert } + b\tanh \sqrt{\vert a\vert k}\,\tau \big),&k > 0 \\ \cos \sqrt{\vert ak \vert }\,\tau \big(\sqrt{\vert k\vert } + b\tan \sqrt{\vert ak \vert }\,\tau \big),&k < 0\\ \end{array} \right.&\Delta p < 0 \\ \end{array} \right. }$$

(5.8)

For nonrotating jet, $V _{\Omega } = 0$, the solution (5.8) is transformed to the simple form

$$\displaystyle{ \lambda (\tau ) =\lambda _{0}\left \{\begin{array}{*{20}c} \begin{array}{*{20}c} \cos \sqrt{ak}\,\tau /\cos \sqrt{a}\,\tau, &k > 0 \\ \cosh \sqrt{a\vert k\vert }\tau /\cos \sqrt{a}\,\tau,&k < 0\\ \end{array} &\Delta p > 0, \\ 1, &\Delta p = 0, \\ \begin{array}{*{20}c} \cosh \sqrt{\vert a\vert k}\,\tau /\cosh \sqrt{\vert a\vert }\,\tau,&k > 0 \\ \cos \sqrt{\vert ak \vert }\,\tau /\cosh \sqrt{\vert a\vert }\,\tau,&k < 0\\ \end{array} &\Delta p < 0. \\ \end{array} \right. }$$

(5.9)

Let us study the modes k = ±2, ±3, ±4, ±5, ±6, , … in a wide range temporary interval, τ > 100, for low initial value of parameter λ ₀,  λ ₀ = 0. 05. Figures 7–10 show dependence λ on dimensionless time τ; the curves correspond to the wave numbers k = ±3, ±4, ±6, ±8, ±16.

Fig. 7

Dependencies λ(τ) for a = 0. 125 and b = 0. 8; modes k = 3,  4,  6,  8,  16

Fig. 8

Function λ(τ) for a = 0. 125 and b = 0. 8; modes k = −3, − 4, − 6, − 8, − 16

Fig. 9

Function λ(τ) for a = −0. 04 and b = 25. 0; modes k = 3,  4,  6,  8,  16

Fig. 10

Function λ(τ) for a = −0. 04 and b = 25. 0; modes k = −3, − 4, − 6, − 8, − 16

It can be seen that for positive value a, which corresponds to positive pressure drop, $\Delta p > 0$ and for wide range of parameter b = 0. 8 ÷ 25, all positive modes, k > 1, are unstable (Fig. 7). This result can be obtained analytically. In fact, see (5.8)

$$\displaystyle{\lambda (\tau ) =\lambda _{0}\frac{1 + (b/\sqrt{k})\tan \sqrt{ak}\,\tau } {1 + b\tan \sqrt{a}\,\tau } \cdot \frac{\cos \sqrt{ak}\,\tau } {\cos \sqrt{a}\,\tau },\quad \Delta p > 0,\quad k > 0.}$$

Thus, λ(τ) → ∞, when $\tau =\pi n/2\sqrt{ak},\ n = 1,\ 2,\ldots,$ i.e., we obtain periodic singular unstable points that are consistent with the results shown in Fig. 7.

All modes with negative k are also unstable (Fig. 8). Really,

$$\displaystyle{\lambda (\tau ) =\lambda _{0}\frac{1 + (b/\sqrt{\vert k\vert })\tanh \sqrt{a\vert k\vert }\,\tau } {1 + b\tan \sqrt{a}\,\tau } \cdot \frac{\cosh \sqrt{a\vert k\vert }\,\tau } {\cos \sqrt{a}\,\tau },\quad \Delta p > 0,\quad k < 0;}$$

hence λ(τ) → ∞, when $\tau =\pi n/2\sqrt{ak},\ n = 1,\ 2,\ldots,$ and at τ → ∞, i.e., we obtain periodic singular unstable points and asymptotic instability. For negative pressure drop corresponding to negative parameter a, all negative modes decreased (Fig. 10), while all positive modes increased (Fig. 9). The results shown in Figs. 9 and 10 may be obtained analytically. Indeed, from (5.8), we have

$$\displaystyle{\lambda (\tau ) =\lambda _{0}\frac{1 + (b/\sqrt{\vert k\vert })\tanh \sqrt{\vert a\vert k}\,\tau } {1 + b\tanh \sqrt{\vert a\vert }\,\tau } \cdot \frac{\cosh \sqrt{\vert ak \vert }\,\tau } {\cosh \sqrt{\vert a\vert }\,\tau },\quad \Delta p < 0,\quad k > 0.}$$

Hence, λ(τ) → ∞, at τ → ∞, for all k < 0, when $\Delta p > 0$, for all k > 0; and for all k > 1, when $\Delta p < 0$, i.e., there is asymptotic instability that is consistent with Figs. 8 and 9. For negative pressure drop, $\Delta p < 0$, one obtains λ(τ) → 0, at τ → ∞, for all negative modes, k < 0, i.e., there is asymptotic stability (compare with Fig. 10). The lines λ(τ) are gathering with increasing | a | as it plays a role of dimensionless frequency in (5.8) and (5.9). In the case of nonrotating jet, when parameter b = 0, and at positive pressure drop (a > 0), both the positive and negative modes become unstable (Figs. 11 and 12) by comparison with the rotational jet (Fig. 7).

Fig. 11

Function λ(τ) for a = 0. 04 and b = 0; modes k = 3,  4,  6,  8,  16

Fig. 12

Function λ(τ) for a = 0. 04 and b = 0; modes k = −3, − 4, − 6, − 8, − 16

For negative pressure drop, all positive modes are unstable (Fig. 9), and negative modes are stable (similar to Fig. 10, i.e., in this case rotation does depend on the jet stability). The rotating velocity affects jet stability so that only two of considered positive modes, k = 4 and 16, become stable. The curves in Figs. 7, 8, 11, and 12 are periodic, so their behavior is shown in the range of one–two periods.

7 Conclusion

The equations that described the flow of rotating annular jets of viscous liquid in an undisturbed ideal medium are obtained and analyzed. The effect of surface tension gravity forces and inner–outer pressure difference on jet behavior was considered. Asymptotic analysis for low viscosity value (high Reynolds numbers) was carried out. It is shown that energy transfer from the rotational to the longitudinal motion takes place. The problem of a laminar jet flow with pressure difference between outer and inner ambient area was formulated additionally.

It is shown that equations which describe this phenomenon can be reduced to Cauchy’s problem for the system of ODE. This equation set was solved by the method of successive approximation. The solution results are in good agreement with test.

Nonlinear analysis of instability shows that the film instability in meridional cross section is developed due to pressure difference. At positive pressure inner–outer difference, $\Delta p > 0$, two positive modes, k = 4,  and16 are stable while all negative modes, k < 0, are unstable. In the case $\Delta p < 0$ all negative modes are stable and all positive modes are unstable. These instabilities in meridional cross section developed due to pressure drop cannot be stabilized by rotation; only two modes, k = 14 and 16, become stable due to rotation.

8 Appendix

In the case of $\varepsilon \equiv {\mathit{Re}}^{-1} = \text{0, Eu} = 0,\ \mathit{Fr} \rightarrow \infty$ the problem (1.5)–(1.7) leads to the system

$$\displaystyle{ \begin{array}{l} \frac{dV _{\tau }} {ds} = \frac{V _{\theta }^{2}} {V _{\tau }R}\sin \psi,\quad \frac{dV _{\theta }} {ds} = -\frac{V _{\theta }} {R} \sin \psi, \\ \frac{d\psi } {ds} = \frac{\cos \psi } {R} \cdot \frac{V _{\theta }^{2}/V _{\tau }-\,{\mathit{We}}^{-1}R} {V _{\tau }-\,{\mathit{We}}^{-1}R},\quad \frac{dR} {ds} =\sin \psi,\quad \frac{dx} {ds} =\cos \psi \\ \end{array} }$$

(7.1a)

with the boundary conditions

$$\displaystyle{ \left.x\right \vert _{s=0} = 0,\quad \left.R\right \vert _{s=0} = 1,\quad \left.V _{\tau }\right \vert _{s=0} = 1,\quad \left.V _{\theta }\right \vert _{s=0} = V _{\Omega },\quad \left.\psi \right \vert _{s=0} =\psi _{0}. }$$

(7.1b)

Substituting the fourth equation into the first and the second ones gives

$$\displaystyle\begin{array}{rcl} & & V _{\tau }\frac{dV _{\tau }} {ds} = \frac{V _{\theta }^{2}} {R} \frac{dR} {ds},\ \ \frac{1} {V _{\theta }} \frac{dV _{\theta }} {ds} = -\frac{1} {R} \frac{dR} {ds},\ \ \frac{d\psi } {ds} {}\\ & & \qquad \quad = \frac{\cos \psi } {R} \cdot \frac{V _{\theta }^{2}/V _{\tau }-{\mathit{We}}^{-1}R} {V _{\tau } -{\mathit{We}}^{-1}R},\ \ \frac{dR} {ds} =\sin \psi,\quad \frac{dx} {ds} =\cos \psi. {}\\ & & {}\\ \end{array}$$

Hence

$$\displaystyle\begin{array}{rcl} & & V _{\tau } = \sqrt{C_{1 } - {C}^{2 } /(2\,{R}^{4 } )},\ \ V _{\theta } = C/R,\ \ \frac{d\psi } {ds} {}\\ & & \quad = \frac{\cos \psi } {R} \cdot \frac{V _{\theta }^{2}/V _{\tau }-{\mathit{We}}^{-1}R} {V _{\tau } -{\mathit{We}}^{-1}R},\ \ \frac{dR} {ds} =\sin \psi,\quad \frac{dx} {ds} =\cos \psi. {}\\ \end{array}$$

Using boundary conditions one obtains

$$\displaystyle{ \begin{array}{l} V _{\tau } = \sqrt{\frac{1} {2}V _{\Omega }^{2}\left (1 - {R}^{-4}\right ) + 1},\quad V _{\theta } = V _{\Omega }/R, \\ \! \frac{d\psi } {ds} = \frac{\cos \psi } {R} \cdot \frac{\left (V _{\Omega }^{2}/{R}^{2}\right )/\left [\frac{1} {2} V _{\Omega }^{2}\left (1-{R}^{-4}\right )+1\right ]-\,{\mathit{We}}^{-1}R} {\frac{1} {2} V _{\Omega }^{2}\left (1-{R}^{-4}\right )+1-\,{\mathit{We}}^{-1}R},\quad \frac{dR} {ds} =\sin \psi,\quad \frac{dx} {ds} =\cos \psi.\\ \end{array} }$$

(7.2)

Proposition 1.

When R = const, ψ = const, V _τ = const, and V _θ = const are the solution to (7.2), (7.1b) it is necessary and sufficient to have the boundary values: $\psi _{0} = 0,\ V _{\Omega } ={ \mathit{We}}^{-1/2}$ .

Proof.

• (1) Necessity. If R = const,  ψ = const, then follow the initial conditions (7.1b) R ≡ 1, ψ ≡ 0, and so the system (7.2) has a simple view:

  $$\displaystyle{\begin{array}{l} R = \text{const} = 1,\quad \psi = \text{const} = 0,\quad V _{\tau } = \text{const} = 1,\quad V _{\theta } = \text{const} = V _{\Omega }, \\ \quad \frac{d\psi } {ds} = -\cos \psi \frac{V _{\Omega }^{2}-\,{\mathit{We}}^{-1}} {1-\,{\mathit{We}}^{-1}} = 0.\\ \end{array} }$$

  The result $V _{\Omega } =\,{ \mathit{We}}^{-1/2}$ proves the necessity.

• (2) Sufficiency. Let $V _{\Omega }$ and ψ ₀ be equal to $V _{\Omega } =\,{ \mathit{We}}^{-1/2},\ \psi _{0} = 0$, and we assume that R ≠ const, V _τ ≠ const, V _θ ≠ const, and ψ ≠ const are the solution to (7.2) and (7.1a,b). Then the constant functions R = 1,  ψ = 0,  V _τ  = 1, and V _θ  = We ^−1∕2 also satisfy the problem as it was proven in the previous point 1. Hence, because of the uniqueness theorem for Cauchy’s problem, only the single solution, namely, $R \equiv 1,\ \psi \equiv 0,\ V _{\tau } \equiv 1,\ V _{\theta } \equiv \,{\mathit{We}}^{-1/2}$, satisfies to (7.2) and (7.1a,b). □