Keywords

13.1 Introduction

Simulating the nonlinear behavior of structures demands a lot of computational effort and therefore developing efficient simulation tools are necessary. Researchers in different fields that normally involve much computation, such as system identification and system reliability, are increasingly interested in nonlinear systems which has spurred in the attempts to develop fast nonlinear simulation methods [1–4].

Nonlinearity in structures can be characterized as being either local or global. Locally nonlinear structures are structures that are mainly linear but have one or more locally nonlinear devices/properties that make the structural behavior nonlinear. Local nonlinearity in mechanical structures often stems from nonlinear structural joints and can make its response highly nonlinear. There are two difficulties in simulating a nonlinear structure, the first one is to make accurate predictions/ simulations of nonlinearity effects in a structure’s response and the next one is the efficiency in simulation in order to simulate the structural behavior fast enough for convenience.

To speed up the simulation of nonlinear structures, several methods have been proposed. Some methods are based on the model reduction of nonlinear structures [5, 6], others are focused on the integration part to make it faster and more stable [1, 2] while others deal with nonlinear elements based on remodeling and piecewise linearization [7].

Avitabile and O’Callahan [8] presented three efficient techniques to treat the nonlinear connection between linear parts. They called them the Equivalent Reduced Model Technique (ERMT), the Modal Modification Response Technique (MMRT), and the Component Element Method(CEM). In MMRT, the coefficient matrices governing the structural response should iteratively be updated using structural dynamics modification [7] in a process done in modal space, then intermediate result should be returned to physical space to check for possible change in linear response. Marinone et al. [3] applied MMRT to three different cases and it was shown that the main efficiency gain was obtained by doing model selection of the systems. In ERMT, the well-known SEREP [9] method was used to reduce the linear system before discrete nonlinear connections were assembled to the system. Thibault et al. [10] applied ERMT and performed case studies.

To tackle the first issue in nonlinear structural simulation, several methods have been proposed in the literature. A comparative study on available methods for obtaining dynamic response of a system with local nonlinearity was presented by Marinone et al. [3].

One of the well-established methods to consider the effect of structural system nonlinearity is the pseudo-force method [11]. In this method the nonlinearity is considered as nonlinear external forces. Felippa and Park [12] used this method to treat the nonlinearity in nonlinear structural dynamics. They implemented the method on first-order system and used the Linear Multistep Method to discretize the equations, i.e. the whole response history of the system was used to find the response of the system in the next iteration. To reduce the required time for finding the response of the system in the next iteration Brusa and Nigro [13] presented a one-step method for discretizing a first-order system. They applied the method on linear systems only. Feng-Bao et al. [14] presented an iterative pseudo-force method for second order systems to treat the non-proportional damping in the structures. They also proved the convergence of the method.

The state-space formulation, see (13.6), is the most common first-order representation of linear systems. To find the system response, integration can be done using numerical integration schemes like the one used by the Runge–Kutta method or other time-stepping schemes based on triangular hold interpolation of the loading [15].

In this paper, we propose a method to efficiently treat localized nonlinearity in a structure. The system is separated by a linearized part and a nonlinear part. The non-linear part is considered as external pseudo forces that act on the linearized system. The response of the system is obtained by iterations. Since the method is presented in linear state-space form, all linear manipulation like similarity transformations and state-space model reduction can easily be exploited. To do integration, time-stepping schemes like the triangular hold interpolation can be used to the advantage. We demonstrate the efficiency, stability and accuracy of the method in comparison with MMRT and Runge–Kutta in numerical examples.

13.2 Theory

The method can be regarded as an iterative pseudo force method applied on first order system that was discretized using linear single step method. We call the method the Pseudo Force in State Space (PFSS) method. To do integration, the triangular hold interpolation is used.

The governing second-order equation of motion for a mechanical structure is

$$ \boldsymbol{M}\ddot{\boldsymbol{q}}+{\boldsymbol{C}}_{\mathrm{L}}\dot{\boldsymbol{q}}+{\boldsymbol{C}}_{\mathrm{NL}}\left(\boldsymbol{q},\dot{\boldsymbol{q}}\right)+{\boldsymbol{K}}_{\mathrm{L}}\boldsymbol{q}+{\boldsymbol{K}}_{\mathrm{NL}}\left(\boldsymbol{q}\right)=\boldsymbol{f}(t) $$
(13.1)

in which M, C and K L are the mass, damping and stiffness of a structure respectively. Subscript L stands for linearized part of the matrices and NL is for the state-dependent nonlinear part. f is the force vector.

Without approximation all nonlinearity can be moved to the RHS side of the equation and to be treated like external force caused be nonlinearities as

$$ {\boldsymbol{M}}_{\mathrm{L}}\ddot{\boldsymbol{q}}+{\boldsymbol{C}}_{\mathrm{L}}\dot{\boldsymbol{q}}+{\boldsymbol{K}}_{\mathrm{L}}\boldsymbol{q}=\boldsymbol{f}+{\boldsymbol{f}}_{\mathrm{NL}} $$
(13.2)

Here,

$$ {\boldsymbol{f}}_{\mathrm{NL}}=-{\boldsymbol{C}}_{\mathrm{NL}}\left(\boldsymbol{q},\dot{\boldsymbol{q}}\right)-{\boldsymbol{K}}_{\mathrm{NL}}\left(\boldsymbol{q}\right) $$
(13.3)

Equation (13.2) can be transformed to a first-order system of equations by introducing the state vector x as

$$ {\boldsymbol{A}}_1\dot{\boldsymbol{x}}+{\boldsymbol{B}}_{\boldsymbol{1}}\boldsymbol{x}=\boldsymbol{u} $$
(13.4)

in which the state vector x and coefficient matrices are

$$ \begin{array}{l}\boldsymbol{x}=\left[\begin{array}{c}\hfill \boldsymbol{q}\hfill \\ {}\hfill \dot{\boldsymbol{q}}\hfill \end{array}\right],\kern0.72em {\boldsymbol{A}}_1=\left[\begin{array}{l@{\quad}l}\mathbf{0}& {\boldsymbol{M}}_{\mathrm{L}}\\ \boldsymbol{I} & \mathbf{0}\end{array}\right],\\ {\boldsymbol{B}}_1=\left[\begin{array}{l@{\quad}l}{\boldsymbol{C}}_{\mathrm{L}} & {\boldsymbol{K}}_{\mathbf{L}}\\ \mathbf{0} & -\boldsymbol{I}\end{array}\right],\kern0.72em \boldsymbol{u}=\left\{\begin{array}{c}\hfill \boldsymbol{I}\hfill \\ {}\hfill \mathbf{0}\hfill \end{array}\right\}\left(\boldsymbol{f}+{\boldsymbol{f}}_{\mathrm{NL}}\right)\end{array} $$
(13.5)

Equation (13.4), can be rewritten in state-space formulation as

$$ \begin{array}{l}\dot{\boldsymbol{x}}=\boldsymbol{Ax}+\boldsymbol{Bu}\\ {}\boldsymbol{y}=\boldsymbol{Cx}+\boldsymbol{Du}\end{array} $$
(13.6)

in which y is the system’s output A, B, C and D are state-space matrices and the matrices A and B of the dynamic equation can be obtained by the following.

$$ \boldsymbol{A}={\boldsymbol{A}}_1^{-\mathbf{1}}\;{\boldsymbol{B}}_1=\left[\begin{array}{c@{\quad}c}\mathbf{0} & -\boldsymbol{I}\\ -{\boldsymbol{M}}_{\mathrm{L}}^{-1*}{\boldsymbol{K}}_{\mathrm{L}}& -{\boldsymbol{M}}_{\mathrm{L}}^{-1*}{\boldsymbol{C}}_{\mathrm{L}}\end{array}\right],\kern0.84em \boldsymbol{B}={\boldsymbol{A}}_1^{-\mathbf{1}}=\left[\begin{array}{c}\mathbf{0} \\ -{\boldsymbol{M}}_{\mathrm{L}}^{-1} \end{array}\right] $$
(13.7)

u is the system’s loading and was defined in (13.5).

To obtain a numerical solution, the continuous-time ordinary differential equation (ODE) of (13.6), needs to be discretized in a time-marching algorithm with time step T. This can be made through the recursive formula

$$ \boldsymbol{x}\left( kT+T\right)={\boldsymbol{A}}_{\mathrm{disc}}\boldsymbol{x}(kT)+{\boldsymbol{B}}_{\mathrm{disc}}\boldsymbol{p}(kT) $$
(13.8)

In which the state at time t = kT + T is obtained from data given by the previous step at t = kT. The exact coefficient matrices of the discretized form can be shown to be

$$ \begin{array}{l}{\boldsymbol{A}}_{\mathrm{disc}}={\mathrm{e}}^{\boldsymbol{A} kT}\\ {}{\boldsymbol{B}}_{\mathrm{disc}}\boldsymbol{p}=\boldsymbol{B}{\displaystyle {\int}_{kT}^{kT+T}{\mathrm{e}}^{\boldsymbol{A}\left( kT+T-\tau \right)}\boldsymbol{p}\left(\tau \right) d\tau}\end{array} $$
(13.9)

The integral expression for the source term B disc p can be established only approximately for a general loading p(t). We use a triangular hold interpolation [15] for this approximation.

To conclude, we use the following algorithm to achieve a solution to the simulation problem:

  1. 1.

    Find K L, C and M of the underlying linear system

  2. 2.

    Establish the state-space matrices (13.7)

  3. 3.

    Do the time discretization as in (13.8)

  4. 4.

    Find the response of the linear system at time step k (u k  = u L,k  + u NL,k )

    1. 4.1.

      For first iteration set the nonlinear force to zero

    2. 4.2.

      Evaluate the non-linear source term by use of (13.3) and (13.5)

  5. 5.

    Check if there is any change in response of the system from previous iteration

    1. 5.1.

      If YES : Update nonlinear force and go to step 4

    2. 5.2.

      If NO: go for next time step and start a new iteration sequence at step 4

The main feature of the algorithm is that the response of the system is found in more than one time step ahead, on the other hand, all available integration scheme are trying to converge to the solution in one time step and then continue to the next step but in this algorithm, by having response at time step kT, the response in a duration (k+1)T to (k+n)T will be found simultaneously. the number of time steps, n, depends on the strength on nonlinearity in the system such that if the system is strongly nonlinear, n=1

13.3 Case Studies

To investigate the accuracy, stability and efficiency of the PFSS method, three case studies were considered and the results were compared with results of the MMRT method and an adaptive time-step Runge–Kutta (RK)method.

Since Runge–Kutta is a well-established method to solve nonlinear ODEs that is conveniently implemented in the Matlab software (as ode45), we use this method to find reference response of the structure. Results from output of other two methods and their deviation from reference response are reported.

13.3.1 A 3DOF System

The structure as shown in Fig. 13.1 consists of three equal masses, four linear springs and one spring with cubic stiffness. Numerical values are: k 1 = k 3 = 20 N/m, k 2 = k 4 = 10 N/m, and m 1 = m 2 = m 3 =1 kg, and c i  = 0.01 k i .

Fig. 13.1
figure 1

3DOF structure with cubic nonlinearity between second and third masses

Full size image

13.3.1.1 Nonlinearity Between Two Masses

The system stimulus consists of a sinusoidal force applied on the second mass with the amplitude 0.5 N and with frequency of 0.5 Hz, i.e. f(t) = 0.5 sin(πt). In this case cubic-stiffness-spring is placed between second and third mass. To simulate the structure, two time step sizes have been chosen; one with T = 0.2 s which results in the solution shown in Fig. 13.2, and another one with a smaller time step T = 0.01 s with results presented in Fig. 13.3.

Fig. 13.2
figure 2

Structure’s response at the third mass with T = 0.2 s. Left: weak nonlinearity k NL = 100 N/m. Right: strong nonlinearity k NL = 10 kN/m. The RHS figure shows that the PFSS produces an unstable response for this time step size (the ODE45 and MMRT do not)

Full size image
Fig. 13.3
figure 3

Structure’s response at the third mass with T = 0.01 s. Left: weak nonlinearity k NL = 100 N/m. Right: strong nonlinearity k NL = 10 kN/m

Full size image

The time response of the third mass of a 40s simulation is presented in Fig. 13.2 using results from all three methods. The left figure shows the structure in a setting with weak nonlinearity in which k NL = 100 N/m3 and the right figure shows the structure’s response in a setting with stronger nonlinearity k NL = 10 kN/m3. The required times to obtain the response by the three methods are presented in Table 13.1.

The algorithmic deviations of the PFSS and MMRT methods are presented in Table 13.2. The deviations are defined by

$$ dev\left(\%\right)=\frac{\left\Vert \boldsymbol{x}-{\boldsymbol{x}}_{\mathrm{RK}}\right\Vert }{\left\Vert {\boldsymbol{x}}_{\mathrm{RK}}\right\Vert}\times 100 $$
(13.10)

where x is either given by the MMRT or the PFSS method and x RK is given by the adaptive time-step Runge–Kutta.

Table 13.1 Required times (in seconds) to find time response of the structure using T = 0.2 s
Full size table

The time steps used to create data for Fig. 13.2, is obviously too long which makes the MMRT inaccurate which results in large deviations in both nonlinear cases. One the other hand the PFSS method gives a small deviation for weak nonlinearity but for stronger nonlinearity it even becomes unstable. To treat these accuracy and stability problems, we simulate both methods with smaller time steps, T = 0.01 s and the results shown in Fig. 13.3.

Table 13.2 Deviation (in %) of the methods as compared with RK
Full size table

The required time to simulate and resulting deviations are presented in Tables 13.3 and 13.4 respectively.

Table 13.3 Required times (in seconds) to find time response of the structure using T = 0.01 s
Full size table
Table 13.4 Deviation (in %) of the methods as compared with RK
Full size table

13.3.1.2 Nonlinearity Affecting Only One Mass

This case is similar to the previous one but the nonlinearity is only connected to the third mass as indicated in Fig. 13.4. The time response of the structure at the third mass is shown in Fig. 13.5. The left picture shows the time response of the third mass for cubic nonlinearity equal to 100 N/m and the right one shows the response at cubic nonlinearity level that equals to 10 kN/m3.

Fig. 13.4
figure 4

3DOF structure with cubic nonlinearity at third mass

Full size image
Fig. 13.5
figure 5

Structure’s response at the third mass with T = 0.01 s. Left: weak nonlinearity k NL = 100 N/m. Right: strong nonlinearity k NL = 10 kN/m

Full size image

At a sample rate T = 0.01 s the required simulation times and the obtained deviations are presented in Tables 13.5 and 13.6 respectively.

Fig. 13.6
figure 6

Clamped beam connected to a spring through a gap and a transverse impulse force applied on the structure at the indicated position. The spring stiffness is k NL. The most relevant node numbers are included

Full size image
Table 13.6 Deviation (in %) of the methods as compared with RK
Full size table

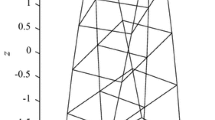
13.3.2 A clamped Beam with Gap Nonlinearity

In this case we considered a beam which is clamped at one end and connected to a spring through a g = 0.127 mm gap at the other end. The beam is shown in Fig. 13.6 and its properties are presented in Table 13.7.

Table 13.5 Required times (in seconds) to find time response of the structure using T = 0.01 s
Full size table
Table 13.7 Properties of the beam model
Full size table

First two nodes were fixed to fulfill the clamped condition. Nonlinearity was placed at node 60 and a transient force applied on node 42. The impulse force was shown in Fig. 13.7. The time response of the structure at the DOF with nonlinearity is displayed in Fig. 13.8. The left figure is for gap and soft spring and the right one is for gap and stiff spring. The required times to simulate the beam response with gap and both soft and stiff spring stiffness is presented in Table 13.8.

Fig. 13.7
figure 7

Impulse force applied to node 42 on beam model

Full size image
Fig. 13.8
figure 8

Time response of the beam model at the node with gap nonlinearity (node 60) and sampling time T = 0.1 ms for 0.4 s duration. Left: soft spring, k NL = 1.7 kN/m. Right: stiff spring, k NL = 17 kN/m

Full size image
Table 13.8 Required times (in seconds) to find time response of the structure using T = 0.1 ms
Full size table

In a case with stronger nonlinear effects we increase the supporting spring stiffness to k NL = 17 KN/m. In order to investigate the influence of the sample rate on the accuracy of the result we consider three different time rates. The results are shown in Fig. 13.9 indicate the results for the PFSS and MMRT methods. The required time to simulate the beam response with stiff spring k NL = 170 KN/m for different sampling rates are listed in Table 13.10.

Fig. 13.9
figure 9

Time response of the beam with hard support spring (k NL = 0.17 MN/m) and gap nonlinearity with different sampling rates T. (Left) PFSS method, (right) MMRT method

Full size image

13.4 Discussion on Numerical Results

As shown in Fig. 13.2 too big time steps can cause big error in the results of both compared methods. In the MMRT method, a too big time step resulted in stable but strongly incorrect results and too big time steps caused the PFSS method to yield unstable results. Both these deficiencies can be cured by decreasing time step as indicated in Fig. 13.3.

It is clear from Tables 13.1 and 13.2 for weak nonlinearity the PFSS method worked about 3 times faster than the MMRT method and about 20 times faster than the adaptive step Runge–Kutta method. The result of the PFSS method is about 9 times more accurate than results of the MMRT method. For the case of strong nonlinearity and too low sample rate the PFSS method became unstable but the MMRT yielded results after 0.05 s but large deviation from results of the Runge–Kutta method.

Table 13.3 shows that the PFSS method obtained the simulation result for the 3DOF structure with weak nonlinearity and time step 0.01 s after 0.06 s which is about 14 times faster than the MMRT method and about 10 times faster than the Runge–Kutta method. The accuracy of the methods, indicated in Table 13.4, show that the PFSS method is 8 times more accurate in this case. For the more strongly nonlinear case, PFSS works about 2.5 times faster and 3 times more accurate than MMRT.

Simulation results for the second 3DOF structure are shown in Fig. 13.5. The required simulation time and result deviation from results of the Runge–Kutta method has been tabulated in Tables 13.5 and 13.6 respectively. Results indicate that under some conditions MMRT can have big deviation from Runge–Kutta results and also it is significantly slower than the here presented PFSS method.

For the beam structure, results have been depicted in Fig. 13.8 show a good match between the results for weak nonlinearity. However, for strong nonlinearity there is deviation between the methods, as is shown Fig. 13.9. Table 13.8 indicates that RK is significantly slower than the other two methods and PFSS is about 12 times faster than MMRT. The main reason for the long simulation time for RK is the fact that stimulus, which is impulse, inserted in very short duration and ode45 could not see it, therefore, a time vector with a very short time step have to send to it. As shown in Table 13.9, PFSS has almost the same accuracy as RK for both cases but MMRT has large deviation from RK in stiff spring case. The convergence of the methods for strongly nonlinear structure, K = 170 KN/m, was considered and Fig. 13.9 indicates that the PFSS method has converged for a time step of 0.1 ms and it took 6.43 s to obtain the results (see Table 13.10) but for the MMRT method no convergence could be found even for time steps as small as 1 μs with results that took 1,429 s to obtain.

Table 13.9 Deviation (in %) of the methods as compared with RK
Full size table
Table 13.10 Required time (in seconds) to simulate the beam response with stiff spring for different sample rates
Full size table

13.5 Conclusions

In this paper Pseudo Force in State Space method, has been presented. This is a method for fast simulation of structures with local nonlinearity. The method has been applied to three different cases and the obtained results have been compared with results of the Runge–Kutta method and Modal Modification Response Technique method.

The results are presented in figures and tables which show three aspects, stability, accuracy and rapidness. In the sense of stability, the method PFSS is conditionally stable but the MMRT and Runge–Kutta produces stable results in these cases. Regarding accuracy, PFSS gives the same accuracy as the adaptive time-step Runge–Kutta method while MMRT in some cases gives the same accuracy and in some other cases it performs worse. Finally, about fastness, the PFSS method is shown to be the fastest of the three while MMRT is faster than Runge–Kutta.