DEIM for the Efficient Computation of Contact Interface Stresses

Abstract

The computational effort for the simulation of reduced order models containing contact stresses is determined by these nonlinear terms. Recent publications suggest the utilization of interpolation methods to overcome this bottleneck. The applicability of the Discrete Empirical Interpolation Method (DEIM) for the efficient computation of contact stresses is demonstrated. The modeling of a mechanical structure containing an interface using zero thickness elements is outlined first. This is followed by a reduction method using joint interface modes as extension to the well known Craig Bampton approach. The basic idea of interpolation methods and a summary of the applied DEIM algorithm is given. Finally the numerical example of a bolted cantilever is investigated for two loadcases and the results are discussed for different trial function bases. It is clearly shown that DEIM can be used to significantly improve the computational efficiency for this type of problems while keeping accuracy at an acceptable level.

41.1 Introduction

This contribution focuses on the efficient consideration of contact stresses within the framework of reduced order models for mechanical systems. Literature and current investigations of the authors clearly point out that the computational effort for the simulation of reduced order models containing contact stresses is determined by these nonlinear terms as the evaluation still takes place on the discretization of the full model. Furthermore a coordinate transformation from generalized coordinates to physical coordinates and the projection of the resulting stresses onto the generalized coordinates is necessary, which leads to an even higher computational effort involved for the interface stress computation compared to the full model.

Interpolation methods are an effective approach to lower the computational effort involved with the evaluation of parametrized functions defined on a spatial domain [6]. Furthermore in [2] the Discrete Empirical Interpolation Method (DEIM) is suggested to lower the computational effort for reduced order models containing nonlinear functions. In this case the former mentioned transformation and projection is only necessary for some few physical coordinates. The scaling of the interpolation functions is determined by collocation of function values and interpolated values at these so called interpolation points.

To demonstrate the applicability of DEIM for efficient computation of joint interface stresses the problem is formulated as single body involving self contact. The theory of zero thickness elements, see [4] and [5], is used to discretize the joint contact. The authors suggest a zero thickness element formulation leading to a contact stress equivalent force vector. This allows for a model order reduction following [3, 8] and fits into the DEIM formulation proposed by [2].

41.2 Problem Formulation

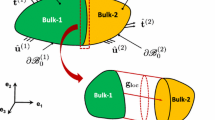
The body $\Omega$ with the surface $\Gamma$ and the contact interface $\Gamma _{jc}$ as depicted in Fig. 41.1a is investigated. As boundary conditions the displacement $\boldsymbol{u}_{d}$ and the stresses $\boldsymbol{t}$ are prescribed on $\Gamma _{d}$ and $\Gamma _{t}$ respectively which are disjunct surface regions of $\Gamma$. The dynamic equilibrium of a physical particle within the domain $\Omega$ at the position denoted by $\boldsymbol{x}$ is given by

$$\displaystyle{ \rho \ddot{\boldsymbol{u}} - div\boldsymbol{S} =\boldsymbol{ k}\quad \forall \boldsymbol{x} \in \Omega }$$

(41.1a)

with the boundary conditions

$$\displaystyle{ \boldsymbol{u} =\boldsymbol{ u}_{d}\quad \forall \boldsymbol{x} \in \Gamma _{d}\quad \text{and}\quad \boldsymbol{S}\boldsymbol{n} =\boldsymbol{ t}\quad \forall \boldsymbol{x} \in \Gamma _{t} }$$

(41.1b)

and the initial conditions for time $t = t_{0} = 0$

$$\displaystyle{ \boldsymbol{u} {= }^{0}\boldsymbol{u}\quad \forall \boldsymbol{x} \in \Omega \quad \text{and}\quad \dot{\boldsymbol{u}} {= }^{0}\boldsymbol{v}\quad \forall \boldsymbol{x} \in \Omega }$$

(41.1c)

where ρ denotes the mass density, $\boldsymbol{u}$ the displacement, $\dot{\boldsymbol{u}} =\boldsymbol{ v}$ the velocity, $\ddot{\boldsymbol{u}} =\boldsymbol{ a}$ the acceleration, $\boldsymbol{S}$ the Cauchy stress tensor, $\boldsymbol{k}$ the imposed force density and $\boldsymbol{n}$ the surface normal pointing outwards. The contact interface $\Gamma _{jc}$ is interpreted as self contact of the body $\Omega$ with $\Gamma _{jc}^{-}$ and $\Gamma _{jc}^{+}$ as the two contacting surfaces. Contact stresses will occur

$$\displaystyle{ \boldsymbol{{S}}^{\pm }\boldsymbol{{n}}^{\pm } =\boldsymbol{ t}_{ jc}^{\pm }\quad \forall \boldsymbol{x} \in \Gamma _{ jc} }$$

(41.1d)

where $\boldsymbol{t}_{jc}^{\pm }$ describes the acting joint contact stresses on the two sides $\Gamma _{jc}^{\pm }$, see Fig. 41.1b.

Fig. 41.1

Body $\Omega$ including joint interface in reference configuration and actual configuration at time t (a) and contact stresses within the joint interface $\Gamma _{jc}$ for contact locations P ⁻ and P ⁺ (b)

41.3 Discretization

To obtain a finite element method (FEM) discretization of the contact problem Eq. (41.1), the principle of virtual work is applied. With the virtual displacements $\delta \boldsymbol{u}$ which are assumed to be small in relation to the body dimension and the according virtual strain tensor $\delta \boldsymbol{\epsilon }$ the resulting weak formulation of the dynamic equilibrium is given by

$$\displaystyle\begin{array}{rcl} \delta {W}^{\Omega }& =& \int \limits _{ \Omega }\rho \ddot{\boldsymbol{u}} \cdot \delta \boldsymbol{ u}\ d\Omega +\sum _{i,j}\int \limits _{\Omega }s_{ij}\delta \epsilon _{ij}\ d\Omega -\int \limits _{\Gamma _{t}}\boldsymbol{S}\boldsymbol{n} \cdot \delta \boldsymbol{ u}\ d\Gamma -\int \limits _{\Gamma _{jc}^{-}}\boldsymbol{{S}}^{-}\boldsymbol{{n}}^{-}\cdot \delta \boldsymbol{ {u}}^{-}\ d\Gamma \\ & & -\int \limits _{\Gamma _{jc}^{+}}\boldsymbol{{S}}^{+}\boldsymbol{{n}}^{+} \cdot \delta \boldsymbol{ {u}}^{+}\ d\Gamma -\int \limits _{ \Omega }\boldsymbol{k} \cdot \delta \boldsymbol{ u}\ d\Omega = 0. {}\end{array}$$

(41.2)

For a discretization $\Omega _{h}$ of the domain $\Omega$ with the nodes $\boldsymbol{x}_{h}$ and the related nodal displacements $\boldsymbol{u}_{h}$ Eq. (41.2) can be rewritten as sum over all elements $\Omega _{h}^{e} \subset \Omega _{h}$ and element surfaces $\Gamma _{h}^{e} \subset \Gamma _{h}$. The virtual work of a single element not adjacent to the contact interface $\Gamma _{jc}$ is given by

$$\displaystyle\begin{array}{rcl} \begin{array}{ll} \delta {W}^{e}& =\int \limits _{\Omega _{h}^{e}}\rho \ddot{\boldsymbol{u}} \cdot \delta \boldsymbol{ u}\ d\Omega +\sum _{i,j}\int \limits _{\Omega _{h}^{e}}s_{ij}\delta \epsilon _{ij}\ d\Omega -\!\int \limits _{\Gamma _{t,h}^{e}}\boldsymbol{S}\boldsymbol{n} \cdot \delta \boldsymbol{ u}\ d\Gamma -\!\int \limits _{\Omega _{h}^{e}}\boldsymbol{k} \cdot \delta \boldsymbol{ u}\ d\Omega = 0.\end{array} & &{}\end{array}$$

(41.3)

For each element the nodal displacement vector $\boldsymbol{u}_{h}^{e} \subset \boldsymbol{ u}_{h}$ can be defined. By using the Matrix of element shape functions $\boldsymbol{{N}}^{e}$ the displacement field $\boldsymbol{{u}}^{e} = \boldsymbol{{N}}^{e}\,\boldsymbol{u}_{h}^{e}$ and the virtual displacement field $\delta \boldsymbol{{u}}^{e} =\boldsymbol{ {N}}^{e}\delta \boldsymbol{u}_{h}^{e}$ can be formulated for each element. Evaluation of the integrals, sum over all elements defined by Eq. (41.3) and implementation of the boundary conditions, see [1], but without consideration of the contact stresses at $\Gamma _{jc}^{-}$ and $\Gamma _{jc}^{+}$ leads to the discretized equations of motion

$$\displaystyle{ \boldsymbol{M}\ddot{\boldsymbol{u}}_{h} +\boldsymbol{ K}\boldsymbol{u}_{h} =\boldsymbol{ f}_{\!ext}. }$$

(41.4)

For an element adjacent to the contact surface $\Gamma _{jc}$ the discretization $\Omega _{h}$ comprises a matching mesh $\Gamma _{jc,h}^{-}$ and $\Gamma _{jc,h}^{+}$ of the two sides $\Gamma _{jc}^{-}$ and $\Gamma _{jc}^{+}$. To handle the contact within the joint interface $\Gamma _{jc}$ the theory of zero thickness elements is a straight forward technique as only small relative movement of the contact partner is expected. Several formulations can be found in literature, e.g. [4] and [5]. For this contribution the stress equivalent nodal force vector of an isoparametric, triangular shaped zero thickness element, depicted in Fig. 41.2a, is formulated. One surface triangle connects to the discretization $\Gamma _{jc,h}^{-}$ and the other one to the discretization $\Gamma _{jc,h}^{+}$.

Fig. 41.2

Triangular shaped zero thickness element (a), arbitrary shaped triangle with local coordinate system (u, v) (b) and uniform triangle with natural coordinates (ξ, η) (c)

For the nodal displacements of the element

$$\displaystyle{ \boldsymbol{u}_{h}^{e,+} ={ \left [\begin{array}{*{10}c} {\boldsymbol{u}_{ 1}^{e}}^{T}&{\boldsymbol{u}_{ 2}^{e}}^{T}&{\boldsymbol{u}_{ 3}^{e}}^{T} \end{array} \right ]}^{T}\quad \text{and}\quad \boldsymbol{u}_{ h}^{e,-} ={ \left [\begin{array}{*{10}c} {\boldsymbol{u}_{ 4}^{e}}^{T}&{\boldsymbol{u}_{ 5}^{e}}^{T}&{\boldsymbol{u}_{ 6}^{e}}^{T} \end{array} \right ]}^{T} }$$

(41.5)

a local coordinate system (u, v, w) where the $\boldsymbol{e}_{w}$ vector is oriented in interface $\Gamma _{jc,h}^{e}$ normal direction as depicted in Fig. 41.2a is used. With these nodal displacements and the Matrix

$$\displaystyle{ \boldsymbol{{N}}^{e} = \left [\begin{array}{*{10}c} \boldsymbol{N}_{ 1} & \boldsymbol{N}_{2} & \boldsymbol{N}_{3} \end{array} \right ]\quad \text{with}\quad \boldsymbol{N}_{i} = diag(N_{i},N_{i},N_{i}) }$$

(41.6)

holding the shape functions $N_{1} = 1 -\xi -\eta$, N ₂ = ξ and N ₃ = η where the natural coordinates of a uniform triangle ξ = ξ(u, v) and η = η(u, v) are depending on the coordinates u and v of the arbitrary shaped element, the displacement fields of both surface triangles

$$\displaystyle{ \boldsymbol{{u}}^{e,+} =\boldsymbol{ {N}}^{e}\boldsymbol{u}_{ h}^{e,+}\quad \text{and}\quad \boldsymbol{{u}}^{e,-} =\boldsymbol{ {N}}^{e}\boldsymbol{u}_{ h}^{e,-} }$$

(41.7)

can be described. Both surface triangles are interpolated using the same shape function definition. With consideration of Newton’s Third Law, the principle of actio and reactio

$$\displaystyle{ \boldsymbol{t}_{jc}^{e} =\boldsymbol{ t}_{ jc}^{e,+} = -\boldsymbol{t}_{ jc}^{e,-} }$$

(41.8)

illustrated in Fig. 41.1b, the virtual work of the zero thickness element is given by

$$\displaystyle\begin{array}{rcl} \delta {W}^{e} =\delta {W}^{e,-}+\delta {W}^{e,+} = -\int \limits _{ \Gamma _{jc,h}^{e,-}}\delta \boldsymbol{{u}}^{e,-}\cdot \boldsymbol{ t}_{ jc}^{e,-}\ d\Gamma -\int \limits _{ \Gamma _{jc,h}^{e,+}}\delta \boldsymbol{{u}}^{e,+} \cdot \boldsymbol{ t}_{ jc}^{e,+}\ d\Gamma =\int \limits _{ \Gamma _{jc,h}^{e,-}}\delta \boldsymbol{{u}}^{e,-}\cdot \boldsymbol{ t}_{ jc}^{e}\ d\Gamma -\int \limits _{ \Gamma _{jc,h}^{e,+}}\delta \boldsymbol{{u}}^{e,+} \cdot \boldsymbol{ t}_{ jc}^{e}\ d\Gamma.& &{}\end{array}$$

(41.9)

The contact stresses, e.g. for normal direction, depend on the gap function

$$\displaystyle{ g ={ \left [\boldsymbol{{u}}^{e,+} -\boldsymbol{{u}}^{e,-}\right ]}^{T}\boldsymbol{e}_{ w} ={ \left [\boldsymbol{{N}}^{e}\boldsymbol{u}_{ h}^{e,+} -\boldsymbol{ {N}}^{e}\boldsymbol{u}_{ h}^{e,-}\right ]}^{T}\boldsymbol{e}_{ w} ={ \left [\begin{array}{*{10}c} \boldsymbol{u}_{h}^{e,+} \\ \boldsymbol{u}_{h}^{e,-} \end{array} \right ]}^{T}{\left [\begin{array}{*{10}c} \boldsymbol{{N}}^{e}&-\boldsymbol{{N}}^{e} \end{array} \right ]}^{T}\boldsymbol{e}_{ w} }$$

(41.10)

via the “constitutive” relation

$$\displaystyle{ \boldsymbol{t}_{jc}^{e} = -t_{ n}\boldsymbol{e}_{w}\quad \text{with}\quad t_{n} = \left \{\begin{array}{@{}l@{\quad }l@{}} 0 \quad &\text{if}\quad g \geq 0, \\ c_{n}g\quad &\text{if}\quad g < 0 \end{array} \right. }$$

(41.11)

with the penalty parameter c _n . For evaluation of the integral in Eq. (41.9) the triangular shaped interface $\Gamma _{jc,h}^{e}$ depicted in Fig. 41.2b is projected onto a uniform triangle as depicted in Fig. 41.2c. The Jacobian $\boldsymbol{J}$ of this transformation is given by

$$\displaystyle{ \left [\begin{array}{c} \dfrac{\partial } {\partial \xi } \\ \dfrac{\partial } {\partial \eta } \end{array} \right ] = \left [\begin{array}{cc} \dfrac{\partial u} {\partial \xi } &\dfrac{\partial v} {\partial \xi } \\ \dfrac{\partial u} {\partial \eta } &\dfrac{\partial v} {\partial \eta } \end{array} \right ]\left [\begin{array}{c} \dfrac{\partial } {\partial u} \\ \dfrac{\partial } {\partial v} \end{array} \right ] =\boldsymbol{ J}\left [\begin{array}{c} \dfrac{\partial } {\partial u} \\ \dfrac{\partial } {\partial v} \end{array} \right ]. }$$

(41.12)

With this transformation the virtual work of the zero thickness element is given by

$$\displaystyle\begin{array}{rcl} \delta {W}^{e} = -\int \limits _{ 0}^{1}\int \limits _{ 0}^{1-\eta }\left [\delta \boldsymbol{{u}}^{e,+} -\delta \boldsymbol{ {u}}^{e,-}\right ] \cdot \boldsymbol{ t}_{ jc}^{e}\ det\boldsymbol{J}\ d\xi \ d\eta = -\int \limits _{ 0}^{1}\int \limits _{ 0}^{1-\eta }{\left [\begin{array}{*{10}c} \delta \boldsymbol{u}_{h}^{e,+} \\ \delta \boldsymbol{u}_{h}^{e,-} \end{array} \right ]}^{T}{\left [\begin{array}{*{10}c} \boldsymbol{{N}}^{e}&-\boldsymbol{{N}}^{e} \end{array} \right ]}^{T}\boldsymbol{t}_{ jc}^{e}\ det\boldsymbol{J}\ d\xi \ d\eta & &{}\end{array}$$

(41.13)

where the stress equivalent nodal force vector of the zero thickness element is found

$$\displaystyle{ \boldsymbol{f}_{contact}^{e} =\int \limits _{ 0}^{1}\int \limits _{ 0}^{1-\eta }{\left [\begin{array}{*{10}c} \boldsymbol{{N}}^{e}&-\boldsymbol{{N}}^{e} \end{array} \right ]}^{T}\ \boldsymbol{t}_{ jc}^{e}\ det\boldsymbol{J}\ d\xi \ d\eta. }$$

(41.14)

Finally Eq. (41.4) is extended with the nodal contact force vectors obtained from the zero thickness elements within the joint interface. The discretization of the contact problem Eq. (41.1) is given by

$$\displaystyle{ \boldsymbol{M}\ddot{\boldsymbol{u}}_{h} +\boldsymbol{ K}\boldsymbol{u}_{h} =\boldsymbol{ f}_{\!ext} +\boldsymbol{ f}_{\!contact}. }$$

(41.15)

41.4 Model Order Reduction

An approximation of the nodal displacements $\boldsymbol{u}_{h}$ in Eq. (41.15) is given by

$$\displaystyle{ \boldsymbol{u}_{h} \approx \boldsymbol{ \Phi }\boldsymbol{q} }$$

(41.16)

with the matrix $\boldsymbol{\Phi }$ holding the displacement trial functions or modes $\boldsymbol{\varphi }_{i}$ and the according generalized coordinates $\boldsymbol{q}$. As described in [3] a mode base

$$\displaystyle{ \boldsymbol{\Phi }_{classic} = \left [\boldsymbol{\Psi }_{CM}\ \boldsymbol{\Phi }_{NM}\right ] }$$

(41.17)

consisting of Constraint Modes $\boldsymbol{\Psi }_{CM}$ and Fixed Boundary Normal Modes $\boldsymbol{\Phi }_{NM}$ is defined. As proposed by [8] for structures containing joints the classic mode base Eq. (41.17) is extended by a set of Joint Interface Modes $\boldsymbol{\Phi }_{JIM}$ which account for the local deformation at the interface. The resulting transformation matrix is given by

$$\displaystyle{ \boldsymbol{\Phi } = \left [\boldsymbol{\Psi }_{CM}\ \boldsymbol{\Phi }_{NM}\ \boldsymbol{\Phi }_{JIM}\right ]. }$$

(41.18)

Substituting (41.16) and (41.18) into Eq. (41.15) and premultiplying with $\boldsymbol{{\Phi }}^{T}$ leads to the reduced equations of motion

$$\displaystyle{ \boldsymbol{M}_{\!red}\,\ddot{\boldsymbol{q}} +\boldsymbol{ K}_{\!red}\,\boldsymbol{q} =\boldsymbol{ f}_{\!red} +\boldsymbol{ {\Phi }}^{T}\boldsymbol{f}_{\! contact}(\boldsymbol{\Phi }\boldsymbol{q}) }$$

(41.19)

where $\boldsymbol{M}_{\!red} =\boldsymbol{ {\Phi }}^{T}\boldsymbol{M}\boldsymbol{\Phi }$ denotes the reduced mass matrix, $\boldsymbol{K}_{\!red} =\boldsymbol{ {\Phi }}^{T}\boldsymbol{K}\boldsymbol{\Phi }$ denotes the reduced stiffness matrix and $\boldsymbol{f}_{\!red} =\boldsymbol{ {\Phi }}^{T}\boldsymbol{f}_{\!ext}$ denotes the projected vector of external forces.

The computational effort is dominated by the last term of the right hand side of Eq. (41.19). The evaluation of the nonlinear contact forces still takes place on the physical coordinates of the unreduced model and additionally requires a transformation from generalized to physical coordinates and a projection of the contact forces onto the generalized coordinates. The computational effort due to the nonlinear term is reduced using a procedure discussed in the next section.

41.5 Interface Stress Computation

41.5.1 POD

The Proper Orthogonal Decomposition (POD) is a method to construct a low dimensional set of ℓ basis vectors $\boldsymbol{t}_{i}$ which approximate the collection of k snapshots $\boldsymbol{t}_{j}^{{\ast}}$ in an optimal sense, see [7]. The resulting basis vectors are a solution to the minimization problem

$$\displaystyle{ \min _{\boldsymbol{t}_{1},\ldots,\boldsymbol{t}_{\ell}}\sum _{j=1}^{k}{\left \|\boldsymbol{t}_{ j}^{{\ast}}-\sum _{ i=1}^{\ell}\left \langle \boldsymbol{t}_{ j}^{{\ast}},\boldsymbol{t}_{ i}\right \rangle \boldsymbol{t}_{i}\right \|}^{2}\quad \text{with}\ \left \langle \boldsymbol{t}_{ i},\boldsymbol{t}_{j}\right \rangle =\delta _{ij}\ \text{for}\ i,j = 1,\ldots,\ell }$$

(41.20)

where $\left \langle.,.\right \rangle$ denotes the inner product of two vectors.

41.5.2 Stress Interpolation

Evaluation of Eq. (41.14) using a numerical integration scheme requires the knowledge of the contact stress vector $\boldsymbol{t}_{jc}^{e}$ at the integration points. The vector containing the discretized contact stress values in normal direction at these locations for each element within the discretized interface $\Gamma _{jc,h}$ is denoted by $\boldsymbol{t}_{n}$. It is assumed that an approximation for the discretized joint contact stresses is given by

$$\displaystyle{ \boldsymbol{t}_{n} \approx \boldsymbol{ T}_{\!n}\,\boldsymbol{p}_{n} }$$

(41.21)

with a base $\boldsymbol{T}_{\!n}$ of orthonormal stress trial functions or stress modes $\boldsymbol{t}_{n,i}$ and the according generalized coordinates $\boldsymbol{p}_{n}$. The stress mode equivalent nodal forces are computed for each element using Eq. (41.14). Formally integration over the element domain, transformation to global coordinates and sum over all elements to achieve the contact force vector $\boldsymbol{f}_{contact}$ in Eq. (41.15) can be expressed using the linear operator $\boldsymbol{A}$. An approximation of the nonlinear term in Eq. (41.19) is given by

$$\displaystyle{ \boldsymbol{{\Phi }}^{T}\boldsymbol{f}_{\! contact}(\boldsymbol{\Phi }\boldsymbol{q}) \approx \boldsymbol{ {\Phi }}^{T}\boldsymbol{A}\,\boldsymbol{T}_{\! n}\,\boldsymbol{p}_{n}. }$$

(41.22)

with unknown generalized coordinates $\boldsymbol{p}_{n}$. The POD method is used to construct a valid base $\boldsymbol{T}_{\!n}$ with the help of several contact stress distribution samples

$$\displaystyle{ \boldsymbol{t}_{n,i}^{{\ast}}\ \text{with}\ i = 1,\ldots,k }$$

(41.23)

obtained from k solutions $\boldsymbol{u}_{h,i}^{{\ast}}$ of the discretized system Eq. (41.15) under different loading conditions. The computation of $\boldsymbol{p}_{n}$ is briefly outlined in the following subsection.

41.5.3 DEIM

The Discrete Empirical Interpolation Method (DEIM) proposed by [2] is an effective method to compute the unknown generalized coordinates $\boldsymbol{p}_{n}$ in Eq. (41.22). Formally this is achieved by a permutation matrix $\boldsymbol{P}$ which is used to extract certain entries of the discretized contact stress vector $\boldsymbol{t}_{n}$. For these entries the contact stresses computed using constitutive relations, e.g. Eq. (41.11), are assumed to be equal to the interpolated contact stresses

$$\displaystyle{ \boldsymbol{{P}}^{T}\boldsymbol{t}_{ n} =\boldsymbol{ {P}}^{T}\boldsymbol{T}_{\! n}\,\boldsymbol{p}_{n}. }$$

(41.24)

If $\boldsymbol{{P}}^{T}\boldsymbol{T}_{\!n}$ is invertible, the generalized coordinates $\boldsymbol{p}_{n}$ can be expressed by the contact stresses at the locations denoted by the permutation matrix

$$\displaystyle{ \boldsymbol{p}_{n} ={ \left [\boldsymbol{{P}}^{T}\boldsymbol{T}_{\! n}\right ]}^{-1}\boldsymbol{{P}}^{T}\boldsymbol{t}_{ n}. }$$

(41.25)

The remaining entries of the contact stress vector $\boldsymbol{t}_{n}$ are interpolated using the base $\boldsymbol{T}_{\!n}$ holding the orthonormal interpolation functions. According to [2] the DEIM algorithm ensures the regularity of $\boldsymbol{{P}}^{T}\boldsymbol{T}_{\!n}$ by selecting the so called interpolation indices defining $\boldsymbol{P}$ from a given POD base $\boldsymbol{T}_{\!n}$. First step of this algorithm is the selection of a unit vector $\boldsymbol{e}_{\wp _{1}}$ to achieve

$$\displaystyle{ \left \vert \boldsymbol{e}_{\wp _{1}}^{T}\boldsymbol{t}_{ n,1}\right \vert = \left \|\boldsymbol{t}_{n,1}\right \|_{\infty } }$$

(41.26)

where $\left \|.\right \|_{\infty }$ denotes the maximum norm of a vector and ℘ ₁ denotes the index of the largest absolute value of $\boldsymbol{t}_{n,1}$. With $\boldsymbol{T}_{n,1} = \left [\boldsymbol{t}_{n,1}\right ]$, $\boldsymbol{P}_{1} = \left [\boldsymbol{e}_{\wp _{1}}\right ]$ and $\boldsymbol{\wp }_{1} = \left [\wp _{1}\right ]$ the DEIM algorithm repeats for i = 2, …, ℓ as follows:

• 1. Determine $\boldsymbol{c}_{i}$ from

  $$\displaystyle{ \left (\boldsymbol{P}_{i-1}^{T}\boldsymbol{T}_{ n,i-1}\right )\boldsymbol{c}_{i} =\boldsymbol{ P}_{i-1}^{T}\boldsymbol{t}_{ n,i} }$$

  (41.27)

• 2. Evaluate

  $$\displaystyle{ \boldsymbol{r}_{i} =\boldsymbol{ t}_{n,i} -\boldsymbol{ T}_{n,i-1}\boldsymbol{c}_{i} }$$

  (41.28)

• 3. Select a unit vector $\boldsymbol{e}_{\wp _{i}}$ where ℘ _i denotes the index of the largest absolute value of $\boldsymbol{r}_{i}$ to achieve

  $$\displaystyle{ \left \vert \boldsymbol{e}_{\wp _{i}}^{T}\boldsymbol{r}_{ i}\right \vert = \left \|\boldsymbol{r}_{i}\right \|_{\infty } }$$

  (41.29)

• 4. Assign

  $$\displaystyle\begin{array}{rcl} \boldsymbol{P}_{i}& =& \left [\boldsymbol{P}_{i-1},\boldsymbol{e}_{\wp _{i}}\right ] {}\end{array}$$

  (41.30a)
  $$\displaystyle\begin{array}{rcl} \boldsymbol{T}_{n,i}& =& \left [\boldsymbol{T}_{n,i-1},\boldsymbol{t}_{n,i}\right ]\ \text{and} {}\end{array}$$

  (41.30b)
  $$\displaystyle\begin{array}{rcl} \boldsymbol{\wp }_{i}& =& \left [\boldsymbol{\wp }_{i-1},\wp _{i}\right ] {}\end{array}$$

  (41.30c)

The vector containing the interpolation indices is denoted by $\boldsymbol{\wp } =\boldsymbol{ \wp }_{\ell}$. According to [2] the permutation matrix constructed in the last iteration is a valid choice $\boldsymbol{P} =\boldsymbol{ P}_{\ell}$ for the permutation matrix in Eq. (41.25).

41.6 Numerical Example

41.6.1 Model Description

The DEIM method for computation of joint interface contact stresses is applied to the model of a bolted cantilever beam for two loading conditions depicted in Fig. 41.3. The first loadcase LC1 is a tip load in vertical direction, the second loadcase LC2 additionally considers a torsional moment.

Fig. 41.3

Resulting displacement of the two substructures (the bolt model is hidden) for LC1 (left) and LC2 (right)

The structure itself consists of two substructures with rectangular shaped cross section (a = 10 mm, b = 20 mm) connected by a single bolt and an overall length of l = 110 mm. All structural components are modeled using a linear elastic material with Young’s Modulus E = 210, 000 N/mm², Poisson ratio ν = 0. 29 and density ρ = 7, 820 kg/m³.

The discretization $\Omega _{h}$ of the full model contains 1, 834 elements and 2, 780 nodes. The CHEXA, CBEAM, RBE2 and RBE3 element formulations of the commercial FEM software package MSC Nastran are used to generate the system matrizes in Eq. (41.4). The joint interface is modeled by zero thickness elements to obtain the contact force vector of the full model in Eq. (41.15). A convergence study regarding the meshsize of the full model is not within the scope of this contribution.

The results of the reduced order model Eq. (41.19) with the nonlinear term substituted by the DEIM based approximation Eq. (41.22) are computed in combination with 2 different types of contact stress trial function bases referenced in Eq. (41.21). These contact stress trial function bases are obtained using the POD snapshot method according to [7]:

• 1. Type 1 (SM id 1) based on a defined set of r < k snapshots Eq. (41.23) (analogous to middle column of Fig. 41.4)

• 2. Type 2 (SM id 2) based on a defined set of k snapshots Eq. (41.23) (analogous to all columns of Fig. 41.4)

Fig. 41.4

Snapshots for obtaining the different contact stress trial function bases

For the investigations within the context of this contribution the inertia effects and the contact shear stresses are neglected. To obtain and postprocess the solution of the resulting equations the software package Scilab is utilized.

The relative error of the gap function in surface normal direction as well as the relative error of the contact stresses in surface normal direction are choosen as evaluation criteria. While the first quantity expresses the influence of the contact stresses onto the structure, the second quantity illustrates whether the computed contact stresses are useful for subsequent computations, e.g. shear stresses due to friction. For a vector $\boldsymbol{y}$ the relative error vector is given by

$$\displaystyle{ \boldsymbol{e}_{rel} = \frac{\boldsymbol{y} -\boldsymbol{ y}_{ref}} {\left \|\boldsymbol{y}_{ref}\right \|_{\infty }} }$$

(41.31)

where $\left \|.\right \|_{\infty }$ denotes the maximum norm of a vector and $\boldsymbol{y}_{ref}$ denotes the reference values obtained from the full model. For computation of the gap function relative error the maximum penetration is used as reference value.

41.6.2 Reference Solution

The parameterization of the contact model Eq. (41.11) is based on a permitted penetration under certain loading conditions. This is checked with solutions obtained from the full model. The resulting values of the gap function and the contact stresses depicted in Fig. 41.5 are comparable with solutions obtained using a commercial FEM code, e.g. ABAQUS in combination with a penalty approach based contact model.

Fig. 41.5

Gap function values (top row) and contact stress values (bottom row) obtained from solutions of the full model

During Model Order Reduction (MOR) in Eq. (41.19) the number of JIM in Eq. (41.18) is increased until the error of the solution is sufficiently small. This is achieved with 50 JIM, the contact stresses are still computed for each node of the joint interface discretization. The resulting relative error values of the gap function and contact stresses are depicted in Fig. 41.6. The largest absolute relative error value is well below 0. 2.

Fig. 41.6

Evaluation of the reduced model utilizing 50 JIMs with node based contact stress computation: gap function relative error values (top row) and contact stress relative error values (bottom row)

41.6.3 Results

The results utilizing stress trial function base type 1 are investigated first. The relative error of the results is depicted in Fig. 41.7. LC1 in combination with only ℓ = 16 trial functions already shows the applicability of the DEIM method for problems containing joint interfaces. The number of operations necessary to obtain these results decreases by a factor 10 compared to the reduced model with node based contact stress computation.

Fig. 41.7

Reduced model utilizing 50 JIMs and DEIM with 16 type 1 trial functions: gap function relative error values (top row) and contact stress relative error values (bottom row)

As the stress trial function base does not include the influence of the torsional moment a physical meaningful solution cannot be obtained for LC2. This clearly shows the importance of a well suited trial function base as the torsional moment can be interpreted as perturbation of LC1. This aspect is even more critical in case of a dynamic simulation without a priori knowledge about the vibrational behavior. The same conclusion is deduced when utilizing a different number of stress modes.

Fig. 41.8

Reduced model utilizing 50 JIMs and DEIM with 16 type 2 trial functions: gap function relative error values (top row) and contact stress relative error values (bottom row)

The results utilizing stress trial function base type 2 are investigated next, the relative error values of the results are depicted in Fig. 41.8. For almost all locations the absolute relative error value of the resulting contact stresses drops below 0. 2 when using the DEIM approach in combination with only ℓ = 16 stress trial functions. It can be concluded that these results show an higher error than those of the reduced model with node based contact stress computation depicted in Fig. 41.6. But if this error level is tolerable the number of operations necessary to obtain a solution decreases by a factor 10 compared to the reduced model with node based contact stress computation.

41.7 Conclusion

The results show that the Discrete Empirical Interpolation Method (DEIM) proposed by [2] can be applied to significantly lower the computational effort involved for joint interface contact stress computation within the framework of reduced order models for mechanical systems.

The results also illustrate that obtaining the required stress trial function base from simulations of the full system can lead to wrong results for a different loading of the structure which is not considered in the stress trial function base. This emphasizes the need for a trial function base covering the whole space of acting interface stresses.