Double Allee Effects on Prey in a Modified Rosenzweig-MacArthur Predator-Prey Model

Abstract

In this work, a modified Rosenzweig-MacArthur predator-prey model is analyzed, which is a particular Gause type model, considering two Allee effect affecting the prey population.

This phenomenon may be expressed by different mathematical expressions; with the form here used, the existence of one limit cycle surrounding a positive equilibrium point is proved.

Conditions to the existence of equilibrium points and their local stability are established; moreover, the existence of a separatrix curve dividing the behavior of trajectories which can have different ω-limit sets.

Some simulations reinforced our results are given and the ecological consequences are discussed.

9.1 Introduction

In current theory of predator-prey dynamics and as consequences of the advancement of the ecological knowledge due to theoretical, empirical, and observational research, more elements are recognized as essential to the phenomenon of predation [27], being incorporated to the study of more complex non-linear mathematical models.

In this work, a Gause-type predator-prey model [16] derived from the reasonably realistic and well-known Rosenzweig-MacArthur model [27] is analyzed, incorporating the Allee effect [13, 26] on the prey growth equation also called depensation in Fisheries Sciences [10, 23].

Any mechanism leading to a positive relationship between a component of individual fitness and the number or density of conspecifics is named as a mechanism of the Allee effect [4], i.e., an Allee effect occurs in populations when individuals suffer a decrease in fitness at low densities [26].

Many ecological mechanisms producing Allee effects are known [25] and distinct causes may generate this phenomenon (Table 1 in [5] or Table 2.1 in [13]). Recent ecological research suggests the possibility that two or more Allee effects can be generated by mechanisms acting simultaneously on a single population (See Table 2 in [5]). The combined influence of some of these phenomena is known as multiple Allee effect [1, 5, 13].

The mathematical formalization of the Allee effect are varied [6, 12, 28], but it is possible to prove that most of them are topologically equivalent [18]. However, some of these forms may produce a change in the number of limit cycles through Hopf bifurcation surrounding a positive equilibrium point in predator-prey models [15, 20].

Many algebraic forms can be employed to describe the Allee effect [6, 12, 25, 31] but it is possible to prove that many of them are topologically equivalent [18]. One of this equations is given by

$$\frac{dx}{dt}=rx\left( 1-\frac{x}{K} \right)\left( 1-\frac{m+n}{x+n} \right)$$

(9.1)

where r scales the prey growth rate, K is the environmental carrying capacity, m is the Allee threshold, and the auxiliary parameter n with n > 0 and m > − n, [6, 7, 28], affecting the overall shape of the per-capita growth curve of the prey.

We affirm that Eq. (9.1) describes double Allee effects, expressed once in the factor $m( x )=x-m$, similarly as in the most usual equation representing Allee effect [3, 12]; a second time is given by the term $r\left( x \right)=\frac{rx}{x+n}$ [31], which can be interpreted as an approximation of a population dynamics where the differences between fertile and non-fertile are not explicitly modelled. Then, we can assume this factor indicates the impact of the Allee effect due to the non-fertile population n [2].

As predator-prey interactions are inherently prone to oscillations [27], it is therefore obvious investigate the Allee effect as a potential mechanism for the creation of population cycles and their related limit cycles from of mathematical point of view [3, 12, 29].

An important objective in these works will be to determine the quantity of limit cycles (trajectories closed and isolated) of this class of non-linear differential equation system associated with the modified Rosenzweig-MacArthur model. We consider that this issue is a good criterion to classify these models, but we not consider this issue in our analysis.

Conditions that guarantee the uniqueness of a limit cycle [21], the global stability of the unique positive equilibrium in predator–prey systems, or non-existence of limit cycles [30], has been extensively studied over the last decades starting with the work by Cheng [8]; results on the existence and uniqueness of limit cycles have been obtained in some papers [8, 22], which can be used to explain many real world oscillatory phenomena in nature [11, 21, 30].

This paper is organized as follows: In Sect. 9.2, we present the model and a topologically equivalent is obtained; in Sect. 9.3, the main properties of this model are presented. In Sect. 9.4, some simulations for verify our results are given. Ecological consequences and a comparative study of the mathematical results are given in Sect. 9.5.

9.2 The Model

Considering the double Allee effect on prey described by (9.1) in the Rosenzweig-MacArthur model [27], the autonomous nonlinear bidimensional differential equation system of Kolmogorov type [16] is given by:

$$ {{X}_{\sigma }}:\left\{ \begin{aligned}& \frac{dx}{dt}=\frac{rx}{x+n}\left( 1-\frac{x}{K} \right)( x-m )-\frac{qx}{x+a}y \\&\\& \frac{dy}{dt}=\left( \frac{px}{x+a}-c \right)y \\ \end{aligned} \right. $$

(9.2)

where x = x(t) and y = y(t) indicate the prey and predator population sizes, respectively for $t\ge 0$ (number of individuals, density or biomass). The parameters are all positives, i. e. $\sigma =\left( r,n,K,q,a,p,c,m \right)\in \mathbb{R}_{+}^{7}\times \mathbb{R}$, with a < K and − K < m < K, having the following biological meanings:

r:

is the intrinsic growth rate or biotic potential of the prey;

K:

is the prey environmental carrying capacity;

m > 0:

is the minimum of viable population (threshold of Allee effect);

n:

is the population size of sterile individuals on prey population;

q:

is the maximum number of prey that necessary can be eaten by a predator in each time unit;

a:

is the amount of prey needed to achieve one-half of q;

p:

is the coefficient of biomass conversion, and

c:

is the natural death rate of predators in absence of prey.

System (9.2) is defined in $\Omega =\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}/x\ge 0,\,y\ge 0 \right\}$.

The analysis must be made separately for the strong Allee effect (m > 0) and weak Allee effect (m ≤ 0), due the number of limit cycles can change with respect to this parameter [20]; in this work we consider only m > 0.

The results will be compared with the Rosenzweig-MacArthur model in which the Allee effect is absent, and with the model studied in [19, 24], where the Allee effect is described by a simpler form, which is topologically equivalent to that used in this work [18].

9.2.1 Topologically Equivalent System

In order to simplify the calculus, we follow the methodology used in [17, 19, 20], making a reparameterization and a time rescaling of system (9.2), given by the function $\varphi :\overline{\Omega }\times \mathbb{R}\to \Omega \times \mathbb{R}$, defined as

$$\varphi \left( u,v,\tau \right)=\left( Ku,\frac{rK}{q}v,\frac{r}{\left( u+\frac{n}{K} \right)\left( u+\frac{a}{K} \right)}\tau \right)=\left( x,y,t \right)$$

with $\overline{\Omega }=\left\{ ( u,v )\in {{\mathbb{R}}^{2}}/u\ge 0,\,v\ge 0 \right\}$. As

$$\det D\varphi \left( u,v,\tau \right)=\frac{{{r}^{2}}{{K}^{2}}}{u\left( u+\frac{n}{K} \right)\left( u+\frac{a}{K} \right)}>0.$$

Then $\varphi$ is a diffeomorphism preserving the orientation of time [9, 14]; the vector field ${{X}_{\mu }}$ is topologically equivalent to the vector field ${{Y}_{\eta }}=\varphi \circ {{X}_{\mu }}$. It take the form ${{Y}_{\eta }}=P\left( u,v \right)\frac{\partial }{\partial u}+Q\left( u,v \right)\frac{\partial }{\partial v}$ and the associated second order differential equations system is

$${{Y}_{\eta }}:\left\{ \begin{aligned}& \frac{du}{d\tau }=u\left( 1-u \right)\left( u-M \right)\left( u+A \right)-u\left( u+N \right)v \\& \\& \frac{dv}{d\tau }=B\left( u+N \right)\left( u-C \right)v \\\end{aligned} \right.$$

(9.3)

with $\eta =( B,C,A,N,M )\in \mathbb{R}_{+}^{2}\times {{( \left] 0,1 \right[ )}^{2}}\times \left] -1,1 \right[$, where $B=\frac{1}{r}\left( p-c \right),$ $C=\frac{ac}{K\left( p-c \right)},A=\frac{a}{K},N=\frac{n}{K}\,\,\text{and}\,M=\frac{m}{K}.$

Clearly, B > 0 if and only if p > c, being a necessary condition for predator to survive; system (9.3) has no ecological sense if B < 0.

For the strong Allee effect it has 0 < M < < 1; so, the equilibria are (0;0), (M;0), (1;0) and (C;L), where $L=\frac{\left( 1-C \right)\left( C+A \right)\left( C-M \right)}{C+N}$.

The point (C;L) lies in the first quadrant, if and only if, 0 < M < C < 1.

The Jacobian matrix of system (9.3) is

$$D{{Y}_{\eta }}\left( u;v \right)=\left( \begin{matrix}D{{Y}_{\eta }}{{\left( u,v \right)}_{11}} & -u\left( u+N \right) \\Bv\left( N-C+2u \right) & -B\left( C-u \right)\left( u+N \right) \\\end{matrix} \right)$$

with $D{{Y}_{\eta }}{{\left( u;v \right)}_{11}}=-4{{u}^{3}}+3\left( 1+M-A \right)+2\left( A-M-v+AM \right)u-\left( AM+Nv \right)$

9.3 Main Results

For 0 < M < < 1, system (9.3) has the following properties:

Lemma 1. Existence of invariant set

The set $\overline{\Gamma }=\left\{ \left( u,v \right)\in {{\mathbb{R}}^{2}}/0\le u\le 1,\,v\ge 0 \right\}$ is a region of positive invariance.

Proof: Since the system (9.3) is of Kolmogorov type [16], the coordinates axis are invariant sets. If u = 1, then $\frac{du}{d\tau }=-v( 1+N )<0.$ Anything the sign of $\frac{dv}{d\tau }=B\left( 1-C \right)\left( 1+N \right)v$, the trajectories enter to the set $\overline{\Gamma }$.

Lemma 2. Boundedness of solutions. The solutions are bounded.

Proof: We use the Poincaré compactification with the change of variables given by $u=\frac{w}{z}\ \text{and}\ v=\frac{1}{z};$ then,

$${{Z}_{\eta }}=\left\{ \begin{aligned}& \frac{dz}{d\tau }=-\frac{w}{{{z}^{3}}}\left( z\left( w+zN \right)\left( w-zC \right) \right)- \\& \quad \quad \frac{w}{{{z}^{3}}}\left( w-z \right)\left( w-zM \right)\left( w-zA \right)+z\left( w+zN \right) \\& \frac{dw}{d\tau }=-\frac{1}{z}\left( w+zN \right)\left( w-zC \right), \\\end{aligned} \right.$$

The equilibrium point (0;0) of vector field Z _η is equivalent to point (0;∞) of system (9.3). Evaluating in (0;0) of vector field Z _η , the zero matrix is obtained. Rescaling the time by the function$\phi :\overline{\Omega }\times \mathbb{R}\to \Omega \times \mathbb{R}$, defined as $\phi \left( w;z;{{z}^{3}}T \right)=\left( w;z;\tau \right)$, we obtain a new polynomial system given by

$${{\widetilde{Z}}_{\eta }}=\left\{ \begin{aligned}& \frac{dz}{d\tau }=-w\left( z\left( w+zN \right)\left( w-zC \right) \right)- \\& \quad w\left( w-z \right)\left( w-zM \right)\left( w-zA \right)+z\left( w+zN \right) \\& \frac{dw}{d\tau }=-{{z}^{2}}\left( w+zN \right)\left( w-zC \right), \\\end{aligned} \right.$$

The Jacobian matrix evaluated in the point (0;0) is $D{{\widetilde{Z}}_{\eta }}( 0;0 )={{\theta }_{2}}$. To desingularize the point (0;0), the technique of blowing-up is used [9, 14]. Using time rescaling defined by $\kappa =\frac{1}{{{I}^{2}}}T$and the directional blowing-up given by ${{\varphi }_{w}}( I;S )=( I;IS )=( w;z )$, we obtain

${{\overset\frown{Z}}_{\eta }}=\left\{ \begin{aligned}& \frac{dI}{d\kappa }=-I( S+I-ASI-MSI+N{{S}^{2}} )+{{I}^{2}}( {{S}^{2}}\beta -AM{{S}^{3}}-CN{{S}^{3}} ) \\& \frac{dS}{d\kappa }=S( S+I-SI-ASI-MSI )+{{S}^{3}}( N-AMSI+I\gamma), \\ \end{aligned} \right.$with $\beta =A-C+M+N+AM$and $\gamma =A+M+AM\text{.}$ We obtain again lies in the first quadrant, and a new directional blowing-up is considered, which is given by ${{\phi }_{S}}\left( E;F \right)=\left( E;EF \right)=\left( I;S \right)$. Using the time rescaling defined by $\lambda =\frac{1}{E}\kappa$ we obtain:

$${{\overline{\overline{Z}}}_{\eta }}=\left\{ \begin{aligned}& \frac{dE}{d\lambda }=E\left( F+1 \right)-F{{E}^{2}}\left( A+M-FN+F\beta E \right)-{{F}^{3}}{{E}^{4}}\left( AM+CN \right) \\& \frac{dF}{d\lambda }=2F\left( F+1 \right)-F{}^\text{2}E\left( 2A+2M-2FN+1 \right)+{{F}^{3}}{{E}^{2}}\left( \beta +\gamma \right) \\& -{{F}^{4}}{{E}^{3}}\left( 2AM+CN \right), \\\end{aligned} \right.$$

After some calculations we obtain

$$D{{\overline{\overline{Z}}}_{\eta }}\left( 0;0 \right)=\left( \begin{matrix}1 & 0 \\0 & 2 \\\end{matrix} \right).$$

Thus, $\det D{{\overline{\overline{Z}}}_{\eta }}( 0;0 )>0$and $\text{tr}D{{\overline{\overline{Z}}}_{\eta }}( 0;0 )>0;$ then, (0;0) is a repeller point of vector field ${{\overline{\overline{Z}}}_{\eta }}.$ By blowing-down of ${{\varphi }_{w}}$ and ${{\phi }_{S}}$ the point (0;0) is a non-hyperbolic repeller of vector fields ${{\overline{Z}}_{\eta }}$ and ${{\overset\frown{Z}}_{\eta }}$, respectively. This implies that the point (0;∞) of ${{Y}_{\eta }}$ is a repeller point and solutions of vector field ${{Y}_{\eta }}$ are bounded.

9.3.1 Nature of Equilibria Over the Axis

Lemma 3. The equilibrium point (0;0) is a hyperbolic attractor for all parameter values.

Proof: Immediate evaluating the Jacobian matrix at this point, since $\det D{{Y}_{\eta }}\left( 0;0 \right)=ABCMN>0$ and $\text{tr}D{{Y}_{\eta }}\left( u;v \right)=-\left( AM+BCN \right)<0.$ Therefore, (0;0) is a locally stable point.

Lemma 4. The equilibrium point P _M  = (M; 0) is

• 1. a hyperbolic repeller, if and only if, $M-C\text{ }>\text{ }0,$

• 2. a hyperbolic saddle point, if and only if, $M-C\text{ }<\text{ }0,$

• 3. a non hyperbolic repeller, if and only if, $M-C\text{ }=\text{ }0.$

Proof: As

$\det D{{Y}_{\eta }}( M;0 )=MB\text{ }( 1-M )\text{ }( A\text{ }+M )\text{ }( M\text{ }+\text{ }N )\text{ }( M-C )$ and $\text{tr}D{{Y}_{\eta }}( M;0 )=B( M-C )( M+N )+M( 1-M )( A+M ).$

• i. If $M-C\text{ }>\text{ }0,$ $\det D{{Y}_{\eta }}\left( M;0 \right)>0$ and $\text{tr}D{{Y}_{\eta }}( M;0 )>0.$ Thus, (M;0) is a hyperbolic repeller.

• ii. If $M-C\text{ }<\text{ }0,$ $\det D{{Y}_{\eta }}( M;0 )<0$; then, (M;0) is a hyperbolic saddle point.

• iii. If $M-C\text{ }=\text{ }0;$ then (C;L) coincides with the point P ₂, and $\det D{{Y}_{\eta }}\left( M;0 \right)=0$; using the Central Manifold Theorem [14], we can proved that point (M;0) is a non hyperbolic repeller.

Lemma 5. The equilibrium point (1;0) is

• 1. a saddle hyperbolic point, if and only if, $1-C\text{ }>\text{ }0,$

• 2. a hyperbolic saddle point, if and only if, $M-C\text{ }<\text{ }0,$

• 3. a non hyperbolic attractor, if and only if, $1-C\text{ }=\text{ }0.$

Proof: We have that

$$ \det D{{Y}_{\eta }}( 1;0 )=-B( A+1 )( 1-M )( 1-C )( N+1 )\quad \text{and} $$

$$\text{tr}D{{Y}_{\eta }}\left( 1;0 \right)=\left( A+1 \right)\left( 1-M \right)+B\left( 1-C \right)\left( N+1 \right)$$

• i. If $1-C\text{ }>\text{ }0,$ $\det D{{Y}_{\eta }}\left( 1;0 \right)<0;$thus (1;0) is a saddle hyperbolic point.

• ii. If $1-C\text{ }<\text{ }0,$then$\det D{{Y}_{\eta }}\left( 1;0 \right)>0$and $\text{tr}D{{Y}_{\eta }}( 1;0 )<0;$ then, (1;0) is a hyperbolic attractor point.

• iii. If $1-C\text{ = }0;$ then (C;L) coincides with (1;0), and$\det D{{Y}_{\eta }}( 1;0 )=0$; using the Central Manifold Theorem [14], it follows that the point (1;0) is a non hyperbolic attractor.

9.3.2 Existence of a Heteroclinic Curve

When the equilibria (M;0) and (1;0) are saddle points, we will demonstrate the existence of a heteroclinic curve for a given condition of parameters.

Theorem 6. Assuming 0 < M < C < 1, the equilibria (M;0) and (1;0) are hyperbolic saddle points. Then, for a subset of parameter values there exists a heteroclinic cycle ${{\gamma }_{h}}$ in the first quadrant containing these equilibria.

Proof: If (M;0) and (1,0) are both saddle points, then their corresponding invariant manifolds W ^s(M;0) and W ^u(1;0) are all one-dimensional objects. Clearly, the α-limit of W ^s(M;0) and the ω-limit of W ^u(1;0) are bounded in the direction of the v-axis. Neither the ω-limit of W ^u(1;0) is on the u-axis.

Let u ^* be such that M < u ^* < 1. Then, there are points (u ^*;v ^s)?W ^s(M;0) and (u ^*;v ^u)? W ^u(1,0), with v ^s and v ^u depending on the parameter values, such that v ^s = s(η) and v ^u = u(η).

Since the vector field Y _η is continuous with respect to the parameters values, then the stable manifold W ^s(M;0) must intersect the unstable manifold W ^u(1;0) for some parameter values. Hence, there exists a point $({{u}^{*}};{{v}^{*}})\in \overline{\Gamma }$ such that ${{v}^{*}}=v_{s}^{*}=v_{s}^{*}$.

Moreover, by uniqueness of solutions of system (9.3), this intersection must occur along a whole trajectory γ_1M, joining the equilibria (1;0) and (M;0). Therefore, the equation s(η) = u(η) defines a codimension-one submanifold in the parameters space, for which the heteroclinic curve γ_1M exists in $\mathbb{R}_{+}^{2}$, connecting the points (1;0) and (M;0).

Then, γ_1M?W ^s(M;0)∩W ^u(1;0) and it lies entirely on a segment of the u-axis and exists for any parameter value such that 0 < M < C < 1.

It follows that a heteroclinic cycle γ_h exists for certain parameter values on the same submanifold. More precisely, γ_h = (1;0)?γ_1M ?(M;0)?γ_M1.

We note that a the existence of a heteroclinic curve joining the points (1;0) and (M;0) is a common property on models with strong Allee effect.

9.3.3 Nature of the Positive Equilibrium Point

In the following we consider 0 < M < X < 1. The equilibrium point (C;L) is in the first quadrant and the Jacobian matrix evaluated at point (C;L) is:

$$ D{{Y}_{\eta }}\left( C;L \right)=\left( \begin{matrix} \left( A+C \right)\mu & -C\left( C+N \right) \\ 0 & B\left( C-M \right)\left( 1-C \right)\left( A+C \right) \\ \end{matrix} \right); $$

$$ \text{with}\quad \mu ( A,C,M,N )=\frac{C( 1-C )( A+2C-M )}{A+C}-\frac{C( C-M )( N+1 )}{C+N} $$

$$\text{and}\quad \det D{{Y}_{\eta }}\left( C;L \right)=BC\left( C+N \right)\left( C-M \right)\left( 1-C \right)\left( A+C \right)>0.$$

Let $Q={{( \text{tr}D{{Y}_{\eta }}( C;L ) )}^{2}}-4\det D{{Y}_{\eta }}( C;L )$; then,

$$Q={{\left( A+C \right)}^{2}}{{\mu }^{2}}-4BC\left( C+N \right)\left( C-M \right)\left( 1-C \right)\left( A+C \right).$$

If Q = 0, then $B=\alpha {{\mu }^{2}}$ where $\alpha =\frac{A+C}{4C\left( C+N \right)\left( C-M \right)\left( 1-C \right)}.$

With the above relations, we can establish the following theorem:

Theorem 7. Let (u ^*;v ^s)?W ^s(M;0) and (u ^*;v ^u)? W ^u(1,0).

7.1 Assuming ${{\varpi }^{\sigma }}>{{\varpi }^{\upsilon }}$, then, $(\text{X;}\Lambda )$ is

a) a local hyperbolic attractor point, if and only if, μ < 0. Moreover,

a.1 If $B<\alpha {{\mu }^{2}}$, is a focus attractor.

a.2 If$B>\alpha {{\mu }^{2}}$, is a node attractor.

b) is a hyperbolic repeller point, if and only if, μ > 0. Moreover,

b.1 If $B<\alpha {{\mu }^{2}}$, is a focus repeller, surrounded by a limit cycle.

b.2 If $B>\alpha {{\mu }^{2}}$, is a node repeller.

c) is a weak focus, at least of order one, if and only if, μ = 0.

7.2 Assuming v^s < v^u; then, (C;L) is a node repeller and (0;0) is globally asymptotically stable.

Proof: It is immediate from the evaluation of the Jacobian matrix.

If 0 < M < C < 1, $\det D{{Y}_{\eta }}( C;L )>0$. So, the nature of (C;L) will be determined by $\text{tr}D{{Y}_{\eta }}( C;L )$ and its sign is determined by μ.

i) Assuming ${{\varpi }^{\sigma }}>{{\varpi }^{\upsilon }}$, it has:

If μ < 0, the point (C;L) is a hyperbolic attractor, meanwhile if μ > 0, the point (C;L) is a hyperbolic repeller.

If Q < 0, then $B>\alpha {{\mu }^{2}}$ and (C;L) is a node.

If Q > 0, then$B<\alpha {{\mu }^{2}}$and (C;L) is a focus.

ii) Assuming ${{\varpi }^{\sigma }}>{{\varpi }^{\upsilon }}$, by the existence and uniqueness theorem ensures that the ω-limit of W ^s(M;0) or W ^u(1;0) are in $\overline{\Gamma }$. As (0;0), (1;0) are saddle points, all path in $\overline{\Gamma }$ has as its ω-limit to (0;0) which is globally asymptotically stable.

Remark 8. When ${{\varpi }^{\sigma }}>{{\varpi }^{\upsilon }}$, the stable manifold W ^s(M;0), the straight line u = 1 and the u-axis determines a subregion $\overline{\Lambda }$ (see left poster in Fig. 9.1), which is closed and bounded, i.e.,

Fig. 9.1

For 0 < M < C < 1, (C;L) is the unique positive equilibrium point. The two possible relative positions between the stable manifold W ^s(M;0) of the saddle point P _M and the unstable manifold W ^u(1;0) of saddle point P ₁ are shown. On the left side v ^s < v ^u and on the right side v ^s > v ^u. Being the vector field Y _η continuous with respect to the parameters values, then the intersection between W ^s(M;0) and W ^u(1;0) occurs

$$\overline{\Lambda }=\left\{ \left( u,v \right)\in \overline{\Omega }/M\le u\le 1,\ 0\le v\le {{v}^{s}}<{{v}^{u}} \right\}$$

is a compact region and the Poincaré-Bendixson Theorem applies there, assuring the existence of a limit cycle. As the born of this limit cycle is through of the Hopf bifurcation, the largest is obtained when v ^s = v ^u, i.e. when the heteroclinic curve γ_1M is reached.

Then, the increase of the diameter of this limit cycle by change of parameters, which will increase until to attain the heteroclinic curve.

Remark 9. To determine the weakness of the focus (C;L), the number of limit cycles bifurcating of a weak (fine) focus must be obtained [9]. The weakness of a focus indicates the number of limit cycles appearing by multiple Hopf bifurcation, i.e., the number of the concentric limit cycles surroumding a weak focus [9].

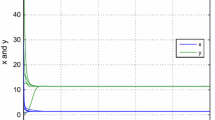
There exist various methods to establish this number being one of them the calculus of the Lyapunov quantities [9, 14]; however, this task that will not be assumed in this work. In Fig. 9.3 we show the existence of a unique limit cycle reinforced the result obtained in theorem 7b.1 (Fig. 9.2, 9.4, 9.5 and 9.6).

9.4 Some Simulations

Fig. 9.2

For A = 0.3, B = 0.2, C = 1.2, M = 0.05 and N = 0.1; there no exists positive equilibrium point. The points (1;0) and (0;0) are local attractors

Fig. 9.3

For A = 0.2, B = 0.5, C = 0.5, M = 0.15 and N = 0.4. The vector field Yh has four equilibrium points in the first quadrant; (0;0) is a attractor point; (M;0) and (1;0) are a saddle point and (C;L) is a repeller, surrounded by a stable limit cycle

Fig. 9.4

For A = 1, B = 0:5, C = 0:6, M = 0:1 and N = 0:2. The vector field Yh has four equilibrium points in the first quadrant; (0;0) is a attractor point, (M;0) and (1;0) are saddle equilibrium points and (C;L) is a node attractor

Fig. 9.5

For A = 0.1, B = 0.3, C = 0.47, M = 0.08 and N = 0.2; the point (C;L) is repeller focus and (0;0) is globally asymptotically stable. In this case, v ^s < v ^u for (u ^*;v ^s) ?W ^s(M;0) and (u ^*;v ^u) ? W ^u(1;0)

Fig. 9.6

For A = 0.1, B = 1, C = 0.25, M = 0.15 and N = 0.115. The vector field Yh has four equilibrium points in the first quadrant; (0;0) is a attractor point; (M;0) and (1;0) are a saddle point and (C;L) is a repeller, and the stable limit cycle collides with the heteroclinic curve

9.5 Conclusions

The existence of interesting dynamics has been shown, for a modified Rosenzweig-MacArthur model [27], a particular case of a Gause type predator-prey model, considering a double Allee effect on prey [1, 4]. The properties are established using a polynomial differential equations system (9.3) topologically equivalent to original system (9.2).

We proved that the model proposed have multiple stable equilibria for a determined set of parameter values and, therefore, different population behaviors can coexist.

As in all models considering strong Allee effect, in system (9.3) there exists a separatrix curve determined by the unstable manifold of equilibrium point (m,0). Then, there are trajectories near of this separatrix, which can have different ω-limit for the same set of parameter values, showing they are highly sensitive to initial conditions. So, for a fixed set of parameters, the following may happen: extinction of two populations, the coexistence for determined population sizes or oscillations of both populations.

Moreover, there are parameter constraints for which the existence of a interior equilibrium point local asymptotically stable or the existence of at least one stable limit cycle generated by Hopf bifurcation has been proved.

We affirm that Eq. (9.1) can be assumed as a paradigm to represent double Allee effect. In fact, without assuming that the population is divided into age or sex class, it can be considered that x = x(t) represents the size of fertile population and n is the non-fertile population (juvenile or oldest individuals) [2]. Populations with strong Allee effects can go extinct at lower levels of mortality by predation; also, when mortality by predation increases and weaker Allee effects can drive population to extinction.

Although extinction of predator or both species are not interesting outcomes from the point of view of population dynamics, system (9.3) it capable for a complete spectrum of dynamical behaviors that can, in principle, characterize this kind of models.

We think it is important for ecologists to be aware of the kind of bistability described for system (9.3), where two potential attractors can exist: (i) the origin; (ii) a positive equilibrium point or a stable limit cycle.