Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In this paper we consider an ad-hoc wireless network with half-duplex links [1] that carries several flows between various source-destination pairs under a slotted-time medium access control (MAC) protocol. We assume that each node in the network has a finite buffer assigned to each flow routed through it, and it is of interest to keep the buffer overflow probabilities at each node below a pre-determined value, in addition to other objectives. Reference [2] uses a class of queue back-pressure random access algorithms (QBRA), where the actual queue-lengths of the flows are used to determine a node’s channel access probabilities. In this distributed algorithm, a node uses the queue-length information in a neighborhood to determine its channel access probability to achieve proportionally fair rates and queue stability. This scheme also has the downside that nodes need to maintain separate queues for each flow routed through it.

For a network of finite-buffer nodes it is of interest to achieve fairness subject to constraints on the buffer overflow probabilities. In [3], the authors present a distributed flow-based access scheme for slotted-time protocols, that is proportionally fair while respecting the bounds on buffer overflow probabilities at each node. The results in this paper imply that packets arriving along different incoming flows into a node can be stored in a common (finite-size) buffer while they are waiting to be serviced, without any violation of the buffer overflow constraints. Since nodes have only a limited amount of available memory to store data packets, maintaining separate queues for each flow can result in significant loss of performance. Our main contributions are:

  1. 1.

    We interpret each flow in the above mentioned wireless network as a tandem of discrete-time queues with constraints that represent primary- and secondary-interference constraints. We also assume there are no capture effects, which means there can be at most one packet arrival at any discrete-time instant. The half-duplex nature of communication prevents the possibility of a simultaneous arrival and departure of packets into a queue. We present an expression for the buffer overflow probability for this class of discrete-time queues.

  2. 2.

    We show that if the objective is keep the buffer overflow probability at each node below a common bound, then it is not necessary to maintain separate queues for each flow routed through a node.

  3. 3.

    The above observation is used in an ns2 implementation of the procedure outlined in [3], and we present simulation results showing the satisfactory performance in terms of fairness and QoS when nodes maintain a single (merged) instead of separate queue for each flow.

The rest of the paper is organized as follows. Section 6.1 presents the network and discrete-time queue models used in the paper. In Sect. 6.2, we show that if all flows in the network have the same bound on the buffer overflow, nodes only need to maintain a single queue. Section 6.3 contains the details of the experimental results verifying the observations of Sect. 6.2. Conclusions are provided in Sect. 6.4.

1 Modeling the Network as a Tandem of Discrete Time Queues

1.1 Wireless Network Model

We assume the following:

  1. 1.

    Time is divided into slots of equal duration.

  2. 2.

    A successful transmission in a time-slot implies collision free data transmission in that slot.

  3. 3.

    The transmitting nodes always have data packets to transmit (i.e. we do not consider the arrival rates of packets for different flows, and assume that all flows have packets to transmit at all times).

  4. 4.

    Nodes cannot transmit and receive packets at the same time.

  5. 5.

    The receipt of more than one packet within the same time-slot will result in a collision.

  6. 6.

    Nodes in the network have a separate buffer of fixed size assigned to each flow routed through it.

  7. 7.

    We also assume there is a unique route for each flow within the network (which would be the case if we used AODV [4] as the routing protocol, for example).

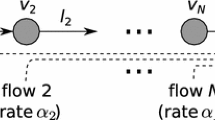
Under the above assumptions, nodes in the wireless network can be seen as discrete time queues with certain arrival and departure rates and a flow in the network passes through a tandem of discrete time queues.

1.2 Buffer Overflow Probability of a Tandem of Discrete-Time Queues

The analysis of Ref. [5] for discrete-time queues that permits simultaneous arrivals and departures of multiple packets at a discrete time instant can be modified to the case of a discrete-time queue where (1) at most one packet arrives at any discrete-time instant, and (2) the simultaneous arrival and departure of packets into/from a queue is not permitted, would result in the following – for a discrete-time queue of capacity M, with a packet arrival probability p a , and a probability p d (p d  > p a ) of a packet departure from a non-empty buffer, the probability of seeing i-many packets at any time-instant in the buffer in steady state is given by the expression

$$\displaystyle{{ \left ( \frac{1-\rho } {1 {-\rho }^{M+1}}\right )\rho^{i} },\;\mbox{ where\ }\rho = \frac{p_{a}} {p_{d}} }$$
(6.1)

For the unrestricted discrete-time queue, Ref. [5] also shows that the joint stationary state probability of a tandem of discrete-time queues is the product of the distributions of each queue taken independently with an arrival probability of p a , which is the probability of packet arrival into the first queue. This result uses the time-reversibility of the underlying Markov-chain and the mutual independence of the simultaneous states of the buffers, That is, the results in [5] can be thought of as the discrete-time analog of Jackson’s result [6] involving tandems of \(M/M/1\) queues.

As mentioned earlier, there are restrictions that one would have to enforce for a discrete-time queue to represent a node in a wireless network. For instance, as a node cannot transmit and receive information at the same time, the simultaneous occurrence of an arrival and a departure from the discrete-time queue at the node cannot be permitted. Secondary interference constraints place additional restrictions on the set of simultaneous events that can occur among neighboring nodes. Reference [7] notes that even for the unrestricted version of the discrete-time queue of Ref. [5], it is intractable to use balance equations to get an expression for the joint stationary probability for tandems of discrete-time queues. The restrictions we impose on the queues are only going to make it harder to use balance equations to arrive at an expression for the joint stationary probability for tandems of queues. It is not hard to construct examples of tandems of restricted, discrete-time queues where it can be shown that the joint stationary probability does not have a product form. In spite of this, it is possible to characterize the marginal probability distribution of each queue in the tandem.

In the restricted, discrete-time queue at most one packet is permitted to arrive, or depart from a single queue of size M. Additionally, there cannot be a simultaneous arrival and departure of a packet from the queue. For such a queue, the analysis of Ref. [5], with appropriate changes, results in the same expression as Eq. 6.1 for the probability of seeing i packets in the buffer at any time-instant. The probability of the queue of size M is non-empty is given by the expression \(\frac{1{-\rho }^{M}} {1{-\rho }^{M+1}} \times \rho \mbox{\ where\ }\rho = \frac{p_{a}} {p_{d}}\) and since the probability of a packet departure from a non-empty queue is p d , the probability of a packet-departure from the discrete-time queue is given by \(\underbrace{\mathop{ \frac{1{-\rho }^{M}} {1{-\rho }^{M+1}} }}\limits _{\leq 1} \times \underbrace{\mathop{\rho }}\limits _{=\frac{p_{a}} {p_{d}} } \times p_{d} < p_{a}.\) That is, the output process of the queue is geometrically distributed with a parameter that is no greater than the input parameter p a . This observation holds for a tandem of discrete-time queues. That is, the output process of each queue is geometrically distributed with a parameter that is no greater than that of the input to the first queue (i.e. p a ). This observation is used in establishing a bound on the buffer-overflow probabilities at each queue in a tandem of discrete-time queues in the following theorem.

Theorem 6.1.1

Consider a tandem of n discrete-time queues, each with buffer-size M, where at any discrete-time instant the probability of a packet-arrival into the first queue is p a , and the probability of a packet-departure from the i-th, non-empty queue is p di , (i = 1,2,…,n). If \(p_{dj} =\min _{i=1,\ldots ,n}\{p_{di}\}\) , and \(\rho _{max}\left(= \frac{p_{a}} {p_{dj}}\right) < \frac{M} {M+1}\) , then, the probability of seeing M packets in the i-th queue (i = 1…n) is no greater than \(\left ( \frac{1-\rho _{max}} {1-\rho _{max}^{M+1}} \right )\rho _{max}^{M}\).

Proof

We first note that \({\left ( \frac{1-\rho } {1{-\rho }^{M+1}} \right )\rho^{M} }\), increases monotonically with respect to ρ if \(\rho \leq \frac{M} {M+1}\). Let p ai be the probability of a packet arrival into the i-th queue, we know p ai  ≤ p a . If \(\rho _{i} = \frac{p_{ai}} {p_{di}}\), since p di  ≥ p dj , it follows that \(\rho _{i} \leq \rho _{max} < \frac{M} {M+1}\). The observation follows directly from the monotonicity property mentioned above.

Let β be an acceptable upper-bound on the buffer overflow probability. A direct consequence of Theorem 6.1.1 is that if we are able to pick a p a such that

$$\displaystyle\eqalign{ \frac{p_{a}} {p_{dj}}(=\rho _{max}) <{ \left [ \frac{\beta } {1+\beta }\right ]}^{1/M},}$$
(6.2)

then the buffer overflow probability at the i-th queue in the tandem of discrete-time queues will be no higher than β at all queues.

In [3], this observation is used in a convex programming solution to the problem of enforcing proportional fairness in the presence of constraints on the buffer overflow probabilities, in ad hoc wireless networks. Typically optimization problems for slotted-time protocols involve selecting the optimal access probabilities for each node such that some performance function is maximized, subject to relevant constraints (for example, [2, 3]).

If a flow is routed through nodes i → j → k, then the probability of packet arrival into (departure from) the discrete-time queue at node j is the single attempt success probability of link (i, j) (link (j, k)). Generalizing this observation, each flow in the network can be modeled as a tandem of restricted, discrete-time queues, where the idiosyncratic constraints of ad-hoc wireless networks are embedded in the expressions for these single attempt link success probabilities (cf. Eq. 6.3, Sect. 6.2). For the present,Footnote 1 each node through which a flow is routed, maintains a restricted, discrete-time queue for that flow.

2 Single Queue vs Multiple Queues

In this section we show that if all the flows in the network have the same requirement on the bound of buffer overflow probability, the nodes in the network do not need to maintain separate queues for each flow.

2.1 Link Success Probability Expression

An ad-hoc wireless network carrying a collection of flows, is represented as an undirected graph G = (V, E), where V represents the set of nodes, and E ⊆ V × V is a symmetric relationship (i.e., \((i,j) \in E \Leftrightarrow (j,i) \in E\)), that represents the set of bi-directional links. We assume all links of the network have the same capacity, which is normalized to unity. The 1-hop neighborhood of node i ∈ V is represented by the symbol N i). When a node i communicates with a node j ∈ N i), we can represent it as an appropriate orientation of the link (i, j) in E, where i is the origin and j is the terminus. The context in which (i, j) ∈ E is used should indicate if it is to be interpreted as a directed edge with i as origin and j as terminus. The set of flows, using a link (i, j) ∈ E with i (j) as origin (terminus), is denoted by \({\cal F}(i,j)\).

When node i intends to transmit data to node j ∈ N i) for the l-th flow (\(l \in {\cal F}(i,j)\)), it would transmit data in the appropriate time-slot with probability \(\tilde{p}_{i,j,l}\). \(\tilde{P}_{i,j} =\sum _{l\in {\cal F}(i,j)}\tilde{p}_{i,j,l}\), denotes the probability that node i transmits data to node j, and \(\tilde{P}_{i} =\sum _{j\in V }\tilde{P}_{i,j}\), denotes the probability that node i will be transmitting to some node in its 1-hop neighborhood for some flow. The probabilities \(\tilde{p}_{i,j,l}\)’s should be chosen such that \(\tilde{{\cal P}}_{i}\) is not greater than unity for any node i ∈ V.

The probability of successful data transmission over link (i, j) ∈ E for flow \(l \in {\cal F}(i,j)\), denoted by \({\cal S}_{i,j,l}\), is given by the expression

$$\displaystyle\eqalign{ {\cal S}_{i,j,l} =\tilde{ p}_{i,j,l} \times \left (1 -\sum _{(j,m)\in E,n\in {\cal F}(j,m)}\tilde{p}_{j,m,n}\right ) \times & & \cr \left \{\prod _{o\in N(j)-\{i\}}\left (1 -\sum _{(o,p)\in E,q\in {\cal F}(o,p)}\tilde{p}_{o,p,q}\right )\right \}.& &{}}<!end array>$$
(6.3)

Assuming there are separate queues for each flow at each node, the probability of a departure, p di l, from the discrete-time queue for the l-th flow in node i (assuming it has a packet to send) is given by the above expression. If i is the source of the l-th flow (i.e. there is always a packet to send at node i) the above expression is the probability of arrival, p a1 l, into the first queue in the tandem (which is located at node j). The above equation also ensures the service-constraint \(\sum _{j\in N(i),l\in {\cal F}(i,j)}p_{di}^{l} \leq 1\).

2.2 Merging Queues

Consider a wireless network where all flows in the network have the same requirement on the bound of the buffer overflow probability stated in the context of Theorem 6.1.1. That is, for any flow l, ρ l max  ≤ ρ max , where \(\rho _{max}^{l} = \frac{p_{a1}^{l}} {p_{dj}^{l}}\), \(p_{dj}^{l} =\min _{ i=1,\ldots ,n}\{p_{di}^{l}\}\), and p ai l (p di l) is the probability of a packet arrival (packet departure, conditioned on the queue at node i, that the l-th flow is routed through, is non-empty).

We assume that all the nodes in the network are accessing the channel with floor access probabilities so as to satisfy the buffer overflow bounds. If ρ max meets the requirement of Eq. 6.2, following Theorem 6.1.1, we have the fact that the probability of a buffer overflow at any node, for any flow, is bounded above by β.

Let us consider a node A, with a total of n flows routed through it, which maintains separate queues for each flow. Additionally, at node A,

  1. 1.

    Let \(\tilde{p}_{l}(\tilde{p}_{i,j,l}\) in Eq. 6.3) be the optimal floor access probability used by node A to transmit packets of flow l in any time slot.

  2. 2.

    \(\hat{P_{l}}\) denotes the probability that the receiving node for flow l and all the one hop neighbors of the receiving node (except transmitting node) are silent in any time slot.

  3. 3.

    l ∈ A implies that flow l routes through node A. The access intensity for any flow l ∈ A is given by \({\rho }^{l} = p_{aA}^{l}/p_{dA}^{l}\ \leq \rho _{max}\), where \(p_{dA}^{l} =\tilde{ p}_{l}\hat{P_{l}}\) (cf. Eq. 6.3).

  4. 4.

    The overall access probability for node is \(\tilde{P}_{A} =\sum\limits _{l\in A}\tilde{p}_{l}\).

Now if n queues are merged into a single queue and for each packet in the queue, node A uses \(\tilde{P}_{A}\) to access the channel, then,

  1. 1.

    The effective arrival rate of the single merged queue is given by ∑ l ∈ A p l aA .

  2. 2.

    The effective departure rate of the single combined queue is given by the expression \(\left (\tilde{P}_{A}\frac{\sum _{l\in A}\hat{P_{l}}p_{aA}^{l}} {\sum _{l\in A}p_{aA}^{l}} \right ).\)

Theorem 6.2.1

The traffic intensity of the merged queue is at most ρ max .

Proof

Let us compute the \(\hat{\rho }\) for the merged queue at node A.

$$\displaystyle\eqalign{ \hat{\rho } = \frac{\sum _{l\in A}p_{aA}^{l}} {\tilde{P}_{A}\left (\frac{\sum _{l\in A}\hat{P_{l}}p_{aA}^{l}} {\sum _{l\in A}p_{aA}^{l}} \right )} = \frac{{\left(\sum _{l\in A}p_{aA}^{l}\right)}^{2}} {\left(\sum _{l\in A}\tilde{p}_{l}\right)\left(\sum _{l\in A}\hat{P_{l}}p_{aA}^{l}\right)} \cr = \frac{{\left(\sum _{l\in A}p_{aA}^{l}\right)}^{2}} {\left(\sum _{l\in A}\left({\left(p_{aA}^{l}\right)}^{2}{/\rho }^{l}\right) +\sum _{l\in A}\tilde{p}_{l}\sum _{j\in A,j\neq l}\hat{P_{j}}p_{aA}^{j}\right)}.{}}<!end array>$$
(6.4)

Now, let us look at one term in the second summand in the denominator,

$$\displaystyle\eqalign{ \tilde{p}_{l}\sum _{j\in A,j\neq l}\hat{P_{j}}p_{aA}^{j}= \tilde{p}_{ l}\sum _{j\in A,j\neq l}\frac{p_{dA}^{j}p_{aA}^{j}} {\tilde{p}_{j}} = p_{aA}^{l}\sum _{ j\in A,j\neq l}{\frac{p_{aA}^{j}\tilde{p}_{l}} {\rho }^{l}\tilde{p}_{j}} \frac{p_{dA}^{j}} {p_{dA}^{l}} {}\cr }<!end array>$$

Using this in (6.4), along with the observation that ρ l < ρ max we have,

$$\displaystyle\eqalign{ \hat{\rho } \leq \frac{\rho _{max}{(\sum _{l\in A}p_{aA}^{l})}^{2}} {(\sum _{l\in A}{(p_{aA}^{l})}^{2} +\sum _{l\in A}\sum _{j\in A,j\neq l}p_{aA}^{l}p_{aA}^{j}\frac{\tilde{p}_{l}} {\tilde{p}_{j}} \frac{p_{dA}^{j}} {p_{dA}^{l}} )} \cr \leq \frac{\rho _{max}{(\sum _{l\in A}p_{aA}^{l})}^{2}} {(\sum _{l\in A}{(p_{aA}^{l})}^{2} +\sum _{l\in A}\sum _{j\in A,j>i}p_{aA}^{l}p_{aA}^{j}(\frac{\tilde{p}_{l}} {\tilde{p}_{j}} \frac{p_{dA}^{j}} {p_{dA}^{l}} + \frac{\tilde{p}_{j}} {\tilde{p}_{l}} \frac{p_{dA}^{l}} {p_{dA}^{j}}))}.{}}<!end array>$$
(6.5)

Let \(x = \frac{\tilde{p}_{l}} {\tilde{p}_{j}}\) and \(y = \frac{p_{dA}^{l}} {p_{dA}^{j}}\), using the fact that \(x/y + y/x \geq 2\), we have, \(\left(\frac{\tilde{p}_{l}} {\tilde{p}_{j}} \frac{p_{dA}^{j}} {p_{dA}^{l}} + \frac{\tilde{p}_{j}} {\tilde{p}_{l}} \frac{p_{dA}^{l}} {p_{dA}^{j}}\right) \geq 2.\) Therefore,

$$\displaystyle{{\left(\sum _{l\in A}p_{aA}^{l}\right)}^{2} \leq \left(\sum _{ l\in A}{(p_{aA}^{l})}^{2} +\sum _{ l\in A}\sum _{j\in A,j>l}p_{aA}^{l}p_{ aA}^{j}\left( \frac{\tilde{p}_{l}} {\tilde{p}_{j}} \frac{p_{dA}^{j}} {p_{dA}^{l}} + \frac{\tilde{p}_{j}} {\tilde{p}_{l}} \frac{p_{dA}^{l}} {p_{dA}^{j}}\right)\right).}$$

Hence, from (6.5), we get, \(\hat{\rho }\leq \rho _{max}\).

Using a single queue instead of multiple queue at each node has the advantage that nodes in the network do not need to maintain separate queue for each flow routed through it, to respect the buffer overflow bound for each flow.

3 Preliminary Results

In this section, we describe the experiments that show how ST-MAC protocol [8] performs when the RTS-signal in the corresponding RTS-slot is transmitted with a probability as determined by the optimization algorithm discussed in [3]. For this, we compare the performance of the ST-MAC protocol using different bounds on the flow’s buffer overflow probabilities (i.e. different traffic intensities). These experiments involved the implementation of the optimization algorithm within the ns2 network simulator [9]. A detailed implementation of the 802.11-MAC protocol already exists as a part of the simulation model.

The results presented in this section, provide an understanding of the performance of the optimization algorithm presented in [3], in terms of fairness and buffer overflow probabilities. It is important to point out that in ns2 network simulator, in addition to transmitting data for unicast flows in the network, nodes also perform additional functions such as route discovery and maintenance using broadcast packets, for example, the broadcasting of route request queries. The simulation results demonstrate the performance of ST-MAC protocol in presence of these additional network traffic.

3.1 Traffic and Mobility Models Used in the Experiments

The pause-time is kept constant and equal to the simulation time (i.e. there is no mobility) in all our experiments. Lucent’s WaveLAN with 2 Mbps bit rates and 250 m-transmission range is used for the radio model. An omnidirectional antenna is used by the mobile/wireless nodes. The carrier sense range is the same as the transmission range in our simulation experiments, i.e. the packets are assumed to interfere with each other only when a receiver is within the transmission range of two sources that are transmitting simultaneously. We chose AODV [4] as the ad hoc routing protocol. Each flow in the network has the same bound on the buffer overflow probability.

In the simulations the retry limit for data packets is set to 4 for 802.11-MAC, which is the default 802.11-MAC long-retry limit. In case of ST-MAC protocol, there is no retry limit, i.e., the nodes keep trying to transmit the packet until its successful. In simulations, at each node a single Drop Tail Queue of size 50 packets was selected as an interface queue for both these protocols.

We then choose ten random source-destination pairs in the network shown in Fig. 6.1a, simulated within a 1,000 × 1,000 m field. Each source generates data packets of 512 bytes each. We run 20 different simulation instances with this fixed network layout and source-destination pairs, by varying the start times of each flow in the network by some milliseconds. Depending on the start time of the flows, AODV chooses different routes for different simulation instances, which are not same in all the instances.

For our simulation comparisons, we compared the following for scenarios:

  • Nodes using 802.11 as MAC protocol, with TCP connections between the source-destination pairs. This provides us with the reference frame, for comparisons using different performance metrics, among the optimization algorithms using different bounds on buffer overflow probabilities and step sizes, when nodes in the network use ST-MAC protocol and CBR traffic.

  • ST-MAC protocol with constant-bit-rate (CBR) flows between each source-destination pair, ρ varying from 0. 86 to 1. 0 for each flow.

The simulation time for each simulation is 620 s. The nodes start using the flow rates and access probabilities given by optimization algorithm [3] after 120 s from the start of the simulation and the simulation continues for additional 500 s. The nodes keep updating the flow rates and access probabilities until the simulation terminates.

In the case of 802.11-MAC protocol, the TCP connections are started when the simulation starts. For ST-MAC, however, we wait a total of 120 s before the nodes start transmitting at optimal rates. During this time, the sources transmit at very low rates so as to prevent any network congestion.

3.2 Results

Figures 6.1b and 6.2a, b show the plots of the average network throughput, packet-delivery ratios and end-to-end delays for different simulation runs of the scenarios mentioned in the earlier section. In case of 802.11-MAC the average packet delivery ratio and end to end delay is low and the because the packets are dropped by 802.11-MAC after four retries. This also contributes to lower the throughput in case of TCP.

In case of ST-MAC protocol, as ρ increases the network throughput increases but at a cost of larger delays and higher packet loss. As the value of ρ is increased, the network delay increases because of increase in queuing delays. Also, we can observe that when ρ = 1, the packet delivery ratio decreases as more packets are getting dropped because of buffer overflows.

Fig. 6.1
figure 1

Simulated network and throughput. (a) Ad hoc wireless network with 100 nodes, 10 connections. (b) Average network throughput

Full size image
Fig. 6.2
figure 2

Network packet delivery ratio and average delay. (a) Average network packet delivery ratio. (b) Average network end to end delay

Full size image

4 Conclusion

Each end-to-end flow in an ad-hoc wireless network of half-duplex nodes using a slotted time protocol can be viewed as a tandem of discrete-time queues with restrictions that capture constraints specific to wireless networks. We derive a bound on the buffer overflow probabilities for each queue in the tandem. We then suppose that all queues, irrespective of the flows they serve, are subject to a common buffer overflow bound. We show that for this case there is no need to maintain separate queues for each flow that is routed through a host. These flows can all be merged into a single queue and served as if there were just one flow, and the buffer overflow bounds will still be met. This observation finds use in the implementation of the distributed algorithm that enforces proportional fairness subject to buffer overflow constraints outlined in Ref. [3]. We present some simulation results of this implementation.