Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

From a phenomenological point of view, the Landau-Lifshitz-Gilbert(LLG) equation is considered to be the basic dynamical equation for describing magnetization/magnetic moment or simply spin \(\mathbf{{S}}(\mathbf{{r}},t)\), including the damping effects [1–3], for bulk materials in applied magnetism. The Landau–Lifshitz (LL) equation can also be deduced in a systematic manner by starting with a lattice spin Hamiltonian with Heisenberg type nearest neighbour interactions, by postulating appropriate spin Poisson brackets, and writing down the Hamilton’s equation of motion for the spins and then taking the classical limit (\(\hbar \rightarrow 0\)) of the quantum spin dynamical equation and then the continuum limit to obtain the LL equation [4, 5]. Then the Gilbert damping term can be introduced phenomenologically [6]. The LLG equation is an extremely interesting nonlinear evolution equation, because of its length constraint, normalized as \(|\mathbf{{S}}|^{2}=1\). Correspondingly it admits a large variety of dynamical structures including spin waves, elliptic function waves, solitary waves, solitons, lumps, dromions, vortices, bifurcations and chaos, spatio-temporal patterns, etc. [5].

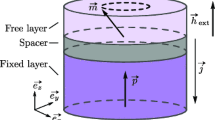
In recent times the study of nonlinear dynamics of spin systems has received renewed interest due to the work of Slonczewski [7] and Berger [8] on the macrospin behaviour of spins of the free layer of a nanospin valve pillar of Fe/Cu/Fe type trilayers due to spin torque effect under the injection of a horizontal spin current in the presence of applied magnetic fields. In the semiclassical representation the corresponding nonlinear evolution is represented by a Landau–Lifshitz–Gilbert–Slonczewski (LLGS) equation [9] which includes an additional term to represent the effect of spin current on the magnetization spin vector. In the case of homogeneous magnetization, the dynamics of the macrospin of the free layer of the nano-valve pillar, the so called spin transfer nano-oscillator (STNO), is effectively a nonlinear oscillator equation exhibiting interesting bifurcation and chaos scenario.

Since the power generated by a single STNO is rather low for microwave generation, it has been recently suggested that the property of synchronization of nonlinear oscillators [10] can be profitably utilized for increased power generation by appropriate coupling of STNOs in series or parallel arrays [11, 12], with or without delay [13, 14]. Even a suitable addition of white noise to the injected current has been shown to lead to in-phase and anti-phase synchronizations of limit cycle oscillations of STNOs [15]. In this article, we investigate the interesting possibility of synchronizing limit cycle oscillations due to the action of a common applied periodically driven external magnetic field leading to synchronization of both in-phase and anti-phase limit cycle oscillations. We also consider the possibility of mass synchronization of coupled phase oscillators of different groups through appropriate coupling as a means of high quality synchronization of STNOs.

2 Heisenberg Ferromagnetic Spin Equation and Extension to STNO

It is well known that the expectation value of the spin angular momentum operator of an electron or equivalently magnetization per unit volume, after normalization, represented as a classical unit vector in three dimensions evolves [16] under the action of a time dependent external magnetic field \(\mathbf{{H}}(t)\) as

$$\begin{aligned} \frac{d\mathbf{{S}}(t)}{dt}=-\gamma _{0}[\mathbf{{S}}(t) \times \mathbf{{H}}(t)], \;\; \mathbf{H} = (H^x,H^y,H^z), \end{aligned}$$
(1)

where \(\mathbf{{S}}^2 = 1,\;\; \mathbf{S} = (S^x,S^y,S^z)\). Here \(\gamma _0\) is the gyromagnetic factor. From a knowledge of the hysteresis curves of ferromagnetic substances where the magnetization saturates, becomes uniform and aligns parallel to the magnetic field, Gilbert [6] introduced the phenomenological damping term to modify Eq. (1) (after suitable rescaling) as

$$\begin{aligned} \frac{d\mathbf{S}}{dt}&=~(\mathbf{{S}} \times \mathbf{{H}}(t))+\lambda \mathbf{{S}} \times [\mathbf{{S}} \times \mathbf{{H}}(t)], \end{aligned}$$
(2)

where \(\lambda \) is the phenomenological Gilbert damping coefficient. Extending the above phenomenological form of the evolution equation for a single spin to a lattice of spins representing a ferromagnetic material, for example a cubic lattice of \(N\) spins with nearest neighbour interactions, onsite anisotropy, demagnetizing field, applied external magnetic field and so on, the evolution equation for the spins can be written [5] as

$$\begin{aligned} \frac{d\mathbf{{S}}_i}{dt}~=~\mathbf{{S}}_i \times \mathbf{{H}}_{eff}+\lambda \mathbf{{S}}_i \times [\mathbf{{S}}_i \times \mathbf{{H}}_{eff}],~~~ i = 1,2,\ldots , N, \end{aligned}$$
(3)

where

$$\begin{aligned} \mathbf{{H}}_{eff}=~&(\mathbf{{S}}_{i+1} + \mathbf{{S}}_{i-1} + A S^x_i \mathbf{n}_x + B S^y_i \mathbf{{n}}_y + C S^z_i \mathbf{n}_z + \mathbf{H}(t) +\cdots ) . \end{aligned}$$
(4)

Here \(A,\;B\) and \(C\) are anisotropy parameters and \(\mathbf{{n}}_x, \mathbf{{n}}_y\) and \(\mathbf{{n}}_z\) are unit vectors. Going over to a continuum limit such that \(\mathbf{{S}}_i(t)=\mathbf{{S}}(\mathbf{{r}},t)\), \(\mathbf{{r}}=(x,y,z)\) and \(\mathbf{{S}}_{i+1}+\mathbf{{S}}_{i-1}=\mathbf{{S}}(\mathbf{{r}},t)+\mathbf{{a}}.\nabla \mathbf{{S}}+\frac{a^2}{2}\nabla ^2\mathbf{{S}}+\) higher order (here \(\mathbf{{a}}\) is the lattice vector), the Landau–Lifshitz–Gilbert (LLG) equation for the spin vector in the form of a vector nonlinear partial differential equation can be written down as

$$\begin{aligned} \frac{\partial \mathbf{S}(\mathbf{r},t)}{\partial t} =&\mathbf{S} \times \mathbf{{H}}_{eff}(\mathbf{r},t) +\mathbf{S} \times (\mathbf{S} \times \mathbf{{H}}_{eff}(\mathbf{r},t)), \end{aligned}$$
(5)
$$\begin{aligned} \mathbf{S}(\mathbf{r},t)=&(S^x(\mathbf{r},t),S^y(\mathbf{r},t),S^z(\mathbf{r},t)),\quad \mathbf{S}^2 = 1, \end{aligned}$$
(6)

and the effective field is given by

$$\begin{aligned} \mathbf{{H}}_{eff}&= \mathbf{{H}}_{\text{ exchange }}+\mathbf{{H}}_{\text{ anisotropy }}+\mathbf{{H}}_{\text{ demag }} +\mathbf{{H}}_{\text{ appl }},\nonumber \\&= (\nabla \mathbf{S})^2 + A S^x \mathbf{{n}}_x + B S^y \mathbf{{n}}_y +C S^z \mathbf{{n}}_z + H_{\text{ demag }} +\mathbf{{H}}(t). \end{aligned}$$
(7)

In the above, \(\mathbf{{H}}_{\text{ demag }}\) is the demagnetizing field of the material and \(\mathbf{{H}}_{app}\) is the applied magnetic field. Equation (5) is a complicated vector nonlinear partial differential equation. Depending upon the nature of the interactions present in the system and the form of \(\mathbf{{H}}_{eff}\), Eq. (5) can admit several kinds of interesting nonlinear dynamical structures. These include spin waves, elliptic function waves, solitary waves, solitons, drominons, vortices, instability induced spatio-temporal patterns, etc. [5]

3 LLGS Equation and the Dynamics of a STNO

The LLG equation has attracted renewed interest in recent times due to intense study of magnetization dynamics in devices such as nanospin valves/pillars in connection with spin torque transfer effect. Slonczewski [7] and Berger [8] have independently shown in 1996 that when a polarized spin current passes through a trilayer of ferromagnetic/nonferromagnetic (conducting)/ferromagnetic materials of size 100 nm or so, a spin torque transfer effect occurs. Slonczewski [7] further showed semiclassically that the influence of spin current can be effectively analysed with the addition of a simple term to the LLG equation as

$$\begin{aligned} \frac{\partial \mathbf{S}}{\partial t} = \mathbf{S} \times [\mathbf{{H}}_{eff}+\lambda (\mathbf{{S}} \times \frac{\partial \mathbf{S}}{\partial t})+ \mathbf{S} \times \mathbf{j}],\quad \mathbf{S}=(S^x, S^y, S^z),~~~ \mathbf{S}^2=1, \end{aligned}$$
(8)

where the spin current term can be given in the form

$$\begin{aligned} \mathbf{j} = \frac{a.\mathbf{S}_P}{f(P)(3+\mathbf{S} . \mathbf{S}_P)},~~~~~f(P)=\frac{(1+P^3)}{4P^{\frac{3}{2}}}. \end{aligned}$$
(9)

Here \(\mathbf{{S}}_p\) is the pinned or fixed direction of the polarized spin current that is normally taken as perpendicular to the direction of flow of current, \(a\) is related to the strength of the spin current and \(f(P)\) is a polarization factor. A simple approximation can be made to the above form of the spin current as

$$\begin{aligned} \mathbf{j}~=~a \mathbf{S}_p. \end{aligned}$$
(10)

Then the spin torque transfer effect can be represented by the Landau–Lifshitz–Gilbert–Slonczewski (LLGS) equation

$$\begin{aligned} \frac{\partial \mathbf{S}}{\partial t} = \mathbf{S} \times \mathbf{{H}}_{eff}+\lambda \mathbf{{S}} \times \left[ \mathbf{{S}} \times \frac{\partial \mathbf{S}}{\partial t} \right] +a \mathbf{{S}} \times [\mathbf{S}\times \mathbf{S}_p], \end{aligned}$$
(11)

where \(\mathbf{{H}}_{eff}\) is as given in Eq. (4).

The LLGS equation can also be written in a more transparent form by projecting the unit spin vector on a stereographic plane [17]

$$\begin{aligned} \omega ~=~ \frac{S^x + i S^y}{(1+S^z)} \end{aligned}$$
(12)

so that Eq. (8) becomes

$$\begin{aligned} i(1-i\lambda )\omega _t&+ \nabla ^2 \omega - \frac{2 \omega ^* (\nabla \omega )^2}{(1+\omega \omega ^*)} + \frac{A}{2} \frac{(1-\omega ^2)(\omega +\omega ^*)}{(1+\omega \omega ^*)}\nonumber \\&+ \frac{B}{2} \frac{(1+\omega ^2)(\omega -\omega ^*)}{(1+\omega \omega ^*)} - C(\frac{1-\omega \omega ^*}{1+\omega \omega ^*})\omega \\ +\,\,\frac{1}{2}(H^x - i j^x)(1-\omega ^2)&+ \frac{1}{2} i (H^y+ij^y) (1+\omega ^2) - (H^z + ij^z)\omega = 0,\nonumber \end{aligned}$$
(13)

where \(\mathbf{j}= a \mathbf{S}_p,~ \omega _t = (\frac{\partial \omega }{\partial t}).\) From the form of Eq. (14) it is clear that the effect of the spin current term \(\mathbf{{j}}\) simply is to change the magnetic field

$$\begin{aligned} \mathbf{{H}}=(H^x,H^y,H^z) \rightarrow (H^x-ij^x,H^y+ij^y,H^z+ij^z). \end{aligned}$$
(14)

Thus one may realize that the effect of spin current and magnetic field complement each other.

Finally, when the free layer of the spin valve is homogeneous, the effect of exchange term in Eq. (11) or (14) can be neglected. The resultant LLGS equation is effectively that of a nonlinear oscillator (after rescaling),

$$\begin{aligned} \frac{d{\mathbf{{S}}}}{dt}=-\gamma {\mathbf{{S}}}\times {\mathbf{{H}}}\,_{eff}+\lambda \mathbf{{S}}\times \frac{d{\mathbf{{S}}}}{dt}-\gamma a{\mathbf{{S}}}\times (\mathbf{{S}}\times \hat{\mathbf{{S}}_{p}}), \end{aligned}$$
(15)

where now

$$\begin{aligned} \mathbf{{S}}=\mathbf{{S}}(t) \end{aligned}$$
(16)

only. Taking \(\mathbf{{H}}_{eff}=-4\pi S_0 S_x \mathbf{{i}}+\kappa S_z\mathbf{{k}}+h_{a3}\mathbf{{k}}\), where the saturation magnetization \(4\pi S_0=8400\) Oe for permalloy film, we can rewrite Eq. (15) equivalently in terms of the stereographic variable \(\omega (t)\) as

$$\begin{aligned} (1-i\lambda )\dot{\omega }&= -\gamma (a-ih_{a3})\omega +i\kappa \gamma \frac{(1-|\omega |^{2})}{(1+|\omega |^{2})}\omega \\&+ \frac{i\gamma 2\pi S_0}{1+|\omega |^{2}}[ (1-\omega ^{2}-|\omega |^{2})\omega +\omega ^*],\;(\dot{\omega }=\frac{d\omega }{dt}).\nonumber \end{aligned}$$
(17)

Here \(\gamma \) is the gyromagnetic ratio. Eq. (15) or (17) may be considered as the LLGS equation describing the dynamics of the macrospin variable of a single STNO. Depending upon the type of interactions, a STNO can exhibit the standard bifurction-chaos scenario of a nonlinear oscillator [18, 19]. In Fig. 1, we represent the phase diagrams in the (\(h_{dc}-a)\) plane indicating periodic regimes, including limit cycles and chaotic behaviour both for isotropic and anisotropic cases with oscillating magnetic field. Here \(\mathbf{{H}}=(h_{dc}+h_{ac}\cos \omega t)\mathbf{{i}}\). Note that periodic oscillations of different types, chaos, period doubling transitions, etc. occur [19].

Fig. 1
figure 1

Regions of chaos in the \(a-h_{a3}\) space, for an applied alternating magnetic field along the \(z\) direction for isotropic a and anisotropic b cases. The dark regions indicate values for which the dynamics is chaotic, i.e, regions where the largest Lyapunov exponent is positive [19]. The white regions are the periodic regimes or limit cycles. Here \(h_{a3}\) is the applied dc magnetic field

Full size image

4 Dynamics of Arrays of STNOs

We next consider an array of two STNOs in the presence of a common applied magnetic field (Fig. 2)

$$\begin{aligned} \mathbf{{H}}_{app}=\mathbf{{H}}(t)=(h_{dc}+h_{ac}\cos \omega t,0,0), \end{aligned}$$
(18)

by the system of LLGS equations of the magnetizations of two STNOs

$$\begin{aligned} \frac{d\mathbf{{S_{1}}}}{dt}&= -\gamma \mathbf{{S_1}}\times \mathbf{{H_1}}_{eff}+\lambda \mathbf{{S_1}}\times \frac{d\mathbf{{S_1}}}{dt}-\gamma a\mathbf{{S_1}}\times (\mathbf{{S_1}}\times \mathbf{{S_{p}}}),\\ \frac{d\mathbf{{S_{2}}}}{dt}&= -\gamma \mathbf{{S_2}}\times \mathbf{{H_2}}_{eff}+\lambda \mathbf{{S_2}}\times \frac{d\mathbf{{S_2}}}{dt}-\gamma a\mathbf{{S_2}}\times (\mathbf{{S_2}}\times \mathbf{{S_{p}}}),\nonumber \end{aligned}$$
(19)

where \(|\mathbf{{S_1}}|^{2}=S_{1x}^{2}+S_{1y}^{2}+S_{1z}^{2}=1\), \(|\mathbf{{S_2}}|^{2}=S_{2x}^{2}+S_{2y}^{2}+S_{2z}^{2}=1\) or equivalently one can write down the corresponding evolution equation for the stereographic variables \(\omega _1(t)\) and \(\omega _2(t)\). Here we take \(\mathbf{{H_1}}_{eff}=\mathbf{{H_2}}_{eff}=\mathbf{{H}}_{eff}\) with appropriate spin number.

Fig. 2
figure 2

The schematic representation of an array of two STNOs placed in the oscillatory external magnetic field

Full size image

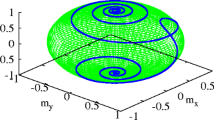
We have numerically integrated the above set of equations and found that both in-phase and anti-phase synchronizations occur in the presence of oscillating magnetic field and spin current. For example, in Fig. 3a, b, we plot the \(\mathbf{{z}}\) component of the spin vectors of the two oscillators for the anisotropic field strength \(\kappa =45\) Oe, external magnetic field strength \(h_{dc}=500 \) Oe and external current \(a=220 \) Oe, both time series and phase space plot. The figure clearly shows the existence of anti-phase synchronization.

Fig. 3
figure 3

The time series (a, c, e, f) and phase space plots (b, d, f, h) of an array of two STNOs with same anisotropy field \(\kappa = 45.0\) (a–d) and with different anisotropy fields \(\kappa _{1} = 45.0\)  Oe, \(\kappa _{2} = 45.1\) (e–h) placed in the oscillating external magnetic field of strength \(h_{ac}=10\) Oe of frequency \(\omega =15~ns^{-1}\), exhibiting anti-phase (a, b, e, f) and in-phase (c, d, g, h) synchronizations. Other parameters are (a, b) \(h_{dc}=500 \) Oe and \(a=220\) Oe, (c, d) \(h_{dc}= 500\) Oe and \(a= 221\) Oe, (e, f) \(h_{dc}=350 \) Oe and \(a=245\) Oe and (g, h) \(h_{dc}=500 \) Oe and \(a=220\) Oe

Full size image

In Fig. 3c, d, we present similar results for a different external magnetic field strength \(h_{dc}=500 \) Oe and external current \(a=221\) Oe with all the other parameters unchanged. It clearly shows the existence of in-phase synchronization of limit cycle oscillations.

In order to confirm that the above synchronization aspects are robust, we present the results of our numerical analysis for the case in which there is a slight mismatch in the system parameters of the two STNOs with the choice of anisotropy strength \(\kappa _1 = 45.0\) for the first oscillator and \(\kappa _{2}=45.1\) for the second oscillator. In Fig. 3e–h we show the in-phase and anti-phase synchronizations for this case.

In Fig. 4 we show the occurrence of synchronization for 100 STNOs for external magnetic field strength \(h_{dc}=500 \) Oe, external current \(a=220\) Oe and anisotropy strength \(\kappa _i\), \(i=1,2,\ldots 100\) distributed randomly between 45 and 46. In the phase space plot, Fig. 4 (right), we show that the 61th STNO is in in-phase with the 17th STNO and in anti-phase synchronization with the 82nd STNO. So we confirm the phenomenon of synchronization in the presence of the external driven magnetic field even for large number of STNOs. For further details on synchronization of STNOs, see Ref. [20].

Fig. 4
figure 4

The time series (left) and phase space (right) plots of an array of 100 nonidentical STNOs shows the anti-phase synchronization. In the right panel we show that the 61th STNO is in in-phase synchronization with the 17th STNO and in anti-phase synchronization with the 82nd STNO

Full size image

5 Mass Synchronization in an Array of STNOs

The dynamics of an array of STNOs can also be represented using models of coupled phase oscillators. For instance, if we consider the synchronization of coupled STNOs via external ac field, we assume that all the STNOs have the same output frequency. According to Ref. [21] the energy injected from the external ac field \(H_{ac}\) to the ith STNO is given as

$$\begin{aligned} E_i=-\mu _0M_SV_0\oint \mathbf{{H_{ac}}} . d\mathbf{{m}}_i, \end{aligned}$$
(20)

where \(\mathbf{{m}}_i\) is the orbit of the small amplitude in-plane oscillation, \(\mu _0\) is the vacuum permeability and \(V_0\) is the volume of the free layer. This energy injected by the ac current is much lesser compared to that injected by the dc current and hence the former can be treated as a perturbation. Thus one can represent the phase dynamics of the ith STNO as

$$\begin{aligned} \dot{\theta _i}= \omega _i- \frac{\sigma }{N}\sum _{j=1}^{N} \sin (\theta _i-\theta _j+\alpha ), i=1,2, \ldots , N, \end{aligned}$$
(21)

where \(\alpha \) is the phase shift. Georges et al. [11] found that in the case of series or parallel arrays, there occurs a problem of impedance-matching where the output power does not increase with the number of oscillators for large values of N if \(NR>> Z_0\) in the case of series arrays and the STNOs shunt each other with the output power increasing as \(N^2\) only if \(NZ_0<<R\); here \(Z_0\) is the load. Hence the authors of [11] proposed hybrid arrays (a combination of series and parallel configuration). In this configuration, the phase of the oscillator \((n,m)\) in the hybrid array can be described by the following equation

$$\begin{aligned}&\dot{\theta _i}^{(\eta )} = \omega _i^{(\eta )} - \sum _{\eta '=1}^{N'}\frac{\sigma _{\eta \eta '}}{N}\sum _{j=1}^{N} \sin (\theta _i^{(\eta )}-\theta _j^{(\eta ')}+\alpha _{\eta \eta '})+\zeta _i^{(\eta )}(t),\\&i=1,2, \ldots , N,\nonumber \end{aligned}$$
(22)

where \(N'\) parallel branches have each \(N\) STNOs connected in series. \(\sigma _{\eta \eta '}\) is the strength of the coupling between the STNOs in \(\eta '\) and those in \(\eta \). Here \(\omega _k^{(\eta )}\) is the natural frequency of the \(k\)th STNO in the branch \(\eta \) and \(\zeta _i^{(1,2)}\) are independent Gaussian white noises with \(\langle \zeta _i^{(\eta )}(t)\rangle =0\) and \(\langle \zeta _i^{(\eta )} (t)\) \(\zeta _j^{(\eta )'}(t) \rangle \) \(=2D^{(\eta )}\delta (t-t')\delta _{ij}\) and \(D^{(\eta )}\) are the noise intensities.

Now, a maximum output power can be harvested if all the STNOs are synchronized; let us call this phenomenon as mass synchronization. In this section let us discuss a method to induce mass synchronization in the system of STNOs that are in hybrid configuration by inducing synchronization in any one of the series or parallel arrays. That is, by inducing synchronization within the STNOs of any one of the series or parallel arrays, mass synchronization can be achieved. For a better understanding of the system configuration, let us refer to the following schematic diagram (Fig. 5).

Fig. 5
figure 5

Schematic representation of system (22) for \(N'=2\). \(\theta _i^{(1)}\) is the source branch and \(\theta _i^{(2)}\) is the target branch. The coupling strengths within the branches are quantified by the parameters \(\sigma _{11}\) and \(\sigma _{22}\). The coupling strengths from the source to the target and the target to the source are quantified by the parameters \(\sigma _{12}=\mu \sigma _{21}\) and \(\sigma _{21}\), respectively [22]

Full size image

In order to acheive mass synchronization, we plan to induce synchronization in any one of the arrays. For the same, we need to quantify the strength of the synchronization within each of the arrays.

We use Kuramoto’s complex order parameter to measure the strength of synchronization within an array. The order parameter can be given as

$$\begin{aligned} z_{\eta }=r_{\eta }e^{i\psi ^{(\eta )}}= \frac{1}{N}\sum _{j=1}^Ne^{i\theta _j^{(\eta )}}. \end{aligned}$$
(23)

When \(r_{\eta }=1\) there is complete synchronization within the \(\eta \)th array and when \(r_{\eta } =0\) there is complete desynchronization in the \(\eta \)th array. When \(r_{\eta }\) takes a value between 0 and 1, there is a partial synchronization in the \(\eta \)th array. We shall use the time average of \(r_{\eta }\) in order to characterize the occurrence of strong synchronization within the corresponding array. Numerically, for \(T=10^5\) units, the occurrence of synchronization within an array can be characterized by \(R_{\eta } > 0.8\). Here \(R_{\eta }\) is the time average of \(r_{\eta }\), that is,

$$\begin{aligned} R_{\eta }=<r_{\eta }>=\frac{1}{T}\int _{0}^{T}r_{\eta }dt. \end{aligned}$$
(24)

In order to find out the dynamical factors that cause the occurrence of mass synchronization, we numerically simulate system (22) using Runge–Kutta fourth order routine. We use a time step of \(0.01\).

We have fixed \(N=1000\) and have assumed a Lorentzian distribution for the oscillator frequencies given by \( g(\omega ^{(\eta )})=\frac{\gamma _{\eta }}{\pi }\bigg [(\omega ^{(\eta )}-\omega _{\eta })^2+\gamma _{\eta }\bigg ]^{-1}, \) where \(\gamma \) is the half width at half maximum and \(\omega _{\eta }\) is the central frequency. We consider a random distributon for the initial phases of the STNOs, distributed between 0 and 2\(\pi \).

Let us now discuss how the occurrence of synchronization in the source branch induces mass synchronization in the other branches as well, leading to an increase in the synchronized output power.

Fig. 6
figure 6

The time average of \(r_\eta \) (a and b) and the time average local and global order parameters, \(R_{avg}\) and \(R_g\), (c and d) for increasing \(\sigma _{11}\) is plotted for two different noise strengths \(D^{\eta }=0.1\) (a and c) and \(D^{\eta }=0.5\) ((b) and (d)) for \(N'=3\), \(\eta =1,2,3\). Here \(\sigma _{\eta \eta }=0.01\), \(\sigma _{\eta 1}=1.5\), \(\sigma _{1\eta }=\mu \sigma _{\eta 1}\), for \(\eta =2,3\), \(\mu =0.1\), \(\alpha _{ij}=\pi /2-0.3\), \(i,j=1,2,3\), \(\gamma _{1,2,3}=0.05\), \(\omega _{1}=1.5\), \(\omega _{2,3}=0.5\), and \(\sigma _{23}=\sigma _{32}=0.01\). The regions DS and SS denote the desynchronization and strong synchronization states characterized by the numerical thresholds of \(R=0.3\) and \(R=0.8\), respectively

Full size image

For the case \(N'=3\) we consider three branches of coupled STNOs each having 1,000 oscillators. We set the values of the coupling parameters as follows: \(\sigma _{\eta \eta }=0.01\), \(\sigma _{\eta 1}=1.5\), \(\sigma _{1\eta }=\mu \sigma _{\eta 1}\), for \(\eta =2,3\), \(\mu =0.1\), \(\alpha _{ij}=\pi /2-0.3\), \(i,j=1,2,3\), \(\gamma _{1,2,3}=0.05\), \(\omega _{1}=1.5\), \(\omega _{2,3}=0.5\), and \(\sigma _{23}=\sigma _{32}=0.01\).

One of the three branches is the source in which synchronization is first established. The other two branches are target branches on to which synchronization will be induced by the synchronized source branch. In Fig. 6a, b we have plotted the time-averaged order parameter of the three branches \(R_1\), \(R_2\) and \(R_3\) against the coupling strength of the source branch, for two different values of noise strengths, namely \(D^{\eta }=0.1\) and \(D^{\eta }=0.5\), respectively. For both the values of noise strengths, we see that when the synchronization of the source branch increases \((R_1)\), the synchronization in the target branches also increases (\(R_2\) and \(R_3\)). The synchronization in the target branch is purely induced by the synchronization in the source branch since the coupling strength of the oscillators within the target branches are \(\sigma _{22}=\sigma _{33}=0.01\).

In Fig. 6c, d we have plotted the local and global order parameters, \(R_{avg}\) and \(R_g\), for \(D^{\eta }=0.1\) and \(D^{\eta }=0.5\), respectively. The local and global order parameters are given by the following expressions:

$$\begin{aligned} R_{avg}&= <\frac{1}{N'}\sum _{\eta '=1}^{N'}r_{\eta '}>,\;\;\;\;\; R_{g}=<|\frac{1}{N'}\sum _{\eta '=1}^{N'}r_{\eta '}e^{i\psi _{\eta '}}|>. \end{aligned}$$
(25)

The local order parameter measures the occurrence of synchronization within a branch, while the global order parameter quantifies the occurrence of synchronization in all the branches, globally in the system. Thus if \(R_g=1\), all the branches in the system are synchronized to a one and the same state.

The occurrence of synchronization in the source and the target branches are not influenced by changes in the strength of the noise in the system. This is evident from Fig. 6 panels (a) and (b), where for both the noise strengths the phenomenon of mass synchronization occurs in a similar manner.

Likewise, the local and the global order parameters also behave in a very similar manner for increasing \(\sigma _{11}\) for two different noise strengths. Thus we conclude that the phenomenon of occurrence of mass synchronization is not affected by the strength of the noise in the system.

6 Analytical Explanation

In order to analytically explain the occurrence of mass synchronization, we analyze system (22) in the continuum limit \(N\rightarrow \infty \). In this limit, the evolution equation for the order parameter for Lorentzian distribution becomes (in the absence of noise)

$$\begin{aligned} \dot{z}_{\eta }&+ (\gamma _{\eta }-i\omega _{\eta })z_{\eta } =\sum _{\eta '=1}^{N'}\frac{\sigma _{\eta \eta '}}{2} \bigg (e^{-i\alpha _{\eta \eta '}}z_{\eta '}-e^{i\alpha _{\eta \eta '}}z_{\eta '}^{*}z_{\eta }^2\bigg ),\\&\qquad \qquad \qquad \qquad \qquad \eta =1,2, \ldots , N'.\nonumber \end{aligned}$$
(26)

Here we use Ott and Antonsen [23] ansatz to derive the amplitude equation (26). From Fig. 6 one can note that the dynamics of the order parameter for all the target branches are similar. Thus one can consider the sate \(r_\eta \simeq r_t\) and \(\psi _\eta \simeq \psi _t\), \(\eta =2,...,N'\) and the amplitude equation (26) becomes (for \(\alpha _{\eta \eta '}=\alpha \))

$$\begin{aligned} \dot{r}_1&= -\gamma _{1}r_{1}+(\frac{1-r_{1}^2}{2})(\sigma _{11}r_{1}\cos (\alpha ) +\mu \sigma _{t1}r_t \cos (\psi _{1}-\psi _{t}+\alpha )),\\ \dot{\psi }_{1}&= \omega _{1}-(\frac{1+r_{1}^2}{2r_{1}})(\sigma _{11}r_{1}\sin (\alpha )\nonumber +\mu \sigma _{t1}r_t \sin (\psi _{1}-\psi _{t}+\alpha )),\end{aligned}$$
(27)
$$\begin{aligned} \dot{r}_{t}&= -\gamma _{t}r_{t}+(\frac{1-r_{t}^2}{2})(\sigma _{tt}r_{t}\cos (\alpha ) +\sigma _{t1}r_1 \cos (\psi _{t}-\psi _{1}+\alpha )), \\ \dot{\psi }_{t}&= \omega _{t}-(\frac{1+r_{t}^2}{2r_{t}})(\sigma _{tt}r_{t}\sin (\alpha )\nonumber +\sigma _{t1}r_1 \sin (\psi _{t}-\psi _{1}+\alpha )), \end{aligned}$$
(28)

where \(\gamma _t=\gamma _\eta \), \(\omega _t=\omega _\eta \), \(\sigma _{1t}=\sum _{\eta '=2}^{N'}\sigma _{\eta \eta '}\) and \(\sigma _{tt}=\sum _{\eta '=2}^{N'}\sigma _{\eta \eta '}\), \(\eta =2,...,N'\). One can assume \(\mu =0\) so that the source strongly (completely) drives the target branches. We have taken \(\mu =0\) for analytical convenience to start with. However, in general one can observe the occurrence of mass synchronization for \(\mu <1\) also as in the case of numerical simulations where \(\mu =\)0.1. Thus when the strength of the synchronization increases in the source it induces synchronization in the targets.

From Eq. (27), for \(\mu =0\), the synchronization of the source is characterized by the stability of the fixed point \(r_1^s=\sqrt{1-2\gamma _1/\bar{\sigma }_{11}}\), where \(\bar{\sigma }=\sigma \cos (\alpha )\). On the other hand, the desynchronization state is characterized by the stability of the fixed point \(r_1^d=0\). When \(\bar{\sigma }_{11}<2\gamma _1\), the fixed point \(r_1^d\) becomes stable and there is no synchronization in the source. In this state the equation for the target branch is given as

$$\begin{aligned} \dot{r}_{t}&= -\gamma _{t}r_{2}+(\frac{1-r_{t}^2}{2})(\sigma _{tt}r_{t}\cos (\alpha ),\; \dot{\psi }_{t}=\omega _{t}-(\frac{1+r_{t}^2}{2r_{t}})\sigma _{tt}r_{t}\sin (\alpha ). \end{aligned}$$
(29)

Again one can check that for \(\bar{\sigma }_{tt}<2\gamma _t\) the fixed point \(r_t=0\) is stable and the target branch is desynchronized. Thus when the source is desynchronized, the target branch is also desynchronized.

On the other hand, when the coupling strength in the source \(\bar{\sigma }_{11}\) increases so that \(\bar{\sigma }_{11}>2\gamma _1\) the fixed point \(r_1^d\) becomes unstable and \(r_1^s\) becomes stable thus establishing synchronization in the source. The synchronization strength of the source increases as \(\sqrt{1-2\gamma _1/\bar{\sigma }_{11}}\). After synchronization in the source is established, Eq. (29) reduces to

$$\begin{aligned} \dot{r}_t&= -\gamma _{t}r_t+(\frac{1-r_t^2}{2})(\sigma _{tt}r_t\cos (\alpha ) +\sigma _{t1}\sqrt{1-2\gamma _1/\bar{\sigma }_{11}} \cos (\psi +\alpha )),\\ \dot{\psi }&= \bar{\omega }-(\frac{1+r_t^2}{2r_t})(\sigma _{tt}r_t\sin (\alpha )\nonumber +\sigma _{t1}\sqrt{1-2\gamma _1/\bar{\sigma }_{11}} \sin (\psi +\alpha )), \end{aligned}$$
(30)

where \(\psi =\psi _t-\psi _1\) and \(\bar{\omega }=\omega _{t}-\omega _{1}+(\sigma _{11}-\gamma _1)\tan (\alpha _{11})\). This equation does not admit the fixed point \(r_t=0\). This means that when synchronization emerges in the source, the target branches also begin to get synchronized. The strength of the synchronization in the target increases according to \(\sigma _{t1}\sqrt{1-2\gamma _1/\bar{\sigma }_{11}}\), eventually leading to synchronization with the target. This result holds good for \(\mu <1\) also as is evident from our numerical findings as depicted in panels (a) and (b) of Fig. 6 for \(\mu =0.1\). Here we can establish that when the source is completely synchronized the target is also completely synchronized. This means that the increase in \(\sigma _{11}\) to a sufficiently high value induces synchronization in the target also apart from inducing synchronization in the source.

7 Summary and Conclusion

We have presented a systematic study of synchronization of STNOs coupled through the external driven periodically varying magnetic field. We have studied in-phase and anti-phase synchronization scenario of two STNOs and extended it to more number of oscillators in the presence of a common oscillating magnetic field. We find that the synchronization is induced though the oscillating magnetic medium. Further, in order to check the practical possibility of this scenario we also find the same phenomenon in the case of two different anisotropic STNOs. We also made a detailed analysis of synchronization in terms of coupled phase models and brought out the phenomenon of mass synchronization.