Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

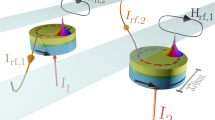
Spin Torque Nano Oscillators (STNO) are a ferromagnet-based electronics component. In certain steady-states, the magnetic moment precesses causing component resistance to oscillate [1]. Based on this oscillating resistance, an STNO can be utilized as a microwave-range voltage oscillator (see Fig. 1). STNOs offer many potential advantages over existing semi-conductor voltage oscillators including small physical size (\(\sim \)10 nm), a large tunable frequency range, and small output linewidths [2]. However, STNOs tested to date have yet to produce adequate power. STNOs need to output at least 1 mW to be applicable [3]. The microwave power generated by an STNO was first measured in 2009 on the order of 100 nW [4]. STNOs cannot be made larger, so an obvious solution to increasing power is to couple multiple oscillators. However, in experiments it has proven difficult to synchronize even two STNOs [5]. Thus we have begun to study the dynamics of coupled STNOs to determine conditions for synchronization. In this article we report our initial findings starting with the model itself. We first explore alternate coordinate systems to reduce the dimension of the model and find a form that is more amenable to later analysis. Both spherical and complex stereographic coordinates are investigated. Next we vary the input current and numerically integrate until steady-state to create qualitative bifurcation diagrams. Bifurcation diagrams are generated for both parallel and series connected STNOs.

2 The Model

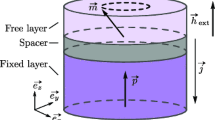
Magnetization in the free ferromagnetic layer is described by the Landau-Lifshitz equation with Gilbert damping and Slonczewski-Berger spin-torque term (LLGS) [6–10]

$$\begin{aligned} \frac{\mathrm{d}\mathbf {m}}{\mathrm{d}t} = \overbrace{-\gamma \mathbf {m}\times \mathbf {H}_{\text {eff}}}^{\displaystyle \text {precession}} \,+\, \overbrace{\lambda \mathbf {m}\times \frac{\mathrm{d}\mathbf {m}}{\mathrm{d}{\textit{t}}}}^{\displaystyle \text {damping}} \,-\, \overbrace{\gamma {a}\;g\left( P,\mathbf {m}\cdot \mathbf {S}_{\textit{p}}\right) \mathbf {m}\times \left( \mathbf {m}\times \mathbf {S}_{\textit{p}}\right) }^{\displaystyle \text {spin transfer torque}}, \end{aligned}$$
(1)

where \(\mathbf {m}\) represents the magnetization of the free ferromagnetic layer in Cartesian coordinates, \(\gamma \) is the gyromagnetic ratio and \(\mathbf {H}_{\text {eff}}\) is the effective field. \(\lambda \) serves as the magnitude of the damping term. In the spin torque term, \(a\) has units \(Oe\) and is proportional to the electrical current density [11]. \(g\) is a function of the polarization factor \(P\), \(\mathbf {m}\), and the fixed-layer magnetization direction \(\mathbf {S}_{\textit{p}}\). To determine the change of field direction with respect to time, we must consider three different classes of torques acting on the field direction \(\mathbf {m}\): effective external magnetic field \(\mathbf {H}_{\text {eff}}\), damping \(\lambda \), and spin transfer torque. \(\mathbf {H}_{\text {eff}}\) is the sum of several factors that can be effectively represented as external fields. The factors that we consider in this fashion are exchange, anisotropy and demagnetization. The actual external, or applied, field rounds out the sum

$$\begin{aligned} \mathbf {H}_{\text {eff}} = \mathbf {H}_{\text {exchange}} + \mathbf {H}_{\text {anisotropy}} + \mathbf {H}_{\text {demagnetization}} + \mathbf {H}_{\text {applied}}. \end{aligned}$$

We model the free layer as a single particle who’s magnetization \(\mathbf {m}\) represents the average of the layer. Thus there is no exchange with adjacent magnetic moments \(\mathbf {H}_{\text {exchange}}=0\).

2.1 Spherical Coordinates

In Eq. (1), \(\mathbf {m}\) has constant magnitude. We confine \(\mathbf {m}\) to the surface of a unit sphere by choosing \(\Vert \mathbf {m}\Vert _2=1\). Thus, spherical coordinates are a natural choice for \(\mathbf {m}\) with the radius \(\rho =1\). In [12], Sun showed that Eq. (1) can be converted to

$$\begin{aligned} \frac{d\theta }{d\tau } =&-\alpha \sin \theta \cos \theta \nonumber \\&- h_{{p}}\left[ \left( \sin \varphi +\alpha \cos \varphi \right) \sin \theta \cos \varphi \right] \nonumber \\&- h\left[ \cos \varphi \sin \psi + \alpha \left( \sin \theta \cos \psi - \cos \theta \sin \varphi \sin \psi \right) \right] \nonumber \\&+ h_{{s}}\left[ \alpha \cos \varphi \sin \phi +\sin \varphi \sin \phi \cos \theta -\cos \phi \sin \theta \right] , \end{aligned}$$
(2)
$$\begin{aligned} \frac{d\varphi }{d\tau } =&-\cos \theta \\&- h_{{p}}\left[ \left( \cos \varphi \cos \theta -\alpha \sin \varphi \right) \cos \varphi \right] \\&- h\left[ {\frac{\sin \theta \cos \psi -\cos \theta \sin \varphi \sin \psi -\alpha \cos \varphi \sin \psi }{\sin \theta }}\right] \\&+ h_{{s}}\left[ {\frac{\cos \varphi \sin \phi -\alpha \sin \varphi \sin \phi \cos \theta }{\sin \theta }}+\alpha \cos \phi \right] , \end{aligned}$$

where \(\theta \) is the angle of inclination and \(\varphi \) is the azimuthal angle. These equations have been time-scaled by \(\frac{\gamma h_k}{1+\lambda ^2}\) (\(h_k\) is the magnitude of anisotropy) and parameters consolidated to: demagnetization magnitude \(h_p\) (\(yz\)-easy-plane), applied field magnitude \(h\), applied field angle from \(z\)-axis \(\psi \) (confined to \(yz\)-plane), spin torque magnitude \(h_s\), and spin torque angle from \(z\)-axis \(\phi \) (also confined to \(yz\)-plane). Ultimately reducing the representation of the system from three dimensions to two.

2.2 Complex Stereographic Projection

A spherical surface can be projected onto a plane by using the complex variable \(\omega \) and the following relationships:

$$\begin{aligned} \omega =\frac{m_x+im_y}{1+m_z} \quad \Rightarrow \quad \mathbf{{m}}= \begin{bmatrix} \displaystyle \frac{\omega +{\bar{\omega }}}{1+\left| \omega \right| ^2} \\ \displaystyle -i\frac{\left( \omega -\bar{\omega }\right) }{1+\left| \omega \right| ^2} \\ \displaystyle \frac{1-\left| \omega \right| ^2}{1+\left| \omega \right| ^2} \end{bmatrix}. \end{aligned}$$
(3)

Building on [11, 13], we reduce Eq. (1) to the form

$$\begin{aligned} {\dot{\omega }} =\,&\frac{\gamma }{1-i\lambda }\Bigg ( -a\omega + i h_{a3}\omega + \frac{ h_{a2}}{2}(1 + {\omega }^2) \nonumber \\&+ im_{\Vert }\kappa \left[ \cos {\theta }_{\Vert }\omega -\frac{1}{2}\sin \theta _{\Vert }\left( \mathrm{e}^{i{\phi }_{\Vert }}-{\omega }^2\mathrm{e}^{-i\phi _{\Vert }}\right) \right] \nonumber \\&-\frac{i4\pi {S_o}}{(1+|\omega |^2)}\bigg [ N_3(1-|\omega |^2)\omega -\frac{N_1}{2}(1-\omega ^2-|\omega |^2)\omega \\&-\frac{N_2}{2}(1+\omega ^2-|\omega |^2)\omega -\frac{(N_1-N_2)}{2}\bar{\omega }\bigg ] \Bigg ), \nonumber \end{aligned}$$
(4)

where \(h_{a2}\) is the magnitude of the applied field in the \(y\)-direction and \(h_{a3}\) is the magnitudes of the applied field in the \(z\)-direction. \(\kappa \) is the anisotropy magnitude who’s direction is determined by \(\theta _\Vert \) and \(\phi _\Vert \). The anisotropy is scaled by \(m_\Vert = \mathbf {m}\cdot \mathbf {e}_\Vert \) where

$$\begin{aligned} \mathbf {e}_{\Vert }= \begin{bmatrix} \sin \theta _{\Vert }\cos \phi _{\Vert }\\[3pt] \sin \theta _{\Vert }\sin \phi _{\Vert }\\[3pt] \cos \theta _{\Vert } \end{bmatrix}. \end{aligned}$$

\(S_0\) is the saturation magnetization. Finally, \(N_1+N_2+N_3=1\) and determine the effective demagnetization field resulting from the shape of the free layer. Now we have a two dimensional expression for the STNO that is close to polynomial form.

Fig. 1
figure 1

Series arrayed STNOs with input current \(I_0\) and output resistance \(R_c\)

Full size image

2.3 Coupling

Coupling is achieved by modeling a simple electrical circuit with STNOs arrayed in series or parallel. Figure 1 depicts the series configuration. The resistance of each STNO \(R_i\) is a function of the angle \(\theta _i\) between \(M\) (fixed layer-green) and \(\mathbf {m}\) (free layer-red):

$$\begin{aligned} R_i = R_{0i} - \varDelta R_{i}\cos {\theta _i}. \end{aligned}$$

Here, \(R_0\) is the median resistance of an STNO and \(\varDelta R\) is the maximum variance in resistance.

3 Numerical Exploration

Numeric simulations have revealed a rich variety of behaviors in a series-array of three STNOs. Figure 2 depicts a few example behaviors found by varying the current \(I\). A high or low current simply causes all of the oscillators to converge to an equilibrium point. However, in the intermediate range there are multiple distinct regimes of oscillatory behavior. All numeric integrations in this diagram use the parameters: \(\lambda = 0.1,\, h=1,\,h_s=-1,\,h_p=5,\,\phi =0,\,\psi =\pi /4,\,R_{0}=2,\,\varDelta R=0.6,\,R_c=50\).

Fig. 2
figure 2

Qualitative bifurcation diagram for 3 STNOs arranged in series and varying parameter \(\varvec{I}\) over the interval [0:3]

Full size image

Performing similar integrations for 3 STNOs coupled in parallel generates the qualitative bifurcation diagram in Fig. 3. As is seen, we find a region of oscillations in \(I\) bound on both sides by fixed points. Within the oscillatory region we discovered six distinct sub-regions. Three sub regions tend to synchronization, two show quasi-periodic motion, and one forms frequency synchronized orbits. All numeric integrations in this diagram use the parameters: \(\lambda = 0.1,\, h=1,\, h_s=-1,h_p=5,\,\phi =0,\,\psi =\pi /4,\,R_{0}=0.1,\,\varDelta R=0.03\), \(R_c=50\).

Fig. 3
figure 3

Qualitative bifurcation diagram for 3 STNOs arranged in parallel and varying parameter \(\varvec{I}\) over the interval [0:7]

Full size image

4 Remarks

The LLGS Eq. (1) is a nonlinear first-order ordinary differential equation confined to the unit sphere \(\Vert \mathbf {m}\Vert _2={\text {1}}\). We are able to reduce the dimension of a system of coupled STNOs by one-third using spherical or complex-stereographic coordinates. Not only does this increase the efficiency of numerics, but will also help in the future with a center manifold reduction. Furthermore, the form of the equations in complex stereographic coordinates is polynomial-like which may be helpful in future analysis.

In the series and parallel electric coupling scenarios, the system experiences all-to-all coupling or \(S_N\) symmetry. Most of the non-synchronous oscillating behaviors observed in Figs. 2 and 3 are consistent with \(S_N \times S^1\) symmetry-breaking Hopf bifurcations. This leads us to believe that we can leverage the work of [14] to determine the existence and stability of non-synchronous oscillations.