Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The wavy-wall channel is one of the enhancement techniques that used to improve the thermal performance of heat exchangers. The heat transfer enhancement in such channel may be achieved by bulk fluid mixing and re-initiation of thermal boundary layer. As the fluid enters a wavy channel, the re-circulation zones occur in trough (crest) of lower (upper) wall of wavy channel and hence improve the mixing of cold fluid with the hot fluid near to the walls of wavy channel.

The disturbed fluid in wavy channel lead to reduce the thickness of thermal boundary layer and increase the temperature gradient near the walls of channel. Because of the importance of heat exchangers in many industrial applications and to design more efficient devices, research on additional techniques for heat transfer enhancement has become essential. For this purpose and due to the poor thermal conductivity of traditional fluids such as water, ethylene glycol and oil, using nanofluids as a cooling fluids in these devices instead of conventional fluids can improve thermal conductivity of fluids and consequently further improvement in the performance of heat exchangers.

Many numerical and experimental studies in the past have been carried out to investigate the heat transfer enhancement in wavy passages using conventional fluids. O’Brien and Sparrow [1] experimentally investigated on the convective heat transfer in triangular-corrugated duct. They were found that the enhancement in heat transfer was around 2.5 over the straight channel but with a grater pumping power requirements. Sparrow and Comb [2] performed experiments to determine flow and heat transfer characteristics in triangular-corrugated duct using water as working fluid. They were observed that heat-transfer coefficient for the smaller spacing between the walls of channel was slightly higher than that for the larger spacing, and the pressure drop penalty was higher as well. Ali and Ramadhyani [3] have been experimentally investigated on the forced convection flow of water flow through triangular-corrugated channel. It was observed that the channel with larger spacing provides better performance than that of smaller spacing. Wang and Vanka [4] numerically investigated on the convective heat transfer in wavy passages. The governing transport equation, in term of curvilinear orthogonal coordinates, have been solved using two-stage fractional step procedure. It was found that the average Nusselt number is slightly increased in steady flow regime. In transitional flow regime, there was a significant increase in heat transfer, but there was a companied by increasing in the friction factor. Fabbri [5] performed a numerical study on the laminar heat transfer flow through composed, smooth and corrugated, walls channel using finite element model. Results showed that the enhancement in heat transfer of the optimum corrugated profile increases as Prandtl and Reynolds numbers increases. Wang and Chen [6] numerically studied on the convection heat transfer in a sinusoidal-wavy channel over the Reynolds number range of 100–700. The governing transport equations in terms of curvilinear coordinates were solved using spline alternating direction implicit method. It was found that there was a slightly augmentation in heat transfer at smaller value of amplitude-wavelength ratio, while at larger amplitude-wavelength ratio, there was a significant enhancement in the rate of the heat transfer. Comini et al. [7] have been numerically studied on the convective heat transfer in wavy channels. The numerical result displayed that the friction factor as well as Nusselt number increase as aspect ratios decreases. Naphon and Kornkumjayrit [8] studied on the convective heat transfer of air flow through channel with one-sided corrugated plate using commercial CFD program. The results displayed that the corrugated walls had a significant influence on the heat transfer augmentation. Zhang and Che [9] numerically investigated the influence of corrugation profile for cross-corrugated plates on thermalhydraulic performance using air as working fluid. The Reynolds number values range of 1,000–10,000. It was found that Nusselt number as well as friction factor were about 1–4 times higher for the trapezoidal-corrugated channel than for the elliptic-corrugated channel.

In this paper, a numerical investigation on the laminar convective heat transfer of copper-water nanofluid in a sinusoidal-wavy channel with phase shift of 0° is carried out for Reynolds number range of 100–800 and nanoparticles volume fraction range of 0–5 %. The governing equations are transformed Cartesian coordinates into body-fitted coordinates and these equations are solved using finite volume method. The effects of nanoparticles volume concentration and Reynolds number on velocity vectors, temperature contours, velocity and temperature profiles, the local skin-friction coefficient, the local Nusselt number, average Nusselt number, pumping power and heat transfer enhancement are presented and analyzed.

2 Problem Description and Mathematical Formulation

2.1 Physical Domain and Assumptions

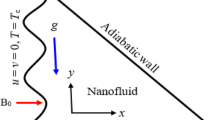
Figure 1 shows the geometry of the present study. It consists of a two parallel plates forming channel with average space between the plates (H) of 10 mm and the phase shift between these walls is 0°. The channel wall is composed of a smooth-adiabatic wall and a wavy-heated wall. The length of each plain (smooth) section that located upstream and downstream of the wavy section is Ls (Ls = 4H), the length of wavy section is Lw (Lw = 12H) and the wave-amplitude is A (A = 0.2H). On the other hand, nanofluid is a homogenous mixture of water and copper nanoparticles with diameter of 100 nm. It can be assumed as Newtonian fluid.

Fig. 1
figure 1

Schematic of the physical model of wavy channel

Full size image

2.2 Computational Domain

In order to develop the computational mesh of the present geometry, the two Poisson equations proposed in Thompson et al. [20] are adopted. The two-dimensional Poisson equations in physical space (x, y) can be written as:

$$\frac{{\partial^{2} \zeta }}{{\partial x^{2} }} + \frac{{\partial^{2} \zeta }}{{\partial y^{2} }} = \,P\,\left( {\zeta ,\eta } \right)$$
(1)
$$\frac{{\partial^{2} \eta }}{{\partial x^{2} }} + \frac{{\partial^{2} \eta }}{{\partial y^{2} }} = \,Q\,\left( {\zeta ,\eta } \right)$$
(2)

where P(ζ, η) and Q(ζ, η) are the control functions which are used to cluster points near the given boundaries. The above equations are transformed to the computational space (ζ, η) by interchanging the dependent and independent variables and then can be expressed as:

$$\beta_{11} \,\frac{{\partial^{2} x}}{{\partial \zeta^{2} }} - 2\beta_{12} \,\frac{{\partial^{2} x}}{\partial \zeta \eta } + \beta_{22} \,\frac{{\partial^{2} x}}{{\partial \eta^{2} }} + J^{2} (P\frac{\partial x}{\partial \zeta } + Q\frac{\partial x}{\partial \eta }) = 0$$
(3)
$$\beta_{11} \,\frac{{\partial^{2} y}}{{\partial \zeta^{2} }} - 2\beta_{12} \,\frac{{\partial^{2} y}}{\partial \zeta \eta } + \beta_{22} \,\frac{{\partial^{2} y}}{{\partial \eta^{2} }} + J^{2} (P\frac{\partial y}{\partial \zeta } + Q\frac{\partial y}{\partial \eta }) = 0$$
(4)

In Eqs. (3) and (4), β11, β12, β22 and J are geometry factors and can be defined as:

$$\begin{aligned} \beta_{11} = & \, x_{\eta }^{2} + y_{\eta }^{2} ,\,\,\beta_{22} = x_{\zeta }^{2} + y_{\zeta }^{2} , \\ \beta_{12} = & \, x_{\zeta } x_{\eta } + y_{\zeta } y_{\eta } ,\quad J = x_{\zeta } y_{\eta } - x_{\eta } y_{\zeta } \\ \end{aligned}$$
(5)

Equations (3) and (4) are solved numerically using Successive Line Over-Relaxation algorithm to determine the values of (x, y) at each point of computational grid [21]. The computational grid which is developed in current study is shown in Fig. 2.

Fig. 2
figure 2

Computational domain of present study

Full size image
Table 1 A summary of the governing equations
Full size table

2.3 Governing Equations

The general form of non-dimensional governing equations for two-dimensional, steady, laminar and incompressible flow in Cartesian coordinates can be written as (Table 1):

$$\frac{\partial (\rho \,u\,\phi )}{\partial x} + \frac{\partial (\rho \,v\,\phi )}{\partial y} = \frac{\partial }{\partial x}\left( {\Gamma \frac{\partial u}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\Gamma \frac{\partial u}{\partial y}} \right) + S_{\phi } (x,y)$$
(6)

Due to the complex geometry (i.e. wavy boundaries) of present study, the governing equations are transformed to a body-fitted coordinate system, and the these equations can be written as [22, 23]:

$$\begin{gathered} \frac{1}{J}\frac{{\partial (\rho \,U^{c} \,\phi )}}{\partial \zeta } + \frac{1}{J}\frac{{\partial (\rho \,V^{c} \,\phi )}}{\partial \eta } = \frac{1}{J}\frac{\partial }{\partial \zeta }\left[ {\frac{{\Gamma_{\phi } }}{J}\,(\beta_{11} \phi_{\zeta } - \beta_{12} \phi_{\eta } )} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{J}\frac{\partial }{\partial \eta }\left[ {\frac{{\Gamma_{\phi } }}{J}\,(\beta_{22} \phi_{\eta } - \beta_{12} \phi_{\zeta } )} \right] + S_{\phi } (\zeta ,\eta ) \hfill \\ \end{gathered}$$
(7)

where Uc and Vc are contravariant velocity components and it can be defined as

$$U^{c} = UY_{\eta } - VX\eta ,\,V^{c} = VX_{\zeta \,} - \,\,UY_{\zeta }$$
(8)

3 Numerical Algorithm

3.1 Discretization of Governing Equations

The governing equations in body-fitted coordinate system are discretized using finite volume method. The diffusion term is discretized using central scheme and the convection term is discretized by power-law scheme. A collocated grid arrangement, in which all physical variables such as velocity, temperature and pressure are stored at the center of control volume, is used (Fig. 3.). The final discretized equation is

$$A_{P}^{\phi } \,\phi_{p} = \sum\limits_{nb} {A_{nb}^{\phi } } \,\phi_{nb} + S_{\phi } \,J\,\Delta \zeta \,\Delta \eta - \,\,\left[ {\left( {\frac{{\Gamma_{\phi } }}{J}\beta_{12} \,\phi_{\eta } \,\Delta \eta } \right)_{w}^{e} + \left( {\frac{{\Gamma_{\phi } }}{J}\beta_{12} \,\phi_{\zeta } \,\Delta \zeta } \right)_{s}^{n} \,\,} \right]\,$$
(9)

In above equation, the terms within the brackets are originated from approximating the diffusion terms on the non-orthogonal grid [24]. The coefficients A involve the flow rate F and diffusion conductivity D and these coefficients can be defined as follows [25]:

$$\begin{aligned} A_{E} = & \, D_{e} \,\hbox{max} \,\,[0,\,\,(1 - 0.1\,\,\left| {\,Pe_{e} \,} \right|)^{5} ] + \,\hbox{max} \,\,[ - F_{e} ,\,0], \\ A_{W} = & \, D_{w} \,\hbox{max} \,\,[0,\,\,(1 - 0.1\,\,\left| {\,Pe_{w} \,} \right|)^{5} ] + \,\hbox{max} \,\,[F_{w} ,\,0] \\ A_{N} = & \, D_{n} \,\hbox{max} \,\,[0,\,\,(1 - 0.1\,\,\left| {\,Pe_{n} \,} \right|)^{5} ] + \,\hbox{max} \,\,[ - F_{n} ,\,0], \\ A_{S} = & \, D_{s} \,\hbox{max} \,\,[0,\,\,(1 - 0.1\,\,\left| {\,Pe_{s} \,} \right|)^{5} ] + \,\hbox{max} \,\,[F_{s} ,\,0] \\ A_{P} = & \, A_{E} + A_{W} + A_{N} + A_{S} , \\ Pe_{i} = & \, \frac{{F_{i} }}{{D_{i} }}; \, \left( {{\text{i}} = \, {\text{ e}},{\text{ w}},{\text{ n}},{\text{ s}}} \right) \\ \end{aligned}$$
(10)

where

$$F_{e} = (\rho \,U^{c} \,\Delta \eta )_{e} ,\,F_{w} = (\rho \,U^{c} \,\Delta \eta )_{w} ,\,F_{n} = (\rho \,V^{c} \,\Delta \zeta )_{n} ,\,F_{s} = (\rho \,V^{c} \,\Delta \zeta )_{s}$$
$$D_{e} = \left( {\frac{{\beta_{11} }}{J}\,\,\Gamma \,\,\frac{\Delta \eta }{\Delta \zeta }} \right)_{e} ,\,D_{w} = \left( {\frac{{\beta_{11} }}{J}\,\,\Gamma \,\,\frac{\Delta \eta }{\Delta \zeta }} \right)_{w} ,\,D_{n} = \left( {\frac{{\beta_{22} }}{J}\,\,\Gamma \,\,\frac{\Delta \zeta }{\Delta \eta }} \right)_{n} ,\,D_{s} = \left( {\frac{{\beta_{22} }}{J}\,\,\Gamma \,\,\frac{\Delta \zeta }{\Delta \eta }} \right)_{s}$$
(11)

The discretised Eq. (9) is iteratively solved using Tri-Diagonal Matrix Algorithm (TDMA) [25]. The system is numerically modeled in a FORTRAN.

Fig. 3
figure 3

Control volume in computational domain of non-orthogonal grid

Full size image

3.2 Pressure Correction Equation

The pressure field can be obtained by coupling of the velocity and pressure equations on a collocated non-orthogonal grid using the SIMPLE algorithm [25]. To illustrate the algorithm, the velocity components u and v can be obtained from

$$u_{p}^{*} = \,\frac{1}{{A_{P}^{u} }}\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{*} \, + b_{u} + (B_{P}^{u} \,\frac{{\partial p^{*} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{*} }}{\partial \eta }\,)$$
(12)
$$v_{p}^{*} = \frac{1}{{A_{P}^{v} }}\sum\limits_{nb} {A_{nb}^{v} } \,v_{nb}^{*} \, + b_{v} + (B_{P}^{v} \,\frac{{\partial p^{*} }}{\partial \zeta }\, + C_{P}^{v} \,\frac{{\partial p^{*} }}{\partial \eta }\,)$$
(13)
$$B_{p}^{u} = - \frac{1}{{A_{P}^{u} }}\,\,\left( {\frac{\partial y}{\partial \eta }} \right)_{p} \,\Delta \zeta \,\Delta \eta ,\,\,\,C_{p}^{u} = \frac{1}{{A_{P}^{u} }}\,\left( {\frac{\partial y}{\partial \zeta }} \right)_{p} \,\Delta \zeta \,\Delta \eta$$
(14)
$$B_{p}^{v} = \,\,\frac{1}{{A_{P}^{v} }}\,\left( {\frac{\partial x}{\partial \eta }} \right)_{p} \Delta \zeta \,\Delta \eta ,\,\,\,C_{p}^{v} = \frac{1}{{A_{P}^{v} }}\,\,\left( {\frac{\partial x}{\partial \zeta }} \right)_{p} \Delta \zeta \,\Delta \eta$$
(15)

and \(b_{u}\) and \(b{}_{v}\) are residues from \(S_{u}\) and \(S{}_{v}\), respectively, after the pressure gradient terms have been removed from them [24]. The pressure gradient terms in Eqs. (12) and (13) are determined by

$$\frac{{\partial p^{*} }}{\partial \zeta } = \frac{{(p_{e}^{*} )_{p} - (p_{w}^{*} )_{p} }}{\Delta \zeta },\,\,\frac{{\partial p^{*} }}{\partial \eta } = \frac{{(p_{n}^{*} )_{p} - \,(p_{s}^{*} )_{p} }}{\Delta \eta }$$
(16)
$$u\, = \,\,u^{*} \, + (B^{u} \,\frac{\partial p\,'}{\partial \zeta }\, + C^{u} \,\frac{\partial p\,'}{\partial \eta }\,),\,\,\,v = \,\,v^{*} \, + (B^{v} \,\frac{\partial p\,'}{\partial \zeta }\, + C^{v} \,\frac{\partial p\,'}{\partial \eta }\,)$$
(17)

where \(P\,'\) is the pressure correction which can be related to the correct pressure \(P\,\) and the guessed pressure \(P^{*}\) as follows:

$$P = \,\,P^{*} \, + \,P\,'$$
(18)

The correction of contravariant velocity components Uc* and Vc* can be defined as

$$U^{c} = U^{c\,*} \, + \,\left( {B^{u} \,y_{\eta } - \,B^{v} \,x_{\eta } } \right)\,\,\frac{\partial p\,'}{\partial \zeta } + \,\left( {C^{u} \,y_{\eta } - \,C^{v} \,x_{\eta } } \right)\,\,\frac{\partial p\,'}{\partial \eta }$$
(19)
$$V^{c} = V^{c\,*} \, + \,\left( {C^{v} \,x_{\zeta } - C^{u} \,y_{\zeta } } \right)\,\,\frac{\partial p\,'}{\partial \eta } + \,\left( {B^{v} \,x_{\zeta } - \,B^{u} \,y_{\zeta } } \right)\,\,\frac{\partial p\,'}{\partial \zeta }$$
(20)

It has to be noted that the last two terms of Eqs. (19) and (20), based on the approximation of Rhie and Chow [24], are ignored if the computational grid is nearly orthogonal. Therefore, these equations can be rewritten as:

$$U^{c} = U^{c\,*} \, + \,B\,\,\frac{\partial p\,'}{\partial \zeta },\,V^{c} = V^{c\,*} \, + \,C\,\,\frac{\partial p\,'}{\partial \eta }$$
(21)

where

$$B = \,B^{u} \,y_{\eta } - \,B^{v} \,x_{\eta } ,\,\,\,C\, = \,\,C^{v} \,x_{\zeta } - C^{u} \,y_{\zeta }$$
(22)

The discretised continuity equation can be written as follows

$$(\rho \,\Delta \eta \,U^{c} )_{e} - (\rho \,\Delta \eta \,U^{c} )_{w} + (\rho \,\Delta \zeta \,V^{c} )_{n} - (\rho \,\Delta \zeta \,V^{c} )_{s} = 0$$
(23)

Substituting the corrected face contravariant velocities into above equations gives

$$A_{P} \,P_{P}^{'} \, = \,A_{E\,} P_{E}^{'} \, + \,A_{W\,} P_{W}^{'} \, + \,A_{N\,} P_{N}^{'} \, + \,A_{S\,} P_{S}^{'} \, + \,S_{m}$$
(24)

where

$$A_{E} = \,(\rho \,\Delta \eta \,B)_{e} ,\,\,\,A_{W} = \,(\rho \,\Delta \eta \,B)_{w} ,\,\,\,A_{N} = \,(\rho \,\Delta \zeta \,C)_{n} ,\,\,\,A_{S} = \,(\rho \,\Delta \eta \,C)_{s}$$
(25)

and Sm is the mass imbalance over the control volume and it can be expressed as

$$S_{m} = \,\,(\rho \,\Delta \eta \,U^{c*} )_{e} - (\rho \,\Delta \eta \,U^{c*} )_{w} + (\rho \,\Delta \zeta \,V^{c*} )_{n} - (\rho \,\Delta \zeta \,V^{c*} )_{s}$$
(26)

3.3 Interpolation of the Face Velocities

The velocity interpolation is performed to calculate the face velocities of control volume on a collocated non-orthogonal grid. For this purpose and to avoid the unreal pressure oscillation, the momentum interpolation method which is proposed by Rhie and Chow [24] is adopted in this study. The discretised u-momentum equation at the nodes P and E can be written as:

$$u_{p}^{{}} = \,\frac{1}{{(A_{P}^{u} )_{P} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + \, b_{u} } \right)_{P} + \frac{1}{{(A_{P}^{u} )_{P} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{P}$$
(27)
$$u_{E}^{{}} = \,\frac{1}{{(A_{P}^{u} )_{E} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + \, b_{u} } \right)_{E} + \frac{1}{{(A_{P}^{u} )_{E} }}\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{E}$$
(28)

In similar manner, the velocity at the east face can be written as:

$$u_{e}^{{}} = \,\frac{1}{{(A_{P}^{u} )_{e} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + \, b_{u} } \right)_{e} + \frac{1}{{(A_{P}^{u} )_{e} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{e}$$
(29)

The first term and the \(1/(A_{P}^{u} )_{e}\) in the second term of the above equation are linearly interpolated as follows:

$$\begin{aligned} \frac{1}{{(A_{P}^{u} )_{e} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + b_{u} } \right)_{e} = \,& f_{e}^{ + } \,\frac{1}{{(A_{P}^{u} )_{E} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + b_{u} } \right)_{E} \\ & + (1 - f_{e}^{ + } )\,\,\frac{1}{{(A_{P}^{u} )_{P} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + b_{u} } \right)_{P} \end{aligned}$$
(30)
$$\,\frac{1}{{(A_{P}^{u} )_{e} }} = \,f_{e}^{ + } \,\,\frac{1}{{(A_{P}^{u} )_{E} }}\, + \,\,(1 - f_{e}^{ + } )\,\,\frac{1}{{(A_{P}^{u} )_{P} }}$$
(31)

where \(\,\,f_{e}^{ + } \,\) is a linear interpolation factor and it can be defined as:

$$\,\,f_{e}^{ + } \, = \frac{{\Delta \zeta_{P} }}{{2\,\,\delta \zeta_{e} }}$$
(32)

Re-arranging Eqs. (27) and (28), gives:

$$\,\frac{1}{{(A_{P}^{u} )_{P} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + b_{u} } \right)_{P} \, = \,\,u_{p}^{{}} - \,\frac{1}{{(A_{P}^{u} )_{P} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{P}$$
(33)
$$\,\frac{1}{{(A_{P}^{u} )_{E} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + b_{u} } \right)_{E} = u_{E}^{{}} \, - \,\,\frac{1}{{(A_{P}^{u} )_{E} }}\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{E}$$
(34)

Substituting Eqs. (33) and (34) in Eq. (30), gives:

$$\begin{aligned} \frac{1}{{(A_{P}^{u} )_{e} }}\left( {\sum\limits_{nb} {A_{nb}^{u} } \,u_{nb}^{{}} \, + b_{u} } \right)_{e} = \, & f_{e}^{ + } \,\left[ {u_{E}^{{}} - \,\frac{1}{{(A_{P}^{u} )_{E} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{E} } \right]\, \\ & + (1 - f_{e}^{ + } )\,\left[ {u_{p}^{{}} - \,\frac{1}{{(A_{P}^{u} )_{P} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{P} } \right] \\ \end{aligned}$$
(35)

Substituting Eq. (35) in Eq. (29), gives:

$$\begin{aligned} u_{e}^{{}} = \,& f_{e}^{ + } \,\left[ {u_{E}^{{}} - \,\,\frac{1}{{(A_{P}^{u} )_{E} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{E} } \right]\, + \,(1 - f_{e}^{ + } )\,\left[ {u_{p}^{{}} - \,\frac{1}{{(A_{P}^{u} )_{P} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{P} } \right] \hfill \\ & + \frac{1}{{(A_{P}^{u} )_{e} }}\,\left( {B_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \zeta }\, + C_{P}^{u} \,\frac{{\partial p^{{}} }}{\partial \eta }} \right)_{e} \hfill \\ \end{aligned}$$
(36)

Re-arranging the above equation, gives:

$$\begin{aligned} u_{e} & = \left[ {f_{e}^{ + } \,u_{E}^{{}} + (1 - f_{e}^{ + } )\,\,u_{p}^{{}} } \right] + \frac{1}{{(A_{P}^{u} )_{e} }}\left( {B_{P}^{u} \frac{{\partial p^{{}} }}{\partial \zeta } + C_{P}^{u} \frac{{\partial p^{{}} }}{\partial \eta }} \right)_{e} - f_{e}^{ + } \frac{1}{{(A_{P}^{u} )_{E} }}\left( {B_{P}^{u} \frac{\partial p}{\partial \zeta } + C_{P}^{u} \frac{\partial p}{\partial \eta }} \right)_{E} \\ & \quad \; - (1 - f_{e}^{ + } )\,\frac{1}{{(A_{P}^{u} )_{P} }}\left( {B_{P}^{u} \,\frac{\partial p}{\partial \zeta } + C_{P}^{u} \frac{\partial p}{\partial \eta }} \right)_{P} \\ \end{aligned}$$
(37)

The velocities at the other faces such west, north and south faces can be obtained using similar procedure.

3.4 Under-Relaxation

In order to slow down the updating of the dependent variables at each iteration to achieve a better convergence behavior, the under- relaxation is applied. Therefore, the under-relaxation factor can be introduced to the discretised equation (Eq. 9) as follows [25]:

$$\frac{{A_{P}^{\phi } }}{{\alpha_{\phi } }}\,\phi_{P} = \sum\limits_{nb} {A_{nb}^{\phi } } \,\phi_{nb} + S_{\phi } \,J\,\Delta \zeta \,\Delta \eta - \left[ {\left( {\frac{{\Gamma_{\phi } }}{J}\beta_{12} \,\phi_{\eta } \,\Delta \eta } \right)_{w}^{e} + \left( {\frac{{\Gamma_{\phi } }}{J}\beta_{12} \,\phi_{\zeta } \,\Delta \zeta } \right)_{s}^{n} \,\,} \right]\, + \frac{{1 - \alpha_{\phi } }}{{\alpha_{\phi } }}\,A_{P}^{o} \,\phi_{P}^{o}$$
(38)

where \(\alpha_{\phi }\) is the under-relaxation factor. Equation (38) can be written as:

$$\frac{{A_{P}^{\phi } }}{{\alpha_{\phi } }}\,\phi_{P} = \sum\limits_{nb} {A_{nb}^{\phi } } \,\phi_{nb} + S_{\phi }^{r} - \,\,\left[ {\left( {\frac{{\Gamma_{\phi } }}{J}\beta_{12} \,\phi_{\eta } \,\Delta \eta } \right)_{w}^{e} + \left( {\frac{{\Gamma_{\phi } }}{J}\beta_{12} \,\phi_{\zeta } \,\Delta \zeta } \right)_{s}^{n} \,\,} \right]\,$$
(39)

where

$$S_{\phi }^{r} = S_{\phi } \,J\,\Delta \zeta \,\Delta \eta + \,\frac{{1 - \alpha_{\phi } }}{{\alpha_{\phi } }}\,A_{P}^{o} \,\phi_{P}^{o}$$
(40)

The under-relaxation is also applied for the pressure correction equation as follows:

$$P^{new} = \,\,P^{*} \, + \,\alpha_{P} \,P\,'$$
(41)

where \(\alpha_{p}\) is the under-relaxation factor for the pressure correction equation. However, the values of under-relaxation factors which are used in the current study are 0.7 for momentum and energy equations and 0.2 for pressure.

4 Boundary Conditions

The corresponding boundary conditions that are used to solve the governing equation based on the non-dimensional expressions are given by:

  1. i.

    Channel inlet:

    $$U = \frac{3}{2}\,\,\left[ {1 - \frac{\eta }{(H/2)}} \right]^{2} ,\,\,V = 0,\,\,\theta = \,\,0,\,\,\, - \frac{H}{2} \le \eta \le \,\,\frac{H}{2}$$
    (42)
  2. ii.

    Along the smooth walls:

    $$U = 0,\,\,V = 0,\,\,\theta = 1$$
    (43)
  3. iii.

    Along the wavy walls:

    $$U = 0,\,\,V = 0,\,\,\frac{\partial \theta }{\partial \eta }$$
    (44)
  4. iv.

    Channel outlet:

    $$\frac{\partial U}{\partial \zeta } = \,\,0,\,\,\frac{\partial V}{\partial \zeta } = \,\,0,\,\,\frac{\partial \theta }{\partial \zeta } = \,\,0\,\,$$
    (45)

5 Physical Properties of Nanofluids

The properties of nanofluid can be expressed as follows:

  1. i.

    Density:

    The effective density of the nanofluid can be expressed as [26]:

    $$\rho_{nf} = (1 - \varphi )\,\rho_{f} + \varphi \,\rho_{p}$$
    (46)
  2. ii.

    Heat capacity:

    The heat capacity of nanofluid is defined as [26]:

    $$(\rho C_{P} )_{nf} = (1 - \varphi )(\rho C_{P} )_{f} \, + \varphi \,(\rho C_{P} )_{p}$$
    (47)
  3. iii.

    Dynamic viscosity:

    The effective dynamic viscosity of the nanofluid is given by [27]:

    $$\frac{{\mu_{nf} }}{{\mu_{f} }} = \frac{1}{{\left( {1 - \varphi } \right)^{2.5} }}$$
    (48)
  4. iv.

    Thermal conductivity:

    The effective thermal conductivity of nanofluid can be determined using the model proposed by Patel et al. [28], as follows:

    $$\frac{{k_{eff} }}{{k_{f} }} = 1 + \frac{{k_{p} \,A_{p} }}{{k_{f} \,A_{f} }} + c\,k_{p} \,Pe\frac{{\,A_{p} }}{{k_{f} \,A_{f} }},$$
    (49)

    where

    $$\frac{{\,A_{p} }}{{A_{f} }} = \frac{{d_{f} }}{{d_{p} }}\frac{\varphi }{{\left( {1 - \varphi } \right)}},$$
    (50)

    and c is the empirical constant and

    $$Pe = \frac{{u_{p} d_{p} }}{{\alpha_{f} }},$$
    (51)

    where up is the Brownian motion velocity of the particles which is defined as:

    $$u_{p} = \frac{{2k_{p} T}}{{\pi \,\mu_{f} \,d_{p}^{2} }}$$
    (52)

6 Performance and Non-dimensional Parameters

After solving the governing equations, the flow and thermal fields of nanofluid in wavy channel are obtained. The local Nusselt number at the walls of wavy wall can be calculated as [4]:

$$Nu_{x} = - \frac{{k_{nf} }}{{k_{f} }}\left[ {\frac{1}{J}\,\left( {X_{\zeta }^{2} + Y_{\zeta }^{2} } \right)^{\,1/2} \,\frac{\partial \theta }{\partial \eta }} \right]_{\zeta ,w}$$
(53)

The average Nusselt number can be obtained by integrating the local Nusselt number over the walls of the wavy wall as follows:

$$Nu_{L} = \frac{1}{{L_{w} }}\int\limits_{{L_{s} }}^{{L_{s} + L_{w} }} {Nu_{x} } \,d\zeta$$
(54)

The local skin-friction coefficient at the wavy wall can be calculated as:

$$C_{fx} = \frac{2}{\text{Re}}\,\left[ {\frac{1}{J}\,\left( {X_{\zeta } \,\frac{\partial U}{\partial \eta } - Y_{\zeta } \,\frac{\partial V}{\partial \eta }} \right)} \right]_{\zeta ,w}$$
(55)

The friction factor can be defined as:

$$f = \Delta p\,\frac{{D_{h} }}{{L_{w} }}\frac{2}{{\rho_{nf} \,u_{in}^{2} }}$$
(56)

The required pumping power can be expressed as:

$$Pumping\,\,power = H\,u_{in} \,\Delta P$$
(57)

The non-dimensional parameters which are used in current study can be defined as follows:

$$X = \frac{x}{{D_{h} }},\,\,Y = \frac{y}{{D_{h} }},\,\,U = \frac{u}{{{\text{u}}_{\text{in}} }},\,\,V = \frac{v}{{{\text{u}}_{\text{in}} }},\,\,\theta = \frac{{T - T_{in} }}{{T_{w} - T_{in} }}$$
(58)
$$P = \frac{p}{{\rho_{nf} u_{in}^{2} }},\,\,\,\text{Re} = \frac{{\rho_{nf} u_{in} D_{h} }}{{\mu_{nf} }},\,\,\,\Pr = \frac{{\mu_{nf} C_{P\,nf} }}{{K_{nf} }}$$
(59)

7 Code Validation and Grid Independence Test

To validate the code that developed in present study, the average Nusselt number for the convective heat transfer of water \((\varphi = 0\;\% )\) flow in sinusoidal-wavy channel is obtained and compared with previous numerical results of Heidary and Kermani [16], see Fig. 4a. Moreover, the average Nusselt number for copper-water nanofluid flowing between two parallel plates has been calculated and compared with previous numerical results of Santra et al. [13] as shown in Fig. 4b. The results are in good agreement. The accuracy of numerical result are generally dependent on the grid size. To test the grid independence, the non-dimensional streamwise velocity as well as the non-dimensional temperature were calculated for different grid size at Re = 500 and \(\varphi = 5\;\%\) as displayed in Fig. 5a, b. The grid size of 401 × 61 can be considered grid-independent and is therefore used throughout all computations. In current study, the computation is terminated when the sum of absolute residual for each parameter over computational domain is less than 1 × 10−5.

Fig. 4
figure 4

Comparison of the results for a water flow in a wavy-wall channel, b copper-water nanofluid flow in a straight channel

Full size image
Fig. 5
figure 5

Grid independence test at Re = 500, \(\varphi \, = \,5\,\%\) and X = 10.5: a Non-dimensional streamwise velocity b Non-dimensional temperature

Full size image

8 Results and Discussion

Laminar convective heat transfer of nanofluid in a wavy channel has studied numerically over Reynolds number ranges of 100–800 and nanoparticles volume concentration of 0–5 %. Figure 6 shows the velocity vectors and temperature contours for Reynolds number of 100, 300, 500 and 800 and nanoparticles volume concentration is 5 %. In general, it can be seen that the velocity vectors as well as temperature contours are asymmetric about x-axis because of the top and bottom walls of wavy channel are in the same phase (i.e. the phase shift between top and bottom walls of wavy channel is 0°). When the nanofluid flow in a wavy channel, the nanofluid must turn to pass through this channel and hence reversal flow appear in trough (crest) of lower (upper) wall. When Reynolds number increases, the velocities for recirculation regions which are in opposite direction to the main flow increase in magnitude. However, the size of recirculation regions increase with increasing in Reynolds number. From temperature contours it can be clearly seen that when Reynolds number increases, thermal boundary layer thickness deceases and the temperature gradient at the walls of wavy channel increases due to improve the mixing of core fluid with the fluid close to the walls of channel. The non-dimensional streamwise velocity distribution at different locations (troughs) along the length of the wavy channel for Reynolds numbers of 100 and 800 at \(\varphi = 5\;\%\) are plotted in Fig. 7a and b. In general, the velocities at the upper and lower walls of the wavy channel are equal to zero due to the non-slip condition is stated at the walls of the channel. It can be observed that the maximum velocity is detected in the upper part of the wavy channel while the minimum velocity, i.e. negative velocity, is detected in the lower part of the channel. In other word, the peak value of the velocity profile is shifted from the centerline of the wavy channel to the upper part of the way channel. Furthermore, the flow attains periodically fully developed profile downstream of the first wave. This behavior is similar to that reported by Bahaidarah et al. [29]. Moreover, the negative velocity in trough of the wavy channel, i.e. re-circulation regions increases in magnitude as Reynolds number increases from 100 to 800. This is can be clearly observed from Fig. 6.

Fig. 6
figure 6

Velocity vectors (left) and temperature contours (right) for different Reynolds numbers at \(\varphi \, = \,5\%\)

Full size image
Fig. 7
figure 7

Variation of non-dimensional streamwise velocity at troughs along the length of the wavy channel for \(\varphi \, = \,5\%\) at a Re = 100, b Re = 800

Full size image

Figure 8a and b show the non-dimensional temperature distribution in the spanwise direction at troughs along the length of the wavy channel for Reynolds numbers of 100 and 800 at \(\varphi = 5\;\%\). Basically, it is found that the magnitude of non-dimensional temperature at the upper and lower heated-walls of wavy channel is equal to one (\(\theta = \,1\)) as stated in the boundary conditions. At Re = 100, the temperature of the fluid in the trough of the lower wall is higher than that in the crest of the upper wall due to the slow down the velocity of the fluid in the re-circulation regions. Also, the temperature increases when the lengthwise (X) increases. As Reynolds number increases, Re = 800, the temperature (temperature gradient) deceases (increases) especially in the trough of the lower wall of wavy channel due to improve the fluid mixing. Figure 9 depicts the distribution of the local skin-friction coefficient along the bottom wall of wavy channel for different nanoparticles volume concentrations for Re = 100 and 800. It should be noted that the local skin-fiction coefficient has a maximum value which is located at crest of the wavy wall. This is because the velocity gradient has a maximum value at this location. While the skin-friction coefficient has a minimum value at the trough of the wavy wall due to low velocity gradient in the reversal flow regions. It is also found that the skin-friction coefficient has a negative value due to reversal flow that appear in trough of wavy channel. Furthermore, as expected, the skin-friction coefficient at Re = 100 is higher than that at Re = 800 because of the skin-friction coefficient is inversely proportional to Reynolds number, see Eq. 55. Moreover, nanoparticles volume concentration has no effect on the local skin-friction coefficient. Figure 10 gives the distribution of the local Nusselt number along the bottom wavy-wall for different nanoparticles volume concentration at Re = 100 and 800. The maximum local Nusselt number occur upstream of the wave-crest, while the minimum value occur downstream of the wave-crest. This is because the velocity as well as the temperature gradients upstream of the wave-crest are higher than that downstream of the wave-crest. Also, it can be noted that the local Nusselt number, especially the peak values, increase as the volume concentration of nanofluid increases due to improve thermal conductivity of nanofluid.

Fig. 8
figure 8

Variation of non-dimensional temperature at troughs along the length of the wavy channel for \(\varphi \, = \,5\%\) at a Re = 100 b Re = 800

Full size image
Fig. 9
figure 9

Local skin friction coefficient distribution along lower wavy-wall for different nanoparticle volume concentration at a Re = 100 b Re = 800

Full size image
Fig. 10
figure 10

Local Nusselt number distribution along lower wavy-wall for different nanoparticle volume concentration at a Re = 100 b Re = 800

Full size image

The average Nusselt number versus Reynolds number at different values of nanoparticles volume concentrations has been presented in Fig. 11. It should be noted that at a specific concentration of the solid particles, the average Nusselt number increases as Reynolds number increases. This because when Reynolds number increases, the fluid mixing in channel is improved due to re-circulation regions that appear in wavy channel and hence the temperature gradient at wall also increases. On other hand, the average Nusselt number increases with increasing in the volume concentration of solid particles at particular Reynolds number because of the addition nanoparticles to the base fluid can improve thermal conductivity of base fluid and consequently improve heat transfer rate. Figure 12 displays the variation of pumping power with Reynolds number for different nanoparticles volume concentrations. It is observed that the required pumping power increases when Reynolds number increase at a particular nanoparticles volume concentrations. Also, the pumping power increases with nanoparticles volume concentrations due to increase the density and viscosity of nanofluid. This is consistent with numerical results of Manca et al. [30]. Figure 13 shows the average Nusselt number for nanofluid flow in a wavy channel over the average Nusselt number for water (conventional fluid) flow in a plain channel (conventional channel) versus Reynolds number at different volume concentrations of nanoparticles. It is found that the enhancement in average Nusselt number increases with Reynolds number and with the nanoparticles volume concentration as well. As mentioned above, nanoparticles suspension and using wavy-wall increase the enhancement in heat transfer due to the enhance thermal conductivity as well as the fluid mixing.

Fig. 11
figure 11

Average Nusselt number versus Reynolds number for different nanoparticle volume concentration

Full size image
Fig. 12
figure 12

Pumping power versus Reynolds number for different nanoparticle volume concentration

Full size image
Fig. 13
figure 13

Average Nusselt number enhancement versus Reynolds number for different nanoparticle volume concentration

Full size image

9 Conclusions

In this study, laminar flow and heat transfer of copper-water nanofluid in a sinusoidal-wavy channel is numerically investigated over Reynolds number range of (100–800) and nanoparticle volume concentration range of (0–5 %). The phase shift between the upper and lower walls of wavy channel is 0°. The non-dimensional governing continuity, momentum and energy equations in terms of curvilinear coordinates are solved using finite volume method. The effects of nanoparticles volume concentration and Reynolds number on the velocity and temperature profiles, the local skin-friction coefficient, the local Nusselt number, average Nusselt number, pumping power and heat transfer enhancement are presented and discussed. Results show that the local Nusselt, the average Nusselt number as well as the average Nusselt number enhancement are significantly increase with the nanoparticle volume concentration, but the required pumping power increases as well. Also, it is found that the nanoparticles volume concentration has no effect on the local skin-friction coefficient. It can be recommended that the using nanofluid in a wavy channels is a suitable way to design more compact heat exchangers with a higher heat transfer performance.