Keywords

1 Introduction

Due to immense potential applications of the flexible thin rotating disks, the significance of their vibration characteristics has been emphasized in recent years. Rotating disks are the principal components in various rotating machinery. Their applications can vary from space structures to torsional disk dampers and from turbine rotors to computer storage devices and brake systems. It is known that dynamic response and stability of rotating disk depends on its rotational speed. It should be noted that to design a rotating disk, the knowledge of modal vibrations and critical speeds are essential.

Vibration of rotating disk can occur as two types, in-plane and out-of-plane bending vibration. In-plane vibration occurs in the radial direction and can be coupled with the causing torsional vibration. Torsional vibration can occur in the disk surface angular displacement only which can vary with the radius. Out-of-plane bending vibration, the so-called transverse vibration, occurs on the direction occurring perpendicular to the plane of rotation.

Depending on the amplitude of vibrations, the established publications have used linear or nonlinear approaches. In the linear methods, the effect of higher-order terms in the strain–displacement relations is neglected. In the nonlinear theory of vibration, the effects of higher-order strain terms are taken into account and for most cases they have given approximate solutions. Based on both of these approaches, disk deflection will become unbounded at critical speeds corresponding to flutter or and divergence instabilities. In fact, in these unstable cases, the disk deflection is increased beyond the acceptable range of linear modal, and it is necessary to use nonlinear analysis for better predictions of the dynamics of spinning disks.

While the linear and nonlinear transverse vibrations of rotating disk have received higher attention; nevertheless, knowledge of the in-plane vibration of rotating disks is also essential for design of rotating disks. In practice, the problem of rotating disks is far more relevant to applications such as computer hard disks, turbine rotors, and circular saw blades. It should be noted that the vibration analysis of rotating disks has more complexities than that of a stationary disk subject to a rotating load. This complexity is due to the Coriolis and centripetal acceleration terms associated with the relative motion of the spinning disk.

The problems of in-plane vibration of rotating disks have been addressed by a few investigators. Bhuta and Jones [1] have presented a solution to the symmetric in-plane vibrations of a thin rotating circular disk for some specific modes. Burdess et~al. [2] presented generalized formulation to consider asymmetric in-plane vibrations, while the effect of rotational speed on forward and backward traveling wave was discussed only for the mode with two nodal diameters. In their study, the equations of motion of a thin rotating disk were derived and a solution was achieved. Moreover, they studied free and forced vibrations and presented their results for the stability and resonant behavior of the disk. Before Chen and Jhu [3], in most of previous studies, the disk was assumed to be full. Chen and Jhu [3] determined the free in-plane vibration of a thin spinning annular disk and investigated the effects of clamping ratio on the natural frequencies and stability of disks. They extended their analysis to study the divergence instability of spinning annular disks clamped at the inner edge and free at the outer boundary. They also considered the effect of a radius ratio on the natural frequencies and critical speeds of the disk. Chen and Jhu [4] derived an analytical solution for the in-plane stress and displacement distributions in a spinning annular disk under stationary edge loads. Their numerical results showed that as the rotational speed of the disk approaches zero, the in-plane stresses and displacements are shown analytically to recover the solution derived through the Airy stress function in the classical theory of linear elasticity. Hamidzadeh and Dehghani [5] investigated the linear in-plane vibration of an elastic rotating disk and studied the effect of rotational speed and radius ratio on natural frequency and elastic stability of fixed–free vibration rotating disks. Hamidzadeh [6] also developed an analytical solution for in-plane vibration of spinning rings. Hamidzadeh’s previous solution for the rotating disk was extended to investigate an analytical method for the determination of modal vibration of high speed double-segment compound rotating disks [7]. More specifically, a systematic approach for a compound rotating disk based on an established solution for linear in-plane vibration of each segment was developed by satisfying the displacements and stresses compatibilities. He also presented variation of the dimension natural frequencies for a number of modes versus non-dimensional speed of rotation for a fixed–free annular disk for the non-dimensional speeds ranging from 0 to 1.5 [8]. Deshpande and Mote [9] studied the stability of a spinning thin disk using a nonlinear strain in order to account changes in stiffness of the disk due to rotation. Their study suggested that the critical speeds were different using the linear strain assumption. Sarfaraz and Hamidzadeh [10] studied the effect of material hysteretic damping of the disk on the natural frequencies and mode shapes of a fixed–free rotating disk by considering constant complex elastic moduli.

This research report represents the linear in-plane free vibration of a thin viscoelastic annular rotating disk. In the development of the analytical solution, two-dimensional elastodynamic theory is employed and the viscoelastic material for the medium is allowed by assuming complex elastic moduli. The mathematical model is reduced to a wave propagation problem and time-dependent and time-independent modes are considered. The general governing equations of motion are derived by implementing plane stress theory. The natural frequencies and respective modal displacements and stresses are achieved by satisfying the inner and outer boundary conditions. The non-dimensional natural frequencies and modal loss factors for different boundary conditions are computed and presented for several modes, specific radius ratios, and material loss factors. Also, the critical speeds for rotating disks and rings are determined. Furthermore, the influences of embedded disk segments with a different material at one of the edges of the main disk on modal parameters are investigated.

2 Governing Equations

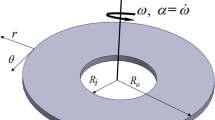
The material of the disk is assumed to be homogeneous, viscoelastic, and isotropic. The disk is rotating at a constant angular speed without any acceleration. The two-dimensional theory of elasticity is applied to derive the stress and strain in polar coordinates. These relationships are then implemented into the dynamic equilibrium equations to derive the governing equations of motion. Figure 22.1 shows the radial and tangential displacements of a point in polar coordinates (r, θ). As it was presented by Hamidzadeh [8], equations of motion in terms of dilatation Δ and elastic rotation ψ or the freely rotating annular disk are given by:

$$ \left.\begin{array}{l}{c}_1^2{\nabla}^2\Delta -\ddot{\Delta}+{\omega}^2\Delta +2\omega \dot{\psi}=-2{\omega}^2\\[6pt] {}{c}_2^2{\nabla}^2\psi -\ddot{\psi}+{\omega}^2\psi -2\omega \dot{\Delta}=0\end{array}\right\} $$
(22.1)

where

$$ \left.\begin{array}{l}\psi =\dfrac{\partial v}{\partial r}-\dfrac{1}{r}\dfrac{\partial u}{\partial \theta }+\dfrac{v}{r},\\[10pt] {}\Delta =\dfrac{\partial u}{\partial r}+\dfrac{1}{r}\dfrac{\partial v}{\partial \theta }+\dfrac{u}{r},\\[10pt] {}{\nabla}^2=\dfrac{\partial^2}{\partial {r}^2}+\dfrac{1}{r}\dfrac{\partial }{\partial r}+\dfrac{1}{r^2}\dfrac{\partial^2}{\partial {\theta}^2},\\[10pt] {}{E}^{*}=E\left(1+ i\eta \right),\\[10pt] {}{G}^{*}=\dfrac{E^{*}}{2\left(1+\nu \right)},\\[10pt] {}{c}_1^2=\dfrac{E^{*}}{\left(1-{\nu}^2\right)\rho },\\[10pt] {}{c}_2^2=\dfrac{G^{*}}{\rho }.\end{array}\right\} $$
(22.2)
Fig. 22.1
figure 1

(a) A typical rotating annular disk, (b) geometry of an annual disk in polar coordinate

Full size image

The functions u and v are radial and tangential displacements. υ, E*, and G* are Poisson ratio and complex elastic and shear moduli for the viscoelastic medium.

3 Solution to Governing Equation

The following solutions can be assumed for Eq. (22.1):

$$ \left.\begin{array}{l}\Delta ={\delta}_0(r)+{\Sigma \Delta}_n(r){e}^{i\left( n\theta + pt\right)},\\[6pt] {}\psi =\Sigma i{\psi}_n(r){e}^{i\left( n\theta + pt\right)}.\end{array}\right\} $$
(22.3)

where Δ n and ψ n are time-dependent functions and δ 0(r) is a time-independent function. Also, Δ is time-dependent dilatation, ψ is time-dependent elastic rotation, n is any integer number, and p is the frequency of vibration. In the time-independent part, δ 0(r) is only a function of r so the solution of that can be given by

$$ \left.\begin{array}{l}{\delta}_0={A}_0{J}_0\left({K}_{1r}\right)+{B}_0{Y}_0\left({K}_1r\right)-2,\\[6pt] {}{K}_1=\dfrac{\omega }{c_1}.\end{array}\right\}$$
(22.4)

The governing equation for time dependence is

$$ \left.\begin{array}{l}{c}_1^2{\nabla}^2\Delta -\ddot{\Delta}+{\omega}^2\Delta +2\omega \dot{\psi}=0\\[6pt] {}{c}_2^2{\nabla}^2\psi -\ddot{\psi}+{\omega}^2\psi -2\omega \dot{\Delta}=0\end{array}\right\}$$
(22.5)

The time-dependent equations have a significant role in determining the natural frequencies and mode shapes of the system. To continue with derivation of the final solution, it is convenient to introduce the following dimensionless variables:

$$ \left.\begin{array}{l}{\Omega}_1=\dfrac{\omega }{c_1}b,{\Omega}_2=\dfrac{p}{c_1}b,\\[10pt] {}{U}_n^{*}=\dfrac{U_n}{b},{V}_n=\dfrac{V_n}{b},\\[10pt] {}{\sigma}_{r_n}^{*}=\dfrac{\sigma_r}{G},{\tau}_{r{\theta}_n}^{*}=\dfrac{\tau_{r\theta}}{G},\\[10pt] {}r*=\dfrac{r}{b},q=\dfrac{c_1}{c_2}.\end{array}\right\}$$
(22.6)

where Ω1 and Ω2 are non-dimensional speed and non-dimensional frequency. Substituting modal expression from Eq. (22.3) into governing Eq. (22.1), the two different ratios of modal elastic rotation to modal dilatation are expressed by the following equations:

$$ \left.\begin{array}{l}{t}_{1n}=\dfrac{\psi_n(r)}{\Delta_n(r)}=\dfrac{2{\Omega}_1^{*}{\Omega}_2^{*}{q}^2}{-{x}_1^{*2}+{q}^2\left({\Omega}_1^{*2}+{\Omega}_2^{*2}\right)},\\[12pt] {}{t}_{2n}=\dfrac{\psi_n(r)}{\Delta_n(r)}=\dfrac{2{\Omega}_1^{*}{\Omega}_2^{*}{q}^2}{-{x}_2^{*2}+{q}^2\left({\Omega}_1^{*2}+{\Omega}_2^{*2}\right)}.\end{array}\right\} $$
(22.7)

where

$$ {x}_1^{*},{x}_2^{*}\,{=}\,\frac{{-}\,\left(1\,{+}\,{q}^2\right)\left({\Omega}_1^2\,{+}\,{\Omega}_2^2\right)\,{\pm}\,\sqrt{{\left[\left(1\,{+}\,{q}^2\right)\left({\Omega}_1^2\,{+}\,{\Omega}_2^2\right)\right]}^2\,{-}\,4\left[{q}^2{\left({\Omega}_1^2\,{-}\,{\Omega}_2^2\right)}^2\right]}}{2}. $$
(22.8)

By using the Bessel function of the first and second kind, the solutions to the wave operators Δ n and ψ n are obtained:

$$ \left.\begin{array}{l}{\Delta}_n(r)={B}_n{J}_n\left({r}^{*}{x}_1^{*}\right)+{C}_n{Y}_n\left({r}^{*}{x}_1^{*}\right)+{D}_n{J}_n\left({r}^{*}{x}_2^{*}\right)+{E}_n{Y}_n\left({r}^{*}{x}_2^{*}\right),\\[6pt] {}{\psi}_n(r)={t}_{1n}{B}_n{J}_n\left({r}^{*}{x}_1^{*}\right)+{t}_{1n}{C}_n{Y}_n\left({r}^{*}{x}_1^{*}\right)+{t}_{2n}{D}_n{J}_n\left({r}^{*}{x}_2^{*}\right)\\[6pt]{}\qquad\quad\ \ +{t}_{2n}{E}_n{Y}_n\left({r}^{*}{x}_2^{*}\right).\end{array}\right\} $$
(22.9)

4 Modal Displacements and Stresses

The radial and tangential displacements in terms of time can be written by the following equations:

$$ \left.\begin{array}{l}u\left(r,\theta, t\right)={U}_n(r){e}^{i\left( n\theta + pt\right)},\\[6pt] {}v\left(r,\theta, t\right)=i{V}_n(r){e}^{i\left( n\theta + pt\right)}.\end{array}\right\} $$
(22.10)

Substituting Eq. (22.9) and these displacements into equations of motions and rearranging, the result yields the modal solution for the non-dimensional radial and tangential displacements:

$$ {\renewcommand\theequation{\normalsize\thechapter.\arabic{equation}}\fontsize{7.5}{10}\selectfont{\left.\begin{array}{l}{U}_n^{*}(r){=}{m}_1^{*}\left(\begin{array}{l}\left[{x}_1^{*}{J}_n^{\prime}\left({r}^{*}{x}_1^{*}\right)+\dfrac{n{t}_1n}{q^2{r}^{*}}{J}_n\right({r}^{*}{x}_1^{*}\left)\right]{B}_n+\left[{x}_1^{*}{Y}_n^{\prime}\right({r}^{*}{x}_1^{*}\left)+\dfrac{n{t}_{1n}}{q^2{r}^{*}}{Y}_n\right({r}^{*}{x}_1^{*}\left)\right]{C}_n\\[3pt] {}{+}\left[{x}_2^{*}{J}_n^{\prime}\left({r}^{*}{x}_2^{*}\right){+}\dfrac{n{t}_{2n}}{q^2{r}^{*}}{J}_n\right({r}^{*}{x}_2^{*}\left)\right]{D}_n{+}\left[{x}_2^{*}{Y}_n^{\prime}\right({r}^{*}{x}_2^{*}\left){+}\dfrac{n{t}_{2n}}{q^2{r}^{*}}{Y}_n\right({r}^{*}{x}_2{}^{*}\left)\right]{E}_n\end{array}\right)\!{+}\\[12pt] {}{m}_2^{*}\left(\begin{array}{l}\left[\dfrac{n}{r^{*}}{J}_n\left({r}^{*}{x}_1^{*}\right){+}\dfrac{t_{1n}}{q^2}{x}_1^{*}{J}_n^{\prime}\right({r}^{*}{x}_1^{*}\left)\right]{B}_n{+}\left[\dfrac{n}{r^{*}}{Y}_n\right({r}^{*}{x}_1^{*}\left){+}\dfrac{t_{1n}}{q^2}{x}_1^{*}{Y}_n^{\prime}\right({r}^{*}{x}_1^{*}\left)\right]{C}_n\\ [3pt] {}{+}\left[\dfrac{n}{r^{*}}{J}_n\left({r}^{*}{x}_2^{*}\right){+}\dfrac{t_{2n}}{q^2}{x}_2^{*}{J}_n^{\prime}\right({r}^{*}{x}_2^{*}\left)\right]{D}_n{+}\left[\dfrac{n}{r^{*}}{Y}_n\right({r}^{*}{x}_2^{*}\left){+}\dfrac{t_{2n}}{q^2}{x}_2^{*}{Y}_n^{\prime}\right({r}^{*}{x}_2^{*}\left)\right]{E}_n\end{array}\right)\\ [3pt] {}\\ [3pt] {}{V}_n^{*}(r){=}{m}_2^{*}\left(\begin{array}{l}\left[{x}_1^{*}{J}_n^{\prime}\left({r}^{*}{x}_1^{*}\right){+}\dfrac{n{t}_1n}{q^2{r}^{*}}{J}_n\right({r}^{*}{x}_1^{*}\left)\right]{B}_n{+}\left[{x}_1^{*}{Y}_n^{\prime}\right({r}^{*}{x}_1^{*}\left){+}\dfrac{n{t}_{1n}}{q^2{r}^{*}}{Y}_n\right({r}^{*}{x}_1^{*}\left)\right]{C}_n\\ [3pt] {}{+}\left[{x}_2^{*}{J}_n^{\prime}\left({r}^{*}{x}_2^{*}\right){+}\dfrac{n{t}_{2n}}{q^2{r}^{*}}{J}_n\right({r}^{*}{x}_2^{*}\left)\right]{D}_n{+}\left[{x}_2^{*}{Y}_n^{\prime}\right({r}^{*}{x}_2^{*}\left){+}\dfrac{n{t}_{2n}}{q^2{r}^{*}}{Y}_n\right({r}^{*}{x}_2{}^{*}\left)\right]{E}_n\end{array}\right)\,{+}\\[12pt] {}{m}_1^{*}\left(\begin{array}{l}\left[\dfrac{n}{r^{*}}{J}_n\left({r}^{*}{x}_1^{*}\right){+}\dfrac{t_{1n}}{q^2}{x}_1^{*}{J}_n^{\prime}\right({r}^{*}{x}_1^{*}\left)\right]{B}_n{+}\left[\dfrac{n}{r^{*}}{Y}_n\right({r}^{*}{x}_1^{*}\left){+}\dfrac{t_{1n}}{q^2}{x}_1^{*}{Y}_n^{\prime}\right({r}^{*}{x}_1^{*}\left)\right]{C}_n\\ [3pt] {}{+}\left[\dfrac{n}{r^{*}}{J}_n\left({r}^{*}{x}_2^{*}\right){+}\dfrac{t_{2n}}{q^2}{x}_2^{*}{J}_n^{\prime}\right({r}^{*}{x}_2^{*}\left)\right]{D}_n{+}\left[\dfrac{n}{r^{*}}{Y}_n\right({r}^{*}{x}_2^{*}\left){+}\dfrac{t_{2n}}{q^2}{x}_2^{*}{Y}_n^{\prime}\right({r}^{*}{x}_2^{*}\left)\right]{E}_n\end{array}\right)\end{array}\!\right\}_{\vphantom{\sum_8}}\!,}} $$
(22.11)

where prime and double prime (′ and ″) represent first and second derivatives of the function and m *1 and m *1 can be presented by:

$$ \left.\begin{array}{l}{m}_1^{*}=-\frac{\Omega_1^{*2}+{\Omega}_2^{*2}}{{\left({\Omega}_1^{*2}-{\Omega}_2^{*2}\right)}^2},\\[1pc] {}{m}_2^{*}=-\frac{2{\Omega}_1^{*2}{\Omega}_2^{*2}}{{\left({\Omega}_1^{*2}-{\Omega}_2^{*2}\right)}^2}.\end{array}\right\} $$
(22.12)

Similarly, the modal radial and shear stresses can be expressed by the following relations:

$$ \left.\begin{array}{l}{\sigma}_r\left(r,\theta, t\right)={\sigma}_{r_n}(r){e}^{i\left( n\theta + pt\right)}\\ {}{\tau}_{r\theta}\left(r,\theta, t\right)=i{\tau}_{r{\theta}_n}(r){e}^{i\left( n\theta + pt\right)}\end{array}\right\} $$
(22.13)

The non-dimensional modal radial and shear stresses can be obtained by substituting from Eqs. (22.9) and (22.11) based on stress–strain relation, and after simplifications they are presented by

$$ {\renewcommand\theequation{\normalsize\thechapter.\arabic{equation}}\fontsize{8}{10}\selectfont{\left.\begin{array}{l}{\sigma}_{r_n}^{*}=\dfrac{\lambda }{G}\left[{B}_n{J}_n\left({r}^{*}{x}_1^{*}\right){+}{C}_n{Y}_n\right({r}^{*}{x}_1^{*}\left){+}{D}_n{J}_n\right({r}^{*}{x}_2^{*}\left){+}{E}_n{Y}_n\right({r}^{*}{x}_2^{*}\left)\right]{+}\\ {}2\left[{s}_1^{*}{x}_1^{*2}{J}_n^{\prime\prime}\left({r}^{*}{x}_1^{*}\right){+}{s}_2^{*}\dfrac{n}{r^{*}}{x}_1^{*}{J}_n^{\prime}\right({r}^{*}{x}_1^{*}\left){-}{s}_2^{*}\dfrac{n}{r^{*2}}{J}_n\right({r}^{*}{x}_1^{*}\left)\right]{B}_n{+}2\left[{s}_1^{*}{x}_1^{*2}{Y}_n^{\prime\prime}\right({r}^{*}{x}_1^{*}\Big)\\ {}{+}{s}_2^{*}\dfrac{n}{r^{*}}{x}_1^{*}{Y}_n^{\prime}\left({r}^{*}{x}_1^{*}\right){-}{s}_2^{*}\dfrac{n}{r^{*2}}{Y}_n\left({r}^{*}{x}_1^{*}\right)\left]{C}_n{+}2\right[{s}_3^{*}{x}_2^{*2}{J}_n^{\prime\prime}\left({r}^{*}{x}_2^{*}\right){+}{s}_4^{*}\dfrac{n}{r^{*}}{x}_2^{*}{J}_n^{\prime}\left({r}^{*}{x}_2^{*}\right)\\ {}{-}{s}_4^{*}\dfrac{n}{r^{*2}}{J}_n\left({r}^{*}{x}_2^{*}\right)\left]{D}_n{+}2\right[{s}_3^{*}{x}_2^{*2}{Y}_n^{\prime\prime}\left({r}^{*}{x}_2^{*}\right){+}{s}_4^{*}\dfrac{n}{r^{*}}{x}_2^{*}{Y}_n^{\prime}\left({r}^{*}{x}_2^{*}\right){-}{s}_4^{*}\dfrac{n}{r^{*2}}{Y}_n\left({r}^{*}{x}_2^{*}\right)\Big]{E}_n\\ {}\\ {}{\tau}_{r{\theta}_n}^{*}=2\left[{s}_2^{*}{x}_1^{*2}{J}_n^{\prime\prime}\left({r}^{*}{x}_1^{*}\right){+}{s}_1^{*}\dfrac{n}{r^{*}}{x}_1^{*}{J}_n^{\prime}\right({r}^{*}{x}_1^{*}\left){-}{s}_1^{*}\dfrac{n}{r^{*2}}{J}_n\right({r}^{*}{x}_1^{*}\left)\right]{B}_n{+}2\left[{s}_2^{*}{x}_1^{*2}{Y}_n\right({r}^{*}{x}_1^{*}\Big)\\ {}{+}{s}_1^{*}\dfrac{n}{r^{*}}{x}_1^{*}{Y}_n^{\prime}\left({r}^{*}{x}_1^{*}\right){-}{s}_1^{*}\dfrac{n}{r^{*2}}{Y}_n\left({r}^{*}{x}_1^{*}\right)\left]{C}_n{+}2\right[{s}_4^{*}{x}_2^{*2}{J}_n^{\prime\prime}\left({r}^{*}{x}_2^{*}\right){+}{s}_3^{*}\dfrac{n}{r^{*}}{x}_2^{*}{J}_n^{\prime}\left({r}^{*}{x}_2^{*}\right)\\ {}{-}{s}_3^{*}\dfrac{n}{r^{*2}}{J}_n\left({r}^{*}{x}_2^{*}\right)\left]{D}_n{+}2\right[{s}_4^{*}{x}_2^{*2}{Y}_n^{\prime\prime}\left({r}^{*}{x}_2^{*}\right){+}{s}_3^{*}\dfrac{n}{r^{*}}{x}_2^{*}{Y}_n^{\prime}\left({r}^{*}{x}_2^{*}\right){-}{s}_3^{*}\dfrac{n}{r^{*2}}{Y}_n\left({r}^{*}{x}_2^{*}\right)\Big]{E}_n\\ {}{-}\left[{t}_{1n}{B}_n{J}_n\left({r}^{*}{x}_1^{*}\right){+}{t}_{1n}{C}_n{Y}_n\right({r}^{*}{x}_1^{*}\left){+}{t}_{2n}{D}_n{J}_n\right({r}^{*}{x}_2^{*}\left){+}{t}_{2n}{E}_n{Y}_n\right({r}^{*}{x}_2^{*}\left)\right]\end{array}\!\!\right\}\!,}} $$
(22.14)

where

$$ \left.\begin{array}{l}{s}_1^{*}={m}_1^{*}+{m}_2^{*}\dfrac{t_{1n}}{q^2},\\[6pt] {s}_2^{*}={m}_2^{*}+{m}_1^{*}\dfrac{t_{1n}}{q^2},\\[6pt] {s}_3^{*}={m}_1^{*}+{m}_2^{*}\dfrac{t_{2n}}{q^2},\\[6pt] {s}_4^{*}={m}_2^{*}+{m}_1^{*}\dfrac{t_{2n}}{q^2}.\end{array}\right\} $$
(22.15)

Using Eqs. (22.11) and (22.14), the modal displacements and stresses at any radius for each part of an annular disk can be expressed in the following form:

$$ \left\{\begin{array}{l}{U}_n^{*}(r)\\ {}{V}_n^{*}(r)\\ {}{\sigma}_{r n}^{*}(r)\\ {}{\tau}_{r\theta n}^{*}(r)\end{array}\right\}=\left[{A}_n(r)\right]\left\{\begin{array}{l}{B}_n\\ {}{C}_n\\ {}{D}_n\\ {}{E}_n\end{array}\right\}, $$
(22.16)

where

$$ \left[{A}_n(r)\right]=\left[\begin{array}{cccc}\hfill {a}_{11}\hfill & \hfill {a}_{12}\hfill & \hfill {a}_{13}\hfill & \hfill {a}_{14}\hfill \\ {}\hfill {a}_{21}\hfill & \hfill {a}_{22}\hfill & \hfill {a}_{23}\hfill & \hfill {a}_{24}\hfill \\ {}\hfill {a}_{31}\hfill & \hfill {a}_{32}\hfill & \hfill {a}_{33}\hfill & \hfill {a}_{34}\hfill \\ {}\hfill {a}_{41}\hfill & \hfill {a}_{42}\hfill & \hfill {a}_{43}\hfill & \hfill {a}_{44}\hfill \end{array}\right]. $$
(22.17)

Elements of A n (r) are in terms of material properties and Bessel functions of first and second kinds. These elements are presented in the above-mentioned paper [8].

5 Natural Frequency Equation

To determine the modal parameters, the boundary conditions must be satisfied. For example, for the fixed–free boundary conditions, it is required that the modal displacements at the inner edge and the modal radial and shear stresses at the outer edge must be zero. By implementing the boundary conditions in Eq. (22.16) and combining them, displacements and stresses at the boundaries are related in the following form:

$$ \left\{\begin{array}{c}{U}_n^{*}(b)\\ {}{V}_n^{*}(b)\\ {}0\\ {}0\end{array}\right\}=\left[{A}_n(b)\right]{\left[{A}_n(a)\right]}^{-1}\left\{\begin{array}{c}{U}_n^{*}(a)\\ {}{V}_n^{*}(a)\\ {}0\\ {}0\end{array}\right\}. $$
(22.18)

Considering that the matrix [A n (b)][A n (a)]− 1 is presented in the following form:

$$ \left[{A}_n(b)\right]{\left[{A}_n(a)\right]}^{-1}=\left[\begin{array}{cccc}\hfill {d}_{11}\hfill & \hfill {d}_{21}\hfill & \hfill {d}_{31}\hfill & \hfill {d}_{41}\hfill \\ {}\hfill {d}_{21}\hfill & \hfill {d}_{22}\hfill & \hfill {d}_{23}\hfill & \hfill {d}_{24}\hfill \\ {}\hfill {d}_{31}\hfill & \hfill {d}_{32}\hfill & \hfill {d}_{33}\hfill & \hfill {d}_{34}\hfill \\ {}\hfill {d}_{41}\hfill & \hfill {d}_{42}\hfill & \hfill {d}_{43}\hfill & \hfill {d}_{44}\hfill \end{array}\right]. $$
(22.19)

Then Eq. (22.18) can be reduced to the following expression in terms of the inner boundary stresses:

$$ \left[\begin{array}{cc}\hfill {d}_{31}\hfill & \hfill {d}_{32}\hfill \\ {}\hfill {d}_{41}\hfill & \hfill {d}_{41}\hfill \end{array}\right]\left\{\begin{array}{l}{U}_n^{*}(a)\\ {}{V}_n^{*}(a)\end{array}\right\}=\left\{\begin{array}{l}0\\ {}0\end{array}\right\}. $$
(22.20)

In order to obtain a nonzero solution for the stresses, the determinant of the matrix in Eq. (22.20) must be zero. This results in the frequency equation for the system:

$$ \left|\begin{array}{cc}\hfill {d}_{31}\hfill & \hfill {d}_{32}\hfill \\ {}\hfill {d}_{41}\hfill & \hfill {d}_{41}\hfill \end{array}\right|=0 $$
(22.21)

The above equation is a function of circumferential wave number n, and other dimensionless parameters including Ω1. For given values of n, a/b, υ, Ω1, and material loss factor η m there are infinite real values for Ω2 that satisfy this equation. It should be noted that the dimensionless frequencies in the rotating coordinate system are given by the absolute values of Ω2:

$$ {\Omega}_R=\left|{\Omega}_2\right|$$
(22.22)

However, for viscoelastic disk, since modulus of elasticity for damping material is complex, then Ω2 in Eq. (22.22) would be complex. In order to obtain the modal loss factor and the natural frequencies for the viscoelastic rotating disks, the following procedures are implemented:

$$ \left.\begin{array}{l}{\Omega}_2^{*}=x+ iy=\sqrt{x^2+{y}^2}{e}^{i\alpha},\\ {}\alpha ={ \tan}^{-1}\frac{y}{x},\\ {}{\Omega}_2^{*2}=\left({x}^2+{y}^2\right){e}^{i2\alpha },\\ {}{\Omega}_2^{*2}=\left({x}^2+{y}^2\right)\left( \cos 2\alpha +i \sin 2\alpha \right),\\ {}{\Omega}_2^{*2}=\left({x}^2+{y}^2\right) \cos 2\alpha \left[1+i \tan 2\alpha \right],\\ {}{\Omega}_2^{*}={\Omega}_2\left(1+i{\eta}_L\right).\end{array}\right\},$$
(22.23)

where η L is modal loss factor and is obtained in following form:

$$ {\eta}_L= \tan 2\alpha$$
(22.24)

and the natural frequencies are given by:

$$ {\Omega}_2=\sqrt{\frac{x^2+{y}^2}{\sqrt{1+{\eta}_L^2}}}.$$
(22.25)

For mode shapes n > 0, if the direction of oscillating wave is the same as that of rotation of the disk (p > 0) in rotating coordinates, the wave is defined as forward wave in rotating coordinates. If the direction of oscillating wave is opposite to that of rotation of the disk (p < 0) in rotating coordinates, the wave is defined as backward wave in rotating coordinates. For mode shapes n < 0, if the direction of oscillating wave is the same as that of rotation of the disk (p F > 0) in fixed coordinates, the wave is defined as forward wave in fixed coordinates. If the direction of oscillating wave is opposite to that of rotation of the disk (p F < 0) in fixed coordinates, then the wave defined as backward wave in fixed coordinates. Thus, the relation between natural frequency in fixed coordinates (p F ) and rotating coordinates (p) and the relation between dimensionless natural frequencies in fixed and rotating coordinate system can be presented by the following equations:

$$ {\Omega}_F=\left|{\Omega}_2+n{\Omega}_1\right|\kern1em for\kern1em {\Omega}_2>0$$
(22.26a)
$$ {\Omega}_F=\left|{\Omega}_2-n{\Omega}_1\right|\kern1em for\kern1em {\Omega}_2<0. $$
(22.26b)

Mode shapes for the in-plane free vibration of a rotating disk can be identified by the number of circular node numbers (m) and the number of nodal diameters (n). It should be noted that the lower modes (m = 0, 1, 2, 3 and n = 0, 1, 2, 3) have been found to be the dominant modes of vibration for vibration of the rotating disks.

6 Natural Frequencies and Critical Speeds

The lowest frequency at which the disk vibrates freely is called the fundamental mode. When the disk is excited at one of its resonance frequencies, respective nodal circle(s) and nodal diameter(s) appear. To determine the natural frequency of the system, the boundary conditions must be satisfied both at the inner radius of the disk (r = a) and the outer radius of disk (r = b). Considering that for the fixed–free rotating disks the modal displacements are zero at the inner radius and modal stresses are zero at the outer radius, then non-dimensional natural frequencies can be determined for any particular non-dimensional rotating speed and a given geometry by using Eq. (22.21).

The variations of the dimensionless natural frequencies of a thin annular disk with Poisson ratio of 0.3 and no material damping in the fixed coordinate for a number of modes are presented here. The boundary conditions considered are free–free, fixed–free, and free–fixed. It should be noted that critical speed for rotating disk is the speed of rotation at which the resonant frequency is zero. Needless to say that in general the annular disk has infinite number of natural frequencies with any combinations of positive integer values for n or m. Thus there are infinite possible numbers of critical speeds for any rotating disk. In this section, the results of the proposed solution are compared with the available data [2, 9]. The comparisons demonstrated excellent agreement among the present result and the available data. This comparison is depicted in Fig. 22.2.

Fig. 22.2
figure 2

Comparison of dimensionless natural frequencies for m = 0 and n = 2 with established results

Full size image

Figure 22.3 presents the variation of dimensionless critical speeds for different modes of free–free boundary conditions versus radius ratios of the rotating disks. Illustrated results show that as the radius ratio increases, the critical speed decreases. In addition, for mode numbers of n = 2 and higher, the critical speed reduces to zero where radius ratio approaches to one. Figure 22.4 demonstrates the variation of dimensionless critical speed for fixed–free rotating disk versus radius ratio for different wave numbers of n. As depicted, since the disk is fixed at the inner and free at the outer radius, as the radius ratio increases, the critical speed increases, and for n = 0, as the radius ratio approaches zero, the critical speed approaches to zero.

Fig. 22.3
figure 3

Variation of dimensionless critical speed versus radius ratio for different modes of free–free rotating disks

Full size image
Fig. 22.4
figure 4

Variation of dimensionless critical speed versus radius ratio for different modes of fixed–free rotating disks

Full size image

Figure 22.5 shows the variations of dimensionless natural frequencies that are experienced in fixed coordinates for free–free conditions versus dimensionless speed for different modes (m, n) and a radius ratio a/b = 0.1. Figures 22.6 and 22.7 show the same results for disk with similar geometry for two different boundary conditions of fixed–free and free–fixed. The presented results are extended for a wide range of dimensionless rotational speed well beyond the speeds previously presented in the established publications. Please note that labels b and f refer to the backward and forward waves in the presented figures.

Fig. 22.5
figure 5

Variation of dimensionless natural frequency versus dimensionless speed for different modes of a free–free disk with a radius ratio a/b = 0.1

Full size image
Fig. 22.6
figure 6

Variation of dimensionless natural frequency versus dimensionless speed for different modes of a fixed–free disk with a radius ratio a/b = 0.1

Full size image
Fig. 22.7
figure 7

Variation of dimensionless natural frequency versus dimensionless speed for different modes of a free–fixed disk with a radius ratio a/b = 0.1

Full size image

7 The Modal Loss Factor of Viscoelastic Rotating Disk

The main objective of this section is to provide an accurate method for predicting the natural frequencies and modal loss factors for in-plane vibration of a rotating annular disk made of viscoelastic material for a specified boundary conditions. The material damping considered is based on typical hysteretic damping with complex elastic moduli. The viscoelastic material can provide the needed structure stiffness with possibility of dissipating vibration energy. To determine the influence of material loss factor on the non-dimensional natural frequencies and their corresponding modal loss factors, computed results for a certain radius ratio of a/b, Poisson’s ratio of 0.3, and wide range of material loss factors are provided in this section.

Figures 22.8, 22.9, and 22.10 show variation of dimensionless modal loss factors versus dimensionless speed for a fixed–free viscoelastic rotating annular disk with a radius ratio 0.2 and different wave numbers. The presented results are for hysteretic damping with material loss factors of 0.05, 0.1, 0.3, 0.5, and 0.7. As shown, each curve presented in Fig. 22.11 depict the effect of different material loss factors on the non-dimensional natural frequencies for the mode associated with m = 2 and n = 2. It could be observed that by increasing wave number of n, modal loss factors are decreased.

Fig. 22.8
figure 8

Variation of dimensionless modal loss factor versus dimensionless speed for a fixed–free rotating disk with different material loss factor for radius ratio 0.2, n = 0, and m = 0 to 3

Full size image
Fig. 22.9
figure 9

Variation of dimensionless modal loss factor versus dimensionless speed for a fixed–free rotating disk with different material loss factor for radius ratio 0.2, n = 1, and m = 0 to 3

Full size image
Fig. 22.10
figure 10

Variation of dimensionless modal loss factor versus dimensionless speed for a fixed–free rotating disk with different material loss factor for radius ratio 0.2, n = 2, and m = 0 to 3

Full size image
Fig. 22.11
figure 11

Variation of dimensionless natural frequency versus dimensionless speed for different hysteretic material damping of a fixed–free disk with a radius ratio 0.2 and mode of n = 2, m = 2

Full size image

8 Natural Frequencies of Rotating Rings

Vibration abatement and structural stability in high speed rotating rings is one of the most prevalent problems in engineering practice. An important step in the study of these rotating structural components is the evaluation of the modal parameters such as mode shapes, natural frequencies, and critical speeds. This information has immense practical importance when designing for these components. It is known that in-plane motion of a point in the medium is combination of radial and circumferential displacements, and the natural frequencies depend on the rotational speed. The literature on dynamic response of rotating rings is mainly restricted to the application of shell or curved beam theories. The ring-like components is of great interest in mechanical systems. For the in-plane vibration of rings, they can be modeled by annular disks with radius ratios very close to one. Thus the general governing equation and natural frequency equation for the rotating annular disk are also valid to determine all the model parameters for ring when its boundary conditions are satisfied. Figures 22.12 and 22.13 show the variation of dimensionless natural frequencies in fixed coordinate versus dimensionless speed of a ring with radius ratio of 0.9 for two different boundary conditions of free–free and fixed–free and different wave numbers of n = 0, 1, 2, and 3 and m = 0.

Fig. 22.12
figure 12

Variation of dimensionless natural frequency versus dimensionless speed for different modes of a free–free ring with a radius ratio 0.9 for different modes

Full size image
Fig. 22.13
figure 13

Variation of dimensionless natural frequency versus dimensionless speed for different modes of a free–fixed ring with a radius ratio 0.9 for different modes

Full size image

9 Effect of Embedded Different Material on Natural Frequencies

This section presents non-dimensional natural frequencies versus dimensionless rotating speeds for compound rotating annular disks with added disk segments with different materials at the inner or outer edge of the main disk. Figure 22.14 illustrates small embedded segments of higher stiffness and density at one of the edges of the rotating disk. Computation was performed to determine the effect of an added disk segment on the dimensionless natural frequency at different rotating speeds. This was done by considering the general solution for stresses and displacement at inner and outer edges of the main disk and the added disk segment using Eq. (22.14). The frequency equation for each mode can be determined by satisfying the compatibility of stresses and displacements at the interface between the main and the added disk segment as well as the boundary conditions of the compound disk. Analysis was conducted for three cases with the same inner to outer radius ratio of 0.2 and fixed–free boundary conditions. In case I, the disk is a single disk made of aluminum. Case II is for an aluminum main disk with added steel disk segment at the inner edge, and case III is an aluminum main disk with added steel disk segment at the outer edge. Non-dimensional frequencies in rotating coordinates for these three cases for a wide range of dimensionless rotating speeds and for t 1 = (b − a)/c = 0.05 and t 2 = (c − b)/c = 0.05 are illustrated in Fig. 22.15a.

Fig. 22.14
figure 14

Case (a): The disk has small segment of higher mass around of outer edge. Case (b): The disk has small segment of higher mass around of inner side

Full size image
Fig. 22.15
figure 15

Variation of dimensionless natural frequencies versus dimensionless speed of rotation for fixed–free disks with/without added segment for t = 0.05 and t = 0.15 for radius ratio of 0.2, n = 0 and m = 0, 1, 2, 3, 4

Full size image

Similar results for t 1 = t 2 = 0.15 are shown in Fig. 22.15b. The presented results are for n = 0, and m = 0, 1, 2, 3, and 4. The modulus of elasticity, mass density, and Poisson’s ratio for aluminum disk and steel are assumed to be (180 GPa, 7,700 kg/m3, and 0.305) and (69 GPa, 2,700 kg/m3, and 0.335), respectively.

10 Conclusion

In this research report, an analytical method has been developed to determine the natural frequency and critical speed for in-plane vibration of a homogeneous, isotropic viscoelastic rotating disk for a wide range of rotational speeds. The modal vibration characteristics of in-plane vibration for annular rotating disks are studied for different types of boundary conditions, i.e., free–free, fixed–free, and free–fixed. The proposed method of solution in this investigation can be effectively applied to determine the modal vibration characteristics of a high speed rotating annular disk. The provided method is capable of computing dimensionless natural frequencies for all modes at any rotating speeds. Furthermore, modal loss factor and stability of a rotating disk with hysteretic material damping ratio have been computed by considering complex natural frequencies. It was observed that the effect of rotational speed on natural frequency depended on the radius ratio, the mode of vibration, Poisson’s ratio, stiffness, mass density of the material, and material damping. The presented solution is also capable of determining modal information for the in-plane vibration of rings by considering the radius ratio of the ring, which is slightly less than 1. Moreover, it was observed that a small segment of a material of higher density and elasticity modulus attached around the inner side of rotating annular disk induced higher natural frequencies and promotes a better dynamic stability for a disk. The presented results can provide a guideline to assist designers by choosing appropriate geometry and material properties to avoid critical speeds and possible resonances for obtaining desired operating speed.