Keywords

1 Introduction

STLF is a very important part of power system operation, and it is also an integral part of the energy management system (EMS). STLF is the basis of optimal operation for power system. Prediction accuracy has a significant impact on safety, quality, and economic performance of the power system. Therefore, it is very important to search more suitable STLF method in order to maximize the prediction accuracy.

On the one hand, the power system load relates to many complex factors, and it is non-linear, uncertain and random. On the other hand, RBF neural network has the abilities of strong self-learning and complex non-linear function fitting, so it is suitable for load forecasting problems. But studies show that there are still many problems to be solved on the RBF neural network algorithm, particularly the parameters identify of RBF network, such as the number of hidden layer nodes, the center and width value in the RBF activation function for each node, and connection weights between the hidden layer nodes and output layer node. These parameters have great impact on the RBF network learning speed and performance. If improper parameters are selected, network convergence will slow, or even result in the network does not converge. In this paper, an improved genetic algorithm is used to optimize the RBF network, and the optimized network is used to forecast power load. Case analysis and calculation show that the method has high accuracy and good applicability.

2 Radial Basis Function Neural Network

2.1 RBF Network Structure

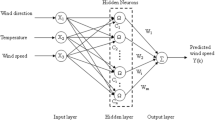
Radial basis function network is a local approximation network, generally including three layers (n inputs, m hidden node, p output). The structure is shown in Fig. 1.

Fig. 1
figure 00361

Radial Gaussian function network topology

Full size image

Basis function of RBF network is commonly used Gaussian function, which can be expressed as

$$ {\phi_i}(x)=\exp \left [\frac{{-{{{\Big\| {X-{c_i}} \Big\|}}^2}}}{{2\sigma_i^2}}\right],i=1,2\cdots, m $$
(1)

Where: \( {\phi_i}(x) \) is the output of the i-th hidden layer node; X is the input sample, \( \mathrm{ x} = ( {{\mathrm{ x}}_1},{{\mathrm{ x}}_2},\ldots,\ {{\mathrm{ x}}_{\mathrm{ n}}} ){{}^{\mathrm{ T}}} \); \( {{\mathrm{ c}}_{\mathrm{ i}}} \) is the center of the Gaussian kernel function of the i-th hidden layer node, having the same number of dimensions with X; \( {\sigma_{\mathrm{ i}}} \) is a variable for the i-th hidden layer node, called normalization constant or the base width [1, 2]. RBF network output is a linear combination of the output of hidden layer nodes.

$$ {y_k}=\sum\limits_{i=1}^m {{w_{ik }}} {\phi_i}(x),k=1,2,\cdots, p $$
(2)

2.2 The Learning Algorithm of Network Parameters

In the section, Gradient descent method is used to study the center \( {{\mathrm{ c}}_{\mathrm{ i}}} \) and the width parameters \( {\sigma_{\mathrm{ i}}} \) of RBF network. For the convenience of discussion, consider the case that the output layer has only one node. Substitute Eq. 1 into Eq. 2:

$$ f(x)=\sum\limits_{i=1}^m {{w_i}} \exp[\frac{{-{{{\left\| {X-{c_i}} \right\|}}^2}}}{{2\sigma_i^2}}] $$
(3)

Let the network desired output is \( {y^d}(x) \), the network energy function can be expressed as:

$$ E=\frac{1}{2}{{\sum\limits_{j=1}^n {\left( {{y^d}({x^{j}})-f({x^d})} \right)}}^{2}} $$
(4)

Let \( f({x^j}) \) substitute into Eq. 4, we can get:

$$ E=\frac{1}{2}{{\sum\limits_{j=1}^n {\left( {{y^d}({x^{j}})-\sum\limits_{i=1}^m {{w_i}} \exp \left[\frac{{-{{{\Big\| {{x^j}-{c_i}} \Big\|}}^2}}}{{2\sigma_i^2}}\right]} \right)}}^{2}} $$
(5)

Let the sample size is L, then

$$ E=\frac{1}{2}{{\sum\limits_{j=1}^n {\sum\limits_{l=1}^L {\left( {{y^d}(x_l^{\; j})-\sum\limits_{i=1}^m {{w_i}} \exp \left[\frac{{-{{{\left\| {x_l^{\; j}-{c_i}} \right\|}}^2}}}{{2\sigma_i^2}}\right]} \right)}}}^{2}} $$
(6)

Remember

$$ \xi \left( {x_l^{\; j},{c_i},{\sigma_i}} \right)=\frac{1}{2}{{\sum\limits_{j=1}^n {\sum\limits_{l=1}^L {\left( {{y^d}(x_l^{\; j})-\sum\limits_{i=1}^m {{w_i}} \exp \left[\frac{{-{{{\left\| {x_l^{\; j}-{c_i}} \right\|}}^2}}}{{2\sigma_i^2}}\right]} \right)}}}^{2}} $$
(7)

Then Eq. 6 becomes

$$ E=\frac{1}{2}\sum\limits_{j=1}^n {\sum\limits_{l=1}^L {(\xi (x_l^{\; j},{c_i},{\sigma_i})} } {)^{2}} $$
(8)

\( {w_i} \) is consider as a constant when you learn center values and width parameters, and you can get the central value and width parameter updating formula which can be represented by:

$$ \eqalign{ {c_i}(t+1)={c_i}(t)-\lambda \frac{{\partial E}}{{\partial {c_i}}}, \hfill \\{\sigma_i}(t+1)={\sigma_i}(t)-\beta \frac{{\partial E}}{{\partial {c_i}}} \hfill \\}<!endgathered> $$
(9)

In Eqs. 9 and 10, λ, β are the learning efficiency of the central value and width parameters. If the formula (8) is substituted into the formula (9) and formula (10), we can get:

$$ {c_i}(t+1)={c_i}(t)-\frac{\lambda }{{2\sigma_i^2}}\sum\limits_{j=1}^n {\sum\limits_{l=1}^L {\xi (x_l^{\; j},{c_i},{\sigma_i})} } \cdot \exp \left[\frac{{-{{{\Big\| {{x^{\; j}}-{c_i}} \Big\|}}^2}}}{{2\sigma_i^2}}\right](x_l^{\; j}-{c_i}) $$
(10)
$$ {\sigma_i}(t+1)={\sigma_i}(t)-\frac{\lambda }{{2\sigma_i^3}}\sum\limits_{j=1}^n {\sum\limits_{l=1}^L {\xi (x_l^{\; j},{c_i},{\sigma_i})} } \cdot \exp \left[\frac{{-{{{\Big\| {{x^{\; j}}-{c_i}} \Big\|}}^2}}}{{2\sigma_i^2}}\right]{{(x_l^{\; j}-{c_i})}^2} $$
(11)

According to the input samples, weights of the output layer can be calculated by using the least squares algorithm of system identification theory. In this paper, the learning algorithm for connection weights between the hidden layer and output layer can be expressed as:

$$ {w_{ik }}(l+1)={w_{ik }}(l)+\eta [y_k^d-{y_k}(l)]{\phi_i}(x) $$
(12)

In the formula: \( y_{{_k}}^d \) is the output to expect; l is the number of iterations; η is the learning rate, general 0 <η <2, to ensure iterative convergence.

3 RBF Network Training Based on Improved Genetic Algorithm

The core of RBF network design is to determine the number of hidden nodes and the central values, and other parameters of basis functions. We will design a neural network to meet the target error as small as possible to ensure that the generalization ability of neural networks. Genetic algorithm (GA) is a randomized search method which simulates biological evolution. This paper presents an improved genetic algorithm (IGA) [3]; the starting point for the algorithm is described as follows. First: to maintain population diversity and prevent premature; second: to improve local search ability of GA; Third: speed up the search; Fourth: to reduce the chance of getting into local extreme value.

3.1 Encoding and Initial Population Generation

That is to say, the RBF network hidden nodes number m, each hidden node center parameters \( {{\mathrm{ c}}_{\mathrm{ i}}} \) and the width parameters \( {\sigma_{\mathrm{ i}}} \) are compiled chromosome, and the collection of these parameters for the network are treated as an individual. In the initialization phase, initial population is generated by completely random method.

3.2 Select Options

Based on the deviation degree of this population, this article defines a selection operator which can bring a diversity of species, which is described as follows:

For a given fitness measure f, so

$$ U({X_j})={\Big| {f({X_j})-\overline{f}(X)} \Big|} $$
(13)

Among them, \( \bar{f}(X)=\frac{1}{N}\sum\limits_{k=1}^N {f({X_k})} \) is the population average fitness; N is the population size, \( f({X_j}) \) is the j-th individual’s fitness value in the group, \( U({X_j}) \) is the deviation degree between individual j and the group mean fitness. Disruptive selection chooses each individual according to the following probability formula:

$$ P\{{Y_i}={X_j}\}=\frac{{U({X_j})}}{{\sum\limits_{k=1}^N {U({X_k})} }},i=1,2,\cdots, M $$
(14)

From geometry, this means that the farther away from the average individual fitness, the higher the chance to be selected, thus corresponding with the fitness of the individual does not have a monotonic, can bring a greater diversity of species.

3.3 Cross Operating

The algorithm uses real number coding, therefore, the corresponding intersection operation can be realized by arithmetic crossover. Arithmetic crossover is defined as a linear combination of two individuals to generate a new breed of individual operations. We can set:

$$ C({X_1},{X_2})=\mu {X_1}+(1-\mu ){X_2} $$
(15)

Among them, \( {X_1},{X_2} \) are two different individuals of the populations. We can take:

$$ \mu =\left\{ \begin{array}{lll} \xi >1,\;\;\;F({X_1})\geq F({X_2}) \hfill \cr \xi <0,\;\;\;F({X_1})< F({X_2}) \hfill \end{array} \right\} $$
(16)

3.4 Mutation Operating

The adaptive mutation operator is used in this paper, and the specific description is as follows: First, if we randomly choose a component in the parent body vector \( x=({x_1},{x_2},\cdots, {x_n}) \), assumption it is the k-th, and then we randomly choose a number \( {{x^{\prime}}_k} \) instead of \( {x_k} \) in its definition interval \( [{a_k},{b_k}] \) to get mutated individuals \( y \), That is \( y=({x_1},{x_2},\cdots {{x^{\prime}}_k},\cdots, {x_n}) \), among them,

$$ x_k^{\prime}=\left\{ \eqalign{ {x_k}+\Delta (T,{b_k}-{x_k}),\;\;\;if\;\;random\ (0,1)=0 \hfill \\{x_k}-\Delta (T,{b_k}-{x_k}),\;\;\;if\;\;random\ (0,1)=1 \hfill \\}<!endgathered> \right\} $$
(17)

Where \( random(0,1) \) is the random number in the interval (0,1); \( \Delta (T,y)\in [0,y] \) is a random number obeying uniform distribution. As T decreases, the greater the likelihood \( \Delta (T,y) \) tends to 0. So that the algorithm searches large fitness individual in a small range and the small fitness individual in a large range, which makes the variation according to solution quality adaptively adjust the search area, which can obviously improve search capabilities [4].

The specific expression of the function \( \Delta (T,y) \) can be taken as:

$$ \Delta (T,y)=y\cdot (1-{r^{{T\lambda }}}) $$
(18)
$$ T=1-\frac{f(x) }{{{f_{\max }}}} $$
(19)

Where \( r \) is random number of the interval [0, 1], \( \lambda \) plays a regulatory role of the local search area, and its value is generally 2–5. \( f(x) \) represents fitness of the individual \( x \), \( {f_{\max }} \) is the biggest fitness value of problem to be solved; Due to \( {f_{\max }} \) is difficult to determine in many problems, we can use rough upper or the largest fitness value of the current population.

3.5 Algorithm Realization

The RBF network structure optimization and parameter learning are carried out in two phases, namely training and evolution. First, randomly generate N individuals to form groups, We use a gradient descent to learn the center \( {{\mathrm{ c}}_{\mathrm{ i}}} \) and width parameters \( {\sigma_{\mathrm{ i}}} \) corresponding to each individual hidden nodes chromosomes in the network, and use the least squares to learn linear weight value \( {w_i} \) of the network; Secondly, We use genetic evolutionary algorithm to optimize hidden nodes, by alternating these two processes to obtain the minimum number of hidden nodes required to meet the error basis functions and have different width parameter of RBF network [5].

In order to use genetic algorithms to solve optimization problems for RBF network structure, Boolean vectors \( {U^T}=\left( {{u_{1, }}{u_{2, }}\ldots, {u_{M, }}} \right) \) \( {u_i}=\left\{ {0,1} \right\} \) is introduced. \( {u_i}=1 \) represents the corresponding hidden node exists; \( {u_i}=0 \) represents the corresponding hidden node does not exist. Each Boolean vectors \( {U^T} \) generate two chromosomes: one center parameters chromosomes, one width parameter chromosomes. Center parameters chromosome \( U_c^T \) and width parameters chromosome \( U_{\sigma}^T \) are coded by real number.

3.6 Example Application

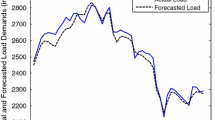
In this paper, to predict the region May 12, 2005 24-point load, we uses 3 months the historical load data of the region Power Grid in 2005, The prediction results are shown in Table 1:

Table 1 The result of load forecasting
Full size table

It can be seen from the table, the maximum relative error of the short-term load forecasting model based algorithm which proposed in this paper is 2.7, and the minimum relative error of it is 0.13. While the maximum relative error of prediction model based on RBF algorithm is 4.51, the minimum relative error is 0.87. It can be seen that the prediction model built in this article can better fit the mapping relationship between the loads; it has better prediction accuracy.

4 Conclusion

According to the deficiencies of RBF neural network and the premature shortcoming of genetic algorithm, this paper presented a radial basis function (RBF) neural network short term load forecasting model based on improved genetic algorithm. The model introduces the real-coded adaptive mechanism for the genetic algorithm. The selection strategy, adaptive crossover and mutation were improved, and its interaction with the gradient descent hybrid operation was used as the RBF network learning algorithm. The experimental results showed that the method can effectively improve the accuracy of load forecasting with good applicability.