A Calculation Approach to Complete Profile of Noncircular Gear Teeth

Abstract

In this paper, the authors propose a practical approach for calculating the complete tooth profile of a noncircular gear based on the fundamental laws of plane gearing and the offset theory of planar curve, together with all details contained in algorithm and numerical solution process. The algorithm not only has a simpler construction and higher calculation efficiency than other published approaches but also no special limitation imposed upon the types of the gear to be dealt with. The approach is explained referring to a machining model using a rack cutter with straight tooth profile to machine the gears; however, it is also applicable to other machining models such as employing a pinion cutter if performing some minor modifications in the algorithm. The effectiveness of the approach is illustrated through a practical example of design and manufacturing for a pair of noncircular gears.

1 Introduction

As a variable transmission ratio mechanism, noncircular gears have early been researched [1]. However, the difficulties in manufacturing significantly restrict the applications. In most of practical utilizations up to now, elliptical gears are employed since the tooth profile machining is relatively easy.

With the advances of NC machining technology, in recent years, the circumstance of noncircular gear manufacture is being improved [2]. Thus, in addition to elliptical gears, the noncircular gear transmissions with more general characteristics attract the attentions of researchers and engineers again. Many new applications of noncircular gears have been reported, for example, a planetary gear train built in high performance bicycle [3], a mechanical hinge with variable stiffness applicable to robot [4], a ratio variation system to transmit power and motion continuously [5], and so on. As an unfortunate fact, however, nowadays only a few makers deal with the noncircular gear manufacturing.

Different from circular gears, the tooth profile of a noncircular gear is generated based on the tooth cutting method, the gear pitch curve type and the cutter tooth profile, and thus it is possible that every tooth has a profile distinct from the others. Most of the published analysis approaches provide a calculation method on the profile belong to the working part, in general, but does not deal with the profile of the root fillet, tip and bottom land of the gear tooth [2, 6]. Only a few published calculation models carry out the whole profile of gear teeth but almost limited to elliptical gears, and the authors hardly explained the necessary details contained in the complex numerical solutions, especially, no model gives the method to calculate the tip land profile of the gear tooth [7–9]. Taking the further research and development of noncircular gear transmissions into consideration, for example, manufacturing a mold to mass-produce gears utilized in small devices or analysing the stress and dynamic characteristic in gear meshing [10], the precise and complete profile date of each tooth is required.

This study aims at developing a practical and efficient calculation approach for the complete profile of all teeth of a noncircular gear that possesses a pre-specified pitch curve and is machined by a rack cutter. The approach with a detailed algorithm is expressed in Chap. 2. Moreover, a practical example of design and manufacturing for a noncircular gear pair is presented in Chap. 3 to demonstrate the effectiveness of the proposed approach. Finally, the main conclusions are summarized in Chap. 4.

2 Calculation Method

2.1 Pitch Curves of Noncircular Gears

Figure 1 shows pitch curves of a noncircular gear pair in meshing. Here, θ and r _θ , ϕ and r _ϕ respectively indicate the rotation angle and pitch curve radius for driving and driven gear, and a is the central distance. The values of θ and ϕ are assigned as positive when the driving gear rotates in clockwise direction and the driven gear in counter clockwise direction; otherwise, assigned as negative. If the angular velocity ratio of both gears, dϕ/dθ, has been pre-specified in a form of function on θ, r _θ and r _ϕ can be defined as the functions of θ and calculated from the following equation.

Fig. 1

Pitch curves of noncircular gear pair

$$ {{\boldsymbol{ r}}_{\theta }}=\frac{{\mathrm{ d}{}\phi /\mathrm{ d}{}\theta }}{{1+\mathrm{ d}\phi /\mathrm{ d}{}\theta }}a\equiv {r_{\theta }}(\theta ),\quad {r_{\phi }}=\frac{1}{{1+\mathrm{ d}\phi /\mathrm{ d}\theta }}a\equiv {r_{\phi }}(\theta ) $$

(1)

For such the pitch curves, it is readily to confirm whether tooth undercutting occurs [7–9]. It should be mentioned that the pitch curve of a gear must be convex if the tooth profile of the gear is machined by a rack cutter, i.e. d² r _θ /dθ ² > 0 and d² r _ϕ /dθ ² > 0.

In Fig. 1, coordinate frames O _θ -x _θ y _θ and O _ϕ -x _ϕ y _ϕ are respectively fixed on the driving and driven gear, whose origins are set at the rotation center of the gears. Point R is a reference position, where θ = 0 and ϕ = 0, to measure the rotation angles. The lengths of pitch curve from Point R, S _θ and S _ϕ , can be obtained as follows:

$$ {S_{\theta }}=\int\nolimits_{{\, 0}}^{{\, \theta }} {\sqrt{{r_{\theta}^2+{{{\left( {\mathrm{d}{r_{\theta }}/\mathrm{d}{\,}\theta } \right)}}^2}}}} \mathrm{d}{\,}\theta =\int\nolimits_{{\, 0}}^{{\, \phi }} {\sqrt{{r_{\phi}^2+{{{\left( {\mathrm{d}{\,}{r_{\phi }}/\mathrm{d}{\,}\phi } \right)}}^2}}}} \mathrm{d}{\,}\phi ={S_{\phi }},\quad \phi =\int\nolimits_{{\, 0}}^{{\, \theta }} {(\mathrm{d}{\,}\phi /\mathrm{d}{\,}\theta )\mathrm{d}{\,}\theta } $$

(2)

2.2 Tooth Profiles of Rack Cutter and Gear

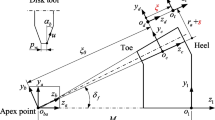
In Fig. 2, the graph (a) illustrates the tooth profile of a rack cutter and the graph (b) the tooth profile of the gear to be machined, where m is the module and α ₀ is the pressure angle of the cutter tooth. In (a), T _a –T _a ′ is straight line that generates the bottom land curve of the gear, G _a –G _a ′ in (b); T _a –T _b and T _a ′–T _b ′ are circular arcs that generate the root fillet curves of the gear tooth, G _a –G _b and G _a ′–G _b ′ in (b); T _b –T _c and T _b ′–T _c ′ are straight lines to generate the working parts of the gear tooth, G _b –G _E and G _b ′–G _E ′ in (b); and T _c –T _d and T _c ′–T _d ′ are circular arcs that do not cut gear blanks in general. The tip land curve, G _E –G _E ′ in (b), is an offset curve of the gear pitch curve, as well as the bottom land curves. In actual noncircular gear manufacturing, the tip land contour has been pre- worked on the blank so this part is not necessary to be cut in tooth profile machining.

Fig. 2

Tooth profiles of rack cutter and gear

2.3 Profile Calculation of Tip Land and Bottom Land of Gear Tooth

For a planar parametric curve r ₁(t) = {x(t), y(t)}as shown in Fig. 3, an offset curve r ₂(t) that moves through a normal distance h from r ₁(t) can be expressed as follows [11]:

Fig. 3

Offset curve of a planar curve

$$ {{\boldsymbol r}_2}(t)=\left\{ {x(t)\mp \frac{{h{y}^{\prime}(t)}}{{\sqrt{{{{{x^{\prime}}}^2}(t)+{{{y^{\prime}}}^2}(t)}}}},\;y(t)\pm \frac{{h{x}^{\prime}(t)}}{{\sqrt{{{{{x^{\prime}}}^2}(t)+{{{y^{\prime}}}^2}(t)}}}}} \right\} $$

(3)

where the symbol ′ indicates a differential on t, the upper sign is for an offset having the same direction and the lower sign for an offset along the opposite direction with respect to the unit normal vector n of r ₁(t). Therefore, substituting the pitch curve, i.e. Eq. 1 that is defined by the rotation angle θ of the driving gear, together with the addendum value h _a or dedendum value h _f into Eq. 3, the profiles of the tip land and bottom land of the gear tooth can be readily calculated, respectively.

2.4 Profile Calculation of Working Part and Root Fillet of Gear Tooth

While using a rack cutter to machine a noncircular gear, the pitch line of the cutter (PLC) performs a pure roll without sliding on the pitch curve of the gear (PCG) and the envelope of movement loci of the cutter teeth forms the tooth profile of the gear. At the same time, the normal line at a contact point of the cutter tooth profile with the gear tooth profile must passes through the pitch point of action. Based on these fundamental laws of plane gearing, we can readily derive the analysis relations for calculating the working part and root fillet profile of machined gear tooth.

Figure 4 illustrates the situation of the i-th tooth of cutter machining the i-th tooth space of gear. We set a reference position on the PLC and PCG, Point R _t and Point R _g , for measuring the rolling distance of both the curves. At this position, the PLC starts to roll on the PCG and the rotation angle θ of the gear is set as 0. At a contact point between both pitch curves, indicated as Point P that corresponds to a gear rotation angle θ _P , the length from Point R _g along the PCG is always equal to that from Point R _t along the PLC. Points P _b , P _c and P _a indicate the intersection points of the PLC with the normal lines at Points T _b , T _c and T _a on the left side of the cutter tooth, which have been defined in Fig. 2. When the gear respectively rotates an angle, θ _b , θ _c or θ _a , Points P _b , P _c or P _a will contact with Point Q _b , Q _c or Q _a on the PCG. Therefore, through substituting the lengths of the points P _b , P _c and P _a along the PLC from Point R _t into Eq. 2 and solving this equation, the values of θ _b , θ _c and θ _a that define the positions of Points Q _b , Q _c and Q _a on the PCG can be obtained.

Fig. 4

Generation of tooth profile within working and root fillet areas

Moreover, as shown in Fig. 4, the normal line of Point T _wj belong to the profile T _b –T _c of cutter tooth passes through the pitch point of action, Point P, so that the position of Point T _wj in the gear coordinate frame O-x _θ y _θ is just the point generated by Point T _wj on the working part of the gear tooth, indicated Point G _wj . Similarly, in O-x _θ y _θ , a point on the root fillet of gear tooth, Point G _tj , is also located at the same position with its generating point T _tj on the tip fillet of cutter tooth, if the normal line of Point T _tj just passes through Point P. Therefore, writing the position vector of Point P as r _θ (θ _P ) = {r _θ (θ _P ), θ _P } in O-x _θ y _θ , the coordinates of the points G _wj and G _tj can be determined from the following equations.

$$ \left\{ \begin{gathered} {x_{gwj }}={r_{\theta }}({\theta_P})\cos {\theta_P}+{L_{wj }}\cos ({\theta_P}+{\alpha_0}+\psi ) \hfill \\ {y_{gwj }}={r_{\theta }}({\theta_P})\sin {\theta_P}+{L_{wj }}\sin ({\theta_P}+{\alpha_0}+\psi ) \hfill \\ \end{gathered} \right. $$

(4)

$$ \left\{ \begin{gathered} {x_{gtj }}={r_{\theta }}({\theta_P})\cos {\theta_P}+({L_{tj }}+{R_a})\cos ({\theta_P}+{\beta_j}+\psi ) \hfill \\ {y_{gtj }}={r_{\theta }}({\theta_P})\sin {\theta_P}+({L_{tj }}+{R_a})\sin ({\theta_P}+{\beta_j}+\psi ) \hfill \\ \end{gathered} \right. $$

(5)

where ψ is the angle of tangential vector of the PCG at r _θ (θ _P ) and the value is given by Eq. 6.

$$ \tan \psi ={r_{\theta }}({\theta_P})/\left(\frac{{\mathrm{ d}{r_{\theta }}}}{{d\theta }}\;\left| {_{{\theta ={\theta_P}}}} \right.\right) $$

(6)

Furthermore, from Fig. 4, the values of L _wj and L _tj in Eqs. 4 and 5 can be obtained as follows:

$$ {L_{wj }}=({S_m}-{S_j})\cos {\alpha_0},\quad {L_{tj }}=H/\sin {\beta_j},\quad \tan {\beta_j}=H/({S_a}-{S_j}) $$

(7)

As shown in Fig. 5, on the other hand, if the normal line of the upper end G _E of the working part of gear tooth corresponds to a pitch point of action, Point P _E , the length from Point R _t to Point P _E along the PLC, S _E , satisfies (8).

Fig. 5

Determination of apex position of tooth working part

$$ {S_E}=\int\nolimits_{{ 0}}^{{ {\theta_E}}} {\sqrt{{{r_{\theta }}{{{(\theta )}}^2}+{{{(\mathrm{ d}{r_{\theta }}/\mathrm{ d}\theta )}}^2}}}\mathrm{ d}\theta } $$

(8)

Instituting the gear rotation angle θ _E , which corresponds to Point P _E , into Eq. 4 instead of θ _P , the coordinates of Point G _E , (x _GE , y _GE ) on the frame O-x _θ y _θ , are obtained. At the same time, Point G _E also lies on the tip land of gear, thus (x _GE , y _GE ) satisfy the following equation.

$$ \left\{ \begin{gathered} {x_{GE }}({\theta_E})={x_{\theta }}({\theta_e})+\frac{{{h_a}y_e^{\prime }}}{{\sqrt{{x_e^{{\prime 2}}+y_e^{{\prime 2}}}}}},\quad {y_{GE }}({\theta_E})={y_{\theta }}({\theta_e})-\frac{{{h_a}x_e^{\prime }}}{{\sqrt{{x_e^{{\prime 2}}+y_e^{{\prime 2}}}}}}, \hfill \\ x_e^{\prime }=\frac{{\mathrm{d}{x_{\theta }}}}{{\mathrm{d}\theta }}\left| {\theta ={\theta_e},\quad y_e^{\prime }=\frac{{\mathrm{d}{y_{\theta }}}}{{\mathrm{d}\theta }}} \right|{\,_{{\theta ={\theta_e}}}} \hfill \\ \end{gathered} \right. $$

(9)

Therefore, solving Eq. 9 together with Eqs. 4, 6, 7, and 8, the values of the rotation angles θ _E and θ _e that determine the position of Point G _E on the PCG can be obtained.

In the above, we have expressed the calculation method on the profile of the left side of a gear tooth space. Using the similar method, the profile of the right side can be calculated, too.

2.5 Calculation Algorithm for Complete profile of Gear Teeth

Under a condition that the central line of the first tooth of rack cutter passes through the reference position on the PLC, the algorithm to calculate the whole profile for all teeth of a driving gear to be machined can be summarized as follows:

• (a) Determine the lengths along the PLC, S _a0, S _b0, S _a0′ and S _b0′, corresponding to the characterizing points on the first cutter tooth, i.e. Points T _a , T _b , T _a ′ and T _b ′ shown in Figs. 2 and 4. Set the cutter tooth number i as 1.

• (b) Let S _a  = S _a0+Δ, S _b  = S _b0+Δ, S _a ′ = S _a0′+Δ and S _b ′ = S _b0′+Δ with Δ = (i − 1)πm. By instituting these pitch line lengths into Eq. 2 and solving this equation, determine the parameter values of corresponding points on the PCG, θ _a , θ _b , θ _a ′ and θ _b ′. Moreover, solve Eq. 9 to determine the values of parameters θ _E , θ _e , θ _E ′ and θ _e ′ with respect to the upper ends of the working part of tooth profile.

• (c) Properly divide the parameter intervals [θ _b , θ _a ] and [θ _a ′, θ _b ′] of the PCG, institute the values θ _tj , θ _tj ′ of each dividing point into Eq. 2 to calculate the corresponding lengths S _tj and S _tj ′ along the PCG, and finally calculate the coordinates of Point G _tj and G _tj ′ belong to the root fillet of the tooth profile with Eq. 5.

• (d) Properly divide the parameter intervals [θ _b , θ _E ] and [θ _E ′, θ _b ′] of the PCG, institute the values θ _wj , θ _wj ′ of each dividing point into Eq. 2 to calculate the corresponding lengths S _wj and S _wj ′ along the PCG, and finally calculate the coordinates of Point G _wj and G _wj ′ belong to the working part of the tooth profile from Eq. 4.

• (e) Properly divide the parameter interval [θ _a ′, θ _a ] of the PCG, institute the values θ _rj of each dividing point into Eq. 3 to calculate the coordinates of Point G _rj belong to the bottom land of the tooth profile. Furthermore, record θ _e as θ _i,L , θ _e ′ as θ _i,R .

• (f) If i ≥ z, go to Step (g); otherwise reset i = i + 1 then go back to Step (b). Here z is the tooth number of the gear.

• (g) Following to the turn of i = 1, 2, …, z, properly divide the parameter interval [θ _i−1,L , θ _i,R ] of the PCG, institute the values θ _sj of each dividing point into Eq. 3 to calculate the coordinates of Point G _sj belong to the tip land of the tooth profile but use θ _z,L instead of θ _0,L in the calculation.

• (h) Stop.

In Step (b), the Newton–Raphson method is used for numerically solving Eqs. 2 and 9. The Simpson’s rule is applied to calculate the integrations of Eqs. 2 and 8.

On the other hand, if we set the central line of the first tooth space of the cutter passing over the reference position of the PLC and employ r _ϕ (θ) instead of r _θ (θ), the above algorithm can be also used to calculate the tooth profiles for the corresponding driven gear.

It should be mentioned that, in the proposed algorithm, an iterative numerical solution process is not necessary for calculating the tip land and bottom land profile of gear tooth, and thus the algorithm is more efficient than other approaches published; at the same time, the programming operation can be completed more readily, too. Moreover, the proposed algorithm is also applicable to calculating the tooth profile of a noncircular gear machined by other types of cutter such as a pinion cutter or a cutter with different tooth profile [12]. In such the situation, only some minor modifications according to the pitch curve or tooth profile of the cutter are required to the algorithm.

3 Practical Example

In order to illustrate the application and effectiveness of the proposed approach, a noncircular gear pair was designed and the complete profiles of both driving and driven gears were machined by a wire electric discharge machine based on the calculated profile data.

In this example, the module is 2.5 mm, the tooth number 42 and the central distance 104.637 mm. In the design, a standard tooth profile was employed for rack cutter, the rate of proportional portion and variable portion in angular velocity ratio was set at 1:0.8833, and a modified constant velocity cam curve [13] was adopted to define the angular velocity in the variable portion. The final angular velocity ratio is shown in Fig. 6. As the profile date, 390 points, 20 points for tip land, 10 points for bottom land, 300 points for working part and 60 points for root fillet, were calculated and recorded for each tooth.

Fig. 6

Angular velocity ratio curve used in the example

Figure 7 illustrates the driving and driven gears meshed at the start position of θ = 0 and ϕ = 0. Figure 8 is a photograph of the machined gears. Through a simple test, it has been confirmed that both gears rotate and mesh very smoothly under a condition of exactly keeping the designed central distance.

Fig. 7

Contours of noncircular gears in the example

Fig. 8

Photograph of machined gears

In addition, Fig. 9 shows two comparisons of tooth profile, the first and the eleventh tooth space for the driving gear, and the first and the twelfth tooth for the driven gear. This result sufficiently illustrates that, for a noncircular gear, the profile may remarkably vary at the different positions of the tooth. Therefore, in order to obtain a correct result, the precise and complete profile date is necessary in an analysis of stress and dynamic characteristic for noncircular gear meshing.

Fig. 9

Comparison of tooth profiles located at different positions

4 Concluding Remarks

In this paper, based on the fundamental laws of plane gearing and the offset theory of planar curve, the authors proposed an efficient approach for calculating the precise and complete profile of each tooth of a noncircular gear machined by a rack cutter; at the same time, also provided necessary explanations for the calculation details contained in algorithm and numerical solutions. The proposed algorithm not only has a simpler construction and requires less calculation than other published approaches but also no special limitation imposed upon the types of the noncircular gear to be dealt with. This approach is also applicable to calculating the tooth profile of a noncircular gear machined by other types of cutter such as a pinion cutter or a cutter with different tooth profile, if some corresponding minor modifications are performed in the algorithm. The effectiveness and applications of the proposed approach has been demonstrated through a practical example of design and machining for a noncircular gear pair.