Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In digital communication systems, adaptive equalizers play a central role in combating signal distortions. Due to bandwidth limitations, the transmission channel may exhibit inter symbol interference (ISI) and an equalizer is used at the receiver to correct the signal distortion caused by the ISI.

In supervised equalization approaches a pilot sequence known by the receiver is periodically sent to help for the minimization of the distance between the desired and the actual output. Whereas, in blind (or unsupervised) equalization ones only some statistical properties of the transmitted signals are needed, to adapt the tap weights of equalizers.

One of the most known algorithms of adaptive blind equalization is the constant modulus algorithm (CMA) [1]. It is known to be robust and requires simple hardware implementation [2].

However, for QAM modulations (non constant modulus), used in high data-rate communications’ systems, the CMA leads to not sufficiently low residual errors for a correct recovering of transmitted signals. Other algorithms, known to be more adapted to QAM symbols, have been proposed in the literature. For instance, the multi-modulus algorithm (MMA) [3] and the extended constant modulus (ECMA) [4] algorithms have been shown to achieve better equalization of QAM signals than does the CMA.

Unfortunately, for high-order QAM modulations, even these algorithms are unable to provide low residual ISI that allow reliable detection of the correct symbols. A way to improve performance CMA, MMA or ECMA, for dense QAM constellations, is to penalize their criteria by terms based on alphabet-matching functions (AMF) which leads to what is called hybrid adaptive blind equalization algorithms. They perform better than their classical counterparts.

One of the first AM criteria has been proposed by Barbarossa and Scaglione [5]. Beasley and Cole-Rhodes combined the MMA and this AM cost functions [6] and showed, using 16-QAM symbols, that the hybrid algorithm outperforms the original dual-mode CMA/AMA [5] and the MMA. In a similar way, He et al. [7] proposed an AM cost function based on even powers of sine functions and combined it with the CMA and demonstrated that hybrid algorithms have higher performance than conventional ones. Blind equalization algorithms are generally based on the minimization of cost functions that measure the closeness of the equalizer output to the constellation points and the stochastic gradient algorithm is commonly used to achieve numerically this minimization.

Our contribution consists of a combination of the ECMA cost function and a modified version of the AM cost function proposed in [5]. The modification is made to account for amplitude and phase information of the transmitted signals, and hence, improve the local convergence which leads to improved global performance. The performance of the derived algorithm has been studied for 16-QAMs (low order) in [8]. But in this work, its effectiveness is shown through simulation for 512-QAM (high order) signaling where performance is compared to those of the conventional MMA and ECMA together with a penalized adaptive version of the extended constant modulus algorithm, based on a squared cosine function [7].

2 Blind Equalization Model

Let us assume that a sequence \((s_n)_{n\in \mathbb {Z}}\) of independent-identically distributed (i.i.d.) symbols, drawn from a QAM constellation, is transmitted over the time invariant channel \(\mathbf{h}\) of length K. The mathematical model for the receiver input at time n is

$$\begin{aligned} x_n=\sum _{l=0}^{K-1}h_l s_{n-l}+\nu _n \end{aligned}$$
(1)

We introduce vectors \({\mathbf {w} }=[w_0,\ldots ,w_{L-1}]^T\) and \(\mathbf {x_n} = [{x_n},\ldots ,x_{n - L + 1}]^T\) where \((\cdot )^T\) denotes transpose, then the equalizer output is

$$\begin{aligned} {z_n} = \mathbf{w}^{-H} \mathbf{x}_n = \sum _{l = 0}^{L - 1} w_l^*x_{n - l}. \end{aligned}$$
(2)

with \((\cdot )^*\) and \((\cdot )^H\) the conjugate and transpose conjugate operators, respectively.

3 MMA and ECMA Algorithms

The idea of the multi-modulus, is to split the cost function into a real and an imaginary part to take account not only for amplitude information but also for phase information, which helps in better equalizing QAM signals than the CMA does.Whereas the extended constant modulus is based on the generalization of the modulus of a complex number.

3.1 MMA Algorithm

The cost function of the MMA to be minimized w.r.t \({\mathbf {w} }\) is given by

$$\begin{aligned} J_{MM} (\mathbf {w}) = \mathbb {E} \left\{ \frac{1}{4} \left( \left( z_{nr}^2 - R_{m} \right) ^{2} + \left( z_{ni}^2 - R_{m} \right) ^{2} \right) \right\} , \end{aligned}$$
(3)

where \(\mathbb {E}\left\{ \cdot \right\} \) denotes expectation and \(z_{nr}\) and \(z_{ni}\) are the real and imaginary part of \(z_n\), respectively. \(R_m\) is a dispersion constant given by

$$\begin{aligned} R_{m}=\frac{{\mathbb {E}}\left\{ (s_{kr})^{4}\right\} }{{\mathbb {E}}\left\{ (s_{kr})^{2}\right\} }=\frac{{\mathbb {E}}\left\{ (s_{ki})^{4}\right\} }{{\mathbb {E}}\left\{ (s_{ki})^{2}\right\} }. \end{aligned}$$
(4)

with \(s_k=s_{kr}+js_{ki}\) a QAM symbol. Letting \(M\) denote the order of the modulation, we have \(s_{nr},~s_{ni} \in \left\{ a_k;\; a_{k} =a_{kr} +j \,a_{ki},\;k=1,..,M\right\} \), with \(a_{kr},~a_{ki}\in \left\{ \pm 1,\pm 3,\ldots ,\pm (\sqrt{M}-1)\right\} \).

Equalizer coefficients are updated from formulas

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathbf {w}_{n + 1}} &{}= {\mathbf {w}_n} - \mu \;{\varphi _n}{\mathbf {x}_n}\\ \\ {\varphi _n} &{}= \left( {z_{nr}^2 - {R_m}} \right) {z_{nr}} - j\left( {z_{ni}^2 - {R_m}} \right) {z_{ni}}. \end{array}\right. \end{aligned}$$
(5)

3.2 ECMA Algorithms

The ECMA algorithm is a particular case of the generalized constant modulus algorithms proposed in [4]. Introducing the generalized complex modulus as

$$\begin{aligned} \left| z_n\right| _p=\left( \left| z_{nr}\right| ^p+\left| z_{ni}\right| ^p\right) ^\frac{1}{p}~, \end{aligned}$$
(6)

for \(p\ge 1\), \(z_{nr}\) and \(z_{ni}\) denoting the real and imaginary part of \(z_n\) respectively, the ECMA criterion is given by

$$\begin{aligned} {J_{ECMA}}(\mathbf{w}) = \mathbb {E}\left\{ \frac{1}{4} {{{\left( {{{\left| {{z_n}} \right| }_4^2} - {R_E}} \right) }^2}} \right\} , \end{aligned}$$
(7)

with the dispersion constant

$$\begin{aligned} R_{4,2}=\frac{{\mathbb {E}}\left\{ \left| s_{k}\right| _{4}^{4}\right\} }{{\mathbb {E}}\left\{ \left| s_{k}\right| _{4}^{2}\right\} }. \end{aligned}$$
(8)

The learning rule for this algorithm is

$$\begin{aligned} {\mathbf w}_{n+1}= {\mathbf w}_n-4\mu \left( \left| z_n\right| _4^2-R_{4,2}\right) \frac{z_{nr}^3-jz_{ni}^3}{\left| z_n\right| _4^2}{\mathbf x}_n~. \end{aligned}$$
(9)

4 Hybrid Algorithms

They combine the CMA, the MMA or the ECMA cost function with an AM-based criterion. The AMF has to vanish at each constellation point, to be symmetric around these points and uniform with respect to them. The former property means that in the case of perfect equalization, the equalizer output coincides with one of the constellation points (zero error). The latter implies that the AMF functions do not favor any data symbol in the alphabet over another.

The AM cost function proposed in [5] is

$$\begin{aligned} {J_{\text {Gauss}}}(\mathbf {w}) = \mathbb {E}\left\{ {1 - \sum \limits _{k = 1}^M {\mathop e\nolimits ^{ - \frac{{{{\left| {{z_n} - {a_k}} \right| }^2}}}{{2{\sigma ^2}}}} } } \right\} \end{aligned}$$
(10)

where \(a_k (k=1,\dots , M)\) are the constellation points and the parameter \(\sigma \) controls the width of the nulls.

The squared cosine AM cost function proposed in [7] has the form

$$\begin{aligned} {J_{\text {Cos}}}(\mathbf {w})=\mathbb {E}\left\{ \cos ^{2}(\frac{z_{nr}\pi }{2d})+\cos ^{2}(\frac{z_{ni}\pi }{2d})\right\} , \end{aligned}$$
(11)

with \(2d\) the minimum distance between symbols.

In our scheme the AM term given by (9), is modified such that the terms of the exponential are split into real and imaginary parts instead of the modulus, as in (10). It transforms to

$$\begin{aligned} J_{\text {MGauss}}(\mathbf {w}) =\mathbb {E}\left\{ \left( 1-\sum _{k=1}^{M}e^{\frac{-\left( z_{nr}-a_{kr}\right) ^2}{2\sigma ^2}}\right) +\left( 1-\sum _{k=1}^{M}e^{\frac{-\left( z_{ni}-a_{ki}\right) ^2}{2\sigma ^2}}\right) \right\} \end{aligned}$$
(12)

We refer to the resulting hybrid algorithms as Cos-ECMA and MGauss-ECMA, if the AM is that given by (10) and (11), respectively.

Hence, combining the ECMA cost function with the modified Gaussian AM term we get

$$\begin{aligned} J_{\text {MGauss}}(\mathbf {w}) =J_{\text {ECMA}}(\mathbf {w})+\beta J_{\text {MGauss}}(\mathbf {w}) \end{aligned}$$
(13)

with \(\beta \) a parameter that trades off between the ECMA and the MGauss terms.

$$\begin{aligned} {\mathbf {w}_{n + 1}} = {\mathbf {w}_n} - \mu \nabla J_{\text {MGauss}} \end{aligned}$$
(14)

5 Numerical Experiment

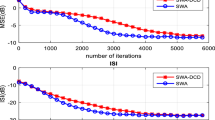
The mean square error (MSE) of the MGauss-ECMA is compared to that of the Cos-ECMA, together with that of the MMA and the ECMA. For comparison, high order 512-QAM symbols are randomly drawn, the equalizer length is set to L = 11 and channel

\(h=[1 \quad 0.1294+0.483j]^T\) is used to transmit these symbols under a signal to noise ratio; SNR \(=\) 40 dB.

The values of the parameters (\(\mu \), \(\beta \) and \(\sigma \)) used in the numerical implementation are \(\mu =6\times 10^{-9}\) and \(\mu =2\times 10^{-9}\) for MMA and ECMA, respectively. Whereas, for Cos-ECMA \(\mu =2\times 10^{-9}\) and \(\beta =1,000\) while for MGauss-ECMA \(\mu =2\times 10^{-9}\), \(\beta =100\) and \(\sigma =0.4\).

Fig. 1
figure 1

Comparison of MSE for 512-QAM signals (SNR \(=\) 40 dB)

Full size image

From Fig. 1, we can notice that the hybrid algorithm Gauss-ECMA has the lowest residual error at steady state (\(-18\) dB). It can also be seen that the Cos-ECMA has a lower residual error than that of ECMA and MMA.

6 Conclusion

The hybrid adaptive blind equalization algorithm combining the ECMA cost function and the modified Gaussian AM cost function (MGauss-ECMA) has been compared to the conventional MMA and ECMA algorithms as well as to hybrid algorithm combining the ECMA and squared cosine function (Cos-ECMA). The simulations performed for the high-order QAM modulation, namely 512-QAM, shows that the two hybrid versions perform much better than conventional ones. However, the MGauss-ECMA lead to lower MSE than the Cos-ECMA.