Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Physicists use (and create) Mathematics as an instrument that allows them to construct and to study mathematical models describing the physical world. As a consequence, each concrete mathematical language used for this purpose reflects in some sense the opinion of physicists that they have about the world at that concrete historical period. This opinion is based on a sum of knowledge obtained from experiments that, in their turn, are made by scientific instruments having their accuracy that bounds our possibility of the observation of physical phenomena. As a result, also mathematical theories describing physical phenomena have their accuracy determined by the accuracy of physical experiments. Obviously, a good theory can also show directions for new experiments and new tools that would confirm or refuse theoretical hypotheses. Thus, there exists a strong link between the mathematical theories describing physical world and the current level of accuracy of physical instruments.

In different historical periods, various mathematical disciplines were used for constructing physical models. Mathematical Analysis is one of them and, obviously, it is widely used in Physics. However, the foundations of Analysis have been developed more than 200 years ago with the goal to develop mathematical tools allowing one to solve problems arising in the real world at that time. Thus, Analysis that we use now does not reflect in itself numerous achievements of Physics of the twentieth century.Footnote 1 For instance, in Physics, the same object can be viewed as either discrete or continuous in dependence of the instrument used for the observation (we see a table continuous when we look at it by eye and we see it discrete (consisting of molecules, atoms, etc.) when we observe it at a microscope). Moreover, physicists together with the result of the observation supply the accuracy of the instrument used for this observation.

In Mathematics, both facts are absent: each mathematical object (e.g., function) is either discrete or continuous and nothing is said about the accuracy of the observation of the mathematical objects and about tools used for these observations. Mathematical notions have an absolute character and the ideas of relativity are not present in it. In some sense, there exists a gap between the physical achievements made in the last two hundred years and their mathematical models that continue to be written using the mathematical language developed two hundred years ago on the basis (among other things) of physical ideas of that remote time.

The point of view presented in this paper tries to fill up this gap. It uses strongly such methodological ideas borrowed from Physics and applied to Mathematics as: the distinction between the object (we speak here about a mathematical object) of an observation and the instrument used for this observation; interrelations holding between the object and the tool used for this observation; the accuracy of the observation determined by the tool. In particular, from this new physical point of view the ways to deal with infinities and infinitesimals are studied. The main attention is dedicated to mathematical languages, more precisely, to numeral systemsFootnote 2 that we use to write down numbers, functions, models, etc. and that are among our tools of investigation of mathematical objects. It is shown that numeral systems strongly influence our capabilities to describe the inhabitants of the mathematical world.

In particular, a new numeral system (see [2–11]) for performing computations with infinite and infinitesimal quantities is used for the observation of mathematical objects and modeling physical phenomena. It is based on the principle ‘The part is less than the whole’ introduced by Ancient Greeks and observed in the physical world. It is applied to all sets and processes (finite and infinite) and all numbers (finite, infinite, and infinitesimal). The new methodology has allowed the author to introduce the Infinity Computer (see the USA patent [11]) working numerically with infinite and infinitesimal numbers. The introduced computational paradigm both gives possibilities to execute computations of a new type and simplifies fields of Mathematics and Computer Science where infinity and/or infinitesimals are required. In order to see the place of the new approach in the historical panorama of ideas dealing with infinite and infinitesimal, see [12] and [13].

The new methodology has been successfully applied for studying fractals [6, 14], percolation [14, 15], optimization algorithms [3, 16], hyperbolic geometry [17], Turing machines [18], cellular automata [19] , infinite series [6–9, 20], etc.

2 A New Methodology for Performing Computations with Infinite and Infinitesimal Quantities

Traditionally, there exist different ways to work with mathematical objects connected to the concepts of infinite and infinitesimal (see, e.g., [1, 21–24] and references given therein). However, it is well known that we work with infinite objects in a way different with respect to the rules that we are used to deal with finite quantities. In fact, there exist undetermined operations (for example, \(\infty -\infty \), 0\(\cdot \infty \), etc.), divergences, etc. It is worthwhile to mention also that the philosophical principle of Ancient Greeks ‘The part is less than the whole’ observed in the physical world around us does not hold for infinities, including infinite cardinals introduced by Cantor, e.g., it follows x+1 = x, if x is an infinite cardinal, although for any finite x we have x+1 \(>\) x.

In order to understand how it is possible to look at the problem of infinity in a new way, let us consider a study published in Science (see [25]) where the author describes a primitive tribe living in Amazonia—Pirahã—that uses a very simple numeral system for counting: one, two, many. For Pirahã, all quantities larger than two are just ‘many’ and such operations as 2+2 and 2+1 give the same result, i.e., ‘many’. Using their weak numeral system Pirahã are not able to see, for instance, numbers 3, 4, 5, and 6, to execute arithmetical operations with them, and, in general, to say anything about these numbers because in their language there are neither words nor concepts for that.

It is important to emphasize that the answer ‘many’ is not wrong, it is just imprecise. Analogously, the answer ‘many’ to the question ‘How many trees are there in the garden in front of our house?’ is correct, but its precision is low. Already these first considerations show us that numeral systems have their accuracy like physical instruments have. This means that when one uses a numeral system, this system defines the accuracy of mathematical results that can be obtained with its help. As a consequence, mathematical truths are not absolute; they are relative to the precision of the numeral systems (and, in general, to the mathematical language) used for their formulation. The understanding of the fact that Mathematics, as all natural sciences, depends on its instruments and is able to provide results that depend on the accuracy of the instruments used for their description is very important.

Pirahã’s numeral system is interesting for us also because its weakness leads to such results as

$$\begin{aligned} `{\text {many}}{\text {'}} + 1 = `{\text {many}}{\text {'}} , `{\text {many}}{\text {'}} + 2 = `{\text {many}}{\text {'}} , `{\text {many}}{\text {'}} + `{\text {many}}{\text {'}} = `{\text {many}}{\text {'}} , \end{aligned}$$
(35.1)

which are very familiar to us in the context of views on infinity used in the traditional calculus:

$$\begin{aligned} \infty + 1 = \infty ,\qquad \qquad \infty + 2 = \infty ,\qquad \qquad \infty + \infty = \infty . \end{aligned}$$
(35.2)

This similarity leads us to the following idea: Probably our difficulty in working with infinity is not connected to the nature of infinity but is a result of inadequate numeral systems used to express infinite numbers. Analogously, Pirahã do not distinguish numbers 3 and 4 not due to the nature of these numbers but due to the weakness of their numeral system.

When we have such mathematical objects as infinite numbers, then even the modern numeral systems used for the observation are not sufficiently precise. The instruments of Pirahã do not allow them to distinguish 3, 4, and other numbers higher than 2. Our modern numeral systems are more precise, they allow us distinguish various finite numbers, but they fail when it is necessary to work with infinite quantities.

The observation made above is important from several points of view; in particular, with respect to the mathematical instruments developed by Cantor (see [21]) who has shown that there exist infinite sets having different number of elements. Cantor has proved, by using his famous diagonal argument, that the cardinality, \(\aleph _0\), of the set, N, of natural numbers is less than the cardinality, C, of real numbers at the interval [0, 1]. Cantor has also developed an arithmetic for the infinite cardinals. Some of the operations of this arithmetic including \(\aleph _0\) and C are given below:

$$\begin{aligned} \aleph _0 + 1 = \aleph _0,\qquad \qquad \aleph _0 + 2 = \aleph _0,\qquad \qquad \aleph _0 + \aleph _0 = \aleph _0,\end{aligned}$$
(35.3)
$$\begin{aligned} \mathrm{C} + 1 = \mathrm{C},\qquad \qquad \mathrm{C} + 2 = \mathrm{C},\qquad \qquad \mathrm{C} + \aleph _0 = \mathrm{C},\mathrm{C} + \mathrm{C} = \mathrm{C}. \end{aligned}$$
(35.4)

Again, it is possible to see a clear similarity with the arithmetic operations used in the numeral system of Pirahã (a detailed discussion related to these issues dealing also with the Continuum Hypothesis see in [10]). This prompts us that, probably, Cantor’s numeral system used to measure infinite sets can be also improved. If we were able to distinguish more infinite numbers we could understand better many processes and objects dealing with the concepts of infinite and infinitesimal (remind the famous phrase of Ludwig Wittgenstein: ‘The limits of my language are the limits of my world.’).

In [2–11] a new numeral system has been developed for performing computations with infinite and infinitesimal quantities using the principle ‘The part is less than the whole’ introduced by Ancient Greeks and observed in the physical world (it is discussed and compared with other approaches in [12] and [13]). The main idea of the new approach consists of the possibility to measure infinite and infinitesimal quantities by different (infinite, finite, and infinitesimal) units of measure.

For this purpose, a new infinite unit of measure expressed by the numeral CD called grossone is introduced as the number of elements of the set, N, of natural numbers. Concurrently with the introduction of grossone in our mathematical language such symbols like \(\infty \), Cantor’s \(\omega \), C from (35.4), all Alephs \(\aleph _0\),\(\aleph _1\), etc. are excluded from the language because grossone ant other numbers constructed with its help not only can be used instead of all of them but can be used with a higher accuracy. Grossone is introduced by describing its properties postulated by the Infinite Unit Axiom [4] added to axioms for real numbers (similarly, in order to pass from the set, N, of natural numbers to the set, Z, of integers a new element—zero expressed by the numeral 0—is introduced by describing its properties).

It is necessary to notice that grossone has both cardinal and ordinal properties as usual finite natural numbers have. The new numeral allows us to construct different numerals expressing different infinite and infinitesimal numbers and to calculate the number of elements of certain infinite sets. For instance, it becomes possible to see that the sets of even and odd numbers have CD/2 elements each. The set, Z, of integers has 2CD + 1 elements (CD positive elements, CD negative elements, and zero). The set B = N \(\backslash \{\mathrm{b}\}, \mathrm{b} \in \) N, has CD\(-1\) elements and the set A = N U { a1; a2 }, a1 \(\notin \) N, a2 \(\notin \) N, has CD + 2 elements.

Note that positive integers larger than grossone do not belong to N but they can be also easily interpreted as the number of elements of certain infinite sets. For instance, \(\mathrm{CD}^{3 }\)is the number of elements of the set V, where

$$\begin{aligned} \mathrm{V} = \{ ( \mathrm{a}_1; \mathrm{a}_2; \mathrm{a}_3 ) : \mathrm{a}_1 \in \mathrm{N}, \mathrm{a}_2 \in \mathrm{N}, \mathrm{a}_3 \in \mathrm{N} \}. \end{aligned}$$

It is worthy to mention that these results do not contradict Cantor’s one-to-one correspondence principle (see [13] and [9, 10] for a detailed discussion). Both Cantor’s numeral system and the new one give correct answers, but their answers have different accuracy. We just use a stronger (with respect to cardinals of Cantor) tool, CD, for the observation of infinite sets that allows us to give more accurate answers than those of Cantor. By using the physical analogy we can say that the lens of our microscope is stronger and we are able to see many different dots where Cantor’s microscope allows him to observe just one dot—countable sets.

Note, that the new numeral system using grossone allows us to avoid records of the type (1)–(4). In fact, it can be easily shown (see [4, 9]) that, for example,

$$\begin{aligned}&\mathrm{CD}/2 < \mathrm{CD} < 2\mathrm{CD} < 2\mathrm{CD}+1 < 2\mathrm{CD}+2 < \mathrm{CD}^{3}/2 < \mathrm{CD}^{3}-1 < \mathrm{CD}^{3}\\&\quad < \mathrm{CD}^{3}+1 < \mathrm{CD}^{3}+2. \end{aligned}$$

Within the sets having cardinality of the continuum it is also possible to distinguish infinite sets having different number of elements expressible in the numeral system using grossone (see [4, 10]):

$$\begin{aligned}&2^\mathrm{CD}-1 < 2^\mathrm{CD} < 2^\mathrm{CD} +1 < 10^\mathrm{CD}-1 < 10^\mathrm{CD} < 10^\mathrm{CD}+1 < \mathrm{CD}^\mathrm{CD}-1\\&\quad < \mathrm{CD}^\mathrm{CD}< \mathrm{CD}^\mathrm{CD}+1 < \mathrm{CD}^\mathrm{CD}+2. \end{aligned}$$

The rules we use to execute arithmetical operations with 0 and 1 work with grossone, as well:

$$\begin{aligned} 0 \cdot \mathrm{CD} = 0, \mathrm{CD} \cdot 0 = 0, \mathrm{CD} - \mathrm{CD} = 0, \mathrm{CD} : \mathrm{CD} =1, \mathrm{CD}^{0}=1, 0^\mathrm{CD}=0, 1^\mathrm{CD}=1. \end{aligned}$$

Since \(\mathrm{CD}^{0}\)=1, a finite number c can be represented in the new numeral system simply as \(\mathrm{cCD}^{0}\)=c, where the numeral c is written down by any convenient numeral system used to write down finite numbers.

The simplest infinitesimal numbers are represented by numerals having only negative powers of grossone that are finite or infinite. The following two numerals are examples of infinitesimals expressed in the new numeral system: 4.2\(\mathrm{CD}^{-3.21}\), 74.56\(\mathrm{CD}^{-33.85\mathrm{CD}}\). The simplest infinitesimal is \(\mathrm{CD}^{-1 }\)being the inverse element with respect to multiplication for CD:

$$\begin{aligned} \mathrm{CD} \cdot \mathrm{CD}^{-1}= 1. \end{aligned}$$

Note that all infinitesimals are not equal to zero. Particularly, it follows \(\mathrm{CD}^{-1 } >\) 0 because \(\mathrm{CD}^{-1 }\)= 1 / CD, i.e., it is a result of division of two positive numbers.

It is necessary to mention that it is not easy to interpret grossone in the framework of the traditional mathematics (including the non-standard analysis). When one tries to compare two languages, it can often happen that their accuracies are different and the translation becomes possible only partially. Moreover, different languages represent the world in different ways (any person knowing more than one language knows that there exist things that can be described better in one language than in another). In linguistics, the relativity of the language with respect to the world around us is well known. This fact has been formulated in the form of the Sapir–Whorf thesis of the linguistic relativity (see [26, 27]). For example, it is impossible to translate to the language of Pirahã the word ’four’ from English maintaining the same accuracy in their language as in English. The same thing happens when we compare the mathematical languages using, on the one hand, such symbols like \(\infty \), Cantor’s \(\omega \), C from (35.4), all Alephs \(\aleph _0\),\(\aleph _1\), etc. and, on the other hand, grossone and other numerals constructed with its help. The accuracies of the two languages are different.

Another crucial problem related to such a translation consists of the fact that in the traditional mathematics (even in the non-standard analysis) very often there is no a clear distinction between numbers (and sets of numbers) and numerals and sets of numerals used to represent numbers.

However, as it happens in Physics, in Mathematics it is also always necessary to indicate the instrument one uses for an observation in order to understand what can be observed. If such a clarification is absent, then ambiguities can easily be encountered. Let us illustrate this affirmation by considering the following set defined by the phrase: the set of all numbers less than three. This phrase seems to identify clearly a set because, without saying it explicitly, we keep in mind that we are speaking about real numbers. So, it is supposed implicitly that the instrument of the observation of the set is a positional numeral system.

However, in different historical periods such implicit suppositions were different. Before discovering negative numbers (for instance, Roman and Greek numeral systems do not include zero and are not able to express negative numbers; in these systems, expression 3–7 was an undetermined form) this was the set of positive numbers less than three. Moreover, before discovering irrational numbers this phrase was defining rational positive numbers less than three. In the language of Pirahã, this set cannot be even defined because they do not know what ‘three’ is. Then, if we use the new approach working with grossone, it can be shown (see [10]) that in dependence on the radix of the positional system used to write down numerals, different sets of real numbers can be observed.

In particular, since the traditional mathematics very often does not pay any attention to the distinction between numbers and numerals, many theories dealing with infinite and infinitesimal quantities have a symbolic (not numerical) character. For instance, many versions of the non- standard analysis are symbolic, since they have no numeral systems to express their numbers by a finite number of symbols (this is necessary for organizing numerical computations). Namely, if we consider a finite n than it can be taken n = 6, or n = 12 or any other numeral consisting of a finite number of symbols. If we consider an infinitesimal h then it is not clear which numerals consisting of a finite number of symbols can be used to write h = \(\dots \) In fact, very often in non-standard analysis texts, a generic infinitesimal h is used and it is considered as a symbol, i.e., only symbolic computations can be done with it. Approaches of this kind leave unclear such issues, e.g., whether the infinite 1/h is integer or not or whether 1/h is the number of elements of an infinite set.

3 Examples of the Usage of the New Computational Methodology

In this section, we give several examples showing how to use the new computational methodology with the new numeral systems using grossone. Examples are chosen in such a way that they can be directly used in modeling physical phenomena.

We start by showing that, in the new language, infinite (both convergent and divergent) series can be substituted by sums with the precisely defined infinite number of items. Since in the new numeral system we have many different infinite integers and we have seen that the symbol \(\infty \) is a kind of ‘many’, such records as

$$\begin{aligned} \mathrm{S}=a_1+a_2+a_3+a_4\ldots \qquad \mathrm{or} \qquad \mathrm{S}= \sum \limits _{i=1}^{\infty } {a_{i} } \end{aligned}$$

become imprecise. In the new language they are just something like “Calculate the sum of \(\mathrm{{a}}_\mathrm{{i}}\) where i goes from 1 to ‘many”’. This means that when we have infinitely many items in a sum, we are in the same situation as with sums having a finite number of items: it is not sufficient to say that the number, n, of items in the sum is finite, it is necessary to fix explicitly the value of n using for this purpose numerals available in a chosen traditional numeral system used for expressing finite numbers, e.g. n = VII or n = 2,000. Analogously, now we should decide (in dependence on the problem we deal with) how many items should be in our sum with an infinite number of items by choosing an appropriate value for n, e.g., n=10CD or n=2000\(\mathrm{CD}^{12}\), see [4, 5, 28] for a detailed discussion.

In problems where the traditional language using \(\infty \) fails and is not able to provide any answer, the new numeral system using grossone allows us to work with expressions involving infinite numbers and to obtain, where it is possible, as results infinite, finite, and infinitesimal numbers. For instance, let us consider two divergent series

$$\begin{aligned} \mathrm{S}_1 = 5 +5 + 5 + {\cdots },\qquad \mathrm{S}2 = 3 + 3 +3 + {\cdots } \end{aligned}$$

Then, by using the traditional language, we are not able to execute such operations like, e.g., S1–S2 or S2 / S1 since both S1 and S2 are divergent series. In the new language, both expressions S1 and S2 are not well defined since the number of items in them is not specified. Instead of series, we should consider the sums S1(k1) and S2(k2), to fix the infinite number of items, k1, in the first sum and the infinite number of items, k2, in the second sum, to calculate the respective results, and then to execute the further required operations, see [4, 5, 28]. For instance, if k1 = 2CD + 2 and \(\mathrm{k}2 = 4\mathrm{{CD}}-1\) then we are able to calculate easily both S1(2CD + 2) and \(\mathrm{S}2(4\mathrm{{CD}}-1)\) and to execute arithmetical operations with the results:

$$\begin{aligned} \mathrm{S}_1(2\mathrm{CD}+2) = 5 (2\mathrm{CD}+2)= 10\mathrm{CD}+10,\quad \mathrm{S}_2(4\mathrm{CD}-1) = 3 (4\mathrm{CD}-1)= 12\mathrm{CD}-3,\\ \mathrm{S}_1(2\mathrm{CD}+2) - \mathrm{S}_2(4\mathrm{CD}-1) = 10\mathrm{CD}+10 - (12\mathrm{CD}-3) = -2\mathrm{CD}+13,\\ \mathrm{S}_1(2\mathrm{CD}+2) + \mathrm{S}_2(4\mathrm{CD}-1)= 10\mathrm{CD}+10 + 12\mathrm{CD}-3 = 22\mathrm{CD}+7,\\ \mathrm{S}_1(2\mathrm{CD}+2) \cdot \mathrm{S}_2(4\mathrm{CD}-1)= 120\mathrm{CD}^{2}+90\mathrm{CD}-30,\\ \mathrm{S}_2(4\mathrm{CD}-1) / \mathrm{S}_1(2\mathrm{CD}+2) = 1.2 -1.5\mathrm{CD}^{-1 }+1.5\mathrm{CD}^{-2}-1.5\mathrm{CD}^{-3}, \end{aligned}$$

where the result of division has been taken with the error that is not higher than O(\(\mathrm{CD}^{-4})\).

The same situation we have with divergent integrals. Namely, records of the type \( \int \limits _{a}^{b} {f\left( x \right) } \) become imprecise if either a = \(-\infty \) or b = \(\infty \), or both. The limits of integration equal to \(-\infty \) or \(\infty \) should be substituted by exact infinite numbers. For instance, if a = \(-6\)CD, b = 3\(\mathrm{CD}^{2}\), and f(x) =\(\mathrm{x}^{2}\), then

$$\begin{aligned} \int \limits _{a}^{b} {f\left( x \right) }= {\bigcirc \!\!\!\!{1}}^6+2{\bigcirc \!\!\!\!{1}}^3, \end{aligned}$$

where the result is the infinite number. By changing any limit of integration (as it happens in the case of finite limits a and b) the result will also change. For instance, by taking the infinitesimal a = 3\(\mathrm{CD}^{-2}\), we have that the integral is equal to \(\mathrm{CD}^{6 }\)–\(\mathrm{CD}^{-6}\). We are able to find easily difference of the two obtained infinite numbers:

$$\begin{aligned} \mathrm{CD}^{6}+ 2\mathrm{CD}^{3}- (\mathrm{CD}^{6}- \mathrm{CD}^{-6}) = 2\mathrm{CD}^{3 }+ \mathrm{CD}^{-6}, \end{aligned}$$

that is the result of integration for a = \(-6\)CD, b = 3\(\mathrm{CD}^{-2}\). By taking the limits a = 3\(\mathrm{CD}^{-2}\), b = 3\(\mathrm{CD}^{2 }\) and by taking f(x) = \(\mathrm{CDx}^{2 }\) we have that the integral, since grossone is a constant and can be put out of the sign of integral, is equal to \(\mathrm{CD}^{7 }\)–\(\mathrm{CD}^{-5}\). Note also that we can easily work with derivatives that can assume infinite (and infinitesimal) values; e.g., if f(x) = \(\mathrm{CDx}^{2 }\) then f’(x) = 2CDx, analogously, if g(x) = \(\mathrm{CD}^{-6} \mathrm{x}^{2 }\) then g’(x) = 2\(\mathrm{CD}^{-6}\) x.

In general, it becomes possible to use infinite and infinitesimal numbers as constants to construct new mathematical objects that are not visible when the traditional mathematical language is used, see [4, 5, 28]. Let us consider, for example, the following discontinuous function that cannot be described by the traditional mathematical language, see Fig. 35.1.

Fig. 35.1
figure 1

Example of a discontinuous function having the point of discontinuity at the infinitesimal point \(\mathrm{CD}^{-10}\) and assuming three different infinite values at this point, on its left, and on its right

Full size image

If we try to describe this function by using the traditional mathematical language working with finite numerals and the symbol \(\infty \), we shall see immediately that we are not able to do this. To be more precise, we can give only a rough qualitative description of this function similar to the following one: The function is \(\infty \) everywhere and it has an infinitesimal jump infinitesimally close to zero. This description has just a qualitative character since in the traditional language there are no numerals allowing us to express different infinite and infinitesimal numbers. In contract, the description presented in Fig. 35.1 is quantitative; it uses new numerals that allow us to write the function easily as follows

Fig. 35.2
figure 2

Examples of two different delta-functions

Full size image
$$\begin{aligned} \mathrm{f}\left( \mathrm{x} \right) = \left\{ {\begin{array}{c} {{\bigcirc \!\!\!\!{1}}^{2} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{x} < {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,} \\ {{\bigcirc \!\!\!\!{1}}^{2} + {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,\,\mathrm{x} = {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,} \\ {{\bigcirc \!\!\!\!{1}}^{2} + 2{\bigcirc \!\!\!\!{1}}^{{ - 1}} ,\mathrm{x} > {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,} \\ \end{array} } \right. \end{aligned}$$

The usage of new numerals allows us to quantify even infinitesimal changes in the structure of objects under consideration. For instance, the following function g(x) is clearly different from the function f(x)

$$\begin{aligned} \mathrm{g}\left( \mathrm{x} \right) = \left\{ {\begin{array}{c} {{\bigcirc \!\!\!\!{1}}^{2} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{x} < {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,} \\ {{\bigcirc \!\!\!\!{1}}^{2} + {\bigcirc \!\!\!\!{1}}^{{ - 1,2}} ,\,\mathrm{x} = {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,} \\ {{\bigcirc \!\!\!\!{1}}^{2} + 2{\bigcirc \!\!\!\!{1}}^{{ - 1}} ,\mathrm{x} > {\bigcirc \!\!\!\!{1}}^{{ - 1}} ,} \\ \end{array} } \right. \end{aligned}$$

even though the difference is infinitesimal; it holds at the point x = \(\mathrm{CD}^{-1}\). Note that the traditional language is able again to give only a qualitative description of g(x); moreover, this description will be the same as for function f(x).

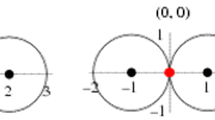
The passage from a qualitative description to quantitative ones is very important when we speak about natural sciences. It allows us to measure infinite and infinitesimal quantities and to distinguish many different objects in cases that are difficult for the traditional mathematics because it is able to see just \(\infty \) or \(\aleph _0\) and \(\aleph _1\). Let us illustrate this fact by considering what the traditional language and the new one can say with respect to the delta-function—the object widely used in Physics.

Informally, it is a generalized function depending on a real x such that it is zero for all values of the x except when x = 0, and its integral from \(-\infty \) to \(\infty \) is equal to one. The new numeral system allows us to distinguish many different delta-functions assuming a concrete infinite value over a concrete infinitesimal interval. Two of them are shown in Fig. 35.2. The first one is equal to CD over the interval [\(-0.5\mathrm{CD}^{-1}\), 0.5\(\mathrm{CD}^{-1}\)] and the second one is equal to \(\mathrm{CD}^{2 }\)over the interval [\(-0.5\mathrm{CD}^{-2}\), 0.5\(\mathrm{CD}^{-2}\)].

We conclude this paper with the hope that the new numeral system allowing us to work numerically with different infinite and infinitesimal numbers on the Infinity Computer (see [11]) will allow physicists and mathematicians to construct new models describing the physical world aroungd us better than it is done actually when the traditional numeral systems are applied for this purpose.