An Approach to the Dodecahedral Conjecture Based on Bounds for Spherical Codes

Abstract

The dodecahedral conjecture states that in a packing of unit spheres in ${\mathfrak{R}}^{3}$, the Voronoi cell of minimum possible volume is a regular dodecahedron with inradius one. The conjecture was first stated by L. Fejes Tóth in 1943, and was finally proved by Hales and McLaughlin over 50 years later using techniques developed by Hales for his proof of the Kepler conjecture. In 1964, Fejes Tóth described an approach that would lead to a complete proof of the dodecahedral conjecture if a key inequality were established. We describe a connection between the key inequality required to complete Fejes Tóth’s proof and bounds for spherical codes and show how recently developed strengthened bounds for spherical codes may make it possible to complete Fejes Tóth’s proof.

1 Introduction

The dodecahedral conjecture states that in a packing of unit spheres in ${\mathfrak{R}\,}^{3}$, the Voronoi (or Dirichlet) cell of minimum possible volume is a regular dodecahedron with inradius one. More precisely, let $\bar{x}_{i}$, i = 1, …, m be points in ${\mathfrak{R}}^{3}$ with $\Vert \bar{x}_{i}\Vert \geq 1$ for each i, and $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$ for all i≠j. Then the points $2\bar{x}_{i}$ can be taken to be the centers of m non-overlapping spheres of radius one which also do not overlap a sphere of radius one centered at x ₀ = 0. The Voronoi cell associated with x ₀ is then

$$\displaystyle{V (\bar{x}_{1},\ldots,\bar{x}_{m}) =\{ x\,\mathrm{:}\,\bar{x}_{i}^{T}x \leq \Vert \bar{ x}{_{ i}\Vert }^{2},\ i = 1,\ldots,m\}.}$$

Let $D \subset {\mathfrak{R}}^{3}$ denote a regular dodecahedron of inradius one, and $\mathrm{Vol}(\cdot )$ denote volume in ${\mathfrak{R}}^{3}$.

The Dodecahedral Conjecture  [5, 6] Let $\bar{x}_{i} \in {\mathfrak{R}}^{3}$, i = 1, …, m with $\Vert \bar{x}_{i}\Vert \geq 1$ for each i, and $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$ for all i≠j. Then $\mathrm{Vol}(V (\bar{x}_{1},\ldots,\bar{x}_{m})) \geq \mathrm{ Vol}(D)$.

The dodecahedral conjecture was stated by L. Fejes Tóth in 1943 [5]. Fejes Tóth’s interest in the conjecture was to obtain a good upper bound on the maximal density of a sphere packing in ${\mathfrak{R}}^{3}$. In particular, the dodecahedral conjecture implies an upper bound of approximately 0.7545, compared to the maximal density of approximately 0.7405 asserted by the Kepler conjecture. Hales and McLaughlin [9] describe a complete proof of the dodecahedral conjecture based on techniques developed by Hales for his proof of the Kepler conjecture. The proof of [9] is believed to be correct, but is difficult to verify due to the many cases and extensive computations required.

Let $R_{D} = \sqrt{3}\tan 3{6}^{\circ }\approx 1.2584$ be the radius of a sphere that circumscribes D, and let $\mathcal{S}_{D} =\{ x \in {\mathfrak{R}}^{3}\,\mathrm{:}\,\Vert x\Vert \leq R_{D}\}$. Fejes Tóth’s 1943 paper contains a proof of the dodecahedral conjecture under the assumption that there are at most 12 i such that $\bar{x}_{i} \in \mathcal{S}_{D}$. In [6, pp. 296–298] Fejes Tóth restates the dodecahedral conjecture and describes an approach that would lead to a complete proof if a key inequality were established. The details of this approach are described in the next section. In Sect. 3 we describe a connection between the key inequality required to complete Fejes Tóth’s proof and bounds for spherical codes. Using constraints from the well-known Delsarte bound for spherical codes, we are able to prove the key inequality for some but not all of the required possible cases. We then consider applying additional constraints from recently described semidefinite programming (SDP) bounds for spherical codes [2]. The use of the SDP constraints improves our bounds, but is not sufficient to eliminate more cases than were already eliminated using the linear programming constraints associated with the Delsarte bound.

In recent work, Hales [7] announced a proof of the “strong” dodecahedral conjecture, which is the original dodecahedral conjecture with surface area replacing volume throughout. The proof methodology of [7] also utilizes Fejes Tóth’s key inequality, which is apparently the basis for a new computational proof of the Kepler conjecture in [8]. These recent developments suggest that continued efforts to provide a direct proof of the key inequality remain a very interesting topic for further research.

2 Fejes Tóth’s Proof

In this section we describe the proof of the dodecahedral conjecture suggested in [6]. The first ingredient is a strengthened version of the result proved in [5].

Theorem 1 ( [6, p. 265]). 

Let $\hat{x}_{i}$ , i = 1,…,m be points in ${\mathfrak{R}}^{3}$ with $\Vert \hat{x}_{i}\Vert \geq 1$ for each i. If m ≤ 12, then $\mathrm{Vol}(V (\hat{x}_{1},\ldots,\hat{x}_{m}) \cap \mathcal{S}_{D}) \geq \mathrm{ Vol}(D)$ .

Note that in Theorem 1 it is not assumed that the points satisfy $\Vert \hat{x}_{i} -\hat{ x}_{j}\Vert \geq 1$, i≠j. Also, the assumption that $\Vert \hat{x}_{i}\Vert < R_{D}$ for each $i$ could be added, since if $\Vert \hat{x}_{i}\Vert \geq R_{D}$ the constraint $\hat{x}_{i}^{T}x \leq \Vert \hat{ x}{_{i}\Vert }^{2}$ in the definition of $V (\hat{x}_{1},\ldots,\hat{x}_{m})$ does not eliminate any points in $\mathcal{S}_{D}$.

The second important component of the argument suggested in [6] is a “point adjustment procedure” that facilitates the use of Theorem 1 when m > 12. For the Voronoi cell $V (\hat{x}_{1},\ldots,\hat{x}_{m})$, let $F_{i}(\hat{x}_{1},\ldots,\hat{x}_{m})$ be the face of $V (\hat{x}_{1},\ldots,\hat{x}_{m}) \cap \mathcal{S}_{D}$ corresponding to the points with $\hat{x}_{i}^{T}x =\Vert \hat{ x}{_{i}\Vert }^{2}$ (it is possible that $F_{i}(\hat{x}_{1},\ldots,\hat{x}_{m}) = \varnothing$).

Point Adjustment Procedure

Step 0.:

Input $\bar{x}_{i}$, $1 \leq \Vert \bar{ x}_{i}\Vert \leq R_{D}$, i = 1, …, m with m > 12 and $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$, i≠j. Let $\hat{x}_{i} =\bar{ x}_{i}$, i = 1, …, m.

Step 1.:

If $\vert \{i\,\mathrm{:}\,1 <\Vert \hat{ x}_{i}\Vert < R_{D}\}\vert < 2$ then go to Step 3. Otherwise choose j≠k such that $1 <\Vert \hat{ x}_{j}\Vert < R_{D}$, $1 <\Vert \hat{ x}_{k}\Vert < R_{D}$, and the surface area of $F_{j}(\hat{x}_{1},\ldots,\hat{x}_{m})$ is less than or equal to that of $F_{k}(\hat{x}_{1},\ldots,\hat{x}_{m})$.

Step 2.:

Let $\delta =\min \{ R_{D} -\Vert \hat{ x}_{j}\Vert,\Vert \hat{x}_{k}\Vert - 1\}$, and

$$\displaystyle{\hat{x}_{j} \leftarrow (\Vert \hat{x}_{j}\Vert +\delta )\frac{\hat{x}_{j}} {\Vert \hat{x}_{j}\Vert },\quad \hat{x}_{k} \leftarrow (\Vert \hat{x}_{k}\Vert -\delta )\frac{\hat{x}_{k}} {\Vert \hat{x}_{k}\Vert }.}$$

Go to Step 1.

Step 3.:

Output $\hat{x}_{i}$, i = 1, …, m.

As pointed out in [6], $R_{D} < \sqrt{2}$ implies that the area of $F_{i}(\lambda _{1}x_{1},\ldots,\lambda _{m}x_{m})$ is monotone decreasing in λ _i . It follows that the adjustment in Step 2 leaves $\sum _{i=1}^{m}\Vert \hat{x}_{i}\Vert$ unchanged, while $\mathrm{Vol}(V (\hat{x}_{1},\ldots,\hat{x}_{m}) \cap \mathcal{S}_{D})$ is nonincreasing.¹ Note that the adjustment in Step 2 is executed at most m − 1 times, since each adjustment decreases $\vert \,\{i\,\mathrm{:}\,1 <\Vert \hat{ x}_{i}\Vert < R_{D}\}\vert$ by at least 1. Then Theorem 1 can be applied if the $\hat{x}_{i}$ output by the procedure have at most 12 i with $\Vert \hat{x}_{i}\Vert < R_{D}$. (Note that the output points $\hat{x}_{i}$ will generally not satisfy $\Vert \hat{x}_{i} -\hat{ x}_{j}\Vert \geq 1$, $i\neq j$, but this assumption is not required in Theorem 1.) This will be the case if the input points $\bar{x}_{i}$ satisfy

$$\displaystyle{ \sum _{i=1}^{m}\Vert \bar{x}_{ i}\Vert \geq 12 + (m - 12)R_{D}. }$$

(1)

To see this, note that there is at most one $\hat{x}_{j}$ with $1 <\Vert \hat{ x}_{j}\Vert < R_{D}$, so if $\vert i\,\mathrm{:}\,\Vert \hat{x}_{i}\Vert = 1\vert \leq 11$ there is nothing to show. Assume on the other hand that $\Vert \hat{x}_{i}\Vert = 1$, i = 1, …, 12. Then (1) and the fact that $\Vert \hat{x}_{i}\Vert \leq R_{D}$ for each i together imply

$$\displaystyle\begin{array}{rcl} \sum _{i=1}^{m}\Vert \hat{x}_{ i}\Vert & =& \sum _{i=1}^{m}\Vert \bar{x}_{ i}\Vert \ \geq \ 12 + (m - 12)R_{D} {}\\ 12 +\sum _{ i=13}^{m}\Vert \hat{x}_{ i}\Vert & \geq & 12 + (m - 12)R_{D} {}\\ (m - 12)R_{D}\ \geq \ \sum _{i=13}^{m}\Vert \hat{x}_{ i}\Vert & \geq & (m - 12)R_{D}, {}\\ \end{array}$$

implying that $\Vert \hat{x}_{i}\Vert = R_{D}$ for i = 13, …, m.

A complete proof of the dodecahedral conjecture thus requires only a proof that (1) holds for any $\bar{x}_{i}$, i = 1, …, m with $1 \leq \Vert \bar{ x}_{i}\Vert \leq R_{D}$ for each i, and $\Vert x_{i} - x_{j}\Vert \geq 1$ for all i≠j. Unfortunately Fejes Tóth was unable to prove (1), even though all evidence suggests that (1) actually holds with R _D replaced by the larger constant $7/\sqrt{27} \approx 1.347$ [6].² Remarkably, the key inequality also appears in Hales’ [7] recent paper that describes a proof of the strong dodecahedral conjecture. In [7] the key inequality is labeled as the inequality L ₁₂, and is written with the value of $R_{D} \approx 1.2584$ rounded up to h ₀: = 1. 26. (It is also assumed that the initial points satisfy $1 \leq \Vert \bar{ x}_{i}\Vert \leq h_{0}$.) A computational proof of the inequality L ₁₂ is apparently the basis for a new proof of the Kepler conjecture in [8].

3 Applying Bounds for Spherical Codes

We now describe an approach to proving the key inequality (1) based on bounds for spherical codes. A set $\mathcal{C} =\{ x_{i}\}_{i=1}^{m} \subset {\mathfrak{R}}^{3}$ is called a spherical z-code if $\Vert x_{i}\Vert = 1$ for each i, and $x_{i}^{T}x_{j} \leq z$ for all i≠j. For example, a packing of unit spheres that all touch (or “kiss”) a unit sphere centered at the origin generates a spherical 1 ∕ 2-code.

To begin we establish that if R is sufficiently small and $\{\bar{x}_{i}\}_{i=1}^{m}$ are points with $1 \leq \Vert \bar{ x}_{i}\Vert \leq R$ for each i and $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$ for all i≠j, then the normalized points $x_{i} =\bar{ x}/\Vert \bar{x}_{i}\Vert$ form a z-code for a suitable value of z.

Lemma 1.

Suppose that $1 \leq \Vert \bar{ x}_{i}\Vert \leq R$ , i = 1,…,m, where $1 \leq R \leq \frac{1+\sqrt{5}} {2}$ and $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$ for all i≠j. Let $x_{i} =\bar{ x}_{i}/\Vert \bar{x}_{i}\Vert$ , i = 1,…,m. Then $x_{i}^{T}x_{j} \leq 1 - \frac{1} {2{R}^{2}}$ for all i≠j.

Proof.

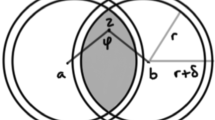
The case R = 1 is trivial. For R > 1 and i≠j, consider the problem

$$\displaystyle\begin{array}{rcl} & \max & \Vert \lambda _{i}x_{i} -\lambda _{j}x{_{j}\Vert }^{2} \\ & \mathrm{s.t.}& 1 \leq \lambda _{i} \leq R,\ 1 \leq \lambda _{j} \leq R.{}\end{array}$$

(2)

The objective in (2) is convex, so the solution lies at an extreme point of the feasible region. Letting $s:= x_{i}^{T}x_{j}$, the value of the objective at the extreme points is:

$$\displaystyle{\lambda _{i}^{2}+\lambda _{ j}^{2}-2s\lambda _{ i}\lambda _{j} = \left \{\begin{array}{@{}l@{\quad }l@{}} 2(1 - s) \quad &\mbox{ if }\lambda _{i} =\lambda _{j} = 1, \\ 1 + {R}^{2} - 2Rs\quad &\mbox{ if }\lambda _{i} = 1,\ \lambda _{j} = R\;\,\text{or}\;\,\lambda _{i} = R,\ \lambda _{j} = 1, \\ 2{R}^{2}(1 - s) \quad &\mbox{ if }\lambda _{i} =\lambda _{j} = R. \end{array} \right.}$$

Obviously the maximum cannot occur at $\lambda _{i} =\lambda _{j} = 1$. Note that the solution value in (2) is at least one, from the assumption that $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$. It follows that if the max occurs at $\lambda _{i} = 1,\ \lambda _{j} = R$ (or equivalently $\lambda _{i} = R,\ \lambda _{j} = 1$) then $1 + {R}^{2} - 2Rs \geq 1$, which is equivalent to $s \leq \frac{R} {2}$. Similarly, if the max occurs at $\lambda _{i} =\lambda _{j} = R$, then $2{R}^{2}(1 - s) \geq 1$, which is equivalent to $s \leq 1 - \frac{1} {2{R}^{2}}$. Finally it is easy to verify that $\frac{R} {2} \leq 1 - \frac{1} {2{R}^{2}}$ for $1 \leq R \leq \frac{1+\sqrt{5}} {2}$. □ 

Next, for $x_{i}\neq x_{j}$ with $\Vert x_{i}\Vert =\Vert x_{j}\Vert = 1$, consider the problem

$$\displaystyle\begin{array}{rcl} & \min & \lambda _{i} +\lambda _{j} \\ & \mathrm{s.t.}& \Vert \lambda _{i}x_{i} -\lambda _{j}x_{j}\Vert \geq 1 \\ & & 1 \leq \lambda _{i} \leq R,\ 1 \leq \lambda _{j} \leq R.{}\end{array}$$

(3)

Note that by Lemma 1 and its proof, if $R \leq \frac{1+\sqrt{5}} {2}$ then (3) is feasible if and only if $x_{i}^{T}x_{j} \leq 1 - \frac{1} {2{R}^{2}}$. The next result gives a complete characterization of the solution value in (3).

Theorem 2.

Let $1 \leq R \leq \frac{1+\sqrt{5}} {2}$, $\Vert x_{i}\Vert =\Vert x_{j}\Vert = 1$ and $s = x_{i}^{T}x_{j} \leq 1 - \frac{1} {2{R}^{2}}$ . Then the solution value in problem (3) is $\lambda _{i}^{{\ast}} +\lambda _{ j}^{{\ast}} = f(s,R)$ , where

$$\displaystyle{f(s,R) = \left \{\begin{array}{@{}l@{\quad }l@{}} 2 \quad &\mathrm{if}\ s \leq \frac{1} {2}, \\ 1 + 2s \quad &\mathrm{if}\ \frac{1} {2} \leq s \leq \frac{R} {2}, \\ R(1 + s) + \sqrt{1 - {R}^{2 } (1 - {s}^{2 } )}\quad &\mathrm{if}\ \frac{R} {2} \leq s \leq 1 - \frac{1} {2{R}^{2}}. \end{array} \right.}$$

Proof.

The case of s ≤ 0. 5 is trivial, so assume that s > 0. 5 and the objective in (3) attains a value $\lambda _{i} +\lambda _{j} = c$, where 2 < c ≤ 2R. Since the constraint $\Vert \lambda _{i}x_{i} -\lambda _{j}x_{j}\Vert \geq 1$ is equivalent to ${(\lambda _{i} +\lambda _{j})}^{2} \geq 1 + 2\lambda _{i}\lambda _{j}(1 + s)$, this implies that we must have

$$\displaystyle{{c}^{2} \geq 1 + 2(1 + s)\lambda _{ i}\lambda _{j}.}$$

To find the minimum possible value of c we are thus led to consider the problem

$$\displaystyle\begin{array}{rcl} & \min & \lambda _{i}\lambda _{j} \\ & \mathrm{s.t.}& \lambda _{i} +\lambda _{j} = c, \\ & & 1 \leq \lambda _{i} \leq R,\ 1 \leq \lambda _{i} \leq R.{}\end{array}$$

(4)

The objective in (4) can be written in the form $\lambda _{i}(c -\lambda _{i})$, which is a concave function, so the solution of (4) must occur at an extreme point of the feasible region. There are two possibilities for the form of such an extreme point, depending on the value of c.

• Case 1: c ≤ 1 + R. In this case the extreme points of (4) have $(\lambda _{i},\lambda _{j})$ equal to (1, c − 1) and (c − 1, 1), both of which have $\lambda _{i}\lambda _{j} = c - 1$. To find the minimum possible value of $c =\lambda _{i} +\lambda _{j}$ in (3), we must find the minimum c ≥ 2 such that

  $$\displaystyle{{c}^{2} \geq 1 + 2(1 + s)(c - 1),}$$

  which is easily determined to be $c = 1 + 2s$. Since by assumption c ≤ 1 + R, this solution applies whenever $1 + 2s \leq 1 + R$, or $s \leq \frac{R} {2}$.

• Case 2: c ≥ 1 + R. In this case the extreme points of (4) have $(\lambda _{i},\lambda _{j})$ equal to (R, c − R) and (c − R, R), both of which have $\lambda _{i}\lambda _{j} = R(c - R)$. To find the minimum possible value of $c =\lambda _{i} +\lambda _{j}$ in (3), we must find the minimum c ≥ 2 such that

  $$\displaystyle{{c}^{2} \geq 1 + 2(1 + s)R(c - R),}$$

  which is easily determined to be $c = R(1 + s) + \sqrt{1 - {R}^{2 } (1 - {s}^{2 } )}$. Since by assumption c ≥ 1 + R, this solution applies whenever $R(1 + s) + \sqrt{1 - {R}^{2 } (1 - {s}^{2 } )} \geq 1 + R$, which is equivalent to $s \geq \frac{R} {2}$. □ 

In Fig. 1 we plot f(s, R _D ) for $\frac{1} {2} \leq s \leq 1 - \frac{1} {2R_{D}^{2}}$. It is evident from the figure, and is easy to prove, that f(s, R _D ) is concave in the interval $\frac{R_{D}} {2} \leq s \leq 1 - \frac{1} {2R_{D}^{2}}$.

Fig. 1

Function f(s, R _D ) from Theorem 2

Now assume that m > 12, $1 \leq \Vert \bar{ x}_{i}\Vert \leq R_{D}$, i = 1, …m, and $\Vert \bar{x}_{i} -\bar{ x}_{j}\Vert \geq 1$ for all i≠j. Let $\lambda _{i} =\Vert \bar{ x}_{i}\Vert$ and $x_{i} = (1/\lambda _{i})\bar{x}_{i}$, i = 1, …, m. Our goal is to prove (1), which can be written as

$$\displaystyle{ \sum _{i=1}^{m}\lambda _{ i} \geq 12 + (m - 12)R_{D}. }$$

(5)

Define $N_{i} =\vert \,\{ j\neq i\,\mathrm{:}\,x_{i}^{T}x_{j} \geq 0.5\}\vert$ to be the number of “close neighbors” of x _i , i = 1, …, m and $\mathcal{N} =\{ (i,j),\ i\neq j\,\mathrm{:}\,x_{i}^{T}x_{j} \geq 0.5\}$. Note that $(i,j) \in \mathcal{N}\;\Longleftrightarrow\;(j,i) \in \mathcal{N}$, and $\vert \mathcal{N}\vert =\sum _{ i=1}^{m}N_{i}$. Moreover we have

$$\displaystyle{\sum _{(i,j)\in \mathcal{N}}(\lambda _{i} +\lambda _{j} - 2) =\sum _{(i,j)\in \mathcal{N}}(\lambda _{i} - 1) + (\lambda _{j} - 1) = 2\sum _{i=1}^{m}N_{ i}(\lambda _{i} - 1).}$$

Applying Theorem 2, it follows that

$$\displaystyle\begin{array}{rcl} 2\sum _{i=1}^{m}N_{ i}(\lambda _{i} - 1)& \geq & \sum _{(i,j)\in \mathcal{N}}[f(x_{i}^{T}x_{ j},R_{D}) - 2] {}\\ \sum _{i=1}^{m}(\lambda _{ i} - 1)& \geq & \frac{1} {2N_{\max }}\sum _{(i,j)\in \mathcal{N}}[f(x_{i}^{T}x_{ j},R_{D}) - 2], {}\\ \end{array}$$

where $N_{\max }:=\max \{ N_{i}\}_{i=1}^{m}$. Thus to prove (5) it suffices to show that

$$\displaystyle{ \frac{1} {2N_{\max }}\sum _{(i,j)\in \mathcal{N}}[f(x_{i}^{T}x_{ j},R_{D}) - 2] \geq 12 + (m - 12)R_{D} - m = (m - 12)(R_{D} - 1). }$$

(6)

To bound N _max we utilize the following result, which is a slight generalization of [1, Lemma 5].

Proposition 1.

Suppose that a spherical triangle with sides a,b,c has cos c ≤ z _c, $0 \leq z_{a} \leq \cos a \leq \cos b \leq z_{b} < 1$, $z_{c} \geq z_{a}z_{b}$ . Let γ be the spherical angle between the sides a and b. Then

$$\displaystyle{\cos \gamma \leq \max \left \{\frac{z_{c} - z_{a}^{2}} {1 - z_{a}^{2}},\ \frac{z_{c} - z_{a}z_{b}} {\sqrt{(1 - z_{a }^{2 })(1 - z_{b }^{2 })}}\right \}.}$$

Lemma 2.

$N_{\max } \leq 6$ . Moreover, for m = 13, if $N_{\max } = 6$ then (5) holds.

Proof.

Applying Proposition 1 with z _a  = 0. 5, $z_{b} = z_{c} = 1 - 1/(2R_{D}^{2}) \approx 0.6843$, we obtain cosγ ≤ 0. 5791, or γ ≥ 54. 6^∘. It follows immediately that N _max ≤ 6, since $7(54.{6}^{\circ }) > 36{0}^{\circ }$. For m = 13, Theorem 2 implies that (5) immediately holds if $x_{i}^{T}x_{j} \geq R_{D}/2$ for any i≠j. Assume alternatively that $x_{i}^{T}x_{j} \leq R_{D}/2$ for all i≠j. Applying Proposition 1 with z _a  = 0. 5, $z_{b} = z_{c} = R_{D}/2 \approx 0.6292$, we obtain cosγ ≤ 0. 5056, or γ ≥ 59. 6288^∘. Hence N _max = 6 is still possible, so assume that N _i  = 6 for some i. Reindexing the points $\{x_{j}\}_{j=1}^{13}$, we can assume that i = 7 and the points $\{x_{j}\}_{j=1}^{6}$, have $x_{j}^{T}x_{(j\mathrm{\,MOD\,}6)+1} \leq R_{D}/2$, j = 1, …, 6. However, the fact that γ ≥ 59. 6288^∘ in each spherical triangle with vertices $x_{7},x_{j},x_{(j\mathrm{\,MOD\,}6)+1}$ also implies that $\gamma \leq 36{0}^{\circ }- 5(59.628{8}^{\circ }) = 61.85{6}^{\circ }$. Since Proposition 1 with z _a  = 0. 5, $z_{b} = R_{D}/2$, z _c  = 0. 6 obtains γ ≥ 62. 18^∘, we can conclude that $x_{j}^{T}x_{(j\mathrm{\,MOD\,}6)+1} \geq 0.6$, j = 1, …, 6. Applying Theorem 2, we conclude that $\lambda _{j} +\lambda _{j+1} \geq 1 + 2(0.6) = 2.2$ for j = 1, 3, 5. It follows that

$$\displaystyle{\sum _{i=1}^{13}\lambda _{ i} \geq 7 + 3(2.2) = 13.6,}$$

which implies (5). □ 

With an upper bound for N _max determined, a lower bound for the left-hand side of (6) can be obtained using the Delsarte bound for spherical codes. Specifically, $\mathcal{C} =\{ x_{i}\}_{i=1}^{m}$ is a spherical z-code in ${\mathfrak{R}}^{3}$, with $z = 1 - 1/(2R_{D}^{2}) \approx 0.6843$. We define the usual distance distribution of the code to be the function $\alpha (\cdot ): [-1,1] \rightarrow \mathfrak{R}_{+}$ defined as

$$\displaystyle{ \alpha (s) = \frac{\vert \{(i,j)\,\mathrm{:}\,x_{i}^{T}x_{j} = s\}\vert } {m}. }$$

(7)

It is then easy to see that α( ⋅) ≥ 0, and

$$\displaystyle{ \sum _{-1\leq s\leq z}\alpha (s) = m - 1. }$$

(8)

Let Φ _k ( ⋅), k = 0, 1, … denote the Gegenbauer, or ultraspherical, polynomials $\Phi _{k}(t) = P_{k}^{(0,0)}(t)$ where $P_{k}^{(s,s)}$ is a Jacobi polynomial. It can be shown [4], [3, Chaps. 9, 13] that

$$\displaystyle{ 1 +\sum _{-1\leq s\leq z}\alpha (s)\Phi _{k}(s) \geq 0,\quad k = 1,2,\ldots. }$$

(9)

From (8) and (9), using k = 1, …, d, a bound on the left-hand side of (6) can be obtained via the semi-infinite linear programming problem

$$\displaystyle\begin{array}{rcl} \mathrm{LP}(m): \qquad & \min & \sum _{0.5\leq s\leq z}m[f(s,R_{D}) - 2]\alpha (s) {}\\ & \mathrm{s.t.}& \ \,\sum _{s\in Z}\alpha (s)\Phi _{k}(s) \geq -1,\quad k = 1,\ldots,d, {}\\ & & \ \,\sum _{s\in Z}\alpha (s) = m - 1,\quad \alpha (s) \geq 0,\quad s \in Z, {}\\ \end{array}$$

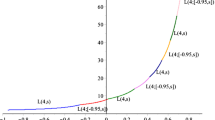
where $Z:= [-1,z]$. For $z = 1 - 1/(2R_{D}^{2})$ the constraints of LP are feasible up to m = 21. (In other words, 21 is the Delsarte bound for the size of this spherical z-code. The maximum cardinality of a z-code for this value of z actually appears to be 20 [10].) Let $v_{\mathrm{LP}}^{{\ast}}(m)$ denote the solution value in LP(m). We obtain an approximate value of $v_{\mathrm{LP}}^{{\ast}}(m)$ for m = 13, …, 21 by numerically solving a discretized version of LP(m) using d = 16, and values of s ∈ Z incremented by 0.002.³ In Fig. 2 we plot the lower bound $v_{\mathrm{LP}}^{{\ast}}(m)/(2N_{\max })$ for the left-hand side of (6) (using N _max = 6, except N _max = 5 for m = 13) and the required value $(m - 1)(R_{D} - 1)$ from the right-hand side of (6). The lower bound based on $v_{\mathrm{LP}}^{{\ast}}(m)$ is sufficient to prove that (5) holds for m ≥ 17.⁴ The value $v_{\mathrm{LP}}^{{\ast}}(13) = 0$ is a consequence of the well-known fact that the Delsarte bound for a 1 ∕ 2-code in ${\mathfrak{R}}^{3}$ is 13, despite the fact that the actual maximal size of such a code is 12. Indeed, this observation means that the approach based on LP(m) has no chance of establishing (5) for m = 13.

Fig. 2

LP bounds for inequality (6)

To prove (5) for 13 ≤ m ≤ 16 requires stronger restrictions on the distance distribution than the constraints (9). The most attractive possibility appears to be the strengthened semidefinite programming constraints from [2]. In particular the constraints in [2] are sufficient to prove that the maximum cardinality of a 1 ∕ 2-code in ${\mathfrak{R}}^{3}$ is 12, which is essential if one is to have any chance of proving (6) for m = 13. Applying the methodology of [2] results in a problem SDP(m) of the form

$$\displaystyle\begin{array}{rcl} \mathrm{SDP}(m):& \min & \sum _{0.5\leq s\leq z}m[f(s,R_{D}) - 2]\alpha (s) {}\\ & \mathrm{s.t.}& 3\sum _{s\in Z}\alpha (s)S_{k}(s,s,1) +\sum { _{s,t,u\in Z}\alpha }^{{\prime}}(s,t,u)S_{ k}(s,t,u) \succcurlyeq -S_{k}(1,1,1), {}\\ & & \ \ \sum _{s\in Z}\alpha (s)\Phi _{k}(s) \geq -1,\quad k = 1,\ldots,d {}\\ & & \ \ \sum _{s\in Z}\alpha (s) = m - 1,\quad \alpha (s) \geq 0,\quad s \in Z {}\\ & & \,\sum {_{s,t,u\in Z}\alpha }^{{\prime}}(s,t,u) = (m - 1)(m - 2),{\quad \alpha }^{{\prime}}(s,t,u) \geq 0,\quad s,t,u \in Z. {}\\ \end{array}$$

In SDP(m), α ^′( ⋅,  ⋅,  ⋅) is the three-point distance distribution

$$\displaystyle{{\alpha }^{{\prime}}(s,t,u) = \frac{\vert \{(i,j,k)\,\mathrm{:}\,x_{i}^{T}x_{ j} = s,x_{i}^{T}x_{ k} = t,x_{j}^{T}x_{ k} = u\}\vert } {m},}$$

and S _k (s, t, u) is a $(d + 1 - k) \times (d + 1 - k)$ symmetric matrix whose entries are symmetric polynomials of degree k in the variables (s, t, u); see [2] for details. (The notation $X \succcurlyeq Y$ means that X − Y is positive semidefinite.) In Fig. 3 we show the bounds $v_{\mathrm{SDP}}^{{\ast}}(m)/(2N_{\max })$ for the left-hand side of (6), as well as the required value $(m - 1)(R_{D} - 1)$ from the right-hand side of (6), for 13 ≤ m ≤ 16.⁵ For comparison we also give the previously described bounds based on $v_{\mathrm{LP}}^{{\ast}}(m)$. As can be seen from the figure, the use of SDP(m) gives a substantial improvement over LP(m) for m = 13, but the magnitude of the difference appears to diminish as m increases, and the improved bound is unable to eliminate any more cases than were eliminated using LP(m).⁶

Fig. 3

LP and SDP bounds for inequality (6)

Although the use of SDP(m) is not sufficient to prove the key inequality (1) for all required m, there are several possible ways in which the approach based on SDP(m) might be strengthened. In particular, since SDP(m) uses the three-point distance distribution, it should be possible to utilize a more elaborate version of Theorem 2 to give lower bounds on terms of the form $\lambda _{i} +\lambda _{j} +\lambda _{k}$. In addition, since the elements of the three-point distance distribution include the triangles in a Delaunay triangulation of the surface of the sphere, it might be possible to add valid constraints that can be derived for the Delaunay triangulation, as in [1]. The possibility that further strengthening of SDP(m) might suffice to establish (1) remains a very interesting topic for ongoing research, especially given the connection between (1) and the recent work of Hales [7, 8] on the Kepler conjecture and related problems.