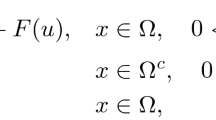Regularity and Unique Existence of Solution to Linear Diffusion Equation with Multiple Time-Fractional Derivatives

Abstract

We consider an initial/boundary value problem for linear diffusion equation with multiple fractional time derivatives and prove the regularity of the solution. The regularity argument implies the unique existence of the solution.

The first named author thanks JASSO Honors Scholarship and the Global COE Program “The Research and Training Center for New Development in Mathematics” at Graduate School of Mathematical Sciences of The University of Tokyo for financial support.

1 Introduction

Let Ω be a bounded domain in $\mathbb{R}^{d}$ with sufficiently smooth boundary ∂Ω and let 0<α ₂<α ₁<1. We consider the following initial/boundary value problem for a diffusion equation with two fractional time derivatives:

(1.1)

(1.2)

and

(1.3)

Here, for 0<α<1, we denote by $\partial_{t}^{\alpha}$ the Caputo fractional derivative with respect to t:

$$ \partial_t^{\alpha}g(t)= \frac{1}{\Gamma(1-\alpha)}\int^t_0 (t- \tau)^{-\alpha} \frac{d}{d \tau }g(\tau)d\tau $$

where Γ is the Gamma function and q∈W ^2,∞(Ω). The space W ^2,∞(Ω) is the usual Sobolev space (Adams [1]). Moreover the operator $-\mathcal{A}$ is a symmetric uniformly elliptic operator, that is,

$$ (-\mathcal{A} u) (x) = \sum^d_{i=1} \frac{\partial}{\partial x_i} \Biggl(\sum^d_{j=1}a_{ij}(x) \frac{\partial}{\partial x_j}u(x) \Biggr) + b(x)u(x), \quad x\in \varOmega , $$

where a _ij=a _ji, 1≤i,j≤d, $a_{ij} \in C^{1}(\overline{\varOmega })$, $b \in C(\overline{\varOmega })$, b(x)≤0 for $x\in \overline{\varOmega }$, and we assume that there exists a constant C ₀>0 such that

$$ C_0\sum^d_{i=1} \xi_i^2 \leq \sum^d_{i,j=1}A_{ij}(x) \xi_i\xi_j, \quad x \in \overline{\varOmega }, \ \xi\in \mathbb{R}^d. $$

In the special case q≡0, (1.1) is a diffusion equation with a single fractional time derivative. For such equations there exists a large and rapidly growing number of publications which we do not intend to list completely: Bazhlekova [3, 4], Eidelman and Kochubei [6], Luchko [12, 13], Prüss [21], Sakamoto and Yamamoto [22]. Also see Agarwal [2], Fujita [7], Gejji and Jafari [8], Mainardi [15–17], Nigmatullin [18], Schneider and Wyss [23].

In this article, we consider the case of multiple fractional time derivatives. Such equations can be considered as more feasible model equations than equations with a single fractional time derivative in modeling diffusion in porous media. In the case where the functions in (1.1) are not dependent on x, we refer to several works and refer for example to Diethelm and Luchko [5], Podlubny [20], Chap. 3, for instance. In particular, in [5], some physical interpretations are given. As for diffusion equations with multiple fractional time derivatives, see Jiang, Liu, Turner and Burrage [10] and Luchko [14] which argue a general number of time fractional derivatives. The article[10] discusses the spatially one dimensional case with constant coefficients where also the spatial fractional derivative is considered, and establishes the formula of the solution, and [14] assumes that the coefficients of the time derivatives are constant to prove unique existence of the solution by the Fourier method as well as the maximum principle and related properties.

Unlike [10] and [14], we treat a general case of x-dependent coefficient of fractional time derivatives. In our case, we cannot apply the Fourier method or obtain an analytic solution. We apply the perturbation method and the theory of evolution equations to prove regularity as well as unique existence of solution to (1.1)–(1.3). Such results should be the starting point for further research concerning the theory of nonlinear fractional diffusion equations, numerical analysis, control theory and inverse problems. In forthcoming papers, we will discuss those subjects.

This paper is composed of four sections including the current section. In Sect. 2, we present the main result for the case of two fractional time derivatives and in Sect. 3 we prove it. Section 4 is devoted to the case of general multiple fractional time derivatives.

2 Main Results

Let L ²(Ω) be the usual L ²-space with the scalar product (⋅,⋅), and H ^ℓ(Ω), $H_{0}^{m} (\varOmega )$ denote the usual Sobolev spaces (e.g., Adams [1]). We set $\Vert a\Vert_{L^{2}(\varOmega )} = (a,a)^{\frac{1}{2}}$.

We define the operator A in L ²(Ω) by

$$ (Au) (x) = (\mathcal{A} u) (x), \quad x \in \varOmega , \qquad \mathcal{D}(A) = H^2(\varOmega ) \cap H^1_0(\varOmega ). $$

Then the fractional power A ^γ is defined for $\gamma \in \mathbb{R}$ (see for instance [19]), and $\mathcal{D} (A^{\gamma}) \subset H^{2\gamma}(\varOmega )$, $\mathcal{D}(A^{\frac{1}{2}})=H^{1}_{0}(\varOmega )$ for example. We note that $\Vert u \Vert _{\mathcal{D}(A^{\gamma})} : =\Vert A^{\gamma}u \Vert _{L^{2}(\varOmega )}$ is a stronger norm than $\Vert u \Vert_{L^{2}(\varOmega )}$ for γ>0.

Since −A is a symmetric uniformly elliptic operator, the spectrum of A is entirely composed of eigenvalues and counting according to the multiplicities, we can set: 0<λ ₁≤λ ₂≤⋯. By $\phi_{n} \in H^{2}(\varOmega ) \cap H^{1}_{0}(\varOmega )$, we denote the orthonormal eigenfunction corresponding to λ _n: Aϕ _n=λ _nϕ _n. Then the sequence $\{ \phi_{n} \}_{n\in \mathbb{N}}$ is an orthonormal basis in L ²(Ω). Moreover, we see that

$$ \mathcal{D}\bigl(A^{\gamma}\bigr) = \Biggl\{ \psi \in L^2( \varOmega ); \sum_{n=1}^{\infty} \lambda _n^{2\gamma}\bigl\vert (\psi,\phi_n) \bigr\vert^2 < \infty \Biggr\} $$

and that $\mathcal{D}(A^{\gamma})$ is a Hilbert space with the norm

$$ \Vert \psi\Vert_{\mathcal{D}(A^{\gamma})} = \Biggl\{ \sum_{n=1}^{\infty} \lambda _n^{2\gamma}\bigl\vert (\psi,\phi_n) \bigr\vert^2 \Biggr\}^{\frac{1}{2}}. $$

Henceforth we associate with u(x,t), provided that it is well-defined, a map u(⋅):(0,T)⟶L ²(Ω) by u(t)(x)=u(x,t), 0<t<T, x∈Ω. Then we can write (1.1)–(1.3) as

(2.1)

Remark 1

The interpretation of the initial condition should be made in a suitable function space. In our case, as Theorem 1 asserts, we have $\lim_{t\to 0} \Vert u(t) - a\Vert_{L^{2}(\varOmega )} = \nobreak 0$.

Moreover we define the Mittag–Leffler function E _α,β by

$$ E_{\alpha,\beta}(z) :=\sum_{k=0}^{\infty} \frac{z^k}{\Gamma(\alpha k+\beta)}, \quad z \in \mathbb{C}, $$

where α>0 and $\beta \in \mathbb{R}$ are arbitrary constants. Using the power series, we can directly verify that E _α,β(z) is an entire function.

Now we define the operators S(t):L ²(Ω)→L ²(Ω), t≥0, by

$$ S(t)a := \sum\limits _{n=1}^\infty (a, \phi_n)E_{\alpha_1,1} \bigl(-\lambda_nt^{\alpha_1} \bigr)\phi_n \quad \mbox{in } L^2(\varOmega ) $$

(2.2)

for a∈L ²(Ω). Then we can prove that S(t):L ²(Ω)⟶L ²(Ω) is a bounded linear operator for t≥0 (e.g., Sakamoto and Yamamoto [22]). Moreover, termwise differentiation is possible and gives

(2.3)

and

(2.4)

for a∈L ²(Ω).

For F∈L ²(Ω×(0,T)) and a∈L ²(Ω), there exists a unique solution in a suitable class (e.g., Sakamoto and Yamamoto [22]) to the problem

(2.5)

(2.6)

This solution is given by

$$ u(t) = \int_0^t A^{-1}S'(t-\tau)F(\tau)d\tau + S(t)a, \quad t > 0. $$

(2.7)

In view of (2.7), we mainly discuss the equation

$$ u(t) = S(t)a - \int_0^t A^{-1}S'(t-\tau)q\partial_t^{\alpha_2}u(\tau)d\tau, \quad 0 < t < T, $$

(2.8)

in order to establish unique existence of solutions to (2.1). Henceforth C denotes generic positive constants which are independent of a in (1.2), but may depend on T, α ₁, α ₂ and the coefficients of the operator A and q.

We can state our first main result.

Theorem 1

We assume thatu∈C((0,T];L ²(Ω)) satisfies (2.8) and

$$ \alpha_1 + \alpha_2 > 1. $$

Then

$$ \bigl\Vert u(t)\bigr\Vert_{H^{2\gamma}(\varOmega )} \le Ct^{-\alpha_1\gamma}\Vert a\Vert_{L^2(\varOmega )}, \quad 0 < t \le T $$

for anyγ∈(0,1).

We may be able to remove the condition α ₁+α ₂>1. On the other hand, Prüss established regularity in case γ=1 for general α ₁,α ₂∈(0,1) under a strong condition on $a \in \mathcal{D}(A)$ (see [21], in particular the perturbation theorem on p. 60).

On the basis of Theorem 1, a standard argument (e.g., Henry [9]) yields

Theorem 2

For anyγ∈(0,1) there exists a mild solution to (2.8) in the space $C((0,T]; \mathcal{D}(A^{\gamma})) \cap C([0,T];L^{2}(\varOmega ))$.

3 Proof of Theorem 1

First we have

$$ A^{\gamma-1}S'(t)a=-t^{\alpha_1-1}\sum _{n=1}^\infty \lambda_n^{\gamma}(a, \phi_n)E_{\alpha_1,\alpha_1}\bigl(-\lambda_nt^{\alpha_1} \bigr) \phi_n \quad \mbox{in}\ L^2(\varOmega ) $$

(3.1)

for a∈L ²(Ω) and γ≥0. Moreover, since

$$ \bigl\vert E_{\alpha_1,\alpha_1}(-\eta) \bigr\vert \le \frac{C}{1+\eta}, \quad \eta > 0 $$

(e.g., Theorem 1.6 on p. 35 in Podlubny [20]), we can prove

(3.2)

and

(3.3)

Now we proceed to the proof of Theorem 1. We set

$$ v(t) := \int_0^t A^{\gamma-1}S'(t- \eta) q\partial_t^{\alpha_2}u({\eta})d\eta, \quad 0 < t < T. $$

By (2.8), we have

$$ A^{\gamma}u(t) = A^{\gamma}S(t)a - v(t), \quad 0 < t < T. $$

Therefore, using

$$ \bigl\Vert u(t)\bigr\Vert_{H^{2\gamma}(\varOmega )} \le C\bigl\Vert A^{\gamma}u(t) \bigr\Vert_{L^2(\varOmega )} $$

(see the beginning of Sect. 2), it is sufficient to estimate $\Vert A^{\gamma}S(t)a\Vert_{L^{2}(\varOmega )} + \Vert v(t)\Vert_{L^{2}(\varOmega )}$. First we will estimate $\Vert v(t)\Vert_{L^{2}(\varOmega )}$. Substituting the definition of $\partial_{t}^{\alpha_{2}}u$ and changing the order of integration, we have

$$ \begin{aligned}[b] v(t) &= \int_0^t A^{\gamma-1}S'(t-\eta)\frac{1}{\Gamma(1-{\alpha_2})} \biggl(\int _0^{\eta}(\eta-\tau)^{-\alpha_2}qu'( \tau)d\tau \biggr)d\eta \\ &= \frac{1}{\Gamma(1-{\alpha_2})} \int_0^t H(t,\tau) qu'(\tau)d\tau, \quad 0 < t < T. \end{aligned} $$

(3.4)

Here we have set

$$ H(t,\tau) = \int_\tau^t A^{\gamma-1}S'(t- \eta) (\eta-\tau)^{-{\alpha_2}}d\eta. $$

Decomposing the integrand and introducing the change of variables η−τ→η we obtain

(3.5)

On the other hand, we have

$$ \begin{aligned} \partial_\tau I_1(t,\tau) = &-\int _0^{t-\tau}A^{\gamma-1} S''(t- \eta-\tau) \bigl(\eta^{-\alpha_2}-(t-\tau)^{-\alpha_2}\bigr)d\eta \\ &{}- \alpha_2\int_0^{t-\tau}A^{\gamma-1}S'(t- \eta-\tau) (t-\tau)^{-{\alpha_2}-1} d\eta \\ &{}- \lim_{\eta\rightarrow t-\tau} A^{\gamma-1}S'(t-\tau-\eta) \bigl[\eta^{-\alpha_2}-(t-\tau)^{-\alpha_2}\bigr]. \end{aligned} $$

By the estimate (3.2) we obtain

According to the mean value theorem, we can choose θ∈(η,t−τ) such that

$$ \bigl\vert (t-\tau)^{\alpha_2} - \eta^{\alpha_2}\bigr\vert = \bigl\vert \alpha_2\theta^{\alpha_2-1}(t-\tau-\eta)\bigr\vert \le \alpha_2\eta^{\alpha_2-1}(t-\tau-\eta). $$

Hence we obtain

by α ₁−α ₁γ>0. This implies

$$ \begin{aligned}[b] \partial_\tau I_1(t,\tau) = &-\int _0^{t-\tau}A^{\gamma-1} S''(t- \eta-\tau) \bigl(\eta^{-\alpha_2}-(t-\tau)^{-\alpha_2}\bigr)d\eta \\ &- \alpha_2\int_0^{t-\tau}A^{\gamma-1}S'(t- \eta-\tau) (t-\tau)^{-{\alpha_2}-1} d\eta, \quad 0 < t < T. \end{aligned} $$

(3.6)

On the other hand, we have

Adding this and (3.6) we obtain

$$ \begin{aligned}[b] \partial_\tau H(t,\tau)= &-\int _0^{t-\tau}A^{\gamma-1}S''(t- \eta-\tau) \bigl(\eta^{-{\alpha_2}}-(t-\tau)^{-{\alpha_2}}\bigr)d\eta \\ &+ A^{\gamma-1}S'(t-\tau) (t-\tau)^{-{\alpha_2}}. \end{aligned} $$

(3.7)

Using (3.7) in (3.4), integrating by parts and using H(t,t)=0 we obtain

We set

$$ B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}, \quad \alpha, \beta > 0. $$

First, by (3.2) and q∈W ^2,∞(Ω) we have

(3.8)

since 1−α ₂>0 and α ₁−α ₁γ>0.

On the other hand, by q∈W ^2,∞(Ω) and u|_∂Ω=0, we have

$$ \bigl\Vert A\bigl(qu(\tau)\bigr)\bigr\Vert_{L^2(\varOmega )} \le C\bigl\Vert qu(\tau)\bigr\Vert _{H^2(\varOmega )} \le C\bigl\Vert u(\tau)\bigr\Vert_{H^2(\varOmega )} \le C\bigl\Vert Au(\tau) \bigr\Vert_{L^2(\varOmega )} $$

and $\Vert qu(\tau)\Vert_{L^{2}(\varOmega )}\le C\Vert u(\tau)\Vert_{L^{2}(\varOmega )}$, that is,

$$ \bigl\Vert A^0\bigl(qu(\tau)\bigr)\bigr\Vert_{L^2(\varOmega )}\le C\bigl\Vert A^0u(\tau) \bigr\Vert_{L^2(\varOmega )}. $$

Hence the interpolation theorem (see for instance Lions and Magenes [11], Theorem 5.1 on p. 27) we obtain

$$ \bigl\Vert A^{\gamma}\bigl(qu(\tau)\bigr)\bigr\Vert_{L^2(\varOmega )} \le C\bigl\Vert A^{\gamma}u(\tau)\bigr\Vert_{L^2(\varOmega )}. $$

Therefore by (3.2) and (3.3), the second term of I ₄(t) can be estimated as follows:

For the last equality, we used α ₁+α ₂>1. Therefore we have

Thus the estimate of $\Vert v(t)\Vert_{L^{2}(\varOmega )}$ is completed.

Next we estimate $\Vert A^{\gamma}S(t)a\Vert_{L^{2}(\varOmega )}$. By Theorem 1.6 (p. 35) in [20], we obtain

$$ \begin{aligned} \bigl\| A^{\gamma} S(t)a\bigr\|^2_{L^2(\varOmega )} &= \Biggl \Vert \sum_{n=1}^\infty (a, \phi_n)\lambda^{\gamma}_n E_{{\alpha_1},1}\bigl(- \lambda_n t^{\alpha_1}\bigr)\phi_n\Biggr \Vert ^2_{L^2(\varOmega )} \\ &\le C\sum_{n=1}^\infty(a, \phi_n)^2 t^{-2\alpha_1\gamma} \biggl(\frac{(\lambda_nt^{\alpha_1})^{\gamma}}{1+\lambda_nt^{\alpha_1}} \biggr)^2 \\ &\leq Ct^{-2\alpha_1\gamma}\|a\|^2_{L^2(\varOmega )}, \end{aligned} $$

and hence

Therefore by an inequality of Gronwall type (see [9], Exercise 3 (p. 190)), we obtain

$$ \bigl\|A^{\gamma} u(t)\bigr\|_{L^2(\varOmega )} \le C\Vert a\Vert_{L^2(\varOmega )}t^{-\alpha_1\gamma}, \quad 0 < t \le T. $$

Thus the proof is completed.

4 Generalization

The results in Sect. 3 shall now be extended to the solution of linear diffusion equation with multiple fractional time derivatives:

and

where 0<α _ℓ<⋯<α ₂<α ₁<1 and q _j∈W ^2,∞(Ω), 2≤j≤ℓ.

As before the lower-order derivatives are regarded as source terms and we consider

$$ u(t) = S(t)a - \int^t_0 A^{-1}S'(t- \tau) \sum_{j=2}^{\ell} q_j \partial _t^{\alpha_j}u(\tau) d\tau, \quad 0 < t < T. $$

(4.1)

Similarly to Theorem 1, we can prove

Theorem 3

We assume thatu∈C((0,T];L ²(Ω)) satisfies (4.1) and

$$ 0 < \alpha_{\ell} < \cdots < \alpha_1, \quad \alpha_1 + \alpha_{\ell} > 1. $$

Then

$$ \bigl\Vert u(t)\bigr\Vert_{H^{2\gamma}(\varOmega )} \le Ct^{-\alpha_1\gamma}\Vert a\Vert_{L^2(\varOmega )}, \quad 0 < t \le T $$

for anyγ∈(0,1). Moreover there exists a mild solution to (4.1) in the space $C((0,T]; \mathcal{D}(A^{\gamma}))\cap C([0,T]; L^{2}(\varOmega ))$withγ∈(0,1).