Keywords

1 Introduction

This paper intends to take a historical journey and visit seemingly landmark events in the development of a certain part of the Path Curvature Theory till the recent past. The targeted audience is mainly the entry level students of any course in Planar Linkages and members of multi-disciplinary groups. Only the events having direct implications for the development of linkages tracing straight line or an arc of a circle are described. The scientific approach to devise a mechanism for tracing longer approximate straight line path was developed almost hundred and fifty years ago. Unfortunately, these methods are forgotten. While executing these steps in the understood sequence, related historical achievements are highlighted to complete the historical saga in this scientific-historical write up.

In 1784 James Watt (1736–1819) invented revolutionary straight-line linkage, generating the crossing pair of straight-line paths. Whatever ensued after this in the domain of linkages for next hundred years is elaborated in depth in [1]. The author has quoted Roberts Willis (1800–1875) with observation- “At present questions of this kind can only be solved by that species of intuition which long familiarity with a subject usually confers upon experienced persons, but which they are totally unable to communicate to others.” Willis was a staunch believer in the systematic and mathematical approach for devising a mechanism to meet the targeted results.

The desire to develop the intuition for identifying coupler points which can individually trace straight line paths or circular arc is implicit in the efforts even before initiation of Industry 1.0 era (c.a. 1784). In the present Industry 4.0 times the problem persists. An apt observation is- “It is interesting to note that the subject has never completely disappeared from the research horizon and indeed, has often bounced back with greater vigor. One reason for this is ….. Intellectual stimulation the study of the subject brings” [2]. Revisiting this long history may reveal some unnoticed gem of concept which is likely to simplify and enrich nascent data-driven approach to synthesis of linkages [3]. Secondly, 5 Axis Vertical Machining Centers are fairly common for generating complex contours by breaking down every pass of the cutter along a complex curve. It is observed that the part programming codes generated with approximate solutions using Taylor-series expansions may be the cause of persisting deviations like tessellation in smooth continuous surfaces [4]. It will be worthwhile to understand the historical development of the path curvature concepts for betterment of controlling strategies like constant feed rates along complex paths.

2 Historical Explorations of Path Curvature

While describing historical mechanisms for drawing the conic curves [5], use of such devices right in the fourth century BC is mentioned. Later on straight edge ruler and a compass were considered ‘divine’. Against a circle, conic curves fascinated geometers of the time for their variable degree of departure from the straight-line form. Gradually ‘kinematic’ curves like cycloid and spirals, traced by a moving tracer appeared on scene.

Analysis of large number of planar curves was to engross mathematicians and geometers for more than two centuries. Related traits of planar curves like Quadrature (area under the curve) and Rectification (measuring perimeter) were to pose challenges right through end of seventeenth century.

A general 2D curve, like in Fig. 1 (L), must have been the source of inspiration for the geometers and mathematicians for quantifying the curvature i.e. degree of departure from the straight path. The tangent drawn at the point where the curvature is to be measured was the most widely used visual aid at that time. At point A, the curvature is higher (as compared to at point B) but the radius is small than that at B. Thus curvature and the radius are inversely related to each other. During the first half of the seventeenth century drawing the tangents to the multitude of the known curves, conic or kinematic, was the challenge for many geometers like Descartes (1596–1650), Fermat (1607–1665), Roberval (1602–1675), Torricelli (1608–1647) etc. [6].

Fig. 1.
figure 1

Visual expression of curvature with tangent and osculating (kissing) circles [7].

Full size image

A general shape curve and its’ varying curvature is shown in Fig. 1 (R). The three circles highlight the degree of departure from the circle which is just ‘kissing’ the curve at the point of tangency. To plot individual osculating circle, three points on the curve with infinitesimal separation, are selected and the circle passing through them is the desired osculating circle. Center of this circle and the radius, from the center to the point under consideration, were of great interest for the mathematicians and geometers of eighteenth and nineteenth centuries. These quantities describe the local curvature of any curve at the point of interest.

In the last decade of seventeenth century, the competition between giants like Newton (1643–1727), Leibniz (1646–1716) and Bernoulli brothers (Jacob and Johann) to solve such problems by use of Differential Geometry was really stiff. Johann Bernoulli (1667–1748) is credited with coining of the term ‘Osculating Circle’ [8]. The term is retained till today.

In Fig. 1(R) it is apparent- Radius of the osculating circle is the local Radius of Curvature of the curve and the curvature is inversely related to it. During second half of the seventeenth century, many great minds were involved in an analysis of curves like cycloids, epicycloids etc. Koetsier has stated that Jacob Bernoulli (1654–1705) published a result on the quantification of curvature of the epicycloids in 1692. Similarly in 1696, G. F. A. Marquis de L’Hopital (1661–1704), a French Mathematician, published work on the curvature of epicycloids, which was to be developed into the most widely used concept for the theory of path curvature, few decades later [9].

In 1583 a young Galileo Galilei (1564–1642) made the observation of constancy of the time period of a swinging pendulum and introduced the concept of time measurement for the specified displacement. Almost one hundred years later, first edition of Principia was published (1687). Acceleration as the second time derivative of displacement gained prime importance in analysis of motion after that. The concept of shortest time elapsed during fall in vertical plane along multiple paths was first proposed by Galileo (Tautochrone). In 1696, Johann Bernoulli proposed the problem of Brachistochrone, and proved it in 1697 using the cycloidal path of descent [10]. Comparison of multiple paths for identification of the fastest option surely calls for understanding of ‘time’ as a parameter.

After Newton’s successful explanation of the elliptical orbits of the planets with Sun at the focus, acceleration as a central cause of continuously varying motion was to become a major contributor for the second school of thought. Analysis of variable speed and acceleration along multitude of known curves gave kinematicians a deeper insight in analyzing coupler point motions. The concept of ‘instantaneous’ values for continuously varying parameters appeared on the scene and terms like e.g. instantaneous center of rotation enhanced understanding of various motions in planar mechanisms.

Two components of acceleration- along path tangent and along path normal became dependable tools for identification of special paths in continuous curves. When component along the normal was absent it resulted into straight line motion and when the component along the tangent was absent it resulted in path along circular arc. Historically path as a geometric consideration preceded the kinematic analysis by few years to few decades.

3 Linkages, Couplers and Coupler Curves

The straight line arrangement of 1784 was revolutionary because it was for the first time motion of an intermediate point on the floating link was being tapped to transform angular oscillatory motion of the input link. This created unlimited options of motion transformation with a single coupler (or connecting rod) four bar chain or kinematic chains with multiple couplers.

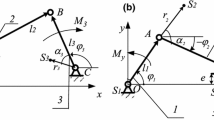
Figure 2 shows a four bar linkage. The crank (O1-A12) and follower/rocker/output link (O2-B12) are pin jointed to the coupler A12-B12. Both the ends of the coupler, A12 and B12, are constrained to move along circular paths. But points on the coupler move along a large variety of paths. To highlight the vast variety of shapes, expanse of the link A12-B12 is expanded and the literature refers to it as the ‘moving plane’. The loci of these points traced in the fixed link plane are called Couple Curves. Historically the first curve to get maximum popularity was traced by the midpoint of the coupler link of Watts’ parallel linkage.

In 1796 Gaspard F. Prony (1755–1839) analyzed Watt’s straight line coupler curve for improvements [11]. Real work on analysis of coupler curves was to gain importance after 1875 [12]. Around same time, Samuel Roberts (1827–1913) could derive the sixth degree algebraic equation to describe the planar coupler curves. Till the end of nineteenth century, the dream of inventing mechanisms to generate exact paths had taken a backseat and applications of the mechanisms with approximate paths matching broadly with the targeted path gained popularity [12]. Nolle has described such applications, straight line or along curves, in details.

In 1875 Samuel Roberts discovered a very special feature of four bar coupler curves- Three different four bar linkages will trace the same coupler curve. In 1878, P. Chebyshev (1821–1894) had independently discovered the same special trait of four bar linkage curves. These linkages were called cognates and this discovery is called Roberts-Chebyshev theorem in the literature. This discovery gives options to the designer working for a particular coupler curve at the application point.

Fig. 2.
figure 2

Variety of coupler curve shapes traced by coupler points of the moving plane

Full size image

The next landmark in design by coupler curve was publication of the Atlas (Analysis of the Four Bar Linkage: It’s Application to Synthesis of Mechanisms) by J. A. Hrones and G. L. Nelson in 1951. With more than 7,300 crank rocker coupler curves designer is likely to complete the selection of suitable crank rocker with minimum compromise.

The concept of thematic atlas of a family of coupler curves was applied to other types of mechanisms like five bar geared mechanisms. The information derived from an atlas is always with some granularity. Many times the best possible solution may be lost between two closely related options available in the atlas. By the beginning of the twentieth century mathematicians had lost the interest in coupler curve analysis. Application Engineers continued using the Atlas for designing of arrangements for numerous application using coupler curves with straight line, circular arc, cusps, symmetry etc.

4 Path Curvature and Euler-Savary Equation

In Fig. 1, the right side curve is shown with three distinct osculating circles. This indicates the varying local radii of path at three locations on the curve. When only geometric parameters of the path segment are considered, then three directed quantities (distances) along the path normal become important parameters for further analysis. These quantities and their inter relationship is discussed in detail in next section.

Koetsier has stated that the earliest precursor for this widely used mathematical relation for analysis of the path curvature is due to Jacob Bernoulli’s (1654–1705) work in 1692 [9]. This is in relation to his work on curvature of epicycloids. The second work on curvature of epicycloids by L’Hospital published in 1696 is better recorded in related history literature.

The next contribution to this important relation is from Leonhard Euler (1707–1783). While working on gear profiles, in 1765, he made some important observations and contributed them to the Academy of Sciences in St. Petersburg [9].

The second contributor, Felix Savary (1797–1841) was working on gear profiles during eighteen thirties. The most widely used relation to locate the center of curvature and the radius of curvature appeared in the present day format after Savary had demonstrated it in multiple situations.

The common form of Euler-Savary equation is given in (1) and it is shown in Fig. 3. The point P12 is the instantaneous center of rotation for the link A12-B12 (the coupler). This point is also the velocity pole. The line originating at P12 and passing through A12 and O1 is called a Pole Ray. This relationship helps in locating point JA on the pole ray. This point of the Pole Ray is the coupler point in the moving plane, whose path at this instant is passing through inflection stage. This is described in the next section. Equation (2) is for locating point JB and Fig. 3 shows its’ location.

$$\frac{1}{{PJ}_{A}}= \frac{1}{PA}-\frac{1}{PO1}$$
(1)
$$\frac{1}{{PJ}_{B}}= \frac{1}{PB}-\frac{1}{PO2}$$
(2)

This expression comes handy when the straight line or circular arc portion of the coupler curves are to be analyzed. The historical aspect of these two paths will be covered in next three sections of this paper.

Fig. 3.
figure 3

Inflection Circle and approximate straight path in the couple curve.

Full size image

5 Special Coupler Curves-I: Straight Line Linkages

Synthesis of approximate straight line linkage by selection of suitable coupler curve does not arrive at a straight forward solution. To appreciate the effort required to accomplish synthesis of even one single linkage, the effort put in by Pafnuty Chebyshev (1821–1894) is worth appreciating. Quoting Ferguson verbatim to highlight the persistence required to create one such special linkage-“In 1853, after visiting France and England and observing carefully the progress of applied mechanics in those countries, he read his first paper on approximate straight-line linkages, and over the next 30 years he attacked the problem with new vigor at least a dozen times” [1]. This indicates why number of named approximate straight line mechanisms is limited and for the exact straight line mechanisms, the number is miniscule.

Fig. 4.
figure 4

Change in the direction of gradient (slope) leads to fairly straight line path

Full size image

Figure 4 shows two general curves. On the left is an open curve and on right is the closed curve which is closer to the coupler curve of any planar mechanism. The point marked on the open curve indicates change in the direction of the slope from concave to convex. This point is called as Inflection point in the curve. The closed curve has more inflection points marked on it. As can be seen, the line drawn to indicate the slope is tangent to the curve. In fact such a line will be indicating presence of a certain straight line path in such curves.

5.1 de Lahire Inflection Circle

This property of curves, understood right at the end of seventeenth century, was put to some landmark observations. In 1706 Philippe de Lahire (1640–1718) published his discovery of the location of the points of the moving plane (coupler Plane) whose paths are undergoing inflection. He has successfully proved this unique property of the moving plane points –“all such points of the moving plane whose paths are undergoing inflection, lie on a circle in the moving plane”. This circle was called the Inflection Circle. This circle shaped locus of coupler points have this trait only at that particular instant of the continued motion. Minor angular displacement of the crank defines a complete new set (i.e. new Inflection Circle) of such points in the moving plane. Thus, in a way, the set of potential coupler points which can trace some approximate straight line path in their coupler curves was reported much before the Watt’s parallel motion linkage was conceived. The recorded history of synthesis of straight line crank rocker does not indicate use of this concept for developing the straight line four bar chains. Since early nineteen fifties, use of Inflection Circle to demonstrate applicability of Euler-Savary equation of path curvature became a common topic in most of the books. The Inflection Circle passing through JA12, JB12 and P12 in Fig. 3 is kind similar explanation. But eighties onwards this has received less attention in published text and overall it is labeled as too theoretical [13, 14].

As shown in Fig. 3, the random coupler points C1-C3 of Fig. 2 lie on the Inflection Circle when the crank O1-A7 is in the given position. Readers can refer [11] for the required steps to use the Euler-Savary equation and plot the Inflection Circle. Interested readers can get the related information about identification of certain Inflection Circle parameters and the identified straight line path from [15].

Fig. 5.
figure 5

Philippe de Lahire (1640–1718) and Jacques Antoine Ch. Bresse (1822–1883)

Full size image

5.2 Bresse Circles

In 1853 Bresse (Fig. 5), then a Lecturer of Mechanical Engineering at Ecole Polytechnic, Paris, analyzed kinematics of coupler points in the moving plane of planar linkages. He was aware of the Euler-Savary equation and the difficulties involved in using it for quantification of the curvature [17]. Following the alternate path and analyzing the acceleration components along the tangent and along the path normal, he identified two loci of special coupler points. One in which the coupler points had only tangential acceleration component was identical with de LaHire Inflection Circle and second one in which the coupler points had only normal component of acceleration is the Normal Circle or Stationary Circle. Both these circles intersect at two points. One of them is a very important point is called as Acceleration Pole. This important contribution to Kinematics also confirmed de Lahires’ discovery of the Inflection Circle.

6 Special Coupler Curves-II: Circular Arc Linkages

In [12] Nolle has collected applications of straight line, circular arc, conic section and special arc coupler curve generating mechanisms. Mathematicians of the nineteenth century were fascinated by this kind of curvilinear motions, but these were really implemented in the applications of the twentieth century. This detailed survey has listed seven straight line applications and only two circular arcs for dwell. In [16], under the title “3.4.8 Examples of Mechanism Design and Analysis Based on Path Curvature”, five different motions along arc of circle are included. As informed in [5], the history of mechanisms to trace the conic curves is much older. In [12] the mere mention of coupler curves with conic sections without any specific application indicates the limited and highly specialized application of these curves. Many of the referred books, published during 1950 to1980, devote more space for straight line mechanisms against other types. In [18] circular arc linkages developed by Chebyshev are included and in [12] a 1934 contribution of Meyer Zur Capellen for analysis of geometric conditions of linkages to have circular arc coupler curves which can have six matching points with real circle.

Unlike the Inflection Circle, role and history of the instantaneous ‘Circling Point Curve’ is less clear. Kurt Hain has credited development of this locus of circular arc tracing coupler points to Reinhold Müller [19]. Müllers’ major publications are dated 1892 to 1897. Coupler curves traced by any point on this Circling Point Curve has a constant rate (equal to zero hence ‘stationary’) of change of the radius of curvature with displacement along the traced coupler curve. This results into a fairly accurate arc of the circle for considerable displacement of the crank.

In [11] it is mentioned that somewhere in 1951 Professor A. S. Hall has re-named the loci of coupler points tracing the coupler curves with circular arcs (i.e. circling point curve) as the ‘Cubic of Stationary Curvature’. In [16], out of five applications of motion along circular path, two motions mention it to be along the Cubic of stationary Curvature.

In Fig. 6, the selected coupler points, C1, C4 and C5 lie on the Circling Point curve or on the Cubic of Stationary Curvature. The locus of such arc tracing coupler points is a third degree equation and is explained in limited number of books, including the detailed discussion and its’ application as given in [11].

Whatever is the significance of the instantaneous Inflection Circle for tracing the approximate straight line path, the Cubic of Stationary Curvature is for tracing coupler curves with circular arcs. However the common factor for both these loci of special coupler points is the use of Euler-Savary equation of the path curvature theory. The vector forms of these relations and of Euler-Savary equation are given in [20].

Fig. 6.
figure 6

Cubic of stationary curvature and combined use of both the concepts to plot Ball’s point

Full size image

Historically the information about pinning the credit for development of the Cubic Curve seems to be more scattered and crediting it to an individual or to a group of individuals seems to be difficult. Search for relevant literature continues.

7 Special Coupler Curves-III: Longer Straight Line Linkages

In Fig. 3, longer approximate straight line path of coupler point C1 is demonstrated. Figure 6 explains the special status of this coupler point at the shown instant. The point C1 is simultaneously on both the special loci of coupler points- the Inflection Circle and the Cubic of Stationary Curvature. By virtue of one locus the traced path has almost zero curvature (or infinite radius) and by the virtue of being in the second locus this zero curvature persists (i.e. is stationary) for a considerable travel of the crank (Fig. 7).

Fig. 7.
figure 7

Sir Robert Stawell Ball (1840–1913)

Full size image

The implications of such a special location of this point (C1) is reflected in its’ coupler curve (Fig. 3 and Fig. 6). This was discovered by the British astronomer Sir Robert Stawell Ball (1840–1913). This concept has been extensively used by Dijksman and the year of publishing of this important discovery by Ball is 1871 [21]. When studied in more depth the alternate name of Undulation Point can be understood. And the recent related literatures like [22] credit it to him by labeling the point as Ball’s point.

8 Conclusion and Discussion

To sum up this Historical-Scientific-Graphical report about evolution of the Path Curvature Theory, few words suffice- Intellectually Stimulating. Geometrical and kinematic considerations for transforming the rotational or oscillatory motion of the input link has engrossed the mathematicians and tinkering technicians for considerable time period. Understanding the contribution of various scholars like de Lahire, Bresse, Muller, Sir R. Ball and other indirect contributors of various time periods, is awe inspiring. The diminishing coverage to these valuable aspects in academics for last few decades is surely a cause of concern. Available resources when these concepts were proposed imposed a great limitation to explore them further. Diameter of the Inflection Circle many times is far more than the limiting size drawing board available. Purely analytical treatment does not excite the reader to same level as graphical representation does.

Like in majority of the domains, work for a data-driven approach for synthesis of linkages has started in earnest. Revisiting evolutionary stages of the domain bolsters the understanding and gives a valuable insight to create a rich background for creating a compact and effective data for the success of numerical methods of modeling. In the present Industry 4.0 paradigm, creating a robust smart system with an efficient background processing system is anticipated.

Revisiting these developmental stages of every concept of the path curvature theory is expected to throw light on their hitherto unexplored aspects. This is anticipated due to a sudden increase in the digital graphics and ability to convert such intricate situations for data-driven decision making. This upsurge in the available facilities coincides with phase of rapidly diminishing interest of the fraternity in such aspects of the path curvature theory. This report rekindles the interest of researchers in these valuable concepts to address the need of easy to follow and effective methodology to complete synthesis of special purpose linkages.