Semi-total Domination in Unit Disk Graphs

Abstract

Let $G=(V, E)$ be a simple undirected graph with no isolated vertex. A set $D\subseteq V$ is a dominating set if each vertex $u\in V$ is either in D or is adjacent to a vertex $v\in D$. A set $D_{t2}\subseteq V$ is said to be a semi-total dominating set if (i) $D_{t2}$ is a dominating set, and (ii) for every vertex $u\in D_{t2}$, there exists a vertex $v\in D_{t2}$ such that the distance between u and v in G is within 2. Given a graph G, the semi-total domination problem is to find a semi-total dominating set of minimum cardinality. The semi-total domination problem is NP-complete for general graphs. It is also NP-complete on some special graph classes, such as planar, split, and chordal bipartite graphs. In this paper, we have shown that it is NP-complete for unit disk graphs. We propose a 6-factor approximation algorithm for the semi-total dominating set problem in unit disk graphs. The algorithm’s running time is O(nk), where n and k are the number of vertices and the size of the maximal independent set of the given UDG, respectively. In addition, we show that the minimum semi-total domination problem in a graph with maximum degree $\mathbb {D}$ admits a $2+\ln {(\mathbb {D}+1)}$-factor approximation algorithm which is an improvement over the best-known result $2+3\ln {(\mathbb {D}+1)}$.

1 Introduction

Let $G=(V,E)$ be a simple undirected graph that may contain multiple components. However, no component in the graph is an isolated vertex. A set $N_G(v)$ denotes the open neighborhood of v in G, and it is defined as $N_G(v)=\{u\in V:uv\in E\}$. On the other hand, the closed neighborhood $N_G[v]$ of v is defined as $N_G[v]=N_G(v)\cup \{v\}$. For any subset $S\subseteq V$, G[S] represents the subgraph induced by the vertex set S in G (i.e., for each $u,v\in S$, $uv\in E(G[S])$ if and only if $uv\in E$).¹ Given two vertices u and v, the distance d(u, v) between u and v is the minimum number of edges that connect u with v in G. A subset $D \subseteq V$ is said to be a dominating set (DS) of G if for each vertex $v\in V$, $|N_G[v]\cap D|\ge 1$. The dominating set with minimum cardinality is called the minimum dominating set, and the size of the minimum dominating set is called the domination number, $\gamma (G)$. A vertex $v\in V$ dominates $N_G[v]$, and a subset $S \subseteq V$ dominates $\bigcup _{v \in S}N_G[v]$. A subset $D_t\subseteq V(G)$ is said to be a total dominating set (TDS) of G if $D_t$ is a dominating set of G, and the vertices in $D_t$ induce a subgraph with no isolated vertex. The total dominating set with minimum cardinality is called the minimum total dominating set, and the size of the minimum total dominating set is called the total domination number, $\gamma _t(G)$. A subset $D_{t2}\subseteq V$ is said to be a semi-total dominating set of G if (i) $D_{t2}$ is a dominating set (domination property), and (ii) for each $u\in D_{t2}$, there exists a vertex $v\in D_{t2}$ such that $d(u,v)\le 2$ (semi-total property). The semi-total dominating set with minimum cardinality is called a minimum semi-total dominating set, and the corresponding cardinality is the semi-total domination number. We denote the semi-total domination number as $\gamma _{t2}(G)$. Given a graph G, the objective of the semi-total dominating set problem is to find a minimum semi-total dominating set.

1.1 Related Work

In computational complexity theory, the dominating set problem is a classical NP-complete problem [6]. Along with the domination problem, its variants are also generally hard in general graphs. So, researchers started exploring the behavior of the domination problem and its variants in different sub-classes of general graphs. The literature on domination and its variants can be found in [7,8,9,10, 13, 18]. In this paper, we focus on semi-total dominating set. The Semi-total dominating set was introduced by W. Goddard et al. [16] in 2015. Since every semi-total dominating set is a dominating set and every total dominating set is a semi-total dominating set, the semi-total domination number is squeezed between the domination number and the total domination number, i.e., for a given graph G, $\gamma (G)\le \gamma _{t2}(G)\le \gamma _t(G)$. In [16], authors showed that if G is a connected graph with n (${\ge }4$) vertices, then $\gamma _{t2}\le \frac{n}{2}$. In the same paper, authors also showed that if G is a graph with n vertices and maximum degree $\mathbb {D}$, then $\gamma _{t2}\ge \frac{2n}{2\mathbb {D}+1}$. Subsequently, Henning and Marcon [13] showed that for a connected graph with at least 2 vertices, $\gamma _{t2}(G)\le \alpha '(G)+1$, where $\alpha '(G)$ is the matching number.² In [1], Asplund et al. studied the semi-total domination in cartesian product graphs and established that for any two graphs G and H, $\gamma _{t2}(G\square H)\ge \frac{1}{3}\gamma _{t2}(G)\gamma _{t2}(H)$. In [4], authors showed that it is NP-complete to recognize the graphs that satisfy $\gamma _{t2}(G)=\gamma _t(G)$ and $\gamma (G)=\gamma _{t2}(G)$. In [11], authors showed that for every connected claw-free cubic graph G of order n, $\gamma _{t2}\le \frac{n}{3}$. In [12], authors showed that the semi-total domination problem remains NP-complete in planar graphs, chordal bipartite graphs and split graphs. They also gave a $2+3\ln {(\mathbb {D}+1)}$-factor approximation algorithm for the minimum semi-total domination problem, where $\mathbb {D}$ is the maximum degree of G.

1.2 Our Contribution

The remaining part of this paper is organized as follows. In Sect. 2, we introduce the required preliminaries and notations. In Sect. 3, we prove that the semi-total dominating set problem is NP-complete in unit disk graphs. Next, in Sect. 4, we propose an O(nk) time 6-factor approximation algorithm for the semi-total domination problem for unit disk graphs. In this section, we also propose a $2+\ln {(\mathbb {D}+1)}$-factor approximation algorithm for the semi-total domination problem for general graphs. Finally, we conclude the paper in Sect. 5.

2 Preliminaries

In this section, we will introduce the required notations and definitions. Let $P=\{p_1,p_2,\dots ,p_n\}$ be a set of n points in $\mathbb {R}^2$. A graph $G=(V,E)$ is said to be a geometric UDG corresponding to the point set P if there exists a one-to-one correspondence between each $v_i\in V$ with $p_i\in P$ and $v_iv_j\in E$ if and only if $\delta (p_i,p_j)\le 1$, where $\delta (.,.)$ is the Euclidean distance between two points in $\mathbb {R}^2$. Let $\varDelta (p)$ denote the unit disk centered at the point $p\in P$ and $\varDelta (P)=\{\varDelta (p): p\in P\}$. The set of disks $\varDelta (P)$ is considered independent if for every pair $p,q\in P$, $p\notin \varDelta (q)$, i.e., $\delta (p,q)>1$. This article often refers to a point as a vertex or node. Given a positive integer i and a vertex u, $N_G^i[u]$ represents the set of all the vertices within distance i from u in G. We often refer to $N_G^1[.]$ as $N_G[.]$.

Next, we list some of the already proven lemmas, theorems, and observations useful in Sect. 3, and Sect. 4.

Lemma 1

[19]. Let $G=(V,E)$ be a planar graph of degree at most 3. The graph G can be embedded in a grid of area $O(|V|^2)$ such that each $v\in V$ lies in a grid point with co-ordinate (5i, 5j), where i and j are integers and each edge $e\in E$ is a finite sequence of consecutive segments of length 5 units along the grid lines.

Lemma 2

[15]. Let $\mathcal {P}$ be a unit disk centered at point p and let S be a set of independent unit disks such that each disk in S contains the point p, then $|S|\le 5$.

Lemma 3

[3]. Given a UDG G, there exists a $\frac{44}{9}$-approximation algorithm for the minimum dominating set problem with running time $O(n^2)$.

Observation 1

[5]. For a given graph G, $\gamma (G)\le \gamma _{t2}(G)$.

3 NP-Completeness

In this section, we focus on the hardness result of the semi-total domination problem and prove that the decision version of the problem is NP-complete in unit disk graphs. We use a reduction from the decision version of the vertex cover (VC) problem in planer graphs of degree at most 3 to the decision version of the semi-total dominating set problem in UDGs. The corresponding decision problems are formally defined as follows:

• The decision version of the VC problem in planar graphs of degree at most 3 (D-VC-PGD3): Given a positive integer k and a planar graph G of degree at most 3, does G has a VC of size at most k?

• The decision version of semi-total dominating set problem in UDGs (D-T2DS-UDGs): Given a positive integer k and a UDG G, does G has a semi-total dominating set of size at most k?

Lichtenstein and David [14] reduced the planar 3SAT problem to the planar vertex cover problem and proved that D-VC-PGD3 is NP-complete. We prove the hardness result of the semi-total dominating set problem in UDGs by making a polynomial time reduction from an arbitrary instance of D-VC-PGD3 to an instance of D-T2DS-UDGs. To prove this, we embed a planar graph $G=(V,E)$ of degree at most 3 in a grid of cell size $5\times 5$ using Lemma 1.

Lemma 4

If $G=(V,E)$ is an instance of D-VC-PGD3 without any isolated vertex, then an instance $G'=(V',E')$ of D-T2DS-UDG can be constructed from G in polynomial time.

Proof

Let $V=\{v_1,v_2,\dots ,v_n\}$ and $E=\{e_1,e_2,\dots ,e_m\}$ be the vertex set and edge set of the given instance G. We construct a graph $G'=(V',E')$ from G by the four steps as given below:

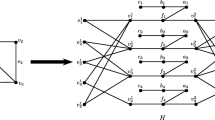
• Step 1 (Embedding): We first embed the graph G on a grid of cell size $5\times 5$ using the algorithm proposed by Biedl et al. in [2]. In this embedding, each edge $e\in E$ is a consecutive sequence of line segment(s) in the grid, where the length of each segment is 5 unit. Let $\ell$ be the total number of line segments used in the embedding. For each vertex $v\in V$, a node point located at a grid having coordinate (5i, 5j) for some integers i and j. Let $p_i$ be the node point at the grid corresponding to vertex $v_i\in V$ for $1\le i\le n$. Let the set of node points be N, i.e., $|N|=|V|=n$. Refer to Fig. 1(a) and (b) for an illustration of the embedding step.

• Step 2 (Inclusion of auxiliary points): In this step, we add some auxiliary points on each segment of the graph after the embedding step as mentioned below: (i) for each $p_ip_j$ corresponding to the edge $v_iv_j\in E$, if the number of segments in $p_ip_j$ is one (length of $p_ip_j$ is exactly 5 unit), then add six points at distances 1, 1.3, 2.1, 2.6, 3.2 and 4 either from $p_i$ or $p_j$ as depicted in Fig. 2(a), (ii) if the number of segments is more than one (length of $p_ip_j$ is greater than 5 unit), then we add a point on each grid point along the line except the node points. We refer to those points as grid points (see the filled square points in Fig. 2). If both the endpoints of any segment are grid points, then add four points on the segment at distances 1, 2, 3, 4 from any of the endpoints of the segment (see Fig. 2(b)); otherwise, add five points at distances 1, 1.9, 2.5, 3 and 4 from node point $p_i$ (Fig. 2(c)). Let A be the set representing the auxiliary points added in this step.

• Step 3 (Inclusion of gadgets): Since each node in the planar graph has degree at most 3 and is embedded within a grid, at least one position at each node point exists to accommodate an extra edge. In this step, we add a gadget as shown in Fig. 2(d) at each node point $p_i$. The gadget at $p_i$ contains 4 points, namely $x_i$, $x'_i$, $y_i$ and $y'_i$. Here, the distances between $p_i$ and $x_i$, $x_i$ and $x'_i$, $x_i$ and $y_i$, $y_i$ and $y'_i$ are 0.9, 0.5, 0.9 and 0.5, respectively. Let S be the number of points added in this step. Since each gadget contains 4 points, therefore, $|S|=4|N|=4n$.

• Step 4 (Construction of UDG): Let $G'=(V',E')$ be the UDG constructed after applying the above 3 steps on graph G, where $V'=N\cup A\cup S$ and $E'=\{uv: u,v\in V' \text { and } \delta (u,v)\le 1\}$.

From Lemma 1, we conclude that the number of segments $\ell =O(n^2)$. Therefore, the upper bound on the number of vertices and the number of edges in $G'$ is $O(n^2)$. Hence, $G'$ can be constructed from G in polynomial time. For the complete illustration of the construction phases, refer to Fig. 1 and Fig. 2.    $\square$

Fig. 1.

(a) A planar graph G, and (b) Embedding of G in a grid

Fig. 2.

(a) Orientation of six points, (b) Orientation of five points, (c) Orientation of four points, (d) Gadget, and (e) Graph $G'$

Fig. 3.

(a) Vertex cover of G, and (b) Semi-total dominating set of $G'$

Theorem 1

D-T2DS-UDGs belongs to the class NP-complete.

Proof

Let $G=(V,E)$ be a unit disk graph. Given a subset $S\subseteq V$ and a positive integer k, we can verify whether S is a semi-total dominating set of G of size at most k or not in polynomial time. Therefore, $D{\text {-}}T2DS{\text {-}}UDGs\in NP$.

To prove $D{\text {-}}T2DS{\text {-}}UDGs$ is NP-hard, we will do a polynomial time reduction from D-VC-PGD3 to D-T2DS-UDGs. Here, we use Lemma 4 to construct an instance $G'=(V',E')$ of D-T2DS-UDGs from an arbitrary instance $G=(V,E)$ of D-VC-PGD3 in polynomial time. Next, we prove the following claim to complete the hardness result of D-T2DS-UDGs.

Claim: G has a vertex cover $S_{vc}$ such that $|S_{vc}|\le k$ if and only if $G'$ has a semi-total dominating set $D_{t2}$ such that $|D_{t2}|\le k+2\ell +2n$.

$(\Longrightarrow )$ Let $S_{vc}$ be a vertex cover of G such that $|S_{vc}|\le k$ and $T_{vc}$ be the set of vertices in $G'$ corresponding to the vertices in $S_{vc}$, i.e., $T_{vc}=\{p_i\in V':v_i\in S_{vc}\}$. Now, we construct two sets $T_a\subseteq A$ and $T_g\subseteq S$ such that $D_{t2}=T_{vc}\cup T_a\cup T_g$ is a semi-total dominating set with cardinality less than or equal to $k+2\ell +2n$. The construction of $T_a$ and $T_g$ are as follows. Since $S_{vc}$ is a vertex cover of G, at least one endpoint of every edge in G is inside $S_{vc}$. Since every edge in G corresponds to a sequence of segments in $G'$, we start from the endpoint, which is inside $T_{vc}$. For each $p_ip_j$ in $G'$ corresponding to each $v_iv_j\in E$, at least one out of $p_i$ and $p_j$ is in $T_{vc}$. Without loss of generality, let $p_i\in T_{vc}$. We traverse from $p_i$ towards $p_j$. While traversing, we leave two vertices next to $p_i$, add a single vertex to $T_a$, and then leave the next vertex and select the next one for $T_a$; again, we leave two vertices. This way, we repeat the process till we reach $p_j$. For each $v_iv_j\in E$, we apply this process to the corresponding $p_ip_j$ in $G'$ and observe that exactly two points from each segment are in $T_a$. So $|T_a|=2\ell$, where $\ell$ is the number of segments in $G'$. In Fig. 3(b), the red cross points are in $T_a$. From each $p_i\in V'$, we choose $x_i$ and $y_i$ for $T_g$. So $|T_g|=2n$. In Fig. 3(b), the red disks are in $T_g$.

Now, we are left to show that the set $D_{t2}$ is a semi-total dominating set of $G'$. Since $x_i,y_i\in T_g\subseteq D_{t2}$ and dominate $p_i$, $x'_i$ and $y'_i$, and $d(x_i,y_i)= 1$ for all $i=\{1,2,\dots ,n\}$, and for each $p_i\in T_{vc}$, there exists a vertex $x_i\in T_g$ such that $d(p_i,x_i)=1$. Hence, the sets $T_{vc}$ and $T_g$ satisfy the semi-total domination. There are three types of segments in $G'$. The types of segments are as follows: (i) segments with two endpoints as node points as depicted in Fig. 2(a), (ii) segments with one endpoint as a node point and another as a grid point as depicted in Fig. 2(b), and (iii) segments with two endpoints as grid points as depicted in Fig. 2(c). We have to show that each segment from each segment type requires at least two points in $D_{t2}$ for semi-total domination.

(i) Segments with two endpoints as node points: Since $S_{vc}$ is a vertex cover of G, at least one out of $v_i$ and $v_j$ is in $S_{vc}$, where $v_iv_j\in E$. Therefore, at least one out of $p_i$ and $p_j$ is in $T_{vc}$. Without loss of generality, let $p_i\in T_{vc}$ (pick any one if both $p_i,p_j\in T_{vc}$). The way graph $G'$ is constructed, there are 6 points on this type of segment excluding the two node points (i.e., $p_i$ and $p_j$). Let us refer to each point on the segment as $z_t$, where $1\le t\le 6$ and t is the position of the point from $p_i$. $p_i$ dominates $z_1$. The selection of $z_3$ and $z_5$ in $T_a$ ensure the domination of $z_2$, $z_4$ and $p_j$ and $d(z_3,z_5)\le 2$ ensures the semi-total property. For a complete illustration, refer to $p_4p_6$ in Fig. 3(b).

(ii) Segments with one endpoint as a node point and another as a grid point: Let $p_i$ and $g_{ijt}$ be the node point and grid point, respectively, where the segment $p_ig_{ijt}$ is in $p_ip_j$, and t represents the position of the grid point from $p_i$. This type of segment contains 5 points. Let the points are $z_1$, $z_2$, ..., $z_5$. (a) If $p_i\in T_{vc}$, then the selection of $z_3$ and $z_5$ in $T_a$ ensures the domination of the segment. (b) If $p_i\notin T_{vc}$, then a point in the other segment connected to $g_{ijt}$ dominates $g_{ijt}$ (since $p_j\in T_{vc}$). Hence, the selection of $z_2$ and $z_4$ ensures the domination of the remaining points in the segment $p_ig_{ijt}$. In either case, the selected two points are within a distance of 2. Hence, it satisfies the semi-total property.

(iii) Segments with two endpoints as grid points: Let $g_{ijt}$ and $g_{ij(t+1)}$ be two grid points and $z_1$, $z_2$, $z_3$ and $z_4$ be the four points on the segment. If so, then at least one grid point is dominated by a point in the other segment connected either to $g_{ijt}$ or $g_{ij(t+1)}$ (since at least one out of $p_i$ or $p_j$ is in $T_{vc}$). Without loss of generality, if $p_i\in T_{vc}$, then the selection of $z_2$ and $z_4$ ensures domination of $z_1$, $z_2$, $z_3$, $z_4$ and $g_{ij(t+1)}$. Since the distance between $z_2$ and $z_4$ is 2, the selection satisfies the semi-total property for the segment.

From the above arguments, we conclude that $D_{t2}=T_{vc}\cup T_a\cup T_g$ is a semi-total dominating set of $G'$. Since $|T_{vc}|\le k$, $|T_a|=2l$ and $|T_g|=2n$, $|D_{t2}|\le k+2\ell +2n$.

$(\Longleftarrow )$ Let $D_{t2}$ be a semi-total dominating set of $G'$ such that $|D_{t2}|\le k+2\ell +2n$. Then, we will show that G has a vertex cover of size at most k. To prove this, we prove the following observations.

• (i) Out of four points in the gadget associated with each $p_i$ in $G'$, at least two points belong to $D_{t2}$.

• (ii) Each segment contributes at least two points to $D_{t2}$.

• (iii) If $p_i$ and $p_j$ in $G'$ corresponds to the end vertices of an edge $v_iv_j\in E$ and if none of them ($p_i$ and $p_j$) is in $D_{t2}$, then there exists one segment whose 3 vertices are in $D_{t2}$ from the segment(s) representing the edge $v_iv_j$, i.e., if there are $\ell '$ number of segments in $G'$ corresponding to the edge $v_iv_j\in E$ such that $p_i,p_j\notin D_{t2}$, then out of $5\ell '+1$ points (excluding $p_i$ and $p_j$) $2\ell '+1$ points are in $D_{t2}$.

• Observation (i): Correspond to each $p_i\in E'$, there are 4 points ($x_i$, $x'_i$, $y_i$ and $y'_i$) in the corresponding gadget. Since $x'_i$ and $y'_i$ are pendant vertices, the selection of any two vertices is sufficient for domination. However, for semi-total domination, it requires either the selection of ($x_i$, $y_i$), ($x_i$, $y'_i$), or ($x'_i$, $y_i$). Hence, in $G'$, $|S\cap D_{t2}|\ge 2n$.

• Observation (ii): Since there are four types of segments. Let us consider a segment, say $s_1$ with 4 points (excluding the endpoints), say $q_1$, $q_2$, $q_3$, and $q_4$. On the contrary, suppose only one vertex is in $D_{t2}$. If so, then just for domination, it requires at least two vertices (since only consecutive points are adjacent). This implies that the segments with more than four vertices on the segment require at least two points for domination. Hence, $|D_{t2}\cap A|\ge 2\ell$, where A and $\ell$ are the set of auxiliary points and the number of segments in $G'$, respectively.

• Observation (iii): Let $\ell '$ be the number of segments in $G'$ correspond to an edge $v_iv_j\in E$. Since only consecutive points are adjacent, two points can dominate at most 5 points in semi-total domination. So the minimum number of points required to dominate (semi-total) $5\ell '+1$ number of points on $\ell '$ segments is $\lceil \frac{5\ell '+1}{5}\rceil \times 2=2\ell '+1$.

Given a semi-total dominating set $D_{t2}$ of $G'$ of size at most $k+2\ell +2n$, we are left to show that by deleting and/or replacing some of the vertices from $D_{t2}$, we can obtain a vertex cover $S_{vc}$ of G of size at most k. Let define a set $S'_{vc}=D_{t2}\setminus S$, then $|S'_{vc}|\le k+2\ell$ (due to claim (i)). Then $S_{vc}=\{v_i\in V|p_i\in S'_{vc}\}$. For each edge $v_iv_j\in E$, if $v_i,v_j\notin S_{vc}$, then there exists a segment on $p_ip_j$ in $G'$, which has 3 points in $D_{t2}$ instead of 2 (refer to claim (ii) and (iii)). For each such edge, add $v_i$ (or $v_j$) to $S_{vc}$. Since every segment contributes at least 2 to $D_{t2}$ and there is $2\ell$ number of such points (refer to claim (ii)), $|S_{vc}|\le k$. Since every edge in G has at least one vertex in $S_{vc}$, $S_{vc}$ is a vertex cover of size at most k. This proves that $D{\text {-}}T2DS{\text {-}}UDGs\in NP{\text {-}}hard$.

Therefore, $D{\text {-}}T2DS{\text {-}}UDGs\in NP{\text {-}}complete$.    $\square$

4 Approximation Algorithms

In this section, we propose a 6-factor approximation algorithm for the semi-total domination problem in UDGs. We also propose a $2+\ln {(\mathbb {D}+1)}$-factor approximation algorithm for the semi-total domination problem for general graphs, where $\mathbb {D}$ is the maximum degree of the graph, which is an improvement over the approximation factor $2+3\ln {(\mathbb {D}+1)}$ given in [12].

4.1 Algorithm for Semi-total Domination in UDGs

Given a geometric unit disk graph $G=(V,E)$ with $V=\{p_1,p_2,\dots ,p_n\}\subseteq \mathbb {R}^2$ as the set of disk centers, Algorithm 1 finds a semi-total dominating set $D_{t2}$ of G. Now, we describe the procedure for finding the set $D_{t2}$. First, we find a maximal independent set $D\subseteq V$ of G to satisfy the domination property (see Lines 2–6 of Algorithm 1). Next, to satisfy the semi-total property, we choose a set of vertices $T\subseteq V$ such that for each $v\in D$, there exists a vertex $u\in D\cup T$ such that $d(u,v)\le 2$. To find such a set T, first, we find each point $u\in D$, which satisfies the semi-total property (see Lines 8–13 of Algorithm 1) and next, we segregate the points (set $\mathcal {U}$) that do not satisfy the semi-total property in D (see Line 14 of Algorithm 1) and then for each point $u\in \mathcal {U}$, we add a point $v\in N_G(u)$ into T (see Lines 15–18 of Algorithm 1). Finally, we report $D_{t2}=D\cup T$ as a semi-total dominating set of G. Lemma 5 and Lemma 6 represent the algorithm’s correctness and time complexity, respectively.

Lemma 5

The set $D_{t2}$ in Algorithm 1 is a semi-total dominating set of G.

Proof

In the first phase, we find a maximal independent set D of G to satisfy the domination property (see Lines 2–6 in Algorithm 1). Next, we segregate the points that do not satisfy the semi-total property in D. Note that, for each vertex $u\in V$, the algorithm finds $S_u=N_G(u)\cap D$. If $|S_u|>1$, then the vertices in $S_u$ satisfy the semi-total property, and hence the vertices in the set $X\subseteq D$ also satisfy the semi-total property (see Lines 8–13). Since $\mathcal {U}=D\setminus X$, the vertices in the set $\mathcal {U}$ do not satisfy the semi-total property, so we choose a one-distance neighbor $v\in V\setminus D$ for each such $u\in \mathcal {U}$ and T is the corresponding set (see Lines 15–18). Since the set T is the set of such one-distance neighbor of each point violating semi-total property in D, the inclusion of T in $D_{t2}$ along with D ensures that for each vertex $u\in D$, there exists another vertex $v\in D\cup T$ such that $d(u,v)\le 2$. Therefore, combinedly, the nominated points in D and T satisfy the domination and semi-total properties. Hence, the set $D_{t2}$ is a semi-total dominating set of G.

Lemma 6

Algorithm 1 runs in O(nk) time.

Proof

The complexity of Algorithm 1 is primarily dominated by the three for loops (see Lines 2–6, 8–13 and 15–18 of Algorithm 1). Let $V=\{p_1,p_2,\dots ,p_n\}$ be the set of disks’ centers corresponding to graph $G=(V,E)$. Let all the disks lie on a plane’s rectangular region $\mathbb {R}$. Let the rectangle’s extreme left and bottom arms represent the x- and y-axis, respectively. Then, we split the plane $\mathbb {R}$ so that the region $\mathbb {R}$ becomes a grid with cell size $1\times 1$. Let [x, y] be the index associated with each cell, where $x,y\in \mathbb {N} \cup \{0\}$. If a point $p\in V$ is located at co-ordinate $(p_x,p_y)$ on $\mathbb {R}$, then the point belongs to a cell with index $[\lfloor {p_x}\rfloor ,\lfloor {p_y}\rfloor ]$.

In the first for loop (see Lines 2–6), Algorithm 1 constructs a maximal independent dominating set D of the input graph G. To do so efficiently, each non-empty cell maintains a list that keeps the points of V chosen for inclusion in D located within that cell. While considering a point $p\in V$ as a candidate for the set D, it only probes into 9 cells surrounding the cell where p lies. That means if p is located at co-ordinate $(p_x,p_y)$, then it searches in each [i, j] cell, where $\lfloor {p_x}\rfloor - 1\leqslant i \leqslant \lfloor {p_x}\rfloor + 1$ and $\lfloor {p_y}\rfloor - 1\leqslant j \leqslant \lfloor {p_y}\rfloor + 1$.³ If there does not exist any point $q\in D$ in those 9 cells such that $p\in \varDelta (q)$, then p is included in D. A height balance binary tree containing non-empty cells is used to store the points that are in D. Since each cell of size $1\times 1$ can contain the centers of at most 3 independent unit disks (since placing the centers on the boundary maximizes the number of independent unit disks in a cell and one disk covers more than one edge in a cell), the processing time to decide whether a point is in D or not requires $O(\log {k})$ time, where $k=|D|$. Thus the time taken to process $|V|=n$ points is $O(n\log {k})$.

In the second for loop (Lines 8–13), Algorithm 1 finds a set $X\subseteq D$ in which each vertex satisfy the semi-total property. To find the set X, it finds $S_u=N_G(u)\cap D$ for each vertex $u\in V$. Now, if $|S_u|>1$, the vertices in $S_u$ satisfy the semi-total property; hence, these vertices collectively represent the set X. Thus, finding a set X requires O(nk) time.

Since each vertex u in $\mathcal {U}$ does not satisfy the semi-total property (i.e., $|S_u|\le 1$), we add a vertex $v\in N_G(u)$ to T (see Lines 15–18). Thus, in the worst case, the time to construct the set T is O(k).

Therefore, in worst case, Algorithm 1 executes in O(nk) time.    $\square$

Lemma 7

In Algorithm 1, $|T|\le |D^*|$, where $D^*$ is an optimal DS of G.

Proof

On contrary assume that $|T|>|D^*|$, i.e., $|\mathcal {U}|>|D^*|$. So, at least one vertex in $D^*$ dominates two or more vertices in $\mathcal {U}$, which leads to a contradiction that there is no vertex $v\in V$ that has more than one neighbor in $\mathcal {U}$.    $\square$

Analysis: The set $D_{t2}$ in Algorithm 1 is a semi-total dominating set of G, where $D_{t2}=D\cup T$ (see Lemma 5). Let $D^*$ and $D_{t2}^*$ be the optimal dominating set and optimal semi-total dominating set of G, respectively. Since D is a maximal independent set of G, from Lemma 2, we have $|D|\le 5|D^*|$. The set T in Algorithm 1 satisfies the semi-total property when added to the independent set D. Note that from Lemma 7, we have $|T|\le |D^*|$. Therefore, using Lemma 2, Lemma 5, Lemma 7 and Observation 1, we conclude the approximation factor of Algorithm 1 as follows:

$$\begin{aligned} |D_{t2}|=|D\cup T|\le |D|+|T|\le 5|D^*|+|D^*| \le 6\times |D^*| \le 6\times |D_{t2}^*| \end{aligned}$$

(1)

Theorem 2

The proposed algorithm (T2DS-UDG) gives a 6-factor approximation result for the semi-total domination problem in UDGs. The algorithm runs in O(nk) time, where n is the number of vertices in the given UDG and k is the size of the maximal independent set.

Proof

The approximation factor and the time complexity result follow from Eq. 1 and Lemma 6, respectively.    $\square$

Corollary 1

The semi-total domination problem achieves a $\frac{53}{9}$-factor approximation result in UDGs with running time $O(n^2)$, where n is the number of vertices in the given UDG.

Proof

From Lemma 3 and Lemma 7, we have $|D|\le \frac{44}{9}|D^*|$ and $|T|\le |D^*|$, respectively. Therefore,

$$\begin{aligned} \begin{aligned} |D_{t2}| & = |D\cup T|\le |D|+|T|\\ & \le \frac{44}{9}|D^*|+|D^*|=\frac{53}{9}|D^*|\\ & \le \frac{53}{9}|D_{t2}^*| \end{aligned} \end{aligned}$$

(2)

   $\square$

Note: In [12], the authors proposed a $2+3\ln {(\mathbb {D}+1)}$-factor approximation algorithm for the semi-total dominating set problem in general graphs. Here, the authors used two sets, namely D and T, to find the semi-total dominating set of the given graph G, where D is a DS and T is a set of vertices such that $D\cup T$ is a semi-total dominating set. The authors used the approximation algorithm for the minimum DS problem to find the set D and the approximation algorithm for the minimum set cover problem to find the set T. Since the approximation factors of the minimum DS and the minimum set cover problems are $1+\ln {(\mathbb {D}+1)}$ and $1+2\ln {\mathbb {D}}$, respectively, the approximation factor of the algorithm in [12] is $2+3\ln {(\mathbb {D}+1)}$. However, to have an improvement over the approximation factor, we can modify the algorithm in [12] by selecting the set T as in Algorithm 1 (the selection of the set T needs the set D to be a dominating set, not necessarily a maximal independent set). Then, by Lemma 7 and Observation 1, the approximation factor of the semi-total domination problem in general graphs is as follows:

$$\begin{aligned} \begin{aligned} |D_{t2}|&=|D\cup T|\le |D| + |T| \le (1+\ln {(\mathbb {D}+1)})|D^*| + |D^*|\\ &\le (2+\ln {(\mathbb {D}+1)})|D^*| \le (2+\ln {(\mathbb {D}+1)}) |D_{t2}^*| \end{aligned} \end{aligned}$$

(3)

Note: Since there exists a polynomial-time approximation scheme (PTAS) for the domination problem in UDGs with approximation factor $(1+\epsilon )$ and time $n^{O(\frac{1}{\epsilon }\frac{1}{\log {\epsilon }})}$, for any $\epsilon >0$ [17]. We have the following corollary.

Corollary 2

The semi-total dominating set problem in UDGs admits a PTAS with approximation factor $(2+\epsilon )$ in time $n^{O(\frac{1}{\epsilon }\frac{1}{\log {\epsilon }})}$.

5 Conclusion

In this paper, we have introduced the concept of semi-total domination to UDGs and shown that the semi-total domination problem in UDGs is NP-complete. Then, we proposed a 6-factor approximation algorithm for the same, with time complexity O(nk), where k is the size of the maximal independent set of the given UDG. In addition, we also proposed a $2+\ln {(\mathbb {D}+1)}$-factor approximation algorithm for general graphs, where $\mathbb {D}$ is the maximum degree of the given graph.