Abstract
This paper focuses on generating test cases from timed symbolic transition systems. At the heart of the generation process are symbolic execution techniques on data and time. Test cases look like finite symbolic trees with verdicts on their leaves and are based on a user-specified finite symbolic path playing the role of a test purpose. Generated test cases handle data involved in time constraints and uninitialized parameters, leveraging the advantages of symbolic execution techniques.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- model-based testing
- timed input/output symbolic transition systems
- symbolic execution
- tioco conformance relation
- test purpose
- test case generation
- uninitialized parameters
1 Introduction
Context. Symbolic execution [7, 13, 15, 20] explores programs or models’ behaviors using formal parameters instead of concrete values and computes a logical constraint on them, the so-called path condition. Interpretations of these parameters satisfying the constraint yield inputs that trigger executions along the desired path. Symbolic execution’s primary application is test case generation, where considering test cases guided by different symbolic paths facilitates achieving high coverage across diverse behaviors. Symbolic execution has been defined first for programs [20] and extended later to models [3, 4, 8, 13, 15, 27] in particular to symbolic transition systems where formal parameters abstract values of uninitialized data variables [4, 15], values of received data from the system’s environment [1, 3, 4, 8, 13, 15, 27], and durations stored in clock variables [4, 27].
Contribution. In this paper, we investigate test case generation from models given as symbolic transition systems that incorporate both data and time. Time is modeled with explicit clock variables, which are treated as a particular case of data variables that occur in guards and constrain the transitions’ firing. Our approach allows for general logical reasoning that mixes data and time through symbolic execution, typically compared to Timed Automata [2], which are models dedicated to time and use tailored zone-based abstraction techniques to handle time. Test cases are built based on a test purpose, defined as a selected symbolic path of the model. We require test purposes to be deterministic, i.e. any system behavior expressed as a trace cannot be executed both on the test purpose and on another symbolic path. By leveraging this determinism property and symbolic execution techniques, we define test cases as tree-like structures [19, 24], presenting the following advantages: (i) data and time benefit from comparable property languages, seamlessly handled with the same symbolic execution techniques; (ii) input communication channels are partitioned into controllable input channels enabling the test case to stimulate the system under test, and uncontrollable input channels enabling observation of data from third parties; (iii) state variables do not need to be initialized, and finally (iv), test cases can be easily executed on systems under test, typically achieved through behavioral composition techniques, such as employing TTCN-3 [26], or by maintaining a test case state at runtime using on-the-fly test case execution [8, 12, 15]. In either case, our test cases are coupled with constraint solving to assess the satisfiability of test cases’ progress or verdict conditions. We provide a soundness result of our test case execution on the system under test in the framework of the timed conformance relation tioco [21] issued from the well-established relation ioco [28]. Finally, we implement our test case generation in the symbolic execution platform Diversity [9].
Paper Plan. We devote Sect. 2 to present timed symbolic transition systems mixing data and time, and in Sect. 3, we define their symbolic execution serving as the foundation for our test case generation. In Sect. 4, we give the main elements of the testing framework: the conformance relation tioco and test purposes. In Sect. 5, we detail the construction of symbolic path-guided test cases. In Sect. 6, we provide some links to related work. In Sect. 7, we provide concluding words.
2 Timed Input/Output Symbolic Transition Systems
Preliminaries on Data Types. For two sets A and B, we denote \(B^A\), the set of applications from A to B. We denote \(\coprod _{i\in \{1,\ldots n\}} A_i\) the disjoint union of sets \(A_1\), ..., and \(A_n\). For a set A, \(A^*\) (resp. \(A^+\)) denotes the set of all (resp. non-empty) finite sequences of elements of A, with \(\varepsilon \) being the empty sequence. For any two sequences \(w,w'\!\in \! A^*\), we denote \(w.w'\!\in \! A^*\) their concatenation.
A data signature is a pair \(\varOmega =(S,Op)\) where S is a set of type names and Op is a set of operation names provided with a profile in \(S^+\). We denote \(V=\coprod _{s\in S}V_s\) the set of typed variables in S with \( type :V\rightarrow S\) the function that associates variables with their type. The set \(\mathcal {T}_{\varOmega }(V)=\coprod _{s\in S}\mathcal {T}_{\varOmega }(V)_{s}\) of \(\varOmega \)-terms in V is inductively defined over V and operations Op of \(\varOmega \) as usual and the function type is extended to \(\mathcal {T}_{\varOmega }(V)\) as usual. The set \(\mathcal {F}_{\varOmega }(V)\) of typed equational \(\varOmega \)-formulas over V is inductively defined over the classical equality and inequality predicates \(t \bowtie t'\) with \(\bowtie \, \in \{ < , \le , = , \ge , > \}\) for any \(t,t'\!\in \! \mathcal {T}_{\varOmega }(V)_{s}\) and over usual Boolean constants and connectives True, False, \(\lnot \), \(\vee \), \(\wedge \) and quantifiers \(\forall x\), \(\exists x\) with x a variable of V. We may use the syntax \(\exists \{ x_1, \ldots , x_n \}\) for the expression \(\exists x_1 \ldots \exists x_n\). A substitution over V is a type-preserving application \(\rho : V \rightarrow \mathcal {T}_{\varOmega }(V)\). The identity substitution over V is denoted \(id_V\) and substitutions are canonically extended on terms and formulas.
An \(\varOmega \)-model \(M = (\coprod _{s\in S}M_s, (f_M)_{f \in Op})\) provides a set of values \(M_s\) for each type s in S and a concrete operation \(f_M:M_{s_1}\times \dots \times M_{s_n}\rightarrow M_s\) for each operation name \(f : s_1 \ldots s_n \rightarrow s\) in Op. An interpretation \(\nu : V \rightarrow M\) associates a value in M with each variable \(v\!\in \! V\), and is canonically extended to \(\mathcal {T}_{\varOmega }(V)\) and \(\mathcal {F}_{\varOmega }(V)\) as usual. For \(\nu \) an interpretation in \(M^V\), x a variable in V and v a value in M, \(\nu [x \mapsto v]\) is the interpretation \(\nu ' \in M^V\) which sends x on the value v and coincides with \(\nu \) for all other variables in V. For \(\nu \in M^V\) and \(\varphi \in \mathcal {F}_{\varOmega }(V)\), the satisfaction of \(\varphi \) by \(\nu \) is denoted \(M\models _{\nu }\varphi \) and is inductively defined w.r.t. the structure of \(\varphi \) as usual. We say a formula \(\varphi \!\in \! \mathcal {F}_{\varOmega }(V)\) is satisfiable, denoted \(Sat(\varphi )\), if there exists \(\nu \!\in \!M^V\) such that \(M\models _{\nu }\varphi \).
In the sequel, we consider a data signature \(\varOmega =(S,Op)\) with \(time \in S\) to represent durations and Op containing the usual operations \(<:time.time\rightarrow Bool\) and \(+:time. time\rightarrow time\), ...An \(\varOmega \)-model M being given, \(M_{time}\) is denoted D and is isomorphic to the set of non-negative real numbers. \(<:time.time\rightarrow Bool\) and \(+:time.time\rightarrow time\) are mapped to their usual meanings.
Timed Input/Output Symbolic Transition Systems (TIOSTS) are automata handling data and time, and defined over a signature \(\varSigma = (A,K,C)\), where:
-
\(A= \coprod _{s\in S}A_s\) and K are pairwise disjoint sets of variables representing respectively data variables and clock variables of type \( time \)
-
and \(C= \coprod _{s\in S}C_s\) is a set of communication channels with the convention \(type(c) = s\) for any \(c \in C_s\). Moreover, channels of type \(s\!\in \! S\) are partitioned into input and output channels, i.e., \(C_s\!=\! C_s^{in}\coprod C_s^{out}\).
We denote \(C^{in}\!=\!\coprod _{s\in S} C_s^{in}\), resp. \(C^{out}\!=\!\coprod _{s\in S} C_s^{out}\), the set of all input, resp. output, channels, regardless of their type.
Interactions of TIOSTS with the environment are expressed in terms of communication actions. The set of communication actions over \(\varSigma \) is \(Act(\varSigma )=I(\varSigma )\cup O(\varSigma )\) where:
-
\(I(\varSigma )=\{c?x~|~c\!\in \! C^{in}, x\!\in \! A_{type(c)}\}\) is the set of input actions, and
-
\(O(\varSigma )=\{c!t~|~c\!\in \! C^{out}, t\!\in \! \mathcal{T}_\varOmega (A \cup K)_{type(c)}\}\) is the set of output actions.
c?x denotes the reception of a value to be stored in x through channel c. c!t denotes the emission of the value corresponding to the current interpretation of term t through channel c. The set of concrete communication actions over C is \(Act(C)=I(C)\cup O(C)\) where:
\(I(C)=\{c?v~|~c\!\in \! C^{in},v\!\in \! M_{type(c)}\}\) and \(O(C)=\{c!v~|~c\!\in \! C^{out},v\!\in M_{type(c)}\}\)
Notations. For \(a\in Act(\varSigma )\) (resp. \(a\in Act(C)\)) of the form c?y or c!y, chan(a) and val(a) denote c and y respectively. For expressiveness concerns, we also use extensions of those actions: either carrying n pieces of data, i.e. \(c!(t_1,\ldots ,t_n)\) or \(c?(x_1,\ldots ,x_n\)), and simple signals c! or c? which are actions carrying no-data.
Definition 1 (TIOSTS)
A TIOSTS over \(\varSigma =(A,K,C)\) is a triple \(\mathbb {G}\!=\!(Q, q_0, Tr )\), where
-
Q is the set of states,
-
\(q_0\!\in \! Q\) is the initial state,
-
\( Tr \) is the set of transitions of the form \((q,act,\phi ,\mathbb {K},\rho ,q')\) with \(q, q'\in Q\), \(act\in Act(\varSigma )\), \(\phi \in \mathcal {F}_{\varOmega }(A\cup K)\), \(\mathbb {K}\subseteq K\) and \(\rho : A\rightarrow \mathcal{T}_\varOmega (A\cup K)\) is a type-preserving function.
In the sequel, given a transition tr of the form \((q,act,\phi ,\mathbb {K},\rho ,q')\), we will access its components by their name, for example, act(tr) for its communication action. We comment on the ingredients of a TIOSTS through the TIOSTS given in Example 1.
Example 1
The TIOSTS \(\mathbb {G}\!=\!(Q,q_0,Tr)\) in Fig. 1 represents a simple Automatic Teller Machine (ATM) with \(Q\!=\!\{q_0,\dots ,q_4\}\) and \(Tr\!=\! \{tr_1,\ldots ,tr_{11} \}\). Its signature introduces two clocks (wclock, rclock), 7 data variables (rid, amt, \( tb \), fee, \(rid\_ret\), stat, \(mid\_ret\)) and 6 channels including 2 input channels ( \( \text {Transc} \), \( \text {Auth} \)) and 4 output channels (\( \text {Debit} \), \( \text {Abort} \), \( \text {Cash} \) and \( \text {Log} \)).
Transition \(tr_1\) : \(q_0\) \( \xrightarrow { { \text {Transc} ? {(amt, tb )}}, [ {True} ] , \{ {wclock} \}, \langle {rid:=rid+1} \rangle } \) \(q_1\) represents a reception on channel Transc of a client withdrawal request for a given amount stored in variable amt and the corresponding bound on processing time stored in variable \( tb \), which can vary due to bank security checks. \(tr_1\) is unconditionally fired (due to the guard True), resets clocks in \(\mathbb {K}\!=\!\{wclock\}\) and updates variable rid with \({rid}\!+\!1\). \(tr_1\) abstracts client interaction and bank processing time retrieval.
Transition \(tr_2\) :
\( q_1\) \( \xrightarrow { { \text {Debit} ! (rid,amt+fee, \text {ATM\_ID} )}, [ {wclock\le 1 \wedge tb \ge 4 \wedge fee > 0 \wedge 10 \le amt \le 1000} ] , \{ {} \}, \langle {} \rangle } \) \(q_2\)
represents an emission of (bank) debit request on channel Debit of the value of rid, the value of the term \(amt+fee\), and the value of the constant \( \text {ATM\_ID} \). \(tr_2\) can be fired if and only if the duration since wclock reset is less than or equal 1, the processing time bound is greater than or equal 4, the ATM fee is strictly positive, and the withdrawal amount in some range (between 10 and 1000).
Other transitions represent debit authorization reception (\(tr_3\)), cash return (\(tr_4\)), logging non-involved debit authorization (\(tr_5\) and \(tr_{9}\)), cancellation upon timeout (\(tr_6\)) or debit refusal (\(tr_7\)), cancellation due to amount out of range or inappropriate processing time bound (\(tr_{10}\)), reception of non-involved debit authorization (\(tr_8\)), and feeless debit request (\(tr_{11}\)).
3 Symbolic Execution of TIOSTS
We use symbolic execution techniques for defining the semantics of TIOSTS: transitions are executed not for concrete values but rather using fresh variables and accumulating constraints on them. Given an TIOSTS \(\mathbb {G} = (Q,q_0,Tr)\) over \(\varSigma = (A,K,C)\), we consider a set F of fresh variables disjoint from TIOSTS variables, i.e. \(F \cap (A\cup K)=\emptyset \), and partitioned with the following subsets:
-
\(F^{ini}\) a set of variables dedicated to initialize variables of \(\mathbb {G}\) ;
-
\(F^{in} = (F^{in}_c)_{c\in C^{in}}\) verifying that variables in \(F^{in}_c\) are of type type(c);
-
\(F^{out} = (F^{out}_c)_{c\in C^{out}}\) verifying that variables in \(F^{out}_c\) are of type type(c);
-
\(F^{dur}\) a set of variables of type time.
For the signature \(\varSigma _F\!=\!(F,\emptyset ,C)\), the set \(Evt(\varSigma _F)\) of symbolic events over \(\varSigma _F\) is \(F_{time} \times (Act(\varSigma _F) \cup \{\_\})\) with \(\_\) for indicating the absence of an action. For \(ev=(z,act)\) in \(Evt(\varSigma _F)\), delay(ev) and act(ev) denote resp. z and act. Intuitively, z is the duration elapsed between the action preceding act and act.
An Execution Context (EC) ec is a data structure of the form \((q, \pi , \lambda , ev, pec)\) composed of pieces of information about symbolic execution:
-
\(q \in Q\), a state (control point) of the TIOSTS reached so far,
-
\(\pi \in \mathcal{F}_{\varOmega }(F)\), a constraint on variables in F, the so-called path condition, to be satisfiable by the symbolic execution to reach ec,
-
\(\lambda : A \cup K \rightarrow \mathcal{T}_{\varOmega }(F)\), a substitution,
-
\(ev \in Evt(\varSigma _F)\), a symbolic event that has been executed to reach ec,
-
pec a predecessor of ec useful to build a symbolic tree in which nodes are ECs and edges connect predecessor ECs to ECs themselves.
For any execution context ec, we note \(q(ec), \pi (ec), \lambda (ec), ev(ec)\) and pec(ec) to denote the corresponding elements in ec. In the same line, we also note act(ec), delay(ec) and chan(ec) for resp. act(ev(ec)), delay(ev(ec)) and chan(act(ev(ec))). For convenience, \(Sat(\pi (ec))\) will be denoted Sat(ec).
Initial ECs are of the form \(ec_0=(q_0,True,\lambda _0,\_,self)\) with: \(\lambda _0\) associating to every variable of A a distinct fresh variable of \(F^{ini}\), and to variables of K the constant 0; "\(\_\)" an identifier indicating the absence of an action to start the system; and self an identifier indicating that , the predecessor of an initial EC is the initial context itself. \(\mathbb {EC(G)}\) denotes the set of all ECs of a TIOSTS \(\mathbb {G}\).
For a non-initial execution context ec, we use the notation pec(ec) \( \xrightarrow []{ev(ec)}\) ec or pec(ec) \( \xrightarrow []{ev(ec)}\) \(ec \in \mathbb{E}\mathbb{C}\) if ec and its predecessor are both in a subset \(\mathbb{E}\mathbb{C}\) of \(\mathbb{E}\mathbb{C}(\mathbb {G})\).
Transitions are executed symbolically from an EC. An example execution on the TIOSTS of Fig. 1 is provided before presenting the general definition.
Example 2
The symbolic execution of transition \(tr_2\) (given in Example 1) from execution context \(ec_1\) results in a successor context \(ec_2\) as follows:
\(ec_1 \xrightarrow []{(\mathbf{z_1}, \text {Debit} ! (\mathbf{ y^{1}_{{D}_{1}} },\mathbf{ y^{1}_{{D}_{2}} },\mathbf{ y^{1}_{{D}_{3}} }))} ec_2\).
Figure 2 provides a summary of both contexts. In the execution context \(ec_1\), the variables fee, rid, \(rid\_ret\), stat, and \(mid\_ret\) are evaluated with fresh initial parameters. The successor context \(ec_2\) is computed by associating the clock wclock with a new duration \(\mathbf{z_1}\) in \(F^{dur}\), indicating the time elapsed since the previous event.
The emission event \((\mathbf{z_1}, \text {Debit} ! (\mathbf{ y^{1}_{{D}_{1}} },\mathbf{ y^{1}_{{D}_{2}} },\mathbf{ y^{1}_{{D}_{3}} }))\) corresponds to the outcome of the symbolic evaluation of the transition action \(act(tr_2)\!=\! \text {Debit} ! (rid,amt+fee, \text {ATM\_ID} )\). The variables \(\mathbf{ y^{1}_{{D}_{1}} }\), \(\mathbf{ y^{1}_{{D}_{2}} }\) and \(\mathbf{ y^{1}_{{D}_{3}} }\) are respectively in \(F^{out}_{ \text {Debit} ,1}\), \(F^{out}_{ \text {Debit} ,2}\) and \(F^{out}_{ \text {Debit} ,3}\)
The evaluation of the transition guard \(\phi (tr_2)\!=\!wclock\!\le \!1\!\wedge \! tb \! \ge \!4 \!\wedge \!fee\!>\!0\!\wedge \!10\!\le \!amt\!\le \!1000\) yields the formula \(\mathbf{z_1}\!\le \!1\!\wedge \!\mathbf{ tb _1}\!\ge \!4 \!\wedge \!\mathbf{fee_0}\!>\!0\!\wedge \!10\!\le \!\mathbf{amt_1}\!\le \!1000\) which together with identification conditions \(\mathbf{ y^{1}_{{D}_{1}} }\!=\!\mathbf{rid_0} +1\), \(\mathbf{ y^{1}_{{D}_{2}} }\!=\!\mathbf{amt_1}+\mathbf{fee_0}\) and \(\mathbf{ y^{1}_{{D}_{3}} }\!=\! \text {ATM\_ID} \) constitutes \(\pi (ec_2)\), the path condition of \(ec_2\). Identification conditions result from the transition action evaluation.
Definition 2 will make clear the computation of the EC’s successors from TIOSTS transitions. While in Example 2, we have illustrated the symbolic execution of a unique transition (\(tr_2\)), we will define symbolic execution by simultaneously executing all the outgoing transitions from a given EC. Following this approach, we can introduce the same symbolic variables for all outgoing transitions as far as they have the same role. Typically, the same fresh duration is employed to represent the time passing in the computation of all the EC’s successors.
Generically, given an execution context ec in \(\mathbb {EC(G)}\), we will access the symbolic variables introduced by the executions from ec with the following notations: \(f^{in}_c(ec)\) for \(c\in C^{in}\), \(f^{out}_c(ec)\) for \(c\in C^{out}\), and \(f^{dur}(ec)\). For convenience, all such fresh variables are available by default with every execution context ec, even if there is no outgoing transition from q(ec) carrying on a given channel c. For \(\alpha \in \{in,out\}\), \(f^\alpha (ec) = \{ f_c^\alpha (ec) ~|~ c \in C^\alpha \}\). In Def 2, to make it easier to read, \(f^{in}_c(ec)\), \(f^{out}_c(ec)\) and \(f^{dur}(ec)\) are respectively denoted as \(x_c\), \(y_c\) and z.
Definition 2 (Symbolic Execution of a TIOSTS)
Let \(\mathbb {G}\!=\!(Q, q_0, Tr )\) be a TIOSTS, \(ec=(q,\pi ,\lambda ,ev,pec)\) be an execution context in \(\mathbb {EC(G)}\), and \(x_c\) be a fresh variable in \(F^{in}_c\) for any \(c\in C^{in}\), \(y_c\) be a fresh variable in \(F^{out}_c\) for any \(c\in C^{out}\) and let z be a fresh variable in \(F^{dur}\).
The successors of ec are all execution contexts \(ec'\) of the form \((q',\pi ',\lambda ',ev',ec)\) verifying that there exists a transition \(tr=(q,act,\phi ,\mathbb {K},\rho , q')\) in Tr and constituents \(\lambda '\), \(ev'\) and \(\pi '\) of \(ec'\) are defined as follows:
-
the substitution \(\lambda ' : A \cup K \rightarrow \mathcal{T}_{\varOmega }(F)\):
$$\begin{aligned} \lambda '(w) = {\left\{ \begin{array}{ll} \lambda '_0(\rho (w)) &{} \textbf{if}\ w \in A \\ 0 &{} \textbf{if}\ w \in \mathbb {K} \\ \lambda '_0(w) &{} \textbf{else} \text { i.e. } {if}\ w \in K \setminus \mathbb {K} \end{array}\right. } \end{aligned}$$(1)where \(\lambda '_0 : A \cup K \rightarrow \mathcal{T}_{\varOmega }(F)\) is the auxiliary function defined as:
$$\begin{aligned} \lambda '_0(w) = {\left\{ \begin{array}{ll} x_c &{} \textbf{if}\ act = c?w \\ \lambda (w)+z &{} \textbf{if}\ w \in K \\ \lambda (w) &{} \textbf{else} \end{array}\right. } \end{aligned}$$(2) -
\(ev'\) is \((z,c?x_c)\) if \(act = c?w\) and is \((z,c!y_c)\) if \(act = c!t\) for a given channel c
-
\(\pi '\) is the formula \(\pi \wedge \lambda '_0(\phi )\) if \(act = c?w\) and is \(\pi \wedge \lambda '_0(\phi ) \wedge (y_c= \lambda '_0(t))\) if \(act = c!t\) for a given channel c.
The symbolic execution \(SE(\mathbb {G})\) of \(\mathbb {G}\) is a couple \((ec_0, \mathbb{E}\mathbb{C})\) where: \(ec_0\) is an arbitrary initial EC, and \(\mathbb{E}\mathbb{C}\) is the smallest set of execution contexts containing \(ec_0\) and all successors of its elements.
Most of the time (e.g., if it is possible to run a cycle of \(\mathbb {G}\) for an arbitrarily long time), \(\mathbb{E}\mathbb{C}\) is an infinite set. The computation of the successors of an execution context translates the standard execution of a transition from that context: \(\lambda '_0\) is an intermediate substitution that advances all clocks by the same fresh duration z to indicate time passing, assigns to a data variable w a fresh variable \(x_c\) if w is the variable of a reception (c?w) and leaves the other data variables unchanged. Then, \(\lambda '\) is defined, for the data variables, by applying \(\lambda '_0\) on the terms defined by the substitution \(\rho \) introduced by tr and, for the clock variables, by resetting the variables of \(\mathbb {K}\) to zero and advancing the other clocks using \(\lambda '_0\). The event action is either \(c?x_c\) (case of a reception c?w) or \(c!y_c\) (case of an emission c!t). The path condition \(\pi '\) is obtained by the accumulation of the condition \(\pi \) of the predecessor context ec and of the guard \(\phi \) of the transition evaluated using \(\lambda '_0\). Moreover, in case of an emission, \(\pi '\) keeps track of the identification condition matching \(y_c\) with the evaluation \(\lambda '_0(t)\) of the emitted term t.
In the sequel, we will denote tr(ec) the transition that allows building the execution context ec. By convention, tr(ec) is undefined for initial contexts.
Example 3
Fig. 3 illustrates parts of the symbolic execution of the ATM example TIOSTS given in Fig. 1.
So far, we have defined the symbolic execution of a TIOSTS without any adjustments related to our testing concerns from TIOSTS. In the following, we will complete the symbolic execution with quiescent configurations, i.e., identifying situations where the system can remain silent. The system is usually expected to react by sending messages when it receives a message from its environment. However, sometimes, it cannot emit an output from any given state [4, 15, 18, 25, 28]. In such a case, the inability of the system to react becomes a piece of information. To make this fact clear we enrich symbolic execution by adding a special output action \(\delta !\) to denote the absence of output in those specific deadlock situations.
Definition 3 (Quiescence enrichment)
The quiescence enrichment \(SE(\mathbb {G})^\delta \) of \(SE(\mathbb {G})\) \(= (ec_0, \mathbb{E}\mathbb{C})\) is \((ec_0, \mathbb{E}\mathbb{C}^\delta )\) where \(\mathbb{E}\mathbb{C}^\delta \) is the set \(\mathbb{E}\mathbb{C}\) enriched by new execution contexts \(ec^\delta \). For each context \(ec=(q,\pi ,\lambda ,ev,pec)\) in \(\mathbb{E}\mathbb{C}\), a new context \(ec^\delta =(q,\pi \wedge \pi ^\delta ,\lambda ,(f^{dur}(ec),\delta !),ec)\) is considered whereFootnote 1:
Let us emphasize that \(\pi ^\delta \) is satisfiable only for contexts ec where there is no choice of values for the variables for triggering from ec a transition carrying an emission. The context could not be considered quiescent if such a choice were possible, i.e. if there would exist an output transition towards an execution context \(ec'\), for which there is an instantiation of variables \(f^{dur}(ec)\) and \(f^{out}_{chan(ec')}(ec)\) making the condition \(\pi (ec')\) true.
Example 4
We discuss some examples from Fig. 3. The execution context \(ec_0\) does not have successors with outputs (\(\pi ^\delta \) is True) which denotes that the ATM is awaiting withdrawal requests or non-involved debit authorizations. This quiescent situation is captured by adding the context \(ec^\delta _0\!=\!(q_0,True,\lambda (ec_0),(\mathbf{z_0},\delta !),ec_0)\). The execution context \(ec_1\) has three successors with outputs, \(ec_2\), \(ec_9\) and \(ec_{10}\). Then, \(\pi ^\delta \) is:
which is not satisfiable. Thus, there is no need to add a quiescent transition from \(ec_1\). The same applies to \(ec_2\) and \(ec_3\).
A symbolic path of \(SE(\mathbb {G})^\delta =(ec_0, \mathbb{E}\mathbb{C}^\delta )\) is a sequence \(p = ec_0.ec_1\ldots ec_n\) where \(ec_0\) is the initial context, for \(i\in [1,n]\), \(ec_i\in \mathbb{E}\mathbb{C}^\delta \), and \(pec(ec_i) = ec_{i-1}\). \(Paths(SE(\mathbb {G})^\delta )\) denotes the set of all such paths. We will use the notation tgt(p) to refer to \(ec_n\), the last context of p. We define the set of traces of a symbolic path p in \(Paths(SE(\mathbb {G})^\delta )\) by:
where \(\nu \) applies to a path p of the form \(p'.ec\) as \(\nu (p)=\nu (p').\nu (ev(ec))\) with the convention \(\nu (ev(ec_0))=\epsilon \) and \(\nu (ev(ec)) = (\nu (z), c ? \nu (x))\) (resp. \((\nu (z), c ! \nu (y))\) or \((\nu (z), \delta !)\)) if ev(ec) is of the form (z, c?x) (resp. (z, c!y) or \((z,\delta !)\)).
By solving the path condition of a given path, we can evaluate all symbolic events occurring in the path and extract the corresponding trace. The set of traces of \(\mathbb {G}\) is defined as :
Symbolic execution of the ATM TIOSTS of Fig. 1
4 Conformance Testing
Conformance testing aims to check that a system under test behaves correctly w.r.t a reference model, a TIOSTS \(\mathbb {G}\) in our case. The test case stimulates the system with inputs and observes the system’s outputs, their temporalities, and the quiescent situations to compare them to those specified by \(\mathbb {G}\). For generality, we propose test cases that control some inputs of the system under test while leaving other inputs driven by systems in its environment. We assume that the test case selects inputs and observes outputs on some channels while it can only observe inputs and outputs on other channels of the system under test. Illustrating with the ATM, a test case provides the ATM with withdrawal requests, and observes withdrawal authorizations received from the bank.
We characterize a Localized System Under Test (LUT) (terminology from [6, 14]) tested in a context where some inputs are not controllable. For this, we partition \(C^{in} = CC^{in} \amalg UC^{in}\) where:
-
\(CC^{in}\) is the set of controllable input channels and
-
\(UC^{in}\) is the set of uncontrollable input channels.
For a set of channels C, we denote \(Evt(C)=D \times Act(C)\) the set of all concrete events that can occur in a trace: an event (d, act) indicates that the occurrence of action act happens d units of time after the previous event. In model-based testing, a LUT is a black box and as such, is abstracted by a set of traces \(LUT \subseteq Evt(C_\delta )^*\) with \(C_\delta = C \cup \{\delta \}\) satisfying additional hypotheses, denoted as \(\mathcal {H}\), ensuring its consistency. Hypotheses \(\mathcal{H}\) gather the following 3 properties, where for \(\sigma _1, \sigma _2\) in \(Evt(C)^*\), d in D and \(ev \in Evt(C)\) we have:
-
stable by prefix: \( \sigma _1 . \sigma _2 \in LUT \Rightarrow \sigma _1 \in LUT \)
-
quiescence: for any \(d<delay(ev)\), \( \sigma _1 .ev \in LUT \Rightarrow \sigma _1 . (d, \delta !) \in LUT \)
-
input complete: for any \(d<delay(ev)\), \(c \in CC^{in}\), \(v \in M\), \( \sigma _1 . ev \in LUT \Rightarrow \sigma _1 . (d, c?v) \in LUT \)
The first hypothesis simply states that every prefix of a system trace is also a system trace. The hypothesis on quiescence states that if an event ev whose action is in act(C) occurs in LUT, then LUT can remain quiescent for any duration strictly less than the delay of the event. The hypothesis on input completeness enables LUT to receive any input on a controllable channel, i.e., an input received from the test case, during the delay of any ev in the LUT.
The semantics of a TIOSTS \(\mathbb {G}\), denoted by \(Sem(\mathbb {G})\), will include traces with the admissible temporary observation of quiescence: if an event \(ev =(d,act)\) is specified in \(\mathbb {G}\) then quiescence can be observed for any duration \(d' < d\). \(Sem(\mathbb {G})\) is then defined as the smallest set containing \({Traces}(\mathbb {G})\) and such that for any \(\sigma \in Evt(C)^*\), \(ev\in Evt(C)\), for any \(d<delay(ev)\):
\( \sigma . ev \in Traces(\mathbb {G}) \Rightarrow \sigma . (d,\delta !) \in Sem(\mathbb {G}) \)
As other previous works [23, 29] have already done to suit their needs, we are now slightly adapting the conformance relation of [21]:
Definition 4 (tioco)
Let C be a set of channels. Let \(\mathbb {G}\) and LUT be resp. a TIOSTS defined on C and a subset of \(Evt(C_\delta )^*\) satisfying \(\mathcal {H}\).
LUT tioco \(\mathbb {G}\) iff for all \(\sigma \in Sem(\mathbb {G})\), for any \(ev\in Evt(C^{out} \cup \{\delta \})\), we have:
The relation tioco states that LUT is in conformance with \(\mathbb {G}\), if and only if after a specified sequence \(\sigma \) observed on LUT, any event produced by LUT as an output or a delay of quiescence, leads to a sequence \(\sigma .ev\) of \(sem(\mathbb {G})\).
Test case generation is often based on the selection of a test purpose which permits to choose a particular behavior in \(\mathbb {G}\) to be tested [4, 8, 15, 17]. As symbolic execution plays a key role both for the semantics of TIOSTS and for testing issues in general, whether it is for the test case generation or the verdict computation, our test purposes will be paths \(tp\in Paths(SE(\mathbb {G})_\delta )\) with satisfiable path conditions, i.e. verifying Sat(tgt(tp)). As outputs are involved in the tioco relation, we require tp to end with an output event, i.e., \(chan(tgt(tp))\in C^{out}\).
Contrary to [15], our test purposes are simple paths and not (finite) subtrees, simplifying the construction of test cases. We will not need to consider the case where the observed behavior on LUT corresponds to several symbolic paths simultaneously. By taking it a step further, to avoid such tricky situations completely, we restrict ourselves to symbolic paths that do not induce non-determinism. In line with [3, 19], we forbid that there are two outgoing transitions of an execution context concerning the same channel which can be covered by the same trace. Unlike [3, 19] which impose determinism conditions at the state level, we deal with uninitialized variables at the path level:
Definition 5 (Test purpose)
Let \(tp \in Paths(SE(\mathbb {G})^\delta )\) be a symbolic path verifying Sat(tgt(tp)) and \(chan(tgt(tp))\in C^{out}\). Let \(\mathbb{E}\mathbb{C}(tp)\) be its set of execution contexts.
tp is a test purpose for \(\mathbb {G}\) if tp satisfies the so-called trace-determinism property:
for ec in \(\mathbb{E}\mathbb{C}(tp)\) and \(ec'\) in \(\mathbb{E}\mathbb{C}(\mathbb {G})\) s.t. \(Sat(ec')\), \(pec(ec) = pec(ec')\), \(tr(ec) \ne tr(ec')\), and \(chan(ec) = chan(ec')\), the following formula is unsatisfiable:
The trace-determinism property simply expresses that from any intermediate execution context of tp, it is impossible to deviate in \(\mathbb {G}\) with a common trace, independently of the initial conditions.
Example 5
The test purpose \(tp=ec_0.ec_1 \ldots ec_4\) given in Fig. 3 satisfies trace-determinism. To support our comments, let us consider a simpler TIOSTS with three transitions (\(tr_1\), \(tr_2\) and \(tr_3\)), with two of them, \(tr_2\) and \(tr_3\), creating a non-deterministic situation:
\(tr_1 : q_0 \xrightarrow []{ \text {Transc} ? amt } q_1\), \(tr_2 : q_1 \xrightarrow []{ \text {Debit} ! amt } q_2\) and \(tr_3 : q_1 \xrightarrow []{ [\; fee > 0\; ] \,,\, \text {Debit} ! amt+fee } q_3\)
The TIOSTS symbolic execution for some initial execution context \(ec_0\) (\( F^{ini} = \{ \mathbf{amt_0}, \mathbf{fee_0} \}\)) can reach execution contexts \(ec_1\) (\(tr(ec_1)=tr_1\), \(pec(ec_1)=ec_0\)), \(ec_2\) (\(tr(ec_2)=tr_2\), \(pec(ec_2)= ec_1\)), and \(ec_3\) (\(tr(ec_3)=tr_3\), \(pec(ec_3) = ec_1\)), building 2 symbolic paths \(ec_0.ec_1.ec_2\) and \(ec_0.ec_1.ec_3\). Respective path conditions are \( \pi (ec_2) = (\mathbf{ y^{1}_{{D}_{}} } = \mathbf{amt_1}) \) and \( \pi (ec_3) = (\mathbf{fee_0} > 0) \wedge (\mathbf{ y^{1}_{{D}_{}} } = \mathbf{amt_1} + \mathbf{fee_0})\) where \(\mathbf{amt_1}\) binds the value received on the channel \(\text {Transc}\) (\(f^{in}_{\text {Transc}}(ec_0)=\mathbf{amt_1}\)) and \(\mathbf{ y^{1}_{{D}_{}} }\) binds the value emitted on the channel \(\text {Debit}\) (\(f^{out}_{\text {Debit}}(ec_1) = \mathbf{ y^{1}_{{D}_{}} }\)).
Given \(tp=ec_0.ec_1.ec_2\), execution contexts \(ec_2\) and \(ec_3\) share the same output channel \(\text {Debit}\) and the same predecessor context \(ec_1\). tp satisfies the trace-determinism property. Indeed, the formula:
\(\big ( \exists \{\mathbf{fee_0},\mathbf{amt_0}\} . (\mathbf{ y^{1}_{{D}_{}} } \!=\! \mathbf{amt_1}) \big ) \bigwedge \big ( \exists \{\mathbf{fee_0},\mathbf{amt_0}\} . (\mathbf{fee_0} \!>\! 0) \wedge (\mathbf{ y^{1}_{{D}_{}} } \!=\! \mathbf{amt_1} \!+\! \mathbf{fee_0}) \big )\)
is not satisfiable because \(\mathbf{amt_1} < \mathbf{amt_1} + \mathbf{fee_0}\) holds as we have \(\mathbf{fee_0} > 0\). A trace cannot belong to distinct paths: if the debit value is the same as what is requested for withdrawal then the trace covers \(ec_2\), else \(ec_3\) is covered.
5 Path-Guided Test Cases
Roughly speaking, a test case \(\mathbb{T}\mathbb{C}\) will be a mirror TIOSTS of a TIOSTS \(\mathbb {G}\), restricted by tp, a test purpose of \(\mathbb {G}\), intended to interact with a LUT that we wish to check its conformance to \(\mathbb {G}\) up to tp. \(\mathbb{T}\mathbb{C}\) will be a tree-like TIOSTS with tp of \(\mathbb {G}\) as a backbone, incorporating the following specific characteristics:
-
execution contexts in \(\mathbb{E}\mathbb{C}(tp)\) constitute the main branch,
-
sink states or leaves are assimilated with a test verdict. Notably, the last execution context tgt(tp) of tp will be assimilated with the \(\text {PASS}\) verdict,
-
from each ec in \(\mathbb{E}\mathbb{C}(tp)\) other than tgt(tp), the outgoing arcs outside tp decline all ways to deviate from tp and directly lead to a verdict state, either an inconclusive verdict or a failure verdict. In Definition 6, we will specify the different ways of constructing these arcs from tp states, leading to a verdict.
In Definition 6, we define \(\mathbb{T}\mathbb{C}\) by enumerating the different cases of transitions to be built according to channel type and tp membership. We now give a few indications for enhancing the readability.
-
Channel roles are reversed: channels in \(CC^{in}\) as well as channel \(\delta \) (resp. \(C^{out} \cup UC^{in}\)) become output (resp. input) channels;
-
Variables of \(\mathbb{T}\mathbb{C}\) will be symbolic variables involved in tp and will be used to store successive concrete events observed on LUT;
-
Any observation on LUT will be encoded as an input transition in \(\mathbb{T}\mathbb{C}\), whether it is an emission from a channel of \(C^{out}\), a reception on a channel of \(UC^{in}\) or a time-out observation.
On the latter, it is conventional to consider that a system that does not react before a certain delay, chosen to be long enough, is in a state of quiescence. The only notable exception is when input transitions of tp give rise to output transitions for \(\mathbb{T}\mathbb{C}\), modeling a situation in which \(\mathbb{T}\mathbb{C}\) stimulates LUT by sending it data. The choice of the data to send is conditioned by two constraints: (i) taking into account the information collected so far and stored in the variables of \(\mathbb{T}\mathbb{C}\) in the first steps, and (ii) the guarantee of being able to reach the last EC of tp, i.e. the verdict \(\text {PASS}\). This will be done by ensuring the satisfiability of the path condition of tp, leaving aside the variables already binded.
We will refer to variables of a symbolic path as follows: forFootnote 2 \(\alpha \in \{in,out\}\), \(f^\alpha (p)=\bigcup _{i \in [1,n)} f^\alpha (ec_i)\) will denote all introduced fresh variables in \(F^\alpha \) used to compute a symbolic path \(p =ec_0.ec_1\ldots ec_n\). Similarly, \(f^{dur}(p) = \{ f^{dur}(ec_i) | i \in [1,n) \}\). Moreover, for a target execution context \(ec_n = tgt(p)\), we denote \(\overline{f}^\alpha (ec_n)\) and \(\overline{f}(ec_n)\) resp. for \(f^\alpha (p)\) and f(p).
Definition 6 (Path-guided test case)
Let tp be a test purpose for a TIOSTS \(\mathbb {G}\). Let us consider the signature \(\widehat{\varSigma } = (\widehat{A}, \widehat{K}, \widehat{C})\) where:
-
\(\widehat{A} = f^{in}(tp) \cup f^{out}(tp)\),
-
\(\widehat{K}=f^{dur}(tp)\),
-
\(\widehat{C}=C_\delta \) such that \(\widehat{C}^{in} = C^{out} \cup UC^{in}\) and \(\widehat{C}^{out} = CC^{in} \cup \{\delta \}\)
A test case guided by tp is a TIOSTS \(\mathbb{T}\mathbb{C}=(\widehat{Q}, \widehat{q_0}, \widehat{Tr})\) over \(\widehat{\varSigma }\) where:
-
\(\widehat{Q} = \big (\mathbb{E}\mathbb{C}(tp) \setminus \{tgt(tp)\} \big ) \cup \mathbb {V}\) where: \(\mathbb {V} = \{\) \(PASS ,\) \(FAIL ^{out},\) \(FAIL ^{dur},\) \(INC ^{out},\) \(INC ^{dur},\) \(INC ^ {ucIn} _ {spec} ,\) \(INC ^ {ucIn} _ {uspec} \) \(\}\),
-
\(\widehat{q_0}=ec_0\),
-
\(\widehat{Tr}\) is defined by a set \(\mathcal{R}\) of 10 rules of the form
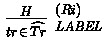 for \(i \in [1,10]\). Such a rule reads as follows: the transition tr is added due to rule Ri to \(\widehat{Tr}\) provided that hypothesis H holds and \(Sat(\phi (tr))\).
for \(i \in [1,10]\). Such a rule reads as follows: the transition tr is added due to rule Ri to \(\widehat{Tr}\) provided that hypothesis H holds and \(Sat(\phi (tr))\).
In writing the rules of \(\mathcal{R}\), we will use the following formulas
\(\begin{array}{lcl} &{}\\ \phi _{stim} &{}:&{} \exists F^{ini} \cup \overline{f}(tgt(tp)) \setminus \overline{f}(ec'). \pi (tp) \\ &{} \\ \phi ^ {obs} _ {spec} &{}:&{} f^{dur} (ec) < TM \wedge (\exists F^{ini}.\pi (ec')) \\ \phi ^ {obs} _ {uspec} &{}:&{} f^{dur} (ec) < TM \wedge \bigwedge _{\begin{array}{c} pec(ec') = ec \\ chan(ec')=c \end{array}}(\forall F^{ini}.\lnot \pi (ec')) \\ &{} \\ \phi ^{\delta }_ {spec} &{}:&{} f^{dur}(ec) \ge TM \wedge \bigvee _{\begin{array}{c} pec(ec')=ec \\ chan(ec') \in C^{out} \cup UC^{in} \cup \{\delta \} \end{array}} (\exists F^{ini}.\pi (ec')) \\ \phi ^{\delta }_ {uspec} &{}:&{} f^{dur}(ec) \ge TM \wedge \bigwedge _{\begin{array}{c} pec(ec')=ec \\ chan(ec') \in C^{out} \cup UC^{in} \cup \{\delta \} \end{array}} (\forall F^{ini}.\lnot \pi (ec')) \\ &{} \end{array} \)
where the constant \(TM \) (Time-out) sets the maximum waiting-time for observing outputs or uncontrollable inputs.

A verdict \(\text {PASS}\) is reached when tp is covered, verdicts \(\text {INC}^m_n\) are reached when traces deviate from tp while remaining in \(\mathbb {G}\), and verdicts \(\text {FAIL}^m\) denote traces outside \(\mathbb {G}\). The annotations n and m provide additional information on the cause of the verdict. Rules R1, R2 and R6, grouped together under the label \(\text {SKIP}\), allow advancing along tp, resp. by stimulating LUT with the sending of data, observing an emission on \(C^{out}\) and observing a reception on \(UC^{in}\). Rule R3 indicates that the last EC of tp, thus the \(\text {PASS}\) verdict, has been reached. Rules R4, R7, R8 and R9, each with a label \(\text {INC}^m_n\) indicate that the observed event causes LUT to leave tp, without leaving \(\mathbb {G}\), resp. by observing an output, an input specified in \(\mathbb {G}\), an input not specified in \(\mathbb {G}\) and a time-out observation. Lastly, rules R5 and R10, resp. labeled by \(\text {FAIL}^{out}\) and \(\text {FAIL}^{dur}\), raise a \(\text {FAIL}\) verdict, for resp. an unauthorized output and an exceeded time-out.
Example 6
In Fig. 4, the test case for \(tp=ec_0.ec_1\ldots ec_4\) (see Example 5) is depicted. Certain verdict states are repeated for readability, and defining rules annotate the transitions. The test case utilizes the \(\text {Transc}\) channel as a controllable input channel for stimulation while observing all other channels. For space considerations, we comment only on some rules.
Rule R1 defines a stimulation action \( \text {Transc} ! (\mathbf{amt_1},\mathbf{ tb _1})\) (transition from \(ec_0\) to \(ec_1\)) constrained by \(\pi (tp)\) to select an appropriate value for \(\mathbf{amt_1}\) and \(\mathbf{ tb _1}\) together with a time of stimulation \(\mathbf{z_0}\) that allows to follow the test purpose. Within \(\pi (tp)\), \(\mathbf{amt_1}\) is limited to some range (\(10\le \mathbf{amt_1} \le 1000\)), \(\mathbf{ tb _1}\) is greater than or equal 4, while \(\mathbf{z_0}\) is unconstrained (a duration measured with clock \(\mathbf{z_0}\)). Non-revealed variables, i.e., other than \(\mathbf{z_0}\), \(\mathbf{amt_1}\) and \(\mathbf{ tb _1}\) appearing in \(\pi (tp)\) are bound by the existential quantifier due to their unknown values at this execution point. The clock \(\mathbf{z_1}\) is reset to enable reasoning on subsequent actions’ duration (measured on \(\mathbf{z_1}\)). Rule R2 defines an observation action \( \text {Debit} ? (\mathbf{ y^{1}_{{D}_{1}} },\mathbf{ y^{1}_{{D}_{2}} },\mathbf{ y^{1}_{{D}_{3}} })\) constrained by \((\mathbf{z_1}\!<\! \text {TM} ) \wedge \exists \mathbf{fee_0} . { \pi ( ec_{2} ) } \) (transition from \(ec_1\) to \(ec_2\)) while rule R5 defines the same observation constrained by \((\mathbf{z_1}\!<\! \text {TM} ) \wedge \forall \mathbf{fee_0} . \lnot \, { \pi ( ec_{2} ) } \wedge \forall \{ \mathbf{fee_0} \} \, . \, \lnot \, { \pi ( ec_{9} ) } \) (transition from \(ec_1\) to \(\text {FAIL}^{out}\)). Both situations are possible: Trace \((0, \text {Transc} ! (50,4)). (0, \text {Debit} ? (1,51, \text {ATM\_ID} ))\) reaches \(ec_2\) whereas \(\text {FAIL}_{out}\) is reached by traces \((0, \text {Transc} ! (50,4)). (0, \text {Debit} ? (1,0, \text {ATM\_ID} ))\) and \((0, \text {Transc} ! (50,4)). (2, \text {Debit} ? (1,51, \text {ATM\_ID} ))\) due resp. to data and time non-compliance. Rule R6 defines an unspecified quiescence \(\delta !\) constrained by \((\mathbf{z_1} \ge \text {TM} ) \wedge \forall \mathbf{fee_0} \, . \lnot { \pi ( ec_{2} ) } \wedge \forall \mathbf{fee_0} \, . \lnot { \pi ( ec_{9} ) } \wedge \forall \mathbf{fee_0} \, .\lnot { \pi ( ec_{10} ) } \) (transition from \(ec_1\) to \(\text {FAIL}^{dur}\)). The trace \((0, \text {Transc} ! (50,4)).(5,\delta !)\) reaches \(\text {FAIL}^{dur}\) (time-out \( \text {TM} \) is set to 5): the time-out is exceeded without the mandatory output on the channel \(\text {Debit}\) being observed. Rule R9 defines a specified quiescence \(\delta !\) (transition from \(ec_1\) to \(\text {INC}^{dur}\) not drawn for space). This case arises when there is still sufficient time to reach \(ec_2\), \(ec_9\) or \(ec_{10}\) (no quiescence applies from \(ec_1\), see Example 4).
A test case \(\mathbb{T}\mathbb{C}\) interacts with a LUT, designed to comply with a TIOSTS \(\mathbb {G}\), to issue a verdict about a test purpose tp. \(\mathbb{T}\mathbb{C}\) is therefore defined as a mirror image of \(\mathbb {G}\): emissions (receptions) in \(\mathbb{T}\mathbb{C}\) correspond to receptions (emissions) of \(\mathbb {G}\) (cf. rules R1 and R2), except uncontrollable channels whose actions are not reversed (cf rule R6). Given a concrete action act (with v for value received or sent), we denote \(\overline{act}\) its mirror action, defined as follows: \(\overline{c!v} = c?v\) for \(c \in C^{out}\), \(\overline{c?v} = c!v\) for \(c \in CC^{in}\) and \(\overline{c?v} = c?v\) for \(c \in UC^{in}\).
We introduce an execution relation that abstracts a synchronized execution of a trace with \(\mathbb{T}\mathbb{C}\):
Definition 7
(Relation execution \(\leadsto _{\mathbb{T}\mathbb{C}}\)). Let \(\mathbb {G}\) be a TIOSTS and tp a test purpose for \(\mathbb {G}\) with \(\mathbb{T}\mathbb{C} = (\widehat{Q},\widehat{q_0},\widehat{Tr})\) the test case guided by tp.
The execution relation \(\leadsto _{\mathbb{T}\mathbb{C}}\subseteq \big ( Evt(C_\delta )^* \times \widehat{Q} \times M^F \big )^2\) is defined by:
for \(ev.\sigma \in Evt(C_\delta )^*\), \(q,q' \in \widehat{Q}\) and for \(\nu , \nu ' \in M^F\), \((ev.\sigma ,q,\nu ) ~\leadsto _{\mathbb{T}\mathbb{C}}~ (\sigma , q',\nu ')\) holds iff there exists \(tr\in \widehat{Tr}\) s.t. \(src(tr)\!=\! q\), \(tgt(tr)\!=\!q'\), \(\nu '(act(tr))=\overline{act(ev)}\) and \(M \models _{\nu '} \phi (tr)\) with \(\nu '\) defined as:
-
if \(ev\!=\!(d,c?v)\) and \(chan(tr)\!=\!c\) then \(\nu '\!=\!\nu [f^{dur}(q)\!\mapsto \!d][ f^{in}_c(q)\!\mapsto \!v]\) ;
-
if \(ev\!=\!(d,c!v)\) and \(chan(tr)\!=\!c\) then \(\nu '\!=\!\nu [f^{dur}(q)\!\mapsto \!d][f^{out}_c(q) \!\mapsto \! v]\) ;
-
else, i.e., \(ev\!=\!(d,\delta !)\) and \(chan(tr)\!=\!\delta \), \(\nu '=\nu [f^{dur}(q)\!\mapsto \!d]\).
Intuitively, a step \((ev.\sigma , q,\nu ) ~\leadsto _{\mathbb{T}\mathbb{C}}~ (\sigma , q',\nu ')\) consists in:
-
reading the first element ev of a trace from a test case state q and an interpretation \(\nu \) synthesizing the known information about the variables in F;
-
finding a transition tr in \(\widehat{Tr}\) whose action matches the mirror action of ev;
-
building a new triple with \(\sigma \) the trace remaining to be read, \(q'\) a successor state of q in \(\widehat{Q}\), and \(\nu '\) the updated interpretation of the variables F.
The execution relation simulates a parallel composition between timed input output systems, synchronizing inputs and outputs. Our formulation deviates from the one in [22] for two essential reasons: the symbolic nature of the test case requires the intermediate interpretations of variables to be memorized, and uncontrollable channels require to adapt the synchronization [11].
Let LUT be a subset of \( Evt(C_\delta )^*\) satisfying \(\mathcal{H}\) and \(\overset{*}{\leadsto }_{\mathbb{T}\mathbb{C}}\) be the reflexive and transitive closure of \(\leadsto _{\mathbb{T}\mathbb{C}}\). Given a LUT trace \(\sigma _0\), we apply the execution relation iteratively from an initial triplet consisting of \(\sigma _0\) a trace, \(\widehat{q_0}\) the initial state and \(\nu _0\) an arbitrary interpretation, to obtain the corresponding test verdict for tp, so that the verdict set obtained from the execution of \(\mathbb{T}\mathbb{C}\) on LUT is defined by:
\(vdt(LUT,\mathbb{T}\mathbb{C})= \{\text {V} ~|~ \exists \sigma _0 \in LUT, \nu _0 \in M^F, (\sigma _0,\widehat{q_0} , \nu _0) ~\overset{*}{\leadsto }_{\mathbb{T}\mathbb{C}} (\sigma ,\text {V}, \nu )\}\).
Theorem 1 states the soundness of the test case execution for detecting errors through the \(\text {FAIL}^{out}\) and \(\text {FAIL}^{dur}\) verdicts. A proof can be found in [5]. Comparable results can be formulated for the other verdicts. Still, those relating to FAIL verdicts are the only ones to guarantee that any discarded system under test does not satisfy the tioco conformance relation.
Theorem 1
Let C be a set of channels. Let \(\mathbb {G}\) and LUT be resp. a TIOSTS defined on C and a subset of \(Evt(C_\delta )^*\) satisfying \(\mathcal {H}\).
If \(LUT~tioco~\mathbb {G}\) then for any test purpose tp for \(\mathbb {G}\) with \(\mathbb{T}\mathbb{C}\) as test case guided by tp, we have \(FAIL ^{out}\not \in vdt(LUT, \mathbb{T}\mathbb{C}) \) and \(FAIL ^{dur}\not \in vdt(LUT, \mathbb{T}\mathbb{C})\).
The test case generation is implemented as a module in the Diversity symbolic execution platform [9]. Resulting test cases are expressed in Diversity’s entry language, allowing their exploration through symbolic execution with the SMT-solver Z3 [10]. For easier execution, we export the test cases from Diversity in JSON format, with transition guards expressed in the SMT-LIB input format for SMT-solvers. Our experiments involved applying this test case generation to the ATM example on an Intel Core i7 processor. Varying the size of the test purposes up to 100 transitions, we observed successful trace-determinism verification for all test purposes. We noted a noticeable increase in generation duration as the test purpose size grew while still remaining feasible. Generating the TIOSTS test case (513 transitions) for the test purpose of 100 transitions took more than 40s, in contrast to only 500 ms for the test purpose of size 4 in Example 6 (31 transitions) resp. 8s for the test purpose of size 50 (138 transitions).
6 Related Work
Existing works for (t)ioco conformance test cases from symbolic models employs two main generation methods: online and offline. Online generation [8, 12, 15] involves dynamically generating test cases while exploring the model during execution on the system under test. In contrast, offline generation [3, 4, 16] focuses on deriving test cases from the model before executing them on the system under test. Some works [8, 12, 15] propose online test case generation using symbolic execution. Yet, these works did not consider time constraints, and in particular, work [8] did not consider quiescence. In [8], a test purpose is a finite path, while in [15], it is a finite symbolic subtree. Both works require maintaining a set of reached symbolic states during test case execution to avoid inconsistent verdicts in case of non-determinism, at the expense of computational resources for tracking the symbolic states and solving their path conditions. Work [4] proposes offline test case generation using a path to compute a timed stimulation sequence for the system under test. The recorded timed output sequence is then analyzed for conformance. This approach lacks control over the value and timing of the next stimulation relative to the observed system behavior, potentially resulting in greater deviations from the test purpose. In [16], objective-centered testers for timed automata are built using game theory. Works [3, 19] propose offline test case generation as tree-like symbolic transition systems and thus restricted to determinism as we do. The test case generation in [19] relies on abstract interpretation to reinforce test case guards on data to keep chances of staying in the test purpose and does not consider time. In [3], symbolic execution techniques are used for data handling, while zone-based abstraction techniques are employed for time. This separation results in less expressive and flexible models, as it cannot extend to incorporate data parameters in the time constraints.
7 Conclusion
This paper presents an offline approach to conformance test case generation from models of timed symbolic transition systems using symbolic execution to handle data and time. Our test purpose is a symbolic path in the model that fulfills a determinism condition to enable the generation of sound tree-like test cases. By distinguishing between controllable inputs (from the test case) and uncontrollable inputs (from other systems), our approach enhances the usability of test cases when the system interacts with other systems (remote in general). This allows our test cases to be used in more liberal configurations, typically those that may appear for distributed systems. It’s worth noting that our test cases include configurations where the resolution time exceeds the stimulation time or overlaps the arrival of an observation. These points will be the subject of future work. Similarly, the experiments described in this paper concern the computation of test cases derived from models that have not yet been used to test systems. This is another avenue for future work.
Notes
- 1.
with the convention that \(\bigwedge \) quantified over empty conditions is the formula True.
- 2.
For i and j in \(\mathbb {N}\) verifying \(i < j\), [i, j) contains the integers from i to \(j-1\) included.
References
Aichernig, B.K., Tappler, M.: Symbolic input-output conformance checking for model-based mutation testing. In: USE@FM 2015, Elsevier (2015). https://doi.org/10.1016/j.entcs.2016.01.002
Alur, R., Dill, D.L.: A theory of timed automata. Theor. Comput. Sci. (1994). https://doi.org/10.1016/0304-3975(94)90010-8
Andrade, W.L., Machado, P.D.L., Jéron, T., Marchand, H.: Abstracting time and data for conformance testing of real-time systems. In: ICST Workshops (2011). https://doi.org/10.1109/ICSTW.2011.82
Bannour, B., Escobedo, J.P., Gaston, C., Le Gall, P.: Off-line test case generation for timed symbolic model-based conformance testing. In: ICTSS (2012). https://doi.org/10.1007/978-3-642-34691-0_10
Bannour, B., Lapitre, A., Le Gall, P., Nguyen, T.: Symbolic path-guided test cases for models with data and time, version of this paper extended with appendix (2023). https://doi.org/10.48550/arXiv.2309.06840
Benharrat, N., Gaston, C., Hierons, R.M., Lapitre, A., Le Gall, P.: Constraint-based oracles for timed distributed systems. In: Yevtushenko, N., Cavalli, A.R., Yenigün, H. (eds.) ICTSS 2017. LNCS, vol. 10533, pp. 276–292. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-67549-7_17
de Boer, F.S., Bonsangue, M.: On the nature of symbolic execution. In: ter Beek, M.H., McIver, A., Oliveira, J.N. (eds.) FM 2019. LNCS, vol. 11800, pp. 64–80. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30942-8_6
van den Bos, P., Tretmans, J.: Coverage-based testing with symbolic transition systems. In: Beyer, D., Keller, C. (eds.) TAP 2019. LNCS, vol. 11823, pp. 64–82. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31157-5_5
CEA: diversity, eclipse formal modeling project. https://projects.eclipse.org/proposals/eclipse-formal-modeling-project (2023)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Escobedo, J.P., Gaston, C., Gall, P.L., Cavalli, A.R.: Testing web service orchestrators in context: a symbolic approach. In: SEFM, pp. 257–267. IEEE Computer Society (2010)
Frantzen, L., Tretmans, J., Willemse, T.A.C.: Test generation based on symbolic specifications. In: FATES (2004). https://doi.org/10.1007/978-3-540-31848-4_1
Frantzen, L., Tretmans, J., Willemse, T.A.C.: A symbolic framework for model-based testing. In: Havelund, K., Núñez, M., Roşu, G., Wolff, B. (eds.) FATES/RV -2006. LNCS, vol. 4262, pp. 40–54. Springer, Heidelberg (2006). https://doi.org/10.1007/11940197_3
Gaston, C., Hierons, R.M., Le Gall, P.: An implementation relation and test framework for timed distributed systems. In: ICTSS (2013). https://doi.org/10.1007/978-3-642-41707-8_6
Gaston, C., Le Gall, P., Rapin, N., Touil, A.: Symbolic execution techniques for test purpose definition. In: TestCom (2006). https://doi.org/10.1007/11754008_1
Henry, L., Jéron, T., Markey, N.: Control strategies for off-line testing of timed systems. Formal Methods Syst. Des. (2022). https://doi.org/10.1007/s10703-022-00403-w
Hessel, A., Larsen, K.G., Mikucionis, M., Nielsen, B., Pettersson, P., Skou, A.: Testing real-time systems using UPPAAL. In: FORTEST (2008). https://doi.org/10.1007/978-3-540-78917-8_3
Janssen, R., Tretmans, J.: Matching implementations to specifications: the corner cases of ioco. In: Hung, C., Papadopoulos, G.A. (eds.) SAC. ACM (2019). https://doi.org/10.1145/3297280.3297496
Jéron, T.: Symbolic model-based test selection. In: Machado, P.D.L. (ed.) SBMF. Elsevier (2008). https://doi.org/10.1016/j.entcs.2009.05.051
King, J.C.: Symbolic execution and program testing. Commun. ACM 19(7), 385–394 (1976)
Krichen, M., Tripakis, S.: Black-box conformance testing for real-time systems. In: Graf, S., Mounier, L. (eds.) SPIN 2004. LNCS, vol. 2989, pp. 109–126. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24732-6_8
Krichen, M., Tripakis, S.: Interesting properties of the real-time conformance relation tioco. In: Barkaoui, K., Cavalcanti, A., Cerone, A. (eds.) ICTAC 2006. LNCS, vol. 4281, pp. 317–331. Springer, Heidelberg (2006). https://doi.org/10.1007/11921240_22
Luthmann, L., Göttmann, H., Lochau, M.: Compositional liveness-preserving conformance testing of timed I/O automata. In: Arbab, F., Jongmans, S.-S. (eds.) FACS 2019. LNCS, vol. 12018, pp. 147–169. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-40914-2_8
Marsso, L., Mateescu, R., Serwe, W.: TESTOR: a modular tool for on-the-fly conformance test case generation. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10806, pp. 211–228. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_13
Rusu, V., Marchand, H., Jéron, T.: Automatic verification and conformance testing for validating safety properties of reactive systems. In: Fitzgerald, J., Hayes, I.J., Tarlecki, A. (eds.) FM 2005. LNCS, vol. 3582, pp. 189–204. Springer, Heidelberg (2005). https://doi.org/10.1007/11526841_14
Standard, E.: Methods for testing and specification (MTS); the testing and test control notation version 3; Part 1: TTCN-3 core language (2005)
von Styp, S., Bohnenkamp, H., Schmaltz, J.: A conformance testing relation for symbolic timed automata. In: Chatterjee, K., Henzinger, T.A. (eds.) FORMATS 2010. LNCS, vol. 6246, pp. 243–255. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15297-9_19
Tretmans, J.: Test generation with inputs, outputs, and quiescence. In: Margaria, T., Steffen, B. (eds.) TACAS 1996. LNCS, vol. 1055, pp. 127–146. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61042-1_42
Tretmans, J., Janssen, R.: Goodbye ioco. In: a journey from process algebra via timed automata to model learning. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-15629-8_26
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Bannour, B., Lapitre, A., Gall, P.L., Nguyen, T. (2024). Symbolic Path-Guided Test Cases for Models with Data and Time. In: Cámara, J., Jongmans, SS. (eds) Formal Aspects of Component Software. FACS 2023. Lecture Notes in Computer Science, vol 14485. Springer, Cham. https://doi.org/10.1007/978-3-031-52183-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-031-52183-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-52182-9
Online ISBN: 978-3-031-52183-6
eBook Packages: Computer ScienceComputer Science (R0)








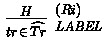 for
for 