Topological Network-Control Games

Abstract

The paper introduces new combinatorial games, called topological network-control games, played on graphs. These games model the influence of competing two parties aiming to control a given network. In a such game given the network, the players move alternatively. At each turn, a player selects an unclaimed vertex and its unclaimed neighbours within distance t. The players obey the topological condition that all claimed vertices stay connected. The goal is to decide which player claims the majority of the vertices at the end of the play. We study greedy, symmetric and optimal strategies. We solve the topological network-control games on various classes of graphs. This progresses our understanding of combinatorial games played on graphs. We prove that finding an optimal winning strategy is a PSPACE-complete problem.

B. Khoussainov—Acknowledges the National Science Foundation of China under Grant No. 62172077.

1 Introduction, Preliminary Definitions and Results

We introduce new combinatorial games played on finite graphs. These games are called topological network-control games. These games model the influence of competing two parties aiming to control the network by preserving connectedness property. Below we present basic definitions, preliminary concepts, related work and our contribution.

1.1 Statement of the Problem

Let $G = (V,E)$ be a finite graph. We assume that the graphs are simple, that is, the graphs are undirected, have no loops and multiple edges. For a vertex $x \in V$ in $G = (V, E)$, and an integer $t \ge 0$, the t-neighbourhood of x, denoted by $\mathcal N_t(x)$, is the set of all vertices at distance at most t from x. So, $\mathcal N_0(x) = {x}$ and $\mathcal N_t(x) \subseteq \mathcal N_{t+1}(x)$ for all $t \ge 0$. Vertices in $\mathcal N_t(x)$ are called t-neighbours of x. For a set of vertices $X \subseteq V \text { in }G = (V,E)$, and an integer $t \ge 0$, the t-neighbourhood of X is denoted by $\mathcal N_t(X) = \cup _{x \in X}\mathcal N_t(x)$. We fix t that will be our parameter.

Now we define topological network-control game played on $G=(V,E)$. There are two players: Player 1 and Player 2. The opponent of Player $\epsilon$, where $\epsilon \in \{0,1\}$, is denoted by Player $\bar{\epsilon }$. Each play consists of rounds. At odd rounds Player 1 moves. At even rounds Player 2 moves. Player 1 starts the first round. At this round the player selects a vertex x and claims (all vertices in) $\mathcal N_t(x)$. Let $X_{2i-1}$ be the set of all vertices claimed by the players by the end of round $2i-1$, $i>0$. At round 2i, where $i > 0$, Player 2 selects a vertex from $\mathcal N_{t+1}(X_{2i-1}) / X_{2i-1}$, and then claims the selected vertex and its unclaimed t-neighbour vertices. Let $X_{2i}$ be the set of all vertices claimed by the players by the end of round 2i, $i>0$. At round $2i+1$, where $i > 0$, Player 1 selects a vertex in $\mathcal N_{t+1}(X_{2i}) / X_{2i}$, and then claims the selected vertex and its unclaimed t-neighbour vertices.

Let t be the round at which no vertices can be claimed. If $X_t=V$, then the play stops. If $V \ne X_t$, then the player whose turn it is at round t, selects a new vertex (from a component with unclaimed vertices) and claims its t-neighbourhood, and the play continues on just as above.

To define a winner, we need a few notations. By $C_{1, 2i+1}$ we denote the set of vertices claimed by Player 1 at the end of round $2i+1$, $i\ge 0$. Similarly, $C_{2, 2i+2}$ denotes the set of vertices claimed by Player 2 at the end of round $2i+2$. If $S_{2i+1}$ is the set of vertices claimed by Player 1 at round $2i+1$, then $C_{1, 2i+1}=C_{1, 2i-1}\cup S_{2i+1}$. Similarly, $C_{2, 2i+2}=C_{1, 2i}\cup S_{2i+2}$.

Once the play stops, let $C_1$ and $C_2$ be all vertices claimed by Player 1 and Player 2, respectively. The sets $C_1$ and $C_2$ partition G.

Definition 1

We say that Player $\epsilon$ wins the play if $|C_{\epsilon }|>|C_{\bar{\epsilon }}|$. If $|C_{\epsilon }|=|C_{\bar{\epsilon }}|$, then we say that the play is a draw.

If G is connected, then the set of claimed vertices is connected at any round. Connectedness is a topological property, and hence we call our games topological network-control game. We assume the reader is familiar with the notion of strategy. A player is the winner of the topological network-control game played on G if the player has a winning strategy. Our goal is twofold. First, we want to solve games by designing algorithms that given a game decide the winner. Second, we want to extract winning strategies for the winners. Note that when $t=0$, Player 1 wins iff |V| is odd. So, we always assume that $t>0$.

1.2 Preliminaries and Basic Results

Assume that the players play the game on G. By (S, v) we denote a move where Player $\epsilon$ selects vertex v and claims the set of vertices S on G. Thus, a play is a sequence $(S_1,v_1)$, $\ldots$, $(S_i, v_i)$ of selected nodes and claimed vertices at each round. The configuration determined by this play is the tuple $(G_i, C_i)$, where

• 1. The set $G_i$ is the sub-graph of G that consists of all unclaimed vertices at the end of the play, and thus $G_i=V\setminus (S_1 \cup S_2 \cup \ldots S_i)$

• 2. The set $C_i$ is a set of vertices which players can select in $G_i$. Thus, $C_i=\mathcal N_{t+1}(S_1 \cup S_2 \cup \ldots S_i) \setminus (S_1 \cup S_2 \cup \ldots S_i)$.

Greedy and monotonic strategies. During a game, the players might follow a greedy strategy.

Definition 2

A greedy strategy is one that, at any round, selects a vertex with the maximal number of unclaimed t-neighbours.

Greedy strategies could be losing strategies.

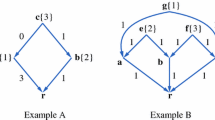
Example 1

Consider the graph in Fig 1. Assume $t=1$. Player 1’s first greedy move is the vertex of degree 5. Player 2 responds by selecting the vertex of degree 4. Then Player 1 greedily selects the vertex of degree 3. Player 2 selects the vertex of degree 4 and wins.

Fig. 1.

Greedy strategy does not always help

However, greedy strategies might be useful if they satisfy monotonicity property. Let (G, C) be a configuration of a play. By max-$deg_t(G,C)$ we denote the maximal cardinality among cardinalities of the sets $\mathcal N_{t}(v)$, where $v\in C$. This corresponds to a greedy move in the configuration (G, C).

Definition 3

A strategy is monotonic if for any play $(S_1,v_1)$, $\ldots$, $(S_i, v_i)$, $\ldots$ consistent with the strategy, max-$deg_t(G_i, C_i) \ge max$-$deg_t(G_{i+1}, C_{i+1})$, where $(G_i, C_i)$ is the configuration determined by the play $(S_1,v_1), (S_2, v_2), \ldots , (S_i, v_i)$.

Example 2

If $G=C$ then Player 1 has a monotonic greedy strategy on (G, C). Moreover, Player 2 can guarantee to lose at most max-$deg_t(G,C)$ vertices.

Lemma 1

Assume that Player 1 has a monotonic greedy strategy on G. Then Player 1 can guarantee to not lose the game.

Proof

Fix a monotonic greedy strategy for Player 1. Let $(S_1,v_1)$, $\ldots$, $(S_n, v_n)$ be a play consistent with the strategy and $(G_0,C_0),\ldots , (G_n,C_n)$ be the corresponding configurations. For all $i=1,\ldots ,\lfloor \frac{n}{2}\rfloor$, $|S_{2i-1}|= max$-$deg_t(G_{2i-2}, C_{2i-2}) \ge max$-$deg_t(G_{2i-1}, C_{2i-1})\ge |S_{2i}|$. Therefore, $\sum _{i=1}^{\lceil \frac{n}{2}\rceil } |S_{2i-1}|\ge \sum _{i=1}^{\lfloor \frac{n}{2}\rfloor } |S_{2i}|$ and Player 1 doesn’t lose.

We apply this lemma to a few examples of graphs. For this, we recall several specific classes of graphs. These graphs will further be studied in this paper.

The path graph of size n, $Path_n$, has vertices $\{1,\ldots ,n\}$ with the edge relation between the consecutive integers. The cycle graph of size $n \ge 3$, $Cycle_n$, is obtained from $Path_n$ by adding the edge between 1 and n. A caterpillar is a tree in which all non-leaf vertices are on a path and leaves are at distance 1 from the path. We call the path the central path. Let G be a caterpillar with central path $Path_n$. A caterpillar is degree-homogeneous if degrees of all vertices along the central path are the same. By $Caterpillar_{n,k}$ we denote the degree-homogeneous caterpillar whose central path is $Path_n$ in which every vertex has degree k. Not hard to see that Player 1 has a monotonic greedy strategy on $Path_n$, $Cycle_n$, and $Caterpillar_{n,m}$. Therefore, we have the following corollary.

Corollary 1

Player 1 never loses $Path_n$, $Cycle_n$, and $Caterpillar_{n,m}$.

Symmetric strategies. Two configurations $(G_1,C_1)$ and $(G_2,C_2)$ are isomorphic if there exists an isomorphism $f:G_1\rightarrow G_2$ from $G_1=(V_1,E_1)$ to $G_2=(V_2,E_2)$ such that for all x in $G_1$ we have $x\in C_1$ iff $f(x) \in C_2$.

Definition 4

Let $f:G_1\rightarrow G_2$ be an isomorphism between two disjoint configurations $(G_1, C_1)$ and $(G_2, C_2)$. Let $(G,C)=(G_1,C_1)\cup (G_2, C_2)$ be the union of $(G_1, C_1)$ and $(G_2, C_2)$: $V=V_1\cup V_2$, $E=E_1\cup E_2$ and $C=C_1\cup C_2$. The symmetric strategy for Player $\epsilon$ is this: if Player $\overline{\epsilon }$ selects x from $G_1$ then Player $\epsilon$ selects f(x); if Player $\overline{\epsilon }$ selects x from $G_2$ then Player $\epsilon$ selects $f^{-1}(x)$.

Lemma 2

If $(G_1,C_1)$ and $(G_2,C_2)$ are isomorphic, then Player 2 guarantees a draw in the configuration $(G,C)=(G_1,C_1)\cup (G_2,C_2)$.

Optimal strategies. Here is a definition of optimal strategies.

Definition 5

Let $w\ge 0$ be an integer. A strategy for Player $\epsilon$ is w -optimal if

• 1. The strategy can guarantee that Player $\epsilon$ wins any play with at least w more vertices independent on the opponent’s strategies.

• 2. The opponent, Player $\bar{\epsilon }$, has a strategy that guarantees that no more than w vertices are lost independent on strategies of Player $\epsilon$.

Let (G, C) be a configuration. We define the integer Opt(G, C) such that player $\epsilon$ faced with the configuration can guarantee a win with at least Opt(G, C) vertices starting at (G, C):

• 1. If $G = \emptyset$ then $Opt(G,C) = 0$.

• 2. If $C=\emptyset$, Player $\epsilon$ can select any vertex $v \in G$ and make corresponding moves (S, v). Let $S_1, \ldots , S_m$ be all possible moves of player $\epsilon$ at (G, C). Let $(G_i,C_i)$ be updated configuration after moving $S_i$ and $n(S_i)$ be the cardinality of $S_i$, $i=1,\ldots , m$. Set $Opt(G,C) = \max _{1\le i \le m}\{n(S_i) - Opt(G_i, C_i)\}$.

Lemma 3

Player $\epsilon$ has an Opt(G, C)-optimal strategy at (G, C). Moreover, the computation of Opt(G, C)-optimal strategy is in PSPACE.

Proof

The case $G = \emptyset$ is clear. Assume that for all $(G',C')$ with $0\le n(G') \le k$ the lemma is true. Let (G, C) be a configuration with $n(G) = k+1$. Let $S_1, \ldots , S_m$ be possible moves at (G, C) . By induction, Player $\bar{\epsilon }$ has an $Opt(G_i,C_i)$-optimal strategy on $(G_i,C_i)$. So Player $\bar{\epsilon }$ guarantees to lose no more than $\max _{1\le i \le m}\{n(S_i) - Opt(G_i, C_i)\}$ vertices, and Player $\epsilon$ guarantees to win at least $\max _{1\le i \le m}\{n(S_i) - Opt(G_i, C_i)\}$ vertices. This implies that $Opt(G,C) = \max _{1\le i \le m}\{n(S_i) - Opt(G_i, C_i)\}$. Showing that Opt(G, C)-optimal strategy can be computed in PSPACE is standard.

1.3 Related Work and Our Contribution

This work belongs to the area of combinatorial games. Typically these games are of finite duration played on spaces of finite configurations. Combinatorial games are usually classified as scoring games and non-scoring games. In scoring games, a player wants to collect a certain amount of points to win the game. Examples of scoring games are graph-grabbing game [13, 23], median game [12], orthogonal colouring game [3], Vertex-Capture Game [8] and the largest connected subgraph game [6, 7]. In non-scoring games, the players aim to put their opponent into a deadlock (e.g., the opponent makes the last move). Examples of non-scoring games are GRIM [1], Nim on graphs [11, 17], Kayles on graphs [9, 10, 18,19,20, 24], game 0.33 [4] Weighted Arc and generalized Kayles [15]. Our games are obviously scoring games as the winner is the one who claims the most number of vertices of the graph. However, one unexpected side of our games is that they exhibit a behaviour of non-scoring games when the game graph G consists of more than one component. Indeed, once players start playing in a component C of G, the players need to claim all the vertices of C before they move to the other components. Therefore, if a player makes the last move on C, then the opponent will start a new component and might gain an advantage. This implies that the players need to take into account the parity of the last move in C. So, when the players play the games on graphs that consists of more than one component, the parties of the last moves on the components matter. This is a typical feature of non-scoring games. Here now we briefly list the main contributions of this work:

1.:

We introduce topological network-control games. These games model the influence of competing parties to control a given network. The restraint is that the players need to ensure connectivity of the set of claimed vertices.

2.:

In combinatorial game theory, understanding games in algebraically simple graphs (such as paths, cycles, trees, etc.) usually constitutes bottleneck problems [2, 5, 14, 16]. That is why we start by studying our games in these classes of graphs. We succeed to characterize some classes of graphs where Player 1 wins. Our proofs are combinatorial and are based on careful analysis of configuration spaces of games. These are presented in Theorems 1, 2, and 3 of Sect. 2.

3.:

As we mentioned above, one novel side of our games is that they exhibit characteristics of both scoring games and non-scoring games. We study this interplay between scoring condition (the number of vertices claimed) and the parity condition (the player moving the last loses) on graphs through two recursively defined functions $F_{even}$ and $S_{odd}$. We then fully describe a non-trivial behaviour of these functions on path graphs. This is presented in Theorem 4 of Sect. 3.

4.:

We fully characterize the graphs $Path_{\ell _1} \cup Path_{\ell _2}$ (disjoint union of two path graphs), where Player 1 wins. Our charcaterization makes use of a computer program that lists all graphs $Path_{\ell _1} \cup Path_{\ell _2}$, where $\ell _1\le 100$ and $\ell _2\le 100$, won by Player 1. See Theorem 5 in Sect. 4. The proof takes into account the interplay between the parity and the number claimed vertices.

5.:

We prove that finding optimal strategies is a PSPACE-complete problem. There are two key difficulties in the proof. The first is that the cardinalities of t-neighbourhoods of unclaimed vertices depend on configurations. In comparison, this does not happen in the Competetive Facility Allocation problem, where coding of a quantified Boolean Formula becomes easy [21]. The second is the connectivity condition put on the set of claimed vertices. These two conditions make it challenging to code PSPACE-complete problems into our games.

We finally mention the recent work by Z. Liang, B. Khoussainov, and M. Xiao on network-control games played on graphs [22]. The work of this paper is a natural and independent follow-up of the control-network games. As opposed to topological network-control games, network-control games lack the connectivity condition of the set of claimed vertices. In particular, in network-control games, players can select and claim vertices with no regards (in terms of connectivity) to already claimed vertices. In this sense, network-control games from [22] do not exhibit characteristics of non-scoring games as we described above. Hence, the proof methods and ideas in this work are, in many ways, orthogonal to those in the study of network-control games. For instance, greedy strategies in network-control games suffice to prove that Player 1 never loses any network-control game. In contrast, we already showed that the greedy strategies in topological network-control games can be losing for Player 1. Furthermore, we do not know if there is graph G where Player 1 loses the topological network-control game.

2 Games on Paths, Cycles, and Caterpillars

The strategies defined above can be used to analyze the topological network-control games on paths, cycles, and caterpillars. Note that by Corollary 1 Player 1 never loses these graphs.

Theorem 1

Player 1 wins the topological network-control games on paths.

Proof

Player 1 wins $Path_n$ with $n \le 2t + 1$ by claiming all vertices in the first move. Assume $n > 2t + 1$. If $n = 2k+1$ then Player 1 has a monotonic greedy strategy on $Path_n$ and by Lemma 1, Player 1 wins $Path_n$. Assume $n = 2k$. Player 1 selects the middle vertex k and claims its t-neighbours $\mathcal N_t(k)$. Both players make greedy moves. In the remaining configuration, Player 2 claims one more vertex at most. Therefore, Player 1 wins 2t vertices. If Player 2 makes non-greedy moves more times, Player 2 will lose more vertices.

Theorem 2

Player 1 wins the game on $Cycle_n$ iff $n \ne 0 \ \mod \ (4t+2)$.

Proof

It is clear that Player 1 wins $Cycle_n$ if $n < 4t + 2$. Assume $n\ge 4t+2$. If $n =0 \mod (4t + 2)$, then both of the players must follow greedy strategies. Otherwise, the player making a non-greedy move loses. Therefore, the last move will be made by Player 2. This guarantees a draw for Player 2 due to the condition on n. Assume $n \ne 0 \mod (4t + 2)$. Player 1 selects p, say $p = 1$, and claimed its t-neighbours $\mathcal N_t(p)$. Assume both players must follow greedy strategies. Because $n \ne 0 \mod (4t + 2)$, Player 1 can claim more vertices than Player 2 in last two rounds. If Player 2 makes non-greedy moves until Player 1 makes more moves, Player 1 will claim more vertices than before.

The proof of the next theorem is more involved but uses the same ideas as the proofs of the theorems above.

Theorem 3

Player 1 wins the games on $Caterpillar_{n,k}$.

3 Parity Vs the Number of Claimed Vertices

Suppose that the game graph G consists of more than one component, say $C_1$ and $C_2$. Even if Player 1 wins topological network-control game on each of these components $C_1$ and $C_2$, this does not guarantee that Player 1 wins G. The reason is that Player 1 might make the last move playing on each of these components. Therefore, once all vertices in one of the components are claimed, Player 2 continues the game by starting the remaining component. Thus, each player has two, somewhat opposing, aims. On the one hand, the player would like to win as many nodes as possible in a given component. On the other hand, the player would like the opponent to make the last move in the current component to take the advantage of the remaining component.

A natural question is thus the following. Assume that the players play the game on connected graph G. How many nodes should a player give up to ensure that the opponent makes the last move? To answer this question, below we provide a general framework, and apply it to the case when the underlying graphs are paths graphs. Even the case of paths turns out to involve non-trivial combinatorial and inductive arguments.

Let (G, C) be a configuration. Let us define two functions $F_{even}(G,S)$ and $S_{odd}(G,C)$. The function $F_{even}(G,S)$ computes the maximal number of vertices won by the first player who starts the game at (G, S) under the assumption that the player can force the opponent to make the last move in the game. Similarly, $S_{even}(G,S)$ computes the maximal number of vertices won by the second player in the game (G, C) under the assumption that the player can force the opponent to make the last move in the game. Note that the value $F_{even}(G,C)$ and $S_{odd}(G,C)$ can be undefined if the player can not force the opponent to make the last move. We defined these functions through mutual recursion as follows:

• Set $F_{even}(\emptyset , \emptyset )=0$ and $S_{odd}(\emptyset , \emptyset )=-\infty$.

• Let $S_1, \ldots , S_m$ be all possible moves of a player at (G, C). Let $(G_i,C_i)$ be the configuration after move $S_i$, $i=1,\ldots , m$. Set

  $$\begin{array}{c} F_{even}(G,C)=\max \{ n(S_i)+S_{odd}(G_i, S_i) \mid i=1, \ldots , m\}\text {, and }\\ S_{odd}(G,C)=\min \{-n(S_i)+F_{even}(G_i, S_i) \mid i=1, \ldots , m\} \end{array}$$

As an example, on graphs $Path_{13}$ and $Path_{18}$, one can compute that we have $F_{even}(Path_{13}, \emptyset )=-1$ and $F_{18}(Path_{18}, \emptyset )=-2$, respectively. Also, from the definitions of $F_{even}$ and $S_{odd}$, we have the following corollary.

Corollary 2

$F_{even}(G,C) \ne -\infty$ if and only if $S_{odd}(G,C) = -\infty$.

It turns out guaranteeing that the opponent makes the last move can be costly even in such graphs as $Path_n$. The proof of the next theorem is based on a careful analysis of $F_{even}$ and $S_{odd}$ functions.

Theorem 4

Consider a game played on $Path_n$ with $t=1$. If $n<3$ then $F_{even}(Path_n) = -\infty$ and $S_{odd}(Path_n) = -n$. Otherwise:

$$ S_{odd}(Path_n) = \left\{ \begin{aligned} -1 - \lfloor \frac{n}{5} \rfloor & \text { if } \ n = 1 \mod 5 \\ - \lfloor \frac{n}{5} \rfloor & \text { if } \ n = 2 \mod 5 \text { and } n\ne 7\\ -3 & \text { if } \ n = 7 \\ -\infty & \ \text {otherwise} \end{aligned} \right. $$

$$ F_{even}(Path_n) = \left\{ \begin{aligned} -\lfloor \frac{n}{5} \rfloor + 4 & \text { if } \ n = 0 \mod 5, n \ne 0 \text { and } n \ne 5\\ -\lfloor \frac{n}{5} \rfloor + 1& \text { if } \ n = 3 \mod 5 \\ -\lfloor \frac{n}{5} \rfloor + 2 & \text { if } \ n = 4 \mod 5 \\ 0 & \text { if } \ n = 0 \\ 1 & \text { if } \ n = 5 \\ -\infty & \ \text { otherwise} \end{aligned} \right. $$

4 Topological Network-Control Games on $Path_{\ell _1} \cup Path_{\ell _2}$

From the previous section, we see that controlling the parity is a challenging task even on path graphs. Our goal is to settle the topological network-control games problem for the class of graphs of the type $Path_{\ell _1} \cup Path_{\ell _2}$. The previous section shows that the players can not rely solely on only greedy strategies or parity control strategies in $Path_{\ell _1} \cup Path_{\ell _2}$. The players need to adapt different strategies, e.g., mixing greedy and parity strategies. Note that Player 1 never loses the game on $Path_{\ell _1} \cup Path_{\ell _2}$. Thus, we aim to characterize those graphs $Path_{\ell _1} \cup Path_{\ell _2}$ where Player 1 guarantees a win. For this section we assume that $t=1$.

Our next Lemma 4 is proved through a computer-assisted technique. The code for the lemma computes the function $Opt(Path_{\ell _1}\cup Path_{\ell _2}, \emptyset )$¹

Lemma 4

Player 2 can guarantee a draw in the game $Path_{\ell _1} \cup Path_{\ell _2}$, where ${1\le \ell _1 \le \ell _2 < 100}$, if and only if $\{\ell _1, \ell _2\}\in \{\{1,1\}$, $\{2,2\}$, $\{7,7\}$, $\{7,6x+5\}$, $\{2,6x\}$, $\{6x,6y\}$, $\{6x+5,6y+5\}\}_{1\le x,y}$.

This lemma can be used to fully characterize those games on $Path_{\ell _1} \cup Path_{\ell _2}$ where Player 2 guarantees a draw. We prove the theorem below based on the analysis of several conditions on $\ell _1$ and $\ell _2$. We showcase our proofs on several cases.

Theorem 5

Player 2 guarantees a draw on $Path_{\ell _1} \cup Path_{\ell _2}$ iff $\{\ell _1, \ell _2\}$ belongs to $\{\{1,1\}$ $,\{2,2\}$ $,\{7,7\}$ $,\{7,6x+5\}$ $,\{2,6x\}$ $,\{6x,6y\}$ $,\{6x+5,6y+5\}\}_{1\le x,y}$.

Proof

Our proof is based on the analysis of 9 cases (and their subcases). By the lemma above we can always assume that either $\ell _1\ge 100$ or $\ell _2 \ge 100$.

Case 1: The parities of $\ell _1$ and $\ell _2$ are different. Without loss of generality, assume $\ell _1$ is odd, $\ell _2$ is even, with $\ell _1 \ge 3$ and $\ell _2 \ge 2$. Then Player 1 wins as follows. The player selects the middle node in the path of odd length (greater than 1) and then uses a greedy strategy. Player 1 wins at least 3 vertices. Even if Player 2 starts the line of even length, the play can win at most 2 vertices. If the length of the odd path graph is 1, then Player starts with the even length path graph and wins two nodes guaranteeing the overall win.

Case 2: $\ell _1 = 4 \ (\mod \ 6)$. Player 1 uses a greedy strategy on $Path_{\ell _1}$ starting from one end of $Path_{\ell _1}$. If Player 2 uses a greedy strategy, then the last move on $Path_{\ell _1}$ is made by Player 2. Hence, in this case Player 1 wins the game. In order to ensure that Player 1 makes the last move in $Path_{\ell _1}$, Player 2 must give up the greedy strategy at least twice. Thus, either Player 1 starts the second line $Path_{\ell _2}$ or wins at least 3 vertices on $Path_{\ell _1}$. In either case, Player 1 wins the game.

Case 3: $\ell _1=3 \ (\mod \ 6)$. Player 1 starts using the greedy strategy on $Path_{\ell _1}$ from one end of the graph. If Player 2 also plays a greedy strategy, then in the last move on $Path_{\ell _1}$, Player 1 will claim 2 vertices instead of greedy 3. In this way, Player 2 makes the last move in $Path_{\ell _1}$. Hence, Player 1 moves to the next line and wins the game. This implies that Player 2 must abandon its greedy strategy on $Path_{\ell _1}$ at least four times. If this happens, Player 1 will have won at least 4 vertices when the play moves to $Path_{\ell _2}$. So Player 1 wins.

Case 4: $\ell _1=2 \ (\mod \ 6)$ with $\ell _1 > 2$. Player 1 makes a move from one side of $Path_{\ell _1}$. In the first round, Player 1 only claims 2 nodes. After that Player 1 will always use a greedy strategy. If Player 2 uses a greedy strategy, then in the last move on $Path_{\ell _1}$ Player 1 claims two vertices (instead of 3). In this case, Player 2 makes the last move in $Path_{\ell _1}$. Hence, Player 1 starts $Path_{\ell _2}$ (with a draw on $Path_{\ell _1}$) and wins the game. Therefore, Player 2 must abandon its greedy strategy while playing on $Path_{\ell _1}$ at least 4 times. In this game Player 2 moves to $Path_{\ell _2}$, where Player 1 won at least 3 vertices in $Path_{\ell _1}$. So, Player 1 wins.

Case 5. $\ell _1 = 1 \ (\mod \ 6)$ with $\ell _1 > 7$. Player 1 makes a move from the middle of $Path_{\ell _1}$, dividing the $Path_{\ell _1}$ into two parts. The length of two parts are $6x_1 + 3, 6x_2 + 1$ respectively. In previous rounds, Player 1 gives up once in first part. After that Player 1 will always use a greedy strategy. If Player 2 uses a greedy strategy, Player 2 makes last move in $Path_{\ell _1}$. Hence, Player 1 starts $Path_{\ell _1}$(loses 1 node on $Path_{\ell _1}$ and wins the game). Therefore Player 2 must abandon its greedy strategy while playing on $Path_{\ell _1}$ at least 3 times. In this game the game moves to $Path_{\ell _2}$, where Player 1 won at least 5 vertices in $Path_{\ell _1}$. So, Player 1 wins.

Case 6. $\ell _1 = 5 \text { and } \ell _2 = 5 \ (\mod \ 5)$. In this case, we show that Player 1 wins on $Path_{\ell _1} \cup Path_{\ell _2}$. Player 1 starts by selecting a vertex in $Path_{\ell _1}$ so that Player 1 wins 1 vertex and Player 2 makes the last move in $Path_{\ell _1}$. Since Player 1 wins on $Path_{\ell _2}$, Player 1 wins the game.

Case 7. $\ell _1 = 5 \ (\mod \ 6)$ and $\ell _2 = 5 \ (\mod \ 6)$ with $\ell _1 > 7 \text { and } \ell _2 > 7$. In this case we show that Player 2 doesn’t lose. W.L.O.G, assume Player 1 starts by selecting a vertex in $Path_{\ell _1}$. Then there are 4 subcases.

Subcase 1: The unclaimed vertices of $Path_{\ell _1}$ consist of two parts L, R where $|L|=6x_1$ and $|R|=6x_2+2$. Consider the play in the unclaimed parts of $Path_{\ell _1}$. If Player 1 applies a greedy strategy all the time, then Player 2 also follows a greedy strategy until the number of unclaimed vertices of L is less than 10. By abandoning greedy strategy for one time in L, Player 2 guarantees that the opponent wins three vertices and makes the last move in $Path_{\ell _1}$. Since Player 2 wins at least 3 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon its greedy strategy at least 6 times in $Path_{\ell _1}$ so that Player 2 makes the last move in $Path_{\ell _1}$. Correspondingly, Player 2 wins 3 vertices in $Path_{\ell _1}$. Since Player 1 wins at most 3 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game.

Subcase 2: The unclaimed vertices of $Path_{\ell _1}$ consist of two parts L, R where $|L|=6x_1+3$ and $|R|=6x_2+5$. If Player 1 applies a greedy strategy all the time, then Player 2 also follows a greedy strategy until the number of unclaimed vertices of L is less than 7. By abandoning greedy strategy for one time, Player 2 guarantees that the opponent wins three vertices and makes the last move in $Path_{\ell _1}$. Since Player 2 wins at least 3 vertices in $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon at least 6 times in $Path_{\ell _1}$ so that Player 2 makes the last move in $Path_{\ell _1}$. Correspondingly, Player 2 wins 3 vertices in $Path_{\ell _1}$. Since Player 1 wins at most 3 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game.

Subcase 3: The unclaimed vertices of $Path_{\ell _1}$ consist of two parts L, R where $|L|=6x_1+1$ and $|R|=6x_2+1$. If both players apply greedy strategy, then Player 1 wins 3 vertices and makes the last move in. Since Player 2 wins at least 3 vertices in $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon at least 6 times in $Path_{\ell _1}$ so that Player 2 makes the last move in $Path_{\ell _1}$. Correspondingly, Player 2 wins 3 vertices in $Path_{\ell _1}$. Since Player 1 wins at most 3 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game.

Subcase 4: The unclaimed vertices of $Path_{\ell _1}$ consist of two parts L, R where $|L|=6x_1+4$ and $|R|=6x_2+4$. If both players apply greedy strategy, then Player 1 wins 3 vertices and makes the last move in. Since Player 2 wins at least 3 vertices in $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon at least 6 times in $Path_{\ell _1}$ so that Player 2 makes the last move in $Path_{\ell _1}$. Correspondingly, Player 2 wins 3 vertices in $Path_{\ell _1}$. Since Player 1 wins at most 3 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game.

Case 8: $\ell _1 = 0 \ (\mod \ 6) \text { and } \ell _2 = 0 \ (\mod \ 6)$. In this case, we show that Player 2 doesn’t lose. W.L.O.G, assume Player 1 starts by selecting a vertex in $Path_{\ell _1}$. Then there are 2 subcases.

Subcase 1: The unclaimed vertices of $Path_{\ell _1}$ consist of two parts L, R where $|L|=6x_1$ and $|R|=6x_2+3$. Assume both players apply greedy strategy and Player 2 abandons its greedy strategy one time in $Path_{\ell _1}$. Then Player 1 wins 2 vertices and makes the last move in $Path_{\ell _1}$. Since Player 2 wins at least 2 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon its greedy strategy at least two times in $Path_{\ell _1}$ so that Player 2 makes the last move in $Path_{\ell _1}$. Correspondingly, Player 2 wins 2 vertices in $Path_{\ell _1}$. Since Player 1 wins at most 2 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game.

Subcase 2: The unclaimed vertices of $Path_{\ell _1}$ consist of two parts L, R where $|L|=6x_1+1$ and $|R|=6x_2+2$. If both players apply greedy strategy, then Player 1 wins two vertices and makes the last move in $Path_{\ell _1}$. Since Player 2 wins at least 2 vertices in $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon its greedy strategy at least two times in $Path_{\ell _1}$ so that Player 2 makes the last move in $Path_{\ell _1}$. Correspondingly, Player 2 wins 2 vertices in $Path_{\ell _1}$. Since Player 1 wins at most 2 vertices on $Path_{\ell _2}$, Player 2 doesn’t lose the game.

Case 9: Player 2 doesn’t lose on the following subcases.

Subcases 1: $\ell _1 = 2 \text { and } \ell _2 = 0 \ (\mod \ 6)$. Note that $\ell _2\ge 100$. If Player 1 starts by selecting a vertex in $Path_{\ell _1}$, then Player 1 wins 2 vertices in $Path_{\ell _1}$. Since Player 2 wins at least 2 vertices in $Path_{\ell _2}$, Player 2 doesn’t lose the game. Therefore, assume Player 1 starts by selecting a vertex in $Path_{\ell _2}$. If both players apply greedy strategy, Player 1 wins 2 vertices and makes the last move on $Path_{\ell _2}$. Since Player 2 wins 2 vertices in $Path_{\ell _1}$, Player 2 doesn’t lose the game. Therefore Player 1 needs to abandon its greedy strategy at least two times in $Path_{\ell _2}$ so that Player 2 makes the last move in $Path_{\ell _2}$. Correspondingly, Player 2 wins 2 vertices in $Path_{\ell _2}$. Since Player 1 wins at most 2 vertices on $Path_{\ell _1}$, Player 2 doesn’t lose the game.

Subcases 2: $\ell _1 = 7 \text { and } \ell _2 = 5 \ (\mod \ 6)$. Note that $\ell _2\ge 100$. If Player 1 starts by selecting a vertex in $Path_{\ell _1}$, then Player 2 can forces Player 1 to select the last move in $Path_{\ell _1}$ and guarantee to lose at most 3 vertices. Since Player 2 wins $Path_{\ell _2}$ with at least 3 vertices, Player 2 doesn’t lose the game. Therefore, assume Player 1 starts by selecting a vertex in $Path_{\ell _2}$. Note that $Opt(Path_{7})=Opt(Path_{6x+5})=2$ where $x>0$. Therefore, following similar proofs of Case 7, one can prove that Player 2 doesn’t lose the game.

Corollary 3

Player 1 wins topological network-control games on $Path_{\ell _1} \cup Path_{\ell _2}$ if and only if $\{\ell _1, \ell _1\}$ satisfies one of the following conditions: (1) $\ell _1$ and $\ell _2$ have different parities, (2) $\ell _1= 4 \ (mod \ 6)$, (3) $\ell _1=3 \ (mod \ 6)$, (4) $\ell _1=2 \ (mod \ 6)$ except for $\{2,2\}$, $\{2,6x\}$, (5) $\ell _1=1 \ (mod \ 6)$ except for $\{1,1\}$, $\{7,7\}$, $\{7,6x+5\}$. In all other cases, Player 2 can guarantee a draw and cannot win.

5 PSPACE-Completeness

The alternating 3-TQBF problem is to determine if a fully quantified Boolean formula $\psi =\exists x_1\forall x_2\exists x_3\ldots \exists x_n\phi (x_1,x_2,\ldots ,x_n)$ is true, where $\phi$ is a conjunction of clauses with three literals. The problem is PSPACE-complete [25]. The optimal topological network-control game problem with parameter t is this:

$$ OTNC (t)=\{\langle G, w\rangle \mid \text {Player 1 has a } w\text {-optimal strategy on game { G}} \}. $$

Let $\psi$ be an alternating 3-TQBF formula with clauses $C_1,\ldots ,C_m$ and variables $x_1, \ldots ,x_n$. W.L.O.G, we assume $n > 1$, n is odd and for each pair of distinct variables $x_i$ and $x_j$, the clauses $x_i\vee \overline{x_i}\vee x_j$ and $x_i\vee \overline{x_i}\vee \overline{x_j}$ are in $\{C_i\}_{i\le m}$. We build a connected graph $G_{\psi }$ with $2n+6n(n+1)m+3m$ vertices and $n+12n(n+1)m+3m+2m^2 \ + \ m(m-1)/2$ edges such that the formula $\psi =\exists x_1\forall x_2\exists x_3\ldots \exists x_n \phi (x_1,x_2,\ldots ,x_n)$ is true iff $F(G_\psi )\ge 6nm+5m+2$. Therefore, we can prove the following theorem.

Theorem 6

The OTNC(1) problem is PSPACE-complete.