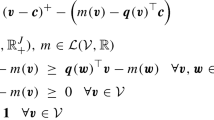Keywords

1 Introduction

We study a variant of the monopoly pricing problem where the seller (‘she’) offers an item to gain maximum benefit. The buyer (‘he’) attaches a private value \(\nu \) to the item offered, and to him this value is a personal monetary equivalent of the item. It indicates the maximum amount of money that he is willing to pay. Consequently, if this value was known to the seller, then she could have simply offered the item at a fixed price \(\nu \) and earned maximally.

However, a prudent buyer would always keep his value strictly private before the seller making her first move in order to not lose his bargaining power. It is therefore impossible for the seller to earn exactly an amount of \(\nu \) from the sale transaction. The seller designs and broadcasts a mechanism that sets out the instructions on how the buyer can communicate with her. A mechanism consists of three parts: the set of messages for the buyer to choose from, the allocation rule, and the payment rule. Once the buyer selects a message that to him is the most favourable, he will pay an amount indicated by the payment rule to the seller and be allotted the item with a certain probability that is specified by the allocation rule. Modern studies of mechanism design largely simplify due to the influential Revelation Principle [18] which allows the seller to restrict her attention to a subclass of direct mechanisms, where the message set is simply chosen as the set of all possible values of the buyer’s private value \(\nu \), without any loss of generality and revenue. In the remainder of the paper, we will henceforth use the terms mechanism and direct mechanism interchangeably.

As \(\nu \) is unknown to the seller, it may be perceived as a random variable that crisply follows a known probability distribution. In this case, [18] and [23] showed that the seller can attain a maximum expected revenue by posting a deterministic price for the item. Although without a doubt this is the most popular variant of the mechanisms currently seen in practice, especially at retail stores, several studies and observations have pointed out the advantages of the seller offering the same item to different buyers at different price points.

The assumption that the seller knows the distribution of the buyer’s private value \(\nu \) itself is not innocuous, and a question concerning the robustness of the so-called optimal mechanism has come under the spotlight [3]. A seller with limited information about \(\nu \) may consider stepping away from maximizing the expected revenue and instead leverage robust optimization (see, e.g., [2, 6]) with an aim to maximize the worst-case revenue. While this approach is methodologically sound, it may recommend a trivial and unrealistically conservative mechanism where the seller keeps the item to herself provided that the uncertainty set for \(\nu \) contains zero.

To address having limited information and also to avoid being superfluously conservative, [24] introduced a minimax regret as a decision criterion; see also [19, 21] for further justifications. Specifically in a sale transaction, the seller’s regret is defined as the difference between the hypothetical revenue that the seller could have earned if she exactly knew \(\nu \) and the actual revenue which is specified by the payment rule. Recently, it was discovered in [13] that the mechanism which attains the smallest worst-case regret is non-trivial, and it involves a piece-wise logarithmic allocation rule and a piece-wise linear payment rule even if \(\nu \) can take a value of zero. The minimax regret criterion has also been adopted in several other papers, for example, [4] and [5], with the latter aptly noting that “a deterministic pricing policy exposes the seller to substantial regret, and that the seller can decrease her exposure by offering many prices,” which underscores the importance of a randomized pricing strategy when a regret-type objective is used by the seller. Slightly differently, [8] and [27] adopted a worst-case relative regret criterion, also known as a competitive ratio, and again the benefit of randomization remains.

The principle of worst-case regret minimization resonates well with that of robust optimization. A duality technique that is frequently leveraged in the robust optimization literature is indispensable for [13] to analytically derive the optimal mechanism that minimizes the seller’s worst-case regret. We refer our readers to [26] for a broader discussion on the link between mechanism design and linear programming as well as the corresponding duality theory.

For the comprehensiveness of our literature review, we remark that a risk-neutral, ambiguity-averse seller may instead use distributionally robust optimization (e.g., [11, 17, 28]) to maximize her worst-case expected revenue when facing the inadequacy of robust optimization in mechanism design. To achieve this, the seller needs to construct an ambiguity set comprising all probability distributions of \(\nu \) that are consistent with her prior information. Listing a few important examples, [5] and [14] adopted a neighbourhood of a reference distribution of \(\nu \) with respect to the Prohorov and the Wasserstein metric, respectively, whereas [20] and [7] considered an ambiguity set that is characterized by the support, the mean, and/or higher order moments. Recently, [9] provided a unified framework for computing the robustly optimal mechanisms under different ambiguity sets of distributions.

Recently, [15] provided a follow-up on an earlier work on globalized robust optimization due to [1] and introduced an alternative to robust optimization known as ‘robust satisficing.’ When the objective function representing cost (or regret) is uncertain, robust optimization computes a solution that minimizes the worst-case cost. On the contrary, robust satisficing determines a solution that, in the nominal scenario, has a cost under the predetermined target and, in all other scenarios, a cost that only proportionately deviates from the same target. Robust satisficing has been numerically shown to produce statistically better decisions than various state-of-the-art benchmarks (see, e.g., [12, 25]), and it also satisfies several axioms from behavioral decision making. Abiding by this new principle, the decision maker needs to specify the ‘nominal scenario’ and to supply the ‘target value,’ which represents the acceptability level of the nominal objective. In this paper, we revisit the monopoly pricing problem with a regret objective that was studied by [13], but we formulate the problem using the robust satisficing ideology instead. Computationally, depending on the convexity and linearity properties of the problem (or the lack thereof), robust satisficing solutions could be exactly determined by Fenchel duality [1] or approximately attained by using either a primal decision rule [15] or a dual linear decision rule [22]. To our knowledge, we are the first to analytically solve a robust satisficing problem of this level of complexity, that is, the infinite dimensionality of the mechanism design problem and the interaction between the two agents (i.e., the buyer and the seller), without any approximation.

We summarize the main contributions of the paper as follows.

  1. 1.

    We use robust satisficing to formulate a mechanism design problem for a monopolist who has an item to liquidate and a regret minimization objective. The problem takes as input parameters the support of the buyer’s value for the item and its nominal value as well as the target regret level that should not be exceeded (that is, the threshold that the seller is willing to tolerate) under the nominal scenario. After mathematically formulating the problem, we derive a probabilistic regret bound based on its solution to provide further justification for this work.

  2. 2.

    We characterize the condition on the problem’s input that is equivalent to the problem’s feasibility. Whenever it is feasible, we analytically propose a candidate solution of the mechanism design problem, which itself is an infinite linear program. We establish that the proposed mechanisms are optimal with respect to the problem’s given input by developing tight lower bounds of the problem. Besides, we also argue that each of these lower bounds has an intimate relationship with the problem’s dual, see our online Appendix B, and we relate a subset of our recommended mechanisms to those from the existing literature on distributionally robust mechanism design.

  3. 3.

    We study two additional variants of the mechanism design problem that are similarly analytically solvable. The first extension assumes that the seller restricts her attention to a class of deterministic posted price mechanisms only, whereas the second relaxes the requirement of the target regret needing specifying.

  4. 4.

    To increase the acceptance and the relevance of the derived optimal mechanism, we interpret it as a randomized posted price mechanism, compute its statistics and compare it with the optimal deterministic posted price mechanism. Besides, we compare our mechanisms with several benchmarks including the worst-case regret minimizing mechanism; see [13], where we numerically show the dominance of our mechanism in terms of the seller’s expected regret and expected revenue, especially when the coefficient of variation of the buyer’s value falls below \(100\%\). Based on our experiment results, we also provide a guideline on how our pricing model should be calibrated.

The rest of the paper is structured as follows. Section 2 discusses how regret could be leveraged as a decision criterion in both robust optimization and robust satisficing settings. Section 3 derives the optimal mechanism for different ranges of the input parameters. Section 4 considers a restricted problem where only deterministic posted price mechanisms are considered, and Sect. 5 studies another variation of the problem where the seller is relieved from choosing the target regret. Finally, Sect. 6 reports the statistics and the performance of the proposed mechanisms in relation to the benchmarks, and Sect. 7 concludes the paper. All proofs can be found in Appendix A, which is available online.

Notation: For a logical expression \(\mathcal {E}\), we define \(\mathbbm {1}(\mathcal {E}) = 1\) if \(\mathcal {E}\) is true; = 0 otherwise, and for any real number x, we denote by \(x^+\) its positive part, that is, \(x^+ = \max \{x,0\}\). We adopt the convention for division by zero that \(a/0 = \infty \) if \(a > 0\); \(= 0\) otherwise. All logarithms have a natural base of e, and it is assumed that \(\log (0) = -\infty \). Besides, the set of all (bounded) Borel-measurable functions from \(\mathcal {D}\) to \(\mathcal {R}\) is denoted by \(\mathcal {L}(\mathcal {D},\mathcal {R})\), and finally the cone of all non-negative Borel measures supported on \(\mathcal {A}\) is denoted by \(\mathcal {M}_+(\mathcal {A})\).

2 Regret Satisficing in Robust Mechanism Design

We consider a prototypical monopoly pricing problem where the seller aims to sell a single product to a buyer. She perceives the value \(\nu \) that the buyer privately assigns to the item as a stochastic-free uncertain variable which could take any value in the interval \([0,\overline{\nu }]\). The vanishing lower bound is justified by the observation that no matter what the product offered is, it can be inconsequential to some people, and the upper bound \(\overline{\nu }\) could perhaps be estimated from the price of a similar yet superior substitute that is currently available in the market; see [10]. If nothing else is known, a direct mechanism that attains the minimum worst-case regret can be found by solving

$$\begin{aligned} \begin{aligned} &\text {minimize} {} & {} \sup _{\nu \in [0,\overline{\nu }]} \nu - m(\nu ) \\ &\text {subject to} {} & {} q \in \mathcal {L}([0,\overline{\nu }],[0,1]), \ m \in \mathcal {L}([0,\overline{\nu }],\mathbb {R}) \\ {} & {} {}& q(\nu )\nu - m(\nu ) \ge 0 {} & {} \forall \nu \in [0,\overline{\nu }] \\ {} & {} {}& q(\nu )\nu - m(\nu ) \ge q(\omega )\nu - m(\omega ) {} & {} \forall \nu ,\omega \in [0,\overline{\nu }], \end{aligned} \end{aligned}$$
(1)

where q and m denote the allocation and the payment rule, respectively. In particular, \(q(\nu )\) represents the probability that the buyer with value \(\nu \) will obtain the item after he makes a payment of amount \(m(\nu )\) to the seller. Besides, Problem (1) assumes that the buyer is risk-neutral and that his expected utility coincides with \(q(\nu )\nu - m(\nu )\). The two inequalities are known as the ‘individual rationality’ and the ‘incentive compatibility’ constraints, respectively. A mechanism is said to be individually rational if it ensures that the buyer’s expected utility is always non-negative, and it is said to be incentive compatible if the buyer can maximize his expected utility by truthfully reporting his true value \(\nu \), which is unknown to the seller when the mechanism is designed. Both of these constraints must hold for a buyer of any value. Finally, the objective function of Problem (1) contains \(\nu -m(\nu )\) which we refer to as a ‘regret’ of the seller since it characterizes the difference between the hypothetical revenue that the seller could have earned if she precisely knew \(\nu \) and the actual revenue that is generated by the mechanism (q, m).

As an allocation of the item is probabilistic, the seller announcing a mechanism is similar to the seller offering a lottery: requesting an upfront payment from the buyer without making a definite promise to deliver the winning prize. Though, a mechanism can be as simple as offering a product at a certain price, say \(p \in \mathbb {R}\). In this case, we can write down the mechanism as

$$\begin{aligned} q(\nu ) = \mathbbm {1}(\nu \ge p) \quad \text {and} \quad m(\nu ) = p \mathbbm {1}(\nu \ge p), \end{aligned}$$

and we shall refer to it as a ‘deterministic posted price mechanism.’ One can readily verify that such a mechanism is always incentive compatible and individually rational. Note that due to the linearity of the constraints involved, even if the price p is chosen at random, \(\tilde{p} \sim \mathbb {P}\), a ‘randomized posted price mechanism’ with

$$\begin{aligned} q(\nu ) = \mathbb {E}_{\mathbb {P}} \left( \mathbbm {1}(\nu \ge \tilde{p}) \right) \quad \text {and} \quad m(\nu ) = \mathbb {E}_{\mathbb {P}} \left( \tilde{p} \mathbbm {1}(\nu \ge \tilde{p}) \right) \end{aligned}$$

is too incentive compatible and individually rational. Amongst others, [7] argued that every incentive compatible and individually rational mechanism with a right-continuous allocation rule can be interpreted as a randomized posted price mechanism.

Essentially, [4] solved the above worst-case regret minimization problem, and subsequently [13] provided an extension to this problem in which the seller has multiple items to sell simultaneously. Similarly, both papers showed that the optimal mechanism consists of a piece-wise logarithm allocation rule and a piece-wise linear payment rule.

In this paper, we are going to take a similar yet fundamentally different approach to the seller’s worst-case regret minimization problem. Instead of using robust optimization, we adopt a recently proposed ‘robust satisficing’ approach and consider the following mechanism design problem.

figure a

In this formulation, we have additional parameters \(\hat{\nu } \in (0,\overline{\nu })\) and \(\tau \in \mathbb {R}\). They represent the nominal value of \(\nu \) and the target regret (see [15]). The target \(\tau \) represents an admissible upper bound of the seller’s regret under the nominal scenario \(\nu = \hat{\nu }\). The additional decision variable k characterizes the maximum level of constraint violation of all other scenarios \(\nu \ne \hat{\nu }\) in relation to their deviation from the nominal counterpart. Problem (\(\mathcal {P}\)) seeks the smallest upper bound on the regret \(\nu - m(\nu )\) of the form \(\tau + k\vert \nu - \hat{\nu } \vert \), parameterized by k. This upper bound takes a minimum value when \(\nu = \hat{\nu }\) and is increasing when the buyer’s value \(\nu \) further deviates from the nominal value \(\hat{\nu }\) in either direction. The inputs \(\hat{\nu }\) and \(\overline{\nu }\) are to be obtained or statistically estimated from the available data, whereas the target \(\tau \) is to be specified by the seller to reflect her risk tolerance level. Throughout, we will refer to the last constraint of Problem (\(\mathcal {P}\)) as the ‘satisficing’ constraint. By construction, the optimal objective value of Problem (\(\mathcal {P}\)) could be infinity if \(\tau \) is too small, and it decreases as \(\tau \) increases. As an upper bound on the nominal regret, i.e., \(\hat{\nu } - m(\hat{\nu })\), that the seller is willing to tolerate, \(\tau \) is a trade-off parameter that the seller could explore. She may leverage a smaller \(\tau \) if she believes that \(\hat{\nu }\) is an adequate representative of the unknown \(\nu \). Conversely, if \(\nu \) is considerably uncertain, she may employ a larger \(\tau \) to get a smaller optimal k and strengthen the regret bound elsewhere as \(\nu \) departs from \(\hat{\nu }\).

The satisficing constraint allows us to draw the following probabilistic regret bound, which serves as an additional motivation for us to study Problem (\(\mathcal {P}\)).

Theorem 1

If \(\nu \sim \mathbb {Q}\) and \(\mathbb {Q}\left( \nu \in [0,\overline{\nu }] \right) = 1\), then

$$\begin{aligned} \mathbb {Q} \left( \nu - m(\nu ) < \tau + \delta \right) \ge 1 - \frac{k}{\delta } \ \mathbb {E}_{\mathbb {Q}} \left[ \vert \nu - \hat{\nu } \vert \right] \end{aligned}$$
(2)

for any \(\delta > 0\) and any (q, m, k) that is feasible in Problem (\(\mathcal {P}\)).

The regret bound in Theorem 1 conforms with the convention of robust satisficing, which yearns for the smallest k so that the probabilistic guarantee is strongest. The theorem also suggests that, if possible, the seller may want to choose \(\hat{\nu }\) to be the median of \(\nu \). On the other hand, if \(\hat{\nu }\) is chosen as the expected value of \(\nu \), then the right-hand side of (2) is completely characterized by the mean absolute deviation of \(\nu \). Other choices of \(\hat{\nu }\) will be presented in the later part of the paper. The fact that this probabilistic guarantee depends explicitly on the input \(\hat{\nu }\) marks a clear distinction between robust satisficing and robust optimization, with the latter focusing on only the worst-case \(\nu \) [16].

Before solving Problem (\(\mathcal {P}\)), we state its feasibility condition as follows.

Theorem 2

Problem (\(\mathcal {P}\)) is feasible if and only if \(\tau > 0\).

Due to Theorem 2, we henceforth always assume that \(\tau > 0\) to avoid trivialities.

3 Optimal Mechanisms

This section contains our main results which are the analytical derivations of the optimal solutions of Problem (\(\mathcal {P}\)) for different values of the seller’s target \(\tau > 0\). We will consider in total four cases depending on the relationship between \(\tau \) and the other inputs to the problem: \(\hat{\nu } \in (0,\overline{\nu })\) and \(\overline{\nu } > 0\).

$$\begin{aligned} \begin{aligned} &\text {I: } &\,& \tau \ge \frac{\overline{\nu }}{e} &\,&\text {II: } &\,& \tau < \frac{\overline{\nu }}{e} \text { and } \tau > \hat{\nu } \\ &\text {III: } &\,& \tau < \frac{\overline{\nu }}{e},\ \tau > \left( 2e^{-1/2}-1 \right) \hat{\nu } \text { and } \tau \le \hat{\nu } \quad &\,&\text {IV: } &\,& \tau \le \left( 2e^{-1/2}-1 \right) \hat{\nu } \end{aligned} \end{aligned}$$

3.1 Analysis of Case I

Proposition 1

If \(\tau \ge \frac{\overline{\nu }}{e}\), then \((q^\star ,m^\star ,0)\) with

$$\begin{aligned} q^\star (\nu ) = \left( 1 + \log \left( \frac{\nu }{\overline{\nu }} \right) \right) ^+ \quad \text {and} \quad m^\star (\nu ) = \left( \nu - \frac{\overline{\nu }}{e} \right) ^+ \end{aligned}$$
(3)

is optimal in Problem (\(\mathcal {P}\)).

Note that this optimal mechanism depends on neither \(\tau \), as long as it is sufficiently large, nor \(\hat{\nu }\). This observation indicates that the regret incurred by the buyer of any value \(\nu \in [0,\overline{\nu }]\) is no more than \(\frac{\overline{\nu }}{e}\), which is consistent with and encapsulates the analysis by [13].

3.2 Analysis of Case II

Proposition 2

If \(\hat{\nu } < \tau < \frac{\overline{\nu }}{e}\), then \((q^\star ,m^\star ,k^\star )\), where

$$\begin{aligned} q^\star (\nu ) = \left( 1 + (1-k^\star ) \log \left( \frac{\nu }{\overline{\nu }} \right) \right) ^+ \quad \text {and} \quad m^\star (\nu ) = (1-k^\star ) \left( \nu - e^{1/(k^\star -1)}\overline{\nu } \right) ^+ \end{aligned}$$
(4)

and \(k^\star \in (0,1)\) is a solution of \(k\hat{\nu } + (1-k)e^{1/(k-1)}\overline{\nu } = \tau \), is feasible in Problem (\(\mathcal {P}\)).

To establish the optimality of mechanism in (4), our strategy is to construct a tight lower bound of Problem (\(\mathcal {P}\)). This lower bound is expressed as the optimal objective value of the following maximization problem

figure b

Note that Problem (\(\mathcal {D}\)) implicitly imposes that any feasible \(\beta \) must be integrable; however, \(\beta \) is not necessarily continuous or monotonic.

Proposition 3

Problem (\(\mathcal {P}\)) is lower bounded by Problem (\(\mathcal {D}\)).

We next establish the tightness of the proposed lower bound, which will in turn imply the optimality of the mechanism defined in (4).

Proposition 4

If \(\hat{\nu } < \tau < \frac{\overline{\nu }}{e}\), then \(\beta ^\star \) which is defined through

$$\begin{aligned} \beta ^\star (\nu ) = {\left\{ \begin{array}{ll} \frac{c}{\nu ^2} &{} \text {if } \nu \in \left[ e^{1/(k^\star -1)}\overline{\nu }, \overline{\nu } \right] , \\ 0 &{} \text {if } \nu \in \left[ 0, e^{1/(k^\star -1)}\overline{\nu } \right) , \end{array}\right. } \end{aligned}$$

where \(k^\star \in (0,1)\) is defined as in Proposition 2 and

$$\begin{aligned} c = \left[ \frac{2-k^\star }{1-k^\star } - e^{1/(1-k^\star )}\frac{\hat{\nu }}{\overline{\nu }} \right] ^{-1}, \end{aligned}$$

is feasible in Problem (\(\mathcal {D}\)) and it attains the objective value of \(k^\star \).

3.3 Analysis of Case III

Proposition 5

If \(\tau < \frac{\overline{\nu }}{e}\) and \(\left( 2e^{-1/2}-1 \right) \hat{\nu } < \tau \le \hat{\nu }\), then \((q^\star ,m^\star ,k^\star )\), where

$$\begin{aligned} q^\star (\nu ) = {\left\{ \begin{array}{ll} 1 + (1-k^\star ) \log \left( \frac{\nu }{\overline{\nu }} \right) &{} \text {if } \nu \in (\hat{\nu }, \overline{\nu }], \\ 1 + \log \left( \frac{\nu }{\overline{\nu }} \right) + k^\star \log \left( \frac{\nu \overline{\nu }}{\hat{\nu }^2}\right) &{} \text {if } \nu \in \left[ \left( \frac{\hat{\nu }^{2k^\star }}{e\overline{\nu }^{k^\star -1}} \right) ^{1/(k^\star +1)} , \hat{\nu } \right] , \\ 0 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$
(5a)

and

$$\begin{aligned} m^\star (\nu ) = {\left\{ \begin{array}{ll} (1-k^\star )(\nu - \hat{\nu }) + (1+k^\star )\left( \hat{\nu } - \left( \frac{\hat{\nu }^{2k^\star }}{e\overline{\nu }^{k^\star -1}} \right) ^{1/(k^\star +1)} \right) &{} \text {if } \nu \in (\hat{\nu }, \overline{\nu }], \\ (1+k^\star ) \left( \nu - \left( \frac{\hat{\nu }^{2k^\star }}{e\overline{\nu }^{k^\star -1}} \right) ^{1/(k^\star +1)} \right) &{} \text {if } \nu \in \left[ \left( \frac{\hat{\nu }^{2k^\star }}{e\overline{\nu }^{k^\star -1}} \right) ^{1/(k^\star +1)}, \hat{\nu } \right] , \\ 0 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$
(5b)

and \(k^\star \in (0,1)\) is a solution of \(\tau + k\hat{\nu } = (1+k) \left( \frac{\hat{\nu }^{2k}}{e\overline{\nu }^{k-1}} \right) ^{1/(k+1)}\), is feasible in Problem (\(\mathcal {P}\)).

Analogously to Case II, Proposition 6 below certifies the optimality of the mechanism from (5).

Proposition 6

If \(\tau < \frac{\overline{\nu }}{e}\) and \(\left( 2e^{-1/2}-1 \right) \hat{\nu } < \tau \le \hat{\nu }\), then \(\beta ^\star \) which is defined through

$$\begin{aligned} \beta ^\star (\nu ) = {\left\{ \begin{array}{ll} \frac{c}{\nu ^2} &{} \text {if } \nu \in \left[ \left( \frac{\hat{\nu }^{2k^\star }}{e\overline{\nu }^{k^\star -1}} \right) ^{1/(k^\star +1)}, \overline{\nu } \right] , \\ 0 &{} \text {if } \nu \in \left[ 0, \left( \frac{\hat{\nu }^{2k^\star }}{e\overline{\nu }^{k^\star -1}} \right) ^{1/(k^\star +1)} \right) , \end{array}\right. } \end{aligned}$$

where \(k^\star \in (0,1)\) is defined as in Proposition 5 and

$$\begin{aligned} c = \left[ e^{{1}/{(1+k^\star )}} \left( \frac{\hat{\nu }}{\overline{\nu }} \right) ^{\frac{1-k^\star }{1+k^\star }} - \frac{2}{1+k^\star } \log \left( \frac{\hat{\nu }}{\overline{\nu }} \right) - \frac{2+k^\star }{1+k^\star } \right] ^{-1}, \end{aligned}$$

is feasible in Problem (\(\mathcal {D}\)) and it attains the objective value of \(k^\star \).

It could be readily observed that the derived optimal mechanism of this case is distinctively similar to the mechanism that maximizes the seller’s worst-case expected revenue when the probability distribution governing the buyer’s value \(\nu \) is ambiguous and only known to have certain mean and support [7, 20]. Here, we discuss this phenomenon more deeply by showing that the mechanism we propose is indeed distributionally robust in some sense.

Corollary 1

For any \(0 < \mu < \frac{2\overline{\nu }}{e}\), then \((q^\star ,m^\star ,k^\star )\) constructed in Proposition 5 when \(\tau = \hat{\nu } \in \left( 0, \frac{\overline{\nu }}{e} \right) \) and \(\hat{\nu } \left( 1 + \log \left( \frac{\overline{\nu }}{\hat{\nu }} \right) \right) = \mu \) satisfies

$$\begin{aligned} (q^\star ,m^\star ) \in {\mathop {\hbox {arg max}}\limits _{q,m}} \left\{ \inf _{\mathbb {Q} \in \mathcal {Q}(\mu )} \left\{ \mathbb {E}_{\mathbb {Q}} \left[ m(\nu ) \right] \right\} : \begin{array}{ll} q \in \mathcal {L}([0,\overline{\nu }],[0,1]),\ m \in \mathcal {L} ([0,\overline{\nu }],\mathbb {R}) \\ q(\nu )\nu - m(\nu ) \ge 0 &{} \forall \nu \in [0,\overline{\nu }] \\ q(\nu )\nu - m(\nu ) \ge q(\omega )\nu - m(\omega ) &{} \forall \nu ,\omega \in [0,\overline{\nu }] \end{array} \right\} , \end{aligned}$$

where the ambiguity set \(\mathcal {Q}(\mu )\) comprises of all probability distributions of \(\nu \) such that

$$\begin{aligned} \mathbb {Q}(\nu \in [0,\overline{\nu }]) = 1 \quad \text {and} \quad \mathbb {E}_\mathbb {Q}[\nu ] = \mu . \end{aligned}$$

To our best knowledge, this observation shows for the first time the relationship between robust satisficing with a regret objective and distributionally robust optimization with a revenue objective. Besides, we numerically compute Corollary 1’s choices of \(\tau \) and \(\hat{\nu }\) for different values of \(\mu \), from which it is observed that to bring forth the distributional robustness for the expected revenue, the seller should choose \(\tau \) and \(\hat{\nu }\) to be smaller than a half of \({\mu }\). Together, Theorem 1 and Corollary 1 highlight the impact of our input parameters in the seller’s regret and in her revenue, respectively.

3.4 Analysis of Case IV

Proposition 7

If \(\tau \le \left( 2e^{-1/2}-1 \right) \hat{\nu }\), then \((q^\star ,m^\star ,k^\star )\), where

$$\begin{aligned} q^\star (\nu ) = {\left\{ \begin{array}{ll} 1 &{} \text {if } \nu \in (\hat{\nu }, \overline{\nu }], \\ 1 + (1+k^\star )\log \left( \frac{\nu }{\hat{\nu }} \right) &{} \text {if } \nu \in \left[ e^{-1/(k^\star +1)}\hat{\nu }, \hat{\nu } \right] , \\ 0 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$
(6a)

and

$$\begin{aligned} m^\star (\nu ) = {\left\{ \begin{array}{ll} (1+k^\star )\left( 1-e^{-1/(k^\star +1)} \right) \hat{\nu } &{} \text {if } \nu \in ( \hat{\nu }, \overline{\nu }], \\ (1+k^\star ) \left( \nu - e^{-1/(k^\star +1)}\hat{\nu } \right) &{} \text {if } \nu \in \left[ e^{-1/(k^\star +1)}\hat{\nu } , \hat{\nu }\right] , \\ 0 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$
(6b)

and \(k^\star \in [1,\infty )\) is a solution of \(\tau + k\hat{\nu } = (1+k) e^{-1/(k+1)}\hat{\nu }\), is feasible in Problem (\(\mathcal {P}\)).

To establish the optimality of the mechanism in (6), we need a different lower bound which is

figure c

Note that Problem (\(\mathcal {D}'\)) implicitly imposes that any feasible \(\beta \) must be integrable.

Proposition 8

Problem (\(\mathcal {P}\)) is lower bounded by Problem (\(\mathcal {D}'\)).

We are now ready to argue that the mechanism suggested in Proposition 7 is indeed optimal.

Proposition 9

If \(\tau \le \left( 2e^{-1/2}-1 \right) \hat{\nu }\), then \(\beta ^\star \) which is defined through

$$\begin{aligned} \beta ^\star (\nu ) = {\left\{ \begin{array}{ll} \frac{c}{\nu ^2} &{} \text {if } \nu \in \left[ e^{-1/(k^\star +1)}\hat{\nu }, \hat{\nu } \right] , \\ 0 &{} \text {if } \nu \in \left[ 0, e^{-1/(k^\star +1)}\hat{\nu } \right) , \end{array}\right. } \end{aligned}$$

where \(k^\star \in [1,\infty )\) is defined as in Proposition 7 and

$$\begin{aligned} c = \left[ e^{1/(k^\star +1)} - \frac{2+k^\star }{1+k^\star } \right] ^{-1}, \end{aligned}$$

is feasible in Problem (\(\mathcal {D}'\)) and it attains the objective value of \(k^\star \).

We summarize the analyses of the four cases in the theorem below.

Theorem 3

Problem (\(\mathcal {P}\)) is solved by the mechanism

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {from Proposition}~1 &{} \text { if } \tau \ge \frac{\overline{\nu }}{e}, \\ \text {from Proposition}~2 &{} \text { if } \tau < \frac{\overline{\nu }}{e} \text { and } \tau > \hat{\nu }, \\ \text {from Proposition}~5 &{} \text { if } \tau < \frac{\overline{\nu }}{e},\ \tau > \left( 2e^{-1/2}-1 \right) \hat{\nu } \text { and } \tau \le \hat{\nu }, \\ \text {from Proposition}~7 &{} \text { if } \tau \le \left( 2e^{-1/2}-1 \right) \hat{\nu }. \end{array}\right. } \end{aligned}$$

All in all, we show that the optimal solution of Problem (\(\mathcal {P}\)) can be determined by using a simple line search to find a value of \(k^\star \) from a certain interval which solves a given characteristic equation. Although for Case IV the upper bound on \(k^\star \) is not explicitly given, we can still without any loss impose that \(k^\star \le \max \left\{ \frac{\hat{\nu }}{\tau }-2,1 \right\} \) which is a valid inequality known from the proof of Theorem 2 in Appendix A, which is available online.

4 Optimal Deterministic Posted Price Mechanisms

Our aim for this section is to derive an optimal deterministic posted price mechanism. We denote by \(p \in [0, \overline{\nu }]\) the posted price which is to be optimized, and we restrict the allocation and payment rule to \(q(\nu ) = \mathbbm {1}(\nu \ge p)\) and \(m(\nu ) = p\mathbbm {1}(\nu \ge p)\). Under this restriction, Problem (\(\mathcal {P}\)) reduces to

$$\begin{aligned} \begin{aligned} &\text {minimize} {} & {} k \\ &\text {subject to} {} & {} p \in [0,\overline{\nu }], \ k \in \mathbb {R}_+ \\ {} & {} {}& \nu - p\mathbbm {1}(\nu \ge p) \le \tau + k \vert \nu - \hat{\nu } \vert {} & {} \forall \nu \in [0,\overline{\nu }]. \end{aligned} \end{aligned}$$
(7)

Unlike Problem (\(\mathcal {P}\)), Problem (7) involves a finite number of decision variables (i.e., p and k). It however still contains an infinite number of constraints, each of which is neither convex nor concave in the posted price p.

Theorem 4

Problem (7) is solved by

$$\begin{aligned} p^\star = {\left\{ \begin{array}{ll} \tau &{} \text {if } \tau \ge \frac{\overline{\nu }}{2}, \\ \text {a root of } \frac{p-\tau }{p-\hat{\nu }} = \frac{\overline{\nu } - p -\tau }{\overline{\nu } - \hat{\nu }} \text { from } (\tau ,\overline{\nu }-\tau ) &{} \text {if } \tau < \frac{\overline{\nu }}{2} \text { and } \tau > \hat{\nu }, \\ \hat{\nu } &{} \text {if } \tau < \frac{\overline{\nu }}{2} \text { and } \tau = \hat{\nu }, \\ \max \left\{ \hat{\nu }-\tau , \text { a root of } \frac{p-\tau }{\hat{\nu }-p} = \frac{\overline{\nu } - p -\tau }{\overline{\nu } - \hat{\nu }} \text { from } (\tau ,\hat{\nu }) \right\} &{} \text {if } \tau < \frac{\overline{\nu }}{2} \text { and } \tau < \hat{\nu }. \end{array}\right. } \end{aligned}$$

Based on Theorem 4 and our earlier results, we can now establish the following observations.

  1. 1.

    The mechanism that is optimal in Problem (\(\mathcal {P}\)) is not necessarily unique. Indeed, when \(\tau \ge \frac{\overline{\nu }}{2}\), the optimal objective value of Problem (\(\mathcal {P}\)) vanishes and it could be solved by a mechanism with either a randomized or a deterministic allocation; see Theorems 3 and 4.

  2. 2.

    The restriction to a class of deterministic posted price mechanisms does not impact the feasibility of Problem (\(\mathcal {P}\)). That is Problem (\(\mathcal {P}\)) is feasible if and only if Problem (7) is. Particularly, both problems are feasible if and only if \(\tau > 0\).

  3. 3.

    Even though Problems (\(\mathcal {P}\)) and (7) share the same necessary and sufficient condition for feasibility, the latter can result in a mechanism that is arbitrarily worse than the former. To see this, we may consider a target \(\tau \in [\frac{\overline{\nu }}{e},\frac{\overline{\nu }}{2})\). The optimal objective value of Problem (\(\mathcal {P}\)) is zero, whereas that of the restricted problem (7) is strictly positive. Suppose otherwise for the sake of contradiction that k can be zero in Problem (7). Its satisficing constraint evaluated at \(\nu \uparrow p\) and \(\nu = \overline{\nu }\) would then imply that both p and \(\overline{\nu } - p\) are smaller than or equal to \(\tau \). Therefore, \(\tau \ge \frac{\overline{\nu }}{2}\) and this observation contradicts with the admissible range of \(\tau \) currently considered.

5 Optimal Target-Free Mechanisms

We will now consider another variant of Problem (\(\mathcal {P}\)) where the seller is relieved from choosing \(\tau \):

$$\begin{aligned} \begin{aligned} &\text {minimize} &\,& k \\ &\text {subject to} &\,& q \in \mathcal {L}([0,\overline{\nu }],[0,1]), \ m \in \mathcal {L}([0,\overline{\nu }],\mathbb {R}), \ k \in \mathbb {R}_+ \\ &\,&\,& q(\nu )\nu - m(\nu ) \ge 0 &\,& \forall \nu \in [0,\overline{\nu }] \\ &\,&\,& q(\nu )\nu - m(\nu ) \ge q(\omega )\nu - m(\omega ) &\,& \forall \nu ,\omega \in [0,\overline{\nu }] \\ &\, &\,& \nu - m(\nu ) \le \hat{\nu } - m(\hat{\nu }) + k\vert \nu - \hat{\nu } \vert &\,& \forall \nu \in [0,\overline{\nu }]. \end{aligned} \end{aligned}$$
(8)

In other words, Problem (8) is obtained by replacing the target regret \(\tau \) which is an explicit input parameter of Problem (\(\mathcal {P}\)) by \(\hat{\nu } - m(\hat{\nu })\), which represents the regret of the mechanism (q, m) under the nominal scenario \(\nu = \hat{\nu }\). Similar to our solution approach in Sect. 3, we perform a case-by-case analysis depending on the value of \(\hat{\nu } \in (0,\overline{\nu })\).

Proposition 10

If \(\hat{\nu } \ge \frac{\overline{\nu }}{e}\), then Problem (8) is solved by the mechanism defined in (3).

Proposition 11

If \(\hat{\nu } < \frac{\overline{\nu }}{e}\), then Problem (8) is solved by the mechanism defined in (4) where \(k^\star \in (0,1)\) satisfies \(e^{1/(k^\star -1)}\overline{\nu } = \hat{\nu }\).

In fact, there are infinitely many mechanisms that solve Problem (8). Indeed, for any \((q^\star ,m^\star ,k^\star )\) that is optimal, we can construct a family of optimal mechanisms of the form \((q^\star ,m^\star -\delta ,k^\star )\), which are parametrized by \(\delta \ge 0\). However, when \(\delta > 0\), these mechanisms are Pareto inefficient as to the seller they would earn a strictly smaller expected revenue (regardless of the probability distribution that governs \(\nu \)), and hence they are of less interest.

Last but not least, we present a distributionally robust interpretation for the mechanism provided in Proposition 11.

Corollary 2

For any \(0 < \mu < \frac{2\overline{\nu }}{e}\), then \((q^\star ,m^\star ,k^\star )\) constructed in Proposition 11 when \(\hat{\nu } \in \left( 0, \frac{\overline{\nu }}{e} \right) \) and \(\hat{\nu } \left( 1 + \log \left( \frac{\overline{\nu }}{\hat{\nu }} \right) \right) = \mu \) satisfies

$$\begin{aligned} (q^\star ,m^\star ) \in {\mathop {\hbox {arg max}}\limits _{q,m}} \left\{ \inf _{\mathbb {Q} \in \mathcal {Q}(\mu )} \left\{ \mathbb {E}_{\mathbb {Q}} \left[ m(\nu ) \right] \right\} : \begin{array}{ll} q \in \mathcal {L}([0,\overline{\nu }],[0,1]),\ m \in \mathcal {L} ([0,\overline{\nu }],\mathbb {R}) \\ q(\nu )\nu - m(\nu ) \ge 0 &{} \forall \nu \in [0,\overline{\nu }] \\ q(\nu )\nu - m(\nu ) \ge q(\omega )\nu - m(\omega ) &{} \forall \nu ,\omega \in [0,\overline{\nu }] \end{array} \right\} , \end{aligned}$$

where the ambiguity set \(\mathcal {Q}(\mu )\) is defined as in Corollary 1.

6 Statistics and Performance of the Optimal Mechanisms

In all cases, the optimal allocation rule of Problem (\(\mathcal {P}\)) is continuous and non-decreasing as well as satisfies \(q^\star (0) = 0\) and \(q^\star (\overline{\nu }) = 1\). Hence, \(q^\star \) admits an interpretation as a cumulative distribution function that is supported on \([0,\overline{\nu }]\), and there exists a random variable \(\tilde{p} \sim \mathbb {P}\) such that

$$\begin{aligned} q^\star (\nu ) = \mathbb {P}\left( \tilde{p} \le \nu \right) = \mathbb {E}_{\mathbb {P}} \left( \mathbbm {1}(\tilde{p} \le \nu ) \right) \quad \forall \nu \in [0,\overline{\nu }]. \end{aligned}$$

Moreover, the optimal mechanism satisfies \(m^\star (0) = 0\). From Lemma 1 in our Appendix A, we further have

$$\begin{aligned} \begin{aligned} m^\star (\nu ) &= q^\star (\nu ) \nu - \int _{0}^{\nu } q^\star (x) \ \textrm{d} x = \int _0^\nu x \ \textrm{d} q^\star (x) = \int _0^{\overline{\nu }} x \mathbbm {1}(x \le \nu ) \ \textrm{d} q^\star (x) \\ &= \mathbb {E}_{\mathbb {P}} \left( \tilde{p}\mathbbm {1}(\tilde{p} \le \nu ) \right) \quad \forall \nu \in [0,\overline{\nu }]. \end{aligned} \end{aligned}$$

We can thus interpret the optimal mechanism \((q^\star ,m^\star )\) as a ‘randomized posted price mechanism’ where the price \(\tilde{p}\) is drawn from the probability distribution \(\mathbb {P}\). Using randomized posted prices offers a distinct advantage to the seller in the sense that it increases the willingness of the buyer to engage in the sale transaction as the buyer has to pay only when he is actually given the item. In contrast, directly implementing the mechanism \((q^\star ,m^\star )\) entails offering a lottery that requires the buyer with a value \(\nu \) to make a payment of amount \(m^\star (\nu )\) regardless of whether or not he will obtain the item, which to him can only happen favourably with a probability of \(q^\star (\nu )\).

We will now carry out a sensitivity analysis to see how the mean price \(\mathbb {E}_{\mathbb {P}} \left( \tilde{p} \right) \) changes with the values of \(\tau \) and \(\hat{\nu }\), and simultaneously we will compare it with the optimal deterministic posted price \(p^\star \) derived in Sect. 4. Throughout the experiment, we assume that . From Fig. 1, it is seen that when \(\tau \) is small, \(\mathbb {E}_{\mathbb {P}}(\tilde{p})\) and \(p^\star \) coincide. As the target \(\tau \) gets increasingly larger (i.e., as the seller gets more uncertainty-conscious), the variance of the optimal random price becomes more sizeable, which justifies the implementation of the more convoluted mechanism we propose. When \(\tau \) reaches a certain threshold, the variance of \(\tilde{p}\) may drop but stay significant nonetheless. Overall, we find that the optimal random price is, on average, at least as large as the optimal deterministic price; hence, the randomized strategy does not only incur a smaller regret but it also has a potential to extract higher revenue from the buyer. Last but not least, we compute and compare the optimal objective value of Problem (\(\mathcal {P}\)), denoted by \(k^\star \), and that of Problem (7), denoted by \(k^\star _{\text {det}}\). These optimal objective values characterize the sensitivity of the regret upper bound with respect to the departure of the buyer’s value \(\nu \) from \(\hat{\nu }\). Regardless of , it can be observed from Fig. 2 (top) that both \(k^\star \) and \(k^\star _{\text {det}}\) change abruptly when \(\tau \le 21.3\% \times \hat{\nu }\). Our recommendation for the seller is therefore to choose the target \(\tau \) above this level, and the larger \(\tau \) is suitable for a seller who prefers to have a stronger safeguard against an uprising regret from any scenario \(\nu \ne \hat{\nu }\). To further appreciate the benefit of the price dispersion, Fig. 2 (bottom left) shows that the randomized pricing strategy can lead to a substantial reduction of the sensitivity level (from \(k^\star _{\det }\) to \(k^\star \)) of at least 12%, and oftentimes the difference between the two strategies is considerably more pronounced. Figure 2 (bottom right) exemplary visualizes the regret bound \(\tau + k\vert \nu - \hat{\nu } \vert \), \(k \in \{ k^\star , k^\star _{\text {det}} \}\), of the two pricing strategies when and .

Fig. 1.
figure 1

The mean (left) and the coefficient of variation (right) of the optimal random price \(\tilde{p}\) under different combinations of \(\tau \) and \(\hat{\nu }\). The accompanied dashed curves (left) show the optimal deterministic prices \(p^\star \).

Full size image
Fig. 2.
figure 2

The comparison between \(k^\star \) and \(k^\star _{\text {det}}\) (in a logarithmic scale) under different combinations of \(\tau \) and \(\hat{\nu }\) as well as the comparison between the corresponding regret upper bounds.

Full size image

Next, we make a statistical comparison between the worst-case regret minimization [13] and the proposed robust regret satisficing frameworks. Retaining the names of the optimization techniques adopted, we shall refer to their recommended mechanisms as ‘robust’ and ‘satisficing’ solutions, respectively. Specifically for this experiment, we work with a target-free model proposed in Sect. 5, we normalize \(\overline{\nu }\) to \(1\$\), and we now model the buyer’s value as a Beta random variable, \(\nu \sim \mathbb {Q}\), with some positive shape parameters \(s_1\) and \(s_2\), and we set \(\hat{\nu }\) as \(\mu = \mathbb {E}_{\mathbb {Q}}[\nu ]\). We consider various combinations of the shape parameters that are consistent with different means from (as when \(\hat{\nu } = \mu > \frac{1}{e} \approx 0.368\), the robust and the satisficing solutions coincide) and coefficients of variation (CV) from \(\{0.1,0.2,\ldots ,2.5\}\). It should be noted that there may be no shape parameters that are compatible with a certain combination of the mean and the CV of \(\nu \) from their stipulated ranges. In such cases, the corresponding entries in Table 1 are painted black, and there are 137 remaining cells in total. Table 1 (left) reports the relative improvement (in %) in terms of the expected regret of the satisficing solution from Proposition 11 over the robust solution from [13], whereas Table 1 (right) similarly reports the relative improvement (in %) in terms of the expected revenue. We observe that, in an overwhelming majority of instances, our target-free robust satisficing mechanism makes a significant improvement. Though, as one would expect, if the variance of \(\nu \) becomes exceptionally large, the seller should carefully and cautiously hedge against this uncertainty, and the standing of the robust solution from [13] remains. In light of this, Table 1 markedly defines the region where the satisficing solution is superior to the robust solution and vice versa.

Table 1. Relative improvement (in %) of the satisficing mechanism over its robust counterpart in terms of the expected regret (left) and the expected revenue (right) under different Beta distributions of the buyer’s value. The entries marked with a star symbol indicate that the improvement exceeds 100%.
Full size table

Finally, we recall that, although natural, we do not necessarily have to set \(\hat{\nu }\) as \(\mu \). For instance, Corollary 2 suggests a value for \(\hat{\nu }\), which will be henceforth denoted by \(\nu ^\dag \in (0,\mu ]\), that enables the seller to earn more on average under the worst-case distribution from the mean-support ambiguity set [7]. We now consider 11 possibilities of \(\hat{\nu }\), namely

$$\begin{aligned} \hat{\nu } \in \left\{ \nu ^\dag + \frac{i}{10}(\mu - \nu ^\dag ): i \in \{0,\ldots ,10\} \right\} . \end{aligned}$$

For each of the 137 distributions \(\mathbb {Q}\) which we experiment with in Table 1, we determine which value of \(\hat{\nu }\) (or equivalently, which \(i \in \{0,\ldots ,10\}\)) earns the highest expected revenue. From Fig. 3, we conclude that the majority of the optimal i’s are either zero or ten highlighting the benefit of the distributionally robust mechanism studied in [7] and our previous choice of the robust satisficing mechanism, respectively, and the seller is recommended to increase the value of \(\hat{\nu }\) when \(\text {CV}\) or \(\mu \) becomes larger. We also compute the expected revenue of the mechanism that corresponds to the optimal \(i \in \{0,\ldots ,10\}\) and compare it with the maximum expected revenue obtained without any restriction besides incentive compatibility and individual rationality, and we find that in more than \(93.4\%\) of the test distributions the difference between the two is no more than .

Fig. 3.
figure 3

The value of \(i \in \{0,\ldots ,10\}\) corresponding to the maximally-earning value of \(\hat{\nu }\) under different Beta distributions of the buyer’s value.

Full size image

7 Conclusions

Inspired by the recent development of the satisficing decision-making paradigm, we propose an innovative way of incorporating regret into the robust monopoly pricing problem. We demonstrate that the resulting optimization problem, which is an infinite linear program, and several of its variants can be solved analytically. We then alternatively express each of our optimal mechanisms as a randomized posted price mechanism since the latter is more widely accepted and readily implementable in practice. We show in our numerical studies both the benefit of randomizing prices and of adopting the satisficing over the traditional robust and distributionally robust approaches. As a by-product, we also give a managerial guideline on how to calibrate the risk-aversion parameter of our problem.