Optimal Item Pricing in Online Combinatorial Auctions

Abstract

We consider a fundamental pricing problem in combinatorial auctions. We are given a set of indivisible items and a set of buyers with randomly drawn monotone valuations over subsets of items. A decision maker sets item prices and then the buyers make sequential purchasing decisions, taking their favorite set among the remaining items. We parametrize an instance by d, the size of the largest set a buyer may want. Our main result asserts that there exist prices such that the expected (over the random valuations) welfare of the allocation they induce is at least a factor $1/(d+1)$ times the expected optimal welfare in hindsight. Moreover we prove that this bound is tight. Thus, our result not only improves upon the $1/(4d-2)$ bound of Dütting et al., but also settles the approximation that can be achieved by using item prices. We further show how to compute our prices in polynomial time. We provide additional results for the special case when buyers’ valuations are known (but a posted-price mechanism is still desired).

1 Introduction

In combinatorial auctions, a set of valuable items is to be allocated among a set of interested agents. Who should get which items in order to maximize the social welfare? This is a fundamental economic question, and a ubiquitous allocation mechanism is to simply set a price for each item and let the agents buy their preferred subset of items under those prices. The study of these mechanisms dates back to the investigations of Leon Walras over a century ago, and is closely related to the notion of Walrasrian equilibrium. Understanding the existence and approximation of Walrasrian equilibrium and related notions under pricing mechanisms has been an active area of research in recent years [3, 4, 13, 14, 20].

In this paper, we follow the approach of online combinatorial auctions and study the welfare achieved by posted-price mechanisms in a very general setup. Specifically, our mechanisms post a price $p_i$ on each item i. Then, buyers with randomly-drawn monotone valuations over the subsets of items arrive in arbitrary order, and upon arrival pick their preferred subset among those items that are left (at the posted prices). Of course, in this generality little can be said about the social welfare induced by posted-price mechanisms, so it is common to parametrize the instances by d, the largest size of a set a buyer might be interested in.¹ This parametrization is interesting from a combinatorial perspective: finding a socially optimal allocation is NP-hard already when $d \ge 3$.² Moreover, if we restrict the buyers’ valuations to be deterministic and single-minded,³ we recover the classic hypergraph matching problem.

Our main result in this paper is to determine the tight approximation guarantee of item pricing as a function of d. Specifically, we prove that there always exist a posted-price mechanism such that the expected welfare of the resulting allocation, when buyers arrive in adversarial order and iteratively purchase their preferred set, is at least a $1/(d+1)$ fraction of the expected welfare of an optimal allocation (Theorem 1). Furthermore, we prove this bound is tight (Proposition 1).

Interestingly, our result generalizes and/or improves upon several results in the literature, which we now provide context for.

1.1 Context and Related Work

Posted-Price Mechanisms. Posted-price mechanisms are ubiquitous within the economics and computation literature due to their simplicity. They are commonly used as subroutines in truthful mechanisms that approximately maximize welfare [1, 2, 8, 9, 19]. They are also used as subroutines in simple mechanisms to approximately maximize revenue in Bayesian settings [5,6,7, 18]. Our work considers the same model (welfare maximization in Bayesian settings) initiated by Feldman et al. [13]. Other works consider restrictions on the valuations such as subadditive [11], while others consider the unrestricted case [10]. Our paper contributes to this line of work by nailing the tight approximation guarantee of posted-price mechanisms in this model for unrestricted valuations over sets of size at most d. In particular, our results improve the bound of $1/(4d-2)$ of Dütting et al. [10], to $1/(d+1)$, which is tight.

Prophet Inequalities. When there is a single item (and thus $d=1$) our problem is equivalent to the single-item prophet inequality and thus our result takes the same form as the classic result of Samuel-Cahn [21], who proved that the optimal prophet inequality (whose factor is 1/2) can be achieved with a single threshold. A special case of our problem when buyers are single-minded corresponds to various multiple-choice prophet inequality settings, and our results improve upon the state-of-the-art. In particular, all prophet inequalities deduced from our main result are non-adaptive: for each element e, a threshold $T_e$ is set at the beginning of the algorithm. Element e is accepted if and only if $w_e \ge T_e$ (and it is feasible to accept e).

When $d=2$ and buyers are single-minded, our problem translates into the matching prophet inequality problem. Our results when $d=2$ therefore extend the 1/3-approximation of Gravin and Wang [16] from bipartite to general graphs. Note that recent work of Ezra et al. [12] provides a .337-approximation in this case, although it sets thresholds adaptively. In the full version, we further contribute to the $d=2$ case by proving that no prophet inequality (adaptive or not) can guarantee better than a 3/7-approximation for the bipartite graph prophet inequality.

For arbitrary d when buyers are single-minded, our problem translates into the d-dimensional hypergraph prophet inequality, which generalizes the prophet inequality problem over the intersection of d partition matroids. Here, a $1/(4d-2)$-approximation was first given by Kleinberg and Weinberg [18], and improved to $1/(e(d + 1))$ by Feldman et al. [15]. A corollary of our main result improves this to $1/(d+1)$, and with non-adaptive thresholds. A lower bound of Kleinberg and Weinberg [18] proves that it is not possible to achieve an $\omega (1/\sqrt{d})$ approximation even for this special case, but it remains an open problem to determine the tight ratio for prophet inequalities for the intersection of d partition matroids (and for the d-dimensional hypergraph prophet inequality).

1.2 A Technical Highlight and Additional Results

The proof of our main result breaks down the expected welfare into the “revenue” and “utility” achieved by setting prices, and searches for properly “balanced thresholds” as in [10, 13, 16, 18]. In particular, we target prices that are “low enough” so that a buyer with high value for some set will choose to purchase it, yet also “high enough” so that the revenue gained when a bidder purchases items they should not receive in the optimal allocation compensates for the lost welfare. In comparison to prior work using a similar approach, the conditions that guarantee such prices are more involved, and we prove their existence using Brouwer’s fixed point theorem.

As our proof makes use of Brouwer’s fixed point theorem, it is inherently non-constructive; however, in the full version, we show that the prices can be efficiently computed by making use of an LP relaxation to cope with the APX-hardness of optimizing welfare, and we further provide a convex optimization formulation to find our fixed point.

In Sect. 4, we consider the special case that arises when valuations are deterministic and buyers are single-minded. In this situation the welfare optimization problem corresponds to matching in a hypergraph with edges of size at most d. So the problem of finding item prices boils down to finding a set of thresholds, one for each vertex, such that the value of the solution in which hyperedges arrive sequentially (for any order) and greedily included in the solution so long as their weight is higher than the sum of the corresponding vertex thresholds, is as close as possible to the optimal solution. For the case of standard matching ($d=2$) we prove that there exist prices guaranteeing a factor of 1/2 of the optimal solution and that there do not exist prices guaranteeing a factor better than 2/3. The tight factor is left as an open problem. More generally, we prove that there are prices obtaining a fraction 1/d of the optimal solution (thus slightly improving our general $1/(d+1)$), and that it is not possible to do better than $\varOmega (1/\sqrt{d})$.

2 Model

In our basic model, we have a (multi)set of items M in which there are $k_j\ge 1$ copies of each item $j\in M$.⁴ The set of buyers, denoted by N, arrive sequentially (in arbitrary order) and buy some of those items. Each buyer $i\in N$ has a valuation function $v_i:2^M \rightarrow \mathbb {R}_+$, which is randomly chosen according to a given distribution $\mathcal {F}_i$ (defined over a set of possible valuation functions). As is standard, we assume that each possible realization of each $v_i$ is monotone (i.e., $A \subseteq B \Rightarrow v_i(A)\le v_i(B)$). We parametrize an instance of the problem by d, the size of the largest set a buyer might be interested in. Thus we assume that if $A\subseteq M$ is such that $|A|>d$, then

$$\begin{aligned} v(A)=\max _{B \subseteq A, |B|=d} v(B). \end{aligned}$$

(1)

Note that while there are $k_i\ge 1$ copies of each item $i\in M$, no single buyer can purchase more than one copy of an item.

In this paper, we are interested in exploring the limits of using item prices as the mechanism to assign items to buyers. In a pricing mechanism, we set item prices $p\in \mathbb {R}_+^M$ and then consider an arbitrary arrival order of the buyers.⁵ Thus, buyer i buys the set of remaining items that optimizes

$$\begin{aligned} \max _{A \subseteq R_i} v_i(A) - \sum _{j \in A} p_j, \end{aligned}$$

(2)

where $R_i$ stands for the remaining items for which there exists at least one unsold copy when i arrives. Note that (2) might be solved by $A=\emptyset$, i.e., buyer i might opt not to buy anything. When there is a tie between different sets, the buyer can choose arbitrarily, meaning that our results need to be valid even for the worst case.⁶

More precisely, if $\sigma$ is the arrival order of the buyers, so that buyer i comes at time $\sigma (i)$, then buyer i gets the set $B_i(\sigma )=\arg \max _{A \subseteq R_i(\sigma )} v_i(A) - \sum _{j \in A} p_j,$ where $R_i(\sigma )=\{j\in M: k_j>|\{\ell \in N: \sigma (\ell )<\sigma (i) \text{ and } j\in B_\ell (\sigma )\}|\}$. With this, given an instance of the problem (determined by M, $k_j$ for all $j\in M$, N, and $\mathcal {F}_i$ for all $i\in N$), the quality measure of a price vector $p\in \mathbb {R}_+^M$ is the worst case (over the arrival orders) expected (over the valuations) welfare of the allocation it induces. Denoting this quantity as ALG(p) we have that

$$ ALG(p):=\min _{\sigma } \mathbb {E}\left( \sum _{i\in N} v_i(B_i(\sigma ))\right) . $$

On the other hand, the benchmark we compare to throughout the paper is the welfare maximizing allocation, OPT, which is defined as

$$ OPT:= \mathbb {E}\left( \max _{A_i,\, i\in N}\left\{ \sum _{i\in N}v_i(A_i):\text { s.t. } |\{i\in N: j\in A_i\}|\le k_j, \text{ for } \text{ all } j\!\in \! M\right\} \right) . $$

We denote by $OPT_i$ the random set that buyer i gets in an optimal allocation.

In Sect. 4 we consider the special case of our problem in which

• (i) valuations are deterministic,

• (ii) there is a single copy of each item ($k_j=1$ for all $j\in M$), and

• (iii) buyers are single-minded, i.e., each buyer i has a set $A_i$, with $|A_i|\le d$, such that $A_i \not \subseteq B \Rightarrow v_i(B)=0, A_i \subseteq B \Rightarrow v_i(B)=v_i(A_i)$.

Interestingly, already in this particular setup, the problem of maximizing the welfare of an allocation corresponds to the classic combinatorial optimization problem of hypergraph matching with hyperedges of size at most d. Indeed, in an optimal allocation buyer i either gets $A_i$ or $\emptyset$, implying that maximizing the (now deterministic) welfare of the allocation is equivalent to finding a subset of pairwise disjoint $A_i$’s of maximum total valuation.

3 Random Valuations

In this section we prove there exists a vector of item prices such that the resulting allocation yields in expectation at least a $1/(d+1)$ fraction of the optimal social welfare. Additionally, we show that this bound is tight.

Theorem 1

There exists a vector of prices $p\in \mathbb {R}_+^M$ such that

$$(d+1)\cdot ALG(p)\ge OPT.$$

To prove the theorem we will make use of the following function. For each $A\subseteq M$ and $i\in N$, we define

$$z_{i,A}(p)= \left[ \mathbb {E}(\mathbbm {1}_{OPT_i=A}\cdot v_i(A))-\mathbb {P}(OPT_i=A)\sum _{j\in A} p_j\right] _+\,,$$

where $[\cdot ]_+$ denotes the positive part. We assume without loss of generality that $|OPT_i|\le d$ for all $i\in N$, so $z_{i,A}(p)=0$ if $|A|>d$. We start by showing a lower bound for ALG(p) in terms of the functions $z_{i,A}(p)$.

Lemma 1

For any vector of prices $p\in \mathbb {R}_+^M$,

$$\displaystyle ALG(p)\ge \min _{C\subseteq M} \left\{ \sum _{j\notin C} k_j\cdot p_j + \sum _{i\in N} \sum _{A\subseteq C} z_{i,A}(p) \right\} . $$

Proof

In this proof we assume the arrival order $\sigma$ is arbitrary, and for simplicity we drop the dependency of $B_i(\sigma )$ and $R_i(\sigma )$ on $\sigma$ and simply denote them by $B_i$ and $R_i$. We separate the welfare of the resulting allocation into revenue and utility, i.e., we separate $\sum _{i\in N} v_i(B_i)$ into

$$ \text {Revenue}= \sum _{i\in N}\sum _{j\in B_i} p_j\;\; \text { and } \;\; \text {Utility}= \sum _{i \in N} \left( v_i(B_i)-\sum _{j\in B_i} p_j\right) . $$

Recall that $R_i$ is the set of items such that there are remaining copies when i arrives. Similarly, denote by R the set of items that have remaining copies by the end of the process. We have that

$$ \mathbb {E}(\text {Revenue})\ge \mathbb {E}\left( \sum _{j\notin R} k_j\cdot p_j\right) . $$

For the utility, for any $i\in N$, by the definition of $B_i$, it holds that

$$\begin{aligned} v_i(B_i)-\sum _{j\in B_i} p_j&=\max _{A\subseteq R_i} \left( v_i(A)-\sum _{j\in A} p_j\right) \end{aligned}$$

Note now that $v_i$ and $R_i$ are independent. Thus, let $(\tilde{v}_i)_{i\in N}$ be independent realizations of the valuations, and $\widetilde{OPT}_i$ the corresponding optimal solution. With this we can rewrite the expected utility of agent i as

$$\begin{aligned} \mathbb {E}\left( \max _{A\subseteq R_i} v_i(A)-\sum _{j\in A} p_j \right) = \mathbb {E}\left( \max _{A\subseteq R_i} \tilde{v}_i(A)-\sum _{j\in A} p_j \right) \ge \mathbb {E}\left( \max _{A\subseteq R} \tilde{v}_i(A)-\sum _{j\in A} p_j \right) . \end{aligned}$$

We replace the maximization over subsets of R with a particular choice, $\widetilde{OPT}_i$, whenever it is contained by R and gives positive utility (otherwise we take $\emptyset$), to obtain the following lower bound.

$$\begin{aligned}&\mathbb {E}\left( \mathbbm {1}_{\{\widetilde{OPT}_i\subseteq R\}}\cdot \left[ \tilde{v}_i(\widetilde{OPT}_i) -\sum _{j\in \widetilde{OPT}_i} p_j\right] _+\right) \\&= \mathbb {E}\left( \sum _{A\subseteq R} \mathbbm {1}_{\{\widetilde{OPT}_i=A\}}\cdot \left[ \tilde{v}_i(A) -\sum _{j\in A} p_j\right] _+\right) \\&= \mathbb {E}\left( \sum _{A\subseteq R} \mathbb {E}\left( \left[ \mathbbm {1}_{\{\widetilde{OPT}_i=A\}}\left( \tilde{v}_i(A) -\sum _{j\in A} p_j \right) \right] _+\right) \right) \ge \mathbb {E}\left( \sum _{A\subseteq R} z_{i,A}(p) \right) . \end{aligned}$$

The last inequality comes from Jensen’s inequality, noting that $[\cdot ]_+$ is a convex function. Summing over all agents, we get that

$$ \mathbb {E}(\text {Utility})\ge \mathbb {E}\left( \sum _{i\in N} \sum _{A\subseteq R} z_{i,A}(p) \right) . $$

Therefore, adding the revenue and the utility we get that

$$\begin{aligned} ALG(p)&\ge \mathbb {E}\left( \sum _{j\notin R} k_j\cdot p_j + \sum _{i\in N} \sum _{A\subseteq R} z_{i,A}(p) \right) . \end{aligned}$$

Replacing the expectation over R with a minimization over subsets of M we obtain the bound of the lemma.    $\square$

Lemma 2

For any vector of prices $p\in \mathbb {R}_+^M$,

$$ OPT\le \sum _{j\in M} k_j\cdot p_j + \sum _{i\in N} \sum _{A\subseteq M} z_{i,A}(p). $$

Proof

We have that OPT equals

$$\begin{aligned} \sum _{i\in N} \mathbb {E}(v_i(OPT_i))&= \mathbb {E}\left( \sum _{i\in N} \sum _{j\in OPT_i} p_j\right) + \sum _{i\in N} \mathbb {E}\left( v_i(OPT_i) - \sum _{j\in OPT_i} p_j \right) . \end{aligned}$$

Now we upper bound these two terms separately. Note that in the first term each item $j \in M$ appears at most $k_j$ times, so

$$ \mathbb {E}\left( \sum _{i\in N} \sum _{j\in OPT_i} p_j\right) \le \sum _{j\in M} k_j \cdot p_j. $$

For the second part we upper bound with the positive part of the difference, and sum over all possible values of $OPT_i$.

$$\begin{aligned}&\sum _{i\in N} \mathbb {E}\left( v_i(OPT_i) - \sum _{j\in OPT_i} p_j \right) \\&\le \sum _{i\in N} \sum _{A\subseteq M} \mathbb {E}\left( \mathbbm {1}_{\{OPT_i=A\}}\left( v_i(OPT_i) - \sum _{j\in OPT_i} p_j \right) \right) \\&\le \sum _{i\in N} \sum _{A\subseteq M} z_{i,A}(p). \end{aligned}$$

Putting together the two upper bounds we obtain the bound on OPT.   $\square$

Lemma 3

There exists a vector of prices $p\in \mathbb {R}_+^M$ that satisfies the equation

$$p_j= \frac{1}{k_j} \sum _{i \in N} \sum _{A\subseteq M: j\in A} z_{i,A}(p). $$

Proof

Denote the set $K=[0,OPT]^M\subseteq \mathbb {R}_+^M$. We define the function $\psi :K\rightarrow K$ as follows. For an element $p\in K$ and $j\in M$, the j-th coordinate of $\psi$ is

$$ \psi _j(p)=\frac{1}{k_j} \sum _{i \in N} \sum _{A\subseteq M: j\in A} z_{i,A}(p). $$

We prove now that $\psi$ is a well defined continuous function, from the compact set K into itself, and therefore it has a fixed point by Brouwer’s theorem. Note that a fixed point of $\psi$ is exactly the vector of prices we are looking for.

Recall that $z_{i,A}(p)=[\mathbb {E}(\mathbbm {1}_{OPT_i=A}\cdot v_i(A))-\mathbb {P}(OPT_i=A)\sum _{j\in A} p_j]_+$, which is a decreasing function of $p_j$, for all $j\in M$. Moreover, note that since $[\cdot ]_+$ is a convex function, $z_{i,A}$ is also a convex function of $p_j$ for all $j\in M$. The monotonicity of $z_{i,A}$ implies that for all $p\in K$ and $j\in M$, $\psi _j(p)\le \psi _j(0)\le \frac{1}{k_j} \mathbb {E}(OPT)$, and therefore $\psi (p)\in K$ for all $p\in K$. The convexity of $z_{i,A}$ implies it is also continuous, so $\psi$ is a continuous function.    $\square$

Proof (of Theorem 1)

Using the vector of prices from Lemma 3 in the bound of Lemma 1 results in

$$\begin{aligned} ALG(p)\ge \sum _{i\in N} \sum _{A\subseteq M} z_{i,A}(p). \end{aligned}$$

To compare to OPT, we use the upper bound of Lemma 2, which shows

$$\begin{aligned} OPT&\le \sum _{j\in M}\sum _{i\in N} \sum _{A\subseteq M:j\in A} z_{i,A}(p) + \sum _{i\in N} \sum _{A\subseteq M} z_{i,A}(p)\\&= \sum _{i\in N} \sum _{A\subseteq M} (|A|+1)\cdot z_{i,A}(p)\\&\le (d+1) \sum _{i\in N} \sum _{A\subseteq M} z_{i,A}(p). \end{aligned}$$

Comparing the two bounds we get that $(d+1)ALG(p)\ge OPT$.   $\square$

To wrap up the section, we establish that the bound of Theorem 1 is best possible, by modifying a simple example of Dütting et al. [10].

Proposition 1

For all d, and all $\delta > 0$, there exists an instance on $|N|=2$ bidders and $|M|=d$ items such that for all p, $ALG(p) = 1$, yet $OPT(p) = d+1-\delta$.

Proof

Consider a set M of exactly d items with a single copy of each, and a very small $\varepsilon >0$. There are two buyers. The first buyer values any nonempty subset of the items at 1. The second buyer only assigns value to getting all d items, and this value is $d-\varepsilon$ with probability $1-\varepsilon$ and it is $1/\varepsilon$ with probability $\varepsilon$. Now we consider setting prices $p_j$ for all $j\in M$. If we set the prices so that $\sum _{j\in M} p_j\le d-\varepsilon$ then there exists an item with price at most $1-\varepsilon /d$. Therefore, the first buyer will get this item and thus the total welfare will be 1. If, on the contrary, buyer one does not purchase an item, then we must have $\sum _{j \in M} p_j \ge d$, and the second buyer will only purchase items with probability $\varepsilon$. In this case, the expected total welfare is also 1. This establishes that $ALG(p) = 1$ for all p. Finally, it is clear that in this instance the optimal welfare is achieved by always assigning all items to the second buyer, which results in an expected welfare of $(d-\varepsilon ) \cdot (1-\varepsilon )+\varepsilon \cdot (1/\varepsilon ) \ge d+1-(d+1)\varepsilon$. Setting $\varepsilon = \delta /(d+1)$ completes the proof.   $\square$

Efficient Computation. Our above proof is nonconstructive as it requires a fixed point computation. However, in the full version of the paper, we show that despite this challenge and others, there exists a polynomial-time algorithm to compute the prices using only demand queries.

4 Single-Minded Valuations

In this section, we consider the special case where there is a single copy of each item ($k_i=1$ for all $i\in M$), buyers’ valuations are deterministic, and buyers are single-minded. The latter means each buyer i has a set $A_i$, with $|A_i|\le d$, such that $A_i \not \subseteq B \Rightarrow v_i(B)=0$ and $A_i \subseteq B \Rightarrow v_i(B)=v_i(A_i)$. The problem of maximizing the welfare of an allocation in this context can be seen as the classic combinatorial problem of hypergraph matching with hyperedges of size at most d, where the buyers correspond to the hyperedges and the items are the vertices. Indeed, in an optimal allocation for this setting buyer i either gets $A_i$ or $\emptyset$, implying that maximizing the welfare of the allocation is equivalent to finding a subset of pairwise disjoint $A_i$’s of maximum total valuation. As this is a traditional problem, in the rest of this section we will refer to hypergraphs, hyperedges and vertices, rather than buyers and items, using the usual notation $G=(V,E)$ and denoting by w(e) the valuation (or weight) of the hyperedge e.

4.1 Matching in Graphs: $d=2$

We first focus on the traditional matching problem, showing that using prices has limits even for this scenario. As argued in Lemmas 4 and 6, there are instances in which no pricing scheme can guarantee recovering more than 2/3 of the optimal solution. This is true even if the graph is bipartite or if there is a unique optimal matching; on the other hand, if both conditions are fulfilled—i.e., the graph is bipartite and there is a unique optimal matching, we show that using the dual prices leads precisely to such optimal solution.

Lemma 4

Prices cannot guarantee obtaining more than 2/3 of the optimal matching, even if the graph is bipartite.

Proof

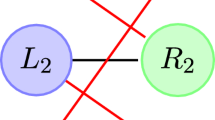
Consider the graph depicted in Fig. 1, in which all edges have unit weight. There are two optimal solutions, given by the black and the red perfect matchings. Assume we have prices that are able to build an optimal solution (i.e., include three edges) regardless of the order in which the edges arrive. This implies that for at least one of the optimal solutions, all the edges will be included if their vertices are available when they arrive. Without loss assume this is the case for the black matching, i.e. for $i=1,2,3,$ we have $p_{L_i}+p_{R_i} \le 1$.

Fig. 1.

Example of a bipartite graph in which, when all edges have the same weight, no pricing scheme can guarantee obtaining more than 2/3 of the optimal solution. (Color figure online)

On the other hand, we need to prevent the red edges to be included if they appear: to see why this is necessary, consider for instance the case in which the edge $(L_1,R_2)$ is not discarded when appearing first; then, if the edge $(L_3,R_3)$ appears second, no more edges could be added. To preclude this, we need to impose that for $i=1,2,3,\, p_{L_i}+p_{R_{(i \text { mod } 3) + 1}}>1$. A contradiction follows by adding these as well as the previous three inequalities.    $\square$

In the case of bipartite graphs, it is natural to consider the usual linear programming formulation, since it has integral optimal solutions. The following lemma shows that when we require the additional hypothesis that there is a unique optimal matching, the prices given by the optimal solution of the dual problem lead to the optimal assignment.

Lemma 5

If the graph $G=(V,E)$ is bipartite and has a unique optimal matching, then such a matching is obtained using the dual prices.

Proof

Because the graph is bipartite, the problem reduces to solving the linear program $\max \{\sum _{e\in E} x_e w(e): \sum _{e \in \delta (v)} x_e\le 1 \text { for all }v\in V,\, x\ge 0\}$, which has an integral optimal solution. Because there is only one optimal matching, the LP has a unique optimal solution $(x_e^*)_{e \in E}$. Consider the prices $(p^*_u)_{u \in V}$ corresponding to an optimal dual solution, satisfying strict complementary slackness.

Consider an edge $e=(u,v)$ that is not part of the optimal matching. Hence, the corresponding primal variable takes the value $x_e^*=0$. By complementary slackness, the corresponding dual constraint is not tight, i.e. $p_u^*+p_v^*>w(e)$. This last condition implies that buyer e will not buy the edge upon arrival. On the other hand, if e is part of the optimal solution, the corresponding dual constraint must be tight (again due to strict complementary slackness), so that those buyers will choose to buy.    $\square$

The assumption of a unique solution is crucial for the dual prices to be useful. Indeed, when there is more than one solution, using the dual prices can be arbitrarily inefficient. Indeed, consider the same example depicted in Fig. 1, but modify the weight of the edges $f=(L_1,R_1)$ and $g=(L_2,R_3)$ to be $\varepsilon$, so that that the optimal solution has value $2+\varepsilon$. On the other hand, consider an edge $e=(u,v)$ and the resulting dual prices $p_u,p_v$: complementary slackness now states that we have $p_u+p_v=w(e)$ iff e is part of any optimal solution. Edge f is part of the black optimal solution, and edge g is part of the red, hence those edges will be bought if the corresponding vertices are available when they appear. In particular, if they are the first two edges to appear, then they will both be in the final solution, and no other edge can be added, leading to a final weight of $2\varepsilon$.

Fig. 2.

Example of a graph in which, when all edges have the same weight, there is a unique optimal matching but no pricing scheme can guarantee obtaining more than 2/3 of its weight.

However, in general graphs, even the uniqueness assumption is not enough. Indeed we have the following result.

Lemma 6

Prices cannot guarantee obtaining more than 2/3 of the optimal matching in a general graph, even if there is only one optimal matching.

Proof

Consider the graph depicted in Fig. 2, where every edge has unit weight. The optimal matching is given by the three black edges with total value of 3. On the other hand, if any red edge enters the solution, the resulting total weight will be at most 2. We now show that any pricing scheme in which every black edge is willing to buy will also include at least one red edge if it comes first. Let $(p_i)_{i=A,\ldots ,F}$ prices such that for every black edge, the sum of the involved vertices is lower than 1. In particular, we have that $p_C+p_D \le 1$, so without loss of generality we assume that $p_C \le 1/2$. If $p_B \le 1/2$ as well, then the red edge (B, C) will want to buy and the proof is complete. Otherwise, i.e. if $p_B>1/2$, it implies that $p_A\le 1/2$ because the black edge (A, B) wants to buy. But this implies that the red edge (A, C) will buy if appearing first.

Finally, if all vertex prices are 1/2, then it is straightforward to see that at least two edges will be added regardless of the order in which they appear.    $\square$

In general, there are item prices that guarantee obtaining at least half of the optimal welfare. This is achieved by splitting the weight of the edges of an optimal matching uniformly between the two corresponding vertices. We present this result in Lemma 8 for general d.

4.2 Hypergraph Matching: $d>2$

We begin this section by proving two negative results. First we show an upper bound of $\sim \sqrt{1/d}$ on the fraction of the optimal solution that can be guaranteed with prices. We then show a specific bound for the case $d=3$, in which we cannot guarantee obtaining more than 1/2 of the optimal welfare. Finally, we provide a pricing scheme that always obtains at least 1/d of the optimal welfare.

Lemma 7

Prices cannot guarantee welfare more than an $\sim \sqrt{1/d}$ fraction of the optimal welfare, even if the arrival order is known.

Proof

Our example is based on constructions for finite projective planes; namely, we will use the fact that if $q-1$ is a prime power there exists a hypergraph on $q^2 - q + 1$ vertices with $q^2 - q + 1$ hyperedges that are q-regular, q-uniform and intersecting, i.e. every pair of hyperedges has at least one shared vertex (see, e.g., [17, Chapter 12] for a reference).

To build our example, we will assume that for each hyperedge there exists a corresponding buyer interested in exclusively that subset of items with a total valuation of q. We will also add one buyer whose only subset of interest is the entire set of items, with a valuation of $d=q^2 - q + 1$. Note that clearly the optimal welfare attainable is $q^2 - q + 1$.

It hence suffices to show that prices cannot achieve welfare greater than q. Assume the buyer interested in the entire set of items arrives last. Note that if there is any edge e such that the sum of the prices of the vertices in e is at most than q, we are guaranteed welfare at most q. However, if every the sum of the prices of the vertices in every hyperedge is more than q, because our graph is q-uniform that means the sum of the prices of all vertices is more than $q^2\,-\,q\,+\,1$, meaning the final buyer would not select anything and the welfare attained is zero. Hence, the total welfare attainable by prices is at most a

$$\frac{q}{q^2 - q + 1} \sim \frac{1}{\sqrt{q^2 - q + 1}}$$

fraction of the optimum.

Finally, if d cannot be written as $q^2\,-\,q\,+\,1$, we replicate the same construction for the largest $d'<d$ that can, and the result holds.    $\square$

When $d=3$ the upper bound given by Lemma 7 is 2/3. We briefly note that this bound can be tightened to 1/2. Our instance consists of a hypergraph $G=(V,E)$ with $V=\{1,2,3,4,5,6\}$ and hyperedges $\{1,2,3\}$, $\{4,5,6\}$, $\{1,2,4\}$, $\{1,3,5\}$, $\{2,5,6\}$, $\{3,4,6\}$ all with unit weight; the short proof that this attains an upper bound of 1/2 is deferred to the full version.

We conclude with our positive result. Consider a hypergraph $G=(V,E)$, with weights $(w(e))_{e\in E}$. To define the prices, take an optimal matching given by the hyperedges $OPT_1,\ldots ,OPT_\ell$. For each $a \in OPT_j$, define $p_a=w(OPT_j)/d$. The prices of the items not covered by the optimal solution are set to $\infty$. The following simple result shows that these prices obtain at least a fraction 1/d of the optimal welfare.

Lemma 8

Consider prices defined as above, and hyperedges arriving in an arbitrary order. Let Q denote the set of edges that are bought. Then

$$\sum _{e \in Q} w(e) \ge \frac{1}{d} \sum _{j=1}^\ell w(OPT_j)$$

Proof

First note that for each $e \in Q$, it must hold that

$$\begin{aligned} w(e) \ge \sum _{i \in e} p_i \end{aligned}$$

(3)

as otherwise the buyer associated to e would have decided not to buy. Therefore

$$\begin{aligned} \sum _{e \in Q} w(e) \ge \sum _{e \in Q} \sum _{i \in e} p_i \end{aligned}$$

(4)

On the other hand, for each $OPT_j$ in the optimal solution, there must be at least one vertex, with its corresponding price $w(OPT_j)/d$ that is covered by the edges in Q. To see this, note that there are two possible cases: either $OPT_j \in Q$ and all its vertices are covered, or $OPT_j \notin Q$, meaning that when $OPT_j$ arrived, at least one of its vertices was not available, i.e., it was covered by an edge previously bought. The result follows directly, noting that in the RHS of (4), we are summing at least once $w(OPT_j)/d$ for each $j=1\ldots ,\ell$.    $\square$