Rectangle Attacks on Reduced Versions of the FBC Block Cipher

Abstract

The FBC block cipher is an award-winning algorithm of the recent Cryptographic Algorithm Design Competition in China, which has three versions: FBC128-128 with a 128-bit block size and a 128-bit key size, FBC128-256 with a 128-bit block size and a 256-bit key size, and FBC256 with a 256-bit block size and a 256-bit key size. The best previously published cryptanalysis results on FBC are an impossible differential attack on 13-round FBC128-128 and a boomerang attack on 13-round FBC128-256. In this paper, we exploit a 12-round rectangle distinguisher with probability $2^{-234}$ of FBC128 and a 16-round rectangle distinguisher with probability $2^{-448}$ of FBC256, and observe that preliminary satisfying ciphertext quartets can be efficiently filtered out by sorting plaintext pairs according to some nibble positions at the ciphertext side during key-recovery phase, and finally we mount rectangle attacks on 14-round FBC128-128, 15-round FBC128-256 and 19-round FBC256 to recover their respective user key. Our attacks break more rounds than any previously published attacks on FBC.

1 Introduction

Aiming to select block cipher and public-key encryption algorithms, the Cryptographic Algorithm Design Competition in China, organised by the Chinese Association of Cryptologic Research under the guidance of State Cryptography Administration Office, started in 2018, and finished in 2020. The FBC block cipher, designed by Feng et al. [5], is an award-winning algorithm of the competition. FBC employs a generalized Feistel structure and has three versions: FBC128-128 with a 128-bit block size and a 128-bit key size, FBC128-256 with a 128-bit block size and a 256-bit key size, and FBC256 with a 256-bit block size and a 256-bit key size, which have a total of 48, 64 and 80 rounds, respectively.

The main published cryptanalytic results on FBC are as follows. In 2019, Ren et al. [13] described a 11-round differential [2] with probability $2^{-122}$ and a 12-round differential attack on FBC128-128, a 10-round linear approximation [11] with bias $2^{-42}$ and an 11-round linear attack on FBC128-128, a 7-round impossible differential [3, 8] and an 11-round impossible differential attack on FBC128-128, and a 12-round boomerang [15] distinguisher with probability $2^{-235.34}$ (more specifically, an amplified boomerang [6] or rectangle [1] distinguisher) and a 13-round boomerang attack on FBC128-256. In 2022, Zhang et al. [16] described 7-round impossible differentials of FBC128 and an impossible differential attack on 13-round FBC128-128.

Being an extension to differential cryptanalysis [2], the boomerang attack [15] treats a block cipher as a cascade of two sub-ciphers and is based on the idea of using two short differentials with larger probabilities instead of a long differential with a smaller probability, under an adaptive chosen plaintext or ciphertext attack scenario. The amplified boomerang attack [6] and the rectangle attack [1] simplify the attack scenario of the boomerang attack to a chosen plaintext or ciphertext attack scenario under a uniformity assumption. The boomerang-style attacks can use more than two differentials, some for the first sub-cipher and the others for the other sub-cipher, and generally assume that the differentials for the sub-ciphers behave independently [7, 12], although boomerang connectivity table tools [4, 14] have recently been proposed for use under certain circumstances.

Table 1. Main cryptanalytic results on FBC

In this paper, we further analyse the security of the FBC block cipher against rectangle attack. First, we exploit a 12-round rectangle distinguisher with probability $2^{-234}$ on FBC128, and observe that during key-recovery phase the output difference of the 12-round distinguisher enables us to obtain preliminary satisfying ciphertext quartets efficiently by sorting the plaintext pairs according to the values of some nibble positions with a zero difference at the ciphertext side, and finally we can use the 12-round rectangle distinguisher to make key-recovery attacks on 14-round FBC128-128 and 15-round FBC128-256, breaking one or two more rounds than the best previously published cryptanalytic results on FBC128-128 and FBC128-256, respectively. Similarly, we exploit a 16-round rectangle distinguisher with probability $2^{-448}$ on FBC256 and use it to mount a key-recovery attack on 19-round FBC256. Table 1 summarises previous and our main cryptanalytic results on FBC. Our attacks are better than any previously published attacks on FBC in terms of the numbers of attacked rounds.

The remainder of the paper is organized as follows. In the next section, we give the notion used throughout this paper and briefly describe the FBC block cipher and Ren et al.’s 13-round FBC128-256 attack. We present our rectangle attacks on FBC128 and FBC256 in Sects. 3 and 4, respectively. Section 5 concludes this paper.

2 Preliminaries

  In this section, we give the notation and briefly describe the FBC block cipher and Ren et al.’s boomerang attack on 13-round FBC128-256.

2.1 Notation

In all descriptions we assume that the bits of an n-bit value are numbered from 0 to $n-1$ from left to right, a number without a prefix represents a decimal number, a number with prefix 0x represents a hexadecimal number, and we use the following notation throughout this paper.

2.2 The FBC Block Cipher

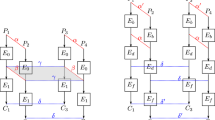
The FBC block cipher employs a 4-branch generalised Feistel structure and has three versions: FBC128-128 with a 128-bit block size and key size, FBC128-256 with a 128-bit block size and a 256-bit key size, and FBC256 with a 256-bit block size and key size, and they have a total of 48, 64 and 80 rounds, respectively. Denote the input and output of the i-th round ($i\ge 0$) by $(X_{i}^0, X_{i}^1, X_{i}^2, X_{i}^3) \in (\mathbb {F}_2^b)^4$ and $(X_{i+1}^0, X_{i+1}^1, X_{i+1}^2, X_{i+1}^3) \in (\mathbb {F}_2^b)^4$ respectively, then the encryption process of the i-th round, as illustrated in Fig. 1, is as follows,

$$\begin{aligned} X_{i+1}^0 = & {} \textbf{F}(X_{i}^0,K_{2i})\oplus X_{i}^1, \\ X_{i+1}^1 = & {} \textbf{F}(X_{i}^3,K_{2i+1})\oplus X_{i}^2\oplus X_{i}^0, \\ X_{i+1}^2 = & {} \textbf{F}(X_{i}^0,K_{2i})\oplus X_{i}^1\oplus X_{i}^3, \\ X_{i+1}^3 = & {} \textbf{F}(X_{i}^3,K_{2i+1})\oplus X_{i}^2, \end{aligned}$$

where b is 32 for FBC128 and 64 for FBC256, $\textbf{F}$ is the round function, and $K_{2i+1}$ and $K_{2i}$ are round keys.

Fig. 1.

One-round encryption of FBC 

The round function $\textbf{F}$ consists of the following three operations:

• Key Addition: Input is XORed with a round key to produce output u.

• Column Transform S: Representing u as $u=(u_0\Vert u_1\Vert u_2\Vert u_3)$, apply the same $4\times 4$-bit bijective S-box S 8 or 16 times in parallel to u to produce output $v=(v_0\Vert v_1\Vert v_2\Vert v_3)$ as ($v_{0,j}\Vert v_{1,j}\Vert v_{2,j}\Vert v_{3,j}$) = $S(u_{0,j}\Vert u_{1,j}\Vert u_{2,j}\Vert u_{3,j})$, where $u_i$ and $v_i$ are 8-bit for FBC128 and 16-bit for FBC256, and $u_{i,j}$ and $v_{i,j}$ are respectively the j-th bit of $u_i$ and $v_i$ ($0\le i\le 3$, $0\le j\le 7$ for FBC128 and $0\le j\le 15$ for FBC256). The S-box specification is given in Table 2.

• Row Transform P: Given input v, the output z is computed as $z=v\oplus (v\lll 3)\oplus (v\lll 10)$ for FBC128, and $z=v\oplus (v\lll 17)\oplus (v\lll 58)$ for FBC256.

Table 2. The S-box of FBC 

At last, to simplify our subsequent descriptions and cryptanalysis, we denote by $\textbf{L}$ the linear operation except the $\text{ F }$ layer in a round, as shown in Fig. 1, and give the details of the Row Transform of FBC128 and FBC256 in Tables 3 and 4, respectively.

Table 3. Details of row transform of FBC128 

Table 4. Details of row transform of FBC256 

2.3 Ren et al.’s Boomerang Attack on 13-Round FBC128-256

Ren et al.’s boomerang attack on 13-round FBC128-256 [13] is actually an amplified boomerang or rectangle attack, which is based on a 12-round (amplified boomerang or rectangle) distinguisher with $2^{-235.34}$. The 12-round distinguisher is made up of two groups of 6-round differentials, where the group of 6-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ for Rounds 0–5 have the same input difference $\alpha =0x00000000000000000100020801000000$ but different output differences $\beta '$: 4096 $\beta '$ with probability $2^{-34}$, 204800 $\beta '$ with probability $2^{-36}$ and 966656 $\beta '$ with probability $2^{-38}$, and the group of 6-round differentials $\varDelta \gamma '\rightarrow \varDelta \delta$ for Rounds 6–11 have the same output difference $\delta$ but different input differences $\gamma '$, which are similar to the 6-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ in the decryption direction. As a result, they obtained a 12-round distinguisher with probability $[4096 \times (2^{-34})^2 +204800 \times (2^{-36})^2 +966656 \times (2^{-38})^2]\times [4096 \times (2^{-34})^2 +204800 \times (2^{-36})^2 +966656 \times (2^{-38})^2]\times 2^{-128} \approx 2^{-107.34} \times 2^{-128}= 2^{-235.34}$ by Biham et al.’s probability formula $\big (\sqrt{\sum _{\beta '}Pr^2[\alpha \rightarrow \beta ']} \cdot \sqrt{\sum _{\gamma '}Pr^2[\gamma '\rightarrow \delta ]}\big )^2 \times 2^{-n}$ of [1] (n is block size), and finally they appended one round at the end of this 12-round distinguisher to attack 13-round FBC128-256 in the following procedure:

• 1. Choose $2^{117.67}$ plaintext pairs with difference $\alpha$, and get the corresponding ciphertext pairs.

• 2. Guess the round key in Round 12, partially decrypt every ciphertext pair to get the corresponding intermediate values immediately after Round 11, XOR each of them with $\delta$, and store the resulting pair in a table.

• 3. Partially decrypt every ciphertext pair with the round key guessed in Step 2 to get the corresponding intermediate values immediately after Round 11, and check whether the resulting pair is in the table of Step 2. If there is a match, the guessed round key may be correct, since it is expected that there is $(2^{117.67})^2 \times 2^{-235.34}=1$ satisfying quartet under the correct key.

3 Rectangle Attacks on 14-Round FBC128-128 and 15-Round FBC128-256

  In this section, we describe a 12-round rectangle distinguisher with probability $2^{-234}$ of FBC128, and present rectangle attacks on 14-round FBC128-128 and 15-round FBC128-256.

3.1 A 12-Round Rectangle Distinguisher with Probability $2^{-234}$ of FBC128

We exploit a 12-round rectangle distinguisher with probability $2^{-234}$ for FBC128, which has a slightly larger probability than Ren et al.’s. Our 12-round distinguisher is made up of a group of 6-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ for the first 6 rounds and a group of 6-round differentials $\varDelta \gamma '\rightarrow \varDelta \delta$ for the last 6 rounds, here the 6-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ have the same input difference $\alpha =0x00000000000000000800004208000000$ but different output differences $\beta '$: 256 $\beta '$ with probability $2^{-32}$ and $7\times 2^{10}=7168$ $\beta '$ with probability $2^{-33}$, and the 6-round differentials $\varDelta \gamma '\rightarrow \varDelta \delta$ have the same output difference $\delta =0x08000000080000420000000008000042$ but different input differences $\gamma '$, which are similar to the 6-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ in the decryption direction. Table 5 gives a 6-round differential $\varDelta \alpha \rightarrow \varDelta \beta '$ with probability $2^{-32}$, and Table 6 gives a 6-round differential $\varDelta \alpha \rightarrow \varDelta \beta '$ with probability $2^{-33}$. The other 6-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ can be easily obtained by changing the output difference of the last round of one of the two 6-round differentials of Tables 5 and 6. The difference distribution table (DDT) of the FBC S-box is given as Table 7 in the appendix.

Table 5. A 6-round differential with probability $2^{-32}$ of FBC128 

Table 6. A 6-round differential with probability $2^{-33}$ of FBC128 

Hence, the 12-round rectangle distinguisher has a probability of $[256 \times (2^{-32})^2 + 7168 \times (2^{-33})^2]\times [256 \times (2^{-32})^2 + 7168 \times (2^{-33})^2]\times 2^{-128} = 2^{-106} \times 2^{-128}= 2^{-234}$.

Fig. 2.

Rectangle attack on 14-round FBC128-128 

3.2 Attacking 14-Round FBC128-128

  We can attack 14-round FBC128-128 by appending one round respectively at the beginning and end of the above 12-round rectangle distinguisher. We assume the attacked 14 rounds are Rounds 0–13, and the 12-round distinguisher is used from Rounds 1–12, as illustrated in Fig. 2. The attack procedure is as follows.

• 1. By the S-box DDT in Table 7, we have $DDT(0x8,0x8) = DDT(0x8,0xA) = DDT(0x2,0x2) = DDT(0x2,0x6) = DDT(0x2,0xA) = DDT(0x2,0xE) = DDT(0x4,0x1) = DDT(0x4,0x4) = DDT(0x4,0xC) = DDT(0x4,0xD)= 4$ and DDT(0x8,  $0x3) =DDT(0x8,0x7)= DDT(0x8,0x9)= DDT(0x8,$ $0xD) = 2$ under the notation $DDT(\varDelta a, \varDelta b)=\#\{x|S(x)\oplus S(x\oplus a)=b\}$. Thus, given the input difference $\alpha$ to Round 1 from the 12-round distinguisher, there are $6\times 4\times 4\times 6 \approx 2^{9.17}$ possible input differences to Round 0, which we denote by $\varDelta _j$ ($j=0,1,\cdots ,2^{9.17}-1$). We choose $2^{117}\times 2^{9.17}=2^{126.17}$ plaintext pairs ($P_i, P_{i,j}$) such that $P_{i,j}=P_i \oplus \varDelta _j$, and obtain their ciphertext pairs ($C_i, C_{i,j}$), where $i=0,1,\cdots ,2^{117}-1$. Clearly, $P_i\oplus P_{i,j}$ = $(0x080000000\star 0000\star \star 0\star 0\star \star \star \star \star 08000042)$.

• 2. Store ($C_i, C_{i,j}$) into a hash table indexed by ($\textbf{L}^{-1}(C_i)[0, 2-8, 10-13, 16,18,$ $24, 26-29], \textbf{L}^{-1}(C_{i,j})[0, 2-8, 10-13, 16,18, 24, 26-29]$), that is, nibbles $(0, 2-8, 10-13, 16,18, 24, 26-29)$ of $\textbf{L}^{-1}(C_i)$ and $\textbf{L}^{-1}(C_{i,j})$, store also ($C_{i,j}, C_i$) into this hash table indexed by ($\textbf{L}^{-1}(C_{i,j})[0, 2-8, 10-13, 16,18, 24,$ $26-29], \textbf{L}^{-1}(C_i)[0, 2-8, 10-13, 16,18,24, 26-29]$), and obtain preliminary satisfying ciphertext quartets $((C_a, C_b),(C_c, C_d))$ such that $\textbf{L}^{-1}(C_a)[0, 2-8, 10-13, 16,18,24, 26-29]=\textbf{L}^{-1}(C_c)[0, 2-8, 10-13, 16,18,24, 26-29]$ and $\textbf{L}^{-1}(C_b)[0, 2-8, 10-13, 16,18, 24, 26-29]=\textbf{L}^{-1}(C_d)[0, 2-8, 10-13, 16,18, 24, 26-29]$, by accessing every table entry to get the preliminary satisfying ciphertext quartets and removing their actually identical counterparts at the corresponding entries. (Note that $((C_{i_0}, C_{i_0,j_0}),(C_{i_1}, C_{i_1,j_1}))$ and $((C_{i_0}, C_{i_0,j_0}),$ $(C_{i_1,j_1}, C_{i_1}))$ are different quartets, but $((C_{i_0,j_0}, C_{i_0}), (C_{i_1,j_1},$ $C_{i_1}))$ and $((C_{i_0}, C_{i_0,j_0}),(C_{i_1}, C_{i_1,j_1}))$ are actually identical quartets, more specifically, two ciphertext pairs $(C_a, C_b)$ and $(C_c, C_d)$ under a table index constitute a preliminary satisfying ciphertext quartet $((C_a, C_b),(C_c, C_d))$, but this quartet appears pairwise with its actually identical counterpart $((C_b, C_a), (C_d, C_c))$ in the whole table, and the entry of the quartet $((C_b, C_a),$ $(C_d, C_c))$ can be immediately determined from the entry of the quartet $((C_a, C_b),(C_c, C_d))$, so it takes only an access to remove a counterpart.) As a result, it is expected that there are approximately $(2^{126.17})^2 \times (2^{-19\times 4})^2=2^{100.34}$ preliminary satisfying ciphertext quartets $((C_a, C_b),(C_c, C_d))$.

• 3. Check whether the $2^{100.34}$ preliminary quartets $((C_a, C_b),(C_c, C_d))$ meet $\textbf{L}^{-1}(C_a)\oplus \textbf{L}^{-1}(C_c)=0x080000000\star 0000\star \star 0\star 0\star \star \star \star \star 08000042$ and $\textbf{L}^{-1}(C_b) \oplus \textbf{L}^{-1}(C_d)=0x080000000\star 0000\star \star 0\star 0\star \star \star \star \star 08000042$, and keep only the satisfying quartets. It is expected that there remain $2^{100.34} \times (2^{-4\times 4})^2=2^{68.34}$ satisfying quartets $((C_a, C_b),(C_c, C_d))$.

• 4. Guess ($K_{26}[1],K_{27}[1,6,7]$), and do as follows.

  • (a) Partially decrypt every remaining quartet $((C_a, C_b),(C_c, C_d))$ to check whether both $(C_a,C_c)$ and $(C_b, C_d))$ produce the difference $\delta$ immediately before Round 13. It is expected that there remains $2^{68.34} \times (2^{-9\times 4})^2=2^{-3.66}<1$ satisfying quartet $((C_a, C_b),(C_c, C_d))$ for every key guess, and $2^{16} \times [1-{2^{68.34} \atopwithdelims ()0}(2^{-9\times 4 \times 2})^0(1-2^{-9\times 4 \times 2})^{2^{68.34}}]\approx 2^{16} \times 2^{-3.71}=2^{12.29}$ guesses of ($K_{26}[1],K_{27}[1,6,7]$) have at least one remaining quartet.

  • (b) For every remaining quartet $((C_a, C_b),(C_c, C_d))$ (if any), get the corresponding $((P_a, P_b),(P_c, P_d))$ and extract the subkeys ($K_0[1],K_1[1,6,7]$) such that $((P_a, P_b),(P_c, P_d))$ produces the difference $\alpha$ immediately after Round 0. (Skip this quartet if there is no satisfying ($K_0[1], K_1[1,6,7]$).)

• 5. For every remaining ($K_0[1], K_1[1,6,7]$), exhaustively search the remaining 112 key bits to determine the 128-bit user key.

The attack requires $2^{126.17}+2^{117}\approx 2^{126.17}$ chosen plaintexts. The memory complexity of the attack is dominated by Step 2, which is $2^{126.17}\times 4\times 16 \times 2=2^{133.17}$ bytes. The time complexity of the attack is dominated by the encryptions of the $2^{126.17}$ chosen plaintexts and Steps 2 and 5, Step 2 has a time complexity of $2^{126.17}\times 2=2^{127.17}$ memory accesses, which is equivalent to $\frac{2^{127.17}}{14\times 2} \approx 2^{122.36}$ 14-round FBC128-128 encryptions under an extreme approximation that a one-round FBC128-128 encryption is approximated as two table lookups, Step 5 has a time complexity of $2^{12.29}\times 2^{112}=2^{124.29}$ 14-round FBC128-128 encryptions, and thus the attack has a total time complexity of $2^{126.17}+2^{122.36}+2^{124.29}\approx 2^{126.59}$ 14-round FBC128-128 encryptions. The attack has an expected success probability of approximately $1-(1-2^{-234})^{2^{234}}\approx 1-\texttt{e}^{-1}\approx 63\%$.

Notice that an usual process for rectangle attack is to check whether the two ciphertext pairs $(C_{i_0},C_{i_1})$ and $(C_{i_0,j_0}, C_{i_1,j_1})$ out of a ciphertext quartet $((C_{i_0},C_{i_1}),(C_{i_0,j_0}, C_{i_1,j_1}))$ could produce the expected $\delta$ difference, but in this 14-round FBC128-128 attack, some nibble positions immediately before the $\textbf{L}$ operation of Round 13 have a determinate zero difference, so $\textbf{L}^{-1}(C_{i_0})[0, 2-8, 10-13, 16,18,24, 26-29] \oplus \textbf{L}^{-1}(C_{i_1})[0, 2-8, 10-13, 16,18,24, 26-29] = \textbf{L}^{-1}(C_{i_0,j_0})[0, 2-8, 10-13, 16,18, 24, 26-29] \oplus \textbf{L}^{-1}(C_{i_1,j_1})[0, 2-8, 10-13, 16,18,$ $24, 26-29]=0$ leads to $(\textbf{L}^{-1}(C_{i_0})[0, 2-8, 10-13, 16,18,24, 26-29], \textbf{L}^{-1}(C_{i_0,j_0})[0,$ $2-8, 10-13, 16,18, 24, 26-29])= (\textbf{L}^{-1}(C_{i_1})[0, 2-8, 10-13, 16,18,24, 26-29], \textbf{L}^{-1}(C_{i_1,j_1})[0, 2-8, 10-13, 16,18, 24, 26-29])$. This is why we can filter out preliminary satisfying ciphertext quartets efficiently by sorting the ciphertext pairs of the chosen plaintext pairs as described in Step 2.

Note that in Step 2 we can make a more refined filtering by further sorting the plaintext pairs according to the values of some nibble positions with a non-zero difference at the ciphertext side, but this is not necessary from the perspective of time complexity.

3.3 Attacking 15-Round FBC128-256

  We can attack 15-round FBC128-256, by appending one round at the end of the above 14-round FBC128-128 attack. As illustrated in Fig. 3, we assume the attacked 15 rounds are Rounds 0–14, the 12-round distinguisher is used from Rounds 1–12, and the attack procedure is as follows.

• 1. Same as Step 1 of the above 14-round FBC128-128 attack.

• 2. Store ($C_i, C_{i,j}$) into a hash table indexed by ($\textbf{L}^{-1}(C_i)[0,2-5,8,10,24,26],$ $\textbf{L}^{-1}(C_{i,j})[0,2-5,8,10,24,26]$), that is, nibbles $(0,2-5,8,10,24,26)$ of $\textbf{L}^{-1}(C_i)$ and $\textbf{L}^{-1}(C_{i,j})$, store also ($C_{i,j}, C_i$) into this hash table indexed by ($\textbf{L}^{-1}(C_{i,j})[0,2-5,8,10,24,26], \textbf{L}^{-1}(C_i)[0,2-5,8,10,24,26]$), and obtain preliminary satisfying ciphertext quartets $((C_a, C_b),(C_c, C_d))$ such that $\textbf{L}^{-1}(C_a)[0,2-5,8,10,24,26]=\textbf{L}^{-1}(C_c)[0,2-5,8,10,24,26]$ and $\textbf{L}^{-1}(C_b)[0,$ $2-5,8,10,24,26]=\textbf{L}^{-1}(C_d)[0,2-5,8,10,24,26]$. It is expected that there are $(2^{126.17})^2 \times (2^{-9\times 4})^2=2^{180.34}$ preliminary satisfying ciphertext quartets $((C_a, C_b),(C_c, C_d))$.

• 3. Guess ($K_{28}[1,6,7],K_{29}[1,3-7]$), and do as follows.

  • (a) Partially decrypt each of the $2^{180.34}$ preliminary quartets $((C_a, C_b),(C_a,$ $C_b))$ to check whether both $(C_a,C_c)$ and $(C_b, C_d))$ produce the difference $0x080000000\star 0000\star \star 0\star 0\star \star \star \star \star 08000042$ immediately before the $\textbf{L}$ operation of Round 13. It is expected that there remain $2^{180.34} \times (2^{-14\times 4})^2=2^{68.34}$ satisfying quartets $((C_a, C_b),(C_c, C_d))$ for every key guess.

  • (b) Guess ($K_{26}[1],K_{27}[1,6,7],K_{28}[3,4],K_{29}[0,2]$), partially decrypt every remaining quartet $((C_a, C_b),(C_c, C_d))$ to check whether both $(C_a, C_c)$ and $(C_b,C_d))$ produce the difference $\delta$ immediately before Round 13. It is expected that there are $2^{68.34} \times (2^{-9\times 4})^2=2^{-3.66}<1$ satisfying quartet $((C_a, C_b),(C_c, C_d))$ for every key guess and $2^{68} \times [1-{2^{68.34} \atopwithdelims ()0}(2^{-9\times 4 \times 2})^0(1-2^{-9\times 4 \times 2})^{2^{68.34}}]\approx 2^{16} \times 2^{-3.71}=2^{64.29}$ guesses of ($K_{26}[1],K_{27}[1,6,7],$ $K_{28}[1,3,4,6,7],K_{29}$) have at least one remaining quartet.

  • (c) For every remaining quartet $((C_a, C_b),(C_c, C_d))$ (if any), get the corresponding $((P_a, P_b),(P_c, P_d))$ and extract the subkeys ($K_0[1],K_1[1,6,7]$) such that $((P_a, P_b),(P_c, P_d))$ produces the difference $\alpha$ immediately after Round 0. (Skip this quartet if there is no satisfying ($K_0[1], K_1[1,6,7]$).)

• 4. For every remaining ($K_{26}[1],K_{27}[1,6,7],K_{28}[1,3,4,6,7],K_{29}$), exhaustively search the remaining 188 key bits to determine the 256-bit user key.

Fig. 3.

Rectangle attack on 15-round FBC128-256 

The attack has a data complexity of approximately $2^{126.17}$ chosen plaintexts, a memory complexity of approximately $2^{126.17}\times 4\times 16 \times 2=2^{133.17}$ bytes and a success probability of $63\%$. The time complexity of the attack is dominated by Step 4, which is $2^{64.29}\times 2^{188}=2^{252.29}$ 15-round FBC128-256 encryptions.

4 Rectangle Attack on 19-Round FBC256

  In this section, we describe a 16-round rectangle distinguisher with probability $2^{-448}$ of FBC256, and present a rectangle attack on 19-round FBC256.

4.1 A 16-Round Rectangle Distinguisher with Probability $2^{-448}$ of FBC256

The 16-round distinguisher is made up of two groups of 8-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ for the first 8 rounds and a group of 8-round differentials $\varDelta \gamma '\rightarrow \varDelta \delta$ for the last 8 rounds, here the 8-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ have the same input difference $\alpha =0x080000000000000048000008000000000000000000000801480$ $0000800000000$ but $2^{6}$ different output differences $\beta '$ with probability $2^{-51}$, and the 8-round differentials $\varDelta \gamma '\rightarrow \varDelta \delta$ have the same output difference $\delta =0x0000000000000$ $000000000000000080148000008000000000800000000000801$ but $2^{6}$ different input differences $\gamma '$ with probability $2^{-51}$, which are similar to the 8-round differentials $\varDelta \alpha \rightarrow \varDelta \beta '$ in the decryption direction. Hence, the 16-round rectangle distinguisher has a probability of $[2^{6} \times (2^{-51})^2]\times [2^{6} \times (2^{-51})^2]\times 2^{-256} = 2^{-448}$.

An 8-round differential $\varDelta \alpha \rightarrow \varDelta \beta '$ is described in detail in Table 8 in the appendix. The other 8-round differentials can be easily obtained by changing the output difference of the last round of the 8-round differential of Table 8.

Fig. 4.

Rectangle attack on 19-round FBC256 

4.2 Attacking 19-Round FBC256

  We can attack 19-round FBC256 by appending one round at the beginning and two rounds at the end of the above 15-round rectangle distinguisher, and we assume the attacked 19 rounds are Rounds 0–18 and the 16-round distinguisher is used from Rounds 1–16, as illustrated in Fig. 4. Slightly different from the above 14-round FBC128-128 attack and 15-round FBC128-256 attack, here we use the early abort technique [9, 10] for a reduced time complexity, by guessing only a small fraction of the unknown required subkey bits at a time in Round 18, instead of guessing all of them at once.

• 1. By the S-box DDT in Table 7, we have $DDT(0x1,0x1) = DDT(0x1,0x5) = DDT(0x8,0x8) = DDT(0x8,0xA) = 4$ and $DDT(0x8, 0x3) =DDT(0x8,$ $0x7)= DDT(0x8,0x9)= DDT(0x8,0xD) = DDT(0x1, 0x3) =DDT(0x1,$ $0x7)= DDT(0x1,0xB)= DDT(0x1, 0xF) =2$. Thus, given the input difference $\alpha$ to Round 1 from the 16-round distinguisher, there are $6\times 6\times 6 \approx 2^{7.75}$ possible input differences to Round 0, which we denote by $\varDelta _j$ ($j=0,1,\cdots ,2^{7.75}-1$). We choose $2^{224}\times 2^{7.75}=2^{231.75}$ plaintext pairs ($P_i, P_{i,j}$) such that $P_{i,j}=P_i \oplus \varDelta _j$, and obtain their ciphertext pairs ($C_i, C_{i,j}$), where $i=0,1,\cdots ,2^{224}-1$. Clearly, $P_i\oplus P_{i,j}$ = (0x0000000000000000080000000000 $0000\star \star 0\star 0\star 0\star 0000\star \star \star \star 0800000000000801)$.

• 2. Store ($C_i, C_{i,j}$) into a hash table indexed by ($\textbf{L}^{-1}(C_i)[0-12,14,18,20,22,$ $24-27,40,42,50,52,54,56-59], \textbf{L}^{-1}(C_{i,j})[0-12,14,18,20,22,24-27,40,42,$ $50,52,54,56-59]$), that is, nibbles $(0-12,14,18,20,22,24-27,40,42,50,52,$ $54,56-59)$ of $\textbf{L}^{-1}(C_i)$ and $\textbf{L}^{-1}(C_{i,j})$, store also ($C_{i,j}, C_i$) into this table indexed by ($\textbf{L}^{-1}(C_{i,j})[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59], \textbf{L}^{-1}(C_i)[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59]$), and obtain preliminary quartets $((C_a, C_b),(C_c, C_d))$ such that $\textbf{L}^{-1}(C_a)[0-12,14,$ $18,20,22,24-27,40,42,50,52,54,56-59]= \textbf{L}^{-1}(C_c)[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59]$ and $\textbf{L}^{-1}(C_b)[0-12,14,18,20,22,24-27,40,42,$ $50,52,54,56-59]=\textbf{L}^{-1}(C_d)[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59]$. It is expected that there are $(2^{231.75})^2 \times (2^{-30\times 4})^2=2^{223.5}$ preliminary satisfying ciphertext quartets $((C_a, C_b),(C_c, C_d))$.

• 3. Check whether the $2^{223.5}$ preliminary satisfying ciphertext quartets $((C_a, C_b),$ $(C_c, C_d))$ meet $\textbf{L}^{-1}(C_a)[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59] \oplus \textbf{L}^{-1}(C_c)[0-12,14,18,20, 22,24-27,40,42,50,52,54,56-59]=0x000000$ $0000000801\star \star 0\star 0\star 0\star 0000\star \star \star \star \star \star \star \star \star \star \star \star 0\star 0\star \star \star \star \star \star \star 0\star 0\star 0\star 0000\star \star \star \star$ and $\textbf{L}^{-1}(C_b)[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59]\oplus \textbf{L}^{-1}(C_b)[0-12,14,18,20,22,24-27,40,42,50,52,54,56-59]=0x0000000000000801\star \star 0\star 0 \star 0\star 0000\star \star \star \star \star \star \star \star \star \star \star \star 0\star 0\star \star \star \star \star \star \star 0\star 0\star 0\star 0000\star \star \star \star$, and keep only the satisfying quartets. It is expected that there remain $2^{223.5} \times (2^{-2\times 4})^2=2^{207.5}$ satisfying quartets $((C_a, C_b),(C_c, C_d))$.

• 4. Guess $K_{37}[0,1,3,12,13]$, partially decrypt each of the $2^{207.5}$ remaining quartets $((C_a, C_b),(C_c, C_d))$ to check whether both $(C_a,C_c)$ and $(C_b,C_d)$ produce $\varDelta X^2_{18}[0-3]=0x0800$. (Note that this can be done by checking the two ciphertext pairs out of a quartet one after the other as introduced in [9].) It is expected that there remain $2^{207.5}\times (2^{-4\times 4})^2 = 2^{175.5}$ satisfying $((C_a, C_b),(C_c, C_d))$ for every key guess.

• 5. Guess $K_{37}[5,7,14,15]$, partially decrypt each of the $2^{175.5}$ remaining quartets $((C_a, C_b),(C_c, C_d))$ to check whether both $(C_a,C_c)$ and $(C_b,C_d)$ produce $\varDelta X^2_{18}[4-7,9,11-15]=0$. It is expected that there remain $2^{175.5}\times (2^{-10 \times 4})^2 = 2^{95.5}$ satisfying $((C_a, C_b),(C_c, C_d))$ for every key guess.

• 6. Guess $K_{36}[13,15]$, partially decrypt each of the $2^{95.5}$ remaining quartets $((C_a, C_b),(C_c, C_d))$ to check whether both $(C_a,C_c)$ and $(C_b,C_d)$ produce $\varDelta X^1_{18}=\varDelta X^3_{18}$. It is expected that there remain $2^{95.5}\times (2^{-9\times 4})^2 = 2^{23.5}$ satisfying $((C_a, C_b),(C_c, C_d))$ for every key guess.

• 7. Guess $(K_{37}[2,9,11],K_{35}[1,13,15])$, partially decrypt each of the $2^{23.5}$ remaining quartets $((C_a, C_b),(C_c, C_d))$ to check whether both $(C_a,C_c)$ and $(C_b,C_d)$ produce $\varDelta X^2_{17}=0x4800000800000000$. It is expected that there remains $2^{23.5}\times (2^{-9\times 4})^2 = 2^{-48.5}<1$ satisfying quartets for every key guess, and $2^{68} \times [1-{2^{23.5} \atopwithdelims ()0}(2^{-9\times 4 \times 2})^0(1-2^{-9\times 4 \times 2})^{2^{23.5}}] \approx 2^{68} \times 2^{-48.5}=2^{19.5}$ guesses of $(K_{37}[0-3,5,7,9,11-15],K_{36}[13,15],K_{35}[1,13,15])$ have at least one remaining quartet. For every remaining quartet $((C_a, C_b),(C_c, C_d))$ (if any), get the corresponding $((P_a, P_b),(P_c, P_d))$ and extract the subkeys $K_1[1, 13,15]$ such that $((P_a, P_b),(P_c, P_d))$ produces the difference $\alpha$ immediately after Round 0. (Skip this quartet if there is no satisfying $K_1[1, 13,15]$.)

• 8. For every remaining $(K_{37}[0-3,5,7,9,11-15],K_{36}[13,15],K_{35}[1,13,15])$, exhaustively search the remaining 188 key bits to determine the 256-bit user key.

The attack has a data complexity of approximately $2^{231.75}+2^{224}\approx 2^{231.75}$ chosen plaintexts, a memory complexity of approximately $2^{231.75}\times 4\times 32\times 2=2^{239.75}$ bytes and a success probability of $1-(1-2^{-448})^{2^{448}}\approx 1-\texttt{e}^{-1}\approx 63\%$. The time complexity of the attack is dominated by the encryptions of the $2^{231.75}$ chosen plaintexts and Step 2, and Step 2 has a time complexity of $2^{231.75}\times 2=2^{232.75}$ memory accesses, which is equivalent to $\frac{2^{232.75}}{19\times 2} \approx 2^{227.51}$ 19-round FBC256 encryptions under an extreme approximation that a one-round FBC256 encryption is approximated as two table lookups. Therefore, the attack has a total time complexity of $2^{231.75}+ 2^{227.51} \approx 2^{231.83}$ 19-round FBC256 encryptions. Note that there are different data-memory-time tradeoffs and we can increase the success probability by using more chosen plaintexts.

5 Conclusion

  The FBC block cipher is an award-winning algorithm of the recent Cryptographic Algorithm Design Competition in China. In this paper, we have presented rectangle attacks on 14-round FBC128-128, 15-round FBC128-256 and 19-round FBC256 to recover their respective user key. These are better than any previously published cryptanalytic results on FBC in terms of the numbers of attacked rounds. Like most cryptanalytic results on block ciphers, our attacks are theoretical in the sense of the independence and uniformity assumptions of rectangle attack, and they do not endanger the security of the full FBC cipher.

Appendix

Table 7. Difference distribution table of the FBC S-box

Table 8. An 8-round differential with probability $2^{-51}$ of FBC256