Coupled Dynamics of an Oscillator Moving in Contact with a Periodically Supported String on Foundation

Abstract

The dynamics of a single degree-of-freedom oscillator moving at a constant velocity in contact with a periodically supported taut string on a continuous foundation is studied. The main objective is to assess the effect of various parameters on the contact stability of the system. The string is assumed to be of infinite extent, and the contact is assumed to be smooth. The system is modeled using the idea of periodic continuation of sub-structure, and the dynamical variables are solved using Fourier transformation and periodicity conditions. The interaction force between the oscillator and the string is determined analytically using the compatibility condition at the contact. The role of the string support parameters and the oscillator parameters on the contact stability are clearly brought out.

1 Introduction

The dynamics of a one-dimensional elastic continuum carrying a traveling transverse force is a classical problem [1]. This has relevance to the dynamics of bridges and railway lines under moving loads in general, and coupled dynamics of the conductor-pantograph system in electric trains in particular [2, 3]. The problem presents significant complexity when the elastic continuum is periodically supported. Moreover, for realistic modeling, the load is considered to be a traveling discrete dynamical system, which adds to the complexity. Addressing this issue motivates the present work.

The dynamics of elastic continua under moving constant force or interaction force of a travelling mechanical systems has been studied by many researchers. Some of these studies relate to fundamental aspects of dynamics of continuous structures (such as string and beams) subjected to moving loads. Gavrilov [4] and Metrikine [5] studied the response of an infinite string on a foundation when subjected to a moving point load. The dynamics of an infinite stretched string on Winkler foundation carrying a moving mass has been presented by Gavrilov [6]. Fox [7] studied the dynamics of periodically supported string subjected to a travelling time-dependent force and a travelling rigid mass. A two-level periodically supported catenary system under a moving constant force has been studied in [8]. Metrikine [9] studied the parametric instablity of a point mass moving on periodically supported infinite string. Mazilu [10] studied the travelling load response of an infinite homogeneous structure consisting of two continuously supported beams numerically using Green’s function method. Beams supported on an elastic half-space subjected to a moving load has been studied in [11]. Dynamic response of beams under moving loads has been presented in [12, 13]. Jezequel [14] analyzed the dynamics of a periodically supported beam to moving load. Dynamics of periodically supported beams on a foundation has been analyzed in [15, 16].

There exists a substantial body of research literature on modeling of catenary-pantograph dynamics that approach the problem completely numerically [17]. Most works either consider the load to be a constant force or a point mass. In recent years, there is a renewed interest in analytical modeling to understand the pantograph-catenary interaction dynamics [18, 19]. In this work, we follow the approach of [8] to first determine the basic response of a periodically supported infinite string on a Winkler foundation to a travelling harmonic force. Using this solution, we expand the string and the oscillator response in Fourier harmonics of the force, and use the contact compatibility condition to solve the steady-state response of the system analytically. Any type of oscillator can be considered in the proposed method. We study the effect of certain parameters on the response of the system. A normalized figure of merit is defined to track the effect of these parameters on the stability of contact between the oscillator and the string.

2 Mathematical Modeling

2.1 Equations of Motion

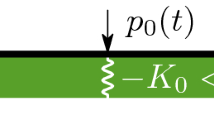
Consider a taut string of infinite extent, as shown in Fig. 1, placed on a visco-elastic foundation (shaded), and periodically supported at discrete points. Such a system is an idealization of a two-level catenary system with periodic supports at the poles. The single degree of freedom tunable oscillator in contact with the string is also shown. The contact between the oscillator and the string, assumed to be force-closed, will be considered stable as long as the interaction force is in the positive vertical direction (upwards) on the string.

Fig. 1.

Schematic figure of an oscillator moving in contact with a periodically supported string on a visco-elastic foundation.

The equation of motion of the taut string between the $n^{th}$ and $(n+1)^{th}$ periodic supports with a moving point force may be written as

$$\begin{aligned} \mu _s W_{,\tau \tau }+\Gamma _sW_{,\tau }+\Sigma _s W-TW_{,X\!X}=F(\tau )\Delta (X-V_o\tau ), \end{aligned}$$

(1)

for $nd\le X\le (n+1)d$, where $\mu _s$ and $W=W(x,t)$ are, respectively, the mass per unit length and transverse displacement field of the string, $\Gamma _s$ and $\Sigma _s$ are the coefficients of damping and stiffness distributions of the foundation, T is the string tension, $F(\tau )$ is the (unknown) interaction force, $V_o$ is the velocity of travel of the force, d is the distance between any two supports, and $\Delta (\cdot )$ is the Dirac-delta distribution. The equation of motion of the oscillator may be written as

$$\begin{aligned} {} & {} M_o\ddot{Y}+K_{op}Y+K_{os}Z=-F(\tau ),\qquad C_o\dot{Z}+K_{os}Z=C_o\dot{Y}, \end{aligned}$$

(2)

where $M_o$, $K_{op}$, $K_{os}$ and $C_o$ are, respectively, the mass, primary stiffness, secondary stiffness and damping parameters of the system, and Y and Z are the displacement variables as shown in Fig. 1. It may be noted that maintenance of contact requires the satisfaction of the compatibility condition

$$\begin{aligned} W(V\tau ,\tau )=Y(\tau ). \end{aligned}$$

(3)

The form of the system (2) is versatile, and can be tuned within the following extreme possibilities (a) compliant undamped oscillator ($K_{os}=0$, or $C_o=0$), (b) stiff undamped oscillator ($C_o\rightarrow \infty$), and (c) damped oscillator ($K_{os}\rightarrow \infty$).

The equations of motion (1)-(2) may be non-dimensionalized to obtain

$$\begin{aligned} {} & {} w_{,tt}+\gamma _sw_{,t}+\sigma _s w-w_{,xx}=f(t)\delta (x-v_ot),\qquad (n-1)\le x\le n, \end{aligned}$$

(4)

$$\begin{aligned} {} & {} m_o\ddot{y}+k_{op}y+k_{os}z=-f(t),\qquad c_o\dot{z}+k_{os}z=c_o\dot{y}, \end{aligned}$$

(5)

where we have used the non-dimensional quantities

$$\begin{aligned} {} & {} \!\!\! w=W/d,\qquad y=Y/d,\qquad z=Z/d,\qquad x=X/d, \qquad t=\tau c/d,\nonumber \\ {} & {} \!\!\! \gamma _s=\frac{\Gamma _sd}{\mu _s c},\qquad \sigma _s=\frac{\Sigma _sd^2}{\mu _s c^2},\qquad f(t)=\frac{F(\tau )}{\mu _s c^2},\qquad \delta (\cdot )=\frac{\Delta (\cdot )}{d},\nonumber \\ {} & {} \!\!\! m_o=\frac{M_o}{\mu _s d},\qquad k_{op}=\frac{K_{op}d}{\mu _s c^2},\qquad k_{os}=\frac{K_{os}d}{\mu _s c^2},\qquad c_{o}=\frac{C_{o}}{\mu _s c},\qquad v_o=\frac{V_o}{c}, \nonumber \end{aligned}$$

and $c=\sqrt{T/\mu _s}$ is the transverse wave speed in the string. With the above definitions, the non-dimensional stiffness and damping coefficients at the periodic support points are, respectively, $K_p=\frac{\kappa _pd}{\mu _s c^2}$ and $D_p=\frac{\delta _p}{\mu _s c}$, where $\kappa _p$ and $\delta _p$ are the corresponding dimensional values.

2.2 Solution Procedure

We are interested in determining the steady-state solution of the system. To this end, we first solve the string equation (4), and the oscillator equations (5) separately for an unknown harmonic force with (non-dimensional) frequency of the form $p\Omega$ for arbitrary choice of integer $p=0,1,\ldots N$ ($p=0$ corresponds to a constant force), where $\Omega =2\pi v_o$ is the fundamental frequency of forcing. In non-dimensional terms, therefore, one can write $f(t)=\textrm{e}^{i p\Omega t}$, which represents a unit (complex) amplitude force, and $i=\sqrt{-1}$.

Using the method of Fourier transform, one can formally write the solution of (4) for the $p^{th}$ harmonic in the $n^{th}$ span as

$$\begin{aligned} w^p(x,t)=\frac{1}{2\pi }\int _{-\infty }^\infty \hat{w}_n^p\, \textrm{e}^{i\omega t}\textrm{d}\omega \end{aligned}$$

(6)

where

$$\hat{w}_n^p=a_{n}^+\textrm{e}^{ik_sx}+a_{n}^-\textrm{e}^{-ik_sx}+\frac{(1/v_o)\textrm{e}^{i(p\Omega -\omega )x/v_o}}{(p\Omega -\omega )^2/v_o^2-k_s^2},$$

$a_{n}^+$ and $a_{n}^-$ are arbitrary constants of integration for the $n^{th}$ span, and $k_s=\sqrt{(\omega ^2-\sigma _s-i\omega \gamma _s)}$. It may be noted that the solution (6) is valid span-wise. Thus, in the $n^{th}$ span with $n-1\le x\le n$, one can put $x=n-1+\chi$, where $\chi \in [0,1]$. One may express the integrand in (6) as

$$\begin{aligned} \hat{H}_n^p(\chi ,\omega ,t)=\left[ a_{n}^+\textrm{e}^{ik_s\chi }+a_{n}^-\textrm{e}^{-ik_s\chi }+\frac{\textrm{e}^{i(p\Omega -\omega )(n-1+\chi )/v_o}}{v_o[(p\Omega -\omega )^2/v_o^2-k_s^2]}\right] \textrm{e}^{i\omega t}, \end{aligned}$$

(7)

where certain constant factors appearing in the homogeneous solution are absorbed in the unknown constants of integration. At the junction of the $n^{th}$ and $(n+1)^{th}$ span, the displacement and force compatibility conditions can be expressed as, respectively,

$$\begin{aligned} {} & {} \hat{H}_n^p(1,\omega ,t)=\hat{H}_{n+1}^p(0,\omega ,t), \end{aligned}$$

(8)

$$\begin{aligned} &\textrm{and}\qquad & -\hat{H}_{n,x}^p(1,\omega ,t)+\hat{H}_{n+1,x}^p(0,\omega ,t)=(K_f+i\omega D_f)\hat{H}_{n+1}^p(0,\omega ,t). \end{aligned}$$

(9)

These two conditions involve 4 unknowns, namely $(a_n^+, a_n^-,a_{n+1}^+,a_{n+1}^-)$. Since we are interested in steady-state periodic solutions, we impose the periodicity condition

$$\begin{aligned} \hat{H}_{n+1}(\chi ,\omega ,t)=\hat{H}_{n}(\chi ,\omega ,t-1/v_o), \end{aligned}$$

(10)

where $1/v_o$ is the time to cover one span. This leads to the relations $a_{n+1}^+=a_n^+\textrm{e}^{-i\omega /v_o}$, and $a_{n+1}^-=a_n^-\textrm{e}^{-i\omega /v_o}$. Using these relations in the compatibility conditions (8)-(9), one can eliminate $(a_{n+1}^+,a_{n+1}^-)$, and solve for $(a_n^+, a_n^-)$ to completely determine the integrand (7). Finally, the solution under unit harmonic forcing can then be obtained from (6). It may be noted that the solution, with the periodicity condition imposed, is identical for any span. We focus on the point of contact (considered at $x=v_ot$) of the string with the oscillator. The displacement at that point may be expressed as $w(v_o t,t)$. Since the solution is periodic with fundamental frequency $\Omega =2\pi v_o$, one can decompose the string displacement at $x=v_ot$ as

$$\begin{aligned} w_p(v_ot,t)=\sum _{q=-\infty }^\infty a_{qp}\textrm{e}^{iq\Omega t}, \end{aligned}$$

(11)

where the complex constants $a_{qp}$ can be determined using the standard method of projections.

The next step is to determine the interaction force f(t) between the oscillator and the string. Since we expect the interaction force to also be periodic, we expand it in Fourier series as

$$\begin{aligned} f(t)=\sum _{p=0}^\infty \frac{f_p}{2}\textrm{e}^{ip\Omega t}+c.c., \end{aligned}$$

(12)

where $f_p$ are complex amplitudes, and the complex conjugate (c.c.) part is treated separately for ease of representation. The displacement of the string at the point of contact with the oscillator can now be written as

$$\begin{aligned} w(v_o t,t) =\sum _{p=0}^\infty \left[ \left( a_{0p}\frac{f_p}{4}+a_{0p}^*\frac{f_p^*}{4}\right) +\sum _{q=1}^\infty \left( a_{qp}\frac{f_p}{2}+a_{(-q)p}^*\frac{f_p^*}{2}\right) \textrm{e}^{iq\Omega t}+c.c.\right] \end{aligned}$$

(13)

Define a row matrix $\textbf{E}=[1,\,\textrm{e}^{i\Omega t},\,\textrm{e}^{i2\Omega t},\,\ldots ]$. Then one can write

$$\begin{aligned} w(v_ot,t)= & {} \textbf{E}\left[ \begin{array}{c} \sum _{p=0}^\infty \left( a_{0p}\frac{f_p}{4}+a_{0p}^*\frac{f_p^*}{4}\right) \\ \\ \sum _{p=0}^\infty \left( a_{1p}\frac{f_p}{2}+a_{(-1)p}^*\frac{f_p^*}{2}\right) \\ \\ \vdots \end{array}\right] +c.c. =\textbf{E}(\textbf{A}{} \textbf{f}+\textbf{B}{} \textbf{f}^*)+c.c., \end{aligned}$$

(14)

where $\textbf{f}=[f_0,\,f_1,\,\ldots ]^T$ is a column vector containing the (unknown) complex force amplitudes, and the matrices $\textbf{A}$ and $\textbf{B}$ can be read out from the preceding expression.

Now the motion of the oscillator under the same interaction force (12) can be written from (5) as

$$\begin{aligned} y(t)=\textbf{E}\left[ \begin{array}{c} \frac{y_0}{2}-\frac{f_0}{2\mathcal{Z}(0)} \\ -\frac{f_1}{2\mathcal{Z}(\Omega )}\\ -\frac{f_2}{2\mathcal{Z}(2\Omega )}\\ \vdots \end{array}\right] +c.c.=\textbf{E}(\textbf{y}_0+\textbf{C}{} \textbf{f})+c.c., \end{aligned}$$

(15)

where $\textbf{y}_0=[\frac{y_0}{2},\,0,\,\ldots ]^T$ is a column matrix with $y_0$ as the unforced position of the oscillator, $\textbf{C}=\textrm{Diag}[-\frac{1}{{2\mathcal Z}(0)},\,-\frac{1}{{2\mathcal Z}(i\Omega )},\,\ldots ]$ is a diagonal matrix, and

$$\begin{aligned} \mathcal{Z}(p\Omega )=-m_op^2\Omega ^2+k_{op}+\frac{ip\Omega c_ok_{os}}{ip\Omega c_o+k_{os}}. \end{aligned}$$

(16)

The compatibility condition between the string and the oscillator (3) requires $w(v_ot,t)=y(t)$ at each harmonic (elements in $\textbf{E}$), implying, from (14)-(15), $(\textbf{A}-\textbf{C})\textbf{f}+\textbf{B}{} \textbf{f}^*=\textbf{y}_0$, which solves as

$$\begin{aligned} \textbf{f}=\left[ (\textbf{A}-\textbf{C})-\textbf{B}(\textbf{A}^*-\textbf{C}^*)^{-1}{} \textbf{B}^*\right] ^{-1}\left[ \mathbf{I-\textbf{B}(\textbf{A}^*-\textbf{C}^*)^{-1}}\right] \textbf{y}_0, \end{aligned}$$

(17)

where $\textbf{I}$ is the identity matrix. The interaction force at the point of contact can now be expressed using (12) as

$$\begin{aligned} f(t)=\frac{1}{2}(\textbf{Ef}+\mathbf{E^*f^*}). \end{aligned}$$

(18)

The contact between the string and the oscillator will be maintained if and only if $f(t)>0$.

3 Numerical Results and Discussion

We have eight non-dimensional parameters in the problem. We fix the values of $K_f=1500$, $D_f=20$, $m_o=2$. For numerical computations, only a finite number of terms are retained in all the infinite sums presented in the previous section. In order to understand the effect of variation of the other parameters on the stability of contact, a normalized Figure of Merit (FoM) is proposed of the form

$$\begin{aligned} \mathcal{J}=\frac{1}{2}\sqrt{\frac{\int _{0}^{1/v_o}[\,f(t)-|f(t)|\,]^2\,\textrm{d}t}{\int _{0}^{1/v_o}[\,f(t)\,]^2\,\textrm{d}t}}, \end{aligned}$$

(19)

which captures the severity of loss of contact over a span of the string. It may be noted that $\mathcal{J}\in [0,1]$.

Fig. 2.

Variation of (a) contact force, and (b) contact transverse displacement with travel distance over a span between two support points at certain values of travel speeds. The values of $v_o$ are in the same order that the arrow marking line cuts the curves.

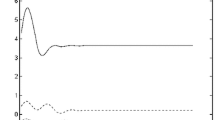
For the numerical calculations, we start by taking the (non-dimensional) parameter values as $\gamma _s=0.6$, $\sigma _s=2.0$, $D_p=0.5$, $K_p=3.5$, $m_o=0.6$, $c_o=0.2$ and $k_{op}=k_{os}=0.4$. The value of $y_0=0.0182$ is considered. The variations of interaction force between the oscillator and the string, and the displacement of the string at the point of contact over one span of travel for certain values of travel speed are presented is Fig. 2. It is observed from Fig. 2(a) that the interaction force becomes negative just after crossing a support point over a range of travel speed. This implies that the contact between the oscillator and the string will be lost in this phase. However, below a critical value of travel speed, the force is positive throughout, and hence, contact will be maintained throughout. Detailed calculation yields the non-dimensional critical speed for the chosen parameter values as $v_o^c=0.48$. The variation of displacement of the string at the contact point over the span in shown in Fig. 2(b). It is to be noted that, with increasing travel speed of the oscillator, the mean displacement is higher, though with a lower variation in the displacement over the span.

Fig. 3.

Snapshots of the string for $t\in [-1.2,1.2]$ in steps of 0.3. Horizontal axis: x, and vertical axis: w

Snapshots of the string at certain time instants are presented in Fig. 4. In the figure, the supports are located at the labeled points. The oscillator location is marked by the highest peak position on the string. The wave reflections are clearly seen as the oscillator crosses the support points.

Fig. 4.

Variation of the FoM value of $\mathcal{J}$ with variation of (a) oscillator mass $m_o$, and (b) support damping $D_p$.

In order to improve the contact force variation and increase the critical speed, we study the effect of parameter variation on the FoM. The variation of $\mathcal{J}$ with variation of the oscillator mass $m_o$ and support damping $D_p$ are shown in Fig. 3. It is observed that increasing (reducing) the mass (support damping) improves the FoM. This opens up an approach to tuning the system parameters to achieve a lower value of $\mathcal{J}$, and possibly increasing the critical speed.

Table 1. Parameter values considered for various cases

Next, we vary the parameters in steps to successively reduce the value of $\mathcal{J}$. Five sets of parameter values that are varied are presented in Tab. 1. The rest of the parameters are held fixed. The variations of $\mathcal{J}$ with travel speed for the five cases are plotted in Fig. 5(a). It is clearly observed that with each successive case, the FoM exhibits marked improvement with the value of $\mathcal{J}$ showing a significant drop. The critical speed for each of the cases considered is shown in Fig. 5(b). It may be noted that the critical could be improved from $v_o^c=0.48$ for Case I to $v_o^c=0.697$ for Case V.

Fig. 5.

(a) Variation of $\mathcal{J}$ with speed of travel $v_o$ for the cases presented in Tab. 1. (b) Critical speed of travel of the oscillator for different cases.

Fig. 6.

Variation of (a) contact force, and (b) contact transverse displacement with travel distance over a span between two support points at certain values of travel speeds for the data of Case V in Tab. 1. The values of $v_o$ are in the same order that the arrow marking line cuts the curves.

Fig. 7.

Snapshots of the string for $t\in [-1.2,1.2]$ in steps of 0.3 with $v_o=0.697$ and parameters corresponding to Case V in Tab. 1. Horizontal axis: x, and vertical axis: w

For the data of Case V, the variation of contact force and displacement of the string at the contact point with distance traveled is shown in Fig. 6. It is observed from Fig. 6(a) that the negativity and variation of contact force is much restricted compared to that observed in Fig. 2(a). Comparing Figs. 2(b) and 6(b), we observe the reduction in variation of the string displacement at the contact point. The shape of the string at certain time instants $t\in [-1.2,1.2]$ in steps of 0.3 with the travel speed $v_o=v_o^c=0.697$ is presented in Fig. 7. Comparing this figure with the one in Fig. 3 reveals some striking differences. Firstly, the amplitude of displacement at the contact point is lower in the case of Fig. 7. Further, the reflected wave amplitude is also lower compared to that observed in Fig. 3.

Fig. 8.

Variation of (a) mean and (b) standard deviation of contact point displacement with travel speed for two cases tabulated in Table 1.

The mean $\langle y\rangle$ and standard deviation $\langle \langle y\rangle \rangle$ of the variation of contact force and string displacement at the contact point with travel speed of the oscillator are presented for Cases I and V in Fig. 8. As noted before, at lower speeds, the variation in the displacement (as indicated by $\langle \langle y\rangle \rangle$) is higher. For Case I, the mean and standard deviation values are higher due to lower values of oscillator mass and foundation stiffness and damping. However, at higher travel speed of the oscillator, the standard deviation is found to increase marginally due to lowering of dynamic stiffness of the string.

4 Summary and Outlook

A study of the coupled dynamics of an oscillator moving in contact with a periodically supported taut string on a visco-elastic foundation is studied. The major objective was to study the causal effect of various parameters on the contact stability. The evolution of the contact force is obtained analytically, and the contact stability is assessed using a figure of merit function defined herein. The critical travel speed of the oscillator for stable contact is determined and improved by appropriate choice of parameters. The role of certain parameters on the contact stability is clearly brought out. This work is expected to lead to a better understanding of the coupled dynamics and improvement in design. In future, we intend to study closely the wave dynamics when the oscillator crosses a support point. Mitigation of disturbance propagation is an important aspect for future studies. This will be particularly relevant for dynamics of multiple pantographs interacting with the overhead cable.