1 Introduction

In this paper, we consider a mechanical system with mixed spectrum of natural oscillations. Namely, we deal with an infinite string with slowly time-varying tension. The string lies on the Winkler foundation with a point inhomogeneity (a concentrated spring of negative stiffness). In the case of a constant string tension, the discrete part of the spectrum for such a system may contain unique (positive) eigenvalue, which is less than the lowest frequency for the string on the uniform foundation. This special natural frequency corresponds to a trapped mode of oscillation with eigenform localized near the spring. The phenomenon of trapped modes was discovered in the theory of surface water waves [1]. The examples of various mechanical systems, where trapped modes can exist, can be found in studies [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].

It is known [2, 7, 9, 19, 24,25,26] that applying non-stationary external excitation to a system possessing trapped modes leads to the emergence of undamped oscillations localized near the inhomogeneity. The large time asymptotics for such oscillation can be found [7, 9, 24,25,26] by means of the method of stationary phase [27, 28]. Gavrilov in [6, 7] suggested an asymptotic procedure based on successive application of two asymptotic methods, namely the method of stationary phase [27, 28] and the method of multiple scales [28, 29] that allows us to investigate non-stationary processes in perturbed systems, with slowly time-varying parameters, possessing trapped modes. In studies [6, 7], the problem concerning non-uniform motion of a point mass along a taut string on the Winkler foundation was considered and solved. Note that later the same problem was reconsidered in paper by Gao et al. [30] in very particular case of uniform motion at a given speed.

The asymptotic procedure suggested in [6, 7] was successfully applied to describe the evolution of the amplitude of the trapped mode of oscillations in a taut string on the Winkler foundation with a point inertial inclusion of time-varying mass [24] and in a taut string on the Winkler foundation with a concentrated spring of negative time-varying stiffness [25]. All problems considered in previous papers [6, 7, 24, 25] are formulated for the Klein–Gordon PDE with constant coefficients. In our recent paper [26], a Bernoulli–Euler beam on the Winkler foundation with a concentrated spring of negative time-varying stiffness is considered. In the latter case, a PDE with constant coefficients is also under consideration. This allows one to verify the obtained analytical results by reduction of the problem to a Volterra integral equation of the second kind with its kernel expressed in terms of the fundamental solution for the corresponding PDE. The integral equation can be easily solved numerically. This was done in all previous studies [6, 7, 24,25,26], and a good mutual agreement between asymptotic and numeric results was demonstrated.

The consideration of the problem for a string with variable tension has some geophysical motivation [17]. In contrast to previous papers [6, 7, 24, 25], the governing equation here is the Klein–Gordon equation with time-varying coefficients. To verify the obtained analytical results, we solve numerically the initial value problem for this PDE using the finite difference method and demonstrate the applicability of the analytical formulas for various types of external excitation and laws governing the varying tension. Some preliminary results concerning this problem were presented in a recent conference publication [25].

Finally, note that very similar problems for structures of finite length were considered in studies [31,32,33,34].

2 Mathematical formulation

We consider transverse oscillation of an infinite taut string on the Winkler elastic foundation. The elastic foundation has a point inhomogeneity in the form of a concentrated spring of a negative stiffness. The schematic of the system is shown in Fig. 1. Introduce the following notation: u(x, t) is the displacement of a point of the string at the position x and time t, \({\mathscr {T}}_0(t)>0\) is the string tension (a given function of time), \(\rho >0\) is the mass of the string per unit length, \(K_0\) is the absolute value for the stiffness \(-K_0\) of the concentrated spring, \(k_0>0\) is the stiffness for the Winkler foundation, \(P_0(t)\) is the unknown force on the string from the spring, and \(p_0(t)\) is the given external force on the string. Quantities \(k_0\), \(K_0\), \(\rho \) are constants. One can choose any orthogonal to the string direction, where \(u(x,t),\ p_0(t)\) and \(P_0(t)\) are assumed to be positive.

Fig. 1
figure 1

The schematic of the system

Full size image

The governing equations are

$$\begin{aligned}&{\mathscr {T}}_0(t)\,u_{xx}-\rho u_{tt} -k_0u=-P_0(t)\,\delta (x), \end{aligned}$$
(1)
$$\begin{aligned}&P_0(t)=K_0u(0,t)+p_0(t). \end{aligned}$$
(2)

Here \(\delta \) is the Dirac delta function.

Now we introduce the dimensionless variables

$$\begin{aligned} \tau =t\sqrt{k_0/\rho },\qquad \xi =x\sqrt{k_0/\hat{{\mathscr {T}}}_0} \end{aligned}$$
(3)

and rewrite governing Eqs. (1), (2) in the following form

$$\begin{aligned}&c^2(\tau )\,u^{\prime \prime }-\ddot{u} -u=-P(\tau )\,\delta (\xi ), \end{aligned}$$
(4)
$$\begin{aligned}&P(\tau )=2u(0,\tau )+2p(\tau ), \end{aligned}$$
(5)
$$\begin{aligned}&\hat{{\mathscr {T}}}_0=\frac{K_0^2}{4k_0}, \end{aligned}$$
(6)
$$\begin{aligned}&c^2={\mathscr {T}}_0/\hat{{\mathscr {T}}}_0,\quad P=P_0/\sqrt{k_0\hat{{\mathscr {T}}}_0},\nonumber \\&2p=p_0/\sqrt{k_0\hat{{\mathscr {T}}}_0} . \end{aligned}$$
(7)

Here and in what follows, we denote by prime the derivative with respect to spatial coordinate \(\xi \) and by overdot the derivative with respect to time \(\tau \). The quantity \(c>0\) is the dimensionless transverse waves speed. The quantities \(u,\ P,\ p\) remain dimensional ones having the dimension of length.

The initial conditions for Eq. (4) can be formulated in the following form, which is conventional for distributions (or generalized functions) [35]:

$$\begin{aligned} u \big |_{\tau <0}\equiv 0. \end{aligned}$$
(8)

Note that according to Eqs. (4), (5), (8), we restrict ourselves to the important particular case of the general problem concerning non-stationary oscillation, where any external excitation (and, in particular, nonzero initial conditions) is applied only to the point of the string under the concentrated spring. One can take into account nonzero initial conditions

$$\begin{aligned} \begin{aligned}&u(0,0)=0,\qquad&\dot{u}(0,0)=2v_0;\\&u(\xi ,0)=0,\qquad&\dot{u}(\xi ,0)=0\qquad (\xi \ne 0); \end{aligned} \end{aligned}$$
(9)

for the velocity of the point under the concentrated spring, introducing of p in the form of [35]

$$\begin{aligned} p=v_0\delta (\tau )+{\bar{p}}(\tau ). \end{aligned}$$
(10)

Here \({\bar{p}}(\tau )\) is a non-singular at \(\tau =0\) function such that \({\bar{p}}(\tau )\big |_{\tau <0}\equiv 0\).

The problem under consideration (4), (5), (8) is symmetric with respect to \(\xi =0\). Integrating (4) over \(\xi =0\) results in the following condition

$$\begin{aligned}{}[u']=-\frac{P(\tau )}{c^2(\tau )}=- \frac{2u(0,\tau )+2p(\tau )}{c^2(\tau )}. \end{aligned}$$
(11)

Here, and in what follows, \([\mu ]\equiv \mu (\xi +0)-\mu (\xi -0)\) for any arbitrary quantity \(\mu \). Due to symmetry, one has \([u']=2u'(\xi +0)\). Thus, the problem for infinite string can be equivalently reformulated as the problem for homogeneous equation

$$\begin{aligned} c^2(\tau )\,u^{\prime \prime }-\ddot{u} -u=0 \end{aligned}$$
(12)

for \(\xi >0\) with boundary condition at \(\xi =0\)

$$\begin{aligned} u'(0,\tau )= -\frac{u(0,\tau )+p(\tau )}{c^2(\tau )}. \end{aligned}$$
(13)

Equivalent formulation (12), (13), (8) is used for numerical calculations (Sect. 5).

3 A string with constant tension

In this section, we consider the infinite string with a constant tension, and thus, \(c={\text {const}}\).

3.1 Spectral problem

Put \(p=0\) and consider the steady-state problem concerning the natural oscillations of the system described by Eqs. (4)–(5). Take

$$\begin{aligned} u={\hat{u}}(\xi )\,\exp (-\mathrm i\varOmega \tau ). \end{aligned}$$
(14)

Let us show that such a system possesses a mixed spectrum of natural frequencies. There exists a continuous spectrum of frequencies, which lies higher than the cutoff (or boundary) frequency: \(|\varOmega |\ge 1\). The modes corresponding to the frequencies from the continuous spectrum are harmonic waves. Trapped modes correspond to the frequencies from the discrete part of the spectrum, which lies lower than the cutoff frequency: \(0<|\varOmega |<1\). We want to demonstrate that for the problem under consideration the only one trapped mode can exist. Trapped modes are modes with finite energy; therefore, we require

$$\begin{aligned} \int _{-\infty }^{+\infty }{\hat{u}}^2\,\mathrm d\xi<\infty ,\qquad \int _{-\infty }^{+\infty }{\hat{u}}'{}^2\,\mathrm d\xi <\infty . \end{aligned}$$
(15)

Now we substitute Eq. (14) in Eq. (4). This yields

$$\begin{aligned} {{\hat{u}}}'' -A^2(\varOmega ){{\hat{u}}}= -\frac{2{{\hat{u}}}(0)}{c^2} \,\delta (\xi ), \end{aligned}$$
(16)

where

$$\begin{aligned} A^2(\varOmega )= \frac{ 1-\varOmega ^2}{c^2}. \end{aligned}$$
(17)

Here, by definition, we assume that

$$\begin{aligned} A(\varOmega )>0 \end{aligned}$$
(18)

for \(0<\varOmega <1\). The dispersion relation for the operator in the left-hand side of (16) is

$$\begin{aligned} \omega ^2 +A^2(\varOmega )=0; \end{aligned}$$
(19)

therefore, the wave number \(\omega \) can be expressed as follows:

$$\begin{aligned} \omega = \pm \, \mathrm iA(\varOmega ). \end{aligned}$$
(20)

The solution of Eq. (16), which satisfies (15), is

$$\begin{aligned} {\hat{u}}(\xi )= {{\hat{u}}}(0) \,\frac{\exp (-A(\varOmega _0)|\xi |) }{c^2A(\varOmega _0)}. \end{aligned}$$
(21)

Calculating the right-hand side of Eq. (21) at \(\xi =0\) yields the frequency equation

$$\begin{aligned} c^2A(\varOmega _0)=1, \end{aligned}$$
(22)

where \(\varOmega _0\) is the trapped mode frequency. Resolving the frequency equation results in

$$\begin{aligned} \varOmega _0^2=1-{c}^{-2}. \end{aligned}$$
(23)

Thus, according to (18), (22), (23), a trapped mode exists and is unique if and only if

$$\begin{aligned} c>1. \end{aligned}$$
(24)

The critical value \(c=1\) corresponds to possibility of localized buckling of the string.

Note that considering initial non-dimensionless problem for Eqs. (4), (5) one can easily show [25] that the trapped mode exists only if

$$\begin{aligned} K_0>0, \end{aligned}$$
(25)

i.e., we deal with a destabilizing spring.

3.2 Inhomogeneous non-stationary problem

Put now \(p\ne 0\). Applying to Eqs. (4)–(5), the Fourier transform in time \(\tau \) results in

$$\begin{aligned} {u}_F'' -A^2(\varOmega ){u_F}= -\frac{2}{c^2}\big ({u_F}(0,\varOmega )+p_F(\varOmega )\big ) \,\delta (\xi ), \nonumber \\ \end{aligned}$$
(26)

where \(u_F(0,\varOmega ),\ p_F(\varOmega )\) are the Fourier transforms of \(u(0,\tau )\) and \(p(\tau )\), respectively. Resolving Eq. (26) with respect to \(u_F(0,\varOmega )\) and applying the inverse transform yields

$$\begin{aligned} u(0,\tau )= & {} \frac{1}{2\pi }\int _{-\infty }^{+\infty }\frac{p_Fe^{-\mathrm i\varOmega \tau }\,\mathrm d\varOmega }{c\sqrt{1-\varOmega ^2}-1} \nonumber \\= & {} -\frac{1}{2\pi c^2}\int _{-\infty }^{+\infty }\frac{p_F(c\sqrt{1-\varOmega ^2}+1)e^{-\mathrm i\varOmega \tau }\,\mathrm d\varOmega }{\varOmega ^2-\varOmega _0^2}. \nonumber \\ \end{aligned}$$
(27)

At first, consider the simplest case \(p=v_0\delta (\tau )\) (\(p_F=v_0)\) that corresponds to the initial conditions (9). To estimate asymptotically the integral in the right-hand side of (27) for large times \(\tau \), we use the method of stationary phase [27, 28]. The principal part of the asymptotics is given by the contributions from poles

$$\begin{aligned} \varOmega =\pm \,\varOmega _0-\mathrm i0 \end{aligned}$$
(28)

of the amplitude function

$$\begin{aligned} \frac{c\sqrt{1-\varOmega ^2}+1}{\varOmega ^2-\varOmega _0^2}. \end{aligned}$$
(29)

The terms \(-\mathrm i0\) in the right-hand side of (28) are taken in accordance with principle of limit absorption. Calculating the contributions from the poles [27, 36] results in

$$\begin{aligned} u(0,\tau )=\frac{2v_0}{\varOmega _0c^2}\sin \varOmega _0 \tau +O(\tau ^{-3/2}), \quad \tau \rightarrow \infty . \nonumber \\ \end{aligned}$$
(30)

One can prove [2] that the principal part of the error term in (30) is given by the contribution from the boundary frequencies (the branching points) \(\varOmega =\pm \,1\). Thus, for the large times, the non-stationary response of the system under consideration is undamped oscillations with the trapped mode frequency \(\varOmega _0\).

Now consider more general case when \(p(\tau )\) is a vanishing as \(\tau \rightarrow \infty \) function such that its Fourier’s transform \(p_F(\varOmega )\) does not have singular points on the real axis. Applying the method of stationary phase to the asymptotic evaluation of the integral in the right-hand side of (27) results in

$$\begin{aligned}&u(0,\tau )=\frac{2|p_F(\varOmega _0)|}{\varOmega _0c^2} \sin \big (\varOmega _0 \tau -\arg p_F(\varOmega _0)\big )+o(1), \nonumber \\&\tau \rightarrow \infty . \end{aligned}$$
(31)

The asymptotic order of the error term in the last formula depends on the properties of \(p_F\).

4 A string with slowly varying tension

Assume that the string tension \({\mathscr {T}}_0\) and, therefore, the dimensionless transverse wave speed c are slowly varying piecewise monotone function of the dimensionless time \(\tau \): \(c=c(\epsilon \tau )\). Here \(\epsilon \) is a formal small parameter. We use an approach [6, 7, 24] based on the modification of the method of multiple scales [29] (Section 7.1.6) for equations with slowly varying coefficients. The corresponding rigorous proof, which validates such asymptotic approach in the case of a one-degree-of-freedom system, can be found in [37]. We look for the asymptotics for the solution under the following conditions:

  • \( \epsilon =o(1), \)

  • \(\tau =O(\epsilon ^{-1}),\)

  • \(c(\epsilon \tau )\) satisfies restriction (24) for all \(\tau \).

To construct the particular solution of (4)–(5), which describes the evolution of the trapped mode of oscillation in the case of slowly varying c, we require that in the perturbed system

  • Frequency equation (23) for the trapped mode holds for all \(\tau \);

  • Dispersion relation (19) at \(\xi =\pm \,0\) holds for all \(\tau \).

Accordingly, we use the following ansatz (\(\tau >0\), \(\xi \lessgtr 0\)):

$$\begin{aligned}&u(\xi ,\tau )=W(X,T)\,\exp \varphi (\xi ,\tau ), \end{aligned}$$
(32)
$$\begin{aligned}&T=\epsilon \tau , \quad X=\epsilon \xi , \end{aligned}$$
(33)
$$\begin{aligned}&{\varphi }'=\mathrm i\,\omega (X,T),\quad {\dot{\varphi }}=-\mathrm i\,\varOmega (X,T), \end{aligned}$$
(34)
$$\begin{aligned}&W(X,T)=\sum _{j=0}^{\infty } \epsilon ^{j}{W_j}(X,T). \end{aligned}$$
(35)

Here the amplitude W(X, T), the wave number \(\omega (X,T)\), and the frequency \(\varOmega (X,T)\) are the unknown functions to be defined in accordance with Eq. (4). The variables \(X,\ T,\ \varphi \) are assumed to be independent. Accordingly, we use the following representations for the differential operators:

$$\begin{aligned}&\displaystyle \dot{(\cdot )}=- \mathrm i\,\varOmega \,\partial _{\varphi }+\epsilon \,\partial _{T},\nonumber \\&\displaystyle \ddot{(\cdot )}=-\varOmega ^2\,\partial ^2_{\varphi \varphi } -2\epsilon \mathrm i\,\varOmega \,\partial ^2_{\varphi T} -\epsilon \mathrm i\, {\varOmega '}_T\,\partial _{\varphi } +O(\epsilon ^2),\nonumber \\&\displaystyle (\cdot )'= \mathrm i\,\omega \,\partial _{\varphi }+\epsilon \,\partial _{X},\nonumber \\&\displaystyle (\cdot )''=-\omega ^2\,\partial ^2_{\varphi \varphi } +2\epsilon \mathrm i\,\omega \,\partial ^2_{\varphi X} +\epsilon \mathrm i\, {\omega }'_X\,\partial _{\varphi } +O(\epsilon ^2). \nonumber \\ \end{aligned}$$
(36)

We require that \(\omega (X,T)\) and \(\varOmega (X,T)\) satisfy dispersion relation (19) and equation

$$\begin{aligned} {\varOmega }'_X+{\omega }'_T=0 \end{aligned}$$
(37)

that follows from (34). Since in the case of a string with constant tension the undamped oscillation can be described by Eq. (31), we assume that

$$\begin{aligned} \varOmega (\pm \, 0,T)=\varOmega _0(T). \end{aligned}$$
(38)

Additionally, we require that

$$\begin{aligned}{}[W]=0,\qquad [\varphi ]=0. \end{aligned}$$
(39)

In Eq. (38), the right-hand side is defined in accordance with frequency equation (22), wherein \(c=c(T)\). The phase \(\varphi (\xi ,\tau )\) should be defined by the formula

$$\begin{aligned} \varphi =\mathrm i\int (\omega \,\mathrm d\xi -\varOmega \,\mathrm d\tau ). \end{aligned}$$
(40)

For large times, integrating formally Eq. (4) with respect to \(\xi \) over the infinitesimal vicinity of \(\xi =0\) taking into account (5), one gets (11), wherein \(p=0\). Now we substitute ansatz (32)–(35) and representations (36) in Eq. (11) and equate coefficients of like powers \(\epsilon \). Taking into account frequency equation (22), and Eq. (38), one obtains that to the first approximation

$$\begin{aligned}{}[W_0{}'_X]=0. \end{aligned}$$
(41)

On the other hand, the quantity in the left-hand side of (41) can be defined by consideration of Eq. (4) at \(\xi =\pm \,0\). To do this, we substitute ansatz (32)–(35) and representations (36) in Eq. (4) and equate coefficients of like powers \(\epsilon \). Taking into account dispersion relation (19) and Eq. (38), one obtains that to the first approximation

$$\begin{aligned} c^2(T)(2\omega \,{W_0}'_X+{\omega }'_X\,{W_0})+ 2\varOmega _0\,{W_0}'_T+{\varOmega _0}'_T\,{W_0}=0 \nonumber \\ \end{aligned}$$
(42)

at \(\xi =\pm \,0\). Due to (37) one has

$$\begin{aligned} {\omega }'_X={\omega }'_\varOmega \,\varOmega '_X= -{\omega }'_\varOmega \,{\omega }'_T, \end{aligned}$$
(43)

where the right-hand side should be calculated in accordance with Eq. (20). Thus, Eqs. (42) and (43) result in

$$\begin{aligned} {W_0}'_X=-\frac{2\varOmega _0 \,{W_0}'_T + (-c^2{\omega }'_\varOmega {\omega }'_T +{\varOmega _0}'_T )\,{W_0}}{2\mathrm i\gamma A(\varOmega _0,T)c^2(T)}, \end{aligned}$$
(44)

where \(\gamma ={\text {sign}}\xi \). Accordingly,

$$\begin{aligned}&{} [{W_0}'_X]= -\frac{\varLambda _2 {W}_0 +\varLambda _1 {W}_0{}'_T}{\mathrm iA(\varOmega _0)c^2}, \end{aligned}$$
(45)
$$\begin{aligned}&\varLambda _1\equiv 2\varOmega _0, \end{aligned}$$
(46)
$$\begin{aligned}&\varLambda _2\equiv c^2 A'_\varOmega (\varOmega _0)A'_T(\varOmega _0) +{\varOmega _0}'_T, \end{aligned}$$
(47)

where the right-hand side of Eq. (45) is taken at \(\xi =0\).

Now, equating the right-hand sides of Eqs. (41) and (45) results in the first approximation equation for \({\bar{W}}_0(T) \equiv W_0(0,T)\):

$$\begin{aligned} \varLambda _2\bar{W}_0+\varLambda _1\bar{W}_0{}'_T=0. \end{aligned}$$
(48)

The general solution of the last equation is

$$\begin{aligned} \bar{W}_0=\frac{C_0}{2}\exp \Big (-\int \frac{ \varLambda _2}{\varLambda _1 }\,\mathrm dT \Big ), \end{aligned}$$
(49)

where \(C_0\) is an arbitrary constant. Using (17), one gets

$$\begin{aligned}&A'_\varOmega =-\frac{\varOmega _0}{c\sqrt{1-\varOmega _0^2}}, \end{aligned}$$
(50)
$$\begin{aligned}&A'_T=-\frac{\varOmega _0\varOmega _0{}'_T}{c\sqrt{1-\varOmega _0^2}} -\frac{c{}'_T}{c^2}\sqrt{1-\varOmega _0^2}. \end{aligned}$$
(51)

Substituting these expressions into (47) yields

$$\begin{aligned} \varLambda _2=\frac{\varOmega ^2_0{\varOmega _0}'_T}{1-{\varOmega }^2_0}+ \frac{\varOmega _0c'_T}{c}+{\varOmega _0}'_T. \end{aligned}$$
(52)

Therefore,

$$\begin{aligned} -\int \frac{ \varLambda _2}{\varLambda _1 }\,\mathrm dT= & {} -\int \frac{\mathrm d\varOmega ^2_0}{4\left( 1-{\varOmega }^2_0\right) } -\int \frac{\mathrm dc}{2c} -\int \frac{\mathrm d\varOmega _0}{2\varOmega _0}\nonumber \\= & {} \frac{1}{4}\ln \left( 1-{\varOmega }^2_0 \right) -\frac{1}{2}\ln c -\frac{1}{2}\ln \varOmega _0. \nonumber \\ \end{aligned}$$
(53)

Substituting the last equation in the right-hand side of Eq. (49) yields the final result

$$\begin{aligned} \bar{W}_0 =C_0\frac{\left( 1-{\varOmega }^2_0\right) ^{1/4}}{2\left( c\varOmega _0\right) ^{1/2}}. \end{aligned}$$
(54)

Taking into account (23), one can rewrite the last formula in two equivalent forms:

$$\begin{aligned} \bar{W}_0 =\frac{C_0}{2\sqrt{c}\,(c^2-1)^{1/4}} =\frac{C_0}{2}\sqrt{\frac{1-\varOmega _0^2}{\varOmega _0}} \end{aligned}$$
(55)

If \(\varOmega _0 \rightarrow +0\) (or, equivalently, \(c\rightarrow 1+0\), \({\mathscr {T}}_0 \rightarrow \frac{K_0^2}{4k_0}+0\)), then

$$\begin{aligned} \bar{W}_0 = \frac{C_0}{2\varOmega _0^{1/2}}+o(1). \end{aligned}$$
(56)

Hence, localized low-frequency oscillations with increasing amplitude precede the localized string buckling.

This result is analogous to the classical result for a one-degree-of-freedom system

$$\begin{aligned} \ddot{y}+{\hat{\varOmega }}^2(\epsilon \tau ) y =0, \end{aligned}$$
(57)

where the following formula

$$\begin{aligned} Y\propto \frac{1}{{\hat{\varOmega }}^{1/2}} \end{aligned}$$
(58)

for the amplitude of free oscillations Y is valid (the Liouville–Green approximation [29]). On the other hand, unlike one-degree-of-freedom system (57), for the system under consideration, formula (56) is valid only in the limiting case \(\varOmega _0 \rightarrow +\,0\). For finite \(\varOmega _0\), dependence (55) is more complicated.

Combining the solution in the form of Eqs. (32)–(35) with its complex conjugate, we get the non-stationary solution as the following ansatz:

$$\begin{aligned} u(0,\tau )\sim 2\bar{W}_0\big (\varOmega _0(T)\big )\sin \left( \int _0^\tau \varOmega _0(T)\,\mathrm dT-D_0\right) , \nonumber \\ \end{aligned}$$
(59)

where \({\bar{W}}_0\) is defined by (55). The unknown constants \(C_0\) and \(D_0\) should be defined by equating the right-hand sides of (31) and (59) taken at \(\tau =0\). This yields

$$\begin{aligned} C_0= & {} \frac{2(c^2(0)-1)^{1/4}}{\varOmega _0(0)c^{3/2}(0)}\,\big |p_F\big (\varOmega _0(0)\big )\big |\nonumber \\= & {} \frac{2\big |p_F\big (\varOmega _0(0)\big )\big |}{c(0)(1-c^{-2}(0))^{1/4}}, \end{aligned}$$
(60)
$$\begin{aligned} D_0= & {} \arg p_F\big (\varOmega _0(0)\big ). \end{aligned}$$
(61)

In the particular case \(p=v_0\delta (\tau )\) that corresponds to initial conditions (9), one has

$$\begin{aligned}&C_0=\frac{2v_0\big (c^2(0)-1\big )^{1/4}}{\varOmega _0(0)c^{3/2}(0)} =\frac{2v_0}{c(0)(1-c^{-2}(0))^{1/4}}, \nonumber \\ \end{aligned}$$
(62)
$$\begin{aligned}&D_0=0. \end{aligned}$$
(63)

In the particular case

$$\begin{aligned} p(\tau )={\bar{p}}_0H(\tau )\exp (-\lambda \tau ), \end{aligned}$$
(64)

where \(H(\tau )\) is the Heaviside function, \({\bar{p}}_0={\text {const}}\), and \(\lambda =\mathrm {const}>0\), one has

$$\begin{aligned}&p_F\big (\varOmega _0(0)\big )=\frac{{\bar{p}}_0}{ \lambda -\mathrm i\varOmega _0(0)}, \end{aligned}$$
(65)
$$\begin{aligned}&\big |p_F\big (\varOmega _0(0)\big )\big |=\frac{|\bar{p}_0|}{\sqrt{\lambda ^2+\varOmega _0(0)^2}}, \end{aligned}$$
(66)
$$\begin{aligned}&\arg \big (p_F\big (\varOmega _0(0)\big )\big )=\arctan \frac{\varOmega _0(0)}{\lambda }. \end{aligned}$$
(67)

Finally, using in the case \(p=v_0\delta (\tau )\) approximate asymptotically incorrect formula (56) instead of correct formula (55) yields

$$\begin{aligned} C_0=\frac{2v_0}{\sqrt{\varOmega _0(0)}\,c^2(0)}=\frac{2v_0}{{\big (1-c^{-2}(0)\big )^{1/4}}\,{c^2(0)}} \end{aligned}$$
(68)

together with formula (63).

5 Numerics

In previous studies [6, 7, 24, 25], we dealt with several problems for the linear Klein–Gordon equation with constant coefficients. Numerical solutions were obtained by means of the reduction in the corresponding problem to an integral Volterra equation of the second kind with its kernel expressed in terms of the fundamental solution of the Klein–Gordon equation. This cannot be done for the problem under consideration in this paper, since now we deal with an equation with time-varying coefficients. To perform the numerical calculations, we use SciPy software.

To verify constructed analytical solution (54), we solve numerically the initial value problem for PDE (12) with boundary condition (13) using the finite difference method. To discretize PDE (12), we use the following implicit difference scheme:

$$\begin{aligned}&(c^i)^2 \frac{u_{j+1}^{i}-2u_j^{i}+u_{j-1}^{i}}{(\varDelta \xi )^2}\nonumber \\&\quad - \frac{u_j^{i+1}-2u_j^{i}+u_j^{i-1}}{(\varDelta \tau )^2}- \frac{u_j^{i+1}+u_j^{i-1}}{2}=0, \end{aligned}$$
(69)

where integers \(i,\ j\) (\(0\le j\le N,\ -1\le i\)) are such that

$$\begin{aligned}&u_j^i=u(j\varDelta \xi ,i\varDelta \tau ), \end{aligned}$$
(70)
$$\begin{aligned}&c^i=c(i\varDelta \tau ). \end{aligned}$$
(71)

This scheme conserves [38, 39] the discrete energy for a nonlinear Klein–Gordon equation with constant coefficients. Numeric boundary conditions that correspond to (13) are taken in the form [40]

$$\begin{aligned}&(c^{i+1})^2\frac{-3u_0^{i+1}+4u_1^{i+1}-u_2^{i+1}}{2\varDelta \xi }\nonumber \\&\quad +\,(c^{i-1})^2\frac{-3u_0^{i-1}+4u_1^{i-1}-u_2^{i-1}}{2\varDelta \xi }\nonumber \\&\quad +\,{(u_0^{i+1}+u_0^{i-1})} + (p^{i+1}+p^{i-1})=0. \end{aligned}$$
(72)

At the right end, we use boundary condition [41]

$$\begin{aligned} u^i_{N}=u^i_{N-1} \end{aligned}$$
(73)

that corresponds to the physical boundary condition \(u'=0\). Actually, the specific form of this boundary condition is not very important in our calculations, since we consider the discrete model of the string with sufficiently large length such that the wave reflections at the right end do not occur.

Numerical initial conditions are

$$\begin{aligned} u^0_j=u^{-1}_j=0. \end{aligned}$$
(74)

All numerical results below are obtained for the case

$$\begin{aligned} \varDelta \xi =0.025,\qquad \varDelta \tau =0.01. \end{aligned}$$
(75)

The dimensional coefficients \(v_0\) and \({\bar{p}}_0\) are taken as \(1\,\mathrm {m}\) and skipped in what follows for the aim of simplicity. Calculating the numerical solutions, which corresponds to \(p=\delta (\tau )\), we approximate the Dirac delta function as follows:

$$\begin{aligned} p=\tau _0^{-1}(H(\tau )-H(\tau -\tau _0)). \end{aligned}$$
(76)
Fig. 2
figure 2

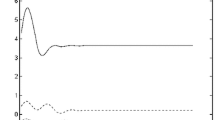
Comparing analytical solution (55), (59), (62), (63) obtained for \(p=\delta (\tau )\) (the red dashed line) and the numerical solution obtained for \(p(\tau )=\tau _0^{-1}(H(\tau )-H(\tau -\tau _0))\) (the blue solid line) in the case \(c^2(\epsilon \tau )={4-\epsilon \tau }\). Here \(\epsilon =0.03,\ \tau _0=0.1\). The localized buckling occurs at \(\tau =100\). (Color figure online)

Full size image
Fig. 3
figure 3

Comparing analytical solution (55), (59), (62), (63) obtained for \(p=\delta (\tau )\) (the red dashed line) and the numerical solution obtained for \(p=\tau _0^{-1}(H(\tau )-H(\tau -\tau _0))\) (the blue solid line) in the case \(c^2(\epsilon \tau )=2+0.9\sin (\epsilon \tau )\). Here \(\epsilon =0.1,\ \tau _0=0.1.\) (Color figure online)

Full size image

A comparison between the analytical and numerical solutions is presented in Figs. 2, 3, 4 and 5. In Fig. 2, we compare the results obtained for the case of \(p=\delta (\tau )\) and monotonically decreasing \(c(\epsilon \tau )\). The asymptotic solution approaches the numeric one very quickly. The localized buckling occurs at \(\tau =100\) that corresponds to the critical value \(c=1\). In Fig. 3, we compare the results obtained for the case of \(p=\delta (\tau )\) and slowly oscillating \(c(\epsilon \tau )>1\). In Fig. 4, we compare the results obtained for the case of \(p(\tau )=H(\tau )\exp (-\lambda \tau )\) and monotonically decreasing \(c(\epsilon \tau )\). Since \(\lambda =0.1\) is taken small enough, the method of the stationary phase gives a reasonable result only after some time (\(\tau \approx 30\)). After that time, the analytical solution approaches the numerical one. Finally, in Fig. 5, we compare the results obtained for the case of \(p=\delta (\tau )\) and monotonically decreasing \(c(\epsilon \tau )\), using approximate asymptotically incorrect formula (56) that corresponds to the Liouville – Green approximation for a one-degree-of-freedom system (57). One can see that in the last case the analytical solution and the numerical one diverge.

Fig. 4
figure 4

Comparing analytical solution (55), (59), (60), (61), (66), (67) (the red dashed line) and the numerical solution obtained for \(p=H(\tau )\exp (-\lambda \tau )\) (the blue solid line) in the case \(c^2(\epsilon \tau )={4-\epsilon \tau }\). Here \(\epsilon =0.03,\ \lambda =0.1\). The localized buckling occurs at \(\tau =100\). (Color figure online)

Full size image
Fig. 5
figure 5

Comparing the approximate asymptotically incorrect analytical solution (56), (59), (68), (63) obtained for \(p=\delta (\tau )\) (the magenta dotted line) and the numerical solution obtained for \(p=\tau _0^{-1}(H(\tau )-H(\tau -\tau _0))\) (the blue solid line) in the case \(c^2(\epsilon \tau )={4-\epsilon \tau }\). Here \(\epsilon =0.03,\ \tau _0=0.1\). The localized buckling occurs at \(\tau =100\). (Color figure online)

Full size image

6 Conclusion

In the paper, we consider a non-stationary localized oscillation of an infinite string with slowly time-varying tension. The string lies on the Winkler foundation with a point elastic inhomogeneity (a concentrated spring with negative stiffness). We restrict ourselves to the important particular case of the general problem concerning non-stationary oscillation, where any external excitation (and, in particular, nonzero initial conditions) is applied only to the point of the string under the concentrated spring. In the case of the string with a constant tension a trapped mode of oscillations exists and is unique if and only if conditions (24), (25) are satisfied. The existence of a trapped mode leads to the possibility of the wave localization near the inhomogeneity in the Winkler foundation. Applying a vanishing as \(\tau \rightarrow \infty \) external excitation to the point of the string under the inclusion leads to the emergence of undamped free oscillations localized near the spring. The most important result of the paper is analytical formulas (55), (59), (60), (61), which allow us to describe for large times such non-stationary localized oscillations in the case of slowly time-varying string tension. The obtained analytical results were verified by independent numerical calculations based on the finite difference method. The applicability of the analytical formulas was demonstrated for various types of external excitation and laws governing the varying tension (see Figs. 2, 3, 4).

We also have shown that localized low-frequency oscillations with increasing amplitude precede the localized string buckling (see (56)). However, unlike the case (57) of a one-degree-of-freedom system with time-varying stiffness, in the framework of the problem under consideration formula (56) is correct only in the limiting case, where the frequency of localized oscillations approaches zero. This fact is also verified by independent numerical calculations (see Figs. 2, 5).

Finally, we note that in order to consider a more general problem, where the external excitation can be applied to an arbitrary point of the string, we need to take into account wave reflections and passing through the discrete inclusion. This makes the problem to be more sophisticated. It may be a subject of a separate future study.