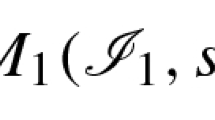The Expressive Power of Revised Datalog on Problems with Closure Properties

Abstract

In this paper, we study the expressive power of revised Datalog on the problems that are closed under substructures. We show that revised Datalog cannot define all the problems that are in PTIME and closed under substructures. As a corollary, LFP cannot define all the extension-closed problems that are in PTIME.

1 Introduction

Datalog and its variants are widely used in artificial intelligence and other fields, such as deductive database, knowledge representation, data integration, cloud computing, etc [8, 11, 13, 18, 19, 23]. As a declarative programming language, it is often used to perform data analysis and create complex queries. The complexity and expressive power is an important issue of the study [1, 5, 19, 21, 22]. With the recursive computing ability, Datalog is more powerful than first-order logic. It defines exactly the polynomial time computable queries on ordered finite structures [9]. Hence, Datalog captures the complexity class PTIME on ordered finite structures. While on all finite structures, the expressive power of Datalog is very limited. It even cannot define the parity of a set [9]. A Datalog program is constituted of a set of Horn clauses. The characteristics of syntax determine the monotonicity properties of its semantics. That is, every Datalog (resp., positive Datalog, the fragment of Datalog where no negated atomic formula occurs in the body of any clauses) definable query is preserved under extensions [3] (resp., homomorphisms [4]). It is natural to ask from the point of view of descriptive complexity that whether Datalog (resp., positive Datalog) captures the polynomial time computable problems that are closed under extensions (resp., homomorphisms). The answer is negative by the work of Afrati et al. who showed that positive Datalog cannot express all monotone queries computable in polynomial time, and the perfect squares problem that is in polynomial time and closed under extensions is not expressible in Datalog [3].

Fig. 1.

The relationship of FO, LFP, PTIME, Datalog and its variants. Datalog$^r$ denotes revised Datalog. pos-$\mathcal {L}$ denotes the positive fragment of $\mathcal {L}$. $\exists \mathcal {L}$ denotes the existential fragment of $\mathcal {L}$. $\mathcal {L}$[FO] denotes the set of $\mathcal {L}$ formulas that are first-order definable. $\mathcal {L}$[H] (resp., $\mathcal {L}$[E]) denotes the set of $\mathcal {L}$ formulas (or problems computable in $\mathcal {L}$) that are preserved under homomorphisms (resp., extensions). The blue arrow shows the containment relationship on Datalog and its variants. The red arrow shows the relationship about the expressive power. The solid arrow implies that the relationship is strict, and the dashed bidirectional arrow implies the equality relationship. The black dotted arrow means whether the relationship is strict is still open.

In model theory, many preservation theorems are proved to show the relationship between the closure properties and the syntactic properties of formulas. Most of these preservation theorems fail when restricted to finite structures. A lot of research about the preservation theorems on Datalog, first-order logic (FO) and least fixpoint logic (LFP) have been conducted on finite structures. Ajtai and Gurevich showed that a positive Datalog formula is bounded iff it is definable in positive existential first-order logic, and every first-order logic expressible positive Datalog formula is bounded [4], where a Datalog formula is bounded if there exists a number n such that the fixpoint of the formula can be reached for any finite structure within n steps. Dawar and Kreutzer showed that the homomorphism preservation theorem fails for LFP, both in general and in restriction to finite structures [6]. That is, there is an LFP formula that is preserved under homomorphisms (in the finite) but is not equivalent (in the finite) to a Datalog formula. The paper [16] studied Datalog with negation and monotonicity, and the expressive power with respect to monotone and homomorphism properties. The papers [7, 20] studied the preservation results under extensions for FO and Datalog. All the results are summarized in Fig. 1.

Revised Datalog (Datalog$^r$) is an extension of Datalog, where universal quantification over intensional relations is allowed in the body of rules. Abiteboul and Vianu first introduced the idea that the body of a rule in Datalog can be universally quantified [2]. The author of the paper showed that Datalog$^r$ equals LFP on all finite structures [10]. In the paper, we study the expressive power of Datalog$^r$ on problems with closure properties, i.e., closed under substructures (or extensions). We conclude that a Datalog$^r$ formula is equivalent to a first-order formula iff it is equivalent to a bounded Datalog$^r$ formula. As the main result of the paper, we show that Datalog$^r$ cannot define all the problems that are in PTIME and closed under substructures. Since Datalog$^r$ equals LFP, and the complement of a substructure-closed problem is extension-closed, as a corollary, LFP cannot define all the extension-closed problems that are in PTIME. This result contributes the strict containment $\mathrm {LFP[E]} \subsetneq \mathrm {PTIME[E]}$ in Fig. 1. A technique of tree encodings for arbitrary structures is used in the proof. For an arbitrary set of structures $\mathcal {K}\in$ EXPTIME, we can encode them into a set of substructure-closed structures $\mathcal {K}'$, where the tree used to encode the structure in $\mathcal {K}$ is exponentially larger. Therefore, $\mathcal {K}'$ is in PTIME. For every structure in $\mathcal {K}'$, there is a characteristic structure $S_{\textbf{T}}$ of it such that they are equivalent with respect to Datalog$^r$-transformations. Since $S_{\textbf{T}}$ can be computed from the structure in $\mathcal {K}$ in logspace, this implies that $\mathcal {K}$ is also in PTIME, contrary to the time hierarchy theorem. Figure 2 shows the sketch of the proof.

Fig. 2.

The idea of the proof for the nondefinability of Datalog$^r$.

The paper is organized as follows: In Sect. 2, we give the basic definitions and notations. In Sect. 3, we recall invariant relations on perfect binary trees, and introduce the technique of tree encodings for arbitrary structures. And we prove the nondefinability results for Datalog$^r$ on substructure-closed problems. Finally, we conclude the paper in Sect. 4.

2 Preliminaries

Let $\tau =\{\textbf{c}_{1},\dots ,\textbf{c}_{m},P_{1},\dots ,P_{n}\}$ be a vocabulary, where $\textbf{c}_{1},\dots ,\textbf{c}_{m}$ are constant symbols and $P_{1},\dots ,P_{n}$ are relation symbols. A $\tau$-structure is a tuple $\textbf{A}=\langle A,\textbf{c}_{1}^{A},\dots ,\textbf{c}_{m}^{A},P_{1}^{A},\dots ,P_{n}^{A}\rangle$ where A is the domain, and $\textbf{c}_{1}^{A},\dots ,\textbf{c}_{m}^{A}$, $P_{1}^{A},\dots ,P_{n}^{A}$ are interpretations of the constant and relation symbols over A, respectively. We assume the equality relation “=” is contained in every vocabulary, and omit the superscript “A” when it is clear from context. We call $\textbf{A}$ finite if its domain A is a finite set. Unless otherwise stated, all structures considered in this paper are finite. We use arity(R) to denote the arity of a relation R, and use “$|\ |$” to indicate the cardinality of a set or the arity of a tuple, e.g., |A| denotes the cardinality of A and $|(x_1,x_2,x_3)|=3$. A finite structure is ordered if it is equipped with a linear order relation “$\le$”, and the successor relation “$\textrm{SUCC}$”, the constants “min” and “max” for the minimal and maximal elements, respectively, with respect to “$\le$”. Let $\textbf{A}=\langle A,\textbf{c}_{1}^{A},\dots ,\textbf{c}_{m}^{A},P_{1}^{A},\dots ,P_{n}^{A}\rangle$ and $\textbf{B}=\langle B,\textbf{c}_{1}^{B},\dots ,\textbf{c}_{m}^{B},P_{1}^{B},\dots ,P_{n}^{B}\rangle$ be two structures. If $B\subseteq A$, $\textbf{c}_{i}^{A} = \textbf{c}_{i}^{B}$ $(1\le i \le m)$, and $P_{j}^{B} = P_{j}^{A} \cap B^{arity(P_j)}$ $(1\le j \le n)$, then we say that $\textbf{B}$ is a substructure of $\textbf{A}$, and $\textbf{A}$ is an extension of $\textbf{B}$.

An r-ary global relation R of a vocabulary $\tau$ is a mapping that assigns to every $\tau$-structure $\textbf{A}$ an r-ary relation $R^{A}$ over A such that for every isomorphism $\pi : \textbf{A} \simeq \textbf{B}$ and every $a_1,\dots ,a_r\in A$, $\textbf{A} \models R^{A}a_1\dots a_r$ iff $\textbf{B} \models R^{B}\pi (a_1)\dots \pi (a_r)$. A query is a global relation. We say that a query $\mathcal {Q}$ is expressible in a logic $\mathcal {L}$ if there is an $\mathcal {L}$-formula that defines $\mathcal {Q}$. Two formulas are equivalent if they define the same query. Given two logics $\mathcal {L}_1$ and $\mathcal {L}_2$, we use $\mathcal {L}_1\le \mathcal {L}_2$ to denote that every $\mathcal {L}_1$-formula is equivalent to an $\mathcal {L}_2$-formula. If $\mathcal {L}_1\le \mathcal {L}_2$ and $\mathcal {L}_2\le \mathcal {L}_1$, then we denote it by $\mathcal {L}_1\equiv \mathcal {L}_2$.

Suppose that a relation symbol X occurs positively in $\varphi (\bar{x})$ and $|\bar{x}|=arity(X)$. Given a structure $\textbf{A}$, we can define a monotonic sequence $X_0, X_1, X_2, \dots$, where $X_0 = \emptyset$ and $X_{i+1} = \{\bar{a} \mid (\textbf{A}, X_i) \vDash \varphi [\bar{a}] \}$ for $i\ge 0$, such that $X_i\subseteq X_{i+1}$. Since $\textbf{A}$ is finite, the sequence will eventually reach a fixpoint.

Definition 1

The least fixpoint logic $\textrm{LFP}$ is an extension of first-order logic by adding the following rule [9]:

• If $\varphi$ is an $\textrm{LFP}$ formula, X occurs positively in $\varphi$, and $|\bar{x}|=|\bar{u}|=arity(X)$, then $[\textrm{LFP}_{\bar{x},X}\varphi ]\bar{u}$ is an $\textrm{LFP}$ formula.

Given an LFP formula $[\textrm{LFP}_{\bar{x},X}\varphi ]\bar{u}$, for any structure $\textbf{A}$ and $\bar{a} \in A^{arity(\bar{a})}$, we have $\textbf{A} \vDash [\textrm{LFP}_{\bar{x},X}\varphi ]\bar{a}$ iff $\bar{a}$ is in the fixpoint of the sequence induced by X and $\varphi$ on $\textbf{A}$.

Proposition 1

 [15, 24] $\textrm{LFP}$ captures $\textrm{PTIME}$ on ordered finite structures.

Definition 2

Let $\tau$ be a vocabulary. A $\textrm{Datalog}$ program $\mathrm {\Pi }$ over $\tau$ is a finite set of rules of the form

$$ \beta \leftarrow \alpha _{1},\dots ,\alpha _{l} $$

where $l\ge 0$ and

• (1) each $\alpha _{i}$ is either an atomic formula or a negated atomic formula,

• (2) $\beta$ is an atomic formula $R\bar{x}$, where R doesn’t occur negatively in any rule of $\mathrm {\Pi }$.

$\beta$ is the head of the rule and the sequence $\alpha _{1},\dots ,\alpha _{l}$ constitute the body. Every relation symbol occurring in the head of some rule of $\mathrm {\Pi }$ is intensional, and the other symbols in $\tau$ are extensional. We use $(\tau ,\mathrm {\Pi })_{\textrm{int}}$ and $(\tau ,\mathrm {\Pi })_{\textrm{ext}}$ to denote the set of intensional and extensional symbols, respectively. We also allow 0-ary relation symbols. If Q is a 0-ary relation, its value is from $\{\emptyset ,\{\emptyset \}\}$. $Q=\emptyset$ means that Q is FALSE and $Q=\{\emptyset \}$ means that Q is TRUE. We use the least fixpoint semantics for Datalog programs. A Datalog formula has the form $(\mathrm {\Pi },P)\bar{x}$, where P is an r-ary intensional relation symbol and $\bar{x}=(x_{1},\dots ,x_{r})$ are variables that do not occur in $\mathrm {\Pi }$. For a $(\tau ,\mathrm {\Pi })_{\textrm{ext}}$-structure $\textbf{A}$ and $\bar{a}=(a_{1},\dots ,a_{r})\in A^r$,

$$ \textbf{A}\models (\mathrm {\Pi },P)\bar{x}[\bar{a}]\text { iff }(a_{1},\dots ,a_{r})\in P_{(\infty )}, $$

where $P_{(\infty )}$ is the least fixpoint for relation P when $\mathrm {\Pi }$ is evaluated on $\textbf{A}$. If P is 0-ary, then $\textbf{A}\models (\mathrm {\Pi },P)\text { iff }P_{(\infty )}=\{\emptyset \}$.

3 $\textrm{Datalog}^r$ on Problems with Closure Properties

3.1 Revised Datalog Programs

Definition 3

In Definition 2, if we replace Condition (1) by

• (1$'$) each $\alpha _{i}$ is either an atomic formula, or a negated atomic formula, or a formula $\forall \bar{y}R\bar{y}\bar{z}$, where R occurs in the head of some rule,

then we call this logic program revised $\textrm{Datalog}$ program, denoted by $\textrm{Datalog}^r$.

Example 1

Let $G =\langle V,E \rangle$ be a directed acyclic graph, and the set of nodes V partitioned into two disjointed sets $V_{\textrm{uni}}$ and $V_{\textrm{exi}}$. The nodes in $V_{\textrm{uni}}$ (resp., $V_{\textrm{exi}}$) are universal (resp., existential). The notion of alternating path is defined recursively. There is an alternating path from $\textbf{s}$ to $\textbf{t}$ in G if

• $\textbf{s} = \textbf{t}$; or

• $\textbf{s}\in V_{\textrm{exi}}$, $\exists x\in V$ such that $(\textbf{s},x)\in E$ and there is an alternating path from x to $\textbf{t}$; or

• $\textbf{s}\in V_{\textrm{uni}}$, $\exists x\in V$ such that $(\textbf{s},x)\in E$, and $\forall y\in V$, if $(\textbf{s},y)\in E$ then there is an alternating path from y to $\textbf{t}$.

The alternating graph accessibility problem is defined as follows:

• Input: A directed acyclic graph $G=\langle V_{\textrm{uni}}\cup V_{\textrm{exi}}, E \rangle$ and two nodes $\textbf{s}, \textbf{t}$.

• Output: Yes if there is an alternating path from $\textbf{s}$ to $\textbf{t}$ in G, otherwise no.

This problem is $\textrm{P}$-complete [14]. The following $\textrm{Datalog}^r$ program $\mathrm {\Pi }$ defines the alternating graph accessibility problem

We have $(\tau ,\mathrm {\Pi })_{\textrm{int}}=\{P_{\textrm{alt}},Q,P_{\textrm{uni}},P\}$ and $(\tau ,\mathrm {\Pi })_{\textrm{ext}}=\{E,V_{\textrm{uni}},\textbf{s},\textbf{t}\}$. The relation $P_{\textrm{uni}}$ saves the nodes in $V_{\textrm{uni}}$ that have a successor. The relation $P_{\textrm{alt}}$ saves the pairs (x, y) such that there is an alternating path from x to y. We use Qxzy to denote that for any $x \in P_{\textrm{uni}}$, either there is no edge from x to z, or there is an alternating path from z to y. For any directed acyclic $(\tau ,\mathrm {\Pi })_{\textrm{ext}}$-structure $\textbf{A}$, we have $\textbf{A}\models (\mathrm {\Pi },P)$ iff there is an alternating path from $\textbf{s}$ to $\textbf{t}$.

The Datalog formulas are preserved under extensions [7], i.e., if a structure $\textbf{B}$ satisfies a Datalog formula $\varphi$ and $\textbf{A}$ is an extension of $\textbf{B}$, then $\textbf{A}$ also satisfies $\varphi$. A directed acyclic graph with an alternating path from $\textbf{s}$ to $\textbf{t}$ can be extended to a directed acyclic graph without any alternating path from $\textbf{s}$ to $\textbf{t}$ by adding new nodes. So Datalog cannot define the alternating graph accessibility problem, which implies that $\textrm{Datalog}^r$ is strictly more expressive than $\textrm{Datalog}$. Allowing universal quantification over intensional relations is essential for $\textrm{Datalog}^r$ to increase its expressive power. With the help of it, every FO(LFP) formula can be transformed into an equivalent $\textrm{Datalog}^r$ formula.

Proposition 2

[10] $\textrm{Datalog}^r\equiv \textrm{LFP}$ on all finite structures.

A Datalog program is positive if no negated atomic formula occurs in the body of any rule. A Datalog formula $(\mathrm {\Pi },P)\bar{t}$ is bounded if there is an $n\ge 0$ such that $P_{(n)}=P_{(\infty )}$ for all structures. A bounded (positive) Datalog formula is equivalent to an existential (positive) first-order formula, and vice versa [9]. Furthermore, a positive Datalog formula is bounded iff it is equivalent to a first-order formula. The statement is false for all Datalog formulas. There is an unbounded Datalog formula that is equivalent to an FO formula, but no bounded Datalog formula is equivalent to it [4]. Unlike Datalog, if an unbounded $\textrm{Datalog}^r$ formula is equivalent to an FO formula, then it must be equivalent to a bounded $\textrm{Datalog}^r$ formula.

Proposition 3

A $\textrm{Datalog}^r$ formula is equivalent to a first-order formula iff it is equivalent to a bounded $\textrm{Datalog}^r$ formula.

Proof

Suppose that a $\textrm{Datalog}^r$ formula is equivalent to a first-order formula $\varphi$. Using the method in [10] we can construct a bounded $\textrm{Datalog}^r$ formula that is equivalent to $\varphi$. For the other direction, the proof in [9] which shows that every bounded $\textrm{Datalog}$ formula is equivalent to an FO formula remains valid for bounded $\textrm{Datalog}^r$ formulas.

3.2 Invariant Relations on Perfect Binary Trees

In [17], Lindell introduced invariant relations that are defined on perfect binary trees, and showed that there are queries computable in PTIME but not definable in LFP. A perfect binary tree is a binary tree in which all internal nodes have two children and all leaf nodes are in the same level. Let $T=\langle V,E,\textbf{root}\rangle$ be a perfect binary tree, where V is the set of nodes, E is the set of edges and $\textbf{root}$ is the root node. Suppose that R is an r-ary relation on V and f is an automorphism of T. Given a tuple $\bar{a}=(a_{1},\dots ,a_{r})\in R$, we write $f(\bar{a})=(f(a_{1}),\dots ,f(a_{r}))$ and $f[R]=\{(f(a_{1}),\dots ,f(a_{r}))\mid (a_{1},\dots ,a_{r})\in R\}$. We say that R is an invariant relation if for every automorphism f, $R=f[R]$. It is easily seen that the equality $=$ and E are invariant relations.

First we give several technical lemmas. The proofs of Lemmas 1, 2, 3, and 5 can be found in the full arXiv version of the paper.

Lemma 1

If $R_{1}$ and $R_{2}$ are r-ary invariant relations, then $\lnot R_{1}$, $R_{1}\cap R_{2}$ and $R_{1}\cup R_{2}$ are also invariant relations.

Lemma 2

Suppose that R is an r-ary invariant relation, $R'$ is a k-ary invariant relation and g is a permutation of $\{1,\dots ,r\}$. Define

$$ \begin{aligned} R_{1} & = \{(a_{g(1)},\dots ,a_{g(r)})\mid (a_{1},\dots ,a_{r})\in R\},\\ R_{2} & = \{(a_{1},\dots ,a_{r},b_{1},\dots ,b_{k})\mid (a_{1},\dots ,a_{r})\in R \text { and }(b_{1},\dots ,b_{k})\in R' \}. \end{aligned} $$

Then $R_{1}$ and $R_{2}$ are also invariant relations.

Lemma 3

Suppose that R is a $(k+r)$-ary invariant relation. Define

$$ \begin{array}{cl} R_{1}= &{} \{(a_{1},\dots ,a_{r})\mid (b_{1},\dots ,b_{k},a_{1},\dots ,a_{r})\in R\text { for all nodes }b_{1},\dots ,b_{k}\}\\ R_{2}= &{} \{(a_{1},\dots ,a_{r})\mid \exists b_{1},\dots ,b_{k} \text { such that }(b_{1},\dots ,b_{k},a_{1},\dots ,a_{r})\in R\}. \end{array} $$

Then $R_{1}$ and $R_{2}$ are also invariant relations.

Let a, b be two nodes of a perfect binary tree T, we use $a\barwedge b$ and d(a) to denote the least common ancestor of a, b and the depth of a, respectively. For example, in Fig. 3 there is a perfect binary tree in which $d(\textbf{root})=0$, $d(a)=1$, $d(c)=d(e)=2$, and $c\barwedge e=\textbf{root}$.

Fig. 3.

A perfect binary tree of depth 3.

Let $(a_{1},\dots ,a_{r})$ be an r-ary tuple of nodes, its characteristic tuple is defined as

$$ \begin{array}{rr} (a_{1},\dots ,a_{r})^{*}= &{} (d(a_{1}),d(a_{1}\barwedge a_{2}),\dots ,d(a_{1}\barwedge a_{r}),\,\\ &{} d(a_{2}),d(a_{2}\barwedge a_{3}),\dots ,d(a_{2}\barwedge a_{r}),\,\\ &{} \dots ,d(a_{r})) \end{array} $$

which is a $\frac{r(r+1)}{2}$-ary tuple of numbers. Let R be an invariant relation, the characteristic relation of R is defined to be

$$ R^{*}=\{(a_{1},\dots ,a_{r})^{*}\mid (a_{1},\dots ,a_{r})\in R\}. $$

Proposition 4

[17] Let $\bar{a}=(a_{1},\dots ,a_{r})$ and $\bar{b}=(b_{1},\dots ,b_{r})$ be two tuples, and R an r-ary invariant relation of a perfect binary tree T.

• $(a_{1},\dots ,a_{r})^{*}=(b_{1},\dots ,b_{r})^{*}$ iff there is an automorphism f of T such that $f(\bar{a})=\bar{b}$.

• If $(a_{1},\dots ,a_{r})^{*}=(b_{1},\dots ,b_{r})^{*}$, then $\bar{a}\in R$ iff $\bar{b}\in R$.

For any two invariant relations $R_{1}$ and $R_{2}$, $R_{1}=R_{2}$ iff $R_{1}^{*}=R_{2}^{*}$.

3.3 Tree Encodings and Characteristic Structures

This section is devoted to the definitions of tree encodings and characteristic structures, and the propositions about the equivalent relationship between them on Datalog$^r$ programs, which will be used in the next section.

Definition 4

Let T be a perfect binary tree, R an r-ary relation on T. R is a saturated relation if for any nodes $a_{1},\dots ,a_{r}$, $b_{1},\dots ,b_{r}$, whenever $d(a_{i})=d(b_{i})\,(1\le i\le r)$, then $(a_{1},\dots ,a_{r})\in R \text{ iff } (b_{1},\dots ,b_{r})\in R$.

The following proposition can be proved easily from the definitions of invariant relations and saturated relations.

Proposition 5

A saturated relation is also an invariant relation.

From now on we make the assumption: $\tau$ is the vocabulary $\{R_{1},\dots ,R_{k}\}$, and $\tau '=\tau \cup \{\textbf{root},E\}$, where $\textbf{root}$ is a constant symbol and E is a binary relation symbol that is not in $\tau$. We define a class of $\tau '$-structures

$$ \begin{array}{r} \mathcal {T}=\{\langle V,\textbf{root},E,R_{1},\dots ,R_{k}\rangle \mid \langle V,E,\textbf{root}\rangle \text { is a perfect binary tree}, \\ R_{1},\dots ,R_{k} \text { are saturated relations on it} \}. \end{array} $$

Definition 5

Let $\textbf{A}=\langle \{0,1,\dots ,h-1\},R_{1}^{A},\dots ,R_{k}^{A}\rangle$ be a $\tau$-structure. The tree encoding of $\textbf{A}$ is a $\tau '$-structure $C(\textbf{A})=\langle V,\textbf{root},E,R_{1}^{T},\dots ,R_{k}^{T}\rangle \in \mathcal {T}$, such that $\langle V,E,\textbf{root}\rangle$ is a perfect binary tree of depth h, and for any relation symbol $R_{i}\,(1\le i\le k)$ and any nodes $a_{1},\dots ,a_{r_i}\in V$,

$$ C(\textbf{A})\models R_{i}^{T}a_{1}\cdots a_{r_{i}} \text{ iff } \textbf{A}\models R_{i}^{A}d(a_{1})\cdots d(a_{r_{i}}) $$

where $r_i$ is the arity of $R_i$, and $d(a_{j})\,(1\le j \le r_i)$ is the depth of $a_{j}$.

Roughly speaking, $C(\textbf{A})$ encodes $\textbf{A}$ in a tree, but its size is exponentially larger. Conversely, given a $\tau '$-structure $\textbf{T}=\langle V,\textbf{root},E,R_{1}^{T},\dots ,R_{k}^{T}\rangle \in \mathcal {T}$, we can compute the $\tau$-structure $\textbf{A}$ encoded by $\textbf{T}$ as follows:

• (1) The domain is $\{0,\dots , h-1\}$, where h is the depth of $\textbf{T}$;

• (2) For each $i=1,\dots ,k$,

  $$ R^A_i = \{(d(a_1), \dots , d(a_{r_i}))\mid \exists a_1,\dots , a_{r_i}\in V \text { such that } \textbf{T}\models R_i^Ta_1\cdots a_{r_i}\}. $$

We use $C^{-1}(\textbf{T})$ to denote the corresponding $\tau$-structure $\textbf{A}$ encoded by $\textbf{T}$. Let $\textrm{FUL}_m = V^m$ be a relation of arity m, where $m\ge 1$ and V is the domain of $\textbf{T}$. Define the vocabulary

$$ \sigma =\{\textbf{0},\textrm{SUCC},R_{\ne },R_{\lnot e},\textrm{FUL}_{m}^{*}\} \cup \{R_{1}^{*},\dots ,R_{k}^{*},(\lnot R_{1})^{*},\dots ,(\lnot R_{k})^{*}\} $$

where $\textrm{FUL}_{m}^{*}$ has arity $\frac{m(m+1)}{2}$, $R_{\ne }$ and $R_{\lnot e}$ have arity 3, $R_i^*$ or $(\lnot R_{1})^{*}$ has arity $\frac{r_i(r_i+1)}{2}$ ($1\le i \le k$ and $r_i$ is the arity of $R_i$).

Definition 6

Given a $\tau '$-structure $\textbf{T}=\langle V,\textbf{root},E,R_{1},\dots ,R_{k}\rangle \in \mathcal {T}$, the characteristic structure $S_{\textbf{T}}$ of $\textbf{T}$ is a $\sigma$-structure

$$ \langle \{0,1,\dots ,h-1\},\textbf{0},\textrm{SUCC},R_{\ne },R_{\lnot e},\textrm{FUL}_{m}^{*}, R_{1}^{*},\dots ,R_{k}^{*},(\lnot R_{1})^{*},\dots ,(\lnot R_{k})^{*}\rangle $$

where h is the depth of $\textbf{T}$, $\textbf{0}$ is a constant interpreted by 0, $\textrm{SUCC}$ is the successor relation on the domain, and $R_{\ne },R_{\lnot e},\textrm{FUL}_{m}^{*}$, $R_{1}^{*},\dots ,R_{k}^{*}$, $(\lnot R_{1})^{*},\dots ,(\lnot R_{k})^{*}$ are the characteristic relations of $\ne ,(\lnot E)$, $\textrm{FUL}_{m},R_{1},\dots ,R_{k}$, $\lnot R_{1},\dots ,\lnot R_{k}$, respectively.

In the following we show that for every Datalog$^r$ program $\mathrm {\Pi }$ on the tree encodings, there is a Datalog$^r$ program $\mathrm {\Pi }^{*}$ on the corresponding characteristic structures such that $\mathrm {\Pi }^{*}$ simulates $\mathrm {\Pi }$. More precisely, $\mathrm {\Pi }^{*}$ handles the characteristic relations of the relations in $\mathrm {\Pi }$. Let $\mathrm {\Pi }=\{\gamma _{1},\dots ,\gamma _{s}\}$ be a Datalog$^r$ program on $\mathcal {T}$. Suppose $X_{1},\dots ,X_{w}$ are all intensional relation symbols in $\mathrm {\Pi }$ and for each rule $\gamma _{i}$, let $n_{\gamma _{i}}$ be the number of free variables occurring in $\gamma _{i}$. Set

$$ m= \max \{n_{\gamma _{1}},\dots ,n_{\gamma _{s}},\textrm{arity}(R_{1}),\dots ,\textrm{arity}(R_{k}),\textrm{arity}(X_{1}),\dots ,\textrm{arity}(X_{w})\}. $$

We shall construct, based on $\mathrm {\Pi }$, a Datalog$^r$ program $\mathrm {\Pi }^{*}$ such that for any Datalog$^r$ formula $(\mathrm {\Pi },P)$, there exists a Datalog$^r$ formula $(\mathrm {\Pi }^{*},P^{*})$, and $\textbf{T}\models (\mathrm {\Pi },P)$ iff $S_{\textbf{T}}\models (\mathrm {\Pi }^{*},P^{*})$ for any $\textbf{T}\in \mathcal {T}$, where P and $P^{*}$ are 0-ary.

Every element of $\textbf{T}$ is a node of a perfect binary tree, while every element of $S_{\textbf{T}}$ is a number which can be treated as the depth of some node. Hence, for each variable x in $\mathrm {\Pi }$, we introduce a new variable $i_{x}$, and for any two variables $x_1, x_2$ in $\mathrm {\Pi }$, we introduce a new variable $i_{x_1\barwedge x_2}$. For a tuple of variables $\bar{x}=x_{1}\cdots x_{r}$, we use the following abbreviations:

$$ \begin{aligned} (\bar{x})^{*} & = i_{x_{1}}i_{x_{1}\barwedge x_{2}}\cdots i_{x_{1}\barwedge x_{r}}i_{x_{2}}i_{x_{2}\barwedge x_{3}}\cdots i_{x_{r-1}\barwedge x_{r}}i_{x_{r}},\\ \forall (\bar{x})^{*} & = \forall i_{x_{1}}\forall i_{x_{1}\barwedge x_{2}}\cdots \forall i_{x_{1}\barwedge x_{r}}\forall i_{x_{2}}\forall i_{x_{2}\barwedge x_{3}}\cdots \forall i_{x_{r-1}\barwedge x_{r}}\forall i_{x_{r}}. \end{aligned} $$

Without loss of generality, we treat $i_{u \barwedge v}$ and $i_{v \barwedge u}$ as the same variable. Additionally, we assume that the 0-ary relation is also an invariant relation, and the characteristic relation of a 0-ary relation is itself.

First we construct a quasi-Datalog$^r$ program $\mathrm {\Pi }'$ as follows. For each rule $\beta \leftarrow \alpha _{1},\dots ,\alpha _{l}$ in $\mathrm {\Pi }$, suppose that $v_{1},\dots ,v_{n}$ are the free variables in it, we add the formula

$$ \textrm{FUL}_{m}v_{1}v_{2}\cdots v_{n-1}v_{n}v_{n}\cdots v_{n} $$

to the body and obtain a new rule

$$ \beta \leftarrow \alpha _{1},\dots ,\alpha _{l},\textrm{FUL}_{m}v_{1}v_{2}\cdots v_{n-1}v_{n}\cdots v_{n}. $$

For each new rule, we

• replace $x=y$ by $i_{x}=i_{x\barwedge y},i_{x\barwedge y}=i_{y}$ (reason: $d(x)=d(x\barwedge y)=d(y)$), for constant $\textbf{root}$, we replace $i_{\textbf{root}}$ by constant $\textbf{0}$, and replace $i_{\textbf{root}\barwedge x}$ also by $\textbf{0}$, since $\textbf{root}\barwedge a=\textbf{root}$ for any node a;

• replace Exy by $i_{x}=i_{x\barwedge y},\textrm{SUCC}i_{x\barwedge y}i_{y}$ (reason: $d(y)=d(x\barwedge y)+1=d(x)+1$);

• replace $x\ne y$ by $R_{\ne }i_{x}i_{x\barwedge y}i_{y}$ (reason: $R_{\ne }$ is the characteristic relation of $\ne$);

• replace $\lnot Exy$ by $R_{\lnot e}i_{x}i_{x\barwedge y}i_{y}$ (reason: $R_{\lnot e}$ is the characteristic relation of $\lnot E$);

• replace $P\bar{x}$ by $P^{*}(\bar{x})^{*}$, where P is in $\{R_{1},\dots ,R_{k},\textrm{FUL}_{m}\}$, or an intensional relation symbol;

• replace $\lnot R\bar{x}$ by $(\lnot R)^{*}(\bar{x})^{*}$, where R is a symbol in $\{R_{1},\dots ,R_{k}\}$;

• replace $\forall y_{1}\cdots \forall y_{t}Py_{1}\cdots y_{t}z_{1}\cdots z_{s}$ by

  $$ \varPsi _{P}=\left( \begin{array}{l} \textrm{FUL}_{m}^{*}(z_{1}z_{2}\cdots z_{s-1}z_{s}\cdots z_{s})^{*}\wedge \\ \forall (y_{1}\cdots y_{t})^{*}\forall i_{y_{1}\barwedge z_{1}}\cdots \forall i_{y_{1}\barwedge z_{s}}\forall i_{y_{2}\barwedge z_{1}}\cdots \forall i_{y_{t}\barwedge z_{s-1}}\forall i_{y_{t}\barwedge z_{s}}\\ \bigr (\textrm{FUL}_{m}^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s}\cdots z_{s})^{*} \rightarrow P^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*}\bigl ) \end{array}\right) $$

  where P is an intensional relation symbol.

By adding $\textrm{FUL}_m$ to each rule of $\mathrm {\Pi }$ and replacing it with $\textrm{FUL}_m^{*}$ in $\mathrm {\Pi }'$, we can restrict to characteristic tuples. $\mathrm {\Pi }'$ is not a Datalog$^r$ program because of $\varPsi _P$. Note that $\varPsi _P$ is equivalent to the Datalog$^r$ formula $(\mathrm {\Pi }_{1},Q_{2})\bar{t}$, where

$$ \begin{aligned} \mathrm {\Pi }_{1}: Q(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*} & \leftarrow \lnot \textrm{FUL}_{m}^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s}z_{s}\cdots z_{s})^{*};\\ Q(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*} & \leftarrow P^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*};\\ Q_{1}(z_{1}\cdots z_{s})^{*} & \leftarrow \forall (y_{1}\cdots y_{t})^{*}\forall i_{y_{1}\barwedge z_{1}}\cdots \forall i_{y_{1}\barwedge z_{s}}\\ &\qquad \! \forall i_{y_{2}\barwedge z_{1}}\cdots \forall i_{y_{t}\barwedge z_{s-1}}\forall i_{y_{t}\barwedge z_{s}}Q(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*};\\ Q_{2}(z_{1}\cdots z_{s})^{*} & \leftarrow Q_{1}(z_{1}\cdots z_{s})^{*},\textrm{FUL}_{m}^{*}(z_{1}z_{2}\cdots z_{s-1}z_{s}\cdots z_{s})^{*}. \end{aligned} $$

The Datalog$^r$ program $\mathrm {\Pi }^{*}$ can be obtained by adding $\mathrm {\Pi }_{1}$ to $\mathrm {\Pi }'$ and changing $\varPsi _{P}$ to $Q_{2}(z_1\cdots z_s)^*$.

Remark 1

We cannot replace $\forall y_{1}\cdots \forall y_{t}Py_{1}\cdots y_{t}z_{1}\cdots z_{s}$ directly by

$$ \forall (y_{1}\cdots y_{t})^{*}\forall i_{y_{1}\barwedge z_{1}}\cdots \forall i_{y_{1}\barwedge z_{s}}\forall i_{y_{2}\barwedge z_{1}}\cdots \forall i_{y_{t}\barwedge z_{s-1}}\forall i_{y_{t}\barwedge z_{s}} P^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*} $$

since there may be $\textbf{T}\in \mathcal {T}$, $\bar{a}\in \textbf{T}$, and an invariant relation P such that

$$ \begin{aligned} \textbf{T} & \vDash \forall y_{1}\cdots \forall y_{t}P y_{1}\cdots y_{t}z_{1}\cdots z_{s}[\bar{a}], \text {and}\\ S_{\textbf{T}} & \nvDash \forall (y_{1}\cdots y_{t})^{*}\forall i_{y_{1}\barwedge z_{1}}\cdots \forall i_{y_{1}\barwedge z_{s}}\forall i_{y_{2}\barwedge z_{1}}\cdots \forall i_{y_{t}\barwedge z_{s-1}}\forall i_{y_{t}\barwedge z_{s}}\\ & \quad P^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*}[(\bar{a})^{*}]. \end{aligned} $$

For example, let $\textbf{T}$ be the structure with the perfect binary tree of Fig. 3 and relation

$$ P=\{(\textbf{root},\textbf{root}),(\textbf{root},a),(\textbf{root},b),(\textbf{root},c),(\textbf{root},d),(\textbf{root},e),(\textbf{root},f)\}. $$

Obviously, we have $\textbf{T} \vDash \forall y P(\textbf{root},y)$. But $S_{\textbf{T}} \nvDash P^{*}(\textbf{0}, 1,1)$ since $(\textbf{0}, 1,1)$ is not the characteristic tuple of any tuple in $\textbf{T}$. This problem can be solved by changing $\forall y_{1}\cdots \forall y_{t}Py_{1}\cdots y_{t}z_{1}\cdots z_{s}$ to the equivalent formula

$$ \textrm{FUL}_{m}z_{1}\cdots z_{s-1}z_{s}\cdots z_{s}\,\wedge \forall y_{1}\cdots \forall y_{t}(\textrm{FUL}_{m}y_{1}\cdots y_{t}z_{1}\cdots z_{s}\cdots z_{s}\rightarrow Py_{1}\cdots y_{t}z_{1}\cdots z_{s}). $$

We replace $\textrm{FUL}_{m}$ and P by their characteristic relations $\textrm{FUL}_{m}^*$ and $P^*$, respectively, to obtain $\varPsi _{P}$. This guarantees that only characteristic tuples are considered.

Example 2

The following Datalog$^r$ program $\mathrm {\Pi }$ computes the transitive closure R of edges E

$$ \begin{aligned} \mathrm {\Pi }: R x_1x_2 & \leftarrow E x_1x_2;\\ R x_1x_3 & \leftarrow R x_1x_2, E x_2x_3. \end{aligned} $$

The corresponding Datalog$^r$ program $\mathrm {\Pi }^*$ below computes the characteristic relation $R^*$ of R.

$$ \begin{aligned} \mathrm {\Pi }^*: R^* i_{x_1} i_{x_1\barwedge x_2} i_{x_2} & \leftarrow i_{x_1}=i_{x_1\barwedge x_2},\textrm{SUCC}i_{x_1\barwedge x_2}i_{x_2}, \\ & \qquad \! \textrm{FUL}_3^* i_{x_1} i_{x_1\barwedge x_2} i_{x_1\barwedge x_2} i_{x_2} i_{x_2} i_{x_2};\\ R^* i_{x_1} i_{x_1\barwedge x_3} i_{x_3} & \leftarrow R^* i_{x_1} i_{x_1\barwedge x_2} i_{x_2}, i_{x_2}=i_{x_2\barwedge x_3},\textrm{SUCC}i_{x_2\barwedge x_3}i_{x_3}, \\ & \qquad \! \textrm{FUL}_3^* i_{x_1} i_{x_1\barwedge x_2} i_{x_1\barwedge x_3} i_{x_2} i_{x_2\barwedge x_3} i_{x_3}. \end{aligned} $$

Lemma 4

Given $\psi _{P}=\forall y_{1}\cdots \forall y_{t}Py_{1}\cdots y_{t}z_{1}\cdots z_{s}$, a structure $\textbf{T}\in \mathcal {T}$, let $\varPsi _{P}$ be defined as above, and $Q_{1}=\{\bar{a}\mid \textbf{T}\models \psi _{P}[\bar{a}]\}$, $Q_{2}=\{\bar{e}\mid S_{\textbf{T}}\models \varPsi _{P}[\bar{e}]\}$. If P is an invariant relation on $\textbf{T}$, then $(Q_{1})^{*}=Q_{2}$.

Proof

Because P is an invariant relation, by Lemma 3 and the definition of $Q_{1}$, we know that $Q_{1}$ is also an invariant relation. We first show that $(Q_{1})^{*}\subseteq Q_{2}$. Suppose that $\bar{e}\in (Q_{1})^{*}$ for some $\bar{e}\in S_{\textbf{T}}$, there must exist a tuple $\bar{a}$ from $\textbf{T}$ such that $\bar{a}\in Q_{1}$, $(\bar{a})^{*}=\bar{e}$, and $\bar{b}\bar{a}\in P$ for all tuples $\bar{b}$ of $\textbf{T}$, i.e.,

$$ \begin{array}{ll} \textbf{T}\models &{} \Bigl (\textrm{FUL}_{m}z_{1}\cdots z_{s-1}z_{s}z_{s}\cdots z_{s}\wedge \\ &{} \forall y_{1}\cdots \forall y_{t}(\textrm{FUL}_{m}y_{1}\cdots y_{t}z_{1}\cdots z_{s}z_{s}\cdots z_{s}\rightarrow Py_{1}\cdots y_{t}z_{1}\cdots z_{s})\Bigr )[\bar{a}]. \end{array} $$

By the definition of $\varPsi _P$ we see that $S_{\textbf{T}}\models \varPsi _{P}[(\bar{a})^{*}]$, which implies $\bar{e}\in Q_{2}$.

To prove $Q_{2}\subseteq (Q_{1})^{*}$, consider an arbitrary tuple $\bar{e}\in S_{\textbf{T}}$ such that $\bar{e}\in Q_{2}$. By the definition of $Q_{2}$ and $\varPsi _{P}$, we have $S_{\textbf{T}}\models \textrm{FUL}_m(z_1\cdots z_sz_s\cdots z_s)^*[\bar{e}]$, so there exists a tuple $\bar{a}$ of $\textbf{T}$ such that $\bar{e}=(\bar{a})^{*}$. On the contrary, assume $\bar{a}\notin Q_{1}$, then there is a tuple $\bar{b}$ such that $\bar{b}\bar{a}\notin P$. Because P is an invariant relation, for any tuples $\bar{b}'$ and $\bar{a}'$, if $(\bar{b}\bar{a})^{*}=(\bar{b}'\bar{a}')^{*}$ then $\bar{b}'\bar{a}'\notin P$. Combing that $P^{*}$ is the characteristic relation of P we conclude that

$$\begin{aligned} S_{\textbf{T}} & \nvDash P^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s})^{*}[(\bar{b}\bar{a})^{*}], \text {and}\end{aligned}$$

(1)

$$\begin{aligned} S_{\textbf{T}} & \vDash \textrm{FUL}_{m}^{*}(y_{1}\cdots y_{t}z_{1}\cdots z_{s}z_{s}\cdots z_{s})^{*}[(\bar{b}\bar{a})^{*}]. \end{aligned}$$

(2)

(1) and (2) give $S_{\textbf{T}}\nvDash \varPsi _{P}[(\bar{a})^{*}]$. Hence, $\bar{e}\notin Q_{2}$, contrary to the assumption that $\bar{e}\in Q_{2}$. Therefore, $\bar{a}$ must be in $Q_1$, which implies $\bar{e}\in (Q_1)^*$.    $\square$

Let P be an intensional relation symbol in $\mathrm {\Pi }$, and $\textbf{T}$ a structure in $\mathcal {T}$. We use $P_{(n)}\,(n>0)$ to denote the relation obtained in the n-th evaluation of $\mathrm {\Pi }$ on $\textbf{T}$ for P, and $P^{\textbf{T}[\mathrm {\Pi }]}$ to denote the relation obtained by applying $\mathrm {\Pi }$ on $\textbf{T}$ for P, i.e., the fixpoint of the sequence $P_{(0)},P_{(1)},P_{(2)},\dots$

Proposition 6

For any intensional relation symbol P in $\mathrm {\Pi }$ and any $\textbf{T}\in \mathcal {T}$, $P^{\textbf{T}[\mathrm {\Pi }]}$ is an invariant relation on $\textbf{T}$ and $(P^{\textbf{T}[\mathrm {\Pi }]})^{*}=(P^{*})^{S_{\textbf{T}}[\mathrm {\Pi }^{*}]}$. Moreover, if P is a 0-ary intensional relation symbol, then $\textbf{T}\models (\mathrm {\Pi },P)$ iff $S_{\textbf{T}}\models (\mathrm {\Pi }^{*},P^{*})$.

Proof

We first show that if P is an intensional relation symbol in $\mathrm {\Pi }$ and $\textbf{T}$ is a structure in $\mathcal {T}$, then $P^{\textbf{T}[\mathrm {\Pi }]}$ is an invariant relation on $\textbf{T}$. Let $P^{1},\dots ,P^{m'}$ be all intensional relation symbols in $\mathrm {\Pi }$. Consider the following formula constructed for each $P^{i}$

$$ \begin{array}{r} \phi _{P^{i}}(\bar{x}_{P^{i}})=\bigvee \{\exists \bar{v}(\alpha _{1}\wedge \cdots \wedge \alpha _{l})\mid P^{i}\bar{x}_{P^{i}}\leftarrow \alpha _{1},\dots ,\alpha _{l}\in \mathrm {\Pi } \text { and }\bar{v}\text { are the}\\ \text {free variables in }\alpha _{1}\wedge \cdots \wedge \alpha _{l} \text { that are different from }\bar{x}_{P^{i}}\}. \end{array} $$

If the relation defined by each $\alpha _{s}$ is an invariant relation, then by Lemmas 1, 2 and 3, we know that the relation defined by $\phi _{P^{i}}$ is also an invariant relation. Each $\alpha _{s}$ is either an atomic (or negated atomic) formula with the relation symbol from $\{=,E,R_{1},\dots ,R_{k}\}$ where the relations defined by them are all invariant relations, or an atomic formula $P^{j}\bar{x}$, or a formula $\forall \bar{y}P^{j}\bar{y}\bar{z}\, (1\le j\le m')$.

When computing the fixpoint of $P^{1},\dots ,P^{m'}$, we set $P_{(0)}^{i}=\emptyset \,(1\le i\le m')$, where $\emptyset$ is an invariant relation. By Lemma 3 we know that if $P^{j}$ is an invariant relation then the relation defined by $\forall \bar{y}P^{j}\bar{y}\bar{z}$ is also an invariant relation. We proceed by induction on n. Suppose that $P_{(n)}^{1},\dots ,P_{(n)}^{m'}$ are invariant relations, then each

$$\begin{aligned} P_{(n+1)}^{i} & =\{\bar{a}\mid (\textbf{T},P_{(n)}^{1},\dots ,P_{(n)}^{m'})\models \phi _{P^{i}}(\bar{x}_{P^{i}})[\bar{a}]\}, \text {or}\\ P_{(n+1)}^{i} & =\{\emptyset \mid (\textbf{T},P_{(n)}^{1},\dots ,P_{(n)}^{m'})\models \phi _{P^{i}}\} \end{aligned}$$

is also an invariant relation. Therefore, the fixpoints $P_{(\infty )}^{1},\dots ,P_{(\infty )}^{m'}$ are invariant relations, i.e., $P^{\textbf{T}[\mathrm {\Pi }]}$ is an invariant relation on $\textbf{T}$.

Next we shall show that $(P^{\textbf{T}[\mathrm {\Pi }]})^{*}=(P^{*})^{S_{\textbf{T}}[\mathrm {\Pi }^{*}]}$. It suffices to prove that $(P_{(n)}^{i})^{*}=(P^{i})_{(n)}^{*}\,(1\le i\le m')$ for each $n\ge 0$. The proof is by induction on n.

Basis: If $n=0$, then $P_{(0)}^{i}=\emptyset$, $(P^{i})_{(0)}^{*}=\emptyset \,(1\le i\le m')$. We have $(P_{(0)}^{i})^{*}=(P^{i})_{(0)}^{*}\,(1\le i\le m')$.

Inductive Step: Assuming $(P_{(k)}^{i})^{*}=(P^{i})_{(k)}^{*}$ $(1\le i\le m')$, we show that $(P_{(k+1)}^{i})^{*}=(P^{i})_{(k+1)}^{*}$ $(1\le i\le m')$. The case where $P^i$ is 0-ary is trivial, in the following we only consider the relation $P^i$ of no 0-ary.

To prove $(P_{(k+1)}^{i})^{*}\subseteq (P^{i})_{(k+1)}^{*}$, suppose $\bar{e}\in (P_{(k+1)}^{i})^{*}$ for some $\bar{e}\in S_{\textbf{T}}$. There must be a tuple $\bar{a}$ of $\textbf{T}$ such that $\bar{a}\in P_{(k+1)}^{i}$ and $\bar{e}=(\bar{a})^{*}$. By the semantics of Datalog$^r$ we know that

$$ P_{(k+1)}^{i}=\{\bar{a}\mid (\textbf{T},P_{(k)}^{1},\dots ,P_{(k)}^{m'})\models \phi _{P^{i}}(\bar{x}_{P^{i}})[\bar{a}]\}. $$

By the definition of $\phi _{P^i}$, there is a rule $P^{i}\bar{x}_{P^{i}}\leftarrow \alpha _{1},\dots ,\alpha _{l}$ in $\mathrm {\Pi }$ such that

$$ \langle \textbf{T},P_{(k)}^{1},\dots ,P_{(k)}^{m'} \rangle \models \exists \bar{v}(\alpha _{1}\wedge \cdots \wedge \alpha _{l})[\bar{a}]. $$

Thus, there exists some $\bar{b}$ such that

$$ \langle \textbf{T},P_{(k)}^{1},\dots ,P_{(k)}^{m'} \rangle \models (\alpha _{1}\wedge \cdots \wedge \alpha _{l})[\bar{a}\bar{b}]. $$

Because $P^{i}\bar{x}_{P^{i}}\leftarrow \alpha _{1},\dots ,\alpha _{l}$ is a rule of $\mathrm {\Pi }$, we can infer that

$$ (P^{i})^{*}(\bar{x}_{P^{i}})^{*}\leftarrow \alpha _{1}',\dots ,\alpha _{l}',\textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*} $$

is a rule of $\mathrm {\Pi }^{*}$, where $\alpha _{1}',\dots ,\alpha _{l}'$ and $\textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*}$ are obtained by replacing $\alpha _{1},\dots ,\alpha _{l},\textrm{FUL}_{m}$ with the corresponding formulas respectively in the construction of $\mathrm {\Pi }^*$. Note that we replace $\forall \bar{y}P\bar{y}\bar{z}$ by $\varPsi _{P}$, and by Lemma 4 the relation defined by $\varPsi _{P}$ is the characteristic relation of that defined by $\forall \bar{y}P\bar{y}\bar{z}$. By the definition of $S_{\textbf{T}}$ and the induction hypothesis $(P_{(k)}^{i})^{*}=(P^{i})_{(k)}^{*}\,(1\le i\le m')$ we deduce that

$$\begin{aligned} \langle S_{\textbf{T}},(P^{1})_{(k)}^{*},\dots ,(P^{m'})_{(k)}^{*}\rangle & \models (\alpha _{1}'\wedge \cdots \wedge \alpha _{l}'\wedge \textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*})[(\bar{a}\bar{b})^{*}],\text {i.e.,}\\ \langle S_{\textbf{T}},(P^{1})_{(k)}^{*},\dots ,(P^{m'})_{(k)}^{*}\rangle & \models \exists \bar{u}(\alpha _{1}'\wedge \cdots \wedge \alpha _{l}'\wedge \textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*})[(\bar{a})^{*}] \end{aligned}$$

where $\bar{u}$ are the free variables in $\alpha _{1}'\wedge \cdots \wedge \alpha _{l}'\wedge \textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*}$ that are different from $(\bar{x}_{P^{i}})^{*}$. Combining $\bar{e}=(\bar{a})^{*}$ we obtain $\bar{e}\in (P^{i})_{(k+1)}^{*}$.

To prove $(P^{i})_{(k+1)}^{*}\subseteq (P_{(k+1)}^{i})^{*}$, suppose $\bar{e}\in (P^{i})_{(k+1)}^{*}$ for some $\bar{e}\in S_{\textbf{T}}$. There must exist a rule

$$\begin{aligned} (P^{i})^{*}(\bar{x}_{P^{i}})^{*}\leftarrow \alpha _{1}',\dots ,\alpha _{l}',\textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*} \end{aligned}$$

(3)

in $\mathrm {\Pi }^{*}$ such that

$$ \langle S_{\textbf{T}},(P^{1})_{(k)}^{*},\dots ,(P^{m'})_{(k)}^{*} \rangle \models \exists \bar{u}(\alpha _{1}'\wedge \cdots \wedge \alpha _{l}'\wedge \textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*})[\bar{e}]. $$

Hence there exists a tuple $\bar{f}\in S_{\textbf{T}}$ such that

$$ (S_{\textbf{T}},(P^{1})_{(k)}^{*},\dots ,(P^{m'})_{(k)}^{*})\models (\alpha _{1}'\wedge \cdots \wedge \alpha _{l}'\wedge \textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*})[\bar{e}\bar{f}]. $$

The formula $\textrm{FUL}_{m}^{*}(\bar{x}_{P^{i}}\bar{v}\tilde{v}')^{*}$ guarantees that $(\bar{a}\bar{b})^{*}=\bar{e}\bar{f}$ and $(\bar{a})^{*}=\bar{e}$ for some tuple $\bar{a}\bar{b}$ of $\textbf{T}$. Because $P_{(k)}^{1},\dots ,P_{(k)}^{m'}$ are invariant relations, by the induction hypothesis $(P_{(k)}^{i})^{*}=(P^{i})_{(k)}^{*}$ $(1\le i\le m')$ we know that

$$ \langle \textbf{T},P_{(k)}^{1},\dots ,P_{(k)}^{m'} \rangle \models (\alpha _{1}\wedge \cdots \wedge \alpha _{l})[\bar{a}\bar{b}] $$

where $\alpha _{1},\dots ,\alpha _{l}$ occur in the rule $P^{i}\bar{x}_{P^{i}}\leftarrow \alpha _{1},\dots ,\alpha _{l}$ that is the original of (3) in $\mathrm {\Pi }$. Hence $\bar{a}\in P_{(k+1)}^{i}$, which implies $\bar{e}\in (P_{(k+1)}^{i})^{*}$. This completes the proof.    $\square$

3.4 Nondefinability Results for Datalog$^r$

The complexity class EXPTIME contains the decision problems decidable by a deterministic Turing machine in $O(2^{n^{c}})$ time. By the time hierarchy theorem, we know that PTIME is a proper subset of EXPTIME. In this section, for every class of structures $\mathcal {K}\in$ EXPTIME, we construct a class $\mathcal {K}'$ of structures that is in PTIME and closed under substructures, and show that if $\mathcal {K}'$ is definable by a Datalog$^r$ formula, then $\mathcal {K}$ is in P, which is impossible.

Let c be a constant, and $\textbf{A}=\langle \{0,\dots , h-1\},$ $R^A_1,\dots , R^A_k\rangle$ a $\tau$-structure. The trivial extension $\textbf{A}^+=\langle \{0,\dots ,h-1,h,\dots , h+h^c-1\}, R^A_1,\dots , R^A_k\rangle$ of $\textbf{A}$ is a $\tau$-structure obtained by adding $h^c$ dummy elements to the domain of $\textbf{A}$ and keeping all other relations unchanged.

For technical reasons we introduce a new unary relation symbol U and let $\tau _U=\tau \cup \{U\}$, $\tau '_U=\tau \cup \{\textbf{root}, E, U\}$. From now on when we speak of a $\tau '_U$-structure

$$\begin{aligned} \textbf{G}=\langle V, \textbf{root}, E, U, R_1,\cdots , R_k\rangle \end{aligned}$$

we assume that

• (1) $\langle V,E,\textbf{root} \rangle$ is a directed acyclic graph and the nodes reachable from $\textbf{root}$ form a binary tree, and

• (2) all relations $U, R_1,\cdots , R_k$ are saturated relations restricted on $T(\textbf{G})$, which is the largest perfect binary subtree of $\textbf{G}$ with $\textbf{root}$ as the root.

It is easy to check that if a $\tau '_U$-structure $\textbf{G}$ satisfies the aforementioned two conditions, then all its substructures also satisfy the two conditions.

Definition 7

Let $\mathcal {K}$ be a class of $\tau$-structures. Define a class $\mathcal {K}'$ of $\tau '_U$-structures such that, for any $\textbf{G}=\langle V,\textbf{root},E,U,R_{1},\dots ,R_{k}\rangle$, let h be the largest number where all nodes in the first h levels of $T(\textbf{G})$ are marked by U, $\textbf{G}\in \mathcal {K}'$ iff the following Condition (1) or Condition (2) holds.

• Condition (1)   

  • (a) The depth of $T(\textbf{G})$ is $h+h^c$.

  • (b) The relations $R_{1},\dots ,R_{k}$ do not hold on any tuple that contains a node in the last $h^c$ consecutive levels of $T(\textbf{G})$.

  • (c) $C^{-1}(T(\textbf{G}))$ is the trivial extension of $C^{-1}(T_h(\textbf{G}))$, where $T_h(\textbf{G})$ is the subtree of $T(\textbf{G})$ by restricting to the first h levels.

  • (d) $C^{-1}(T_h(\textbf{G}))\in \mathcal {K}$ when ignoring the relation U.

• Condition (2)   

  • (a) The depth of $T(\textbf{G})$ is strictly less than $h+h^c$.

Proposition 7

Let $\mathcal {K}$ be an arbitrary class of $\tau$-structures decidable in $2^{n^c}$ time, where n is the cardinality of the structure’s domain, and $\mathcal {K}'$ defined as above. Then

• (i) $\mathcal {K}'$ is closed under substructures;

• (ii) $\mathcal {K}'$ is decidable in $\textrm{PTIME}$.

Proof

To prove (i), suppose that $\textbf{G}$ is a $\tau '_U$-structure in $\mathcal {K}'$, then it satisfies either Condition (1) or Condition (2) in Definition 7. Let $\textbf{H}$ be an arbitrary substructure of $\textbf{G}$. If $\textbf{G}$ satisfies Condition (2), then $\textbf{H}$ also satisfies Condition (2), and is in $\mathcal {K}'$. Suppose that $\textbf{G}$ satisfies Condition (1), then the perfect binary tree $T(\textbf{H})$ either equals $T(\textbf{G})$, which implies $\textbf{H}$ satisfies Condition (1), or the depth of $T(\textbf{H})$ is less than that of $T(\textbf{G})$, which implies $\textbf{H}$ satisfies Condition (2). Altogether, $\textbf{H}\in \mathcal {K}'$.

To prove (ii), let $\textbf{G}$ be an arbitrary $\tau '_U$-structure, we just need to do the following steps to check whether $\textbf{G}\in \mathcal {K}'$:

• (1) Check that $\langle V, E\rangle$ is a directed acyclic graph.

• (2) Check that all nodes reachable from $\textbf{root}$ form a binary tree.

• (3) Compute $T(\textbf{G})$, the largest perfect binary subtree with $\textbf{root}$ as root.

• (4) Check that $U,R_1,\dots ,R_k$ are saturated relations on $T(\textbf{G})$.

• (5) Compute the largest number h such that all nodes in the first h levels of $T(\textbf{G})$ have property U.

• (6) Check whether the depth of $T(\textbf{G})$ is less than $h+h^c$.

• (7) If the depth of $T(\textbf{G})$ is $h+h^c$, then check whether (b), (c) and (d) in Condition (1) of Definition 7 hold.

Note that $C^{-1}(T_h(\textbf{G}))$ has h elements and $\mathcal {K}$ is decidable in $2^{n^c}$ time, the statement (d) in Condition (1) of Definition 7 can be verified in polynomial time since if the depth of $T(\textbf{G})$ is $h+h^c$ then the input size is at least $2^{h+h^c}$.    $\square$

Let $\mathcal {K}$ and $\mathcal {K}'$ be defined as in Proposition 7. For an arbitrary $\tau$-structure $\textbf{A}$, let $\textbf{A}_U$ be the $\tau _U$-structure obtained by marking every element in $\textbf{A}$ by U, $\textbf{A}^+_U$ the trivial extension of $\textbf{A}_U$ by adding $|A|^c$ elements, and $\textbf{T}$ the $\tau '_U$-structure such that $C^{-1}(\textbf{T})=\textbf{A}^+_U$. If $\mathcal {K}'$ is axiomatizable by a Datalog$^r$ formula $(\mathrm {\Pi },Q)$, then

$$\begin{aligned} \textbf{A}\in \mathcal {K}\quad \text{ iff }\quad \textbf{T}\in \mathcal {K}'\quad \text{ iff }\quad \textbf{T}\models (\mathrm {\Pi },Q). \end{aligned}$$

(4)

Define the vocabulary

$$ \sigma _U=\{\textbf{0},\textrm{SUCC},R_{\ne },R_{\lnot e},\textrm{FUL}_{m}^{*},U^{*},R_{1}^{*},\dots ,R_{k}^{*},(\lnot U)^{*},(\lnot R_{1})^{*},\dots ,(\lnot R_{k})^{*}\}. $$

By Definition 6, we can compute $\textbf{T}$’s characteristic structure that is a $\sigma _U$-structure

$$ \begin{array}{lr} S_{\textbf{T}}= &{} \bigl \langle \{0,1,\dots ,|A|+|A|^c-1\},\textbf{0},\textrm{SUCC},R_{\ne },R_{\lnot e},\textrm{FUL}_{m}^{*},U^{*},\\ &{} R_{1}^{*},\dots ,R_{k}^{*},(\lnot U)^{*},(\lnot R_{1})^{*},\dots ,(\lnot R_{k})^{*}\bigr \rangle \end{array} $$

where $\textbf{0}$ is interpreted by 0, $\textrm{SUCC}$ is the successor relation on the domain and $R_{\ne },R_{\lnot e}$, $\textrm{FUL}_{m}^{*},U^{*}$, $R_{1}^{*},\dots ,R_{k}^{*},(\lnot U)^{*},(\lnot R_{1})^{*}, \dots , (\lnot R_{k})^{*}$ are the characteristic relations of $\ne ,(\lnot E)$, $\textrm{FUL}_{m},U$, $R_{1}, \dots$, $R_{k}$, $\lnot U,\lnot R_{1},\dots ,\lnot R_{k}$, respectively. By Proposition 6, we know there is a Datalog$^r$ formula $(\mathrm {\Pi }^*, Q^*)$ such that $\textbf{T}\models (\mathrm {\Pi },Q)$ iff $S_{\textbf{T}}\models (\mathrm {\Pi }^*, Q^*)$. Combining (4), we have $\textbf{A}\in \mathcal {K}$ iff $S_{\textbf{T}}\models (\mathrm {\Pi }^*,Q^*)$.

Lemma 5

$S_{\textbf{T}}$ is logspace computable from $\textbf{A}$.

By Lemma 5, we know that $S_{\textbf{T}}$ is computable from $\textbf{A}$ in polynomial time. Hence, $\mathcal {K}$ is in PTIME. Since $\mathcal {K}$ is an arbitrary class in EXPTIME, this would imply EXPTIME=PTIME, which contradicts the time hierarchy theorem. So we must have:

Proposition 8

There is a problem in $\textrm{PTIME}$ and closed under substructures but not definable in $\textrm{Datalog}^r$.

If a problem is closed under substructures, then its complement is closed under extensions. By Proposition 2, we can obtain the following corollary.

Corollary 1

$\textrm{DATALOG}^r\mathrm {[E]} = \mathrm {LFP[E]} \subsetneq \mathrm {PTIME[E]}$.

4 Conclusion

Revised Datalog is an extension of Datalog by allowing universal quantification over intensional relations in the body of rules. On all finite structures, Datalog$^r$ is strictly more expressive than Datalog, and has the same expressive power as that of LFP. In classical model theory, the closure properties of a formula are usually related to some syntactic properties. Many preservation theorems have been proven to reflect this relationship. When restricted to finite structures, most of these preservation theorems fail. Due to the syntax and semantics of Datalog, we can treat it as the dual of SO-HORN logic, which is closed under substructures [12]. It follows that Datalog is closed under extensions. A lot of work has been conducted between Datalog and FO (or LFP) to study the closure property. In this paper, we study the expressive power of revised Datalog on the problems that are closed under substructures. We show that Datalog$^r$ cannot define all the problems that are in PTIME and closed under substructures. As a corollary, LFP cannot define all the extension-closed problems that are in PTIME. A method of tree encodings for arbitrary structures is used in the proof. If we replace the extension closure property by the homomorphism closure property, it is still open whether the statement also holds. This is desirable for future work.