Controller Synthesis for Reactive Systems with Communication Delay by Formula Translation

Abstract

The problem of automated reactive synthesis has been well studied by researchers. We consider a setting that is common in practice, wherein there is a communication delay between the (synthesized) controller and the (controlled) plant, such that symbols emitted by either component reach the other component after a delay. We address the problem of synthesizing a controller that can assure the given temporal property at the remote plant despite delay. We consider two variants of this setting, one where the delay is a constant over the entire trace, and the other where the delay could increase over time (upto an upper bound), and propose approaches for both these settings. We state and prove soundness and completeness results for both our approaches. We have implemented our approaches, and evaluated them on the standard SYNTCOMP 2022 suite of temporal properties. The results provide evidence for the robustness and practicality of our approaches.

1 Introduction

Reactive synthesis is the problem of automatically inferring a correct-by- construction controller, that can control an environment or plant to ensure that all runs of the plant satisfy a given temporal property. This is a classical problem, that has been extensively studied over several decades. We cite a selection of papers [5, 6, 10, 13], and refer the interested reader to a recent book chapter [1] for a comprehensive view.

The classical controller synthesis setting assumes instant (delay-free) communication of input and output symbols between the controller and the controlled plant. However, delay in the flow of information between controller and plant is common in real life settings, due to issues like distance between the plant and controller, or network congestion. For instance, this is recognized in the Controller Area Network (CAN) protocol for vehicular control [4, 19], and in protocols for the remote control of satellites [2, 11]. Researchers often devise carefully handcrafted solutions to account for delay in individual protocols [15, 18], but this can be complicated and error prone.

The formal methods research community has been aware of this issue, and has proposed a few techniques that can synthesize controllers while accounting for communication delay [3, 5, 16]. Our work has the same broad objective, and we address the scenario where we are given a Linear Temporal Logic (LTL) property as specification. We make the following contributions in this paper:

• Previous researchers have focused on the setting where the delay between the two sides is fixed and constant throughout the infinite trace (e.g., 2 time units of delay). For the first time in the literature to the best of our knowledge, we identify the issue of variable delay that can arise in real systems, formulate this problem mathematically, and propose an approach to solve it.

• We propose a novel approach that reduces controller synthesis from LTL specifications in the presence of delay to the problem of LTL synthesis without delay. We devise techniques (for fixed delay and variable delay) that emit a delay-adjusted, translated LTL formula. This formula can be fed to any classical (no-delay) LTL synthesis tool. This makes our approach efficient, flexible, and capable of leveraging future advances in classical synthesis. Previous approaches [3, 5], in contrast, involved extensions to specific synthesis approaches. (Additionally, they did not address variable delay.)

• We implement our approach, and evaluate it on a standard set of 1075 benchmarks. Our results show that our approach is more efficient than a baseline approach [3] that targets fixed delay, and gives acceptable performance in the more-complex variable delay setting.

The rest of this paper is organized as follows. Section 2 provides background that is required in the rest of the paper. Section 3 presents our fixed-delay approach, while Sect. 4 presents our variable-delay approach. Section 5 presents an add-on feature to our approach – an unrealizability filter. Section 6 presents our implementation and evaluation, Sect. 7 discusses related work, while Sect. 8 concludes the paper and suggests future work directions.

2 Background

In this section we provide brief background on classical notions of plant, controller, and controller synthesis, in the absence of delay.

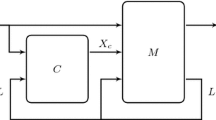
We are concerned with synchronous, reactive systems. Such a system consists of two players, the first player being the controller, while the second player being the plant (or environment). A trace of the system is an infinite sequence of steps. The plant observes a subset of signals from a given output set O in each step, and emits a subset of signals from a given input set I in each step. Each subset of I is called an input symbol while each subset of O is called an output symbol.

Definition 1 (Controller)

A controller is a transducer $C=(Q, 2^{I}$, $2^{O}, \delta , \omega , q_0)$ where Q is the finite set of controller states, $q_0$ is the initial controller state, $2^{I}$ is the input alphabet of the transducer, $2^{O}$ is the output alphabet of the transducer, $\delta : Q \times 2^{I} \rightarrow Q$ is the state transition function, and $\omega : Q \times 2^{I} \rightarrow 2^{O}$ is the output function.

Definition 2 (Trace generated by a controller)

A trace generated by a controller $(Q, 2^{I}$, $2^{O}, \delta , \omega , q_0)$ is a function $t: \mathbb {N}\rightarrow 2^{I \cup O}$, such that:

$t[0] \cap O = \omega (q_0, t[0] \cap I)$,

$\forall i > 0. \ t[i]\cap O = \omega (\delta ^i(q_0, t), t[i] \cap I)$,

where $\delta ^i(q_0, t) = q_0$, if $i = 0$, and $\delta ^i(q_0, t) = \delta (\delta ^{i-1}(q_0, t), t[i-1])$, if $i > 0$

Note, we use t[i] to denote the symbols mapped to $i \in \mathbb {N}$ by the trace t, which is intuitively the content of the trace t at step i. Intuitively, the controller, while in a state $q \in Q$ in step i of the current trace t, receives the input symbol $t[i] \cap I$ emitted by the plant in step i, and responds by emitting the output symbol $t[i] \cap O \equiv \omega (q, t[i] \cap I)$ and by transitioning to the state $\delta (q, t[i] \cap I)$ in the same step.

A linear temporal logic [12] (LTL) formula on symbol set $I \cup O$ is syntactically defined using the following grammar:

$\varPsi = x \mid \lnot \varPsi \mid \varPsi \wedge \varPsi \mid \varPsi \vee \varPsi \mid X \varPsi \mid F \varPsi \mid G \varPsi \mid \varPsi U \varPsi$, where $x \in I \cup O$.

Definition 3 (Trace satisfying LTL specification)

If t is a trace, then for any $i \ge 0$, the suffix of t starting at step i, denoted as t(i), is said to satisfy an LTL formula as defined below.

$$\begin{aligned} t(i) \models {\left\{ \begin{array}{ll} x &{}\text {if}\; x \in t[i] , x \in (I \cup O )\\ \lnot \varPsi &{}\text {if}\; t(i) \not \models \varPsi \\ \psi \wedge \varphi &{}\text {if}\; t(i) \models \psi \; \text {and}\; t(i) \models \varphi \\ \psi \vee \varphi &{}\text {if}\; t(i) \models \psi \; \text {or}\; t(i) \models \varphi \\ X \varPsi &{}\text {if}\; t(i+1) \models \varPsi \\ F \varPsi &{}\text {if} \; \exists k \ge i. \, t(k) \models \varPsi \\ G \varPsi &{}\text {if}\; \forall k \ge i. \, t(k) \models \varPsi \\ \psi U \varphi &{}\text {if}\; \exists k \ge i. \, t(k) \models \varphi { and} \forall n \in [i\ldots k). \, t(n) \models \psi \\ \end{array}\right. } \end{aligned}$$

The trace t is said to satisfy a LTL formula $\varPsi$ if $t(0) \models \varPsi$.

Definition 4 (Controller meeting a temporal specification)

A controller is said to meet a given temporal specification $\varPsi$ ($\varPsi$ being an LTL formula) if and only if every trace generated by the controller satisfies $\varPsi$.

Definition 5 (Realizable specification)

A specification $\varPsi$ is said to be realizable (under no delay) if and only if there exist a controller that meets the specification.

Fig. 1.

(a) Controller $C_1$, meeting specification $G((r \Rightarrow X(g \vee X(g))) \wedge (\lnot r \Rightarrow \lnot X( g \wedge (X (g )))))$, (b) A trace generated by the controller

Figure 1(a) depicts a controller that meets the specification given in the caption of the figure. The part before the ‘/’ on each transition denotes an input symbol, the part after the ‘/’ denotes the corresponding output symbol according to the $\omega$ function, while the target state of the transition denotes the result of the $\delta$ function. A “-” indicates that any symbol is ok. In this example, the set $I = \{r\}$ while the set $O = \{g\}$. In fact, in illustrations throughout this paper, we will assume this same input set I and output set O. We use the notation ‘$\lnot x$’ in a set to indicate that the signal x is not an element of the set.

Note that if a given plant provides certain guarantees on its behavior, e.g., that it will not emit signal r in two consecutive steps, such guarantees can be encoded in LTL and treated as an assumption. The given specification can be amended to the form assumption $\Rightarrow$ specification, and a controller that meets this amended specification can be constructed.

Automatically synthesizing a controller that meets a given LTL-formula specification is a theoretically and practically important problem. It is important because it enables correctness by construction. It is a well-studied problem, and many interesting approaches have been proposed in the literature [1]. Numerous practical tools have been developed for this problem [7], and in fact our approach, which we present in the subsequent sections, is designed to be able to use any of these approaches as a blackbox.

3 Fixed Delay

The setting we address is that of delay between the plant and controller. That is, the output symbol emitted by either player at a step will potentially reach the other player at a later step. This effectively means the reactive system evolves as a pair of traces $t_c, t_p$, where $t_c$ is the trace observed by the controller and $t_p$ is the trace observed by the plant, rather than as a single trace t that is commonly visible to both players. This notion of a trace pair has not been proposed in closely related previous works. In this section and the next, we consider the setting where delay is fixed in both directions; i.e., there exist a pair of constants $(d_ cp , d_ pc )$, both being non-negative integers, such that each output symbol (resp. input symbol) from the controller (resp. plant) reaches the plant (resp. controller) after $d_ cp$ (resp. $d_ pc$) steps. This delay setting has been considered by previous researchers [3, 5] as well. It can be easily seen that in this setting, it is enough to consider delay in one direction (any one direction). That is, a controller that meets an LTL-formula specification in the presence of delays $(d_ cp , d_ pc )$ will also meet the same specification in the presence of delays (d, 0) or (0, d), where $d = d_ pc + d_ cp$. Hence, in the remainder of our presentation, we assume that the delays in the two directions are (0, d), where d is a given constant.

3.1 Definitions

Definition 6 (Trace pair under delay)

A trace pair $(t_c, t_p)$ under delay d is a pair of traces $t_c$ and $t_p$ such that: (1) The first d steps of $t_c$ have the special $\epsilon _i$ in place of an input symbol, indicating that no input symbol has arrived so far from the plant. Every other step in both traces has an input symbol and an output symbol, similar to the no-delay setting, (2) For any step i, $t_c[i] \cap O = t_p[i] \cap O$, meaning the symbol emitted by the controller reaches the plant without any delay, and (3) For any step i, $t_c[i+d] \cap I = t_p[i] \cap I$, meaning input symbols reach the controller after d steps of delay.

Definition 7 (Trace pair satisfying a specification)

A trace pair $(t_c, t_p)$ under delay d is said to satisfy a specification if $t_p$ satisfies the specification.

Definition 8 (Controller feasible under delay)

A controller (see Definition 1) is said to be feasible under delay d if there is a path of d consecutive transitions going out from the initial state $q_0$ such that all transitions in this path are labeled “-” for the input symbol. (Such edges can be traversed upon receiving any input symbol or even upon $\epsilon _i$.)

Definition 9 (Trace pair generated by a controller)

A trace pair $(t_c, t_p)$ under delay d is said to be generated by a controller C if $t_c$ is generated by C (see Definition 2).

Definition 10 (Controller meeting a specification under delay)

A controller is said to meet a given specification $\varPsi$ under delay d if and only if each trace pair $(t_c, t_p)$ under delay d that is generated by the controller is such that $t_p$ satisfies $\varPsi$.

Definition 11 (Realizable specification under delay)

A specification $\varPsi$ is said to be realizable under delay d if and only if there exists a controller that meets the specification under delay d.

Fig. 2.

Controller feasible under delay = 2

Fig. 3.

A sample trace pair $(t_c, t_p)$ under delay = 2. $(t_c,t_p)$ satisfies the specification $G((r \Rightarrow X(g \vee X(g))) \wedge (\lnot r \Rightarrow \lnot X( g \wedge (X (g )))))$.

Figure 2 depicts a controller that is feasible under delay $d=2$. This controller can be seen to meet the specification given in the caption of Fig. 1 under delay $d=2$. The trace pair depicted in Fig. 3 is under delay = 2, and can be seen to be generated by the controller in Fig. 2. This trace pair satisfies the specification. The dashed arrows in Fig. 3 indicate of the flow of symbols in both directions.

3.2 Results on Control Under Delay

An specification that is realizable without delay may not be realizable in the presence of delay. For instance, consider the specification $G (r \Leftrightarrow g)$, where r is an input signal and g is an output signal. A controller that emits g (resp. $\emptyset \in O$) in the same step when it sees r (resp. $\emptyset \in I$) meets the specification when there is no delay. However, this specification is not realizable in the presence of any delay $d > 0$, as whatever the controller emits in the first step (without knowledge of the input), the plant could potentially emit a symbol in the first step to violate the specification. Similarly, a specification that is realizable under a certain delay may not remain realizable under higher values of delay.

Say a specification is realizable under delay $d_1$ and under delay $d_2$, $d_1 < d_2$. A controller that meets the specification under delay $d_1$ may not necessarily meet the same specification under delay $d_2$. For instance, the controller in Fig. 1 can meet the specification in the caption of that figure under no delay, but not under delay = 2 because in the first two steps $t_c$ will neither satisfy r nor $\lnot r$. As mentioned earlier, the controller in Fig. 2 meets this specification under delay = 2.

A controller that meets a specification under delay $d_2$ can be easily shown to meet the same specification under any $d_1$ such that $d_1 < d_2$ (and hence no delay also). The input symbols emitted by the plant can be held in a buffer and delayed by an extra $d_2 - d_1$ steps, and then any trace pair generated by the controller will satisfy the specification. In other words, the set of realizable specifications under (fixed) delay is a strict subset of realizable specifications under no delay.

3.3 Controller Synthesis

It is natural for a user to specify a temporal formula $\varPsi$ that they require all plant-side traces to satisfy. This is the because the plant is the main component of interest to the user, and normally one requires all plant-side traces to satisfy a specification that one requires irrespective of whether there is delay or not, or what the amount of delay is. We hence address the problem of automatically synthesizing a controller C that meets a given specification $\varPsi$ under a given amount of delay d.

By the definitions given in Sect. 3.1, if the above-mentioned controller C generates any trace pair $(t_c, t_p)$, then $t_p$ will satisfy $\varPsi$ (as desired by the user). However, $t_c$ may not satisfy $\varPsi$. Our approach is to construct a transformed LTL formula $tr _f(\varPsi )$, such that any such $t_c$ satisfies $tr _f(\varPsi )$. $tr _f(\varPsi )$ is obtained by replacing every leaf x in the formula $\varPsi$, where x is an element of the input set I, with $X^d (x)$, where $X^d$ means d (nested) occurrences of the LTL “next” operator X, and d is the given total delay. We then supply $tr _f(\varPsi )$ to any existing (no-delay) controller synthesis approach, treating the approach as a blackbox, and return the controller synthesized by the approach as the desired controller C that meets $\varPsi$ under delay d.

To illustrate our approach, consider our running example specification . The transformed LTL formula $tr _f(\varPsi )$, with $d=2$, is . The to-be transformed leaves and the transformed portions have been highlighted for clarity. The controller shown in Fig. 2 was obtained using the synthesis tool Strix [10] by providing $tr _f(\varPsi )$ as input. We already discussed in Sect. 3.1 that this controller meets the specification $\varPsi$ under delay = 2.

As another example, consider the specification $\varPsi = G(r \Leftrightarrow g)$. The transformed specification in this case with $d=2$ is $G(X(X(r)) \Leftrightarrow g)$. This formula is unrealizable in reality (and as per Strix), and indeed this specification $\varPsi$ is unrealizable under delay = 2 as we had discussed in Sect. 3.2.

3.4 Soundness and Completeness

Lemma 1

For any trace pair $(t_c, t_p)$ under delay d, for any LTL formula $\varPsi$, $t_p$ satisfies $\varPsi$ iff $t_c$ satisfies $tr _f(\varPsi )$.

Intuitively, the above property holds because $t_c$ is identical to $t_p$ except that the input symbol in each step of $t_p$ has been shifted to the right by d steps in $t_c$, and that is the exact difference between $\varPsi$ and $tr _f(\varPsi )$ as well. We give a proof for the above lemma in an appendix (the proof is by structural induction on $\varPsi$). The appendix is available in a long-term repository https://doi.org/10.6084/m9.figshare.c.6608452 associated with this paper.

Theorem 1 (Soundness)

Any controller C synthesized by our approach meets the given specification $\varPsi$ under the given delay d.

Proof: By construction of C, all traces generated by C satisfy $tr _f(\varPsi )$. This means, for any trace pair $(t_c, t_p)$ generated by C, $t_c$ satisfies $tr _f(\varPsi )$. Therefore, by Lemma 1, for any trace pair $(t_c, t_p)$ generated by C, $t_p$ satisfies $\varPsi$. $\Box$

Theorem 2 (Completeness)

Our approach returns a controller whenever the given specification $\varPsi$ is realizable under the given delay d.

Proof: If $\varPsi$ is realizable under delay d, it means there exists a controller $C'$ that is feasible under delay d and that meets the given property $\varPsi$ under delay d. That is, every trace pair $(t_c, t_p)$ under delay d that is generated by $C'$ is such that $t_p$ satisfies $\varPsi$. It is easy to see that for any trace $t_c'$ that $C'$ can generate, there exists a (unique) trace $t_p'$ such that $(t_c', t_p')$ is a trace pair under delay d. Therefore, by Lemma 1, it follows that all traces generated by $C'$ satisfy $tr _f(\varPsi )$. This means that the controller synthesis approach that we invoke as a black box with input specification $tr _f(\varPsi )$ will necessarily this declare this specification to be realizable, and will necessarily return a controller C (which may or may not be equal to $C'$). $\Box$

4 Variable Delay

In this section we consider the more challenging setting of variable delay. Here, as the trace (pair) evolves over time, the delay from each side to the other can increase. At each step, the delay can be equal to or greater than the delay in the previous step, subject to given minimum and maximum delays, $d_l$ and $d_u$, applicable in each direction over the entire trace. Variable delay occurs in practice due to variations in environmental conditions (such as network congestion, or interference) that cause delays. To our knowledge ours is the first paper to propose, formulate, and solve the problem of controller synthesis in the presence of variable delay.

4.1 Definitions

Definition 12 (Trace pair under variable delay)

A trace pair under variable delay $(d_l, d_u)$, where $d_l$ and $d_u$ are non-negative integers such that $d_u \ge d_l$, (we drop the word variable in the rest of this section for brevity), is a pair of traces $t_c$ and $t_p$ such that:

• 1. There exist two infinite sequences $d_ cp$ and $d_ pc$ corresponding to this trace pair, each one being a monotonically non-decreasing sequence of integers from the interval $[d_l,d_u]$.

• 2. The output symbol emitted by $t_c$ at its step 0 will reach $t_p$ at its step 0. That is, intuitively, the plant trace starts when it receives the first output symbol from the controller. Subsequently, for each $i > 0$, the output symbol emitted at the controller’s step i will reach the plant at its step $i + d_ cp [i] - d_ cp [0]$. In other words, $t_c[i] \cap O \, = \, t_p[i + d_ cp [i] - d_ cp [0]] \cap O$, for all $i \ge 0$.

• 3. For any index k such that there exists no i such that $i + d_ cp [i] - d_ cp [0]$ is equal k, $t_p[k] \cap O$ will be empty, and $t_p[k]$ will contain the special symbol $\epsilon _o$ to indicate that no output symbol was received in this step (due to increase in delay in the controller to plant direction). We assume that the communication channel between the plant and controller is enhanced in a way that it assures this behavior.

• 4. The input symbol emitted by $t_p$ at its $i^ th$ step, for any $i \ge 0$, reaches the plant in its step $corr (i)$, where $corr (i)$ is equal to $i + d_ cp [0] + d_ pc [i]$. In other words, $t_p[i] \cap I \, = \, t_c[ corr (i)] \cap I$, for all $i \ge 0$. ($d_ cp [0]$ gets added to account for the delayed start of $t_p$ relative to $t_c$, as discussed in the previous point.)

• 5. Analogous to $\epsilon _o$, the controller receives a special symbol $\epsilon _i$ in any step in which it receives no input symbol from the plant due to increase in delay in the plant to controller direction.

Intuitively, $d_ cp [i]$ indicates the delay (in number of steps) from controller to plant for the symbol emitted by the controller in its $i^ th$ step. $d_ pc$ has an analogous meaning, but from the plant to the controller. Note, the transition from a lower delay to a higher delay can happen anywhere in the (infinite) trace, or need not happen at all, and a bounded number of delay transitions can occur in each direction (at most $d_u - d_l$, to be particular).

Fig. 4.

(a) A sample trace pair $(t_c, t_p)$ under variable delay (0, 1). $(t_c, t_p)$ satisfies the specification $G((r \Rightarrow (g \vee X(g \vee X g))) \wedge (\lnot r \Rightarrow \lnot ( g \wedge (X (g \wedge X g )))))$. (b) A controller that meets this specification under variable delay.

Figure 4(a) depicts a sample trace pair under delay (0, 1). Here, $d_ cp [0]$ and $d_ cp [1]$ are zero, while the remaining entries in the $d_ cp$ sequence are one. $d_ pc [0]$ to $d_ pc [3]$ are zero, while $d_ pc [4]$ onward are one. Notice the presence of $\epsilon _o$ and $\epsilon _i$ at the delay transition points. The dashed arrows indicate the flow of symbols visually.

We update the definition of a trace satisfying an LTL formula (see Definition 3), to say that if trace $t_c$ (resp. $t_p$) has $\epsilon _i$ (resp. $\epsilon _o$) in index $t_c[i]$ (resp. $t_p[i]$), then it is interpreted as $t_c[i]$ (resp. $t_p[i])$ not satisfying x (and satisfying $\lnot x$) for any $x \in I$ (resp. $x \in O$).

The analogues of Definition 7 and Definitions 9–11 apply in the variable delay setting as well, simply by substituting each occurrence of the wording “under delay d” with “under delay $(d_l,d_u)$”. Since $\epsilon _i$’s can arrive at any point in the controller-side trace $t_c$ (and not necessarily in the beginning), and since $\epsilon _i$ is interpreted as all input signals being off, any controller (see Definition 1) is also a feasible controller under variable delay.

Figure 4(b) depicts a controller that meets the specification shown in the caption of the figure. Part (a) in the figure depicts one of the trace pairs generated by this controller. Note that in $t_c[4]$, the controller interprets $\epsilon _i$ as $\lnot g$ and hence emits $\lnot g$.

4.2 Results on Control Under Variable Delay

A temporal property $\varPsi$ that is realizable under fixed delay $d \, = \, d_u + d_u$ is not necessarily realizable under variable delay $(d_l, d_u)$. In other words, the set of realizable specifications under variable delay is a strict subset of realizable specifications under fixed delay. As an example, consider the specification G(g), where g is an output element. This specification is met by the controller that emits g continuously, both under no delay and any amount of fixed delay. However, this specification is not realizable under variable delay for any delay bound, because $t_p$ can receive up to $d_u$ $\epsilon _o$’s, and the steps where it receives $\epsilon _o$’s do not satisfy g.

Any controller C that meets any specification $\varPsi$ under variable delay $(d_l,d_u)$ also necessarily meets the same specification under fixed delay $d_u + d_u$. This is because any fixed-delay trace pair under delay $d_u + d_u$ is also a trace pair under variable delay, with all elements of $d_ pc$ and $d_ cp$ being equal to $d_u$.

4.3 Controller Synthesis

As in the fixed delay setting, we propose a LTL formula translation scheme $tr _v$. The approach then is to use any (no-delay) synthesis approach as a blackbox to synthesize a controller that realizes the property $tr _v(\varPsi )$, where $\varPsi$ is the given LTL formula.

A Naive Proposal. A naive proposal would be to model the translation similar to our fixed delay approach, and basically replace every leaf $x \in I$ in $\varPsi$ with the disjunction $X^{2 d_l} {x} \vee X^{{2 d_l}+1} {x} \vee \ldots \vee X^{{2 d_u}} {x}$ (in place of $X^d x$ in the fixed delay setting). The intuitive reason for this proposal is that if $(t_c, t_p)$ are a trace pair under delay $(d_l,d_u)$, and if x and y are the input and output symbols at a plant step $t_p[i]$, and if y was earlier emitted by the controller at step $t_c[k]$, then x would be received by the controller in the range of steps $t_c[k + 2 d_l]$ to $t_c[k + 2 d_u]$ due to the properties of trace pairs under delay. Therefore, since we would like $t_p$ to satisfy $\varPsi$ and $t_c$ to satisfy $tr _v(\varPsi )$, input symbol leaves in $\varPsi$ would need to be moved forward by $2 d_l$ to $2 d_u$ steps, and this is implemented using the transformation proposed above.

However, the proposal above is not sound. Consider the LTL specification G(g). Its translation would be G(g) itself (as it does not refer to the input symbol r). Now, G(g) is realizable under no-delay, but the controller that results from synthesis, which emits g continuously, does not meet the specification in the presence of variable delay as the steps of $t_p$ that receive $\epsilon _o$ do not satisfy g. This motivates the need for a more sophisticated transformation scheme.

Our Proposed Scheme. In order to solve the issue above, we introduce a set of reflected elements $R = \{o' \, | \, o \in O\} \cup \{\epsilon _o'\}$. We also demand a (further) enhancement to the communication medium such that if the plant emits $x \in 2^I$ to the controller at any step $t_p[i]$, then the communication medium actually sends out $x \cup \{y' \, | \, y \text { is in } O \text { or } y \text { is } \epsilon _o, y \in t_p[i]\}$ to the controller at this step. For instance, in Fig. 4, $\{r, g'\}$ would be sent out at $t_p[0]$ and would reach the controller at $t_c[0]$, with $g'$ being reflected back because g was received in $t_p[0]$. Similarly, $\epsilon _o'$ would be reflected back from $t_p[2]$, and therefore $\{r,\epsilon _o'\}$ would reach the controller at $t_c[2]$. Only $\epsilon _i$ would reach $t_c[4]$, with no input or reflected elements reaching. And $t_p[4]$ would not reflect $g'$ as g was not received in this step. Intuitively, reflected elements give information to the controller on when its (previously emitted) output symbols reached the plant.

$$\begin{aligned} tr _v^g(\varPsi ) = {\left\{ \begin{array}{ll} x, &{}\text {if }\varPsi = x \text { and } x \in I\\ y', &{}\text {if }\varPsi = y \text { and } y \in O\\ \lnot tr _v^g(\varPsi _1), &{} \text {if } \varPsi = \lnot \varPsi _1 \\ tr _v^g(\varPsi _1)\ \wedge \ tr _v^g(\varPsi _2), &{}\text {if }\varPsi = \varPsi _1 \wedge \varPsi _2 \\ tr _v^g(\varPsi _1)\ \vee \ tr _v^g(\varPsi _2), &{}\text {if }\varPsi = \varPsi _1 \vee \varPsi _2\\ X\big (\epsilon _i\, U \, (\lnot \epsilon _i\wedge { tr _v^g(\varPsi _1)})\big ), &{} \text {if }\varPsi = X\varPsi _1\\ F\big (\lnot \epsilon _i\wedge tr _v^g(\varPsi _1)\big ), &{} \text {if }\varPsi = F\varPsi _1\\ G\big (\epsilon _i\, U \, (\lnot \epsilon _i\wedge { tr _v^g(\varPsi _1)})\big ), &{}\text {if }\varPsi = G\varPsi _1\\ (\epsilon _i\, U \, (\lnot \epsilon _i\wedge { tr _v^g( \varPsi _1)}))\, U \, (\epsilon _i\, U \, (\lnot \epsilon _i\wedge { tr _v^g( \varPsi _2)})), &{} \text {if }\varPsi = \varPsi _1 \, U \, \varPsi _2 \\ \end{array}\right. } \end{aligned}$$

The translation function $tr _v^g$ defined above forms the core of our translation scheme. We now illustrate it with a couple of examples. For now, treat $tr _v(\varPsi )$ as being equal to $\epsilon _i\, U \, (\lnot \epsilon _i\wedge { tr _v^g(\varPsi )})$. $tr _v(G(g))$ yields $\epsilon _i\, U \, (\lnot \epsilon _i\wedge {(G(\epsilon _i\, U \, (\lnot \epsilon _i\wedge {g'})))})$. The intuition behind the translation is that if g is to occur in all steps of $t_p$, then the reflected $g'$ must occur infinitely often in $t_c$ (once corresponding to each step in $t_p$), and any steps of $t_c$ that do not have $g'$ must have received nothing (i.e., $\epsilon _i$) from the plant. The other cases in the definition above follow the same intuition. Note, during controller synthesis from the translated formula, the reflected elements as well as $\epsilon _o'$ (in addition to the elements in I) must be treated as input elements, as they come from the plant to the controller.

A formula such as F(g) is realizable under variable delay. A controller that continually emits g meets this specification under variable delay (for any $(d_l,d_u)$). However, $tr _v(F(g)) = \epsilon _i\, U \, (\lnot \epsilon _i\wedge {(F(\lnot \epsilon _i\wedge g'))})$ is not realizable and will not yield a controller when fed to a blackbox synthesis tool, as $g'$ is technically an input symbol and hence appears to be entirely in the hands of the (adversial) plant. What is missing in the translation $tr _v^g$ is an assertion that the controller can at any time force a $g'$ to appear later in its input by emitting a g at this time. We therefore define $tr _v(\varPsi )$ to be equal to $\varPsi _ as \, \Rightarrow \, \epsilon _i\, U \, (\lnot \epsilon _i\wedge {( tr _v^g(\varPsi ))})$, where:

$$ \begin{aligned} \varPsi _ as = & \bigwedge _{y \in O} G\left( y \, \Rightarrow \, \bigvee _{i \in [2 d_l, 2 d_u]} X^i y' \right) \wedge \bigwedge _{x \in I \cup R} G\left( x \Rightarrow \lnot \epsilon _i\right) \ \wedge \\ & \bigwedge _{y \in O} \left( GF (y') \, \Rightarrow GF (y)\right) \ \wedge \ \bigwedge _{y \in O} \left( GF (\lnot y') \, \Rightarrow GF (\lnot y)\right) \ \wedge \ FG(\lnot \epsilon _i) \end{aligned} $$

We call $\varPsi _ as$ a trace pair characterization, which is a formula that specifies properties of any trace $t_c$ such that there exists a $t_p$ such that $(t_c, t_p)$ is a trace pair. The first conjunct in the definition above captures the assertion that we had mentioned above, while the remaining four conjuncts capture other properties of trace pairs under delay when reflection is employed. Coming back to the example, it is easy to see that $\varPsi _ as \Rightarrow \epsilon _i\, U \, (\lnot \epsilon _i\wedge {(F(\lnot \epsilon _i\wedge g'))})$ is realizable, and is met by the controller that continually emits g. Intuitively, the last conjunct in the definition of $\varPsi _ as$ assures that at some point $\epsilon _i$’s will stop appearing (reason: there can be atmost $d_u$ occurrences of $\epsilon _i$’s in a trace), while the first conjunct assures that after $\epsilon _i$’s stop appearing each g emitted by the controller will cause $g'$ to appear in a subsequent step.

4.4 Properties of Our Approach

Lemma 2

For any trace pair $(t_c, t_p)$ under variable delay $(d_l, d_u)$, for any LTL formula $\varPsi$, and for any index i, $t_p(i)$ satisfies $\varPsi$ iff $t_c( corr (i))$ satisfies $tr _v^g(\varPsi )$, where $corr (i)$ equals the expression $i + d_ cp [0] + d_ pc [i]$. (Proof provided in appendix.)

Theorem 3 (Soundness)

Any controller C synthesized by our approach meets the given specification $\varPsi$ under the given delay $(d_l,d_u)$.

Proof: Consider any trace pair $(t_c, t_p)$ under delay $(d_l, d_u)$ generated by C. C was constructed to realize the formula $\varPsi _ as \Rightarrow \epsilon _i\, U \, (\lnot \epsilon _i\wedge {( tr _v^g(\varPsi ))})$. It can be seen that by definition of $\varPsi _ as$, since $(t_c, t_p)$ is a trace pair under delay $(d_l, d_u)$, $t_c$ must satisfy $\varPsi _ as$. Since $t_c$ was generated by C, it then follows that $t_c$ also satisfies $\epsilon _i\, U \, (\lnot \epsilon _i\wedge {( tr _v^g(\varPsi ))})$. From this, and by the properties possessed by trace pairs under delay, it follows that $t_c( corr (0))$ satisfies $tr _v^g(\varPsi )$. Therefore, by Lemma 2, $t_p(0)$ (i.e., $t_p$) satisfies $\varPsi$. $\Box$

Unlike, in the fixed delay setting, our approach as presented above does not offer a completeness guarantee. That is, a specification that is realizable under delay may be declared as unrealizable. For example, consider the property $\varPsi = G(\lnot g)$. This specification is in reality met by the controller that continually emits $\lnot g$. However, the translated formula $tr _v(\varPsi ) \, = \, \varPsi _ as \Rightarrow \epsilon _i\, U \, (\lnot \epsilon _i\wedge {(G(\epsilon _i\, U \, (\lnot \epsilon _i\wedge {(\lnot g')})))})$ will be declared as unrealizable when it is fed to any no-delay controller synthesis tool. Intuitively, the reason is that $\varPsi _ as$ should ideally also assert that for any $i, i+1$, the steps of $t_c$ between $t_c[ corr (i)]$ and $t_c[ corr (i+1)]$ contain only $\epsilon _i$’s, but it does not.

To summarize, the $\varPsi _ as$ we have defined is a sound trace pair characterization, but not a complete one. A trace pair characterization is sound if for any trace pair $(t_c, t_p)$ under delay $(d_l,d_u)$, $t_c$ is guaranteed to satisfy the characterization. This soundness was invoked in the proof of Theorem 3 above. A trace pair characterization can be called complete, if, for any trace $t_c$ that satisfies the characterization, there exists a trace $t_p$ such that $(t_c, t_p)$ is trace pair under delay $(d_l, d_u)$. Our approach is basically parametric on the trace pair characterization used, and our approach will be sound (resp. complete) if the characterization is sound (resp. complete). It may be possible to devise a complete trace pair characterization, but it is likely to lead to high synthesis complexity.

5 Unrealizability Filter

A lot practical properties tend to be unrealizable under delay, and the blackbox synthesis approach may expend a lot of time to detect unrealizability of the transformed formula in such cases. We therefore propose a novel, efficient, syntax-based heuristic that detects if a given formula is unrealizable under delay. The heuristic is sound, in that it never mis-classifies a realizable property as unrealizable. The heuristic is not guaranteed to detect all unrealizable properties, so whenever it does not give a classification, the synthesis blackbox will need to be invoked.

We first introduce a pre-requisite function IOIS that is used by the filters. For the given property $\varPsi$, IOIS($\varPsi$) returns a logical formula in conjunctive normal form. Any atomic fact in the formula is of the form (x, l), where x is an input literal or an output literal. Input literals are input elements or their negations (e.g., r, $\lnot r$), while output literals are output elements or their negations (e.g., g, $\lnot g$). l is in general a finite set of closed intervals in the non-negative integers domain. Due to space limitations, we provide the full definition of IOIS in the appendix. For illustration, if $\varPsi \equiv G((r \Rightarrow X g) \wedge (\lnot r \Rightarrow X \lnot g))$, then IOIS($\varPsi$) happens to yield the following formula, which is a conjunction of two conjuncts: $\big ((\lnot r, [0,0]) \vee (g, [1,1])\big )$ $\wedge$ $\big ((r, [0,0]) \vee (\lnot g, [1,1])\big )$. The intuition is that any plant side trace $t_p$ can satisfy $\varPsi$ only if it satisfies IOIS($\varPsi$). An atomic fact (x, l) is satisfied by a trace $t_p$ iff for some index $i \in l$, $t_p[i]$ satisfies x.

Two literals are said to be contradictory if one is a negation of the other. For e.g., $\lnot r$ and r. For a given non-negative integer d, a conjunct $C_i$ is said to be d-bounded if it contains exactly one atomic fact with an output literal, contains at least one atomic fact with an input literal, and $\max (W) - \min (V) < d$, where W is the interval-set associated with the output literal in the conjunct, and V is the union of the interval sets associated with all input intervals in the conjunct. A conjunct is said to be a tautology if it contains two contradictory input literals, and the interval-sets associated with these two input literals are overlapping.

We now define the fixed-delay filter for a given total delay d as follows: It classifies the given $\varPsi$ as unrealizable if IOIS($\varPsi$) contains two conjuncts $C_i$ and $C_j$ such that (a) both conjuncts contain exactly one output literal each, (b) these two output literals are contradictory, (c) the interval sets associated with both these output literals are the same, and each of these interval sets is a unit-interval (i.e., of total width 1), (d) $C_i$ or $C_j$ (or both) are d-bounded, and (e) neither conjunct is a tautology.

The intuition is that a d-bounded conjunct contains input literals and an output literal close enough that the controller cannot use the input symbols in $t_c$ to decide whether to emit the output literal or its negation in order to satisfy the conjunct. Therefore, if two conjuncts have opposite output literals required at the same step in the trace, whichever conjunct the controller tries to satisfy, the other conjunct can be falsified by the adversarial plant.

The example provided earlier in this section indeed gets classified as unrealizable by our filter when $d=2$. Intuitively, the property is unrealizable because the controller has to send a g or a $\lnot g$ before it comes to know whether the step in $t_p$ that precedes the step where this g or $\lnot g$ will be received emitted r or $\lnot r$.

We now define two variable-delay filters. The first filter for the variable-delay setting simply invokes the fixed-delay filter defined above with $d = d_u + d_u$ (see Sect. 4.2 for the justification). The second filter classifies the given $\varPsi$ as unrealizable if IOIS($\varPsi$) contains a conjunct C such that (a) all output literals in the conjunct are positive (i.e., not of the form ‘$\lnot g$’), (b) the total number of positions in the union of the interval sets corresponding to the output literals in the conjunct (i.e., not counting more than once the positions that occur in multiple interval-sets) is less than or equal to $d_u - d _l$, and (c) the conjunct is not a tautology. The intuition is that such a conjunct becomes falsified if $d_u - d_l$ $\epsilon _i$’s happen to occur in all positions in the above-mentioned union.

6 Empirical Evaluation

We have implemented both our fixed delay and variable delay approaches. Our approaches accept LTL specifications in the standard TLSF format. We use Syfco [9] as a front-end to parse TLSF, and implement our formula translation using Haskell (as that is Syfco’s supported language). Our filter implementations are also Syfco and Haskell based. We selected Strix [10] as the blackbox tool to perform synthesis using our translated formulas. Strix was in Number 1 position among all competing synthesis tools in SYNTCOMP 2022 synthesis competition [7, 8]. SYNTCOMP is a pre-eminent annual contest for (no-delay) synthesis tools. For our evaluations, we selected all 1075 TLSF benchmarks (i.e., LTL specifications) used in the SYNTCOMP 2022 contest.

We are not aware of any other tool that performs delay synthesis from given LTL specifications. Therefore, to serve as a baseline, we obtained a recently released tool by Chen et al. [3], from the web site mentioned in their paper. This tool addresses strategy inference from safety games under fixed-delay. Since they do not accept LTL as input directly, and only accept a game graph with a safety winning condition, we need to first translate LTL specifications to safety game graphs. We do this using the “k-bounded safety approximation” feature provided in Owl [14], which is a widely used library for analysis of automata and LTL specifications. The bound specifies the maximum number of visits to final states tolerated during safety game translation (as any finite number of visits is winning). For any LTL property, there exists a (potentially exponentially high) value of k at which the translation is guaranteed sound. To keep the translation time tractable, we have specified an upper limit of $k=10$. Therefore, Owl will stop at this value of 10, or at a value less than 10 if it finds a sound safety game for this lower value. In cases where Owl stops at value 10, the safety game graph Owl returns may not be sound. However, we enforce the limit of $k=10$ so that Owl will finish within practical time limits. Empirically we observe a loss of soundness in some cases (details of which we will provide later). The running times comparison is hence the more interesting takeaway from this baseline study.

6.1 Our Results

Table 1. Summary of results

Table 1 summarizes the results from our runs. Each row represents a run of a tool or approach on all 1075 benchmarks. To keep the total time of the runs tractable, and also to facilitate uniform comparisons, we use a timeout of 720 s per benchmark in each run. The columns indicate the name of the run, number of benchmarks found realizable, number of benchmarks found unrealizable, number of benchmarks on which analysis was stopped due to the timeout being hit, number of benchmarks on which the corresponding tool encountered errors/exceptions during processing, and finally the total wall clock time of the run (on all 1075 benchmarks). All our runs were done on a server with an Intel Xeon W-2295 processor and 256 GB of RAM. Our tool, and certain artifacts from our runs, are available in our repository https://doi.org/10.6084/m9.figshare.c.6608452.

The ‘No delay’ run is a baseline, and represents a run of Strix directly on the given benchmarks, without any delay translation. 187 benchmarks hit the timeout, while the rest were declared realizable (500 of them) or unrealizable (388 of them). The average time to process a single benchmark is 136 s.

Fixed Delay. We now discuss the next two rows, which depict information about runs of our fixed-delay approach, with delay $d = 4$ and $d = 10$, respectively. For each benchmark, out of the 720 s allotted, we use the first 20 s to run two separate filters sequentially. The first filter is our filter, described in Sect. 5. The second is a run of Strix on the untranslated formula, to see if declares unrealizability. Recall that as per the discussion in Sect. 3.2, if a specification is unrealizable with no-delay, it must be unrealizable with delay. Our run script kills each filter after 10 s, and proceeds to run Strix on the translated formula of the benchmark (with a budget of 700 s) if neither filter declares unrealizability.

The ‘# Realizable’ column indicates that 248 benchmarks (out of a maximum possible 500) were found realizable with delay $d= 4$, while 206 were found realizable when the delay is increased to $d=10$. This is consistent with our theoretical claims of higher-delay realizability implying lower-delay realizability and delay realizability implying no-delay realizable. Note that what used to be a realizable or unrealizable benchmark under no-delay could have migrated to the timeouts category in the fixed-delay runs.

The ‘# Unrealizable’ column shows the break up of the number of benchmarks found unrealizable by the filters (the number before the “+”) and the number of benchmarks not removed by the filters but subsequently found to be unrealizable by Strix when applied on the translated formula. It is notable that the filters are very effective, and identify 463 benchmarks are unrealizable (under both delay values). This is a major reason why the fixed-delay total wall-clocks times are not very high. It only 33% higher than the no-delay wall-clock time at $d=4$, and 91% higher at the very high delay value of $d=10$. It is notable that since our fixed-delay approach is sound and complete, any benchmark that is declared as realizable (resp. unrealizable) will necessarily belong to the declared category. It is also notable that with $d = 4$, the number of timeout runs we encounter is only a little more than with the no-delay run despite the complexity of having to account for delay. We are very encouraged by this result about the efficiency of our approach.

Variable Delay. In the variable-delay runs, we employ a total of four filters sequentially, with a time budget of 10 s for each filter (per benchmark). The first two filters were presented at the end of Sect. 5. The next two filters are (a) a run of Strix on the original untranslated formula $\varPsi$, and (b) a run of Strix on $\varPsi$ after it is translated as per the fixed-delay translation, with $d = d_u + d_u$. The reasoning behind these two applications of Strix as filters is provided in Sect. 4.2. If none of the four filters detects a benchmark as unrealizable, then we proceed to run Strix on the (variable-delay) translated formula, with a budget of 680 s.

The next two rows in Table 1 depict information about runs of our variable-delay approach, with delay (1, 2) and (1, 5) respectively. Recall that if a specification is realizable under variable delay (1, 2) (resp. (1, 5)), it must be realizable under fixed-delay with $d = 4$ (resp. $d = 10$). The data indicates that a substantially smaller number of benchmarks were found to be realizable. Part of the reason for this is that realizability indeed is less likely to hold with variable delay than with fixed delay, based on manual analysis of real specifications. But the other reason is the substantial numbers of benchmarks on which Strix threw exceptions when applied to the translated properties (even though they were syntactically valid). Many of these exceptions contained a message such as “Too many elements to create power set: 65 > 30”. We suspect that many of these translated formulas may be too large for Strix. We have some future work ideas to try to mitigate this effect, which we discuss at the end of the paper.

In the variable delay runs, the benchmarks found unrealizable by the filters are guaranteed to be unrealizable. However, due to the incompleteness of our trace pair characterization $\varPsi _ as$, some of the benchmarks that were declared unrealizable by Strix (25 in the (1, 2) run and 3 in the (1, 5) run) could potentially be realizable. Despite the prevalence of Strix errors, we are encouraged that on 56% to 69% of benchmarks, i.e., 567 + 39 with delay (1, 2) and 700 + 37 with delay (1, 5), our approach gives definitive results. In all cases, our formula translation is very fast (less than 1 s per benchmark).

Sample Properties. To give a taste for what kind of properties become unrealizable under different settings, we manually extract core unrealizable portions from real properties and present them here. Properties $(F G (\lnot r_0)) \Leftrightarrow (G F (g))$ and $G ( r_0 \Leftrightarrow (X r_1))$ are unrealizable even without delay. The property $G (r \Leftrightarrow (X g))$ is realizable without delay but not realizable under fixed delay $d = 2$. The specification $(G ((r_0) \rightarrow (((r_1) \leftrightarrow (X (g_1)))\ U\ (g_0))))$ is realizable under fixed-delay $d = 2$ but unrealizable under variable delay (1, 2). The design of our unrealizability filter gives a more principled feel for causes of unrealizability (applicable in many, not all, benchmarks).

6.2 Comparison with Chen et al.’s Tool

The last row in Table 1 depicts information about our run of Chen et al.’s synthesis tool. This row is to be compared with the “FD $d = 4$” row which is about our corresponding approach. From the last row, it is seen that 618 benchmarks faced a timeout. Among these, 524 faced the 720 s timeout during the LTL to safety game translation within Owl itself, while the remaining 94 faced a timeout within the synthesis tool. To ensure the uniform total 720 s budget, the time budget we gave to the synthesis tool was 720 s minus the time taken during the LTL to safety game translation. The 197 error cases were all encountered within their synthesis tool.

Of the 90 benchmarks declared realizable, 17 were found unrealizable by our tool. Additionally, 40 of the declared unrealizable specifications were declared realizable by our tool. Since our fixed-delay tool is provably sound and complete, and because their synthesis tool is also presumably correct, we suspect these mis-classifications occur due to potential unsoundness in the initial LTL to safety game translation, as discussed at the beginning of this section.

We cannot conclude about the efficiency of Chen et al.’s tool per-se from this comparison. However, LTL to safety game conversion is inherently an expensive operation. Whereas, LTL synthesis tools like Strix are heavily optimized using heuristics. The takeaway is that when one’s input is an LTL specification, it is useful to have a way to synthesize directly than to have to go via a determinized safety game construction.

7 Related Work

There is a rich literature in the classical LTL synthesis space, where the problem is to synthesize a controller from an LTL specification, with the controller and plant communicating via input/output symbols, in the absence of delay. Pnueli et al. [13] propose a seminal solution for this problem, based on determinization of automata. This approach has been extended with numerous practical optimizations, and is in fact used in the tool Strix that we have used in our evaluations. The time complexity of classical synthesis is in general double exponential in the size of the LTL specification.

An early work that investigated controller synthesis in the presence of delay was by Tripakis et al. [16]. They address the problem of supervisory control, and not input/output symbol based control, which is our setting. In supervisory control, the controller can block the plant from taking a transition by observing the event associated with the proposed transition. They address a restricted class of specifications of the form that every event a must eventually be followed by an event b. They allow multiple controllers to simultaneously control the plant; each controller can observe a subset of events without any delay, and observes the events corresponding to the other controllers’ subsets with delay. There is no empirical evaluation reported in this paper.

Finkbeiner et al. [5] studied various extended versions of the controller synthesis for symbol-based control. Their approach is to construct an alternating parity automaton from the given LTL specification, which accepts (infinite) run trees that represent winning strategies for the controller. The authors describe how the automaton can be transformed to handle distributed systems, where there are multiple controllers, and environments where there is (fixed) delay. There is no empirical evaluation in this paper. The practical tool Bosy [6] that was introduced subsequently is based on this approach, and uses a SAT-solver formulation to try to find a controller within a given size bound k whose unfoldings are accepted run trees. This tool does not appear to support delay.

Winter et al. [17] recently investigated a problem that they call delay games. Their notion of delay is not similar to ours, and does not model communication delay between plant and controller. Rather, the controller is allowed to skip playing in its turns, while the plant keeps playing and emitting input symbols. Effectively the controller gains a lookahead into the plant’s behavior before it chooses to play, and hence this broadens the class of realizable specifications beyond what is realizable under no-delay.

The closest related work to ours is by Chen et al. [3]. We have partially described their work already in Sect. 6. They address fixed delay only, that too on a given 2-player game graph with a safety winning condition. They first present a naive proposal that reduces the strategy inference problem to delay-free games by exploding the game graph by pairing each game graph state with a queue configuration. As this is expensive, they subsequently present an optimized strategy that increases the queue lengths iteratively, pruning uncontrollable states along the way, until the queue lengths reach the given delay d. They do not explicitly address LTL specifications. LTL specifications would first need to be determinized to obtain a game graph, and this incurs exponential cost.

8 Conclusions and Future Work

In conclusion, to the best of our knowledge, our work is the first one to identify and address the problem of variable delay. We also investigate how variable delay relates theoretically to fixed delay. Ours is also the first approach to solve delay synthesis using LTL formula translation. The advantages of this approach are its relative simplicity, flexibility in terms of being able to automatically leverage efficiency improvements to classical (no-delay) synthesis approaches that may emerge in the future, and substantial empirically observed performance gain compared to a closely related and recent baseline approach [3].

In future work we plan to investigate if our variable delay translation can be made more efficient, and can possibly be made complete. Both of these would need (differing) changes to the trace pair characterization $\varPsi _ as$. We would like to try blackbox synthesis tools other than Strix within our implementation. Conceptually, we would like to extend our approach to distributed control, where there are multiple controllers, with differing delays to the plant.