Keywords

1 Introduction

MOGA is extensively employed in diverse fields such as engineering, science, medicine, management, finance, etc. A couple of examples [1, 2] showcase its effectiveness in addressing crucial multi-objective optimization problems in recent times. The widespread adoption of MOGA in industrial applications has significantly elevated its significance, making it a highly valued domain.

1.1 Prerequisites

This portion presents an exploration of the essential terminologies and pertinent concepts related to multi-objective optimization problems.

Definition 1 (Multi-objective Optimization Problem(MOP))

Multiobjective optimization is a method utilized to improve multiple objectives concurrently, considering their mutual influence and any existing constraints. It aims to find optimal solutions that enhance two or more objectives simultaneously. The formal definition of the MOP is as follows:

$$\text {Min/Max}\quad z_m(x), \quad m = 1, 2, \ldots , M;$$
$$\text {s.t.,}\quad w_j(x)\ge 0, \quad j = 1, 2, \ldots , J;\quad y_k(x) = 0, \quad k = 1, 2, \ldots , K;$$
$$x_i^{(L)} \le x_i \le x_i^{(U)} \quad i = 1, 2, \ldots , n;$$

A solutionFootnote 1, denoted as \(x \in \mathbb {R}^n\), is a vector consisting of n decision variables: \(x = (x_1, x_2, \ldots , x_n)^T\). In this context, M, J, and K represent the number of objectives that require optimization, denoted by \(z_m\), the number of inequality constraints denoted by \(w_j\), and the number of equality constraints denoted by \(y_k\), respectively. The lower and upper bounds of \(x_i\) are denoted as \(x_i^{(L)}\) and \(x_i^{(U)}\), respectively, where \(i = 1, 2, \ldots , n\) [3]. The mapping of decision space points to objective space points is illustrated in Fig. 1.

Fig. 1.
figure 1

Decision Space to Objective Space Mapping. The red points found in the objective space represent the members of the Pareto front. (Color figure online)

Full size image

Definition 2 (Domination Relation)

A solution \(\alpha \) \(\in \mathcal D\) (Decision Space) is said to dominate another solution \(\beta \) \(\in \mathcal D\) if both the following conditions hold together:

  1. 1.

    In terms of all the objective functions, the solution \(\alpha \) can not be worse than the solution \(\beta \).

  2. 2.

    There exists at least one objective function for which \(\alpha \) is strictly better than \(\beta \) [3].

Definition 3 (Pareto Optimal Set)

A solution is deemed Pareto optimal when there is no other solution that can improve one objective without worsening another. The set of all Pareto optimal solutions is the “Pareto optimal set”, and their corresponding objective points form the “Pareto front” [3].

For example, in Fig. 1, the red solutions in the decision space form the Pareto optimal set, while the red points in the objective space depict the Pareto front.

1.2 Literature Survey

There have been several mechanisms to solve the MOPs, including SPEA2 [4], MOGA [5], NSGA-II [6], IBEA [7], NSGA-III [8], and more. Among these, NSGA-II stands out as one of the most popular approaches. NSGA-II comprises two main constituents: Fast Non-dominated Sorting (FNDS) and Crowding Distance. FNDS having the computational complexity of \(O(MN^2)\), generates non-dominated fronts, with M and N being the number of objective functions and population size respectively. Although other non-dominated sorting approaches exist, for example, a recursive mechanism having a computational complexity of \(O(N log^{M-1}N)\) by Jensen et al. [9], they become ineffective when two different solutions are with the same objective function value. Tang et al. introduced a fast approach for generating the non-dominated set using the arena’s principle [10]. Zhang et al. introduced an important method called Efficient Non-dominated Sorting (ENS), which encompasses two variations: one employing sequential search (ENS-SS) and the other utilizing binary search (ENS-BS) [11]. However, no existing algorithm in the literature achieves better time complexity in the worst-case scenario than \(O(MN^2)\) for non-dominated sorting while remaining complete.

1.3 Gap Identification and Motivation

To address the issues discussed in Sect. 1.2, we have offered a pivot-based non-dominated sorting that intends to provide a complete, correct, and time-efficient algorithm that generates non-dominated fronts.

1.4 Structure of the Paper

This paper is structured into the following four sections. First, “Introduction” in Sect. 1, covers the background information, literature review, and gap analysis. Followed by “Methodology” in Sect. 2, which explains the proposed technique and provides information about the relevant dataset. Section 3 is dedicated to “Result and Analysis”, where the completeness and accuracy of the proposed method are demonstrated and discussed. Finally, the “Conclusion” is presented in Sect. 4.

2 Methodology

For a clear understanding of the methodology, we introduce the concept of Pivot.

Definition 4 (Pivot)

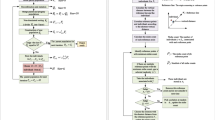
Pivot points refer to the mapped solutions from a decision space to an objective space where there is at least one objective function that achieves the optimal value. This optimal value can be either the maximum value if the objective function aims to maximize or the minimum value if the objective function aims to minimize. In a typical multi-objective optimization, there can be a combination of possibilities for both maximization and minimization. Figure 2 depicts the flow diagram of the mechanism, with an explanation of pivot points.

Fig. 2.
figure 2

Flow Diagram of the Pivot-based Deterministic Non-dominated Sorting Approach. a. Snippet of a demo data set in an objective space with each column representing five different objective functions. b. Five Pivot points for five objective functions. c. Comparing all points in the objective space with the pivot point(s) to check whether they are worse or in a non-dominated relation with the pivot point(s). d. The recursive process of generating fronts until the “left” buffer, used to hold all other elements excluding the current front’s pivot points and its non-dominated points, is empty.

Full size image

2.1 Benchmark Data-Set Specification

Zitzler-Deb-Thiele-1 (ZDT-1) Test Suite. The construction of the ZDT problem suite is rooted in a 30-variable problem (\(n=30\)) that exhibits a convex Pareto-optimal set [14].

min \(z_1(x)\); min \(z_2(x)= g(x)h(z_1(x), g(x))\);

where two objectives need minimization, the function g(x) is typically used to represent convergence, and it is common for \(g(x) = 1\) for Pareto-optimal solutions. The definition of the ZDT-1 test suite is as follows:

$$z_1(x) = x_1; g(x) = 1 + \frac{9}{n-1}\sum _{i = 2}^n x_i; h(z_1, g) = 1 - \sqrt{\frac{z_1}{g}}; 0 \le x_i \le 1 $$

where, \(i = 1,\ldots , n\).

The Vehicle Crashworthiness Problem. This real-life application-based benchmark involves optimizing the level of safety in the event of a crash and is characterized as a problem with three objectives and no constraints [13]. This problem involves five decision variables, \(x_1\), \(x_2\), \(x_3\), \(x_4\), and \(x_5\). Three objective functions: \(z_1\), \(z_2\), and \(z_3\) are depicted as follows:

$$\begin{aligned} z_1(x) = 1640.2823 + 2.3573285x_1 + 2.3220035x_2\\ + 4.5688768x_3 + 7.7213633x_4 + 4.4559504x_5 \end{aligned}$$
$$\begin{aligned} z_2(x) = 6.5856 + 1.15x_1 - 1.0427x_2 + 0.9738x_3 + 0.8364x_4 - 0.3695x_1x_4 \\ + 0.0861x_1x_5 + 0.3628x_2x_4 - 0.1106x_1x_1 - 0.3437x_3x_3 + 0.1764x_4x_4 \end{aligned}$$
$$\begin{aligned} z_3(x) = -0.0551 + 0.0181x_1 + 0.1024x_2 + 0.0421x_3 - 0.0073x_1x_2 + 0.024x_2x_3 \\ - 0.0118x_2x_4 - 0.0204x_3x_4 - 0.008x_3x_5 - 0.0241x_2x_2 + 0.0109x_4x_4 \end{aligned}$$

Deb-Thiele-Laumanns-Zitzler-1 (DTLZ-1). This involves n decision variables and is defined as follows [15]:

Minimize:

$$f_{1}(\vec {x}) = \frac{1}{2}x_{1}x_{2} \cdots x_{M-1}(1 + g(\vec {x}))$$

\(f_{i}(\vec {x}) = \frac{1}{2}x_{1}x_{2} \cdots (1-x_{i-1}) \cdots (1-x_{M-1})(1 + g(\vec {x})),\quad i=2,\ldots ,M-1\)

$$f_{M}(\vec {x}) = \frac{1}{2}(1-x_{1})(1 + g(\vec {x}))$$

where \(\vec {x} = (x_1, x_2, \ldots , x_K)\) depicts the decision variables, and \(g(\vec {x})\) is a nonlinear function given by:

$$g(\vec {x}) = \sum _{i=K-M+1}^{K}(x_{i} - 0.5)^2 - \cos (20\pi (x_{i}-0.5))$$

The decision variables are subject to the following constraints:

$$0 \le x_i \le 1, \quad i=1,\ldots ,K$$

OneMinMax and Leading Ones and Trailing Zeros (LOTZ). The OneMinMax benchmark was originally suggested by Giel and Lehre (2010) as a two-objective version of the well-known ONEMAX benchmark. Laumanns, Thiele, and Zitzler (2004) introduced a benchmark called LOTZ. The benchmarks mentioned here contain objective functions that are of maximization type [12]. \(z: \{0, 1\}^n \rightarrow \mathbb {N} \times \mathbb {N}\)

OneMinMax Function is defined by:

$$\begin{aligned} z(x) = (z_1(x), z_2(x)) = (n-\sum _{i = 1}^n x_i, \sum _{i = 1}^n x_i); \forall x =(x_1, x_2,.....,x_n) \in \{0, 1\}^n \end{aligned}$$

The LOTZ function is defined as follows:

$$\begin{aligned} z(x) = (z_1(x), z_2(x)) = (\sum _{i = 1}^n \prod _{j = 1}^i x_j, \sum _{i = 1}^n \prod _{j = 1}^n (1-x_j)); \forall x \in \{0, 1\}^n \end{aligned}$$

2.2 Pivot-Based Deterministic Non-dominated Sorting

The algorithm takes input as the mapped solutions from the decision space and outputs non-overlapping decomposed Front(s), where the first Front represents the Pareto Front. Algorithm 1 shows the Pivot-based Deterministic Non-dominated Sorting.

figure a

3 Result and Analysis

The result yielded for different benchmark functions are shown in Fig. 3. The result of the suggested Pivot-based algorithm is evaluated using the ZDT-1 bi-objective benchmark function to compare the fast non-dominated sorting and the proposed approach. In the sample of 500 elements in the objective space, both methods successfully position all elements on the Pareto Front. This indicates the presence of a single front, where all 500 elements in the sample are mutually non-dominated. This information is visualized as a diamond shape in Fig. 3. The analysis extends to the “Vehicle Crashworthiness” benchmark, which involves three objective functions and is examined using both fast non-dominated sorting and the proposed approach. In this case, the entire objective space is divided into eight fronts, with each front containing an equal number of elements for both methods. These fronts are represented by a brown-coloured asterisk sign. The consistency of this outcome is observed across all other benchmark functions showcased in Fig. 3 where yellow square, green triangle, and brown cross are used respectively for DTLZ - 1, LOTZ, and OneMinMax front representation, thereby affirming the validity of the proposed algorithm.

Fig. 3.
figure 3

Number of Fronts and corresponding elements generated using the proposed method and the Fast Non-dominated Sorting.

Full size image

3.1 Completeness and Correctness of the Algorithm

Formation of pivots followed by placement of an objective space element in a suitable front in respect of the pivot undergo exhaustive exploration in a deterministic sense. Hence, assigning a newly explored element in an appropriate Front can not but be procedurally complete.

3.2 Complexity of the Proposed Algorithm

The Algorithm proposed in Algorithm 1 consists of two nested for loops in steps 3 and 5, which iterate N times, where N represents the number of mapped solutions in the objective space. In the worst-case scenario, this algorithm requires \(O(N^2)\) time to finish. Additionally, step 10 includes another loop that iterates M times, where M is the number of objective functions. Step 1, on the other hand, takes O(MN) time to complete. Consequently, the algorithm’s best-case, average-case, and worst-case time complexity is respectively, \(\varOmega (MN^2)\), \(\varTheta (MN^2)\), \(O(MN^2)\), which is similar to respective cases of the Fast Non-dominated Sorting phase in NSGA-II and NSGA-III. Furthermore, no worse than any existing non-dominated sorting algorithm, which is complete, in the worst-case scenario.

4 Conclusion

The pivot-based framework has a number of benefits. First off, the idea is simple and straightforward to put into practice. Second, it covers all the solutions in the decision space by effectively dividing them into non-overlapping fronts using the mapped objective space values, needless to mention which ensures the categorization of the quality of the solutions. Last but not least, it accomplishes these advantages in a time-efficient way that isn’t worse than current state-of-the-art methods. The effectiveness of the suggested approach is validated by comparisons with multiple benchmark multi-objective optimization functions that exist in the literature. Despite being a novel, complete, and correct approach, the algorithm cannot handle streamed or online data. Our efforts in the future will be directed towards addressing this particular issue in the algorithm.