Abstract
In this paper, we introduce game-theoretic semantics (GTS) for Qualitative Choice Logic (QCL), which, in order to express preferences, extends classical propositional logic with an additional connective called ordered disjunction. In particular, we present a new semantics that makes use of GTS negation and, by doing so, avoids contentious behavior of negation in existing QCL-semantics.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Preferences are a key research area in artificial intelligence, and thus a multitude of preference formalisms have been described in the literature [12]. An interesting example is Qualitative Choice Logic (QCL) [6], which extends classical propositional logic by the connective  called ordered disjunction.
called ordered disjunction.  states that F or G should be satisfied, but satisfying F is more preferable than satisfying only G. This allows to express soft constraints (preferences) and hard constraints (truth) in a single language.
states that F or G should be satisfied, but satisfying F is more preferable than satisfying only G. This allows to express soft constraints (preferences) and hard constraints (truth) in a single language.
For example, say we want to formalize our choice of pizza toppings: we definitely want tomato-sauce (t); Moreover, we want either mushrooms (m) or artichokes (a), but preferably mushrooms. This can easily be expressed in QCL via the formula  . This formula has three models in QCL, namely \(M_1 = \{t,m,a\}\), \(M_2 = \{t,m\}\), and \(M_3 = \{t,a\}\). QCL-semantics then ranks these models via so-called satisfaction degrees. The lower this degree, the more preferable the model. In this case, \(M_1\) and \(M_2\) would be assigned a degree of 1 and \(M_3\) would be assigned a degree of 2, i.e., \(M_1\) and \(M_2\) are the preferred models of this formula.
. This formula has three models in QCL, namely \(M_1 = \{t,m,a\}\), \(M_2 = \{t,m\}\), and \(M_3 = \{t,a\}\). QCL-semantics then ranks these models via so-called satisfaction degrees. The lower this degree, the more preferable the model. In this case, \(M_1\) and \(M_2\) would be assigned a degree of 1 and \(M_3\) would be assigned a degree of 2, i.e., \(M_1\) and \(M_2\) are the preferred models of this formula.
In the literature, QCL has been studied with regards to possible applications [13], computational properties [4], and proof systems [3]. However, not all aspects of QCL-semantics are uncontroversial. For example, a QCL-formula F is not logically equivalent to its double negation \(\lnot \lnot F\), as all information about preferences is erased by \(\lnot \). This issue has been addressed by Prioritized QCL (PQCL) [1], which defines ordered disjunction in the same way as QCL but changes the meaning of the classical connectives, including negation. While PQCL solves QCL’s problem with double negation, it in turn introduces other controversial behavior, e.g., a formula F and its negation \(\lnot F\) can be satisfied by the same interpretation. No alternative semantics for QCL is known to us that addresses both of these issues at the same time.
In order to tackle these issues, we develop game-theoretic semantics (GTS) for QCL, embedding choice logics in the rich intersection of the fields of game-theory and logics [2, 11, 15]. Building on the concepts of rational behavior and strategic thinking, GTS offer a natural dynamic viewpoint of dealing with truth and preferences. Originally, GTS go back to Jaakko Hintikka [10], who designed a win/lose game for two players, called Me (or I) and You, both of which can act in the role of Proponent or Opponent of a formula F over an interpretation \(\mathcal {I}\). The game proceeds by rules for step-wise reducing F to an atomic formula. It turns out that I have a winning strategy for this game if and only if F is classically true over \(\mathcal {I}\). Most importantly, negation in GTS is interpreted as dual negation, [14]: at formulas \(\lnot G\), the game continues with G and a role switch.
To capture not only truth but also preferences, we extend the two-valued game of Hintikka with more fine-grained outcomes and introduce a game-theoretic interpretation of ordered disjunction. Moreover, we reinterpret negation in QCL using game-theoretic methods. From our GTS we extract a new logic we call Game-induced Choice Logics (GCL), where negation behaves as in classical logic.
2 Qualitative Choice Logic (QCL)
We now recall QCL [6]. \(\mathcal {U}\) denotes an infinite set of propositional variables. An interpretation \(\mathcal {I} \subseteq \mathcal {U}\) is a set of variables, with \(a \in \mathcal {U}\) true under \(\mathcal {I}\) iff \(a \in \mathcal {I}\).
Definition 1 (QCL-formula)
The set \(\mathcal {F}\) of QCL-formulas is built inductively: if \(a \in \mathcal {U}\), then \(a \in \mathcal {F}\); if \(F \in \mathcal {F}\), then \((\lnot F) \in \mathcal {F}\); if \(F, G \in \mathcal {F}\), then \((F \circ G) \in \mathcal {F}\) for  .
.
The semantics of QCL is based on two functions: optionality and satisfaction degree. The satisfaction degree of a formula can be a natural number or \(\infty \) and is used to rank interpretations (lower degrees are better). The optionality of a formula represents the maximum finite satisfaction degree the formula can obtain and is used to penalize interpretations that do not satisfy F in  .
.
Definition 2 (Optionality in QCL)
The optionality of QCL-formulas is defined inductively as follows: (i) \(\textrm{opt}(a) = 1\) for \(a \in \mathcal {U}\), (ii) \(\textrm{opt}(\lnot F) = 1\), (iii) \(\textrm{opt}({F \wedge G}) = \textrm{opt}({F \vee G}) = \max (\textrm{opt}(F),\textrm{opt}(G))\), and (iv)  .
.
Definition 3 (Satisfaction Degree in QCL)
The satisfaction degree of QCL-formulas under an interpretation \(\mathcal {I}\) is defined inductively as follows:

If \(\textrm{deg}_\mathcal {I}(F) = k\) we say that \(\mathcal {I}\) satisfies F to a degree of k. If \(\textrm{deg}_\mathcal {I}(F) < \infty \) we say that \(\mathcal {I}\) (classically) satisfies F, or that \(\mathcal {I}\) is a model of F. A crucial notion in QCL is that of preferred models, i.e., models with minimal degree.
Definition 4 (Preferred Model under QCL-semantics)
Let F be a QCL-formula. An interpretation \(\mathcal {I}\) is a preferred model of F iff \(\textrm{deg}_\mathcal {I}(F) < \infty \) and, for all interpretations \(\mathcal {J}\), \(\textrm{deg}_\mathcal {I}(F) \le \textrm{deg}_\mathcal {J}(F)\).
Satisfaction degrees are bounded by optionality, i.e., either \(\textrm{deg}_\mathcal {I}(F) \le \textrm{opt}(F)\) or \(\textrm{deg}_\mathcal {I}(F) = \infty \) must hold. As stated earlier, optionality is used to penalize non-satisfaction: given  , if \(\textrm{deg}_\mathcal {I}(F) < \infty \) we get
, if \(\textrm{deg}_\mathcal {I}(F) < \infty \) we get  ; if \(\textrm{deg}_\mathcal {I}(F) = \infty \) we get
; if \(\textrm{deg}_\mathcal {I}(F) = \infty \) we get  .
.
Moreover, ordered disjunction is associative under QCL-semantics, which means that we can simply write  to express that we must satisfy at least one of \(A_1,\ldots ,A_n\), and that we prefer \(A_i\) to \(A_j\) for \(i < j\).
to express that we must satisfy at least one of \(A_1,\ldots ,A_n\), and that we prefer \(A_i\) to \(A_j\) for \(i < j\).
Example 1
Consider  . Then \(\textrm{opt}(F) = 3\), \(\textrm{deg}_\emptyset (F) = \infty \), \(\textrm{deg}_{\{b\}}(F) = 3\), \(\textrm{deg}_{\{a\}}(F) = 2\), and \(\textrm{deg}_{\{a,b\}}(F) = 1\). Thus, \(\{a\},\{b\},\{a,b\}\) are models of F while \(\{a,b\}\) is also a preferred model of F.
. Then \(\textrm{opt}(F) = 3\), \(\textrm{deg}_\emptyset (F) = \infty \), \(\textrm{deg}_{\{b\}}(F) = 3\), \(\textrm{deg}_{\{a\}}(F) = 2\), and \(\textrm{deg}_{\{a,b\}}(F) = 1\). Thus, \(\{a\},\{b\},\{a,b\}\) are models of F while \(\{a,b\}\) is also a preferred model of F.
Now consider \(F' = F \wedge \lnot (a \wedge b)\). Again, \(\textrm{deg}_\emptyset (F') = \infty \), \(\textrm{deg}_{\{b\}}(F') = 3\), and \(\textrm{deg}_{\{a\}}(F') = 2\). However, \(\textrm{deg}_{\{a,b\}}(F') = \infty \). Since it is not possible to satisfy \(F'\) to a degree of 1, \(\{a\}\) is a preferred model of \(F'\).
An alternative semantics for QCL has been proposed in the form of PQCL [1]. Specifically, PQCL changes the semantics for the classical connectives (\(\lnot ,\vee ,\wedge \)), but defines ordered disjunction ( ) in the same way as QCL. For our purposes it suffices to note that negation in PQCL propagates to the atom level, meaning that \(\lnot (F \wedge G)\) is assigned the satisfaction degree of \(\lnot F \vee \lnot G\), \(\lnot (F \vee G)\) is assigned the degree of \(\lnot F \wedge \lnot G\), and
) in the same way as QCL. For our purposes it suffices to note that negation in PQCL propagates to the atom level, meaning that \(\lnot (F \wedge G)\) is assigned the satisfaction degree of \(\lnot F \vee \lnot G\), \(\lnot (F \vee G)\) is assigned the degree of \(\lnot F \wedge \lnot G\), and  is assigned the degree of
is assigned the degree of  .
.
3 Comments on Negation
While choice logics are a useful formalism to express both soft constraints (preferences) and hard constraints (truth) in a single language, existing semantics (such as QCL and PQCL) are not entirely uncontroversial. Table 1 shows how negation acts on ordered disjunction in both systems: negation in QCL erases preferences, while in PQCL it is possible to satisfy a formula and its negation at the same time (\(\{a\}\) and \(\{b\}\) classically satisfy both  and
and  ). Moreover, in PQCL, the satisfaction degree of \(\lnot F\) does not only depend on the degree and optionality of F (\(\{a\}\) and \(\{a,b\}\) satisfy
). Moreover, in PQCL, the satisfaction degree of \(\lnot F\) does not only depend on the degree and optionality of F (\(\{a\}\) and \(\{a,b\}\) satisfy  to degree 1, but \(\{a\}\) satisfies
to degree 1, but \(\{a\}\) satisfies  to degree 2 while \(\{a,b\}\) does not satisfy
to degree 2 while \(\{a,b\}\) does not satisfy  at all).
at all).
We will make use of game-theoretic negation to define an alternative semantics for the language of QCL. Our main goal is to define a negation that acts both on hard constraints as in QCL and soft constraints as in PQCL. Specifically, we will ensure that (i) the satisfaction degree of \(\lnot F\) depends only on the degree of F, (ii) formulas and their negation can not be classically satisfied by the same interpretation, (iii) formulas are equivalent to their double negation.
 in QCL (equivalent to \(\lnot a \wedge \lnot b\)) and PQCL (equivalent to
in QCL (equivalent to \(\lnot a \wedge \lnot b\)) and PQCL (equivalent to  ).
).4 A Game for Ordered Disjunction
In this section, we introduce GTS for the language of QCL. As a first step, let us briefly recall Hintikka’s game [10] over a classical propositional formula F and an interpretation \(\mathcal {I}\). There are two players, Me and You, both of which can act in the role of Proponent (\(\textbf{P}\)) or Opponent (\(\textbf{O}\)). The game starts with Me as \(\textbf{P}\) of the formula F and You as \(\textbf{O}\). At formulas of the form \(G_1 \vee G_2\), \(\textbf{P}\) chooses a formula \(G_i\) that the game continues with. At formulas of the form \(G_1 \wedge G_2\) it is \(\textbf{O}\)’s choice. At negations \(\lnot G\), the game continues with G and a role switch. The outcome of the game is a propositional variable a. The player currently in the role of \(\textbf{P}\) wins the game (and \(\textbf{O}\) loses) iff \(a\in \mathcal {I}\). Otherwise, \(\textbf{P}\) wins and \(\textbf{O}\) loses. It turns out that I have a winning strategy for the game iff \(\mathcal {I}\models F\).
The first question we must answer in order to introduce our GTS for QCL is how ordered disjunction should be handled in a game-theoretic setting. We propose the following solution: at  it is \(\textbf{P}\)’s choice whether to continue with \(G_1\) or with \(G_2\), but this player prefers \(G_1\). My aim in the game is now not only to win the game but to do so with as little compromise to My preferences as possible. Thus, it is natural to express My preference of \(G_1\)-outcomes \(O_1\) over \(G_2\)-outcomes \(O_2\) via the relation \(O_2 \ll O_1\).
it is \(\textbf{P}\)’s choice whether to continue with \(G_1\) or with \(G_2\), but this player prefers \(G_1\). My aim in the game is now not only to win the game but to do so with as little compromise to My preferences as possible. Thus, it is natural to express My preference of \(G_1\)-outcomes \(O_1\) over \(G_2\)-outcomes \(O_2\) via the relation \(O_2 \ll O_1\).
The second question to answer is how the classical connectives should interact with the newly introduced preferences \(\ll \) between outcomes. For \(G_1 \wedge G_2\) and \(G_1 \vee G_2\) it suffices to simply combine the preferences of \(G_1\) and \(G_2\), as we will see. For \(\lnot G\), the preferences associated with G will be inverted in order to ensure that negation not only acts on hard constraints but also on soft constraints.
Formally, game states will be either of the form \(\textbf{P}:F\) or \(\textbf{O}:F\), where F is a QCL-formula and “\(\textbf{P}\)” and “\(\textbf{O}\)” signify that I currently act in the role of Proponent and Opponent respectively. Each game state appears in the game tree defined below. Every node is labeled with either “I” (when it is My turn) or “Y” (when it is Your turn). If the game reaches a game state g, then the player whose turn it is chooses a child of g in the game tree where the game continues. The relation \(\ll \) captures My preferences on outcomes, as motivated above.
Definition 5 (Game Tree)
We inductively define the game tree \(T(\textbf{P}:F)=(V,E,l)\) with (game) states V and edges E. Leafs of T are called outcomes and are denoted \(\mathcal {O}(T)\). The labeling function l maps nodes of T to the set \(\{I,Y\}\). Moreover, we define a partial order \(\ll \) over outcomes.
-
\((R_a)\) \({T}(\textbf{P}:a)\) consists of the single leaf and \(\ll _{\textbf{P}:a} = \emptyset \).
-
\((R_\lnot )\) \({T}(\textbf{P}:\lnot G)\) consists of a root labeled “I”, the immediate subtree \({T}(\textbf{O}:G)\), and \(\ll _{\textbf{P}:\lnot G}\) equal to \(\ll _{\textbf{O}:G}\).
-
\((R_\wedge )\) \({T}(\textbf{P}: G_1 \wedge G_2)\) consists of a root labeled “Y” and immediate subtrees \({T}({\textbf{P}:G_1}), {T}({\textbf{P}:G_2})\). The preference is given by \(\ll _{\textbf{P}:G_1 \wedge G_2} = \ll _{\textbf{P}:G_1 } \! \cup \! \ll _{\textbf{P}:G_2}\).
-
\((R_\vee )\) \({T}(\textbf{P}: G_1 \vee G_2)\) consists of a root labeled “I” and immediate subtrees \({T}({\textbf{P}:G_1}), {T}({\textbf{P}:G_2})\). The preference is given by \(\ll _{\textbf{P}:G_1 \wedge G_2} = \ll _{\textbf{P}:G_1 } \! \cup \! \ll _{\textbf{P}:G_2}\).
-

 consists of a root labeled “I” and the immediate subtrees \({T}({\textbf{P}:G_1}),{T}({\textbf{P}:G_2})\). Moreover,
consists of a root labeled “I” and the immediate subtrees \({T}({\textbf{P}:G_1}),{T}({\textbf{P}:G_2})\). Moreover, 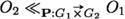 iff \(O_1 \in \mathcal {O}(T(\textbf{P}:G_1))\) and \(O_2 \in \mathcal {O}(T(\textbf{P}:G_2))\), or \(O_2 \ll _{\textbf{P}:G_j} O_1\) for \(j\in \{1,2\}\).
iff \(O_1 \in \mathcal {O}(T(\textbf{P}:G_1))\) and \(O_2 \in \mathcal {O}(T(\textbf{P}:G_2))\), or \(O_2 \ll _{\textbf{P}:G_j} O_1\) for \(j\in \{1,2\}\).
The tree \(T(\textbf{O}:F)\) is defined analogously to \({T}(\textbf{P}:F)\), except that labels are swapped and preferences are switched, i.e., \(O_1 \ll _{\textbf{O}:F} O_2\) iff \(O_2 \ll _{\textbf{P}:F} O_1\).
The game tree from Example 2
Example 2
Figure 1 depicts the game tree for  . Note that
. Note that  is labeled “Y” since roles are switched in
is labeled “Y” since roles are switched in  . The order on outcomes is given by \({\textbf{P}:c} \ll {\textbf{P}:b} \ll {\textbf{P}:a}\) and \({\textbf{O}:a} \ll {\textbf{O}:d}\).
. The order on outcomes is given by \({\textbf{P}:c} \ll {\textbf{P}:b} \ll {\textbf{P}:a}\) and \({\textbf{O}:a} \ll {\textbf{O}:d}\).
An outcome \(\textbf{P}: a\) is true in \(\mathcal {I}\) iff \(a \in \mathcal {I}\). Conversely, \(\textbf{O}: a\) is true iff \(a \not \in \mathcal {I}\). An outcome O is a winning outcome w.r.t an interpretation \(\mathcal {I}\) iff O is true in \(\mathcal {I}\).
To evaluate an interpretation via a game tree, we introduce the payoff function \(\delta _\mathcal {I}\) which will respect My preferences \(\ll \) on My winning outcomes. Given outcome O, let \(\pi _\ll (O) = O_1,..., O_n\) be the longest \(\ll \)-chain starting in O, i.e. \(O_1 = O\), all \(O_i\) are pairwise different, and \(O_i \ll O_{i+1}\) for \(1 \le i < n\). The length of \(\pi _\ll (O)\) is \(|\pi _\ll (O)| = n\).
Definition 6 (Payoff)
\(\delta _{\mathcal {I}}\) maps outcomes of a game tree T into \(Z := (\mathbb {Z} \setminus \{0\},\trianglelefteq )\). The ordering \(\trianglelefteq \) is the inverse of the natural ordering on \(\mathbb {Z}^-\) and on \(\mathbb {Z}^+\) and for \(k \in \mathbb {Z}^-, \ell \in \mathbb {Z}^+\) we set \(k \triangleleft \ell \), i.e. \(-1 \triangleleft -2 \triangleleft \ldots \triangleleft 2 \triangleleft 1\). For an outcome \(O \in \mathcal {O}(T)\), we setFootnote 1
We write \(\delta \) instead of \(\delta _\mathcal {I}\) if \(\mathcal {I}\) is clear from context.
Winning outcomes are ascribed a payoff in \(\mathbb {Z}^+\) and losing outcomes have a payoff in \(\mathbb {Z}^-\). Intuitively, it is better for Me to have a higher payoff with respect to \(\trianglelefteq \). If both \(O_1\) and \(O_2\) are winning outcomes (or if they both are losing outcomes), then \(\delta _\mathcal {I}(O_1) \triangleleft \delta _\mathcal {I}(O_2)\) iff \(O_1 \ll O_2\). If \(O_1\) is a losing outcome and \(O_2\) is a winning outcome, then \(\delta _\mathcal {I}(O_1) \triangleleft \delta _\mathcal {I}(O_2)\). See Fig. 2 for a graphical representation of winning ranges and preferences.
Example 3 (Example 2 cont.)
The winning outcomes for \(\mathcal {I} = \{a\}\) are \({\textbf{P}:a},{\textbf{O}:d}\) with \(\delta ({\textbf{P}:a}) \,{=}\, 1\), \(\delta ({\textbf{P}:b}) \,{=}\, -2\), \(\delta ({\textbf{P}:c}) \,{=}\, -1\), \(\delta ({\textbf{O}:a}) \,{=}\, -1\), \(\delta ({\textbf{O}:d}) \,{=}\, 1\).
We are now ready to formally define the notion of a game.
Definition 7 (Game)
A game \(\textbf{NG} = (T(\textbf{Q}:F),\delta _\mathcal {I})\), also written \(\textbf{NG}(\textbf{Q}:F,\mathcal {I})\), is a pair, where \(T(\textbf{Q}:F)\) is a game tree and \(\delta _\mathcal {I}\) is a payoff-function with respect to some interpretation \(\mathcal {I}\).
The goal of both players is to win the game with as little compromise as possible, and thus force the opponent in as much compromise as possible. To this end, we must consider the optimal strategies that both players have at their disposal. A strategy \(\sigma \) for Me in a game can be understood as My complete game plan. For every node of the game tree labeled “I”, \(\sigma \) tells Me to which node I have to move.
Definition 8 (Strategy)
A strategy \(\sigma \) for Me for the game \(\textbf{NG}\) is a subset of the nodes of the underlying tree such that (i) the root of T is in \(\sigma \) and for all \(v\in \sigma \), (ii) if \(l(v) = I\), then at least one successor of v is in \(\sigma \) and (iii) if \(l(v) = Y\), then all successors of v are in \(\sigma \). A strategy for You is defined symmetrically. We denote by \(\varSigma _I\) and \(\varSigma _{Y}\) the set of all strategies for Me and You, respectively.
Conditions (i) and (iii) make sure that all possible moves by the other player are taken care of by the game plan. Note that each pair of strategies \(\sigma _I \in \varSigma _{I}\), \(\sigma _{Y} \in \varSigma _{Y}\) defines a unique outcome of \(\textbf{NG}\), which we will denote by \(O(\sigma _I,\sigma _{Y})\). We abbreviate \(\delta (O(\sigma _I,\sigma _{Y}))\) by \(\delta (\sigma _I,\sigma _{Y})\). A strategy \(\sigma _I^*\) for Me is called winning if, playing according to this strategy, I win the game, no matter how You move, i.e. for all \(\sigma _{Y} \in \varSigma _{Y}\), \(\delta (\sigma _I^*, \sigma _{Y})\in \mathbb {Z}^+\). An outcome O that maximizes My pay-off in light of Your best strategy is called maxmin-outcome. Formally, O is a maxmin-outcome iff \(\delta (O) = \max ^{\trianglelefteq }_{\sigma _I} \min ^\trianglelefteq _{\sigma _{Y}} \delta (\sigma _I,\sigma _{Y})\) and \(\delta (O)\) is called the maxmin-value of the game. A strategy \(\sigma _I^*\) for Me is a maxmin-strategy for \(\textbf{NG}\) if \(\sigma _I^* \in \textrm{arg}\max ^{\trianglelefteq }_{\sigma _I} \min ^\trianglelefteq _{\sigma _{Y}} \delta (\sigma _I,\sigma _{Y})\), i.e. the maximum is reached at \(\sigma _I^*\). Minmax values and strategies for You are defined symmetrically.
The class of games that we have defined falls into the category of zero-sum perfect information games in game theory. They are characterized by the fact that the players have strictly opposing interests. In these games, the minmax and maxmin value always coincide and is referred to as the value of the game.
Example 4 (Example 2 cont.)
I have a winning strategy for \(\mathcal {I} = \{a,d\}\): if you move to the left at the root, I will reach \(\textbf{P}:a\) with optimal payoff 1. If You go to the right instead, You still cannot win the game but You can minimize My payoff by reaching \(\textbf{O}:a\) with \(\delta (\textbf{O}:a)=2\) instead of \(\textbf{O}:d\) with \(\delta (\textbf{O}:d)=1\). Thus, the value of the game is 2.
Now let \(\mathcal {I} = \{d\}\) with payoffs \(\delta _\mathcal {I}({\textbf{P}:c}) = -1\), \(\delta ({\textbf{P}:b}) = -2\), \(\delta ({\textbf{P}:a}) = -3\), \(\delta ({\textbf{O}:a}) = 2\), \(\delta ({\textbf{O}:d}) = -2\). In this game, I have no winning strategy: if You move to the left at the root, it is best for Me to reach \({\textbf{P}:a}\) with payoff \(-3\). If You move to the right, You can force \({\textbf{O}:d}\) with payoff \(-2\). Thus, it is better for You to move to the right at the root note, giving us the game value \(-2\).
5 Game-Induced Choice Logic (GCL)
To examine the properties of our GTS and compare it with QCL, we extract a novel degree-based semantics for the language of QCL from our game \(\textbf{NG}\). The resulting logic will be called Game-induced Choice Logic (GCL). Syntactically, GCL is defined in the same way as QCL (cf. Definition 1), i.e., F is a GCL-formula iff F is a QCL-formula. The optionality function of GCL is denoted by \(\textrm{opt}^{\mathcal {G}}\) and defined in the same way as \(\textrm{opt}\) (cf. Definition 2), except for negation.
Definition 9 (Optionality in GCL)
The optionality of GCL-formulas is defined inductively as follows: (i) \(\textrm{opt}^{\mathcal {G}}(a) = 1\) for \(a \in \mathcal {U}\), (ii) \(\textrm{opt}^{\mathcal {G}}(\lnot F) = \textrm{opt}^{\mathcal {G}}(F)\), (iii) \(\textrm{opt}^{\mathcal {G}}({F \wedge G}) = \textrm{opt}^{\mathcal {G}}({F \vee G}) = \max (\textrm{opt}^{\mathcal {G}}(F),\textrm{opt}^{\mathcal {G}}(G))\), (iv)  .
.
The degree-function of GCL is denoted by \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}\), and maps pairs of formulas and interpretations to values in the domain \((Z,\trianglelefteq )\) (cf. Definition 6).
Definition 10 (Satisfaction Degree in GCL)
The satisfaction degree of GCL-formulas under an interpretation \(\mathcal {I}\) is defined inductively as follows:

If \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \in \mathbb {Z}^+\), then \(\mathcal {I}\) classically satisfies F (\(\mathcal {I}\) is a model of F). In contrast to QCL, those interpretations that result in a higher degree relative to the ordering \(\trianglelefteq \) are more preferable, which is why we take the maximum degree for disjunction and the minimum degree for conjunction. However, since \(\trianglelefteq \) inverts the order on \(\mathbb {Z}^+\), a degree of 1 is considered to be higher than a degree of 2. Preferred models are defined analogously to QCL (cf. Definition 4).
Definition 11 (Preferred Model under GCL-semantics)
Let F be a GCL-formula. An interpretation \(\mathcal {I}\) is a preferred model of F iff \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \in \mathbb {Z}^+\) and, for all interpretations \(\mathcal {J}\), \(\textrm{deg}_\mathcal {J}^{\mathcal {G}}(F) \trianglelefteq \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\).
We are now ready to show that \(\textbf{NG}\) and GCL are semantically equivalent, which will allow us to examine properties of \(\textbf{NG}\) via GCL. As a first step, we show that the the notion of optionality, which must be defined a-priori in degree-based semantics, arises naturally in our game.
Proposition 1
The longest \(\ll \)-chain in \(\mathcal {O}({\textbf{Q}:F})\) has length \(\textrm{opt}^{\mathcal {G}}(F)\), where \(\textbf{Q} \in \{\textbf{P},\textbf{O}\}\).
Proof
By structural induction. For the base case \(F = a\), where \(a \in \mathcal {U}\), this clearly holds, as \(\textrm{opt}^{\mathcal {G}}(a) = 1\).
Induction step: for the inductive hypothesis we assume that for two GCL-formulas A, B the longest \(\ll \)-chain \(O_1,\ldots ,O_k\) in \(\mathcal {O}({\textbf{Q}:A})\) has length \(k = \textrm{opt}^{\mathcal {G}}(A)\) and the longest \(\ll \)-chain \(O'_1,\ldots ,O'_\ell \) in \(\mathcal {O}({\textbf{Q}:B})\) has length \(\ell = \textrm{opt}^{\mathcal {G}}(B)\).
\(F = \lnot A\): since negation results in a role switch with inverted preferences, the longest \(\ll \)-chain in \(\mathcal {O}({\mathbf {Q'}:\lnot A})\), where \(\mathbf {Q'} \in \{\textbf{P},\textbf{O}\} \setminus \{\textbf{Q}\}\), is \(O_k,\ldots ,O_1\) with length \(k = \textrm{opt}^{\mathcal {G}}(A) = \textrm{opt}^{\mathcal {G}}(\lnot A)\).
\(F = (A \wedge B)\): Note that \(\ll _{\textbf{Q}:A \wedge B} = \ll _{\textbf{Q}:A } \cup \ll _{\textbf{Q}:B}\). Moreover, \(\mathcal {O}({\textbf{Q}:A})\) and \(\mathcal {O}({\textbf{Q}:B})\) are disjoint, i.e., the longest \(\ll \)-chain in \(\mathcal {O}({\textbf{Q}:A \wedge B})\) has length \(\max (k,\ell ) = \max (\textrm{opt}^{\mathcal {G}}(A),\textrm{opt}^{\mathcal {G}}(B)) = \textrm{opt}^{\mathcal {G}}(A \wedge B)\).
\(F = (A \vee B)\) is analogous to \(F = (A \wedge B)\).
 : by construction of
: by construction of  (cf. Definition 5), the longest \(\ll \)-chain in
(cf. Definition 5), the longest \(\ll \)-chain in  is \(O_1,\ldots ,O_k,O'_1,\ldots ,O'_\ell \) with a length of
is \(O_1,\ldots ,O_k,O'_1,\ldots ,O'_\ell \) with a length of  . \(\square \)
. \(\square \)
The following results express semantic equivalence between \(\textbf{NG}\) and GCL. The key is to show that the degree-based semantics captures My preferences in the game as induced by the choice connective  .
.
Theorem 1
The value of \(\textbf{NG}(\textbf{P}:F,\mathcal {I})\) is \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\). The value of \(\textbf{NG}(\textbf{O}:F,\mathcal {I})\) is \(-\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\).
Proof
We fix an interpretation \(\mathcal {I}\). For this proof, we introduce some handy notation: for a game state \(\textbf{Q}:F\), let \(d(\textbf{Q}:F)\) denote the maxmin-value and \(O(\textbf{Q}:F)\) the maxmin-outcome of the game \(\textbf{NG}(\textbf{Q}:F,\mathcal {I})\), and \(W(\textbf{Q}:F)\) and \(L(\textbf{Q}:F)\) the set of its winning and losing outcomes, respectively. Let \(\delta ^{\textbf{Q}:F}_\mathcal {I}\) denote the payoff function for the game \(\textbf{NG}(\textbf{Q}:F,\mathcal {I})\). We proceed by structural induction on F, starting with the cases where \(\textbf{Q} = \textbf{P}\).
\(F = a\): This game consists of a single node v. The longest \(\ll \)-chain starting at v has length 1. Therefore, \(d({\textbf{P}:a}) = 1\) iff \(a\in \mathcal {I}\) iff \(\textrm{deg}_\mathcal {I}^\mathcal {G}(a) = 1\), and \(d({\textbf{P}:a}) = -1\) iff \(a\notin \mathcal {I}\) iff \(\textrm{deg}_\mathcal {I}^\mathcal {G}(a) = -1\).
\(F = G_1 \vee G_2\): In the first round, I choose between \(\textbf{P}:G_1\) and \(\textbf{P}:G_2\). By the inductive hypothesis, the values of these games are \(\textrm{deg}_\mathcal {I}^\mathcal {G}(\textbf{P}:G_1)\) and \(\textrm{deg}_\mathcal {I}^\mathcal {G}(\textbf{P}:G_2)\), respectively. Since I am looking to maximize My payoff, I move to the subgame with maximal payoff:
\(F = G_1 \wedge G_2\) is analogous to \(F = G_1 \vee G_2\).
 : From the fact that \(\delta _\mathcal {I}\) respects \(\ll \) for the winning outcomes of both players and the game rule of
: From the fact that \(\delta _\mathcal {I}\) respects \(\ll \) for the winning outcomes of both players and the game rule of  , we observe the following facts: First, if the \(G_1\)-game is winning for Me, I go to \(G_1\) in the first round. Secondly, if \(G_1\) is losing and \(G_2\) is winning, I go to \(G_2\). And thirdly, if both games are losing, I go to \(G_1\). Since all outcomes of the \(G_2\)-games are in \(\ll \)-relation to all outcomes of the \(G_1\)-game, we have by Proposition 1 for all outcomes O:
, we observe the following facts: First, if the \(G_1\)-game is winning for Me, I go to \(G_1\) in the first round. Secondly, if \(G_1\) is losing and \(G_2\) is winning, I go to \(G_2\). And thirdly, if both games are losing, I go to \(G_1\). Since all outcomes of the \(G_2\)-games are in \(\ll \)-relation to all outcomes of the \(G_1\)-game, we have by Proposition 1 for all outcomes O:
The last case comes from the fact that \(O \gg O'\) for all \(O' \in \mathcal {O}(\textbf{P}:G_2)\), Proposition 1 and the definition of \(\delta _\mathcal {I}\). We now use the inductive hypothesis: in the first case from above, \(O({\textbf{P}:F}) \in W({\textbf{P}:G_1})\) and therefore \(d({\textbf{P}:F}) = d({\textbf{P}:G_1}) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(G_1)\). In the second case, \(O({\textbf{P}:F}) \in W({\textbf{P}:G_2})\) and therefore \(d({\textbf{P}:F}) = d({\textbf{P}:G_2})+\textrm{opt}(G_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(G_2)+\textrm{opt}(G_1)\). Finally, in the third case, \(O({\textbf{P}:F}) \in L({\textbf{P}:G_1})\) and therefore \(d({\textbf{P}:F}) = d({\textbf{P}:G_1})-\textrm{opt}(G_2) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(G_2)-\textrm{opt}(G_2)\).
\(F = \lnot G\): The game continues at \({\textbf{O}:G}\). Therefore, using the inductive hypothesis, \(d({\textbf{P}:F}) = d({\textbf{O}:G}) = -\textrm{deg}_\mathcal {I}^{\mathcal {G}}(G) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\).
Cases where I am in the role of Opponent are similar. For example, let us consider \({\textbf{O}: G_1 \wedge G_2}\). In the first move I choose between the two subgames \({\textbf{O}:G_1}\) and \({\textbf{O}:G_2}\). I seek to maximize My payoff, so I go to the subgame with maximal value. Therefore, using the inductive hypothesis,
The argument can be adapted analogously for the other logical connectives. \(\square \)
Negation in our new semantics behaves as desired. To see this, compare the discussion in Sect. 3 to statements (i–iii) in Proposition 2 below. Intuitively, negation in GCL preserves information on preferences by allowing for degrees of dissatisfaction. For example, the formula  can only be satisfied by \(\emptyset \). However, we must also inspect the interpretations that do not satisfy the formula: \(\{b\}\) results in a degree of \(-2\) while \(\{a\}\) and \(\{a,b\}\) result in a degree of \(-1\), meaning that \(\{b\}\) is more preferable than \(\{a\}\) and \(\{a,b\}\).
can only be satisfied by \(\emptyset \). However, we must also inspect the interpretations that do not satisfy the formula: \(\{b\}\) results in a degree of \(-2\) while \(\{a\}\) and \(\{a,b\}\) result in a degree of \(-1\), meaning that \(\{b\}\) is more preferable than \(\{a\}\) and \(\{a,b\}\).
Moreover, De Morgan’s laws still hold in GCL, and ordered disjunction is still associative (see statements (iv–vi) in Proposition 2).
Definition 12 (Equivalence)
Two GCL-formulas F and G are equivalent, written \(F \equiv G\), iff \(\textrm{opt}^{\mathcal {G}}(F) = \textrm{opt}^{\mathcal {G}}(G)\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(G)\) for all \(\mathcal {I} \subseteq \mathcal {U}\).
Proposition 2
The following holds:
-
(i)
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \! = \! \textrm{deg}_\mathcal {J}^{\mathcal {G}}(F) \iff \textrm{deg}_\mathcal {I}^{\mathcal {G}}(\lnot F) \! = \! \textrm{deg}_\mathcal {J}^{\mathcal {G}}(\lnot F)\)
-
(ii)
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \in \mathbb {Z}^+ \iff \textrm{deg}_\mathcal {I}^{\mathcal {G}}(\lnot F) \in \mathbb {Z}^-\)
-
(iii)
\(F \equiv \lnot \lnot F\)
-
(iv)
\(\lnot (F \wedge G) \equiv \lnot F \vee \lnot G\)
-
(v)
\(\lnot (F \vee G) \equiv \lnot F \wedge \lnot G\)
-
(vi)

Proof
Statements (i–iii) follow by definition of negation in GCL, i.e., \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(\lnot F) = - \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\). Let us consider statements (iv–vi):
-
(i)
First, note that \(\textrm{opt}^{\mathcal {G}}(\lnot (F \wedge G)) = \textrm{opt}^{\mathcal {G}}(F \wedge G) = \max \{\textrm{opt}(F),\textrm{opt}(G)\} = \max \{\textrm{opt}(\lnot F),\textrm{opt}(\lnot G)\} = \textrm{opt}^{\mathcal {G}}(\lnot F \vee \lnot G)\). Moreover, for any \(\mathcal {I} \subseteq \mathcal {U}\), we have \(\deg _\mathcal {I}(\lnot (F \wedge G)) = -\textrm{min}_\trianglelefteq \{\deg _\mathcal {I}(F),\deg _\mathcal {I}(G)\} = \textrm{max}_\trianglelefteq \{-\deg _\mathcal {I}(F),-\deg _\mathcal {I}(G)\} = \deg _\mathcal {I}(\lnot F \vee \lnot G)\).
-
(ii)
Analogous to (iv).
-
(iii)
Associativity of \(\wedge , \vee \) follows from associativity of \(\min \)/\(\max \) over any total order like Z (cf. Definition 6). For example: \(\textrm{min}_\trianglelefteq \{a,\textrm{min}_\trianglelefteq \{b,c\}\} = \textrm{min}_\trianglelefteq \{a,b,c\} = \textrm{min}_\trianglelefteq \{\textrm{min}_\trianglelefteq \{a,b\},\textrm{min}_\trianglelefteq \{c\}\}\). We now show associativity of
 . Let
. Let  . \(\textrm{opt}^{\mathcal {G}}(F_1) = \textrm{opt}^{\mathcal {G}}(F_2)\) is immediate. Let \(\mathcal {I}\) be an arbitrary interpretation. We can show \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_2)\) by distinguishing all cases for \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A), \textrm{deg}_\mathcal {I}^{\mathcal {G}}(B), \textrm{deg}_\mathcal {I}^{\mathcal {G}}(C) \in \{\mathbb {Z}^-,\mathbb {Z}^+\}\).
. \(\textrm{opt}^{\mathcal {G}}(F_1) = \textrm{opt}^{\mathcal {G}}(F_2)\) is immediate. Let \(\mathcal {I}\) be an arbitrary interpretation. We can show \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_2)\) by distinguishing all cases for \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A), \textrm{deg}_\mathcal {I}^{\mathcal {G}}(B), \textrm{deg}_\mathcal {I}^{\mathcal {G}}(C) \in \{\mathbb {Z}^-,\mathbb {Z}^+\}\).-
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\). Then \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_2) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(A)\). Moreover,
 and therefore \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(A)\).
and therefore \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(A)\). -
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^-\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\). Then
 and
and  . Thus, \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_2) = \textrm{opt}^{\mathcal {G}}(A) + \textrm{deg}_\mathcal {I}^{\mathcal {G}}(B)\).
. Thus, \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_1) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F_2) = \textrm{opt}^{\mathcal {G}}(A) + \textrm{deg}_\mathcal {I}^{\mathcal {G}}(B)\). -
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^-\), \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^-\), and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(C) \in \mathbb {Z}^+\). Then
 and
and 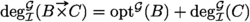 . Observe that
. Observe that  and thus
and thus  .
. -
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^-\), \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^-\), and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(C) \in \mathbb {Z}^-\). Then
 . Thus,
. Thus,  q. \(\square \)
q. \(\square \)
-
While GCL deviates from QCL, the two logics agree when it comes to classical satisfaction, as expressed by the following result.
Proposition 3
\(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}(F) < \infty \).
Proof
By structural induction. Let \(\mathcal {I} \subseteq \mathcal {U}\). For the base case \(F = a\), where \(a \in \mathcal {U}\), we distinguish two cases: If \(a \in \mathcal {I}\), then \(\textrm{deg}_\mathcal {I}(a) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(a) = 1\). If \(a \not \in \mathcal {I}\), then \(\textrm{deg}_\mathcal {I}(a) = \infty \) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(a) = -1\).
Induction step: the I.H. is that \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}(A) < \infty \), and that \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}(B) < \infty \).
\(F = \lnot A\): \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(\lnot A) \! \in \! \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \! \in \! \mathbb {Z}^-\) iff \(\textrm{deg}_\mathcal {I}(A) \! = \! \infty \) iff \(\textrm{deg}_\mathcal {I}(\lnot A) \! < \! \infty \).
\(F = (A \wedge B)\): \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A \wedge B) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}(A) < \infty \) and \(\textrm{deg}_\mathcal {I}(B) < \infty \) iff \(\textrm{deg}_\mathcal {I}(A \wedge B) < \infty \).
\(F = (A \vee B)\): \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A \vee B) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) or \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\) iff \(\textrm{deg}_\mathcal {I}(A) < \infty \) or \(\textrm{deg}_\mathcal {I}(B) < \infty \) iff \(\textrm{deg}_\mathcal {I}(A \vee B) < \infty \).
 : analogous to \(F = (A \vee B)\). \(\square \)
: analogous to \(F = (A \vee B)\). \(\square \)
Moreover, if we allow negation only in front of classical formulas, QCL and GCL agree even when it comes to (positive) satisfaction degrees.
Proposition 4
If F is a QCL-formula in which negation is only applied to classical formulas, \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \in \mathbb {Z}^+\) implies \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) = \textrm{deg}_\mathcal {I}(F)\).
Proof
By structural induction. Let \(\mathcal {I} \subseteq \mathcal {U}\). In this proof, \(\min _\trianglelefteq \) and \(\max _\trianglelefteq \) are relative to \(\trianglelefteq \) (cf. Definition 6) while \(\min _\le \) and \(\max _\le \) are relative to the regular order on integers.
Base case: let F be a classical formula. Assume \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(a) \in \mathbb {Z}^+\). By Proposition 3 this implies \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) < \infty \). Thus, \(\textrm{deg}_\mathcal {I}(F) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) = 1\).
Induction step: let A and B be formulas such that negation only appears in front of classical formulas, i.e., if \(\lnot G\) is a subformula of A or B then G is a classical formula. The I.H. is that \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) implies \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) = \textrm{deg}_\mathcal {I}(A)\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\) implies \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) = \textrm{deg}_\mathcal {I}(B)\).
\(F = (A \wedge B)\): assume \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A \wedge B) \in \mathbb {Z}^+\). Then we have \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\). This means that, \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A\wedge B) = \min _\trianglelefteq (\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A),\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B)) = \max _\le (\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A),\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B)) = \max _\le (\textrm{deg}_\mathcal {I}(A),\textrm{deg}_\mathcal {I}(B)) = \textrm{deg}_\mathcal {I}(A\wedge B)\).
\(F = (A \vee B)\): assume \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A \vee B) \in \mathbb {Z}^+\). Then either \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) or \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\). If both \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\) the proof is analogous to \(F = (A \wedge B)\). Suppose \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^+\) and \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^-\) (the other case is symmetric). By Proposition 3, \(\textrm{deg}_\mathcal {I}(B) = \infty \). Thus, \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A\vee B) = \max _\trianglelefteq (\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A),\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B)) = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) = \textrm{deg}_\mathcal {I}(A) = \min _\le (\textrm{deg}_\mathcal {I}(A),\textrm{deg}_\mathcal {I}(B)) = \textrm{deg}_\mathcal {I}(A\vee B)\).
 : assume
: assume  . If
. If  . If \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^-\), then \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\). By Proposition 3, \(\textrm{deg}_\mathcal {I}(A) = \infty \). Then
. If \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(A) \in \mathbb {Z}^-\), then \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(B) \in \mathbb {Z}^+\). By Proposition 3, \(\textrm{deg}_\mathcal {I}(A) = \infty \). Then  . Note that \(\textrm{opt}^{\mathcal {G}}(A) = \textrm{opt}(A)\) holds because negation is only applied to classical formulas in A, and, except for negation, optionality is defined equivalently in QCL and GCL. \(\square \)
. Note that \(\textrm{opt}^{\mathcal {G}}(A) = \textrm{opt}(A)\) holds because negation is only applied to classical formulas in A, and, except for negation, optionality is defined equivalently in QCL and GCL. \(\square \)
Note that Propositions 3 and 4 do not hold if we substitute QCL for PQCL. Regarding Proposition 3, recall that, in PQCL, an interpretation may classically satisfy a formula F and its negation \(\lnot F\) (see Sect. 3), which is not possible in GCL. As for Proposition 4, classical conjunction and disjunction are defined differently in PQCL compared to QCL and GCL.
Lastly, we investigate the computational complexity of GCL (and therefore our game \(\textbf{NG}\)). Familiarity with complexity classes \(\textsf{P}\), \(\textsf{NP}\), and \(\textsf{coNP}\) is assumed. Moreover, the complexity class \(\varTheta _{2}^\textsf{P}\) contains the problems solvable in polynomial time with access to \(O(\log (n))\)-many \(\textsf{NP}\)-oracle calls [16]. We consider decision problems pertaining to the preferred models of a formula.
Definition 13
We define the following two decision problems:
-
PMChecking: given a GCL-formula F and an interpretation \(\mathcal {I}\), is \(\mathcal {I}\) a preferred model of F?
-
PMContainment: given a GCL-formula F and a variable \(x \in \mathcal {U}\), is there a preferred model \(\mathcal {I}\) of F such that \(x \in \mathcal {I}\)?
For QCL, PMChecking is \(\textsf{coNP}\)-complete while PMContainment is \(\varTheta _{2}^\textsf{P}\)-complete [4]. Intuitively, PMChecking is \(\textsf{coNP}\)-complete for QCL since we must go through all other interpretations to check that our given interpretation \(\mathcal {I}\) results in an optimal degree. The same is true in the case of GCL.
Proposition 5
PMChecking is \(\textsf{coNP}\)-complete for GCL.
Proof
\(\textsf{NP}\)-membership of the complementary problem: given a GCL-formula F and an interpretation \(\mathcal {I}\), compute \(k = \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\) (this can be done in polynomial time) and check whether \(k \in \mathbb {Z}^+\). If no, then \(\mathcal {I}\) is not a preferred model and we are done. If yes, non-deterministically guess an interpretation \(\mathcal {J}\) and check whether \(k \triangleleft \textrm{deg}_\mathcal {J}^{\mathcal {G}}(F)\). If yes, then \(\mathcal {I}\) is not a preferred model, i.e. \((F,\mathcal {I})\) is a yes-instance for the complementary problem of PMChecking.
\(\textsf{coNP}\)-hardness by reduction from UnsatFootnote 2: given a classical formula F, we construct the GCL-formula

where a is a fresh variable that does not occur in F. It holds that F is unsatisfiable iff \(\{a\}\) is a preferred model of \(F'\):
Assume F is unsatisfiable. Note that \(\{a\}\) satisfies \(F'\) to a degree of 2. Moreover,  can not be satisfied to a degree more preferable than 2. Thus, to satisfy \(F'\) to a degree of 1 we must satisfy F, which is not possible.
can not be satisfied to a degree more preferable than 2. Thus, to satisfy \(F'\) to a degree of 1 we must satisfy F, which is not possible.
Assume F is satisfiable, i.e., there is some interpretation \(\mathcal {I}\) that satisfies F. Note that we can assume \(a \not \in \mathcal {I}\), since a is a fresh variable. Then \(\mathcal {I}\) satisfies \(F'\) to a degree of 1. But \(\{a\}\) satisfies \(F'\) to a degree of 2. \(\square \)
As for PMContainment, \(\varTheta _{2}^\textsf{P}\)-completeness in the case of QCL can intuitively be explained by the fact that we must first find the optimal degree m for the given formula F. This can be done via binary search, using \(O(\log (\textrm{opt}(F)))\) \(\textsf{NP}\)-oracle calls. Then, a last oracle call suffices to guess an interpretation \(\mathcal {I}\) and check whether \(\textrm{deg}_\mathcal {I}(F) = m\) and \(a \in \mathcal {I}\). This algorithm can be adapted for GCL.
Proposition 6
PMContainment is \(\varTheta _{2}^\textsf{P}\)-complete for GCL.
Proof
\(\varTheta _{2}^\textsf{P}\)-membership: let F be a GCL-formula and \(a \in \mathcal {U}\). First, using an \(\textsf{NP}\)-oracle call, check whether there is some interpretation \(\mathcal {I}\) such that \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) \in \mathbb {Z}^+\). If no, then F has no preferred models and we have a no-instance. If yes, we continue. We conduct a binary search over \((1,\ldots ,\mathrm {opt^{\mathcal {G}}}(F))\). At each step of the binary search we use an \(\textsf{NP}\)-oracle call to check whether there is some interpretation \(\mathcal {I}\) such that \(k \trianglelefteq \textrm{deg}_\mathcal {I}^{\mathcal {G}}(F)\), where k is the current mid-point of the binary search. If yes, we continue the binary search over \((1,\ldots ,k-1)\), otherwise we continue with \((k+1,\ldots ,\mathrm {opt^{\mathcal {G}}}(F))\). In this way, we find the optimal degree m with which F can be satisfied, i.e., every preferred model of F must satisfy F to a degree of m. The binary search requires \(O(\log (\mathrm {opt^{\mathcal {G}}}(F)))\) \(\textsf{NP}\)-oracle calls. Note that \(\mathrm {opt^{\mathcal {G}}}(F)\) is linear in the size of F, since  . Finally, we make one last \(\textsf{NP}\)-oracle call to guess an interpretation \(\mathcal {I}\) and check whether \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) = m\) and \(a \in \mathcal {I}\).
. Finally, we make one last \(\textsf{NP}\)-oracle call to guess an interpretation \(\mathcal {I}\) and check whether \(\textrm{deg}_\mathcal {I}^{\mathcal {G}}(F) = m\) and \(a \in \mathcal {I}\).
\(\varTheta _{2}^\textsf{P}\)-hardness: in the \(\varTheta _{2}^\textsf{P}\)-hardness proof of PMContainment for QCL (see Proposition 19 in [4]), a formula \(F'\) is constructed in which negation is only applied to atoms, i.e., if \(\lnot G\) is a subformula of \(F'\) then G is a propositional variable. By our Proposition 4, this means that an interpretation \(\mathcal {I}\) is a preferred model of \(F'\) in QCL if and only if \(\mathcal {I}\) is a preferred model of \(F'\) in GCL. Thus, the same construction used in the hardness proof of QCL works for GCL. \(\square \)
We have shown that the complexity of GCL with respect to preferred models is the same as that of QCL. Note that the complexity of PQCL has not been formally investigated yet (to the best of our knowledge).
6 Conclusion
We propose a game-theoretic semantics (GTS) for the language of Qualitative Choice Logic (QCL), and thereby show that GTS are well-suited for languages in which soft and hard constraints are expressed in a single language.
We extract the degree-based Game-induced Choice Logic (GCL) from our GTS and show equivalence between the two formalisms. By leveraging game-theoretic negation, our new semantics avoids the contentious behavior of negation in QCL and Prioritized QCL (PQCL) while retaining desirable properties such as associativity of ordered disjunction. Moreover, we show that the complexity of GCL is the same as that of QCL when it comes to preferred models.
Regarding future work, our game semantics can be lifted to a provability game [8, 9] by which a cut-free sequent calculus can be obtained. We also plan to investigate how our approach can be adapted to formalisms related to QCL such as other choice logics [4, 5] or the recently introduced lexicographic logic [7].
Notes
- 1.
Notice the flipped \(\ll \)-sign in the second case.
- 2.
In the \(\textsf{coNP}\)-complete Unsat problem we are given a classical formula F and ask whether \(\mathcal {I} \not \models F\) for all interpretations \(\mathcal {I}\).
References
Benferhat, S., Sedki, K.: Two alternatives for handling preferences in qualitative choice logic. Fuzzy Sets Syst. 159(15), 1889–1912 (2008)
van Benthem, J.: Logic in Games. MIT Press, Cambridge (2014)
Bernreiter, M., Lolic, A., Maly, J., Woltran, S.: Sequent calculi for choice logics. In: Blanchette, J., Kovács, L., Pattinson, D. (eds.) IJCAR 2022. LNCS, vol. 13385, pp. 331–349. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-10769-6_20
Bernreiter, M., Maly, J., Woltran, S.: Choice logics and their computational properties. Artif. Intell. 311, 103755 (2022)
Boudjelida, A., Benferhat, S.: Conjunctive choice logic. In: ISAIM 2016, Fort Lauderdale, Florida, USA, 4–6 January 2016 (2016)
Brewka, G., Benferhat, S., Berre, D.L.: Qualitative choice logic. Artif. Intell. 157(1–2), 203–237 (2004)
Charalambidis, A., Papadimitriou, G., Rondogiannis, P., Troumpoukis, A.: A many-valued logic for lexicographic preference representation. In: KR 2021, Online event, 3–12 November 2021, pp. 646–650 (2021)
Fermüller, C.G., Metcalfe, G.: Giles’s game and the proof theory of Łukasiewicz logic. Stud. Logica 92(1), 27–61 (2009)
Freiman, R.: Games for hybrid logic. In: Silva, A., Wassermann, R., de Queiroz, R. (eds.) WoLLIC 2021. LNCS, vol. 13038, pp. 133–149. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-88853-4_9
Hintikka, J.: Logic, Language-Games and Information: Kantian Themes in the Philosophy of Logic. Clarendon Press, Oxford (1973)
Hodges, W., Vänänen, J.: Logic and games. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University, fall 2019 edn. (2019)
Pigozzi, G., Tsoukiàs, A., Viappiani, P.: Preferences in artificial intelligence. Ann. Math. Artif. Intell. 77(3–4), 361–401 (2016)
Sedki, K., Lamy, J., Tsopra, R.: Qualitative choice logic for modeling experts recommendations of antibiotics. In: Proceedings of the Thirty-Fifth International Florida Artificial Intelligence Research Society Conference, FLAIRS 2022, Hutchinson Island, Jensen Beach, Florida, USA, 15–18 May 2022 (2022)
Tulenheimo, T.: Classical negation and game-theoretical semantics. Notre Dame J. Form. Logic 55(4), 469–498 (2014)
Vänänen, J.: Models and Games. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2011)
Wagner, K.W.: Bounded query classes. SIAM J. Comput. 19(5), 833–846 (1990)
Acknowledgements
We thank the anonymous reviewers for their feedback. This work was funded by the Austrian Science Fund (FWF) under grants P32830 and P32684, the Vienna Science and Technology Fund (WWTF) under grant ICT19-065, and partially funded by the EU (Marie Skłodowska-Curie RISE) project MOSAIC, grant 101007624.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Freiman, R., Bernreiter, M. (2023). Truth and Preferences - A Game Approach for Qualitative Choice Logic. In: Gaggl, S., Martinez, M.V., Ortiz, M. (eds) Logics in Artificial Intelligence. JELIA 2023. Lecture Notes in Computer Science(), vol 14281. Springer, Cham. https://doi.org/10.1007/978-3-031-43619-2_37
Download citation
DOI: https://doi.org/10.1007/978-3-031-43619-2_37
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43618-5
Online ISBN: 978-3-031-43619-2
eBook Packages: Computer ScienceComputer Science (R0)





 consists of a root labeled “I” and the immediate subtrees
consists of a root labeled “I” and the immediate subtrees 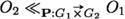 iff
iff 


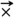 . Let
. Let  .
.  and therefore
and therefore  and
and  . Thus,
. Thus,  and
and 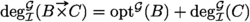 . Observe that
. Observe that  and thus
and thus  .
. . Thus,
. Thus,  q.
q.