Inflation of Hyperelastic Curved Tubes

Abstract

This paper deals with the problem of inflation of curved thin-walled hyperelastic tubes. Nonlinear elastic membrane theory and the Fung model of material are used. Tubes with elliptic cross-sections are considered. The influence of internal pressure on tube curvature and the shape of its cross-section is investigated.

13.1 Introduction

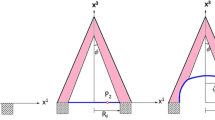
Thin-walled straight and curved tubes are a structural element of many technical systems and living objects, such as vessel walls, pipelines, pneumatic structures, soft robots and devices. They are often loaded by internal pressure. A straight tube of constant thickness under internal pressure remains a straight tube with deformed cross-section and length. Inflation leads to change a cross-section and curvature of tube. This effect is widely used in Bourdon pressure tubes (Feodos’ev 1949).

At present, two directions of research can be distinguished in the inflation problem of a curved tube. In the first case, nonlinearity of the displacement problem is taken into account, but the linear strain theory is used Feodos’ev (1949), Levyakov (1997). In the second case, nonlinearity of displacements and strains is considered. In the framework of membrane theory, such a problem is presented in Kolesnikov (2011a), Kolesnikov (2015). This approach is valid for thin-walled tubes of hyperelastic material at large strains.

The tube inflation problem is a special case of the more general problem of pure bending of a tube under internal pressure, Libai and Simmonds (1988), Zubov (2001). For straight tubes, this problem has been studied in Koga (1972), Haseganu and Steigmann (1994), Haughton and McKay (1996) and Kolesnikov and Zubov (2009). The curved tubes are considered in Kolesnikov (2011b), Levyakov (2017) and Kolesnikov et al. (2019). The works show that the internal pressure increases the bending stiffness of the tube.

Studies of inflation of curved thin-walled tubes made of hyperelastic material are presented in Kolesnikov (2011a), Kolesnikov (2015). In Kolesnikov (2011a), circular cross-section tubes made of Mooney–Rivlin and neo-Hookean material are considered. It is shown that the tube unbends under inflation. That is, the curvature of the centre line decreases. In Kolesnikov (2015), the tubes of neo-Hookean material with elliptical cross-section are investigated. It is shown that at the beginning of inflation the cross-section of the tube tends to a circular shape. Depending on the ratio of the semi-axes, the tube is either bent or unbent. After the cross-section becomes close to circular, the tube unbends under inflation. A peculiarity of the behaviour of the neo-Hookean material is its instability under biaxial tension. This appears, for example, in straight or curved tube inflation as the existence of two different shapes of the tube corresponding to the same pressure. And also the pressure has a maximum on the curve “pressure–cross-sectional radius”.

In this paper, we consider the inflation problem of curved thin-walled tubes of constant thickness made of Fung material. The problem is solved within the framework of the nonlinear theory of elastic membranes. The aim of this work is to investigate the influence of the cross-section shape and the material parameters of the tube on its behaviour under the internal pressure. The monitored parameters are the curvature of the centre line and the average radius of the cross-section.

13.2 Inflation of Pressurized Curved Tube

In this paper, we will base on the previously presented mathematical model of inflating of a curvilinear thin-walled tube (Kolesnikov 2015), which is a special case of pure bending of an inflated curvilinear tube (Kolesnikov et al. 2019). In this section, we give the basic relations of this model.

In the initial state, the membrane surface is defined by the following equations:

$$\begin{aligned} \begin{aligned} \nonumber & \boldsymbol{\textrm{r}} = x_1(s) \boldsymbol{\textrm{i}}_1 + x_2(s) \boldsymbol{\textrm{e}}_2, \quad s \in [0; S], \quad t \in [0;T]. \\ & \boldsymbol{\textrm{e}}_2 = \boldsymbol{\textrm{i}}_2 \cos {\beta t} + \boldsymbol{\textrm{i}}_3 \sin {\beta t}, \quad \boldsymbol{\textrm{e}}_3 =-\boldsymbol{\textrm{i}}_2 \sin {\beta t} + \boldsymbol{\textrm{i}}_3 \cos {\beta t} . \end{aligned} \end{aligned}$$

The membrane remains a curvilinear tube with changed curvature and cross-section under internal pressure. Its surface can be described as Libai and Simmonds (1988), Zubov (2001)

$$\begin{aligned} \begin{aligned} & \boldsymbol{\textrm{R}} = X_1(s) \boldsymbol{\textrm{i}}_1 + X_2(s) \boldsymbol{\textrm{E}}_2, \\ & \boldsymbol{\textrm{E}}_2 = \boldsymbol{\textrm{i}}_2 \cos {B t} + \boldsymbol{\textrm{i}}_3 \sin {B t}, \quad & \boldsymbol{\textrm{E}}_3 = - \boldsymbol{\textrm{i}}_2 \sin {B t} + \boldsymbol{\textrm{i}}_3 \cos {B t}. \end{aligned} \end{aligned}$$

(13.1)

Here, B is the unknown new curvature of the central axis, and $X_1(s)$ and $X_2(s)$ are unknown functions describing the cross-section of the inflated tube.

Let’s introduce the principal stretch ratios of elongation $\lambda _1$, $\lambda _2$ and the angle of the tangent to the cross-section $\psi$:

$$\begin{aligned} \lambda _1(s) = \sqrt{\frac{ {X_1'}^2 + {X_2'}^2 }{ {x_1'}^2 + {x_2'}^2 }}, \quad \lambda _2(s) = \sqrt{\frac{ B^2 X_2^2 }{ \beta ^2 x_2^2 }}, \quad \tan {\psi (s)} = \frac{X_2'}{X_1'}. \end{aligned}$$

(13.2)

The equilibrium equations of the membrane in this case can be written in the form Kolesnikov (2015), Kolesnikov et al. (2019)

$$\begin{aligned} & X_1'(s) = \sqrt{g_{11}} \lambda _1 \cos {\psi }, \quad X_2'(s) = \sqrt{g_{11}} \lambda _1 \sin {\psi }, \end{aligned}$$

(13.3)

$$\begin{aligned} & \lambda _2'(s) = B \sqrt{\frac{g_{11}}{g_{22}}} \lambda _1 \sin {\psi } - \frac{g_{22}'}{2 g_{22}} \lambda _2. \end{aligned}$$

(13.4)

$$\begin{aligned} & \frac{\partial ^2\,W}{\partial \lambda _1^2} \lambda _1' = \left( \frac{\partial W}{\partial \lambda _2} - \lambda _1 \frac{\partial ^2\,W}{\partial \lambda _1 \lambda _2} \right) B \sqrt{\frac{g_{11}}{g_{22}}} \sin {\psi } - \nonumber \\ & - \left( \frac{\partial W}{\partial \lambda _1} - \lambda _2 \frac{\partial ^2\,W}{\partial \lambda _1 \lambda _2} \right) \frac{g_{22}'}{2 g_{22}} - \frac{h'}{h} \frac{\partial W}{\partial \lambda _1}, \end{aligned}$$

(13.5)

$$\begin{aligned} & \frac{\partial W}{\partial \lambda _1} \psi ' = B \sqrt{\frac{g_{11}}{g_{22}}} \frac{\partial W}{\partial \lambda _2} \cos {\psi } + \frac{\xi }{h} \sqrt{g_{11}} \lambda _1 \lambda _2. \end{aligned}$$

(13.6)

The principal stress resultants in the membrane are determined by the equations

$$\begin{aligned} L_1 = \frac{h}{\lambda _2} \frac{\partial W}{\partial \lambda _1}, \quad L_2 = \frac{h}{\lambda _1} \frac{\partial W}{\partial \lambda _2}. \end{aligned}$$

(13.7)

We assume that the cross-section of the tube is closed. The boundary conditions for the unknown functions at the points $s=0, S$ are their periodicity. The boundary conditions at the ends ($t=0, T$) of the tube are satisfied in the integral sense. In this problem, the resultant force and the resultant couple of the stresses in the membrane and the internal pressure are equal to zero:

$$\begin{aligned} \int \limits _0^S{\sqrt{G_{11}} L_2 ds} - \xi \Sigma = 0, \end{aligned}$$

(13.8)

$$\begin{aligned} \int \limits _0^S{\sqrt{G_{11}} L_2 (X_2 - X_{C2}) ds} = 0. \end{aligned}$$

(13.9)

Here $X_{2C}$ is the centre of mass of the area bounded by the membrane contour in the cross-sectional plane. For a given potential energy function of deformation, the static problem of an elastic membrane is reduced to the boundary value problem for the system of ordinary differential equations (13.3)–(13.6) with parameter B. The boundary value problem is solved numerically by the shooting method.

13.3 Results

In this paper, we consider a tube made from incompressible Fung material. The strain energy function is given as

$$\begin{aligned} W = \frac{\mu }{2 \gamma } \left( \text {e}^{\gamma (I_1 - 3)} - 1 \right) , \quad I_1 = \lambda _1^2 + \lambda _2^2 + \frac{1}{\lambda _1^2 \lambda _2^2}. \end{aligned}$$

(13.10)

A correct choice of dimensionless parameters will give results independent of the material parameter $\mu$. Below results will be presented for the material parameter $\gamma = 5$, 0.2 and 0.05. Also, for comparison, some results will be presented for the neo-Hookean material, including those from Kolesnikov (2015).

We assume that the thickness $h = 0.001$ is constant and that the cross-section of the curved tube is elliptical and defined by the equations

$$\begin{aligned} x_1(s) = r_1 \sin {s}, \quad x_2(s) = \beta ^{-1} - r_2 \cos (s), \quad s \in [0; 2 \pi ]. \nonumber \end{aligned}$$

Also we assume that $T = \pi /(2 \beta )$.

Next we consider the curved tube with the curvature of the central axis $\beta = 0.1$. The cross-sectional dimensions $r_1$ and $r_2$ are given in Table 13.1. The number in the first line corresponds to the curve number in Figs. 13.1, 13.2, 13.3, 13.4, 13.5, 13.6, 13.7, 13.8 and 13.9. As will be shown below, the shape of the cross-section has a significant influence on the deformation of the curved tube. During inflation, the curved tube bends or unbends in the plane $\boldsymbol{\textrm{e}}_2 \boldsymbol{\textrm{e}}_3$. The tube 5 has a circular cross-section. The cross-section of the tubes 1–4 is an ellipse extended along the axis $\boldsymbol{\textrm{i}}_1$ and flattened along the axis $\boldsymbol{\textrm{e}}_2$. For the tubes 6–9, the cross-section is elongated along the $\boldsymbol{\textrm{e}}_2$-axis and flattened along the $\boldsymbol{\textrm{i}}_1$-axis.

To present the results, we introduce a dimensionless pressure $p^*$ and a relative curvature $B^*$ as follows:

$$\begin{aligned} \nonumber p^* = \frac{\xi r_0}{\mu h}, \quad B^* = \frac{B}{\beta } . \end{aligned}$$

In addition, we introduce dimensionless parameters characterizing the deformed cross-section

$$\begin{aligned} & R_1 = \max { \left\{ \frac{2 X_1(s)}{r_1 + r_2}, s \in [0; \pi ] \right\} }, \end{aligned}$$

(13.11)

$$\begin{aligned} & R_2 = \frac{X_2(\pi ) - X_2(0)}{r_1 + r_2}, \quad R_0 = \frac{R_1 + R_2}{r_1 + r_2} . \end{aligned}$$

(13.12)

The deformed cross-section is not an ellipse. However, we can correspond parameters $R_1$ and $R_2$ to the semi-axes $r_1$ and $r_2$ of the initial elliptical cross-section. The parameter $R_0$ will be called the mean radius of the deformed cross-section. In the present work, we consider the undeformed cross-sections such that their mean radii are 1, as can be seen from Table 13.1.

Table 13.1 The cross-section parameters

In this work, we investigate the effect of the material parameter $\gamma$ and the elliptical cross-section on the curvature of the inflated tube B and the mean radius of cross-section $R_0$. Figures 13.1, 13.2 and 13.3 show the relationship between the curvature of central axis $B^*$ and pressure $p^*$. The solid lines correspond to the results for the Fung material with parameter $\gamma = 5$, 0.2 and 0.05, respectively. The dotted lines correspond to the results for the neo-Hookean material. The curve numbers in the figures correspond to the column numbers in Table 13.1.

Fig. 13.1

The pressure $p^*$ versus the curvature $B^*$ ($\gamma = 5$)

Fig. 13.2

The pressure $p^*$ versus the curvature $B^*$ ($\gamma = 0.2$)

Fig. 13.3

The pressure $p^*$ versus the curvature $B^*$ ($\gamma = 0.05$)

Up to a certain pressure $p^*$, the “curvature–pressure” curves for the tubes made of Fung material coincide with one for the tubes made of neo-Hookean material. At $\gamma = 5$, the magnitude of this pressure $p^* \approx 0.4$, at $\gamma = 0.2$ – $p^* \approx 0.5$, at $\gamma = 0.05$ – $p^* \approx 0.6$. The tube 5 with a circular cross-section gradually unbends under pressure increasing, i.e. the curvature decreases. For the tubes 1–4, for which $r_1 > r_2$, the curvature first decreases dramatically, i.e. the tubes unbend sharply under the internal pressure. The greater the ratio $r_1/r_2$, the more the tube unbends. The curvature then continues to decrease, but at a much slower rate. For the tubes 6–9, for which $r_1 < r_2$, the curvature first increases dramatically, that is, the tubes bend sharply under the internal pressure. The smaller the ratio $r_1/r_2$, the more the tube bends. Then the curvature begins to slowly decrease, i.e. the tube begins to unbend.

Further, the behaviour of a tube made of Fung material depends on the material parameter $\gamma$ and differs significantly from that for neo-Hookean tube. At $\gamma = 5$ (Fig. 13.1) for pressures $p^* > 0.4$, the curvature slowly monotonically decreases with increasing pressure. At $\gamma = 0.2$ (Fig. 13.2) for pressures $p^* > 0.5$ the curvature first decreases, reaching a minimum, then slowly increases with increasing pressure. At $\gamma = 0.05$ (Fig. 13.3) for pressures $p^* > 0.6$ the curve “curvature–pressure” has a loop and a self-intersection point, after which the curvature increases with increasing pressure.

The change in curvature of the tube is related to the deformation of its cross-section. As it is shown in Kolesnikov (2015) that for a curvilinear tube of neo-Hookean material, for $r_1 \in [0.5, 1.5]$ and $r_2 \in [0.5, 1.5]$ the deviation from a circular shape is less than $5\%$ at $p^* > 0.01$. Figures 13.4, 13.5 and 13.6 show the relationship between the ratio of characteristic cross-sectional dimensions $R_1/R_2$ and the pressure $p^*$. As we can see from the figures, the ratio of the characteristic dimensions of the cross-section tends rapidly towards 1. That is, the shape of the deformed cross-section of the curved tube tends to be circular. The elliptical cross-section flattened along the axis $\boldsymbol{\textrm{e}}_2$ (the tubes 1–4) tends the circular shape faster than the cross-section flattened along the axis $\boldsymbol{\textrm{i}}_1$ (the tubes 6–9).

Fig. 13.4

The pressure $p^*$ versus the ratio $R_1 / R_2$ ($\gamma =5$)

Fig. 13.5

The pressure $p^*$ versus the ratio $R_1 / R_2$ ($\gamma =0.2$)

Fig. 13.6

The pressure $p^*$ versus the ratio $R_1 / R_2$ ($\gamma =0.05$)

Since the cross-section of the inflated tube is close to circular, let us consider the relationship between the average radius $R_0$ and pressure $p^*$ shown in Figs. 13.7, 13.8 and 13.9. The solid black lines show the dependence $R_0$–$p^*$ for the tubes made of Fung material at $r_1\le r_2$, and the solid grey lines correspond to $r_1 > r_2$. The thin dotted lines show the dependences of the mean radius for curvilinear tubes of neo-Hookean material. The thick grey dashed line in Figs. 13.7, 13.8 and 13.9, coinciding with the line 5, shows the relation between the radius of a straight tube (cylindrical membrane) and the pressure. That is, for circular curved tubes, a small curvature (in this work, the initial curvature $\beta = 0.1$) has little effect on the deformation of the cross-section.

At the start of inflation, the change in the mean radius depends on the ratio $r_1/r_2$. For the tubes 1–4 with the elliptical cross-section flattened along the axis $\boldsymbol{\textrm{e}}_2$ ($r_1 > r_2$) the mean radius increases sharply, then the curve “mean radius–curvature” becomes similar to the relationship for the tube 5 with circular cross-section, but with a rightward shift (grey curves in Figs. 13.7, 13.8 and 13.9). The more $r_1/r_2$ differs from one, the greater the amount of shift. For the tubes 6–9 with the elliptical cross-section flattened along the axis $\boldsymbol{\textrm{i}}_1$ ($r_1 < r_2$), the dependence of the mean radius $R_0$ on pressure $p^*$ decreases at the beginning of inflation (black curves in Fig. 13.7, 13.8 and 13.9), then it starts increasing with increasing pressure. For tubes where $r_1/r_2 = r_2/r_1$, the curves $R_0$–$p^*$ become very close at $p^* > 0.1$. At $\gamma = 0.05$, the dependence of the mean radius $R_0$ has a descending region and a local minimum, as we can see in Fig. 13.9.

We note that for very small pressures and hence deformations we failed to obtain a numerical solution of the nonlinear differential equations, so for the tubes 1–4 and 6–9 in Figs. 13.1, 13.2 and 13.3 the curves do not start from point $B^* = 1$, and in Figs. 13.7, 13.8 and 13.9 the curves do not start from point $R_0 = 1$, which would correspond to the undeformed state of the tubes. Besides, for the tube 6–9 (Figs. 13.7, 13.8 and 13.9), the dependence $R_0$–$p^*$ should have a sharp growth at very low pressures ($p^* < 0.01$) and reach a local maximum. After that the mean radius decreases, which has already been calculated numerically. We note that at very low pressures and hence deformations, the use of the membrane theory becomes incorrect, as the influence of the bending stiffness will be significant. In addition, at the beginning of inflation of curved tubes, areas of compression are formed in their, which quickly disappear with increasing pressure, as shown in Kolesnikov (2015). The inflation of curved tubes within small deformations has been previously investigated, e.g. by Feodos’ev (1949), Levyakov (1997). The effects of a significant change in curvature of a curved tube with a flattened cross-section is used in manometers (the Bourdon tube) (Feodos’ev 1949; Levyakov 1997).

Fig. 13.7

The pressure $p^*$ versus the average radius $R_0$ ($\gamma =5$)

Fig. 13.8

The pressure $p^*$ versus the average radius $R_0$ ($\gamma =0.2$)

Fig. 13.9

The pressure $p^*$ versus the average radius $R_0$ ($\gamma =0.05$)

Figures 13.10 and 13.11 show how the tube deforms during inflation using the tubes 9 and 1 as examples, respectively. The curves $p^*$–$B^*$ show in the figures, on which the points $P_k^m$ ($k=1,9$, $m=1,\ldots ,7$) are marked and the corresponding shapes of the longitudinal and cross-sections are shown. The grey lines show the initial shapes for comparison.

The points $P_k^m$ ($k=1,9$, $m=1,\ldots ,7$) corresponding to the shapes shown in Figs. 13.10 and 13.11 are marked in Fig. 13.9. As we can see from Fig. 13.9, the points $P_{1,9}^3$ correspond to the local maximum pressure, after which the mean radius increases as the internal pressure decreases. The points $P_{1,9}^5$ correspond to the local minimum of the curves $R_0$–$p^*$.

Fig. 13.10

Planform and cross-sectional views of a deformed tube 9 ($\gamma =0.05$)

Fig. 13.11

Planform and cross-sectional views of a deformed tube 1 ($\gamma =0.05$)

13.4 Conclusions

In this work, we consider the problem of an initially curved thin-walled tube made of hyperelastic material. Due to the small thickness and predominantly tensile stresses, the bending stiffness of the tube walls is neglected and the nonlinear theory of elastic membranes is used. The mechanical properties of the hyperelastic material are described by the Fung strain energy function.

A straight tube changes cross-section and length under inflation. A curved tube additionally changes the curvature. A tube made of neo-Hookean material has a specific behaviour. There is a maximum internal pressure after which the cross-section radius increases under the pressure decreases. This is usually associated with unstable of the tube (Gonçalves et al. 2008; Pearce and Fu 2010; Zubov and Karyakin 2011; Guo et al. 2016; Wang et al. 2019). For the curved tube made of the neo-Hookean material, the mean radius shows the same behaviour. Additionally, the curvature of the tube is reduced.

The elliptical cross-section of a thin-walled curved tube tends to circular shape when inflated. But as long as the pressures are small and they are not yet completely circular, the behaviour of the tubes is very different for different elliptical shapes. Some tubes are sharply unbent, other tubes are bent. This is a well-known effect, in particular used for pressure measurement with Bourdon tubes (Feodos’ev 1949; Levyakov 1997). But for thin-walled highly elastic tubes, rather quickly the cross-section becomes circular, as shown in this paper and in Kolesnikov (2015). Further, as the pressure increases, the behaviour of the tubes becomes similar to that of a tube with a circular cross-section. Their mean radius increases and the curvature decreases (for the neo-Hookean tubes). The difference in the initial shift of the curves “curvature–pressure” to one side or the other depends on the ratio of the semi-axes of the initial elliptical cross-section.

The Fung material has two material parameters. One parameter can be excluded by the introduction of dimensionless parameters, and the other parameter denoted as $\gamma$ cannot be excluded. Up to a certain value of pressure and deformation, a tube made of Fung material has a behaviour similar to the neo-Hookean tube. As the pressure increases, its behaviour begins to differ. The curvature–pressure relation exhibits three possible behaviours depending on the value of $\gamma$: monotonic decrease in curvature, decrease and then increase in curvature (for small $\gamma$); existence of a loop (for even smaller $\gamma$).

The change in curvature is associated with a change in the cross-section. For pressures that are not very small, the monotonicity of the “curvature–pressure” curve corresponds to the constant sign of the curvature of the “mean radius–pressure” curve. For the nonmonotonic “curvature–pressure” curve, the sign of the curvature of the “mean radius–pressure” curve changes, but the curvature itself remains monotonic. For the “curvature–pressure” curve that has a loop, the “mean radius–pressure” curve not only changes the sign of the curvature, but also ceases to be monotonically increasing. The local maximum and minimum on the “radius–pressure” curve is a known fact for straight tubes (Pearce and Fu 2010; Zubov and Karyakin 2011; Wang et al. 2019). This is usually associated with structural instability. According to the theory, the tube jumps from the maximum to the second ascending branch of the curve. In experiments, this is due to local bulging. When the cross-section of the tube increases locally and sharply. And then this extension is extended to the entire tube (Gonçalves et al. 2008; Guo et al. 2016; Wang et al. 2019). For the curved tube, the mechanisms appear to be the same. From the point of local maximum pressure, there will be a transition to the second ascending branch of the solution with an abrupt change in cross-section and curvature.