Intelligent Reentry Guidance with Dynamic No-Fly Zones Based on Deep Reinforcement Learning

Abstract

Aimed at avoiding multiple dynamic no-fly zones and satisfying path constraints and terminal constraints in the reentry process of hypersonic glide vehicles, intelligent reentry guidance based on deep reinforcement learning is developed. Firstly, the guidance is decoupled as longitudinal guidance and lateral guidance. The lateral guidance provides the sign of the bank angle to adjust the heading direction while the longitudinal guidance outputs the magnitude of the bank angle through the artificial intelligence interface. Then, the reentry guidance simulation is mapped to a Markov Decision Process, in which the essential elements including state, action, and reward are defined or designed adaptively. Finally, the policy neural network is trained by the twin delayed deep deterministic policy gradient (TD3) algorithm. By selecting proper hyperparameters and network architecture, the policy neural network is able to converge. Simulations imply that under the influence of dynamic no-fly zones, initial state errors, and kinds of online dispersion, the proposed guidance can avoid all the no-fly zones and reach the target accurately with all the satisfied path constraints.

20.1 Introduction

There has been increasing attention to hypersonic glide vehicles (HGV) due to their high speed, wide flight space, and strong maneuver capability [1,2,3,4,5,6]. After decades of development, reentry guidance has formed a relatively complete methodological system. For HGV, the task complexity and real-time performance are challenging in the future. For example, there are several dynamic no-fly zones whose information is not clear before the flight. HGV is requested to avoid all the no-fly zones and arrive at the specified target area under the premise of satisfying multiple path constraints and terminal constraints. With the help of artificial intelligence, HGV can fly out novel trajectories different from traditional algorithms and complete the mission.

The conventional guidance methods mainly include reference trajectory guidance [7,8,9] and predictor–corrector guidance [10,11,12,13]. For guidance issues with no-fly zones, current methods mainly include trajectory optimization, lateral guidance design, and route planning method. In trajectory optimization methods, the no-fly zones constraint is modeled in the optimization model and the problem is solved by off-line optimization algorithms. Zhao et al. [14] applied the Gauss pseudo-spectral method (GPM) to the multi-phase of the reentry problem and used waypoints to the complete optimization of the trajectory with no-fly zones. Zhao and Song [15] proposed a multiphase convex programming method for the path, waypoint, and no-fly zone constraints, and they solve the second-order conic problem (SOCP) problems with the help of the open-source solver ECOS. Zhang et al. [16] developed a time-optimal memetic whale optimization method based on GPM, which is excellent in both global searching and local convergent, and the simulation shows that the method is competitive in entry trajectory optimization with no-fly zones. The advantage of optimization methods is that by relying on strong search capability, the feasible solution is guaranteed if the scene parameters are in the range of dynamic ability. On the other hand, the computational complexity is commonly huge and not able to implement online with real-time performance.

There are many works based on lateral guidance design and route planning methods. Liang and Ren [17] presented a tentacle-based guidance method to satisfy the no-fly zone constraint, in which the sign of bank angle is determined by the feedback of tentacles. Gao et al. [18] proposed an improved tentacle-based bank angle transient lateral guidance method for avoiding static, dynamic, or unknown no-fly zones. Considering the concise mathematical expression and practicability, the artificial potential field (APF) method and its improved version are applied in reentry guidance with no-fly zone constraints. Zhang et al. [19] combined APF and velocity azimuth angle error threshold in lateral guidance to reduce heading error and avoid no-fly zones. Li et al. [20] proposed an improved APF method, in which the passing waypoints and avoiding no-fly zones problem is transformed into generating the reference heading angle. Li et al. [21] designed an adaptive cross corridor based on the concept of repulsion force in the APF method and the corridor is practicable for conventional guidance logic and avoiding no-fly zones logic. Hu et al. [22] presented an improved APF method for complex distributed no-fly zones, in which the reference heading angle is calculated according to geographic coordinate velocity and the designed potential field function. It can be seen that the methods based on APF are easy to achieve rapid real-time performance and robust to multiple complex no-fly zones. However, the design of the attractive and repulsive potential field is relevant to no-fly zones and other distances, which lacks robustness to unknown scenes and errors.

During recent decades, artificial intelligence technology has experienced rapid development and has been applied in lots of fields. More recently, deep reinforcement learning (DRL) shows excellent decision-making ability in complex high dimension tasks. DRL takes features of tasks as input and output decision results directly, naturally, the end-to-end characteristic makes it easy to handle different tasks. There are some applications of DRL in HGV or avoiding no-fly zones. For example, Yuksek et al. [23] used reinforcement learning and proposed a planning method for the unmanned aerial vehicle, which can avoid no-fly zones and ensure the time-of-arrival constraint.

In DRL algorithms, the AC (actor-critic) framework plays an important role, in which the policy from the actor is used to generate decision actions and the critic is in charge of evaluating the actions in the current state of the environment. Based on policy gradient theory, there is a family of progressive algorithms: deterministic policy gradient (DPG) [24], deep deterministic policy gradient (DDPG) [25], twin delayed deep deterministic policy gradient (TD3) [26], distributed distributional deterministic Policy Gradients (D4PG) [27]. Considering that the guidance command of HGV is generated according to its flight state, the guidance process can be seen as a decision-making mission. And the irreversibility of flight trajectory makes it easy to build a Markov decision process (MDP), that the problem can be solved by the TD3 algorithm.

The purpose of this paper is to develop an intelligent guidance method for reentry problems with several dynamic no-fly zones and constraints. The contributions of this paper can be summarized as follows: The reentry problem with several dynamic no-fly zones is described as an MDP. In MDP, the state is defined by parameters of HGV, the current no-fly zone, and the target. The guidance command of HGV is defined as the action of the agent, which can be seen as the output of a policy neural network and learned by training. Secondly, the action is trained by the TD3 algorithm. Finally, the converged policy network is invoked online with a tremendous real-time performance, which is an advantage in online guidance.

This paper is arranged as follows. Section 20.2 describes the reentry model with no-fly zones. Section 20.3 introduces the general principles of DRL and the TD3 algorithm. Section 20.4 proposes intelligent guidance based on TD3. Section 20.5 shows the training results and verifies the proposed method in simulations. Finally, the conclusions of this work are in Sect. 20.6.

20.2 Problem Model

20.2.1 Dynamics Equations in Reentry Process

Suppose the earth is a spherical non-rotating sphere, the dynamics equations in the reentry process are given by:

$$ \left\{ {\begin{array}{*{20}l} {\dot{V} = - \frac{D}{m} - g\sin \gamma } \hfill \\ {\dot{\gamma } = \frac{L\cos \sigma }{{mV}} - \left( {\frac{g}{V} - \frac{V}{r}} \right)\cos \gamma } \hfill \\ {\dot{\psi } = \frac{L\sin \sigma }{{mV\cos \gamma }} + \frac{V\cos \gamma \sin \psi \tan \phi }{r}} \hfill \\ {\dot{r} = V\sin \gamma } \hfill \\ {\dot{\theta } = \frac{V\cos \gamma \sin \psi }{{r\cos \phi }}} \hfill \\ {\dot{\phi } = \frac{V\cos \gamma \cos \psi }{r}} \hfill \\ \end{array} } \right. $$

(20.1)

where V is the Earth-relative velocity, γ is the flight-path angle, ψ is the heading angle of velocity, r is the distance between the Earth center and HGV, θ is the longitude, ϕ is the latitude, m is the mass of HGV, g is the gravitational acceleration, σ is the bank angle. L and D represent the aerodynamic lift and drag respectively, which are expressed by

$$ \left\{ {\begin{array}{*{20}l} {D = \frac{1}{2}\rho V^2 C_D S_m } \hfill \\ {L = \frac{1}{2}\rho V^2 C_L S_m } \hfill \\ \end{array} } \right. $$

(20.2)

where ρ is the atmospheric density, S_m is the reference area of HGV, C_D and C_L are the drag coefficient and lift coefficient respectively, which depend on the Mach number and angle of attack (AOA).

20.2.2 Constraints in Reentry Process

During the reentry flight, there are several hard path constraints: the maximum heating rate Q̇_max, the maximum dynamic pressure q_max, and the maximum aerodynamic overload n_max. HGV is required to satisfy these constraints:

$$ \left\{ {\begin{array}{*{20}l} {\dot{Q} = k_Q \rho^{0.5} V^{3.15} < \dot{Q}_{\max } } \hfill \\ {q = \frac{1}{2}\rho V^2 < q_{\max } } \hfill \\ {n = \frac{{\sqrt {D^2 + L^2 } }}{m} < n_{\max } } \hfill \\ \end{array} } \right. $$

(20.3)

where Q̇ is the heating rate, q is the dynamic pressure, n is the aerodynamic overload, k_Q is a constant.

Assume that no-fly zones are described as infinite-height cylinders with a central point (θ_i, φ_i) and radius R_i. Then the constraint of no-fly zones is expressed as:

$$ S_i = R_e \arccos (\cos \phi \cos \phi_i \cos (\theta - \theta_i ) + \sin \phi \sin \phi_i ) > R_i + \Delta S $$

(20.4)

where S_i is the distance between HGV and the central point of the ith no-fly zone, R_e is the radius of the earth and ΔS is a safe threshold.

Terminal constraints include altitude, velocity, and distance to the target.

$$ \left\{ {\begin{array}{*{20}l} {\Delta H(t_f ) = |H(t_f ) - H^* | \le \Delta \tilde{H}} \hfill \\ {\Delta S(t_f ) = |V(t_f ) - V^* | \le \Delta \tilde{V}} \hfill \\ {s(t_f ) \le s^* } \hfill \\ \end{array} } \right. $$

(20.5)

where t_f represents the final flight time, H^*, V^*, and s^* are the required altitude, velocity, and distance respectively. In this paper, $\Delta \tilde{H} = 1000\;{\text{m}},\;\Delta \tilde{V} = 20\;{\text{m/s}},\;s^* = 300\;{\text{km}}.$

20.2.3 Guidance Scheme

Longitudinal Guidance

In reentry guidance, the terminal constraints of altitude and velocity are combined as an energy-form variable e

$$ e = \frac{1}{r} - \frac{V^2 }{{2\mu }} $$

(20.6)

where μ is the Earth's gravitational constant. If the Earth rotation is ignored, e is monotonically increasing, which can be set as the termination condition of dynamics integration.

If the final height and velocity are determined, the terminal energy is determined:

$$ e^* = \frac{1}{r^* } - \frac{{V^{*2} }}{2\mu } $$

(20.7)

The integration of dynamics will last until the termination condition is met: e ≥ e^*.

During the reentry process, the trajectory is decided by the AOA α and the bank angle σ. Usually, the AOA profile is a piecewise linear function of velocity or energy. In this paper the AOA is expressed as:

$$ \alpha = \left\{ {\begin{array}{*{20}l} {\alpha_{\max } } \hfill & {V \ge \tilde{V}} \hfill \\ {\alpha_0 + \frac{{\alpha_{\max } - \alpha_{0} }}{V_1 - V_2 }(V - V_2 )} \hfill & {\tilde{V}_2 < V < \tilde{V}} \hfill \\ {\alpha_{0} } \hfill & {V \le \tilde{V}_2 } \hfill \\ \end{array} } \right. $$

(20.8)

where α_max is the max AOA of HGV, α₀ is the AOA when the lift-drag radio gets the maximum value, $\tilde{V}_1$ and $\tilde{V}_2$ are designed values.

The purpose of longitudinal guidance is to generate the magnitude of the bank angle to satisfy the request for height, velocity, and other path constraints. In conventional guidance algorithms, the magnitude of the bank angle is updated iteratively to make the final distance error s(t_f) decrease to 0. In this paper, the magnitude of the bank angle is generated by the intelligent algorithm.

Lateral Guidance

The purpose of lateral guidance is to generate the sign of bank angle to make HGV avoid the no-fly zones and fly to the target. Hence, the lateral guidance in this paper is divided into two phases. In the first phase, there is a closest no-fly zone near the route of HGV, so lateral guidance is designed to avoid the no-fly zone. In the second phase, after all the no-fly zones are avoided, the lateral guidance is designed to satisfy the terminal constraints. Because the velocity and height constraints are satisfied by the termination condition of dynamics integration, the purpose of the second phase can be seen as to decrease the terminal range error. In the first phase, the relative position of the current no-fly zone is described in Fig. 20.1. The LOS (line of sight) angle of the ith no-fly zone ψ_i is calculated by:

$$ \begin{aligned} \lambda_i & = \arccos (\sin \phi \sin \phi_i + \cos \phi \cos \phi_i \cos (\theta - \theta_i )) \\ \psi_i & = \arccos \frac{\sin \phi_i - \sin \phi \cos \lambda_i }{{\cos \phi \sin \lambda_i }} \\ \end{aligned} $$

(20.9)

Fig. 20.1

HGV and current no-fly zone

where λ_i is the geocentric angle between HGV and the ith no-fly zone.

In Fig. 20.1, the horizontal axis represents the east and the vertical axis represents the north. According to the direction of V, there are four areas: I, II, III, and IV. When HGV is in the II area, it should output a negative bank angle to decrease ψ and avoid the current no-fly zone quickly. Conversely, When HGV is in the III area, it should output a positive bank angle to increase ψ. When HGV is in the I and IV area, it should output a negative and positive bank angle respectively to increase the angle between V and LOS direction |Δψ_i|. There is a criterion for whether the current ith no-fly zone has been avoided:

$$ |\Delta \psi_i | = |\psi - \psi_i | > 90^{\circ} $$

(20.10)

which means that when the HGV passes through the II area and enters the I area, the sign of the bank angle should keep minus until the criterion (20.10) is satisfied. Similarly, When HGV is in the III and IV area, it should output a positive bank angle.

Hence, in the first phase, the sign of the bank angle is decided by:

$$ {\textit{sign}}(\sigma ) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\psi > \psi_i } \hfill \\ { - 1} \hfill & {\psi \le \psi_i } \hfill \\ \end{array} } \right. $$

(20.11)

In the second phase, the LOS angle of target ψ_tar is expressed as:

$$ \begin{aligned} \psi_{tar} & = \arccos \frac{{\sin \phi_{tar} - \sin \phi \cos \lambda_{tar} }}{{\cos \phi \sin \lambda_{tar} }} \\ \lambda_{tar} & = \arccos (\sin \phi \sin \phi_{tar} + \cos \phi \cos \phi_{tar} \cos (\theta - \theta_{tar} )) \\ \end{aligned} $$

(20.12)

where λ_tar is the geocentric angle between HGV and the target.

The sign of the bank angle is decided by the lateral corridor:

$$ {\textit{sign}}(\sigma ) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\Delta \psi > \Delta \psi_{up} } \hfill \\ {{\textit{sign}}(\sigma )} \hfill & {\Delta \psi_{low} \le \Delta \psi \le \Delta \psi_{up} } \hfill \\ { - 1} \hfill & {\Delta \psi < \Delta \psi_{low} } \hfill \\ \end{array} } \right. $$

(20.13)

where Δψ = ψ−ψ_tar, is the heading error, Δψ_up and Δψ_low are the upper and lower bound:

$$ \Delta \psi_{up} = \left\{ {\begin{array}{*{20}l} {\psi_1 + \frac{\psi_2 - \psi_2 }{{V_2 - V_1 }}(V - V_1 )} \hfill & {V_1 < V \le V_2 } \hfill \\ {\psi_2 } \hfill & {V_2 < V \le V_3 } \hfill \\ {\psi_2 + \frac{\psi_3 - \psi_2 }{{V_4 - V_3 }}(V - V_3 )} \hfill & {V_3 < V \le V_4 } \hfill \\ \end{array} } \right. $$

(20.14)

where V₁ = 2000 m/s, V₂ = 3500 m/s, V₃ = 6500 m/s, V₄ = 7000 m/s, ψ₁ = 2°, ψ₁ = 2°, ψ₁ = 10°. The corridor is shown in Fig. 20.2.

Fig. 20.2

Corridor of heading angle error

20.3 TD3 Algorithm

20.3.1 Deep Reinforcement Learning

Commonly the sequential decision-making problem can be modeled as a Markov Decision Process (MDP), in which there are elements including state, action, and reward. The object who makes decisions is called an agent and the agent is in a dynamic environment. The agent can interact with the environment State is a variable that can describe the features of the environment. The agent takes an action or decides according to the state. Then the environment is transformed from state S₁ to the next state S₂. At the same time, the agent gets a reward from the environment. The interaction progress will last until some termination condition is met. So there is a tuple <S_i, A_i, S_i+1, R_i> at every interaction time. For the agent, the goal is to maximize the total discounted reward in the whole process:

$$ G_t = \sum_{k = 0}^\infty {\lambda^k R_{t + k + 1} } $$

(20.15)

where λ is the discount rate which determines the present value of future rewards.

In RL, the agent's policy π is a mapping from states to probabilities of selecting some possible action, and π(a|s) means the probability that A_t = a if S_t = s.

The action-value function for policy π is q(s, a):

$$ q_\pi (s,a) = E_\pi [G_t |S_t = s,A_t = a] = E_\pi \left[ {\sum_{k = 0}^\infty {\lambda^k R_{t + k + 1} } |S_t = s,A_t = a} \right] $$

(20.16)

Similarly, the state-value function v_π(s) is defined as:

$$ v_\pi (s) = E_\pi [G_t |S_t = s] = E_\pi \left[ {\sum_{k = 0}^\infty {\lambda^k R_{t + k + 1} } |S_t = s} \right] $$

(20.17)

There is an optimal action-value function q^*(s, a) which satisfies that:

$$ q^* (s,a) = {\mathop {\max }\limits_\pi } q_\pi (s,a),\forall s \in {\mathcal{S}} $$

(20.18)

At this point, the policy π^* is called the optimal policy. In DRL, the policy is implemented by a neural network parameterized by θ^π. This is implemented by a neural network parameterized by θ^Q. The purpose of DRL training is to find the optimal parameters θ^π and θ^Q, which means that the best policy for the agent is found.

20.3.2 TD3 Algorithm

The baseline algorithm used in this paper for the neural network training is the twin delayed deep deterministic policy gradient (TD3), which is an improved version of the deep deterministic policy gradient (DDPG). In DDPG, there is a policy network actor parameterized by π (s| θ^π) and an evaluation network critic parameterized by Q (s, a| θ^Q). The input of the actor is the state of the environment s and it outputs the actions a. The input of the critic is the combination of s, a and it outputs the approximate action-value function Q (s, a). And two target networks are designed to make the training process stable, the target actor network parameterized by π′(s| θ^π’) and the target critic network parameterized by Q′(s, a| θ^Q’).

The update of the critic is based on the gradient descent method. According to the Bellman Equations, the loss of critic L(θ^Q) is expressed as:

$$ L(\theta^Q ) = {\mathbf{\mathbb{E}}}[(r(s_t ,a_t ) + \lambda Q^{\prime}(s_{t + 1} ,\pi^{\prime}(s_{t + 1} |\theta^{\pi^{\prime}} )|\theta^{Q^{\prime}} ) - Q(s_t ,a_t |\theta^Q ))^2 ] $$

(20.19)

By updating the parameter θ^Q, the critic is closer and closer to the optimal Q(s, a), which means that the evaluation of action is getting accurate gradually.

The actor π(s, a|θ^π) is updated according to the theory of policy gradient:

$$ \begin{array}{*{20}l} {\nabla_{\theta^\pi } J \approx {\mathbf{\mathbb{E}}}_{s_t \sim \xi } [\nabla_{\theta^\pi } Q(s,a|\theta^Q )|_{s = s_t ,a = \pi (s_t ,\theta^\pi )} ]} \hfill \\ {\quad \quad \quad \quad = {\mathbf{\mathbb{E}}}_{s_t \sim \xi } [\nabla_a Q(s,a|\theta^Q )_{s = s_t ,a = \pi (s_t )} \nabla_{\theta^\pi } \pi (s|\theta^\pi )_{s = s_t } ]} \hfill \\ \end{array} $$

(20.20)

where J is the objective to be optimized and ξ is the distribution of state.

Compared with DDPG, twin delayed deep deterministic policy gradient (TD3) has three improvements. First of all, TD3 provides two different critic networks including critic 1 parameterized by $Q_1 (s,a|\theta^{Q_1 } )$ and critic 2 parameterized by $Q_2 (s,a|\theta^{Q_2 } )$. In the training process, the smaller output value of critic 1 and critic 2 is set as the target Q value, which can overcome the overestimation of the Q value.

$$ y = r(s_t ,a_t ) + \lambda \min \{ Q^{\prime}_1 (s_{t + 1} ,\tilde{a}_{t + 1} |\theta^{Q^{\prime}_1 } ),Q^{\prime}_2 (s_{t + 1} ,\tilde{a}_{t + 1} |\theta^{Q^{\prime}_2 } )\} $$

(20.21)

where the next action is calculated by

$$ \tilde{a}_{t + 1} = \pi^{\prime}(s_{t + 1} |\theta^{\pi^{\prime}} ) + \varepsilon $$

(20.22)

where ε ~ clip ($\rm{\mathcal{N}}$ (0, $\tilde{\sigma}$), −c, c) is the clipped noise in the range of [−c, c], in which $\tilde{\sigma}$ is the variance of the noise.

The loss of critic 1 L($\theta^{Q_1 }$) and the loss of critic 2 L($\theta^{Q_2 }$) are

$$ \left\{ {\begin{array}{*{20}l} {L(\theta^{Q_1 } ) = {\mathbf{\mathbb{E}}}[(y - Q(s_t ,a_t |\theta^{Q_1 } ))^2 ]} \hfill \\ {L(\theta^{Q_2 } ) = {\mathbf{\mathbb{E}}}[(y - Q(s_t ,a_t |\theta^{Q_2 } ))^2 ]} \hfill \\ \end{array} } \right. $$

(20.23)

Secondly, the update of policy is delayed, which means that TD3 updates critic networks more frequently than the actor and gets a higher quality policy update. The delayed update is meaningful because only if the critic is accurate, the improvement of policy is valuable.

Thirdly, TD3 adds a small amount of random noise to the target policy in Eq. (20.22), and the noise is clipped to keep the target close to the original action, in which way target policy smoothing is realized.

The three target networks are updated periodically:

$$ \left\{ {\begin{array}{*{20}l} {\theta^{\pi^{\prime}} \leftarrow (1 - \tau )\theta^\pi + \tau \theta^{\pi^{\prime}} } \hfill \\ {\theta^{Q^{\prime}_1 } \leftarrow (1 - \tau )\theta^{Q_1 } + \tau \theta^{Q^{\prime}_1 } } \hfill \\ {\theta^{Q^{\prime}_2 } \leftarrow (1 - \tau )\theta^{Q_2 } + \tau \theta^{Q^{\prime}_2 } } \hfill \\ \end{array} } \right. $$

(20.24)

where τ is the soft update factor.

20.4 Intelligent Guidance Law Based on TD3

20.4.1 Framework for Intelligent Guidance

In this section, the TD3-based guidance is proposed.

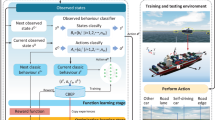
Firstly, the reentry including the no-fly zones process is normalized into two functions (scenario initialization function and policy cycle function) and the interfaces are open to the TD3 algorithm. In the scenario initialization function, the motion parameters of HGV are initialized randomly within a certain range. The information of N no-fly zones is also set randomly. At each policy step, HGV gets a magnitude command of the bank angle and generates the sign of the bank angle according to lateral guidance. The simulation proceeds until the energy e > e^* or any path constraint is not satisfied. Then, the transformation from the reentry process to MDP is accomplished. The kinematical parameters of HGV are mapped to states, and the guidance command of bank angle is designed as the action. The reward function is designed according to whether avoiding the no-fly zones and arriving at the neighborhood of the target. Finally, based on TD3, the algorithm goes into operation as is shown in Fig. 20.3.

Fig. 20.3

Algorithm flow of intelligent guidance law

20.4.2 Markov Decision Process

The fundamental variables in MDP are defined as follows. Firstly, we divide the glide phase into two phases. In Phase I, there is one no-fly zone in HGV's flight path, which need to be avoided. In Phase II, HGV has passed through all the no-fly zones, so it needs to fix its path and approach the target.

• (1) States

The basic state of the HGV agent in Phase I is defined as s = s_I = [V, γ, ψ, r, θ, ϕ, 1, θ_now, ϕ_now, R_now, V^*], where θ_now, ϕ_now, and R_now are the longitude, latitude, and geocentric distance of current no-fly zone, which can uniquely express the features of the current situation. Considering dynamic no-fly zones, the information about no-fly zones is unknown before the flight.

Then, after the HGV has passed through all the no-fly zones, the state in Phase II is redefined as s = s_II = [V, γ, ψ, r, θ, ϕ, 0, θ_tar, ϕ_tar, H^*, V^*], where θ_tar, ϕ_tar are the longitude, latitude of the target. The design of s_II aims to guide the HGV to the target.

• (2) Actions

Since the AOA is decided by profile and the sign of the bank angle is decided by lateral guidance, the action of the agent is mapped to the magnitude of the bank angle. So no matter what phase the HGV is in, the action is defined as a ∈ [0, σ_max], where σ_max is the maximum bank angle. Then the command of bank angle σ_cmd is obtained:

$$ \sigma_{cmd} = {\textit{sign}}(\sigma ) \cdot a $$

(20.25)

where the sign of the bank angle sign(σ) is given by lateral guidance.

• (3) Rewards

The reward function plays a decisive role in guiding HGV to avoid the no-fly zones and achieve the target accurately. The reward function is shown as follows:

$$ R_I = \left\{ {\begin{array}{*{20}l} {10,} \hfill & {|\psi - \psi_i | > 90^{\circ} } \hfill \\ {0,} \hfill & {|\psi - \psi_i | \le 90^{\circ} } \hfill \\ \end{array} } \right. $$

(20.26)

where R_I is the no-fly-zone-related reward. The design of R_I means that when the HGV passes through the current no-fly zone, the agent will get a positive reward.

$$ R_{{\text{II}}} = \left\{ {\begin{array}{*{20}l} {50 + \frac{40 - 50}{{300 - 0}}(s(t_f ) - 0),} \hfill & {s(t_f ) \le 300} \hfill \\ {40 + \frac{10 - 40}{{500 - 300}}(s(t_f ) - 300),} \hfill & {300 < s(t_f ) \le 500} \hfill \\ {10,} \hfill & {500 < s(t_f ) \le 2000} \hfill \\ {1,} \hfill & {s(t_f ) > 2000} \hfill \\ \end{array} } \right. $$

(20.27)

where s(t_f) is the terminal distance error (unit km) and R_II is the target-related reward in the second phase. The piecewise linear functions are designed to guide the agent to reduce the final distance to the target. When HGV is in Phase I and Phase II, the reward is R_I and R_II respectively.

20.4.3 Steps of the Algorithm

Based on TD3, the intelligent reentry guidance is proposed as follows:

20.4.4 Structures of Neural Networks

The structure of the actor is shown in Table 20.1 and the structure of the two critics is shown in Table 20.2.

Table 20.1 Structure of the actor

Table 20.2 Structure of the critics

20.5 Verification and Simulation

20.5.1 Parameters Settings

The hardware device used in the simulation is Intel-i5 CPU, RTX 3060Ti GPU, and 16GB RAM. The software used for training is PyTorch and Python. The hyperparameters in the training are given in Table 20.3.

Table 20.3 Hyperparameters in the training

HGV parameters are set according to the common aero vehicle (CAV-H). The mentioned parameters in simulation are set as follows: m = 907 kg, g = 9.8066 m/s², S_m = 0.4839 m², ρ₀ = 1.225 kg/m³, β = 0.000141, R_e = 6378004 m, k_Q = 5 × 10^–5, q_max = 100 kPa, n_max = 3, Q̇_max = 2000 kW/m², V_re = 2500 m/s, ΔS = 1000 m, α_max = 20°, α₀ = 10°, $\tilde{V}_1$ = 5000 m/s, $\tilde{V}_2$ = 3000 m/s, σ_max = 85°. The number of no-fly zones is 3. The integration step size is 0.01 s and the guidance (policy) step size is 200 s.

The random parameters used in simulations are shown in Table 20.4.

Table 20.4 Range of random parameters in simulations

20.5.2 Training Result of Policy Network

After the training of 6665 episodes, the policy network converges. The average returns and success rates in the latest 100 episodes are shown in Fig. 20.4.

Fig. 20.4

Average return and success rates in the latest 100 episodes

At the end of the training process, the success rates reach and stabilize at 100%, which means that the policy network can output stable and valid commands. The average return fluctuates slightly in the range of 70–80, which coincides with the design of reward in Eqs. (20.26) and (20.27).

20.5.3 Verifications on Random Trajectories

The well-trained policy network is verified in random simulation.

• (1) Scene 1.

The parameters of HGV and target are: θ₀ = 1.270°, ϕ₀ =  − 3.734°, V₀ = 7000 m/s, H₀ = 65 km, γ =  − 0.1°, ψ₀ = 86.286°, θ_tar = 71.163°, ϕ_tar = 2.212°, H_tar = 30.020 km, V^* = 2482.800 m/s. The parameters of three no-fly zones are listed in Table 20.5.

Table 20.5 Parameters of no-fly zones in scene 1

The simulation results are shown in Figs. 20.5, 20.6, 20.7 and 20.8.

Fig. 20.5

Ground track of HGV in scene 1

Fig. 20.6

Space trajectory of HGV in scene 1

Fig. 20.7

States curves of HGV in scene 1

Fig. 20.8

Path constraints curves of HGV in scene 1

• (2) Scene 2.

The parameters of HGV and target are: θ₀ = 3.059°, ϕ₀ = 3.008°, V₀ = 6823.816 m/s, H₀ = 65.891 km, γ₀ =  − 0.1°, ψ₀ = 95.121°, θ_tar = 69.605°, ϕ_tar =  − 3.514°, H_tar = 28.203 km, V^* = 2545.289 m/s. The parameters of three no-fly zones are listed in Table 20.6.

Table 20.6 Parameters of no-fly zones in scene 2

The simulation results are shown in Figs. 20.9, 20.10, 20.11 and 20.12.

Fig. 20.9

Ground track of HGV in scene 2

We can see from Fig. 20.5, 20.6, 20.7, 20.8, 20.9, 20.10, 20.11 and 20.12 that in the two scenes, HGV can pass through all the dynamic no-fly zones and reach the target. In the flight process, all the path constraints are satisfied. The terminal errors of constraints are shown in Table 20.7.

Fig. 20.10

Space trajectory of HGV in scene 2

Fig. 20.11

States curves of HGV in scene 2

Fig. 20.12

Path constraints curves of HGV in scene 2

Table 20.7 Terminal errors in the scenes

Under the influence of initial parameter perturbation and aerodynamic deviations, HGV agent can satisfy all the constraints and avoid dynamic no-fly zones.

20.6 Conclusions

Based on deep reinforcement learning, an intelligent method for reentry guidance with dynamic no-fly zones is studied in the paper. First of all, the mathematical model of HGV is established. Facing the dynamic no-fly zones, the reentry process of HGV is divided into two phases and the guidance scheme is given accordingly. Then, the problem is transformed into a Markov decision process, where the action is used to output guidance commands. State and reward are designed according to the flight phase. With the help of the TD3 algorithm, the policy network is trained to converge. Finally, the policy network is verified on random trajectories and proved to be robust to dynamic parameters of no-fly zones and other deviations.