Locating Period Doubling and Neimark-Sacker Bifurcations in Parametrically Excited Rotors on Active Gas Foil Bearings

Abstract

In this work, parametric excitation is introduced in a fully balanced flexible rotor mounted on two identical active gas foil bearings. The active gas foil bearings change the top foil shape harmonically with a specific amplitude and frequency. The deformable foil shape is approximated by an analytical function, while the gas pressure distribution is evaluated by the numerical solution of the Reynolds equation for compressible flow. The harmonic variation of the foil shape generates a respective variation in the bearings’ stiffness and damping properties and the system experiences parametric resonances and antiresonances in specific excitation frequencies. The nonlinear gas bearing forces generate bifurcations in the solutions of the system at certain rotating speeds and excitation frequencies; period doubling and Neimark-Sacker bifurcations are noticed in the examined system, and their progress is evaluated as the two bifurcation parameters (rotating speed and parametric excitation frequency) are changed, though a codimension-2 numerical continuation of limit cycles. It is found that at specific range of excitation frequency there are parametric anti-resonances and the bifurcations collide and vanish. Therefore, a bifurcation-free operating range is established and the system can operate stable at a wide speed range.

1 Introduction

Systems with multiple degrees of freedom (MDoF) and periodically changing physical properties (parametrically excited systems) have gathered both the mathematical and engineering interest of the last few decades [1,2,3]. If the parameters of the excitation strategy are carefully chosen, the existing damping properties of the system will be more efficiently used [4, 5]. Therefore, the stability of an initially unstable system will potentially be retained. The aforementioned phenomenon is called parametric antiresonance and can be interpreted as beneficial modal interaction. In current work, parametric excitation is introduced in a realistic model of a high speed, turbopump rotor, mounted on two identical gas foil bearings.

One of the first attempts to implement parametric excitation in realistic rotor models has been done in [6], where the potential to stabilize an equilibrium position was investigated. The stabilization of limit cycles was investigated in [7], where a turbine rotor, modeled with finite element method (FEM), was mounted on adjustable oil film bearings. The works hereby referred, do not consider complex rotor models coupled to active gas foil bearings (AGFBs) and do not examine the type of the occurring bifurcations. Additionally, numerical continuation methods for limit cycles and their bifurcations have been recently applied in simplistic nonlinear rotor bearing systems. In [8,9,10], simplified models of high-speed rotors were coupled to floating ring bearings, while in [11,12,13,14] Jeffcott rotor models on simple oil film bearings were investigated. Recent studies, focusing mainly on the bearing models, studied the bifurcation sets of simplistic rotor models on adjustable oil bearings [15] and on gas foil bearings [16] without implementing parametric excitation. In current work, a lot of emphasis was given on the programming of a robust and time efficient continuation method, applicable to parametrically excited, complex rotor bearing systems with multiple degrees of freedom.

A nonlinear approach of the elastoaerodynamic problem is straightly adopted. Common assumptions about the gas lubrication problem are introduced and the Reynolds equation for the compressible gas flow is solved using a Finite Difference Method [FDM]. The Simple Elastic Foundation Model (SEFM) is adopted for the representation of the bump foil behavior. The structure consists of linear elements of stiffness and damping in the radial direction while the top foil is considered massless. Parametric excitation is introduced by a sinusoidal displacement of the outer, deformableringwith predefined amplitude and frequency, and a harmonic variation in bearing’s stiffness and damping properties is generated. This can practically be achieved using piezo-actuators [17]. In general, there are various experimental and theoretical investigations which show that increased damping and stabilization is possible using closed loop control techniques such as hydraulic servo systems [18]. In current work, an open loop, periodic excitation strategy is proposed, the frequency of which should be close to the lower critical speeds.

The periodic solutions of the parametrically excited and perfectly balanced rotor-bearing systems are considered as solutions of nonlinear Boundary Value Problems (BVPs) and are evaluated using the explicit Runge-Kutta scheme [19], as it is found to be more robust method than the widely known collocation method. The corresponding solution branches are evaluated using the most reputable continuation method, the pseudo-arc length continuation method [20,21,22,23]. This method has the primary advance to study MDoF systems where the nonlinear equations of motion can be many [24] and the occurring bifurcations of various types. Similar continuation methods are applied in order to accurately predict period doubling (PD) and Neimark-Sacker (NS) bifurcations as two bifurcation parameters, the rotating speed and the excitation frequency are changed. Finally, the type of the occurring Neimark-Sacker bifurcations is investigated [25]. All the aforementioned methods are programmed by the authors directly from the notes [20, 23, 26]. The motion of unbalanced rotors under the effect of parametric excitation has quasi periodic characteristics resulted by the simultaneous excitation and synchronous frequency and should be studied using the theory of nonlinear normal modes. Nevertheless, using time integration algorithms, the authors verified that balance quality grades for turbopump rotors do not dramatically affect the phenomenon of parametric antiresonance.

2 Analytical Model of the Parametrically Excited Rotor with AGFBs

2.1 Elastoaerodynamic Lubrication and Resulting Gas Forces

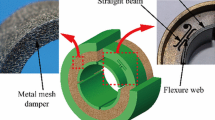
A gas foil bearing with active configuration is presented in Fig. 1 in a schematic representation of the working principles. Under the assumptions of a) isothermal gas film, b) laminar flow, c) no slip boundary conditions, d) continuum flow, e) negligible fluid inertia, f) ideal isothermal gas law ($p/\rho = ct$), g) negligible entrance and exit effects and negligible curvature of the gas film, the compressible gas flow is described by the Reynolds equation, given in Eq. (1). This equation is written in dimensionless form and it is an implicit function of dimensionless time and journal and foil kinematics.

$$\frac{\partial }{{\partial \overline{x}}}\left( {\overline{p}\overline{h}^{3} \frac{{\partial \overline{p}}}{{\partial \overline{x}}}} \right) + \kappa^{2} \frac{\partial }{{\partial \overline{z}}}\left( {\overline{p}\overline{h}^{3} \frac{{\partial \overline{p}}}{{\partial \overline{z}}}} \right) = \overline{\Omega }\frac{\partial }{{\partial \overline{x}}}\left( {\overline{p}\overline{h}} \right) + 2\frac{\partial }{\partial \tau }\left( {\overline{p}\overline{h}} \right)$$

(1)

Since analytical solution for Eq. (1) cannot be defined, the Finite Difference Method (FDM) is used to approximate the gas pressure distribution. At first, the Reynolds equation is rewritten, defining the first time derivative of the pressure distribution, in Eq. (2).

$$\dot{\overline{p}} = \frac{1}{{2\overline{h}}}\frac{\partial }{{\partial \overline{x}}}\left( {\overline{p}\overline{h}^{3} \frac{{\partial \overline{p}}}{{\partial \overline{x}}}} \right) + \frac{\kappa }{{2\overline{h}}}\frac{\partial }{{\partial \overline{z}}}\left( {\overline{p}\overline{h}^{3} \frac{{\partial \overline{p}}}{{\partial \overline{z}}}} \right) - \frac{{\overline{\Omega }}}{{2\overline{h}}}\frac{\partial }{{\partial \overline{x}}}\left( {\overline{p}\overline{h}} \right) - \frac{{\overline{p}\dot{\overline{h}}}}{{\overline{h}}}$$

(2)

The pressure domain is converted into a grid of $i = 1, \ldots ,N_{{\overline{x}}} + 1$ and $j = 1, \ldots ,N_{z} + 1$ mesh points ($i$ and $j$ are the indices in the circumferential and axial direction, see Fig. 1), upon which, the first order partial derivatives of Eq. (2) are expressed with backward differences and the second order partial derivatives are expressed by central differences. It should be noted that the elastoaerodynamic lubrication problem of Eq. (2) includes the dimensionless parameters of gas pressure $\overline{p}$, gas film thickness $\overline{h}$, spatial coordinates in the circumferential and axial direction $\overline{x} = \theta ,\overline{z}$ respectively, dimensionless time $\tau$, dimensionless rotating speed $\overline{\Omega }$, the ratio $\kappa = R/L_{b}$.

Fig. 1.

(a) Representation and key design properties of the gas foil bearing under the effect of parametric excitation force acting on the outer ring, (b) modeling of the bump foil and the respective forces acting on the components of the gas foil bearing.

The gas film thickness is defined in Eq. (3) for both the continuous and discrete spatial coordinates, where $\overline{q} = \overline{q}\left( \theta \right)$ or $\overline{q}_{i} = \overline{q}\left( {\theta_{i} } \right)$ is the dimensionless foil deformation in radial direction, see Fig. 1.

$$\,\begin{array}{*{20}c} {\overline{h} = 1 - \overline{x}_{j} \cos \theta - \overline{y}_{j} \sin \theta + \overline{q},}\,\,\,\, & {\overline{h}_{i} = 1 - \overline{x}_{j} \cos \theta_{i} - \overline{y}_{j} \sin \theta_{i} + \overline{q}_{i} } \\ \end{array}$$

(3)

The symmetry of the gas lubrication problem in the axial direction is taken into account with the boundary conditions described in Eq. (4). These conditions are also expressed in the continuous and the discrete domain.

$$\begin{array}{*{20}c} {\overline{p}\left( {\tau ,\theta_{0} ,\overline{z}} \right) = \overline{p}\left( {\tau ,\theta_{0} + 2\pi ,\overline{z}} \right) = 1,}\,\,\,\, & {\overline{p}_{1,j} = \overline{p}_{Nx + 1,j} = 1} \\ {\frac{{\partial \overline{p}}}{{\partial \overline{z}}}|_{{\overline{z} = 1/2}} = 0,} & {\frac{{\overline{p}_{i,Nz/2} - \overline{p}_{i,Nz/2 - 1} }}{{\Delta \overline{z}}} = 0} \\ \end{array}$$

(4)

It is of high importance to note that, when integrating the pressure distribution over the bearing’s surface in order to compute the impedance gas forces, sub ambient pressure values are neglected. The Gümbel boundary condition is imposed and in terms of numerical calculations, if the dimensionless fluid pressure is lower than $1$, then it is replaced by 1; in this way the pressure in the cavitated areas is neglected.

The schematic representation of the widely known Simple Elastic Foundation (SEF) model for the bump foil structure is also depicted at Fig. 1. According to the aforementioned model, the structure consists of equally valued linear elements of dimensionless stiffness $\overline{k}_{f}$ (with the corresponding compliance $\overline{a}_{f} = 1/\overline{k}_{f}$) and damping $\overline{c}_{f}$ in the radial direction, while the top foil is considered massless, see Fig. 1. Its stripes along the axial direction are assumed to remain parallel to the bearing surface during their motion. Therefore, no axial direction is needed for the description of the top foil motion. Instead, only the mean axial gas pressure $\overline{p}_{m}$ is necessary. This pressure, is given in Eq. (5), in the continuous and the discrete domain, in the dimensional and the dimensionless form.

$$p_{m} \left( \theta \right) = \frac{1}{{L_{b} }}\int_{0}^{{L_{b} }} {p\left( \theta \right)dz} ,\,\,\,\,p_{m,i} = \frac{1}{{L_{b} }}\sum\limits_{j = 2}^{{N_{Z} }} {\left( {p_{i,j} \Delta z} \right)} ,\,\,\,\,\,\overline{p}_{m,i} = \frac{1}{{N_{Z} }}\sum\limits_{j = 2}^{{N_{Z} }} {\left( {\overline{p}_{i,j} } \right)}$$

(5)

Given the fact that the top foil’s motion is synchronous to the pressure excitation, the structural damping coefficient can be expressed as $\overline{c}_{f} = \eta \cdot \overline{k}_{f}$, where $\eta$ denotes the loss factor. Generally, the dimensionless foil stiffness coefficient $\overline{k}_{f}$ is related to some specific physical properties of the bump. According to [27], the dimensional foil compliance $a_{f}$ can be analytically approximated by the following formula:

$$a_{f} = \frac{{2p_{0} S_{bf} }}{{c_{r} E_{bf} }}\left( {\frac{{l_{bf} }}{{t_{bf} }}} \right)\left( {1 - v_{bf}^{2} } \right)$$

(6)

where $S_{bf}$ is the pitch of bump foil, $l_{bf}$ is half bump foil’s length, $t_{bf}$ is bump foil’s thickness and $E_{bf} ,v_{bf}$ are Young’s modulus and Poison’s ratio of the bump foil respectively.

Therefore, the dimensionless foil stiffness coefficient can be defined as:

$$\overline{k}_{f} = \overline{k}_{b} = \frac{{c_{r} }}{{a_{f} p_{0} }}$$

(7)

As it is clearly stated in the Introduction, the parametric excitation is implemented by a predefined harmonic variation of the bearing’s outer ring ${\overline{\mathbf{q}}}_{r} = \left\{ {\overline{q}_{r,i} } \right\}$. Therefore, the radial displacement $\overline{q}_{i}$ of the i^th top foil’s stripe under the effect of the mean axial gas pressure and the parametric excitation is defined in Eq. (8), see also Appendix.

$$\dot{\overline{q}}_{i} = \dot{\overline{q}}_{r,i} + \frac{{[\overline{p}_{m,i} - \overline{k}_{f} (\overline{q}_{i} - \overline{q}_{r,i} )]}}{{\overline{c}_{f} }},\,\,\,\,i = 2,3,...,N_{x}$$

(8)

Finally, it is denoted $\Delta \overline{x} = 2\pi /N_{{\overline{x}}} ,\,\,\,\Delta \overline{z} = 1/N_{z}$ and the nonlinear gas forces can be evaluated according to Eq. (9).

$$\begin{gathered} \overline{F}_{x}^{B} = - \int\limits_{0}^{2\pi } {\int\limits_{0}^{1} {(\overline{p} - 1)\cos \theta \,d\theta \,d\overline{z} = - \sum\limits_{i = 2}^{{N_{x} }} {\sum\limits_{j = 2}^{{N_{z} }} {(\overline{p}_{i,j} - 1)\cos \theta_{i} \,\Delta \overline{x}\,\Delta \overline{z}} } } } \hfill \\ \overline{F}_{y}^{B} = - \int\limits_{0}^{2\pi } {\int\limits_{0}^{1} {(\overline{p} - 1)\sin \theta \,d\theta \,d\overline{z} = - \sum\limits_{i = 2}^{{N_{x} }} {\sum\limits_{j = 2}^{{N_{z} }} {(\overline{p}_{i,j} - 1)\sin \theta_{i} \,\Delta \overline{x}\,\Delta \overline{z}} } } } \hfill \\ \end{gathered}$$

(9)

2.2 Condensed Rotor Model

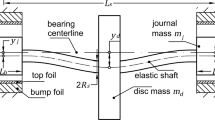
A representative turbopump rotor, mounted on two identical AGFBs and designed to operate above 20 kRPM is implemented in the current work,see Fig. 2. The rotor has complex geometry with different material properties, directly related to the temperature distribution among its length, and additional masses in various locations. Thus the rotor is discretized with cylindrical finite elements, each one having two nodes and a total of eight degrees of freedom $x_{i}$, two transverse displacements and two tilting angles per node. The individual beam element matrices of inertia, stiffness and gyroscopy are properly summated and finally construct the corresponding global matrices. The global damping matrix follows the classical Rayleigh formula and the equations of motion for the whole rotor system in dimensionless form are derived in Eq. (10). On the right-hand side, gas bearing forces $\left\{ {\overline{F}_{i}^{B} } \right\}$ are evaluated according to the aforementioned elastoaerodynamic approach and they are the only source of nonlinearity in the rotor-bearing system. Additionally, gravity forces $\left\{ {\overline{F}_{i}^{G} } \right\}$ are composed supposing that the mass of each element is equally divided to the two nodes of the element.

$$\left[ {{\overline{\mathbf{M}}}} \right]\left\{ {\ddot{\overline{x}}_{i} } \right\} + \left( {\left[ {{\overline{\mathbf{C}}}} \right] + \left[ {{\overline{\mathbf{G}}}} \right]} \right)\left\{ {\dot{\overline{x}}_{i} } \right\} + \left[ {{\overline{\mathbf{K}}}} \right]\left\{ {\overline{x}_{i} } \right\} = \left\{ {\overline{F}_{i}^{B} } \right\} + \left\{ {\overline{F}_{i}^{G} } \right\}$$

(10)

Fig. 2.

Schematic representation of a slender high-speed rotor supported on two identical GFBs. Finite element discretization, bearing span $L_{s}$, and master and slave nodes are also depicted.

The rotor model described in Eq. (10) is then reduced using the Guyan (static) reduction method. The selection of master (retained) nodes has been performed in order to match the dynamic response of the full system to this of the reduced one in terms of unbalance response and modal properties. It should be noted herethat the harmonic variation of $\overline{q}_{i}$ seems to be efficient if its frequency is around specific damped natural frequencies of the linearized rotor-bearing model. Therefore, it is of great importance the reduction method to be held carefully. In current work, the number of total master nodes is 7, including both the overhang nodes and 5 almost equally distributed rotor nodes. By definition, only transverse displacements at each node are retained and the equations of motion for the reduced rotor system in dimensionless form are derived in Eq. (11).

$$\left[ {{\overline{\mathbf{M}}}_{r} } \right]\left\{ {\ddot{\overline{x}}_{m,i} } \right\} + \left( {\left[ {{\overline{\mathbf{C}}}_{r} } \right] + \left[ {{\overline{\mathbf{G}}}_{r} } \right]} \right)\left\{ {\dot{\overline{x}}_{m,i} } \right\} + \left[ {{\overline{\mathbf{K}}}_{r} } \right]\left\{ {\overline{x}_{m,i} } \right\} = \left\{ {\overline{F}_{r,i}^{B} } \right\} + \left\{ {\overline{F}_{r,i}^{G} } \right\}$$

(11)

The reduced rotor model equations of motion can now be converted to the following set of first order ordinary differential equations (ODEs), where ${\overline{\mathbf{y}}}_{m} = \left\{ {\overline{y}_{m,i} } \right\} = \left\{ \begin{gathered} \left\{ {\dot{\overline{x}}_{m,i} } \right\} \hfill \\ \left\{ {\overline{x}_{m,i} } \right\} \hfill \\ \end{gathered} \right\}$ and $\left\{ {\overline{F}_{r,i} } \right\} = \left\{ {\overline{F}_{r,i}^{B} } \right\} + \left\{ {\overline{F}_{r,i}^{G} } \right\}$.

$$\left\{ {\dot{\overline{y}}_{m,i} } \right\}_{28 \times 1} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{14 \times 14} } & {{\mathbf{I}}_{14 \times 14} } \\ {\left( { - {\overline{\mathbf{M}}}_{r}^{ - 1} {\overline{\mathbf{K}}}_{r} } \right)_{14 \times 14} } & { - {\overline{\mathbf{M}}}_{r}^{ - 1} \left( {{\overline{\mathbf{G}}}_{r} + {\overline{\mathbf{C}}}_{r} } \right)_{14 \times 14} } \\ \end{array} } \right]\left\{ {\overline{y}_{m,i} } \right\}_{28 \times 1} + \left\{ \begin{gathered} {\mathbf{0}}_{14 \times 1} \\ {\overline{\mathbf{M}}}_{r}^{ - 1} \left\{ {\overline{F}_{r,i} } \right\}_{14 \times 1} \\ \end{gathered} \right\}$$

(12)

2.3 Composition of the Parametrically Excited Rotor-Bearing System

The aerodynamic lubrication problemin Eq. (2) renders $N_{x} - 1$ first order ODEs, with respect to the time derivative of the dimensionless nodal pressures, in Eq. (13).

$${{\dot{\overline{\mathbf{p}}}}} = {\mathbf{f}}_{{\mathbf{B}}} \left( {{\overline{\mathbf{p}}},{\overline{\mathbf{q}}},{\overline{\mathbf{q}}}_{r} ,{\overline{\mathbf{y}}}_{m} } \right)$$

(13)

In turn, the structural problem renders another $N_{x} - 1$ first order ODEs. Equation (8) can alternatively be written in the following form.

$${{\dot{\overline{\mathbf{q}}}}} = \left\{ {\dot{\overline{q}}_{i} } \right\} = {\mathbf{f}}_{{\mathbf{F}}} \left( {{\overline{\mathbf{p}}},{\overline{\mathbf{q}}},{\overline{\mathbf{q}}}_{r} } \right)$$

(14)

The reduced rotor model equations of motion, see Eq. (12), can be written in the form:

$${{\dot{\overline{\mathbf{y}}}}}_{m} = {\mathbf{f}}_{R} \left( {{\overline{\mathbf{p}}},{\overline{\mathbf{y}}}_{m} } \right)$$

(15)

The nonlinear rotor-gas bearing system is defined by the following first order ODEs, where ${\overline{\mathbf{s}}} = \left\{ {\begin{array}{*{20}c} {{\overline{\mathbf{p}}}} & {\begin{array}{*{20}c} {{\overline{\mathbf{q}}}} & {{\overline{\mathbf{y}}}_{m} } \\ \end{array} } \\ \end{array} } \right\}^{T}$. It should be noted that due to the periodic variation of the bearing’s outer ring dimensionless time still appears explicitly in Eq. (16).

$${{\dot{\overline{\mathbf{s}}}}} = {\mathbf{f}}\left( {{\overline{\mathbf{s}}},\overline{\Omega },\overline{\Omega }_{ex} ,\tau } \right)$$

(16)

In order for the limit cycle solutions to be efficiently evaluated by the explicit Runge-Kutta method, the aforementioned system should be converted to autonomous and this can be achieved by augmenting an oscillator with two degrees of freedom whose unique solution is a harmonic function of frequency $\overline{\Omega }_{ex}$, see Eq. (17).

$$\begin{gathered} \dot{\overline{s}}_{N + 1} = f_{N + 1} = \overline{s}_{N + 1} + \overline{\Omega }_{ex} \overline{s}_{N + 2} - \overline{s}_{N + 1} \left( {\overline{s}_{N + 1}^{2} + \overline{s}_{N + 2}^{2} } \right) \\ \dot{\overline{s}}_{N + 2} = f_{N + 2} = - \overline{\Omega }_{ex} \overline{s}_{N + 1} + \overline{s}_{N + 2} - \overline{s}_{N + 2} \left( {\overline{s}_{N + 1}^{2} + \overline{s}_{N + 2}^{2} } \right) \\ \end{gathered}$$

(17)

Finally, the autonomous system of first order ODEs is defined in Eq. (16), where ${{\tilde{\overline{\mathbf{s}}}}} = \left\{ {{\overline{\mathbf{s}}}^{T} \,\,s_{N + 1} \,\,s_{N + 2} } \right\}^{T}$ and ${\tilde{\mathbf{f}}} = \left\{ {{\mathbf{f}}^{T} \,\,f_{N + 1} \,\,\,f_{N + 2} \,} \right\}^{T}$.

$${{\dot{\tilde{\overline{\mathbf{s}}}}}} = {\tilde{\mathbf{f}}}\left( {{{\tilde{\overline{\mathbf{s}}}}},\overline{\Omega }} \right)$$

(18)

3 Quality of Bifurcations of the Dynamic System

3.1 Location and Continuation of Limit Cycles

Away to find isolated periodic solutions (limit cycles) of the Dynamic System defined in Eq. (18) should be established. If the system poses a stable limit cycle, then it is reasonable to approximate it by numerical integration with an initial condition which belongs to the basin of attraction of the cycle. Given an initial guess for the limit cycle ${{\tilde{\overline{\mathbf{s}}}}}_{0}$ and an initial guess for the cycle period $T_{0} = 2\pi /\overline{\Omega }_{ex}$ it is possible to formulate a periodic Boundary Value Problem (BVP), see Eq. (19) on a fixed time interval $[0,1]$ $[0,1]$.

$$\left\{ \begin{gathered} \frac{{d{{\tilde{\overline{\mathbf{s}}}}}}}{{d\tau_{1} }} - {\rm T}{\tilde{\mathbf{f}}}\left( {{{\tilde{\overline{\mathbf{s}}}}},\overline{\Omega }} \right) = {\mathbf{0}} \hfill \\ {{\tilde{\overline{\mathbf{s}}}}}(1) - {{\tilde{\overline{\mathbf{s}}}}}(0) = {\mathbf{0}} \hfill \\ \int\limits_{0}^{1} {\left\langle {{{\tilde{\overline{\mathbf{s}}}}},{{\tilde{\overline{\mathbf{s}}}}}_{0} } \right\rangle } \,d\tau_{1} = 0 \hfill \\ \end{gathered} \right.$$

(19)

The first two conditions define a periodic solution to the partially defined BVP but not uniquely, since any time shift of such a solution, is another solution. Therefore, an extra condition has to be appended, known as phase condition, in order to select one and only periodic solution among all those corresponding to the cycle. The phase condition appended in current work is called integral phase condition and it is a necessary condition for a local minimum of the distance between ${{\tilde{\overline{\mathbf{s}}}}},{{\tilde{\overline{\mathbf{s}}}}}_{0}$ with respect to any time shifts. The aforementioned problem can be reduced to finite dimensional problem using the explicit Runge-Kutta discretization scheme and solved for the unknown periodic solution ${{\tilde{\overline{\mathbf{s}}}}}^{*}$ and the unknown period $T^{*}$.

By definition, the periodic solution of the problem defined in Eq. (19) depends on the dimensionless rotating speed $\overline{\Omega }$. The problem of computing the curve ${{\tilde{\overline{\mathbf{s}}}}}^{*} \left( {\overline{\Omega }} \right)$ belongs to the general case of finite dimensional continuation problems. The numerical solution of the continuation problem means computing a sequence of ${{\tilde{\overline{\mathbf{s}}}}}_{1}^{*} ,{{\tilde{\overline{\mathbf{s}}}}}_{2}^{*} ,{{\tilde{\overline{\mathbf{s}}}}}_{3}^{*} ,...$ Approximating the curve ${{\tilde{\overline{\mathbf{s}}}}}^{*} (\overline{\Omega })$. This sequence is generated by an initial point ${{\tilde{\overline{\mathbf{s}}}}}_{0}$ which is sufficiently close to the curve. In current work, the continuation algorithm implements a predictor-corrector method called pseudo-arc length continuation method. For more detailed information, the reader may refer to [22].

3.2 Location and Continuation of Codim1 Bifurcations of Limit Cycles

The problem of locating Codim 1 bifurcations of limit cycles is a more delicate problem and, in this case, should be approached again as BVP, since there are periodic solutions whose multipliers have magnitude much smaller than 1. In the case ofFlip (period- doubling) bifurcation, a vector-valued function ${\overline{\mathbf{v}}}(\tau_{1} )$ is introduced and a non-periodic BVP is considered on the fixed time interval in Eq. (18). The first three conditions specify the periodic BVP defined in Eq. (19), the fourth condition is the linearization of Eq. (18) around the periodic solution ${{\tilde{\overline{\mathbf{s}}}}}$, the fifth condition corresponds to the flip bifurcation condition and the last one provides a normalization to ${\overline{\mathbf{v}}}(\tau_{1} )$. This problem can be reduced to its finite dimensional form using the explicit Runge-Kutta discretization scheme and solved for the unknowns ${{\tilde{\overline{\mathbf{s}}}}}^{*} ,\,\,T^{*} ,\,\,{\overline{\mathbf{v}}},\,\,\overline{\Omega }$. .In the case of Secondary Hopf (Neimark Sacker) bifurcation, a complex eigen-function ${\overline{\mathbf{w}}}\left( {\tau_{1} } \right)$ and the scalar variable $\theta_{m}$ (which parameterizes the critical multipliers) are introduced and the non-periodic BVP is considered on the fixed time interval in Eq. (20).

$$\left\{ \begin{gathered} \frac{{d{{\tilde{\overline{\mathbf{s}}}}}}}{{d\tau_{1} }} - {\rm T}{\tilde{\mathbf{f}}}\left( {{{\tilde{\overline{\mathbf{s}}}}},\overline{\Omega }} \right) = {\mathbf{0}} \hfill \\ {{\tilde{\overline{\mathbf{s}}}}}(1) - {{\tilde{\overline{\mathbf{s}}}}}(0) = {\mathbf{0}} \hfill \\ \int\limits_{0}^{1} {\left\langle {{{\tilde{\overline{\mathbf{s}}}}},{{\tilde{\overline{\mathbf{s}}}}}_{0} } \right\rangle } \,d\tau_{1} = 0 \hfill \\ \frac{{d{\overline{\mathbf{v}}}}}{{d\tau_{1} }} - {\rm T}\frac{{\partial {\tilde{\mathbf{f}}}}}{{\partial {{\tilde{\overline{\mathbf{s}}}}}}}\left( {{{\tilde{\overline{\mathbf{s}}}}},\overline{\Omega }} \right){\overline{\mathbf{v}}} = {\mathbf{0}} \hfill \\ {\overline{\mathbf{v}}}(1) + {\overline{\mathbf{v}}}(0) = {\mathbf{0}} \hfill \\ \int\limits_{0}^{1} {\left\langle {{\overline{\mathbf{v}}},{\overline{\mathbf{v}}}} \right\rangle } \,d\tau_{1} = 0 \hfill \\ \end{gathered} \right.$$

(20)

$$\left\{ \begin{gathered} \frac{{d{{\tilde{\overline{\mathbf{s}}}}}}}{{d\tau_{1} }} - {\rm T}{\tilde{\mathbf{f}}}\left( {{{\tilde{\overline{\mathbf{s}}}}},\overline{\Omega }} \right) = {\mathbf{0}} \hfill \\ {{\tilde{\overline{\mathbf{s}}}}}(1) - {{\tilde{\overline{\mathbf{s}}}}}(0) = {\mathbf{0}} \hfill \\ \int\limits_{0}^{1} {\left\langle {{{\tilde{\overline{\mathbf{s}}}}},{{\tilde{\overline{\mathbf{s}}}}}_{0} } \right\rangle } \,d\tau_{1} = 0 \hfill \\ \frac{{d{\overline{\mathbf{w}}}}}{{d\tau_{1} }} - {\rm T}\frac{{\partial {\tilde{\mathbf{f}}}}}{{\partial {{\tilde{\overline{\mathbf{s}}}}}}}\left( {{{\tilde{\overline{\mathbf{s}}}}},\overline{\Omega }} \right){\overline{\mathbf{w}}} = {\mathbf{0}} \hfill \\ {\overline{\mathbf{w}}}(1) - e^{{i\theta_{m} }} {\overline{\mathbf{w}}}(0) = {\mathbf{0}} \hfill \\ \int\limits_{0}^{1} {\left\langle {{\overline{\mathbf{w}}},{\overline{\mathbf{w}}}} \right\rangle } \,d\tau_{1} = 0 \hfill \\ \end{gathered} \right.$$

(21)

The meaning of the augmented conditions in Eq. (21) is similar with the meaning of the augmented conditions in Eq. (20). It is suggested this problem to be written in its real form.Then it should be discretized using the Runge-Kutta scheme and finally solved for the unknowns ${{\tilde{\overline{\mathbf{s}}}}}^{*} ,\,\,T^{*} ,\,\,{\overline{\mathbf{w}}},\,\,\theta_{m} ,\,\,\overline{\Omega }$. The presented BV problems can also be used to continue generic Flip (PD) and Secondary Hopf bifurcations (NS) of limit cycles. They are called fully extended augmented BVPs since the augmented conditions for the location of Codim 1 bifurcation can be replaced by one and only equation using bordering techniques analytically presented in [22].

It is important to note that Eq. (20) and Eq. (21) do not consider the degeneracy conditions of the corresponding bifurcations. Generally, the finite dimensional problem, arising after proper discretization of Eq. (19) is solved using the damped Newton method, analytically presented in [19]. Based on the Jacobian matrix of the aforementioned system of nonlinear equations, one can approximate the monodromy matrix of the isolated periodic solution, using a method similar to this presented in [26]. All the criteria to determine local flip (period doubling) and secondary Hopf (Neimark – Sacker) bifurcations arise from the eigenvalues of the monodromy matrix, called Floquet multipliers.

More specifically, supposing that all the non-degeneracy conditions hold, if there is one pair of complex eigenvalues on the unlit circle, $\lambda_{1,2} (\overline{\Omega }) = r(\overline{\Omega })e^{{i\theta (\overline{\Omega })}} ,\,r = 1,\,\,0 < \theta < \pi$, then Neimark-Sacker bifurcation occurs. The non-degeneracy conditions indicate that $e^{ik\theta } \ne 1,\,k = 1,2,3,...$ (absence of strong resonances), $\frac{dr}{{d\overline{\Omega }}} \ne 0$ and $d \ne 0$, where $d$ stands for a coefficient involved in the normal form of Neimark – Sacker bifurcation, see [25].

The case of Flip bifurcation is simpler. Supposing again that all the non-degeneracy conditions hold, if there is one real eigenvalue on the unit circle $\lambda_{3} \left( {\overline{\Omega }} \right) = - 1$, then period doubling bifurcation occurs. The non-degeneracy conditions now indicate that $\frac{{d\lambda_{3} }}{{d\overline{\Omega }}} \ne 0$ and $c \ne 0$, where $c$ stands for a coefficient in the normal form of period doubling bifurcation, see [25].

4 Results

In Fig. 3 full bifurcation sets for four different values of the dimensionless foil stiffness coefficient $\overline{k}_{b}$ and for three different values of the maximum dimensionless vertical displacement of the outer ring $\overline{\delta }$ are depicted. According to the literature, in theoretical investigations $\overline{k}_{b}$ varies from 0.1 to 100. In our specific case, $\overline{k}_{b}$ belongs to the aforementioned range and enhances the phenomenon of parametric antiresonance as much as possible. The evaluation of generic Neimark – Sacker bifurcations for bigger than presented values of $\overline{k}_{b}$ was numerically difficult, thus omitted.

The minimum value of $\delta$ is selected so as not to affect the threshold speed of instability of the reference rotor – bearing system. The maximum value of $\delta$ generally depends on the outer ring’s physical properties, the power supply availability and the excitation frequency. In our case, the maximum value is selected in order to avoid numerical difficulties in the continuation of Neimark Sacker bifurcations. Currently, alternative methods of continuation of Neimark-Sacker bifurcations are studied in order to overcome the aforementioned numerical difficulties.

Fig. 3.

Full bifurcation set for a) $\overline{k}_{b} = 3$, , b) $\overline{k}_{b} = 10$, c) $\overline{k}_{b} = 20$ and $\overline{k}_{b} = 50$.

The occurring Neimark-Sacker bifurcations as the two bifurcation parameters $\overline{\Omega },\,\,\overline{\Omega }_{ex}$ change are depicted for eachvalue of the dimensionless stiffness coefficient. The progress of period doubling bifurcations is evaluated by solving Eq. (20) in the context of a sequential continuation method and the progress of Neimark-Sacker bifurcations is evaluated by solving Eq. (19) in the context of the same continuation method, for simplicity reasons.

It can be safely concluded that excitation frequencies around which parametric resonances and antiresonances occur can be approximately predicted by Eq. (22), where $\overline{\Omega }_{j,k}$ denote the dimensionless critical speeds of the rotor-bearing system.

$$\overline{\Omega }^{1}_{{ex,{\text{int}} }} \simeq \frac{{2\overline{\Omega }_{j} }}{n},\,\,\overline{\Omega }^{2}_{{ex,{\text{int}} }} \simeq \frac{{\left| {\overline{\Omega }_{j} \pm \overline{\Omega }_{k} } \right|}}{n},\,\,\,j,k,n = 1,2,3,...$$

(22)

The denominator $n$ denotes the order of the parametric resonance or antiresonance. In these results, only first and second order resonances and antiresonances are found. As it is expected, the strength of such phenomena is enhanced as the dimensionless parameter $\overline{\delta }$ is increased. It is additionally observed that this strength is enhanced as the dimensionless stiffness coefficient is increased. Both the dimensionless parameters mentioned above are related to the variation of the bearing clearance. Therefore, it can be concluded that the greater the variation in clearance, the greater the difference in the threshold speed of instability is.

Around some of the excitation frequencies of interest given by Eq. (22) and under specific circumstances, period doubling bifurcations occur too. For instance, it is observed that for the lowest value of the dimensionless parameter $\overline{\delta }$ no period doubling bifurcation occurs. As this parameter increases, further bifurcations appear. In contrast, as the dimensionless stiffness coefficient increases, only Neimark-Sacker bifurcations appear. Finally, it is of high importance to note that in all examined cases there are zones of excitation frequencies at which the stability threshold of the rotor-bearing system is enhanced, and no other type of bifurcation occurs.

Fig. 4.

Response envelope for a) $\overline{k}_{b} = 3$, b) $\overline{k}_{b} = 10$, c) $\overline{k}_{b} = 20$, and d) $\overline{k}_{b} = 50$.

The transient response of the rotor system is depicted in Fig. 4 for some operating conditions of interest. For each of the different foil stiffness values $\overline{k}_{b} = 3,10,20,50$, the excitation frequencies where antiresonance occurs are selected from the stability maps in Fig. 3. These are found to be $\overline{\Omega }_{ex} = 0.63,\,0.70,\,0.72,\,0.74$ respectively. The transient response of the system is evaluated under the parametric excitation of $\overline{\Omega }_{ex}$ as before, and for the amplitude of excitation force to render $\overline{\delta } = 0.2$. The transient response is evaluated with time integration of the system in Eq. (16) and the envelop of response is depicted in each of Figs. 4a, 4b,4c,4d in the lower chart, together with the response envelop evaluated by sequential continuation of the limit cycles. The Floquet multipliers of each limit cycle motion depict the quality of bifurcations when these occur. At all cases depicted in the aforementioned charts, the system experiences a Neimark-Sacker bifurcation at the ending speed of c.a. $\overline{\Omega } = 1.2$ and this is considered as the threshold speed of instability. However, at the case of Fig. 4a, the system experiences period doubling bifurcation in much lower rotating speed, c.a. $\overline{\Omega } = 0.4$ and stable limit cycles are generated; in Fig. 4a, and at the lower chart one may notice the unstable limit cycles and the stable limit cycles where the system oscillates after the PD bifurcation. In the upper charts of Figs. 4b,4c,4d one may notice the lower threshold speed of instability at c.a. $\overline{\Omega } = 0.95$ when parametric excitation is of low frequency, e.g. $\overline{\Omega }_{ex} = 0.2$. In Fig. 4a, and in the upper chart, the threshold speed of instability appears at $\overline{\Omega } = 1.1$ and this is due to the fact that the foil is compliant enough ($\overline{k}_{b} = 3$) and dissipation of energy takes place due to the higher motion of the foil. Considering the above, parametric excitation provides increase of the threshold speed of instability up to 30% at the specific application. More design sets are currently investigated by the authors.

For clear observation of bifurcation trees of period doubling bifurcations occurring, bifurcation diagrams are depicted in Fig. 5.

Fig. 5.

Bifurcation diagrams during and after a flip (period doubling) bifurcation

As one may notice in Fig. 5 (top), around the excitation frequency of interest the unstable limit cycles where the system oscillates after PD are distributed in a wide range of rotating speeds.

The transient response of the unbalanced rotor system under the effect of parametric excitation is compared with the response of the balanced one in Fig. 6, for some operating conditions of interest. Generally, for turbopump rotors $G = 6.3,\,2.5$ balance quality grades are considered. For each of the dimensionless foil stiffness values $\overline{k}_{b} = 3,\,\overline{k}_{b} = 50$, the excitation frequencies at which parametric antiresonance occurs are selected, and two balance quality grades are applied ($G = 6.3,\,G = 1$). As one may notice in Figs. 6a and 6b the phenomenon of parametric antiresonance is not affected by any level of unbalance.

Fig. 6.

Evaluation of periodic response applying numerical continuation of limit cycles, and quasi-periodic response applying time integration for the respective design and operating parameters as depicted.

Time integration is the only tool in this paper to evaluate the quasi-periodic response under the simultaneous parametric and unbalance excitation; the time response proves that the stability threshold (NS bifurcation) is very similar in both periodic and quasi-periodic solutions, in the status of parametric antiresonance. In the case of compliant bump foil depicted in Figs. 6c and 6d where higher unbalance is applied, still the above comment holds. However, as the unbalance becomes higher, the quality of response includes further characteristics, which should be studied with the appropriate tools for quasi periodic solution evaluation, in future work.

5 Conclusions

This work proves that parametric antiresonance is feasible in slender, high-speed rotors mounted on active gas foil bearings. Slender rotors retrieve stability in high rotating speeds under the effect of periodic load acting on the deformable ring of the gas foil bearings. A nonlinear approach for the elastoaerodynamic problem is adopted, according to which, the compressible gas flow is described by the Reynolds Equation and the bump foil’s behavior is represented by the simple elastic foundation model. Based on the following conclusions, this paper aims to raise further concerns on parametrically excited rotating systems.

The investigation of full bifurcation sets at a wide range of rotating speed and excitation frequency and amplitude indicates that the zone of excitation frequencies at which para-metric resonances or antiresonances occur can be approximated using Eq. (20), existing in literature since long. The strength of both parametric resonance and antiresonance depends on the variation of the bearing clearance (amplitude of exciting force). The greater the variation of the clearance, the greater the difference in the threshold speed of instability is. Based on the literature, see [28] and on personal experience, authors firmly believe that all the aforementioned conclusions regarding the correlation between the threshold speed of instability and the variation in foil stiffness coefficient and clearance are valid for a wide range of slender rotors mounted on AGFBs.

Parametric antiresonance and modal interaction are two simultaneous phenomena, and it is of quite interest to study the energy flow between the interacting modes. This can be achieved by comparing the unbalance response of a parametrically excited rotor with the unbalance response of the same rotor mounted on conventional gas foil bearings (without parametric excitation). It should be noted that in the former case, the rotor-bearing system has quasi periodic characteristics due to the simultaneous synchronous and parametric excitation. Harmonic balance is currently under investigation in order to be embedded in the corresponding continuation scheme. It is furthermore of quite interest to evaluate the type of the occurring Neimark-Sacker bifurcations (subcritical/supercritical). This can be straight forward achieved by approximating the normal form of Neimark Sacker bifurcations. The validity of the coefficients involved in this normal form is currently under investigation.

Appendix: Implementation of Parametric Excitation

The deformation of a ring with the physical and geometrical properties like Poisson’s ratio $v_{r}$, Young’s modulus of elasticity, inner/outer radius $R_{i,r} ,R_{o,r}$ and polar moment of inertia $I$, is evaluated with approximate analytical formulas obtained by the strength of materials. The effect of a periodic vertical load $F_{0} \left( {1 + \sin \left( {\overline{\Omega }_{ex} \tau } \right)} \right)$ is the deformation in the horizontal ($dh$) and vertical ($dv$) direction of the ring, see also Fig. 1, as defined in Eq. (21). The constants $\kappa_{1}$ and $\kappa_{2}$ included are defined in Eq. (22).

$$\begin{gathered} dh = q_{r} \left( {\theta = 0,\pi ,\tau } \right) = \frac{{F_{0} }}{2}\frac{{R_{o,r}^{3} }}{{4.2 \cdot 10^{11} I_{r} }}\left( {\frac{2}{\pi }\kappa_{2}^{2} - \kappa_{2} + \frac{{\kappa_{1} }}{2}} \right)\left( {1 + \sin (\overline{\Omega }_{ex} \tau )} \right) \\ dv = q_{r} \left( {\theta = \pi /2,3\pi /2,\tau } \right) = \frac{{ - F_{0} }}{2}\frac{{R_{o,r}^{3} }}{{4.2 \cdot 10^{11} I_{r} }}\left( {\frac{\pi }{4}\kappa_{1} - \frac{{2\kappa_{2}^{2} }}{\pi }} \right)\left( {1 + \sin (\overline{\Omega }_{ex} \tau )} \right) \\ \end{gathered}$$

(23)

Given the corresponding derivatives with respect to the dimensionless time $d\dot{h},\,d\dot{v}$, the deformation of the outer ring and its rate of change in the circumferential direction are evaluated in Eq. (23), where $\overline{q}_{r} = q_{r} /c_{r}$ and $\dot{\overline{q}}_{r} = \dot{q}_{r} /c_{r}$.

$$\kappa_{1} = 1 - \frac{{\left( {R_{o,r}^{4} - R_{i,r}^{4} } \right)}}{{2R_{i,r}^{2} \left( {R_{o,r}^{2} - R_{i,r}^{2} } \right)}} + \frac{{1.33\left( {1 + 2v_{r} } \right)R_{o,r} }}{{\pi \left( {R_{o,r}^{2} - R_{i,r}^{2} } \right)}},\,\,\,\,\kappa_{2} = 1 - \frac{{\left( {R_{o,r}^{4} - R_{i,r}^{4} } \right)}}{{2R_{i,r}^{2} \left( {R_{o,r}^{2} - R_{i,r}^{2} } \right)}}$$

(24)

$$\begin{gathered} q_{r} = q_{r} \left( {\theta ,\tau } \right) = \sqrt {\left[ {\left( {R_{i,r} + dh} \right)\cos \theta } \right]^{2} + \left[ {\left( {R_{i,r} + dv} \right)\sin \theta } \right]^{2} } - R_{i,r} \\ \dot{q}_{r} = \dot{q}_{r} \left( {\theta ,\tau } \right) = \frac{{\left[ {\left( {R_{i,r} + dh} \right)\cos \theta } \right]\left[ {d\dot{h}\cos \theta } \right] + \left[ {\left( {R_{i,r} + dv} \right)\sin \theta } \right]\left[ {d\dot{v}\sin \theta } \right]}}{{q_{r} + R_{i,r} }} \\ \end{gathered}$$

(25)