Keywords

1 Introduction

Ground deformation can be studied by satellite Interferometric Synthetic Aperture Radar (InSAR) [1]. In the Differential InSAR (DInSAR) techniques, two radar images capturing the same region but taken at different times are compared to produce a map (i.e., interferogram). The map shows ground displacement along the sensor’s line of sight between two acquisition times [2]. However, its main limitation is related to the accuracy caused by spatial and temporal decorrelation (atmospheric delay, topographic errors, etc.) between the two signals. This can be overcome (at least for some particular points, called Persistent Scatterers), with the Advanced-DInSAR (A-DInSAR) technique, which consists of combining a large number of SAR images (multi-image technique). The Persistent Scatterer InSAR (PS-InSAR) technique is an Advanced Differential Synthetic Aperture Radar Interferometry (A-DInSAR) method to obtain the temporal evolution of displacements for stable radar reflectors, in terms of temporal coherence and amplitude stability, in the investigation area: the so-called Persistent Scatterers PSs [3]. PS-InSAR has been widely applied for different hazard investigations, from local-scale deformation processes (e.g., those affecting a single building or structure) to large-scale deformation processes (e.g., landslides, subsidence, tectonic deformations, etc.). The potential of A-DInSAR measurements for landslides detection, mapping, and characterization has been widely investigated to reconstruct the history of deformations through PS time series analysis [4,5,6,7].

A-DInSAR technique allows the study of trend changes in time series, reflecting the deformations observed in differential interferograms. The time series of deformation processes are non-stationary, i.e., exhibit trends, jumps, and wavelike components that change frequency and amplitude over time. Several methods were examined to analyze and evaluate the relations between landslides and triggering phenomena, in particular, heavy rainfalls [8, 9]. Heavy rainfall can determine an increase in velocity trends of time series, providing interesting information about the processes that governed the slope behavior [10]. A possible correlation between the rain and the activation of a deformation phenomenon has been highlighted in [11] through the analysis of Sentinel-1 interferograms and rainfall data. The deformation phenomena detected during the interferometric analysis were mostly concentrated during high rainfall periods, showing that rain could be considered the main triggering/accelerating factor of the studied landslides.

To investigate the possible influence of one phenomenon on another, one may process their time series by several statistical methods. For example, the Pearson correlation coefficient is a common statistical metric that shows the strength and direction of a linear relationship between two variables, denoted by r [12]. However, this metric only shows the possible linear dependency between two phenomena, e.g., deformation processes and rainfall. The deformation processes such as landslides, discovered by the PS time series, are often sampled unevenly because of many reasons, such as sensor defect, storage, and economy. Therefore, methods that can rigorously consider irregularities in sampling and values of such time series are extremely demanding. To analyze the correlation of PS and rainfall in non-stationary time series, we have to take into account that they may also have different sampling rates with missing values. In addition, there might exist some time delay between the wavelike components of the time series, e.g., a time delay between the annual cycles of vegetation and climate or between the annual cycles of interferometric baseline length and temperature [13, 14].

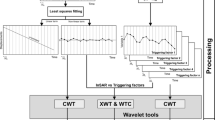
The traditional wavelet coherence and cross-wavelet transform have been used in many applications to study possible relationships between two phenomena in the time-frequency domain [15, 16]. However, these techniques have some limitations. For example, at higher frequencies or small wavelet scales, peaks in the spectrograms/scalograms and cross-spectrograms/scalograms get smoothed out, resulting in a reduction of power that can be misleading [17]. Another limitation of these methods is that the time series should be evenly spaced with no missing values. The Least-Squares Wavelet (LSWAVE) software [18, 19] is designed to process any type of time series regardless of how they are sampled. This software contains several tools each designed for a particular purpose described in more detail in Sects. 2.4, 2.5, 2.6, and 2.7.

The main goal of this study is to highlight the potential of the LSWAVE software for analyzing and investigating the possible relationships between PS-InSAR and precipitation time series. A rainfall time series, obtained from the nearest weather station to an area in the Municipality of Borghi, Italy, affected by landslides, is selected. Then its possible impact on the ground deformation is investigated by performing correlation and coherency analyses with the ascending- and descending-orbital geometries of the PS-InSAR time series. The results of these analyses are demonstrated in Sect. 3. Finally, the discussion and conclusions are provided in Sects. 4 and 5, respectively.

Fig. 1
figure 1

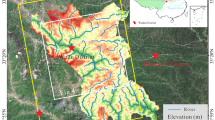
Geographical location of the case study within the municipality of Borghi on 10 m resolution digital elevation model [20]. The closest rainfall and temperature stations to the studied area are represented by a blue triangle and a red diamond respectively (arpae database https://www.arpae.it/). This map was generated with QGIS which is a free and open-source geographic information system (GIS).

Full size image

2 Materials and Methods

2.1 Study Region

The study area, which comprises the municipality of Borghi, is located in the typical hilly landscape of the eastern part of the Forlì-Cesena province (Emilia Romagna Region, Northern Italy, [21]) (Fig. 1). The local geology is represented by a turbiditic sequence (flysch) composed of marly and pelitic rocks in alternation with fractured sandstone layers [22, 23]. The consequence of such a heterogeneous alternation of hard and soft rock layers is an intense slope instability that affects the study area, expressed in relatively small and shallow slides, earth flows, and complex landslides. According to the national-scale historical landslides archive IFFI (Inventario Dei Fenomeni Franosi in Italia [24]), the majority of these landslides are classified as active or dormant. The main triggering factor for the activation or reactivation of landslides is related to long and intense rainfall during the whole year, or rapid snowmelt during the springtime (March and April [25,26,27]).

2.2 Datasets

The meteorological data (rainfall and temperature) used herein are provided by the Arpae agency and freely downloaded from https://www.arpae.it/. The A-DInSAR dataset used in this study consists of 265 SAR images from the archives of the Italian Space Agency (ASI) acquired from 2010 to 2019 in both orbital geometry:

  • Ascending orbital geometry: 119 images in Single Look Complex (SLC) format acquired by the COSMO-SkyMed satellites from 18 February 2011 to 03 August 2019;

  • Descending orbital geometry: 146 images in Single Look Complex (SLC) format acquired by the COSMO-SkyMed satellites from 23 August 2010 to 01 September 2019.

The COSMO-SkyMed constellation consists of four satellites, launched from 2007 to 2010, at an orbital height of 619.6 km and an orbital inclination of 97.86\(^{\circ }\). All satellites are equipped with high-resolution X-band radar (3.1 cm wavelength), capable of observing through cloud cover and during the night. The repeat cycle is 16 days, and the revisit capability is variable because every single satellite will have a near revisit time of 6 days. The policy on data acquisition of satellite missions, e.g., background missions (continuous acquisition for the same areas) versus on-demand acquisitions, affects the availability of data. Since the COSMO-SkyMed satellite mission has both military and civil purposes, the available archived images are not exactly one every 6 days. Therefore, the dataset is not continuous over time. The PS-InSAR time series values often contain outliers because of the technical issues of the PSI method during the stack gathering from the SAR data, the atmospheric phase estimation, and the deformation model used [28].

The selected PS-InSAR time series exhibit a mean cumulative displacement (expressed in mm) of \(-91.3\) mm (DESC) and \(-61.7\) mm (ASC) in the time interval of data acquisition (2011–2019 for the ascending geometry and 2010–2019 for the descending one). The area of interest was carefully chosen within a quiescent landslide reported in the IFFI database (IFFI-0400794100 [24]). Furthermore, the possible correlation with intense rain events was emphasized by the presence of strong accelerations within a small time window in the time series.

2.3 Pearson Correlation Method

The correlation between pairs of series can be measured to determine how much two time series vary together. The most common quantitative measure of correlation is the Pearson correlation coefficient, denoted by r, which can be computed to determine the strength and direction of the relationship between two variables [29]. The Pearson correlation coefficient is essentially a normalized measurement of the covariance that indicates how far away the data points are from the best fitting line, defined by Eq. (1):

$$\begin{aligned} r_{xy} = \frac{\sum _{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum _{i=1}^n (x_i-\overline{x})^2} \sqrt{\sum _{i=1}^n (y_i-\overline{y})^2}}, \end{aligned}$$
(1)

where \(\overline{x}\) and \(\overline{y}\) are the means of variables x and y, respectively. The Pearson correlation coefficient has a value between \(-1\) and \(+1\). This metric reflects only the linear association between two sets of data to find how well they are related, ignoring other types of relationships or correlations. Furthermore, \(x_i\) and \(y_i\) should ideally be measurements corresponding to time \(t_i\) when applying Eq. (1) to find the linear dependency between two time series. This means that if the two time series have different sampling rates, one should first resample the time series to match their corresponding times before Pearson correlation analysis. Thus, the correlation result will also depend on the resampling method.

2.4 Least-Squares Spectral Analysis (LSSA)

The LSSA is a spectral analysis method for processing unevenly sampled time series that may have trends or jumps ([30]). A least-squares spectrum (LSS) can be estimated by choosing a frequency set and trend constituents, such as linear, quadratic, or cubic. The LSS can be plotted as frequency vs. amplitude or frequency vs. percentage variance. To obtain a LSS, trend and sinusoidal functions at each given frequency are fitted to the time series via the least-squares optimization. Mathematically, let

$$\begin{aligned} \nonumber {f}= \begin{bmatrix} f(t_1) \\ f(t_2) \\ \vdots \\ f(t_n) \end{bmatrix}\!, ~~{c_k}= \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_q \\ c_{k,1} \\ c_{k,2} \end{bmatrix}\!,\qquad \qquad \qquad \qquad \\ {\varPhi }_k= \begin{bmatrix} \phi _1(t_1)&{} \phi _2(t_1)&{}\cdots &{}\phi _q(t_1)&{} \cos (2\pi \omega _k t_1) &{} \sin (2\pi \omega _k t_1) \\ \phi _1(t_2)&{} \phi _2(t_2)&{}\cdots &{}\phi _q(t_2)&{} \cos (2\pi \omega _k t_2) &{} \sin (2\pi \omega _k t_2) \\ \vdots &{} \vdots &{} \cdots &{}\vdots &{} \vdots &{} \vdots \\ \phi _1(t_n)&{} \phi _2(t_n)&{}\cdots &{}\phi _q(t_n)&{} \cos (2\pi \omega _k t_n) &{} \sin (2\pi \omega _k t_n) \end{bmatrix}\!, \end{aligned}$$
(2)

where \(f(t_j)\) is the measurement estimated at time \(t_j\), \(\omega _k\) is a cyclic frequency, \(\phi _\ell \) is a constituent of known form, and \(c_k\) is the coefficient vector being estimated by the least-squares method. For example, if \(\phi _1(t_j)=1\) and \(\phi _2(t_j)=t_j\) for \(1\le j\le n\), then \(c_1\) and \(c_2\) will be the intercept and slope of a linear trend to be estimated. The following cost function is minimized in LSSA after an optimization process.

$$\begin{aligned} \Psi \big (c_k\big )=\big (f- \varPhi _k c_k\big )^\textrm{T} \big (f-\varPhi _k c_k\big ), \end{aligned}$$
(3)

where \(\mathrm T\) is transpose. Thus, the estimated coefficient vector will be

$$\begin{aligned} \hat{c}_k=\big (\varPhi _k ^\textrm{T}\varPhi _k\big )^{-1}\varPhi _k ^\textrm{T} f. \end{aligned}$$
(4)

The amplitude of the sinusoid at \(\omega _k\) is the square root of the sum of squares of the last two elements of \(\hat{c}_k\). Since the first q columns in \(\varPhi _k\) are fixed, the amplitude estimation using Eq. (4) is not computationally efficient, especially when estimating LSS for a large set of frequencies. More details for computational optimization of Eq. (4) can be found in [17, Supplementary Materials].

To obtain the percentage variance LSS, the time series may first be de-trended. Then the LSS may be estimated for the residual time series, a process that takes into account the correlation between the removed trend and the sinusoids at each frequency. More precisely, let \(r(t_j)\) be the estimated residual at time \(t_j\), i.e., the original measurement minus the fitted trend value at \(t_j\). The normalized or percentage variance LSS (after multiplying by 100) of the residual series is calculated by the following formula:

$$\begin{aligned} s_k =\sum _{j=1}^n r(t_j)\Big (\hat{c}_{k,1}\cos (2\pi \omega _k t_j)+\hat{c}_{k,2}\sin (2\pi \omega _k t_j)\Big )\Big /\sum _{j=1}^n r(t_j)^2, \end{aligned}$$
(5)

where \(\hat{c}_{k,1}\) and \(\hat{c}_{k,2}\) are the last two elements of \(\hat{c}_{k}\) in Eq. (4).

The graph of estimated amplitudes of the fitted sinusoids versus their frequencies shows the amplitude LSS while the percentage variance LSS shows the contribution amount of the estimated sinusoids to the residual time series versus the frequencies. Note that when the trend is also fitted, both amplitude and percentage variance LSS are obtained for the residual series while the effect of trend removal is considered in the LSS estimation.

Assuming the normality of time series values, LSS in Eq. (5) will follow the beta distribution [31]. From this statement, if a spectral peak value is larger than the critical value at a certain significance level (e.g., 0.01), then the peak is statistically significant at 99% confidence level.

2.5 Least-Squares Cross-Spectral Analysis (LSCSA)

The LSCSA is a time series decomposition method that simultaneously processes two time series together for calculating coherency and phase differences between the harmonic components of the time series [32]. To obtain the least-squares cross-spectrum (LSCS) for two time series, first, the LSS of each time series is obtained, and then the LSSs are multiplied by each other. The stochastic significance of a peak in LSCS is also based on the normality assumption of the two time series whose values are also statistically independent. The discrepancy between the estimated phases can determine the time delay between the harmonics. For example, the phase difference of \(60^\circ \) at frequency 2 cycles/year indicates that the harmonic in the first time series leads/lags by about 30 days from the harmonic in the other time series. Note that the season-trend fit is applied to the entire time series in both LSSA and LSCSA. Therefore, the estimation of components whose frequencies and/or amplitudes change over time is an overall average and so not accurate locally [32, 33].

2.6 Least-Squares Wavelet Analysis (LSWA)

The LSWA, an extension of LSSA, can process non-stationary time series that may not be evenly sampled [32, 33]. In LSWA, a least-squares wavelet spectrogram (LSWS) is computed by sliding a window over time whose size is inversely proportional to the frequency, i.e., as the frequency increases the window size decreases, allowing a more accurate estimation of short-duration waves. The number of observations or measurements within a window is called the window size or segment size.

Spectrograms are usually displayed as time versus frequency versus amplitude or time versus frequency versus percentage variance. The LSWA also estimates the phases of sinusoids. To obtain LSWS, a windowing technique is implemented. Within each sliding window, LSSA is applied to estimate a spectral peak corresponding to that window using Eqs. (4) or (5). In other words, for each time and each frequency, the amplitude or percentage variance is estimated by simultaneously fitting the trend and sinusoids at the given frequency to the segment within the sliding window located at the given time. The percentage variance shows how much the residual segment contains the sinusoids at a given frequency.

A Gaussian function may be used to define weights for time series values within each window. Therefore, the values toward the window center get higher weights (more important) than the values toward the margins of the window (less important) during the season-trend estimation. This results in a smooth spectrogram, i.e., an optimal time-frequency resolution. Furthermore, the weights are useful when there exist missing values in non-stationary time series, so the values further away from the window center receive relatively lower weights. In fact, the Gaussian weights and harmonics in the LSWA model are like the Morlet wavelet in the least-squares sense [17, 32]. Note that the window location and window center are the same when the time series is evenly sampled or an equally spaced set of times is selected for estimating the spectrogram.

Like LSSA, the spectrogram peaks can be statistically assessed with the normality assumption. Note that in some applications, this assumption may not be valid but has no effect on the estimation of a spectrogram. In other words, regardless of whether the time series values are normally distributed or not, a spectrogram can still be estimated. A stochastic confidence level surface, shown herein as a gray surface, can show which spectrogram peaks are significant stochastically [32]. In other words, if a peak stands above the surface, then it is statistically significant.

2.7 Least-Squares Cross-Wavelet Analysis (LSCWA)

The least-squares cross-wavelet analysis (LSCWA) is a time-frequency decomposition technique proposed for coherency analysis and estimating phase differences between the harmonics of two time series [32, 33]. LSCWA can be directly applied to time series that are sampled at different time intervals, and it can account for the measurement errors. Moreover, the cross-spectrograms in LSCWA have higher time-frequency resolution compared to the ones in XWT [17].

The Least-squares cross-wavelet spectrogram (LSCWS) is obtained from the multiplication of the spectrograms of the two time series [32]. Since the time series may have different sampling rates, a common time vector is selected first that can be either the union of the time vectors in both time series or any equally spaced time vector whose values are within the common time interval of the two time series. The cross-spectrograms are plotted as time versus frequency versus percentage variance (coherency). The percentage variance shows the coherency amount between the harmonics of two time series segments—the higher the percentage variance, the higher the coherency and vice versa [17, Supplementary Materials].

The LSCWA also estimates the phase differences between the harmonics fitted to time series segments. The phase difference is a number between \(-180\) and \(180^\circ \), and it is usually plotted by an arrow on the 2D view of the cross-spectrogram. For example, arrows pointing to the positive and negative directions of the time axis mean that the harmonics are in-phase and out-of-phase, respectively. Arrows pointing to the positive and negative direction of the frequency axis mean that the harmonic in the second time series lags and leads the one in the first time series by \(90^\circ \), respectively [14]. Given the frequency, the estimated angle can be converted to time.

When the time series values are statistically independent and normally distributed, a confidence level surface can identify whether an estimated peak in the cross-spectrogram is statistically significant [32]. The MATLAB and Python software packages developed for LSSA, LSCSA, LSWA, and LSCWA are comprehensively described in [18, 19].

3 Results

3.1 Results of Traditional Methods

The relationship between temperature and rainfall variability was investigated by using monthly averages of temperature and cumulative rainfall (Fig. 2). These data were calculated from the daily cumulative temperature and rainfall for the 2011–2019 time period. Borghi municipality climate is classified as warm and temperate (Cfa, the acronym for humid subtropical climate, according to the Köppen-Geiger climate classification [34]). Temperatures are at their highest from June to August (summer) while they are at their lowest from December to February (winter) (Fig. 2a). The average temperature is 11.9 \(^{\circ }\)C. Rainfall amount is significant throughout the year, with an average annual rainfall of 74.3 mm. Even the driest month (August) has an average rainfall of 41.8 mm.

Fig. 2
figure 2

The climate charts showing the temperature and rainfall of Borghi municipality during the 2011–2019 time period. The monthly mean temperature and cumulative rainfall, a show a decrease in the rain during the summer season (from June to August) when the mean temperature increases. The Pearson coefficient, b indicates a poor negative correlation between the two variables. The box plots of rainfall c and temperature, d reveal a great variability during months. The outliers are shown by gray hexagons, and the horizontal lines inside the boxes show the median values

Full size image

There is no statistically significant linear correlation between mean temperature and cumulative rainfall, as highlighted by Fig. 2b. This lack of correlation can be due to the different trends of temperature and rainfall. As underlaid by the annual mean temperature and cumulative rainfall trends, the rainfall seems to show no seasonal tendency (Fig. 2c), while the temperature is characterized by an annual periodicity (Fig. 2d). Both rainfall and temperature exhibit significant monthly variability.

Fig. 3
figure 3

Top three panels: PS-InSAR time series for both ascending (ASC) and descending (DESC) satellite orbits and cumulative rainfall time series. The red curves show the filtered and daily resampled time series. Bottom three panels: Pearson correlation results between the selected daily time series

Full size image

The analysis of the correlation is not straightforward for unevenly spaced time series, as PS-InSAR. To face this problem, the original unevenly spaced time series were butter-filtered and resampled daily in order to remove outliers and obtain equidistant points of measure (Top panels of Fig. 3). The correlations between PS (ascending and descending) and rainfall time series are underlined in the bottom panels of Fig. 3. On one hand, the Pearson correlation coefficient shows that the ascending and descending PS time series are positively correlated with \(r\simeq 1\) (p-value \(< 0.01\)). On the other hand, a strong negative relationship between PS and rainfall time series is highlighted by the r-value close to \(-1\) (p-value \(< 0.01\)). Since the occurrence of landslides can be directly caused by intensive rainfall, identifying an increasing change in rainfall could determine the identification of a change in the occurrence of landslides. Overall, traditional methods of correlation do not allow the analysis of the quantitative relationship between the volume of rainfall and landslide occurrence for the identification of triggers.

3.2 The LSWAVE Results

The percentage variance and amplitude spectra and spectrograms for rainfall and temperature time series are illustrated in Fig. 4. The linear trend is used for both LSSA and LSWA. Interestingly, there is no statistically significant annual component at 99% confidence level in the rainfall time series (Fig. 4a). Furthermore, from the LSS, there is no statistically significant seasonal component in the rainfall time series while the LSWS shows short-duration seasonal components in the years 2012, 2014, 2015, 2016, and 2018 (shown in reddish). The amplitude spectrogram in Fig. 4b also shows relatively higher estimated amplitudes for the seasonal components at 4–5 cycles/year (period of 2–3 months) in 2015 and 2018.

The temperature time series shows a dominant annual component that is statistically significant in both LSS and LSWS (cf. Fig. 4c). On the other hand, the amplitude spectrogram illustrated in Fig. 4d clearly shows the amplitude of the temperature has decreased since 2011 while this cannot be observed from LSS amplitude because LSS only shows frequency versus amplitude not time-frequency versus amplitude.

Fig. 4
figure 4

The percentage variance and amplitude spectra and spectrograms for a, b rainfall and c, d temperature time series. The red lines in LSSs displayed in panels, a and c show the critical values at 99% confidence level. Also, the gray color map is the stochastic surface at 99% confidence level

Full size image

Figure 5 shows the LSCSs and LSCWSs of the climate and PS-InSAR displacement time series. A linear trend was estimated and removed from each segment when estimating LSCWSs in panels (a)–(d) and from each time series when estimating LSCSs in panels (a) and (b) while a cubic trend was fitted and removed from the displacement time series when estimating LSCSs in panels (c) and (d).

One can see from Fig. 5a that the annual cycles of temperature and rainfall time series are coherent at 99% confidence level though the percentage variance is very low (about 2%). Arrows displayed on the significant annual peaks are pointing to the left, meaning that the annual cycles of temperature and rainfall are almost out-of-phase. The estimated phase difference using LSCSA is approximately \(-170^\circ \). This means that when the annual cycle of the temperature reaches its maximum value, the annual cycle of the rainfall reaches its minimum value and vice versa. Note that Fig. 3b only showed a weak negative correlation (\(r\simeq -0.16\)) but neither showed the seasonality nor temporal change.

From Fig. 5b, a statistically significant coherency can be observed for the annual components, where the annual cycle of time series for the ascending geometry leads the one for the descending geometry by about one to two months over time. The cross-spectral peaks are not estimated for the locations with data gaps (e.g., between the end of 2016 and early 2017).

Interestingly, the short-duration seasonal components of displacement (ascending geometry) and rainfall at 4–5 cycles/year (about 2–3 months period) toward the end of 2014 are coherent at 99% confidence level (cf., Fig. 5c), with approximately \(120^\circ \) or one month phase difference. In other words, as the rainfall value increases, the displacement value decreases. It is also known that landslides occurred toward the end of 2014.

The annual cycle in the years 2013 and 2018 for rainfall lags the one for the displacement (descending geometry) by about one month, see Fig. 5d. This is in agreement with the fact that there were landslides in the years 2013 and 2018. Furthermore, in the year 2016 both LSCWSs, illustrated in Fig. 5c, d, show statistically significant coherency at 3 cycles/year with about \(90^\circ \) phase difference. This indicates that the four-month cycle of the displacement time series leads the one in the rainfall by approximately one month which could mean that the rainfall might have played a significant role in the ground deformation. Note that landslides also occurred during 2016.

Fig. 5
figure 5

The cross-spectra and cross-spectrograms of climate and PS-InSAR time series. The red lines in LSCSs show the critical values at 99% confidence level. Also, the gray color map represents the stochastic surface at 99% confidence level. The white arrows on LSCWSs show the local phase differences. Arrows pointing to the right, left, top, and bottom indicate that the seasonal cycles of the segments in the first time series are in-phase, out-of-phase, leads, and lags with/from the ones in the second time series, respectively. To avoid displaying too many arrows on LSCWSs, arrows are displayed only for some of the most significant peaks

Full size image

4 Discussion

As observed in Fig. 4a, there was no statistically significant annual component at 99% confidence level in the rainfall time series as opposed to a significant annual component that usually exists in rainfall time series in other regions (e.g., [13, 17]). The annual amplitude attenuation over time in the temperature time series was also an interesting observation. From the negative Pearson correlation (\(r\simeq -0.16\)) and the direction of the arrows displayed on the annual peaks in Fig. 5a, it can be deduced that the warm summers tended to be drier and cool winters tended to be wetter in this study region—like the results in some other regions (e.g., [35, 36]).

As demonstrated in Fig. 5, the seasonal cycles of the displacement time series generally led the ones in the rainfall time series by nearly one month during major landslides. The least-squares spectral and wavelet analyses did not show any statistically significant annual component in the rainfall time series while the annual component of the rainfall was weakly coherent with the one in the displacement time series which could have also triggered the landslides. Before applying the Pearson correlation analysis, the time series had to be aggregated, i.e., the displacement time series had to be regularized and resampled so that both displacement and rainfall data align in time. However, the LSWAVE tools did not require any such pre-processing and were directly applied to process the climate and displacement time series with different sampling rates and gaps.

The impact of rainfall on ground deformation requires further investigation. For example, the wavelike components of the displacement time series could have been created by several factors, such as possible biases created during the InSAR data pre-processing steps, and land cover and climate change. Applying the methods mentioned herein to process displacement and rainfall time series for other regions may help in a better understanding of their relationships which is subject to future work.

5 Conclusions

We briefly reviewed the tools in the LSWAVE software and showed how they may be utilized to investigate possible relationships between rainfalls and displacement time series derived by PS-InSAR (both ascending and descending geometry) in the municipality of Borghi, Italy. We also investigated the relationship between rainfalls and temperature in the study region. We highlighted what additional information one can obtain when using these tools as compared to traditional ones like Pearson correlation analysis. The tools in the LSWAVE software were directly applied to unevenly sampled time series having different sampling rates without any filtering and/or aggregation. As for future work, we shall generate geospatial maps using these tools for investigating possible spatiotemporal relationships between rainfalls and displacement time series. We hope that such analyses help geologists to better understand the pattern of landslides and their triggering factors.