Keywords

1 Introduction

This work concerns the interval-valued intuitionistic fuzzy set (IVIFS) model [2]. Any IVIFS evaluates every alternative of a set by means of an interval-valued intuitionistic fuzzy number (IVIFN). In turn, an IVIFN shares characteristics of both intuitionistic fuzzy numbers (IFN) [3, 11] and interval-valued fuzzy numbers [9, 13].

Not surprisingly, the research about IVIFSs closely resembles the intuitionistic fuzzy set (IFS) case. In addition to the study of arithmetic operations and algebraic manipulations, a number of works contributed to the field with their inspection of other topics. For example, scores and accuracies were defined that produced comparison laws [12, 14]. Also aggregation operators, or decision-making methodologies, in the framework of IVIFSs were considered by other authors. In fact, aggregation operators and comparison laws have taken part in many decision making (DM) strategies [7, 16, 19]. This includes the case of multi-attribute decision making (MADM).

It is noteworthy that in order to define aggregation operators for either IFSs or IVIFSs, one simply needs to be able to aggregate their constituent IFNs and IVIFNs. Two fundamental methodologies can be identified. One uses operational laws for IFNs, respectively, IVIFNs, to produce aggregation operators for IFNs and IFSs, respectively, IVIFNs and IVIFSs. Another methodology makes use of aggregation operators on crisp numbers. Nevertheless, often the intricacy of the IVIFS model generates long formulas, the intuitive interpretation of which is lost.

This work investigates the utilization of two operational transformation techniques –that represent one IVIFN by two related IFNs in a constructive manner– for the smooth aggregation of IVIFNs, and for MADM in this framewok. These transformation techniques were recently introduced in [1]. One focus will be the derivation of scores and accuracies of IVIFNs from the scores and accuracies of the two IFNs that characterize them. With both tools –transformation techniques and scores/accuracies– it is possible to put forward respective flexible MADM methodologies in the framework of IVIFSs –one for each transformation technique. We just need to use an aggregation operator on IFNs to aggregate the IFNs that characterize the IVIFNs that define each IVIFS, according to the corresponding transformation, and then use a comparison law (for example, one that is based on scores and accuracies) to prioritize the alternatives characterized by the IVIFSs. We argue that in fact, if the aggregation operator and comparison law for IFNs remain fixed, both methodologies are equivalent. Finally, this common methodology will be compared with existing solutions.

The rest of this article is organized as follows. We recall some necessary concepts and results in Sect. 2. In particular, we state the two transformation theorems for IVIFNs and their intuitive background. Visual representations illustrate the main ideas and the two theorems. Section 3 contains our results. Some conclusions end this work in Sect. 4.

2 Preliminary Concepts

In this article X will be a fixed set of alternatives, and D[0, 1] will be the set of all closed intervals that are included in \(\mathcal{I}= [0,1]\).

By an orthopair we mean a pair \((\mu , \nu )\in \mathcal{I}\times \mathcal{I}\), thus \(0\leqslant \mu , \nu \leqslant 1\). This orthopair is an intuitionistic fuzzy number (also, IFN) when \( \mu + \nu \leqslant 1\) [20]. Henceforth \(\mathbb {A}\) will denote the set of all IFNs.

Definition 1

Suppose that \((\mu _1, \nu _1)\), \((\mu _2, \nu _2)\) are orthopairs. Then we define the following two orthopairs:

  • \((\mu _1, \nu _1)\vee (\mu _2, \nu _2) = (\max \{\mu _1, \mu _2\}, \max \{\nu _1, \nu _2\})\), and

  • \((\mu _1, \nu _1)\wedge (\mu _2, \nu _2) = (\min \{\mu _1, \mu _2\}, \min \{\nu _1, \nu _2\})\).

We shall also need the following two partial orders \(\preccurlyeq \) and \(\leqslant _L\) on the set of all orthopairs: suppose that \((\mu _1, \nu _1)\), \((\mu _2, \nu _2)\) are orthopairs, then we declare

  • \((\mu _1, \nu _1)\preccurlyeq (\mu _2, \nu _2)\) if and only if \(\mu _1 \leqslant \mu _2\) and \(\nu _2 \leqslant \nu _1\) [3], and

  • \((\mu _1, \nu _1)\leqslant _L(\mu _2, \nu _2)\) if and only if \(\mu _1 \leqslant \mu _2\) and \(\nu _1 \leqslant \nu _2\) [5].

The IFNs \(\textbf{1}= (1, 0)\) and \(\textbf{0}= (0, 1)\) are, respectively, the top and bottom elements of the partial order \(\preccurlyeq \).

The partial order \(\leqslant _L\) defined on \(\mathcal{I}\times \mathcal{I}\) can be generalized to a partial order on \(\mathcal{I}\times {\mathop {\ldots }\limits ^{n}} \times \mathcal{I}\) in the following manner: if \((a_1, {\ldots } , a_n), (b_1, {\ldots } , b_n) \in \mathcal{I}\times {\mathop {\ldots }\limits ^{n}} \times \mathcal{I}\), then the notation \((a_1, {\ldots } , a_n)\leqslant _L(b_1, {\ldots } , b_n)\) is equivalent to \(a_i \leqslant b_i\) for each i.

2.1 Intuitionistic Fuzzy Sets: Concepts and operations

The concept of interval-valued intuitionistic fuzzy set was initiated by K. Atanassov. For this reason, many authors use the term Atanassov’s intuitionistic fuzzy sets.

Definition 2

(Atanassov [3]). An intuitionistic fuzzy set (also, IFS) A over X is \( A = \{ \langle x, ( \mu _A(x), \nu _A(x) ) \rangle |\, x\in X \} \), with the condition that for each \(x\in X\) \(( \mu _A (x), \nu _A (x) )\) is an IFN.

The set of all IFSs over X will be denoted by IFS(\(X\)).

On occasions the intuitionistic fuzzy set A is abbreviated as \(A = \langle \mu _A, \nu _A \rangle \).

It is assumed that \(\mu _A,\nu _A : X \rightarrow [0,1]\) represent the membership degree (MD) and non-membership degree (NMD) of each element \(x\in X\) to the intuitionistic fuzzy set A.

The concepts defined for orthopairs (hence, for IFNs) in Definition 1 can be applied to IFSs too. Consider the case of the two partial orders defined there. To extend them, let \(A= \langle \mu _A, \nu _A \rangle \) and \(B= \langle \mu _B, \nu _B \rangle \) be two IFSs. Then the notation \(A\leqslant _L B\), respectively, \(A\preccurlyeq B\), means \(( \mu _A (x), \nu _A (x) ) \leqslant _L ( \mu _B (x), \nu _B (x) )\), respectively, \(( \mu _A (x), \nu _A (x) )\preccurlyeq ( \mu _B (x), \nu _B (x) )\), for every \(x\in X\). Of course, the IFSs \(A\wedge B\) and \(A\vee B\) can be given with the corresponding pointwise definitions. Importantly, it is not guaranteed that \(A\vee B\) produces an IFS when A and B are IFSs (see Fig. 1 below). We can only assure that \(A\vee B\) produces an orthopair fuzzy set (associating an orthopair with each \(x\in X\)).

Some algebraic concepts have been extended to IFSs and IFNs:

Definition 3

 [3]. The union and intersection of \(A= \langle \mu _A, \nu _A \rangle \) and \(B= \langle \mu _B, \nu _B \rangle \), two IFSs, are, respectively,

$$\begin{aligned} { A\cup B = \{ \langle x, ( \max \{\mu _A(x), \mu _B(x)\}, \min \{\nu _A(x), \nu _B(x) \} ) \rangle |\, x\in X \} } \end{aligned}$$
(1)
$$\begin{aligned} { A\cap B = \{ \langle x, ( \min \{\mu _A(x), \mu _B(x)\}, \max \{\nu _A(x), \nu _B(x) \} ) \rangle |\, x\in X \} } \end{aligned}$$
(2)

Subsethood is defined by:

$$\begin{aligned} A\subseteq B \Leftrightarrow (\mu _A(x), \nu _A(x)) \preccurlyeq ( \mu _B(x), \nu _B(x) ) \text{ for } \text{ all } x\in X. \end{aligned}$$
(3)

The concepts of union and intersection of IFSs induce union and intersection of IFNs. Both operators produce respective IFNs as follows: let \((\mu _1, \nu _1)\), \((\mu _2, \nu _2)\) be IFNs, then

$$\begin{aligned} (\mu _1, \nu _1) \cup (\mu _2, \nu _2) = ( \max \{\mu _1, \mu _2\}, \min \{\nu _1, \nu _2 \} ),\end{aligned}$$
(4)
$$\begin{aligned} (\mu _1, \nu _1) \cap (\mu _2, \nu _2) = ( \min \{\mu _1, \mu _2\}, \max \{\nu _1, \nu _2 \} ). \end{aligned}$$
(5)

Figure 1 illustrates concepts defined in this section. We consider two cases. When \((\mu _1, \nu _1)\), \((\mu _2, \nu _2)\) are IFNs, we can observe that \(I_1\vee I_2\) may not produce an IFN.

Fig. 1.
figure 1

Visual representation of Definition 1 and Eqs. (4) and (5). Both \(I_1\) and \(I_2\) are IFNs in the two figures.

Full size image

Remark 1

Suppose that \(I_1\) and \(I_2\) are IFNs. Then one has:

\(I_1 \leqslant _L I_2 \Leftrightarrow I_1 \vee I_2 = I_2 \Leftrightarrow I_1 \wedge I_2 = I_1\), and also

\(I_1 \preccurlyeq I_2 \Leftrightarrow I_1 \cup I_2 = I_2 \Leftrightarrow I_1 \cap I_2 = I_1 \).

In order to compare IFNs by their performance, standard rules use their scores and accuracies since [20, Definition 1]. The score of \(J=(\mu , \nu )\), an IFN, was defined in [8] as \(S(J)=\mu - \nu \). Higher scores are preferable, however ties appear often. A tie-breaking rule in the case of equal scores uses the respective accuracies of the IFNs. The accuracy of J was defined in [10] as \(H(J)=\mu + \nu \).

To mention but one antecedent of transformation techniques in the framework of IFSs, we recall that Atanassov and Gargov [2] defined a bijection between IFS(\(X\)) and the set of all interval-valued fuzzy sets [13]. Both this bijection and its inverse mapping are defined by explicit expressions. We shall not use them in this article.

2.2 Interval-Valued Intuitionistic Fuzzy Sets: Concepts and Results

The concept of interval-valued intuitionistic fuzzy set was initiated by Atanassov and Gargov:

Definition 4

(Atanassov and Gargov [2]). An interval-valued intuitionistic fuzzy set (IVIFS) A over X is \( A = \{ \langle x, ( \mu ^A(x), \nu ^A(x) ) \rangle |\, x\in X \} \), with the condition that for each \(x\in X\), \( \mu ^A (x) = [ \mu _L^A(x), \mu _M^A(x)]\in D[0,1]\), \(\nu ^A (x) = [ \nu _L^A(x), \nu _M^A(x)]\in D[0,1]\) and \(\mu _M^A(x) + \nu _M^A(x) \leqslant 1\).

The set of all IVIFSs over X will be denoted by IVIFS(\(X\)).

Any pair \(([\mu , \mu '], [\nu , \nu '])\in D[0,1]\times D[0,1]\) such that \(\mu '+\nu '\leqslant 1\) is an interval-valued intuitionistic fuzzy number (also, IVIFN) [19]. Equivalently, an IVIFN is a pair \(P=([\mu , \mu '], [\nu , \nu '])\in D[0,1]\times D[0,1]\) with the property that \((\mu ',\nu ')\) is an IFN. Its score is \(s(P) = \frac{1}{2}(\mu -\nu + \mu ' - \nu ')\), and \(h(P)=\frac{1}{2}(\mu +\mu '+\nu + \nu ')\) is its accuracy [19]. As in the case if IFNs, IVIFNs with higher scores are preferable, and accuracy is used to break ties between IVIFNs with equal score.

Other scores that attempt to improve the performance of the definition above include the next formulas from [14]:

$$ s_{wc1}(P) = \frac{ \mu + \mu ' + \sqrt{ \mu ' \nu ' } (1 - \mu - \nu ) + \sqrt{ \mu \nu } (1 - \mu '- \nu ') }{2}, \text{ and } $$
$$ s_{wc2}(P) = \frac{ ( \mu + \mu ' ) ( \mu + \nu ) - ( \nu + \nu ') ( \mu ' + \nu ') }{2}. $$

Alternative expressions for the accuracy have been proposed too [12], remarkably,

$$ m(P) = \mu + \nu -1 + \frac{1}{2}(\nu + \nu ') = \frac{ \mu - (1 - \mu - \nu ) + \mu ' - (1 - \mu ' - \nu ' ) }{2}, \text{ and } $$
$$ l(P) = \frac{ \mu + \mu ' - \nu ' ( 1-\mu ' ) - \nu ( 1-\mu ) }{2}. $$

The basic set-theoretic operations (subsethood, union, and intersection), plus arithmetic manipulations (sum and multiplication) were extended to IVIFSs [2, 4]. With their help, and other operational laws (such as Einstein’s sum and product [16]) novel averaging operators were produced that rely on renewed arithmetic operations on IVIFSs. The Einstein operational laws were also used to the purpose of aggregation for multi-attribute decision-making in both [17] and [15].

Now we proceed to recall two structural theorems proven in [1]. Both are concerned with related transformation techniques that allow us to study IVIFN by means of pairs of suitable IFNs. Their respective intuitive foundations are represented by corresponding figures below in this section.

First Bijection. To state the first transformation theorem, we need to define a subset \(\mathcal {O}_1\subseteq \) IFS(\(X\)) \(\times \) IFS(\(X\)) as follows:

$$\begin{aligned} \mathcal {O}_1 = \{ (A_1, A_2) \, \vert A_1 \, \preccurlyeq A_2, A_1 \vee A_2 \in \textrm{IFS}(X) \}. \end{aligned}$$
(6)

Now we are ready to define the following \(f_1 : \textrm{IVIFS}(X) \longrightarrow \mathcal {O}_1\). Let \(A = \{ \langle x, ( \mu ^A(x), \nu ^A(x) ) \rangle |\, x\in X \}\in \textrm{IVIFS}(X)\) such that for each \(x\in X\), we write \( \mu ^A (x) = [ \mu _L^A(x), \mu _M^A(x)]\), \(\nu ^A (x) = [ \nu _L^A(x), \nu _M^A(x)]\). Then \(f_1 (A) = (I_1^A, I_2^A)\) is given by the formulas:

$$\begin{aligned} I_1^A(x) = (\mu _L^A(x), \nu _M^A(x) ), \, I_2^A(x) = (\mu _M^A(x), \nu _L^A(x) ) \end{aligned}$$
(7)

for each \(x\in X\). In addition, consider the mapping \((f_1)^{-1} : \mathcal {O}_1 \longrightarrow \textrm{IVIFS}(X)\) defined as follows. For any \((I_1, I_2)\in \mathcal {O}_1\) such that \(I_i = \{ \langle x, ( \mu _i(x), \nu _i(x) ) \rangle |\, x\in X \}\), \(i=1, 2\), consider

$$\begin{aligned} A_{(I_1, I_2)} = \{ \langle x, ( [\mu _1(x), \mu _2(x)], [\nu _2(x), \nu _1(x)] ) \rangle |\, x\in X \} \end{aligned}$$
(8)

and let \((f_1)^{-1} (I_1, I_2) = A_{(I_1, I_2)}\).

Theorem 1

[1]. The mapping \(f_1 : \textrm{IVIFS}(X) \longrightarrow \mathcal {O}_1\) is a bijection, and its inverse mapping is \((f_1)^{-1} : \mathcal {O}_1 \longrightarrow \textrm{IVIFS}(X)\).

Second Bijection. To state the second transformation theorem, we need to define another subset \(\mathcal {O}_2\subseteq \) IFS(\(X\))\(\times \)IFS(\(X\)) as follows:

$$\begin{aligned} \mathcal {O}_2 = \{ (A_1, A_2)\in \textrm{IFS}(X)^2 \, \vert \, A_1 \leqslant _L A_2 \}. \end{aligned}$$
(9)

Now we are ready to define the following \(f_2 : \textrm{IVIFS}(X) \longrightarrow \mathcal {O}_2\). Consider \(A = \{ \langle x, ( \mu ^A(x), \nu ^A(x) ) \rangle |\, x\in X \}\in \textrm{IVIFS}(X)\) such that for each \(x\in X\), we write \( \mu ^A (x) = [ \mu _L^A(x), \mu _M^A(x)]\), \(\nu ^A (x) = [ \nu _L^A(x), \nu _M^A(x)]\). Then \(f_2 (A) = (J_1^A, J_2^A)\) is given by the formulas:

$$\begin{aligned} J_1^A(x) = (\mu _L^A(x), \nu _L^A(x) ), \, J_2^A(x) = (\mu _M^A(x), \nu _M^A(x) ) \end{aligned}$$
(10)

for each \(x\in X\). In addition, consider the mapping \((f_2)^{-1} : \mathcal {O}_2 \longrightarrow \textrm{IVIFS}(X)\) defined as follows. For any \((I_1, I_2)\in \mathcal {O}_2\) such that \(I_i = \{ \langle x, ( \mu _i(x), \nu _i(x) ) \rangle |\, x\in X \}\), \(i=1, 2\), consider

$$\begin{aligned} A^{(I_1, I_2)} = \{ \langle x, ( [\mu _1(x), \mu _2(x)], [\nu _1(x), \nu _2(x)] ) \rangle |\, x\in X \} \end{aligned}$$
(11)

and let \((f_2)^{-1} (I_1, I_2) = A^{(I_1, I_2)}\).

Theorem 2

[1]. The mapping \(f_2 : \textrm{IVIFS}(X) \longrightarrow \mathcal {O}_1\) is a bijection, and its inverse mapping is \((f_2)^{-1} : \mathcal {O}_1 \longrightarrow \textrm{IVIFS}(X)\).

The intuitive performance of Theorems  1 and 2 is illustrated in Fig. 2.

Fig. 2.
figure 2

Visual representation of the transformations \(f_1\) and \(f_2\) stated in Theorems 1 and  2.

Full size image

3 Results

Note that the transformations \(f_1\) and \(f_2\) stated in Theorems 1 and  2 operate on IVIFSs. By considering their constituent IVIFNs, they also induce respective transformations that associate each IVIFN with respective pairs of IFNs. To reduce notational burden, we denote those transformations of IVIFNs by the same names, i.e., \(f_1\) and \(f_2\). And we shall refer to these reduced specifications for IVIFNs in this section.

3.1 Scores and Accuracies

We proceed to prove that the transformations \(f_1\) and \(f_2\) enable us to compute the standard scores, respectively, accuracies, for IVIFNs if we know the scores, respectively, accuracies, of their associated IFNs. We do this in the next result:

Proposition 1

Let \(P=([\mu , \mu '], [\nu , \nu '])\) be an IVIFN. For \(i=1, 2\), let \(f_i(P)=(I^i_1, I^i_2)\), so that all \(I^1_1\), \(I^1_2\), \(I^2_1\), \(I^2_2\) are IFNs. Then

$$\begin{aligned} s(P) = \frac{1}{2} (S(I^1_1)+S(I^1_2)) = \frac{1}{2} (S(I^2_1)+S(I^2_2)) \end{aligned}$$
(12)

and

$$\begin{aligned} h(P) = \frac{1}{2} (H(I^1_1)+H(I^1_2)) = \frac{1}{2} (H(I^2_1)+H(I^2_2)). \end{aligned}$$
(13)

Proof

By definition, \(f_1(P)=(I^1_1, I^1_2)\) means \(I^1_1 = (\mu , \nu ')\) and \(I^1_2 = (\mu ', \nu )\), whereas \(f_2(P)=(I^2_1, I^2_2)\) means \(I^2_1 = (\mu , \nu )\) and \(I^2_2 = (\mu ', \nu ')\). Proofs follow from direct computations. Notice that we can prove the equalities

$$ s(P) = \frac{1}{2}(\mu -\nu + \mu ' - \nu ') = \frac{1}{2} (S(I^1_1)+S(I^1_2)) = \frac{1}{2} (S(I^2_1)+S(I^2_2)) $$

because \(S(I^1_1) = \mu - \nu '\), \(S(I^1_2) = \mu ' - \nu \), \(S(I^2_1) = \mu - \nu \), \(S(I^2_2) = \mu ' - \nu '\). Similarly, the equalities

$$ h(P)=\frac{1}{2}(\mu +\mu '+\nu + \nu ') = \frac{1}{2} (H(I^1_1)+H(I^1_2)) = \frac{1}{2} (H(I^2_1)+H(I^2_2)) $$

follow from \(H(I^1_1) = \mu + \nu '\), \(H(I^1_2) = \mu ' + \nu \), \(H(I^2_1) = \mu + \nu \), \(H(I^2_2) = \mu ' + \nu '\).

Both \(f_1\) and \(f_2\) associate one IVIFN with two IFNs. Proposition 1 proves that in each case, the score/accuracy of the IVIFN can be computed as the arithmetic average of the scores/accuracies of the two IFNs that are linked to them.

3.2 Aggregation

The main purpose of [1] was to use the theoretical advancements proven by Theorems 1 and 2 in order to design flexible strategies for the aggregation of IVIFSs. This achievement was then applied to group decision making with the help of scores. In this section we complement the information given in [1].

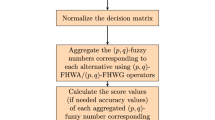
The strategy that was developed in [1] is summarized by Algorithm 1. As said above, here we concentrate in IVIFNs, but [1] worked in the framework of IVIFSs. So Algorithm 1 has been modified accordingly.

figure a

The Effect of Replacing the Representation Theorem. Although [1] did not consider the algorithm that uses the other representation theorem (i.e., \(f_1\) at step 1 and then \(f_1^{-1}\) at step 3), below we state that the reason is that both algorithms are the same:

Proposition 2

If we replace \(f_2\) with \(f_1\) in Algorithm 1, then the aggregate output does not change.

A formal proof of this proposition is long and tedious, but straightforward. Hence we omit it here.

3.3 Multi-attribute Decision Making Using Representation Theorems

Once an IVIFS is associated with an IVIFN (e.g., with the utilization of Algorithm 1 or any other methodology), it is possible to use the scores and accuracies of IVIFNs defined in Sect. 2.2 to rank the IVIFSs [1]. The next section explains this issue and compares the results with existing methodologies.

MADM: A Comparative Analysis. Another exercise that was missing in [1] is a comparative analysis with respect to existing aggregation methodologies. We do this in this section. We shall use data from a case study described in [19]. To simplify matters, consider the three IVIFSs described in Table 1. They are from [19, Section 4], although that article studies ten IVIFSs.

Table 1. Three projects and their characteristics.
Full size table

In Table 1, each project \(A_i\) is characterized by its performance in terms of three attributes, namely, \(B_1\), \(B_2\) and \(B_3\). Then [19] suggest that the overall performance of each \(A_i\) can be faithfully described by the aggregate IVIFNs of their corresponding IVIFNs. Once these IVIFNs are computed, the projects are ranked from highest to lowest score of the aggregate IVIFNs that summarize them. We supplement their exercise with the calculation of scores by \(s_{wc1}\) and \(s_{wc2}\).

We shall compare the results obtained with this methodology, and with the flexible Algorithm 1 (or its counterpart with \(f_1\)). We shall refer to two examples of aggregation operators on IFNs. Both use a weighting vector \(v = (v _1, \ldots , v _n)\), which therefore satisfies \(v _1+ \ldots + v _n=1\) and \(v _i\in \mathcal{I}\) for all \(i=1, \ldots , n\) [6, Def. 2.5]. Now when \(I_i = ( \mu _{i}, \nu _{i} ) \) are IFNs , \(i=1, \ldots , n\):

  • \(\textrm{IWAM}_{v }(I_1, \ldots , I_n) = ( \sum _{i=1}^n {v _i}\mu _{i}, \sum _{i=1}^n {v_i} \nu _{i} )\) [5, Eq. (13)] defines the intuitionistic fuzzy weighted arithmetic mean associated with v.

  • \(\textrm{IFWG}_{v }(I_1, \ldots , I_n) = ( \prod _{i=1}^n \mu _{i}^{ v_i }, 1 - \prod _{i=1}^n (1 - \nu _{i} )^{v _i})\) [20, Definition 2] defines the intuitionistic fuzzy weighted geometric mean associated with v.

It is timely to explain that a version of \(\textrm{IFWG}_{v }\) has been defined that incorporates the foundations of the OWA operator, and it was named \(\textrm{IFOWG}_{ v } \). And also, that many other aggregation operators on IFNs have been proposed in the literature.

In our comparison, we shall use the vector of weights \(v=(0.5,0.3,0.2)\) that formed part of the aggregation methodology of [19]. And we shall compare the results obtained by [19] and by the application of Algorithm 1 with \(\textrm{IWAM}_{v }\) and \(\textrm{IFWG}_{v }\). In each case, we work with three score rankings that correspond to the formulas given in Sect. 2.2. Tables 2 and 3 summarize the elements that motivate our subsequent discussion. Notice that we do not need to compute accuracies, since ties do not appear in the score-based comparisons.

Table 2. Aggregate IFNs and scores of the projects in Table 1.
Full size table
Table 3. Three scores for the projects in Table 1.
Full size table

We can observe that the choice of the decision making mechanism is not innocuous. Indeed, the prioritization recommended by each methodology varies:

  • If we use [19], the recommendation is \(A_{10} \succ A_{9} \succ A_{1}\) regardless of score selection.

  • If we use Algorithm 1 (either with \(\textrm{IWAM}_{v }\) or with \(\textrm{IFWG}_{v }\)), the recommendation becomes \(A_{10} \succ A_{1} \succ A_{9}\) regardless of score selection.

Hence the decision between \(A_{1}\) and \(A_{9}\) is different. The recommendations by Algorithm 1 coincide in declaring \( A_{1} \succ A_{9}\), however the procedure in [19] consistently declares \( A_{9} \succ A_{1}\).

4 Concluding Remarks

This work has shown that the operational transformation techniques rendered in [1] deserve further attention. We have not yet exploited the full capabilities of Algorithm 1, because other aggregation operators can be used and their performance compared with the cases studied so far.

In addition, it is possible to pose the problem of relating the alternative scores \(s_{wc1}\) and \(s_{wc2}\), and accuracies m and l, defined in Sect. 2.2 with our transformations. Proposition 1 is our source of inspiration. And a similar exercise can be done for the membership uncertainty index and hesitation uncertainty index of an IVIFV defined in [18] to guarantee the anti-symmetry of ranking method.

We expect to return to these issues in the future.