Keywords

1 Introduction

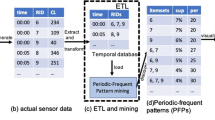
Partial periodic pattern mining is an important knowledge discovery technique to find all patterns exhibiting partial periodic behavior in a temporal database. The basic model of partial periodic pattern mining is as follows [4]: Let \(I = \{i_1, i_2, ..., i_n\}\) be the set of n items appearing in a database. A set of items \(X \subseteq I\) is called an itemset. An itemset containing m items is called a m-itemset. The length of this itemset is m. A transaction t consists of timestamp, and an itemset. That is \(t = (ts, Y)\), where ts represents the transaction time and Y is an itemset. A temporal database TDB is an ordered collection of transactions, i.e. \(TDB = \{t_1, t_2, \cdot \cdot \cdot , t_k\}\), where \(k=|TDB|\) represents the total number of transactions. Let \(ts_{min}\) and \(ts_{max}\) be the minimum and maximum timestamps of all the transactions in TDB, respectively. For a transaction \(t = (ts, Y)\), such that \(X \subseteq Y\), it is said that X occurs in t and such a timestamp is denoted as \(ts^X\). The total number of transactions containing X in TDB is defined as the frequency of X and denoted as freq(X). That is, \(freq(X) = |TS^X|\). Let \(ts^X_j,~ ts^X_k \in TS^X\), \(1\le j < k \le m\), denote any two consecutive timestamps in \(TS^X\). An inter-arrival time of X denoted as \(iat^X = (ts^X_{k} - ts^X_j)\). Let \(IAT^X=\{iat^X_1,iat^X_2,\)- \(\cdots ,iat^X_k\}\), \(k=sup(X)-1\), be the list of all inter-arrival times of X in TDB. An inter-arrival time of X is said to be periodic (or interesting) if it is no more than the user-specified period (per). A \(iat^X_i\in IAT^X\) is said to be periodic if \(iat^X_i\le per\). Let \(\widehat{IAT^X}\) be the set of all inter-arrival times in \(IAT^X\) with \(iat^X \le per\). That is, \(\widehat{IAT^X}\subseteq IAT^X\) such that if \(\exists iat_k^X\in IAT^X:~iat^X_k\le per\), then \(iat^X_k\in \widehat{IAT^X}\). The period-support of X, denoted as PS(X)=\(|\widehat{IAT^X}|\). Given a temporal database (TDB), period (per), and minimum period-support (minPS), the problem of partial periodic pattern mining is to find all patterns in TDB that have periodic-support no less than minPS.

Uday et al. [4] described a pattern-growth algorithm to find desired patterns in a temporal database. Ravi et al. [6] extend this model to discover the partial periodic patterns in columnar temporal databases. However, this model’s widespread adoption and successful industrial application were hindered by this obstacle: “minPS and per are two key constraints that make partial periodic pattern mining practicable in real-world applications. They are used to prune the search space and limit the number of patterns generated. Unfortunately, setting these two constraints for an application is an open research problem and may require a profound knowledge of the application’s background.” With this motivation, this paper proposes a solution of finding top-k partial periodically occurring patterns in a temporal database.

The contribution of this paper is as follows. First, we propose an extended model of finding top-k partial periodic patterns in a temporal database. Two constraints, namely k and per, were employed to find the interesting top-k partial periodic patterns having the highest minPS value in the database. A novel concept known as dynamic minimum periodic support was introduced to reduce the search space and computational cost-effectively. We also introduce an efficient algorithm, called top-k Partial Periodic Pattern Miner (k-3PMiner), to find all the desired patterns. Experimental results on synthetic and real-world databases demonstrate that our algorithm is memory and runtime efficient.

The rest of the paper is organized as follows. Section 2 presents the extended model of top-k partial periodic patterns and the proposed algorithm. Section 3 reports the experimental results. Finally, Sect. 4 concludes the paper with research directions.

2 Proposed Algorithm

2.1 Basic Idea: Dynamic Minimum Periodic-Support

Reducing the enormous search space is challenging as our model does not employ any constraint to reduce the search space. Finding candidate items (or 1-items) play a crucial role in discovering complete set of top-k partial periodic patterns. Algorithm 1 describes finding all candidate items that exist in a database to construct c3PList. Algorithm 2 descibes the procedure of finding all the top-k partial periodic patterns in a database.

figure a
figure b
figure c

3 Experimental Results

Since there exists no algorithm to find Top-k partial periodic patterns in temporal databases using k constraint, we evaluated our algorithm k-3PMiner with naïve algorithm, The naïve algorithm involves the following two steps: (i) finding all partial periodic patterns in a temporal database using 3P-Growth algorithm [5] and (ii) generating top-k partial periodic patterns from all partial periodic patterns by performing another sorting.

3.1 Experimental Setup

Our k-3PMiner algorithm was developed in Python 3.7 and executed on a Gigabyte R282-z94 rack server machine containing two AMD EPIC 7542 CPUs and 600 GB RAM. The operating system of this machine is Ubuntu Server OS 20.04. The experiments have been conducted on both synthetic (T10I4D100K) and BMS-WebView-1 and real-world Pollution databases.

The T10I4D100K is a sparse synthetic database generated using the procedure described in [2]. This database contains 870 items and 100,000 transactions. The minimum, average, and maximum transaction lengths of this database are 1, 10, and 29 respectively. The BMS-WebView-1 is a sparse database containing 59,602 transactions and 497 items. The minimum, average, and maximum transaction lengths of this database are 1, 10, and 76 respectively.

The Pollution database is a high dimensional real-world database provided by Japanese Ministry of the Environment developed the Atmospheric Environmental Regional Observation System (AEROS) [3] to tackle air pollution problems. Each transaction contained the following information: timestamp in hours, station identifiers that have recorded \(PM_{2.5}\) values no less than 16 \(\mu g/m^3\). The resulting database, Pollution, contained 1600 items and 720 transactions. The minimum, average, and maximum transaction lengths are 11, 460, and 971, respectively. The k3P-miner code and the databases were provided at [1] of our experiments.

3.2 Evaluation of both the Algorithms by Varying only k

Figures 1a, 1b, 1c shows the top-k partial periodic patterns discovered on different T10I10D100K, BMS-WebView-1 and Pollution databases by varying k value, respectively. The per values are set at 2000, 1000 and 250 (in count) respectively. For Naïve algorithm the minPS values are set at 100, 30, 250 (in count) respectively. As k increases, the number of top-k patterns also increases.

Figures 2a, 2b, and 2c show the time consumed at a different number of k values in T10I10D100K, BMS-WebView-1 and Pollution databases, respectively. It can be observed that an increase in k increases the runtime to find all top-k partial periodic patterns being generated at different k values. As k increases, the number of patterns to be mined increases, resulting in time consumption.

Figures 3a, 3b, and 3c show the memory consumed at a different number of k values in T10I10D200K, BMS-WebView-1 and Pollution databases, respectively. It can be observed that an increase in k increases the memory to find all top-k partial periodic patterns being generated at different k values.

Fig. 1.
figure 1

top-k patterns on various databases by varying k

Full size image
Fig. 2.
figure 2

Runtime evaluation on various databases by varying k

Full size image
Fig. 3.
figure 3

Memory evaluation on various databases by varying k

Full size image

3.3 Scalability Test

In this experiment, we have used the Kosarak database, which is a huge database having 9,90,000 transactions (in count). We have divided this database into five segments, each consisting of 200,000 transactions. We have evaluated the performance of k-3PMiner by adding each successive segment to the ones that came before it. The runtime requirements and memory consumption k-3PMiner for each segment of the Kosarak database are shown in Fig. 4a and 4b, when \(k=200\). The following are some noteworthy findings that can be derived from these figures: (i) runtime requirements of k-3PMiner increases almost proportionally as database size grows. (ii) memory requirements of k-3PMiner where we can observe same as 4a.

Fig. 4.
figure 4

Scalability of k-3PMiner

Full size image

4 Conclusions and Future Work

In this paper, we have proposed an efficient depth-first search algorithm, called top-k Partial Periodic Pattern Miner (k-3PMiner), to find all desired patterns in big temporal databases. We have solved the open research problem of setting minPS and per constraints by introducing a novel upper-bound measure named dynamic minimum periodic support. An in-depth examination of the proposed k-3PMiner approach on four synthetic and real-world databases revealed that its memory consumption and runtime are efficient and highly scalable. As for future work, we will work on discovering top-k partial periodic patterns in uncertain databases.