Keywords

1 Introduction

Focusing is a technique introduced by Andreoli for reducing permutative non-determinism in proof search. It was originally applied to the cut-free sequent calculus of classical first-order linear logic [3] and subsequently ported to many other proof systems [9]. Andreoli’s key idea was the organization of root-first proof search in the alternation of two distinct phases: the asynchronous phase, where invertible rules are eagerly applied, and the synchronous phase, where non-invertible rules are applied on a selected formula which is brought under focus.

Focusing still retains a large amount of non-determinism in proof search, since many different formulae can possibly be brought under focus. Specifically, the non-determinism introduced by inessential permutative conversions is not resolved. Typically, a linear logician would solve this issue by leaving the sequent calculus and moving to a graphical representation of proofs, such as Girard’s proof nets [7]. Chaudhuri et al. [6] showed that it is not necessary to depart from the sequent calculus formalism to represent canonical derivations wrt. the equational theory generated by the permutative conversions. They introduce a multi-focused sequent calculus where multiple formulae can simultaneously be brought under focus and decomposed during the synchronous phase. They then present a rewriting system on multi-focused proofs whose normal forms are maximally multi-focused. These are derivations f which, at the beginning of each synchronous phase, always pick the largest number of formulae to bring under focus among the multi-focused derivations which are equivalent to f wrt. the equational theory of permutative conversions. In this sense, maximally multi-focused proofs exhibit the maximal amount of parallelism. Chaudhuri et al. showed that these are equivalent to proof nets for unit-free multiplicative classical linear logic. Multi-focusing and maximality have subsequently been applied to other deductive systems [4, 5], in particular variants of intuitionistic logic [12, 13].

This work serves as a starting point for a comprehensive study of maximal multi-focused deductive systems for a large class of substructural logics. It is well-known that many substructural logics enjoy normalization procedures targeting variants of proof nets, e.g. the Lambek calculus [8]. Nevertheless, an extensive study of maximally multi-focused proofs for these logics is missing. We believe this to be especially beneficial for the development of proof-theoretic investigations of logical systems in interactive theorem provers, such as Agda or Coq, where the graphical syntax of proof nets would be harder to implement than sequent calculi, whose inference rules are standard example of inductive type families.

We initiate this endeavor by considering skew non-commutative multiplicative linear logic (SkNMILL), a weak substructural logic recently introduced by the author in collaboration with Uustalu and Wan [16]. This logic is a semi-associative and semi-unital variant of Lambek calculus (with only one residual): it validates structural rules of associativity \((A \otimes B) \otimes C \rightarrow A \otimes (B \otimes C)\) and unitality \(\textsf{I}\otimes A \rightarrow A\) and \(A \rightarrow A \otimes \textsf{I}\), but none of their inverses. Uustalu et al. introduce a cut-free sequent calculus for SkNMILL whose sequents are triples of the form \(S \mid \varGamma \vdash A\), where S is an optional formula (called stoup), \(\varGamma \) is an ordered list of formulae and A is a single formula. A peculiarity of this calculus is that left logical rules act exclusively on the formula in the stoup position, never on formulae in context \(\varGamma \). This makes this sequent calculus a good candidate for initiating the formal study of maximal multi-focusing of substructural logics: during the synchronous phase, at most two formulae can be brought under focus, the stoup formula and the succedent formula. From this perspective, the sequent calculus of SkNMILL is among the “simplest” deductive system which enjoys non-trivial multi-focusing.

The study of SkNMILL was initially motivated by its categorical semantics in the skew monoidal closed categories of Street [15]. These categories arise naturally in semantics of programming languages [1], while semi-associativity has found strong connections with combinatorial structures such as the Tamari lattice and Stasheff associahedra [10, 20]. From a category-theoretic perspective, the maximal multi-focusing procedure described in this paper provides a solution to the coherence problem for skew monoidal closed categories.

The paper starts with a brief introduction of SkNMILL and its cut-free sequent calculus. It continues with a presentation of a sound and complete multi-focused sequent calculus. As expected, the latter does not resolve all the permutative non-determinism, but its introduction is pedagogically useful as it sets the stage for the more involved maximally multi-focused sequent calculus. The latter uses a system of tags, similarly employed by Uustalu et al. in their calculus of normal forms [16], which are inspired by Scherer and Rémy’s saturation technique [14]. Tags are used to keep track of new formulae appearing in context from the application of invertible rules and to decide whether multi-focusing on both the stoup and succedent formulae is admissible or not.

An important contribution of this project is the formalization of the maximal multi-focusing calculus for SkNMILL and the proof of its correctness in the Agda proof assistant. The code, containing all the material presented in the paper, can be found at:

https://github.com/niccoloveltri/multifocus-sknmill

2 The Sequent Calculus of SkNMILL

We recall the definition of the sequent calculus for SkNMILL originally introduced in [16]. Formulae are generated by the grammar \(A,B \,::\,= X \ | \ \textsf{I}\ | \ A \otimes B \ | \ A \multimap B\), where X comes from a fixed set \(\textsf{At}\) of atomic formulae, \(\textsf{I}\) is a multiplicative unit, \(\otimes \) is a multiplicative tensor and \(\multimap \) is a linear implication. Formulae \(\textsf{I}\) and \(A \otimes B\) are positive while \(A \multimap B\) is negative.

A sequent is a triple of the form \(S \mid \varGamma \vdash A\), where the succedent A is a single formula (as in non-commutative multiplicative linear logic NMILL) and the antecedent is divided in two parts: an optional formula S, called stoup, and an ordered list of formulae \(\varGamma \), called context. The metavariable S always denotes a stoup, i.e. S can be a single formula or empty, in which case we write \(S = -\).

Derivations of a sequent \(S \mid \varGamma \vdash A\) are inductively generated by the rules in Fig. 1. There are a few important differences with the sequent calculus of NMILL: 1) left rules can only act on the formula in stoup position, not on formulae in context; 2) the right \(\otimes \)-rule, when read bottom-up, forces the formula in the stoup (whenever it is present) to move to the stoup of the first premise, it cannot move to the antecedent of the second premise; 3) as in NMILL, there are no structural rules of exchange, weakening and contraction, but there is a new structural rule \(\textsf{pass}\) which moves the leftmost formula in context to the stoup, whenever the latter is empty.

As in NMILL  rules \(\textsf{IL}\), \(\otimes \textsf{L}\) and \({\multimap }\textsf{R}\) are invertible, while the other logical rules are not. The structural rule \(\textsf{pass}\) is also non-invertible. Two forms of cut are admissible, since the cut formula can either be located in the stoup or in the context of the second premise. A general axiom, or identity, rule is also admissible.

figure a

A stoup S is called irreducible if it is either empty, an atom or a negative formula. This means that the stoup formula cannot be further reduced using left invertible rules \(\textsf{IL}\) and \(\otimes \textsf{L}\) in root-first proof search. Analogously, a succedent formula A is irreducible when it is atomic or positive, so it cannot be reduced by the right invertible rule \({\multimap }\textsf{R}\).

Fig. 1.
figure 1

Sequent calculus for SkNMILL.

Full size image
Fig. 2.
figure 2

Equivalence of derivations in the sequent calculus.

Full size image

We consider an equivalence relation \(\circeq \) on sets of derivations. This is the congruence generated by the pairs of derivations in Fig. 2, which are permutative conversions. The congruence \(\circeq \) has been chosen to serve as the proof-theoretic counterpart of the equational theory of skew monoidal closed categories [15]. In fact, there exists a syntactic skew monoidal closed category which has formulae of \(\texttt {SkNMILL}\) as objects, and morphisms between formulae A and B are given by the set of derivations of \(A \mid ~ \vdash B\) quotiented by the equivalence relation \(\circeq \). This category is the free skew monoidal closed category generated by the set \(\textsf{At}\). We refer to [16] for more details on categorical semantics.

We employ the following convention for naming formulae and stoups:

P

positive formula

N

negative formula

Q

positive or atomic formula

M

negative or atomic formula

T

irreducible stoup (− or M)

3 A Multi-focused Sequent Calculus

We now present a multi-focused sequent calculus for SkNMILL, which draws inspiration from the one given by Chaudhuri et al. for multiplicative-additive classical linear logic [6]. Inference rules are given in Fig. 3. As in the original formulation by Andreoli [3], the (multi-)focused calculus describes, in a declarative fashion, a root-first proof search strategy in the original sequent calculus.

Fig. 3.
figure 3

Multi-focused sequent calculus for SkNMILL.

Full size image

In this calculus, sequents can take four forms, corresponding to four distinct phases of proof search:

\(S \mid \varGamma \Uparrow A\)

asynchronous (or invertible)

\(S \mid \varGamma \Downarrow A\)

synchronous (or focusing)

\(S \mid \varGamma \Downarrow _\textsf{lf}Q\)

left synchronous

\(T \mid \varGamma \Downarrow _\textsf{rf}A\)

right synchronous

Proof search starts in asynchronous phase \(S \mid \varGamma \Uparrow A\). In this phase, invertible rules are repeatedly applied until both the stoup formula (when present) and the succedent formula become irreducible. We have fixed an order on invertible rules and decided to apply \({\multimap }\textsf{R}\) before \(\textsf{IL}\)/\(\otimes \textsf{R}\), which is enforced by asking the succedent formula in the left invertible rules to be positive or atomic (so we use our notation Q).

Proof search then progresses to the synchronous phase via the rule \(\textsf{foc}\). At this point we can choose to focus on the stoup or succedent position.

If we pick the first option, the irreducible stoup T is brought under focus with an application of rule \(\mathsf {foc_L}\). The context is split in two parts \(\varGamma \) and \(\varDelta \) and the left focusing phase initiates in the first premise. A proof of \(T \mid \varGamma \Downarrow _\textsf{lf}Q\) consists of repeated application of left synchronous rules \(\textsf{pass}\) and \({\multimap }\textsf{L}\) on stoup T and context \(\varGamma \), until the stoup formula becomes the positive or atomic formula Q, at which point the left focus is “blurred” by the rule \(\mathsf {blur_L}\). In synchronous phase, blurred formulae are surrounded by a dashed box . We use notation , with b a Boolean value, to denote a formula which is possibly blurred: and . Blurred formulae are used to remember that a certain left or right synchronous phase has been performed.

If we pick the second option, proof search proceeds by bringing the succedent formula Q under focus with an application of rule \(\mathsf {foc_R}\). The context is split in two parts \(\varGamma \) and \(\varDelta \) and the right focusing phase initiates in the second premise. The right focusing phase consists of repeated applications of the right synchronous rule \(\otimes \textsf{R}\). The optional formula T in sequent \(T \mid \varDelta \Downarrow _\textsf{rf}Q\) indicates whether the right focusing phase terminates when the succedent formula becomes negative or atomic (in which case \(T = M\)) or it terminates with an application of \(\textsf{IR}\) (in which case \(T = -\)). In the first case, the succedent formula M is blurred by the rule \(\mathsf {blur_R}\). The notation is an abbreviation for: , when \(T = M\), while its set of proofs is a singleton if \(T = -\). In other words, \(\mathsf {foc_R}\) does not have a first premise in case the proof of the second premise ends with \(\textsf{IR}\).

A couple of observations on left- and right-focusing. A peculiarity of the sequent calculus in Fig. 3, when compared with other (multi-)focused calculi appearing in the literature, e.g. the one in [6], is that, during the application of non-invertible rules in the focusing phase, one of the premises always releases the focus. In rule \(\otimes \textsf{R}\), the right premise releases the focus on the succedent formula, and similarly for the first premise in rule \({\multimap }\textsf{L}\). Without the loss of focus in these premises, the multi-focused sequent calculus would not be complete wrt. the calculus in Fig. 1, e.g. the sequent \(X \mid Y \otimes Z \Uparrow X \otimes (Y \otimes Z)\) would not admit a derivation. This behaviour was already present in the focused sequent calculi for the \(\otimes \)- and \((\textsf{I},\otimes )\)-fragments of the sequent calculus, originally studied by Zeilberger et al. [17, 20].

The design of rule \(\mathsf {foc_L}\), with a whole left-focusing phase compressed in a proof of \(T \mid \varGamma \Downarrow _\textsf{lf}Q\), is chosen specifically for the purpose of maximal multi-focusing, where we will be interested in whether a certain left-focusing phase has happened rather than the specific left synchronous rules that have been applied. Notice also that in the first premise \(T \mid \varGamma \Downarrow _\textsf{lf}Q\) of \(\mathsf {foc_L}\) there is no need to keep track of the succedent formula A since it is not affected by left synchronous rules, and similarly for the context \(\varDelta \) of the second premise. Analogous observations apply to the second premise of \(\mathsf {foc_R}\).

When the (left-) right-focusing phase terminates, one can subsequently choose to focus on the (succedent) stoup formula. If the execution of both left- and right-focusing lead to a valid derivation, they can be performed in any order, first left then right, or vice versa. When no formula is under focus anymore, we unfocus and continue proof search in asynchronous phase. In order to unfocus, formulae that were previously under focus, which are now blurred, must have switched their polarity, which is reflected in the side condition \(\textsf{UT}(b,c,S,A)\) of rule \(\textsf{unfoc}\) (\(\textsf{UT}\) stands for “unfocusing table”):

b

c

\(\textsf{UT}(b,c,S,A)\)

0

0

0

0

1

\(A = N\)

1

0

\(S = P\)

1

1

\(S = P \vee (S = X \wedge A = N)\)

The stoup formula must be positive if it was under focus (\(b=1\)) but the succedent was not (\(c=0\)). Dually, the succedent formula must be negative is it was under focus (\(c = 1\)) and the stoup formula was not (\(b = 0\)). If both formulae were under focus (\(b = 1 \wedge c = 1\)), one of them must have changed its polarity: either the stoup formula has become positive or, if it had become (or stayed) atomic, the succedent formula has become negative. Unfocusing also requires that at least one formula was previously under focus, hence the condition \(b \vee c\) must be true.

For a sequent with atomic stoup and positive succedent \(X \mid \varGamma \Uparrow P\) (or, dually, negative stoup and atomic succedent), one can choose whether to focus on the stoup formula or not, and both choices may lead to a valid proof. For an example, consider the valid sequent \(X \mid ~ \Uparrow (Y \multimap (X \otimes Y)) \otimes I\). This situation was also present in the multi-focused calculus for classical linear logic [6], where in similar circumstances one was given the choice of focusing on negated atoms or not.

Invertible rules are easily proved to be admissible in the \(\Uparrow \) phase (with a general formula as succedent), and similarly \(\textsf{IR}\) and \(\textsf{ax}\).

Proposition 1

The following rules are admissible:

figure h

Rule \(\otimes \textsf{R}\) of Fig. 1, with \(\vdash \) replaced everywhere by \(\Uparrow \), is also admissible, but showing this requires more work. We prove the admissibility of a macro inference rule corresponding to multiple application of \(\otimes \textsf{R}\). To this end, given a formula A and a list of formulae \(\varGamma = B_1,\dots ,B_n\), define \(A \otimes ^* \varGamma = (((A \otimes B_1) \otimes B_2) \otimes \dots ) \otimes B_n\), which is simply A when \(\varGamma \) is empty. If \(\varGamma \) is non-empty, we write \(A \otimes ^+ \varGamma \). Define also \(\varGamma \multimap ^* A = B_1 \multimap (B_2 \multimap (\dots \multimap (B_n \multimap A)))\) and similarly \(\varGamma \multimap ^+ A\) when \(\varGamma \) is non-empty.

Proposition 2

Let \(\overrightarrow{\varDelta } = \varDelta _1,\dots ,\varDelta _n\) be a list of contexts and \(\overrightarrow{B} = B_1,\dots ,B_n\) a list of formulae, both non-empty. The following rule is admissible:

figure i

where \(\{ - \mid \varDelta _i \Uparrow B_i \}_{i}\) is a collection of premises \(- \mid \varDelta _i \Uparrow B_i\) for each \(1 \le i \le n\).

Proof

The proof proceeds by inspecting the polarity of formula A and then by induction on the structure of the derivation \(f : S \mid \varGamma \Uparrow A\). When A is negative, we need to strengthen the statement for the induction on f to succeed. So we prove the admissibility of the more general rule:

figure j

The context \(\varLambda \) serves as an accumulator for dealing with the case \(f = {\multimap }\textsf{R}(f')\):

figure k

which type checks since \(\varLambda {\multimap }^+ (A' {\multimap } B') = (\varLambda ,A') {\multimap }^+ B'\). Another representative case is \(f = \textsf{foc}(f')\), where right-focusing can immediately be executed:

(1)

We now move to the admissibility of left-synchronous rules. To this end, we introduce an inductive ternary (proof-relevant) relation \(A \rightsquigarrow _{\textsf{li}}S\mid \varGamma \) which holds when the antecedent \(S\mid \varGamma \) is obtained by repeated applications of left-invertible rules on the antecedent \(A \mid ~\), where A is in the stoup and the context is empty:

figure l

Given a proof \(\ell : A \rightsquigarrow _{\textsf{li}}S\mid \varGamma \), we can turn a derivation \(f : S \mid \varGamma ,\varDelta \Uparrow C\) into a derivation \(\textsf{inv}_{\textsf{li}}(f,\ell ) : A \mid \varDelta \Uparrow C\):

(2)

Proposition 3

The following rules are admissible:

figure m

Proof

We only discuss \({\multimap }\textsf{L}^+\). Proving its admissibility proceeds by inspecting the polarity of formula B and then by induction on the structure of the derivation \(g : B \mid \varDelta \Uparrow C\). When B is positive, we need to strengthen the statement for the induction to succeed. We prove the admissibility of the more general rule:

figure n

The additional assumption \(\ell :B \rightsquigarrow _{\textsf{li}}S\mid \varLambda \) serves as an accumulator for dealing with the cases when g is a left-invertible rule and it allows to state that the proof of the third premise is a subderivation of sequent \(B \mid \varDelta \Uparrow C\) in the sense depicted in (2). A representative case is \(g = \textsf{foc}(g)\), where we can immediately execute left-focusing, obtaining a derivation dual to the one in (1).

The multi-focused sequent calculus in Fig. 3 is sound and complete wrt. the sequent calculus in Fig. 1. In the upcoming theorem and in the rest of the paper, we also write \(S \mid \varGamma \vdash A\) and \(S \mid \varGamma \Uparrow A\) for the sets of proofs of the corresponding sequents.

Theorem 1

There exist functions \(\textsf{focus}: S \mid \varGamma \vdash A \, \rightarrow \, S \mid \varGamma \Uparrow A\) and \(\textsf{emb}: S \mid \varGamma \Uparrow A \, \rightarrow \, S \mid \varGamma \vdash A\), turning sequent calculus derivations into multi-focused derivations, and vice versa.

Proof

Function \(\textsf{emb}\) is obtained by erasing all phase-shifting rules and dashed boxes around blurred formulae. Function \(\textsf{focus}\) is defined by induction on the structure of the input derivation, noticing that each rule in Fig. 1 has an admissible counterpart in the multi-focused sequent calculus, which follows from Propositions 1, 2 and 3.

Multi-focused proofs are not canonical wrt. to the equational theory in Fig. 2. When the stoup formula is negative and the succedent is positive, we have the choice of whether left-focusing and subsequently unfocus, right-focusing and subsequently unfocus, or performing both left- and right-focusing before unfocusing, and the latter can also be achieved in two distinct ways. For example, there exist four distinct proofs of \(X \multimap \textsf{I}\mid X , Y \Uparrow (Z \multimap Z) \otimes Y\) which correspond to four \(\circeq \)-related derivations in the unfocused sequent calculus. As discussed before, in general we also have the choice of whether focusing on atomic formulae or not, which further increases the amount of non-determinism.

Fig. 4.
figure 4

Equivalence of derivations in the multi-focused sequent calculus.

Full size image

It is possible to fully capture this remaining non-determinism in a congruence relation \(\circeq _\Uparrow \) on derivations of sequents \(S \mid \varGamma \Uparrow A\). This is inductively specified simultaneously with congruences \(\circeq _\Downarrow \), \(\circeq _\textsf{lf}\) and \(\circeq _\textsf{rf}\). The generators of this collection of relations are exhibited in Fig. 4. Notice that all these generators belong to the relation \(\circeq _\Downarrow \). This means that \(\circeq _\Uparrow \) is the smallest equivalence relation which rules \({\multimap }\textsf{R}\), \(\textsf{IL}\) and \(\otimes \textsf{L}\) respect (in the sense that they send \(\circeq _\Uparrow \)-related premises to \(\circeq _\Uparrow \)-related conclusions), and moreover \(f \circeq _\Downarrow g\) implies \(\textsf{foc}(f) \circeq _\Uparrow \textsf{foc}(g)\).

We can show that functions \(\textsf{focus}\) and \(\textsf{emb}\) respect congruences \(\circeq \) and \(\circeq _\Uparrow \), and moreover define an equivalence between sets of proofs in the different sequent calculi, strengthening the statement of Theorem 1.

Theorem 2

Functions \(\textsf{focus}\) and \(\textsf{emb}\) underlie an isomorphism between the set of proofs of a sequent \(S \mid \varGamma \vdash A\) quotiented by the equivalence relation \(\circeq \) and the set of proofs of \(S \mid \varGamma \Uparrow A\) quotiented by the equivalence relation \(\circeq _\Uparrow \).

Details about the proof can be found in our Agda formalization.

4 Maximal Multi-focusing Using Tags

In order to design a calculus of permutative-canonical derivations, we have to answer the following question: in which situation does a right-focusing phase need to be performed strictly before a left-focusing phase? And dually, when must left-focusing be done before right-focusing? Consider the valid sequent \(X \multimap Y \mid Z \Downarrow (X \multimap Y) \otimes Z\). Attempting to focus on the stoup formula would fail, because no splitting of the context, consisting of the singleton formula Z, leads to a valid derivation. We would be able to appropriately split the context only after performing right-focusing, specifically after an application of \(\otimes \textsf{R}\), and a subsequent application of \({\multimap }\textsf{R}\). This is because the formula X, that we would like to send to the first premise during left-focusing, is not initially in context, it becomes available only after right-focusing.

Dually, consider the valid sequent \(X \multimap (Y \otimes Z) \mid X \Downarrow Y \otimes Z\). It is not hard to see that any attempt to focus on the succedent formula would fail. But after left-focusing and an application of \(\otimes \textsf{L}\), right-focusing becomes possible and leads to a valid proof. This is because the formula Z, which should be sent to the second premise by \(\mathsf {foc_R}\), appears in context only after executing the left-focusing phase. Another simple example is given by the valid sequent \(- \mid X \otimes Y \Downarrow X \otimes Y\). Again left-focusing, specifically \(\textsf{pass}\), must happen before right-focusing, since the formula Y is not in context and cannot otherwise be sent to the second premise during right-focusing.

We need a mechanism for keeping track of new formulae appearing in context from applications of invertible rules \(\otimes \textsf{L}\) and \({\multimap }\textsf{R}\). In proof search, when we choose to perform left-focusing but we decide to postpone right-focusing, after releasing the focus we have to justify this decision by showing that the subsequent application of \(\mathsf {foc_R}\) splits the context in-between new formulae that appeared in context only after the termination of the left-focusing phase. And dually if right-focusing strictly precedes left-focusing.

We employ a mechanism from the recent work of Uustalu et al. [16] which was inspired by Scherer and Rémy’s saturation for intuitionistic logic [14]. Formulae appearing in a sequent will now be decorated with a superscript Boolean value, which we call a tag: \(A^0\) or \(A^1\). Stoups are also tagged: \(S^0\) or \(S^1\). Tagged contexts consist of tagged formulae. Sequents in the maximally multi-focused sequent calculus also take four forms:

\(S \mid \varGamma \Uparrow _{\textsf{m}}A\)

asynchronous

\(S \mid \varGamma \Downarrow _{\textsf{m}}A\)

synchronous

\(S \mid \varGamma \Downarrow _\textsf{lfm}Q\)

left synchronous

\(T \mid \varGamma \Downarrow _\textsf{rfm}A\)

right synchronous

The above are all triples consisting of a tagged stoup S (or an irreducible tagged stoup T in the last case), a tagged context \(\varGamma \) and a tagged formula A (or an irreducible tagged formula Q in the third case). If in a sequent we do not want to specify the tag of a tagged formula, we simply write it without superscript. Given a tagged formula A, we also write \(A^0\) when we want to replace the tag of A by 0 and \(A^1\) when the tag is replaced by 1. These conventions also apply to tagged stoups and contexts in a sequent.

Tags serve two purposes:

  1. 1.

    They are used to remember which (if any) among left- or right-focusing was not performed during the preceding focusing phase. If the stoup is \(S^1\), only right-focusing was previously executed. Dually, if the succedent formula is \(A^1\), only left-focusing took place.

  2. 2.

    In case one (and only one) among the stoup and the succedent has tag 1, new formulae moved to context via the application of invertible rules are also assigned tag 1. So tags are used to remember which formulae in context are new.

Fig. 5.
figure 5

Maximally multi-focused sequent calculus for SkNMILL.

Full size image

Inference rules for the maximally multi-focused sequent calculus are displayed in Fig. 5. In the premise of rule \({\multimap }\textsf{R}\), the stoup S and the formula A must have the same tag t: if the stoup is \(S^1\) in the conclusion, so left-focusing did not happen in the previous synchronous phase, we track the new formula A moving to the right-most end of the context by assigning it tag 1. Similarly for tagged formulae \(A^t\) and \(Q^t\) in the premise of rule \(\otimes \textsf{L}\).

Proof search starts again in asynchronous phase, where initially the sequent is \({S^0} \mid {\varGamma ^0} \Uparrow _{\textsf{m}}{A^0}\). At this point of the search, this phase is analogous to the one in the multi-focused calculus of Fig. 3. Tag 1 may start to appear with an application of \(\textsf{unfoc}\). If left-focusing was not performed, so \(b = 0\), then the stoup is given tag 1, which in the rule is denoted \(S^{\lnot b}\). If right-focusing was not executed, so \(c = 0\), then the succedent has given tag 1, so it becomes \(A^{\lnot c}\). If either the stoup or the succedent has tag 1, new formulae moved to the context via applications of \({\multimap }\textsf{R}\) and \(\otimes \textsf{L}\) are also assigned tag 1.

If we want to left-focus, we first inspect the tag of the stoup formula. If it is \(T^1\), we need to justify why left-focusing was not performed together with right-focusing in the preceding synchronous phase. This can be done by requiring a formula tagged with 1 to appear in \(\varGamma \), which is the meaning of the side condition \(1 \in \varGamma \) in the premise of \(\mathsf {foc_L^1}\). Proof search continues with a stoup formula \({Q^0}\). Dually, if we want to right-focus and the succedent is \(Q^1\), and moreover T is non-empty, we require a formula tagged with 1 to appear in \(\varDelta \) when applying \(\mathsf {foc_R^1}\). When T is empty, so the right-focusing phase terminates with \(\textsf{IR}\), there is no need to check whether \(\varDelta \) contains formulae tagged with 1, since right-focusing could not have happened together with the preceding left-focusing phase. Phases \(\Downarrow _\textsf{lfm}\) and \(\Downarrow _\textsf{rfm}\) are omitted in Fig. 5, since they are the same as \(\Downarrow _\textsf{lf}\) and \(\Downarrow _\textsf{rf}\) in Fig. 3 but with all formulae in sequents having tag 0, and \(\Uparrow \) replaced by \(\Uparrow _{\textsf{m}}\) in the premises of \({\multimap }\textsf{L}\) and \(\otimes \textsf{R}\).

When releasing the focus via \(\textsf{unfoc}\), stoup and succedent must have tag 0, meaning that all the reasons for “not maximally focus” in a preceding focusing phase must have been successfully justified. Apart from tags, there are a couple of differences with the multi-focused system in Fig. 3.

  1. 1.

    In synchronous phase, we have the choice of first applying \(\mathsf {foc_L}\) and then applying \(\mathsf {foc_R}\), i.e. we remove non-determinism in the choice of left- or right-focusing when both are executable. In Fig. 5 this can be observed in \(\mathsf {foc_L}\), where succedents cannot be blurred.

  2. 2.

    Another difference lays in the treatment of atomic formulae. The axiom rule \(\textsf{ax}\) requires the atomic formula to have tag 0 and to be blurred in both positions. More generally, each derivation of \(X \mid \varGamma \Downarrow _{\textsf{m}}A\) necessarily focuses on the stoup and each derivation of \(S \mid \varGamma \Downarrow _{\textsf{m}}X\) necessarily focuses on the succedent.

All tags from a maximally multi-focused derivation can be removed to obtain a proof in the non-maximally multi-focused sequent calculus. More interestingly, each multi-focused derivation can be normalized to a maximally multi-focused one.

Theorem 3

There exist functions

$$ \begin{array}{l} \textsf{max}_\odot : S \mid \varGamma \odot A \, \rightarrow \, {S^0} \mid {\varGamma ^0} \odot _\textsf{m} {A^0} \\ \textsf{untag}_\odot : {S^0} \mid {\varGamma ^0} \odot _{\textsf{m}} {A^0} \, \rightarrow \, S \mid \varGamma \odot A \end{array} $$

for all \(\odot \in \{\Uparrow ,\Downarrow ,\Downarrow _\textsf{lf},\Downarrow _\textsf{rf}\}\), turning multi-focused proofs into maximally multi-focused ones, and vice versa.

Proof

We only sketch the construction of \(\textsf{max}_\Downarrow \), which is the most challenging function to define. We refer the interested reader to the associated Agda formalization for the complete proof. The input derivation can either be: (i) an application of \(\mathsf {foc_R}\) followed by \(\textsf{ax}\) or \(\textsf{unfoc}\); (ii) an application of \(\mathsf {foc_L}\) followed by \(\textsf{ax}\) or \(\textsf{unfoc}\); (iii) an application of both \(\mathsf {foc_L}\) and \(\mathsf {foc_R}\). In case (iii), we can safely apply both \(\mathsf {foc_L}\) and \(\mathsf {foc_R}\) in the maximally multi-focused calculus. The most interesting cases are (i) and (ii) when the focus is subsequently released. We only look at case (i) when the input derivation is of the form \(f = \mathsf {foc_R}(\textsf{unfoc}(f'),r)\) for some \(f' : S \mid \varGamma \Uparrow M\) and \(r : M \mid \varDelta \Downarrow _\textsf{rf}Q\). To deal with this case, we prove the following rule admissible:

figure o

The proof proceeds by checking whether M is atomic or negative. In the latter case we further need to generalize the statement and prove the admissibility of

figure p

We proceed by induction on the structure of the proof of the first premise \({g : {T^0} \mid {\varGamma ^0},{\varLambda ^0} \Uparrow _{\textsf{m}}{A^0}}\). We look at the case \(g = \textsf{foc}(\mathsf {foc_L}(l,\textsf{unfoc}(h)))\) for some \(l : {T^0} \mid {\varOmega ^0} \Downarrow _\textsf{lfm}{P^0}\) and \(h : {P^0} \mid {\varXi ^0} \Uparrow _{\textsf{m}}A^1\). In this case, we have the equality of contexts \(\varOmega ,\varXi = \varGamma ,\varLambda \) and we check whether \(\varLambda \) is split between \(\varOmega \) and \(\varXi \), or it is fully contained in \(\varXi \).

  1. 1.

    If \(\varLambda = \varPhi ,\varXi \) and \(\varOmega =\varGamma ,\varPhi \) for some non-empty \(\varPhi \), then multi-focusing on both stoup and succedent is not possible. We return:

    figure q

    The double-line rule is the equality rule (we simply rewrite the contexts).

  2. 2.

    If \(\varGamma = \varOmega ,\varPhi \) and \(\varXi = \varPhi , \varLambda \), then multi-focusing on both stoup and succedent is possible. We return:

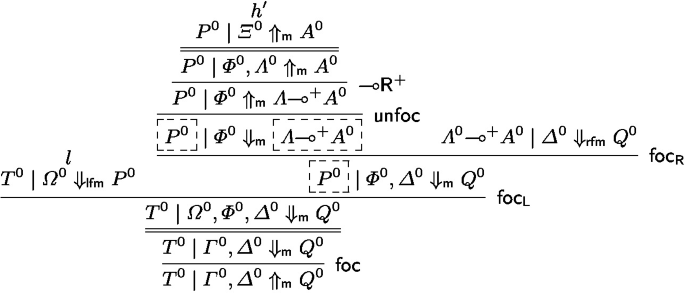
    figure r

    where \(h'\) is obtained from h by turning all applications of rules \(\mathsf {foc_L^1}\) and \(\mathsf {foc_R^1}\) in h to \(\mathsf {foc_L}\) and \(\mathsf {foc_R}\).

It is possible to show that proofs in the maximally multi-focused calculus are canonical wrt. the equational theory in Fig. 4 on multi-focused derivations. Therefore, by Theorem 2, they are also canonical wrt. the equational theory in Fig. 2 on unfocused derivations.

Theorem 4

Functions \(\textsf{max}_\Uparrow \) and \(\textsf{untag}_\Uparrow \) underlie an isomorphism between the set of proofs of a sequent \(S \mid \varGamma \Uparrow A\) quotiented by the equivalence relation \(\circeq _\Uparrow \) and the set of proofs of \({S^0} \mid {\varGamma ^0} \Uparrow _{\textsf{m}}{A^0}\).

We refer the reader to our Agda formalization for details about the proofs.

Corollary 1

Functions \(\textsf{max}_\Uparrow \circ \textsf{focus}\) and \(\textsf{emb}\circ \textsf{untag}_\Uparrow \) underlie an isomorphism between the set of proofs of a sequent \(S \mid \varGamma \vdash A\) quotiented by the equivalence relation \(\circeq \) and the set of proofs of \({S^0} \mid {\varGamma ^0} \Uparrow _{\textsf{m}}{A^0}\).

Proof

By Theorems 2 and 4.

5 Conclusions

SkNMILL is a relatively weak logic, low in the substructural hierarchy and with a restricted selection of logical connectives. Nevertheless, its simplicity allows to properly investigate complex proof-theoretic procedure such as maximal multi-focusing, which can be potentially extended to sequent calculi for richer logics. Porting the technique to extensions of SkNMILL with other structural laws, such as full associativity/unitality (recovering the Lambek calculus without left residual) or exchange (as in the sequent calculus of symmetric skew monoidal categories [18]), should be relatively straightforward. Extensions with additive connectives will make things more complicated. To this end, it would be interesting to study semantic approaches to maximal multi-focusing, akin to normalization-by-evaluation [2, 19] or (proof-relevant) semantic cut elimination [11].

Uustalu et al. [16] define a normalization procedure for SkNMILL using tags, which is also inspired by focusing. Their canonical derivations arise as normal forms of the confluent and strongly normalizing rewriting system obtained by orienting the equations in Fig. 2 from left to right. This means that, during root-first proof search, invertible rules are again applied first, but the application of non-invertible rules \(\textsf{pass}\) and \({\multimap }\textsf{L}\) is prioritized over \(\otimes \textsf{R}\). Moreover, focus is released after each application of a non-invertible rule and the asynchronous phase is immediately resumed. Maximal multi-focusing, on the other hand, is unbiased with respect to the application of non-invertible rules. We plan to further investigate the relationship between the normal forms of the two normalization strategies, for SkNMILL and other substructural logics.