Keywords

1 Introduction

Spiral galaxies are complex dynamical systems. Their global morphology is the result of dynamical processes taking place mainly in their stellar component (disk and bulge), in the gas that lies in the equatorial plane of the galaxy and in the dark matter halo that surrounds the disk. The stellar and the gaseous components interact among themselves, as well as with the dark matter halo. The evolution of each one of these components has to take into account the presence of the others and their dynamical evolution. In order to understand the dynamics of the structures, which are observed in this type of galaxies, we have to understand the global dynamics of a complex system.

The structures that appear in disk galaxies, are the bars, the spiral arms and the rings (nuclear, inner and outer). Galaxies with prominent and well-defined spiral arms are called “grand design”. The presence of the spiral arms may be accompanied by the presence of a bar and so we speak about normal (non-barred) and barred spiral galaxies. A typical grand design example (NGC 5248) is given in Fig. 1.

A major contribution to the field came in the 1990s, with the development of near-infrared detectors. Observations in near-infrared wavelengths allowed the imaging of the old stellar population of the disk, which traces much better the mass distribution than observations in the optical. The conspicuous differences in the morphologies of a galaxy in near-infrared and optical images, gives valuable information to be used as input in theoretical modeling. Stellar models have to be compared with data from near-infrared observations, while gaseous models with morphologies encountered mainly in the optical.

Fig. 1
figure 1

The grand-design spiral galaxy NGC 5248 dominates in the lower left corner of the figure. In the upper part of the image are discernible a disk galaxy with a ring and a disk galaxy with an edge-on orientation. (Observation in B filter with the 2.2 m ESO/MPA telescope, La Silla, Chile, by Patsis, Heraudeau & Grosbøl, 2000)

Full size image

Plausible assumptions that reduce the degree of complexity of a galactic system are necessary in order to be able to construct models that reproduce the dynamical behavior of galactic disks, remaining, to a large degree, realistic. There are two main ways of studying the dynamics of galaxies. Either by means of N-body simulations, or by means of orbital models. N-body models are self-consistent, combine the evolution of the stellar and gaseous components and offer the possibility to include a live dark matter halo (see [1] for a review). Although such models are the best way to describe the time evolution of galactic systems, it is difficult to study with them the details of the dynamical phenomena that are in action as the system evolves. For that purpose have been used orbital models, simple in their initial set up, in most cases in the form of autonomous Hamiltonian systems that refer to the stellar dynamics of the galaxy (for a complete introduction in the subject see [2]). The potentials used are either well behaving analytic functions that match general properties of galactic disks (see e.g. Chap. 2 in [3]) or, in some cases, potentials that have been estimated directly from near-infrared images of specific galaxies (e.g. [4, 5]).

A key element for understanding galactic disk dynamics is to find out the location of the resonances between the epicyclic frequency, \(\kappa (R)\), and the angular velocity of the stars, \(\Omega (R)\), in the rotating with pattern speed \(\Omega _p\) frame of reference (R is the radial distance of a test particle, in cylindrical coordinates). Especially the resonances \(\kappa /(\Omega (R) - \Omega _p)=\pm 2/1\) (Inner and Outer Lindblad resonances respectively), the 4/1 resonance (defined in a similar way as the 2/1 one), as well as corotation, a resonance for which \(\Omega (R)= \Omega _p\), play a crucial role for understanding the dynamics of barred and spiral galaxies. These resonances are defined on the equatorial plane of the galaxy. However, in the same way, we can specify vertical resonances, between the vertical frequency of the stars, \(\nu (R)\) and \(\Omega (R) - \Omega _p\) (see e.g. [6]).

2 Order and Chaos

2.1 Two Dimensional (2D) Models

As their name indicates, disk galaxies are flat objects. Thus, two-dimensional (2D) modeling has been extensively used as a good approximation for their study. The initial idea was to associate ordered motion in the vicinity of stable periodic orbits with the reinforcement of morphological features. Stable periodic orbits trap around them regular orbits, which remain close to the periodic ones forever. In this way they enhance the local density and thus they enhance structures that have a certain similarity with the topology of the periodic orbits (see e.g. Chap. 2 in [2]). This is a straightforward scenario, that gave the following results:

  • The most well appreciated result of nonlinear orbital theory in galactic disk dynamics, concerns the orbital content of galactic bars. The bars of barred-spiral galaxies are supported by orbits trapped around stable periodic orbits of the family “x1”, the orbits of which have elliptical-like shapes [7]. Beyond the inner 4/1 resonance, towards corotation, the existing families of periodic orbits in rotating barred potentials are mainly unstable and practically are found within a chaotic zone. This zone prevents the bars reaching corotation [8]. In this case Order forms a structure and Chaos hinders its extent beyond a certain distance, approaching the region characterized by \(\Omega (R) \approx \Omega _p\), in which we find the Lagrangian equilibrium points [9].

  • In the absence of a bar, a bisymmetric spiral pattern is also supported by a backbone of elliptical x1 orbits, which however precess in a characteristic way, so that their apocenters are aligned with the loci of the spiral arms. In this way the stars stay longer time in the apocenters regions and enhance locally the surface density of the disk, forming the arms. This is the idea of the classic density wave theory [10] expressed by means of periodic orbits (see Fig. 3 in [11]).

    The essential parameters for assessing this hypothesis, are the pattern speed and the amplitude of the spiral perturbation, i.e. of the spiral arms. The pattern speed determines the location of the resonances and consequently the local morphology of the model, while the amplitude of the perturbation defines the degree of nonlinearity, in other words the importance of chaotic phenomena. The response morphology can be directly compared with images of galaxies, while the presence of chaotic phenomena affects, among others, kinematic features, such as the profile of the dispersion of velocities in the disks. Such profiles provide constraints for the appearance of chaotic phenomena. Both quantities (pattern speed and amplitude of the spirals) are very difficult to be estimated from observations. Thus, modeling is needed, so that the right values can be deduced by comparing the situation predicted by the models with the observational data.

    In normal (non-barred) spiral models it has been realized that an open spiral structure has major problems crossing the 4/1 resonance region. Due to the rhomboidal shape of the orbits in this region and their relative orientation, the 4/1 resonance becomes a main obstacle for the continuation of the spiral structure towards corotation [12, 13]. This time it is not the presence of Chaos, but the misalignment of the building blocks (i.e. of the periodic orbits) that imposed the damping of the density wave. A set of self-consistency tests have shown that this is the case for the symmetric part of grand-design galaxies of Hubble types Sb to Sc. Such spiral patterns rotate slowly, so that the end of their symmetric parts corresponds to the 4/1 resonance, while the estimated amplitudes are characterized by perturbing forces of the order of 5–10% with respect to the axisymmetric background. On the other hand, the tightly wound arms of Sa galaxies, could be modeled with spirals with 1% perturbation in the forces and could reach corotation [14]. However, in both cases, i.e. in models with big and small pitch angles, order dominates and this is reflected to the observed velocity dispersions in real galaxies (see e.g. [15, 16]). The relation between pitch angle, amplitude of the perturbation and pattern speed is also recently investigated in [17].

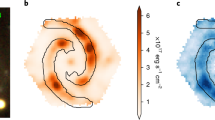
    Gaseous response models have confirmed the above results. In addition, the inclusion of asymmetries in the imposed potentials, for example in the form of \(m = 1\) components, made the models able to reproduce at the right place even secondary features appearing in images of open spiral galaxies, such as asymmetric bifurcations of the arms (see e.g. Fig. 4 in [18]). The inner symmetric part of the grand-design has been always identified with the location of the 4/1 resonance, while off-phase, with respect to the imposed spiral perturbation, extensions, could be found between 4/1 and corotation in the responses (see also the results of three dimensional models in [19]). In all the above cases, the most sensitive parameter in order to obtain a morphological similarity of the model with the modeled galaxy was the pattern speed (\(\Omega _p\)). This should be that slow, as to put corotation beyond the end of the inner symmetric part of the spiral arms. Later, models that have considered kinematic data as well, have also confirmed this result, by pushing corotation at, or beyond, the end of the overall observed spiral structure [20]. A characteristic, gaseous (by means of Smoothed Particle Hydrodynamics, SPH) response model for open normal spirals (pitch angle \(25^{\circ }\)) is given in Fig. 2. The model includes, besides a main \(m = 2\) logarithmic spiral component, also an \(m=1\) term, with the same pattern speed and shape as the \(m=2\) one. The ratio of the amplitudes \(A_{m=1}/A_{m=2}=0.15\), while the relative force perturbation at the end of the symmetric part of the spiral pattern is of the order of 10% of the axisymmetric force. The long arrows in Fig. 2 point to the locations of the end of the symmetric part of the spiral pattern, at the 4/1 resonance region, while the short, thicker, arrows at larger distances from the center, point to weak extensions of the arms, to which we refer in the next paragraph.

  • Another mechanism for supporting the spiral structure of galaxies started being discussed in the middle 2000s, applied to barred-spiral systems. Mainly two groups, elaborated the idea that the spiral structure observed beyond the ends of the bars in this type of galaxies is guided primarily by the unstable manifolds emanating from the unstable Lagrangian points L1, L2 at the corotation region [21, 22]. The idea has been presented earlier [23], without a detailed description of the dynamical mechanism. The later was known in studies of the three-body problem, however without relating it with the support of an emerging structure in that case [24, 25]. According to this mechanism, stars following the paths dictated by the manifolds are on chaotic orbits, as their Lyapunov numbers indicate, so the formed spirals, have been called “chaotic” spirals. Evidence that the orbital content of these spirals is associated with the so-called “hot orbital” population [26] is given in [27]. Such chaotic orbits in autonomous Hamiltonian systems have Jacobi constants, \(E_J\), larger than those of L1 and L2 and for some time they may exhibit a 4/1-resonance orbital behaviour inside corotation. They enhance the spiral arms of the barred-spiral morphology as they cross corotation through the bottlenecks formed by the isocontours of the effective potential at various \(E_J\)’s. They are of the same type of orbits as those building the envelope of the bar in the case of NGC 4314 studied in [28]. Further orbits of this type have been presented in [29], in models for NGC 1300. Since in the chaotic seas we can find unstable periodic orbits around the equilibrium points (Lyapunov orbits) as well as unstable periodic orbits belonging to the 4/1, 6/1 etc. families, it is natural to conclude that all the families of unstable periodic orbits near and beyond corotation contribute to the same phenomenon [30]. Manifolds of unstable 4/1 periodic orbits associated with the reinforcement of chaotic spirals have been presented in [31]. Besides the spirals, the same mechanism has been proposed for explaining several types of rings observed around the bars ([22, 32] and subsequent papers by the same authors). Also in this case, orbits classified by chaos indicators as “chaotic”, reinforce a well defined morphological structure. Models in which the two mechanisms for supporting two different spiral patterns coexist, as the one presented in Fig. 2 (the arrows point to two different sets of spiral arms), lead to rare, but known grand design morphologies, as in the cases of NGC 1566 or NGC 5248 [31, 33]. In these cases the inner spiral structure is supported by regular orbits trapped around precessing x1 periodic orbits, while the outer spiral structure by chaotic orbits that cross the region of the L1 and L2 points and continue beyond corotation. These spiral arms are those indicated with the short arrows in Fig. 2. The main difference among the regular and the chaotic spirals is in the flow of material in their regions. In arms supported by regular orbits, the flow is accross the arms, while in chaotic spirals, the flow is in general along them [27, 33].

Fig. 2
figure 2

An SPH response model to a logarithmic spiral potential with pitch angle \(25^{\circ }\) that includes a main \(m=2\) and a secondary \(m=1\) component. The long arrows point to the end of the inner, symmetric spiral arms, at the 4/1 resonance, while the short arrows at larger distances to a weak continuation of the spiral arms beyond corotation, which are formed following the mechanism of “chaotic” spirals (see text)

Full size image

2.2 Three Dimensional (3D) Models

Disk galaxies can be considered in a first approximation as two dimensional objects. However, the inner part of the bars extends well above the equatorial plane of the galaxy, reaching heights up to 2 kpc in some cases, forming a characteristic boxy, peanut-shape morphology when viewed edge-on. In some cases the side-on profiles of galactic bars outline the pronounced morphology of an “X” shape [34]. These structures, and their relation with bars, have been identified in early N-body simulations [35].

The study of the orbital content of the peanuts, has been based on the analysis of the stability of families of periodic orbits in 3D autonomous Hamiltonians [36] as a parameter of the system, usually \(E_J\), varies [37,38,39,40]. The main dynamical mechanism proposed to be in action in this case, is again that of regular orbits trapped around stable periodic orbits. A family that offers the appropriate orbital content to make this scenario feasible, is the 3D bifurcation of x1 at the vertical 2/1 resonance, called x1v1 [38].

As indicated in [40] (their Fig. 11), the “X” structure is not formed as the density is enhanced along the shape of the orbits of x1v1, but it appears along the maxima heights from the equatorial plane, of successive orbits of this family. An example of such a backbone of stable x1v1 orbits supporting a X/peanut structure in a Ferrers bar model [37, 38] is given in Fig. 3.

Fig. 3
figure 3

A set of successive stable x1v1 periodic orbits in a Ferrers bar model in a nearly side-on projection. The wings of the X are formed along the |z|-maxima of the orbits, i.e. along the directions indicated with the arrows

Full size image

The study of 3D autonomous Hamiltonian systems is a field, where various nonlinear phenomena appear and affect their evolution, such as inverse bifurcations, collisions of bifurcations and complex instability [36]. Especially complex instability, a kind of orbital instability that appears when the four eigenvalues of the \(4 \times 4\) monodromy matrix MFootnote 1, are complex and off the unit circle (see e.g. [38]), appears in orbits that may participate in supporting the peanut for considerable time intervals [40]. This is one more case in which chaotic orbits contribute to the reinforcement of structures by behaving for times significant for the dynamical scales of the system we study, as regular. Essentially, we have to do with the phenomenon of stickiness [41], which is ubiquitous in galactic stellar dynamics and upgrades the role of chaotic orbits in supporting structures.

3 Discussion

Nowadays there is a general consensus among researchers working in the field that the observed structures are the result of the interplay between Order and Chaos. Usually, both situations coexist in structure-supporting models. Regular orbits are the building blocks of the structures in most of the cases, but not in all of them. The alternative is sticky orbits near the borders of an island of stability in the phase space of a 2D dynamical system, or orbits remaining sticky near the unstable asymptotic curves of unstable periodic orbits in chaotic seas of the phase space. Examples of sticky orbits of the first kind are those supporting outer boxy envelopes of barred galaxies [28] or inner boxy structures in the central regions of the bars [42, 43]. Orbits sticky to unstable asymptotic curves, are those supporting the spiral arms outside corotation. An extreme example of an ansae-type bar supported mainly by chaotic orbits is given in [29]. In a case presented in that paper, the shape of the bar is defined by the shape of the isocontours of the effective potential, allowing particles in chaotic motion to visit all regions inside the area outlined by the ansae-type isocontour (see their Figs. 2 and 3).

It is not always easy to distinguish which mechanism is behind an observed morphological feature in a real galaxy. For example, the outer boxiness of a bar may be due to regular orbits trapped around boxy 4/1 resonance orbits, or due to chaotic orbits sticky to tiny stability islands in the 4/1 resonance region. When we see a pair of spiral arms emerging from the ends of a bar, we may conclude that they are due to chaotic orbits associated with Lyapunov orbits around L1 and L2, provided that the ends of the bar are close enough to the Lagrangian points. However, the ratio of the corotation radius, \(R_c\), to the length of the semi-major axis of a bar, \(R_b\), is in general \(1<R_c/R_b<1.4\) [44], while in some cases it can be assumed even larger, reproducing successfully barred-spiral morphologies (see e.g. models in [31, 33]. For bars that end away from the Lagrangian points, other mechanisms have to be invoked for explaining the spirals.

In that respect, imaging in the optical and in the near-infrared, as well as detailed kinematic data, are always needed to be compared with the predictions of the models in order to qualify the best scenario behind the emergence of a specific morphological feature.