An Elastoplastic Framework Accounting for Changes in Matric and Osmotic Suction in Unsaturated Non-expansive Clays

Abstract

The mechanical behaviour of clays is significantly influenced by their salinity and degree of saturation, which are expected to change in both natural and anthropogenic environments. This influence is triggered by fabric changes. Capillary forces, related to changes in the degree of saturation, and electrochemical interactions, related to changes in salinity, affect differently the interaction between particles. However, at the continuum scale, it is possible to pinpoint some common characteristics. This paper focuses on the modelling capabilities of an elasto-plastic framework formulated to reproduce the behaviour of unsaturated non-expansive clays exposed to changes in matric and osmotic suction, by introducing osmotic suction on BBM-like models in terms of its effects on the normal compression line. The model, calibrated on experimental data on Boom clay (Mokni et al., 2014) and remoulded loess (Zhang et al., 2022), has been implemented in the Thebes code and used to predict material response under selected chemo-hydro-mechanical paths.

1 Introduction

Changes in the degree of saturation and the chemical composition of the pore fluid have significant effects on clay behaviour, as they affect volume, permeability, retention properties, compressibility and shear strength. In presence of severe safety requirements, the combined effect of the degree of saturation and pore fluid chemistry should thus be considered for design. In particular, unsaturated clays with salts dissolved in the pore fluid are subjected not only to matric suction, but also to osmotic suction, which is related to the molar concentration of the dissolved salt in the pore fluid. Both matric and osmotic suction changes affect the evolution of clay microstructure, and thus the unsaturated clay behaviour. As evidenced by microstructural observations, clay microstructure consists of clay clusters or aggregates, whose size evolves not only with water content but also with pore water salinity, with relevant effects on clay macro-porosity (see, e.g., Musso et al. (2013)). Constitutive models at the continuum scale accounting for microstructure changes have been developed for expansive clays, while less attention has been paid to the hydro-chemo-mechanical behaviour of non-expansive clays. Starting from the experimental evidence on saturated non-expansive clays presented in Torrance (1974) and Musso et al. (2022), this contribution proposes a constitutive framework capable of reproducing the mechanical effects of simultaneous matric and osmotic suction changes. The approach relies on the similarity between the phenomenological effects of matric and osmotic suction on the mechanical behaviour in the compression plane, which in turn depends on fabric evolution (Scelsi et al., (2021)). In this work, a simple constitutive model has been obtained by joining the Barcelona Basic Model (BBM, Alonso et al. (1990)) and the model proposed by Musso et al. (2022) (MSD model). The model, implemented in the Thebes code (Abed and Sołowski, (2017), (2022)), is used to simulate experiments on compacted Boom clay (Mokni et al., (2014)) and a remoulded loess (Zhang et al., (2022)), subjected to different stress paths at varying matric and osmotic suctions.

2 Constitutive Framework

Matric suction is related to capillary forces, acting on solid particles in granular materials and on clusters/aggregates of clay particles. Soil deposition and compaction may induce an ‘open fabric’ (Alonso et al., (1990)), related to the existence of macro-voids between the clusters/aggregates. Phenomenological evidence of the presence of an open fabric is the fact that, under Normally Consolidated conditions, a higher matric suction allows the material to sustain larger net stresses. Then, the Normal Compression Line (NCL) in the net stress – void ratio plane ($\upsigma$-u_a, e) moves at higher void ratios with matric suction. In such conditions, a higher matric suction implies then also a larger elastic domain. Consistently, if an unsaturated material with an open fabric is subjected to wetting at constant stress, a reduction in matric suction makes the current void ratio non-compatible with the applied stress and compressive plastic strains develop (the so-called wetting induced collapse). This aspect has been modelled by the so-called Loading-Collapse (LC) curve, as proposed by Alonso et al. (1990) in the BBM model and then recognized as a fundamental feature in any constitutive model for unsaturated soils. However, it is acknowledged that also pore water salinity influences the fabric of non-expansive clays, depending on the soil formation process and the electrochemical environment. When deposition occurs in salty water, non-expansive clays tend to have a “flocculated” fabric, characterized by the presence of larger macro-porosity between clay clusters, with respect to the face-to-face aggregated fabric formed in freshwater. Although less pronounced, similar effects were detected also for compacted clays, at least at sufficiently low-stress levels. Consistently with the evidences for unsaturated soils, Musso et al. (2022) proposed a link between the fabric of non-expansive clayey materials and their phenomenological behaviour, highlighting that the position of the NCL moves towards higher void ratios (open fabric) and its slope changes with increasing pore fluid salinity. Thus, as suggested by experimental evidence (see e.g. Torrance (1974), Musso et al. (2022)), when salinity decreases, compressive irreversible strains are anticipated, in the same way as wetting induces the collapse of unsaturated soils. However, if the material is strongly over-consolidated (i.e. closed fabric), desalinization induces swelling, consistently with the increase of repulsive forces between particles caused by the increase in thickness of the double layer. The analogy with matric suction also works for mechanical loading at constant osmotic suction, as its increase induces an increase in the size of the elastic domain.

2.1 Matric Suction Effect: Barcelona Basic Model

The classical BBM, developed in the framework of hardening elastoplasticity, uses net stress $\upsigma ^{{\prime \prime }} =\upsigma - u_{a}$ and matric suction s = u_a − u_w as independent variables, where σ, u_w and u_a are the total stress, pore water pressure and pore air pressure, respectively. As the water content influences the soil fabric, BBM defines the Normal Compression Lines (NCL) for different values of suction in the v – ln ($p^{\prime \prime }$) plane as:

$$ v = N_{s} - \lambda_{s} \,\ln \,\frac{{p^{{\prime \prime }} }}{{p_{r} }} $$

(1)

where N_s is the specific volume for a reference mean stress p_r and λ_s is the slope of the Normal Compression Line. Both N_s and λ_s are functions of suction (see Fig. 5). BBM assumes the loading-collapse (LC) yield curve in the s – $p^{\prime \prime }$ plane as:

$$ p_{0} = p_{r} \cdot \left( {\frac{{p_{0}^{*} }}{{p_{r} }}} \right)^{{\frac{{\lambda_{0} - k}}{{\lambda_{s} - \kappa }}}} $$

(2)

where p₀ is the pre-consolidation pressure at matric suction s, $p_{0}^{*}$ is the isotropic pre-consolidation pressure at full saturation (s = 0) and λ₀ is the slope of the normal compression line in saturated conditions. Equation (2) introduces the dependence of the size of the yield surface on suction. In particular, the larger the matric suction, the larger the size of the yield surface.

2.2 Osmotic Suction Effect: The Musso-Scelsi Della Vecchia Model

Musso et al. (2022) proposed a constitutive model (MSD model in the following) based on the Terzaghi effective stress $\upsigma ^{{\prime }}$ and on osmotic suction π. Osmotic suction has been set to depend on the chemical activity of the components in solution and, at low concentrations, can be described by the van’t Hoff equation, as π = icRT, being i the number of dissolved species, c the molar concentration of the electrolyte, R the universal gas constant and T the absolute temperature. As the pore fluid chemistry influences the soil fabric, the normal compression line in the semilogarithmic plane v-ln($p^{{\prime }}$) depends on the saline concentration:

$$ v = N_{c} - \lambda_{c} \,\ln \,\frac{{p^{{\prime }} }}{{p_{rc}^{{\prime }} }} $$

(3)

where the intercept N_c and slope of the Normal Compression Line $\uplambda_{\text{c}}$ are both functions of the osmotic suction, while $p_{{{\text{rc}}}}^{{\prime }}$ is a reference pressure (here taken as 1 kPa). The original expression of the yield curve in the $\uppi - p^{{\prime }}$ plane can be found in Musso et al (2022), but assuming that the dependence of the volumetric virgin compressibility $\uplambda$ on the pore fluid salinity for non-expansive clays is quite limited (i.e. $\uplambda_{\text{c}}$  =  $\uplambda_{0}$) and that N₀ = N_c, the evolution of the size of the yield surface with osmotic suction for an isotropic stress state can be simplified as

$$ p_{c}^{{\prime }} = p_{0}^{*} \cdot \left( {\frac{{\pi + \pi_{ref} }}{{\pi_{ref} }}} \right)^{{\frac{{\kappa_{\pi } }}{{\lambda_{0} - \kappa }}}} $$

(4)

where $p_{c}^{{\prime }}$ is the preconsolidation pressure corresponding to osmotic suction π and $\upkappa _{\uppi }$ is the elastic logarithmic volumetric stiffness related to changes in osmotic suction. Like in the BBM, plastic strains may develop due to either a reduction of the osmotic suction or a stress change.

2.3 Combining Matric and Osmotic Suction Effects

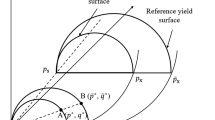
For soils where the pore liquid is pure water, the BBM links the saturated preconsolidation pressure $p_{0}^{ * }$ to the unsaturated yield mean net stress, p₀, through Eq. (2). Following the same rationale, the chemo-mechanical model introduces a relation between the preconsolidation pressure for the material saturated with distilled water, $p_{0}^{ * }$, and the yield mean effective stress for material saturated with saline solutions, $p_{{\text{c}}}^{{\prime }} {(}\uppi {)}$, through Eq. (4). Both yield curves in the $p^{\prime}$ − s plane and in the $p^{\prime}$ - π plane play the role of the Loading Collapse (LC) curve and have similar trends (see Fig. 1). The approach proposed to combine the effect due to partial saturation and salinity is to add them in terms of LC curve, thus introducing osmotic suction in BBM as an ‘equivalent’ matric suction s_π. Introducing in the BBM changes in the matric suction s_π equivalent to the osmotic suction would cause similar effects to those caused by the osmotic suction changes in the MSD model. According to the MSD model, when a saline pore fluid is present, the preconsolidation pressure increases from $p_{0}^{ * }$ to $p_{{\text{c}}}^{{\prime }}$. The equivalent matric suction s_π is the matric suction that would be obtained from the LC curve of the BBM passing from the saturated pre-consolidation pressure, $p_{0}^{ * }$, to $p_{{\text{c}}}^{{\prime }}$, as depicted in Fig. 3. Therefore, imposing that p₀ = $p_{{\text{c}}}^{{\prime }}$, the expression of λ_s(s_π) can be obtained from Eq. (2):

$$ \lambda_{s} = \left( {\lambda_{0} - \kappa } \right) \cdot \frac{{\ln \frac{{p_{0}^{*} }}{{p_{r} }}}}{{\ln \frac{{p_{c}^{^{\prime}} }}{{p_{r} }}}} + \kappa $$

(5)

Exploiting the link between the compressibility dependence on matric suction in BBM, modified to reproduce the increase in compressibility for increasing matric suction (see, e.g. Della Vecchia et al., (2013)), the following expression for the equivalent matric suction is obtained (see Scelsi et al, (2021), for details):

$$ s_{\pi } = - \frac{1}{\beta }\,\ln \,\left[ {\frac{{\lambda_{s} + \lambda_{0} \left( {r - 2} \right)}}{{\lambda_{0} \left( {r - 1} \right)}}} \right] $$

(6)

where r is a parameter already present in the original BBM formulation. The equivalence of the microstructural effects of both matric and osmotic suction leads to a common LC curve for both effects. BBM is finally enhanced by introducing an equivalent suction $s_{\psi }$, used in the same way as suction in the original BBM:

$$ s_{\psi } = s_{{}} + s_{\pi } $$

(7)

Fig. 1.

Procedure to obtain the equivalent matric suction

A yield surface for the first-ever chemical loading has been also introduced, to reproduce the plastic volumetric strain related to the change in soil structure upon the first salinization, as

$$ \pi = \pi_{0} $$

(8)

The maximum osmotic suction ever experienced by the soil π₀ should also be converted to an equivalent matric suction s_π0 in order to be introduced to model. Once this yield locus is reached, the plastic volumetric strain increment is evaluated as:

$$ d\varepsilon_{vs}^{p} = - \frac{{\lambda_{\pi } }}{v}\frac{{ds_{\pi ,0} }}{{\left( {s_{\pi ,0} + p_{atm} } \right)}} $$

(9)

where λ_π is the stiffness parameter for changes in (osmotic) suction for virgin states of the soil.

3 Model Predictions

3.1 Compacted Boom Clay

Mokni et al (2014) performed oedometer tests to investigate the hydro-mechanical response of compacted Boom clay (a kaolinitic-illitic clay of low-medium activity) subjected to different matric and osmotic suction. Figures 2 and 3 show the experimental results and model prediction with respect to the distinct effects of matric and osmotic suction on the compression behaviour of compacted Boom clay. Specimens had been obtained by mixing dry Boom clay powder with saline solutions (4M, 5.4M of NaNO₃, corresponding to $\uppi$  = 11000 kPa and 20000 kPa, respectively). After compaction, specimens have been subjected to either s = 500 kPa or s = 0 kPa (saturated conditions) and finally loaded and unloaded at constant suction. It is evident that the similar fabric effects are also inducing a similar mechanical response in the compression plane. Model predictions are satisfactory not only along constant suction paths, but also in terms of salinization path ($\uppi$  = 31 MPa) at constant matric suction (s = 500 kPa), as shown in Fig. 4. The chemo-mechanical path applied consists of a mechanical loading at constant matric suction up to the vertical stress of 50 kPa, followed by salinization at constant vertical stress and subsequent loading/unloading. In all the simulations, ${\text{p}}_{0}^{*}$ has been set equal to 90 kPa, p_r = 3000 kPa and $\uppi _{0}$ = 1 kPa. Model parameters used for the simulations are summarized in Table 1. When not defined in the paper, parameter nomenclature is consistent with Alonso et al. (1990) and Musso et al. (2022).

3.2 Remoulded Loess

Experimental data (Zhang et al., (2022)) on a remoulded loess coming from the Gansu Province (China) have been also exploited to check the predictive capabilities of the proposed constitutive framework. The remoulded loess had been statically compressed in oedometer to a void ratio of 0.53. Oedometer tests were then performed, by loading the specimens up to 25 kPa and then exposing them to a given value of total suction $\uppsi _{0}$ (via relative humidity control). Due to the lack of information related to the as-prepared suction of the specimens, the drying stage has not been simulated and, according to the volume change data presented by Zhang et al. (2022), the change in the void ratio of this stage has been considered negligible. Later, samples had been soaked with different solutions (i.e. distilled water, NaCl solution, Na₂SO₄ solution), corresponding to several values of input osmotic suction $\uppi _{{{\text{in}}}}$ and finally subjected to a standard oedometer loading/unloading, up to a maximum vertical stress of 1600 kPa. The model has been used to reproduce material response in the compression plane. Material parameters related to unsaturated soil behaviour have been calibrated on the test involving soaking with distilled water. According to the very small deformation upon drying-wetting paths, the parameter $\upkappa _{{\text{s}}}$ has been set equal to 0.001. Figure 5 shows the experimental data and model predictions for soaking tests with two different saline solutions, i.e. a 0.29 mol/l Na₂SO₄ solution and a 0.17 mol/l NaCl solution (corresponding to input osmotic suctions of $\uppi _{{{\text{in}}}}$ = 1.39 MPa and $\uppi _{{{\text{in}}}}$ = 0.74 MPa, respectively). Initial total suctions $\uppsi _{0}$ were equal to 14.0 MPa and 20.6 MPa, respectively. In this case, the presence of compressive volumetric strain upon soaking is evident. From the modelling point of view, this volumetric strain is related to the first salinization path, rather than a collapse upon wetting. This evidence is consistent with the elastic reloading path evident in the compression curve after soaking, which would not be present after a wetting induce collapse path. Model parameters used for the simulations are again summarized in Table 1. As for the initial values of the internal variables, ${\text{p}}_{0}^{*}$ has been set equal to 50 kPa, p_r = 3000 kPa and $\uppi _{0}$ = 5 kPa.

Table 1. Model parameters

Fig. 2.

Effect of matric suction on the compression behaviour of Boom clay (data from Mokni et al, 2014).

Fig. 3.

Effect of osmotic suction on the compression behaviour of Boom clay (data from Mokni et al, 2014).

Fig. 4.

Chemo-mechanical loading path on compacted Boom clay (data from Mokni et al, 2014).

Fig. 5.

Chemo-mechanical loading path on remoulded loess (data from Zhang et al, 2022).

4 Conclusions

Microstructural observations on low-medium activity clay materials show that both the increase in matric suction and pore fluid salt concentration may cause a transition from an open to a close fabric. This evidence allows the introduction of a constitutive framework for soils partially saturated with saline solutions, where both salinity and degree of saturation change simultaneously. In this paper, we proposed a simple elastoplastic model, joining together the well-known BBM with a recently published model, MSD, capable of accounting for the salinity of the pore fluid. The model introduces the effect of the osmotic suction in the BBM as an equivalent matric suction, i.e. a matric suction in the BBM which causes the same effects on void ratio as those caused by the osmotic suction in the MSD model. The model is able to well reproduce the stiffness changes of the soil induced by the suction variations and the plastic chemical deformations that develop when the clayey material is exposed for the first time to an increase in osmotic suction. Remarkably, it is formulated within a simple and widespread framework, without requiring the introduction of new parameters. The similar effects of osmotic and matric suctions in fact allow introducing a unique framework for soils partially saturated with saline solutions, where salinity and saturation changes are expected, thus reproducing and predicting the behaviour of moderate plasticity clays. However, the extension of model framework to unsaturated highly expansive clays would require the introduction of a double-porosity approach and further research.