Abstract
In this paper, we consider tight multi-user security under adaptive corruptions, where the adversary can adaptively corrupt some users and obtain their secret keys. We propose generic constructions for a bunch of primitives, and the instantiations from the matrix decisional Diffie-Hellman (MDDH) assumptions yield the following schemes:
-
(1)
the first digital signature (SIG) scheme achieving almost tight strong EUF-CMA security in the multi-user setting with adaptive corruptions in the standard model;
-
(2)
the first public-key encryption (PKE) scheme achieving almost tight IND-CCA security in the multi-user multi-challenge setting with adaptive corruptions in the standard model;
-
(3)
the first signcryption (SC) scheme achieving almost tight privacy and authenticity under CCA attacks in the multi-user multi-challenge setting with adaptive corruptions in the standard model.
As byproducts, our SIG and SC naturally derive the first strongly secure message authentication code (MAC) and the first authenticated encryption (AE) schemes achieving almost tight multi-user security under adaptive corruptions in the standard model. We further optimize constructions of SC, MAC and AE to admit better efficiency.
Furthermore, we consider key leakages besides corruptions, as a natural strengthening of tight multi-user security under adaptive corruptions. This security considers a more natural and more complete “all-or-part-or-nothing” setting, where secret keys of users are either fully exposed to adversary (“all”), or completely hidden to adversary (“nothing”), or partially leaked to adversary (“part”), and it protects the uncorrupted users even with bounded key leakages. All our schemes additionally support bounded key leakages and enjoy full compactness. This yields the first SIG, PKE, SC, MAC, AE schemes achieving almost tight multi-user security under both adaptive corruptions and leakages.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Cryptography aims to provide two fundamental security guarantees: privacy and authenticity. Centered around privacy and authenticity, a variety of cryptographic primitives are developed, including public-key encryption (PKE), symmetric encryption (SE), digital signature (SIG), message authentication code (MAC), signcryption (SC), authenticated encryption (AE), etc. To rigorously define security notions for these primitives, proper security models have to be set up according to their working environments and the adversaries’ attacking abilities. Along the path of proving security, PKE and SE are defined with indistinguishability under chosen plaintext/ciphertext attacks (IND-CPA/CCA), SIG and MAC are defined with existential unforgeability under chosen message attacks (EUF-CMA), and SC and AE with both privacy (Priv) and authenticity (Auth). To prove a specific primitive construction achieves the security goals, the most important technique is security reduction. Roughly speaking, a security reduction establishes a link from an adversary \(\mathcal {A}\) against the security of a primitive to another adversary \(\mathcal {B}\) solving a well-studied computationally hard problem, such as the decisional Diffie-Hellman (DDH) and learning with errors (LWE) problems, with approximately the same running time. The ratio of \(\mathcal {A}\)’s advantage \(\epsilon _{\mathcal {A}}\) to \(\mathcal {B}\)’s advantage \(\epsilon _{\mathcal {B}}\) is defined as the loss factor \(\ell :=\epsilon _{\mathcal {A}}/\epsilon _{\mathcal {B}}\), which measures the quality of the security reduction.Footnote 1 If \(\ell \) is a small constant, we call the reduction tight. Tight security is more desirable than non-tight one, since it enables a theoretically-sound instantiation without the need to compensate a security loss by increasing key lengths or group sizes, and allows universal key-length recommendations for applications. Many works (e.g., [10, 15, 16, 18, 22, 26]) also consider the tightness notion called almost tight, where \(\ell \) depends at most linearly (or even better, logarithmically) on the security parameter \(\lambda \). For ease of exposition, we will use the term “tight” to denote “(almost) tight” as conventionally did [15, 16, 18, 22, 26], but we will detail the security loss in the security theorems and scheme comparisons to reflect almost tightness.
Tight Multi-user Security Under Adaptive Corruptions (\({{{\textbf {MU}}}^{\textsf{c}}}\)). Cryptographic primitives are usually deployed in multi-user settings. But most of the security models for the primitives only consider single user. This is acceptable, since single-user security generally implies multi-user security via a security reduction called hybrid argument. But the price is a large loss factor \(\ell \) at least nQ, where n is the number of users and Q the number of instances per user [6]. Considering billions of users and trillions of running instances over Internet, the security loss \(\ell \) can be as large as \(2^{60}\). Such a large loss factor does hurt and has to be taken into account in the security parameter configuration during the deployment of primitives over Internet. To avoid a large loss factor that varies with the number of users and/or the number of target instances, many works [15, 16, 21] (to name a few) focus on primitive design with tight multi-user security.
Compared with a single-user setting, a multi-user environment becomes more involved and leaves more opportunities to adversaries implementing new attacks. An important attack is key corruption in that the adversary takes full control of some users and of course their keys. This happens since some adversary may snatch secrets from some user by system hacking or from key exposure due to the user’s bad key management. Therefore, it is reasonable for us to consider Multi-User security under corruptions, which we denote \({\textsf{MU}^{\textsf{c}}}\) or more precisely \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{XX}\) with notion \(\textsf{XX}\) depending on the primitive.Footnote 2 The existing works on \({\textsf{MU}^{\textsf{c}}}\) indicates that pursuing tight \({\textsf{MU}^{\textsf{c}}}\) security is not easy, as shown below.
Technical Difficulties in Achieving Tight \({{{\textbf {MU}}}^{\textsf{c}}}\) Security. As pointed out in [12, 18], there is a seemingly paradoxical technical problem needing to be addressed for proving tight \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of SIG. On the one hand, the security reduction algorithm has to know the signing keys of all users so that it can successfully answer adversary’s adaptive corruption query without resorting to a guessing strategy. On the other hand, the reduction algorithm should also be able to extract an answer to the underlying computationally hard problem from the adversary’s forged signature. However, if the reduction knows all the signing keys, it should be able to forge a signature by itself without the adversary.
There exist similar technical problems in achieving tight \({\textsf{MU}^{\textsf{c}}}\) security for other primitives. For example, to achieve tight \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CPA}/\textsf{CCA}\) security for PKE, the security reduction algorithm has to know the secret keys of all users to avoid the loss factor incurred by a guessing strategy. On the other hand, it should also be able to extract an answer from the adversary’s guessing of challenge bit. This seems to lead to a similar paradox since the reduction can decrypt the challenge ciphertexts to learn the challenge bit by itself if it knows all the secret keys.
Impossibility Results on Tight \({{{\textbf {MU}}}^{\textsf{c}}}\) Security. In fact, there is a line of research which showed impossibility results on tight \({\textsf{MU}^{\textsf{c}}}\) security for a class of PKE, SIG, MAC and AE schemes that meet certain conditions.
-
PKE. Bader et al. [5] proved that there exists no tight security reduction from \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CPA}/\textsf{CCA}\) security of PKE to non-interactive assumptions, if the relation between public key and secret key is “unique” or “re-randomizable”.
-
SIG. The above impossibility result for PKE also applies to \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of SIG, except that the relation is defined for the verification key and signing key [5]. Alternatively, if the signing algorithm is a deterministic one, there exists no tight security reduction from \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of SIG to bounded-round assumptions [30].
-
MAC. Morgan et al. [30] showed that if MAC is a deterministic one, then there exists no tight security reduction from \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of MAC to bounded-round assumptions.
-
AE. Jager et al. [23] proved that if AE satisfies a minimal key uniqueness, any reasonable reduction from \({\textsf{MU}^{\textsf{c}}}\) to single-user security is not tight.
These impossibility results indicate that it is not an easy job to obtain tight \({\textsf{MU}^{\textsf{c}}}\) Security. However, it does not eliminate all hopes as long as we can find ways bypassing the conditions leading to the impossibility results.
Possibility Results on Tight \({{{\textbf {MU}}}^{\textsf{c}}}\) Security. There are very few constructions in the literature proved to have tight \({\textsf{MU}^{\textsf{c}}}\) security, even in the Random Oracle (RO) model.
-
PKE. To the best of our knowledge, only one PKE scheme in [27] is proved to be tightly multi-user multi-challenge CCA secure under adaptive corruptions (\({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\)). Its security proof relies on the RO model.
-
SIG. Gjøsteen and Jager [17] and Pan and Wagner [33] proposed tightly \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure SIG schemes in the RO model. Bader et al. [4] constructed a tightly \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure SIG scheme in the standard model. Its tree-based component makes the signature non-compact. Recently, Han et al. [18] designed a new \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure SIG in the standard model. Their scheme enjoys compact signature while having non-compact public parameters (consisting of over a thousand group elements).
It is more desirable to pursue strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of SIG, which even guarantees the hardness for adversary to forge a new signature for an already signed message, thus additionally ensuring “non-malleablility” of signatures. Strongly \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure SIG has important applications in building more complex primitives such as SC [3] and authenticated key exchange (AKE) [12], where it can help SC to achieve ciphertext integrity (authenticity) [7] and AKE to achieve strong notion of “matching conversations” security [8] (see more discussions in [12]). One may want to resort to the Generalized Boneh-Shen-Waters (GBSW) transform [35] to convert a (non-strongly) secure SIG scheme to a strongly secure one, with the help of chameleon hash functions. However, the GBSW transform was originally proposed in the single-user setting, and was recently extended to the multi-user setting in [28], but without the consideration of corruptions. As noted in [28], it seems difficult to show that the GBSW transform also works under corruptions and preserves the tightness, i.e., converting a tightly \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure SIG scheme to a tightly and strongly \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure one. The reason is, the resulting SIG scheme contains the trapdoor of chameleon hash in its secret key, thus corruption of secret key means revealing of trapdoor, which is not supported by the security of chameleon hash [28].
Up to now, only one SIG scheme in a recent work [12] is proved to have tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security, based on the RO model.
-
SignCryption(SC). In [9], Bellare and Stepanovs defined multi-user security for SC to cover both insider and outsider security. Their security notions are essentially multi-user CCA security under adaptive corruptions which considers both privacy (\({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}\)) and authenticity (\({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Auth}\)). They also designed a SC scheme with security proved in the RO model.
-
MAC and AE. Note that SIG naturally implies a MAC scheme and SC implies an AE scheme. As far as we know there is no approach to tight \({\textsf{MU}^{\textsf{c}}}\)- \(\textsf{CMA}\) security other than derived from SIG. Similar statement holds for AE.
Up to now, there exists no PKE scheme achieving tight \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security, no SIG and MAC achieving tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security, and no SC and AE achieving tight \( {\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) in the standard model. The challenges are:
Can we fill the aforementioned blanks on tight \({\textsf{MU}^{\textsf{c}}}\) security in the standard model? Can we step even forward by considering tight multi-user security under not only adaptive corruptions but also key leakages?
1.1 Our Contributions
We propose generic constructions for a bunch of primitives and prove their tight multi-user security under adaptive corruptions and key leakages.
-
We propose generic constructions of SIG, PKE, SC, MAC, AE and prove their \({\textsf{MU}^{\textsf{c}}}\) security with tight security reductions. The instantiations yield the following concrete schemes from the matrix DDH (MDDH) assumptions [14] (which corresponds to the standard DDH, k-Linear assumptions under different parameters) over asymmetric pairing groups in the standard model:
-
the first PKE scheme achieving almost tight \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security;
-
the first SIG scheme achieving almost tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security;
-
the first SC scheme achieving almost tight \( {\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) security;
-
the first MAC scheme achieving almost tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMVA}\) security;
-
the first AE scheme achieving almost tight \( {\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) security.
Moreover, all our schemes are fully compact, i.e., all the parameters, keys, signatures, ciphertexts consist of only a constant number of group elements.
-
-
We formalize stronger multi-user security notions for the primitives under not only adaptive corruptions but also key leakages, denoted by \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\). In addition to \({\textsf{MU}^{\textsf{c}}}\), the \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security protects the uncorrupted users even if adversary also obtains bounded leakage information on their secret keys.
Key leakage [2, 32] is closely related to corruption, especially in the multi-user setting, and \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) is a natural strengthening of \({\textsf{MU}^{\textsf{c}}}\). The reason is as follows. Existing \({\textsf{MU}^{\textsf{c}}}\) security considers an “all-or-nothing” setting, where secret keys of users are either fully exposed to adversary (“all”) or completely hidden to adversary (“nothing”), and it protects the uncorrupted users. In realistic environments, there would naturally be users whose secret keys are only partially leaked to adversary (“part”). These users sit in a situation that is neither “all” nor “nothing”. The new \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security additionally takes into account the security of these users. Hence the new \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security considers a more natural and more complete setting of “all-or-part-or-nothing”.
Thanks to the leakage resilience property of the building blocks, the almost tight \({\textsf{MU}^{\textsf{c}}}\) security of all our SIG, PKE, SC, MAC, AE schemes can be further strengthened to support key leakage, thus achieving almost tight \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security.
-
At the heart of our constructions is new technical tool called Publicly-Verifiable Quasi-Adaptive Hash Proof System and a set of new properties for it. These, together with our novel tight proof strategies for handling corruptions, help us circumvent the seemingly paradoxical technical problems.
We refer to Table 1 and Table 2 for comparisons of our SIG and PKE with known schemes, respectively.
In summary, our work shows that almost tight \({\textsf{MU}^{\textsf{c}}}\) security (and even together with full compactness) for SIG, PKE, SC, MAC and AE are achievable in the standard model. Moreover, our MDDH-based schemes support bounded key leakages as well, thus our work also provides the first schemes achieving almost tight \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security, no matter in the standard model or RO model.
2 Technical Overview
In this section, we provide a technical overview of our results. We show the main ideas in our generic constructions of SIG and PKE, and give a high-level overview of their tight \({\textsf{MU}^{\textsf{c}}}\) security proofs in Subsect. 2.1 and Subsect. 2.2, respectively. We describe our SC, MAC and AE constructions and how to optimize them in Subsect. 2.3. Then in Subsect. 2.4, we explain the instantiations from the MDDH assumptions and explain why our aforementioned constructions support key leakage and achieve tight \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security. Finally, in Subsect. 2.5, we compare our technique with existing techniques for tight \({\textsf{MU}^{\textsf{c}}}\) security.
2.1 Our SIG: Technical Overview
Our starting point is a useful tool called Quasi-Adaptive Hash Proof System (QA-HPS), which was proposed by Han et al. [20] for achieving tight leakage resilient security of PKE. QA-HPS generalizes HPS [11] with a collection \(\mathscr {L}= \{ \mathcal {L}_\rho \}_\rho \) of NP-languages (\(\mathcal {L}_\rho \subseteq \mathcal {X}\)) and a family of projection functions \(\alpha _{(\cdot )}\). The projection key is determined by \(pk:=\alpha _{\rho }(sk)\), hence depends on language \(\mathcal {L}_\rho \). Meanwhile, QA-HPS has two ways of computing the hash value \(\varLambda _{sk}(x)\): the public evaluation \(\textsf{Pub}(pk, x, w)\) for the instance \(x\in \mathcal {L}_\rho \) with witness w, and the private evaluation \(\textsf{Priv}(sk, x)\) for \(x\in \mathcal {X}\). Its correctness requires \(\textsf{Pub}(pk, x, w)=\textsf{Priv}(sk, x)=\varLambda _{sk}(x)\) for \(x\in \mathcal {L}_\rho \). Moreover, the subset membership problem (SMP) asks the computational indistinguishability of  and
and  .
.
Another technical tool is Quasi-Adaptive Non-Interactive Zero-Knowledge argument (QA-NIZK) proposed by Jutla and Roy [24], where the common reference string \(\textsf{crs}\) depends on language \(\mathcal {L}_{\rho }\). For tag-based QA-NIZK [25], there are two ways of generating a proof \(\pi \) for \(x \in \mathcal {L}_{\rho }\) w.r.t. tag \(\tau \): \(\textsf{Prove}(\textsf{crs}, \tau , x, w)\) using a witness w for \(x \in \mathcal {L}_{\rho }\), and the simulator \(\textsf{Sim}(\textsf{crs}, \textsf{td}_{\textsf{crs}}, \tau , x)\) using a trapdoor \(\textsf{td}_{\textsf{crs}}\). With \(\textsf{Vrfy}_{\textsf{NIZK}}(\textsf{crs}, \tau , x, \pi )\), one can verify whether \(\pi \) is a valid proof. Perfect zero-knowledge requires that the proofs generated by \(\textsf{Prove}\) and \(\textsf{Sim}\) are identically distributed. Besides, unbounded simulation-soundness (USS) [1, 22, 34] stipulates that a PPT adversary cannot prove a false statement \(x \notin \mathcal {L}_{\rho }\), even if it can obtain multiple simulated proofs for instances not necessarily in \(\mathcal {L}_\rho \).
QA-HPS and HPS have found wide applications in designing PKE [11], MAC [13], etc. However, there are rarely applications in building SIG schemes, mainly because the designated-verifier style inherent in (QA)HPS is insufficient to support public verification of SIG. To fill the gap, we propose a new tool.
Publicly-Verifiable QA-HPS. The core technical tool underlying our SIG construction is a Publicly-Verifiable variant of QA-HPS, or PV-QA-HPS in short, which enables public verification of hash values with an extra verification key. We introduce a verification key generation function \(\nu (\cdot )\) to compute verification key \(vk:=\nu (sk)\), and a verification algorithm \(\textsf{Vrfy}_{\textsf{HPS}}(vk, x, hv)\) to check whether an element \(hv\) equals the hash value \(\varLambda _{sk}(x)\) of x with the help of \(vk\).
We also define two important properties for PV-QA-HPS, which play essential roles in the tight security reduction of our SIG.
-
Verification soundness. It is a computational property requiring that, given all secret/verification key pairs \(\{ (sk_i, vk_i) \}_{i \in [n]}\), it is hard for any PPT adversary to come up with an index \(i^* \in [n]\), an instance \(x^*\in \mathcal {X}\) and a hash value \(hv^*\) which is false but passes the verification w.r.t. key pair \((sk_{i^*}, vk_{i^*})\), i.e., \(hv^*\ne \varLambda _{sk_{i^*}}(x^*)\) but \(\textsf{Vrfy}_{\textsf{HPS}}(vk_{i^*}, x^*, hv^*)=1\).
-
\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-One-Time(OT)-extracting. It is a statistical property parameterized by two language collections \(\mathscr {L}_0 = \{ \mathcal {L}_{\rho _0} \}_{\rho _0}\) and \(\mathscr {L}= \{ \mathcal {L}_\rho \}_\rho \). It demands that the hash value \(\varLambda _{sk}(x^*)\) for any \(x^*\in \mathcal {L}_{\rho } \in \mathscr {L}\) retains a large enough min-entropy, even conditioned on the verification key \(vk=\nu (sk)\) and the projection key \(pk_{\rho _0}=\alpha _{\rho _0}(sk)\) w.r.t. language \(\mathcal {L}_{\rho _0} \in \mathscr {L}_0\). This min-entropy makes sure that any (unbounded) adversary is unable to guess the correct hash value \(\varLambda _{sk}(x^*)\), except with a negligible probability.
Our SIG from PV-QA-HPS and QA-NIZK. The building blocks for our SIG construction consists of a PV-QA-HPS scheme \(\textsf{PVQAHPS}= (\alpha _{(\cdot )}, \nu (\cdot ), \textsf{Pub},\) \(\textsf{Priv}, \textsf{Vrfy}_{\textsf{HPS}})\) for both language \(\mathcal {L}_\rho \in \mathscr {L}\) and language \(\mathcal {L}_{\rho _0} \in \mathscr {L}_0\)Footnote 3, a tag-based \(\textsf{QANIZK}= ( \textsf{Prove}, \textsf{Vrfy}_{\textsf{NIZK}}, \textsf{Sim})\) for \(\mathcal {L}_\rho \) and a collision-resistant hash function \(H\). The signing and verification keys of SIG are just the secret key \(sk\) and verification key \(vk=\nu (sk)\) of \(\textsf{PVQAHPS}\). The signature for message m isFootnote 4

The verification of SIG checks \(\textsf{Vrfy}_{\textsf{HPS}}( vk, x, d) = 1\) and \( \textsf{Vrfy}_{\textsf{NIZK}}( \textsf{crs}, \tau , x, \pi ) = 1\).
In the strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security model, adversary \(\mathcal {A}\) adaptively issues user-message pairs (i, m) to the signing oracle and obtains valid signatures \(\sigma \). It can also issue corruption queries and get the corresponding signing keys. \(\mathcal {A}\) tries to output a fresh and valid forgery \((i^*, m^*, \sigma ^*) \notin \{ (i, m, \sigma ) \}\) for an uncorrupted user \(i^*\).
Our tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security proof goes with three steps. See also Fig. 1 for a graphical high-level overview.
-
Step 1. Switch language from \(\mathcal {L}_{\rho }\) to \(\mathcal {L}_{\rho _0}\) for signing queries. Through signing queries, \(\mathcal {A}\) obtains a bunch of tuples \((i, m, \sigma =(x, d,\pi ))\), where \(\sigma \) is a valid signature of \(m\) under \(sk_i\).
-
According to the perfect zero-knowledge of \(\textsf{QANIZK}\), the computation of \(\pi \) by \(\textsf{Prove}\) can be replaced by \(\textsf{Sim}\) without any witness of \(x \in \mathcal {L}_{\rho }\).
-
By the hardness of (multi-fold) SMP, the samplings of all x can be changed from
 to
to  .
. -
For \(x\in \mathcal {L}_{\rho _0}\) with witness w, \(d := \textsf{Priv}(sk_i, x)=\textsf{Pub}(\alpha _{\rho _0}(sk_i), x, w)\). So

Now \(\alpha _{\rho _0}(sk_{i})\) (out of the whole \(sk_i\)) suffices for generating \(\sigma \).
-
-
Step 2. Restrict language from \(\mathcal {X}\) to \(\mathcal {L}_{\rho }\) in the forgery. \(\mathcal {A}\)’s forgery \((i^*, m^*,\) \(\sigma ^*=(x^*, d^*, \pi ^*))\) is successful if it is fresh and passes the validity check \(\textsf{Vrfy}_{\textsf{HPS}}( vk_{i^*}, x^*, d^*) = 1 \wedge \textsf{Vrfy}_{\textsf{NIZK}}( \textsf{crs}, \tau ^*, x^*, \pi ^*) = 1\) with \(\tau ^* := H(vk_{i^*}, m^*)\).
-
By the verification soundness of \(\textsf{PVQAHPS}\), the check of \(\textsf{Vrfy}_{\textsf{HPS}}( vk_{i^*}, x^*,\) \(d^*) = 1\) can be replaced by \(d^*=\textsf{Priv}(sk_{i^*}, x^*)\).
-
The USS property of \(\textsf{QANIZK}\) makes sure that \(x^*\in \mathcal {L}_{\rho }\) in the forgery, except with a negligible probability.
-
-
Strategy for corruptions in reductions. Note that in the above two steps, when reducing to SMP or \(\textsf{QANIZK}\), the reduction algorithms can choose all users’ signing keys themselves. As for the verification soundness of \(\textsf{PVQAHPS}\), the reduction algorithm gets all users’ signing keys from its own challenger. Therefore, all of them are able to handle \(\mathcal {A}\)’s adaptive corruption queries.
-
Step 3. \(\mathcal {A}\)’s forgery fails due to the \(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting property. Now all information about \(sk_{i^*}\) that \(\mathcal {A}\) learns from the signing queries is limited to the projection key \(\alpha _{\rho _0}(sk_{i^*})\) on language \(\mathcal {L}_{\rho _0}\). On the other hand, \(x^*\) in \(\mathcal {A}\)’s forgery is restricted in \(\mathcal {L}_{\rho }\) and \(\mathcal {A}\) wins only if \(d^*=\textsf{Priv}(sk_{i^*}, x^*)\). By the \(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting property of \(\textsf{PVQAHPS}\), \(\mathcal {A}\) hardly succeeds.
How We Circumvent the Seemingly Paradoxical Technical Problem. Now we conclude how we circumvent the paradoxical technical problem for achieving tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of SIG: our proof goes with a constant number of computationally indistinguishable changes to arrive at a final game where the technical problem has turned into a statistical one.
-
(1)
All the reduction algorithms to computational properties or problems possess the signing keys of all users to handle adaptive corruption queries.
-
(2)
After arriving at a statistical problem (\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting property), it is hard for the adversary to forge valid signature information-theoretically.
How We Circumvent the Existing Impossibility Results. Below we explain how we circumvent the impossibility results on tight \({\textsf{MU}^{\textsf{c}}}\) security. Recall that the impossibility results apply to a SIG scheme when the relation between the verification key and the signing key is “unique” or “re-randomizable” [5], or the signing algorithm is a deterministic one [30].
Firstly, the signing algorithm of our SIG is not a deterministic one since it samples a random element x from \(\mathcal {L}_\rho \) with witness w.
Next, we show that the relation between the verification key \(vk= \nu (sk)\) and the signing key \(sk\) of our SIG is neither “unique” nor “re-randomizable”, by the properties we defined for PV-QA-HPS.
-
The relation is not “unique” due to the statistical \(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting property of PV-QA-HPS. Suppose, towards a contradiction, that the relation is unique, then an (unbounded) adversary can uniquely determine \(sk\) from \(\nu (sk)\), and thus break the property easily by computing \(hv^* = \varLambda _sk(x^*)\) for any \(x^* \in \mathcal {L}_\rho \).
-
The relation is not “re-randomizable” due to the verification soundness property of PV-QA-HPS. Suppose, towards a contradiction, that the relation is re-randomizable, then for any user \(i^* \in [n]\), an adversary can resample another \(sk'_{i^*}\) from \(vk_{i^*}\) and \(sk_{i^*}\), such that \(vk_{i^*} = \nu (sk_{i^*}) = \nu (sk'_{i^*})\). Then the adversary picks \(x^*\) from \(\mathcal {X}\) uniformly, computes \(hv^* = \varLambda _{sk'_{i^*}}(x^*)\) using \(sk'_{i^*}\), and outputs \((i^*, x^*, hv^*)\). On the one hand, since \(vk_{i^*}\) is also the verification key of \(sk'_{i^*}\), i.e., \(vk_{i^*} = \nu (sk'_{i^*})\), \(hv^*\) passes the verification w.r.t. \(vk_{i^*}\), i.e., \(\textsf{Vrfy}_{\textsf{HPS}}(vk_{i^*}, x^*, hv^*) = 1\). On the other hand, we have \(sk'_{i^*} \ne sk_{i^*}\) with high probability (\(\ge 1/2\), by the fact that the relation between \(vk\) and \(sk\) is not unique, as shown above), thus \(hv^* = \varLambda _{sk'_{i^*}}(x^*) \ne \varLambda _{sk_{i^*}}(x^*)\) with high probability. Consequently, the adversary breaks the verification soundness with high probability.
Of course, being neither “unique” nor “re-randomizable” nor “deterministic” is only a necessary condition for tight \({\textsf{MU}^{\textsf{c}}}\) security. To achieve tight \({\textsf{MU}^{\textsf{c}}}\) security, the cooperation of PV-QA-HPS and QA-NIZK in the design of our SIG as well as the nice properties of PV-QA-HPS play the most important roles.
2.2 Our PKE: Technical Overview
Our PKE is built upon the recent work [20], where the concept of QA-HPS was proposed to construct PKE with tight leakage resilient security. That tight security heavily relies on two statistical properties of QA-HPS: key-switching and universal. Intuitively, \(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching requires that conditioned on a projection key \(\alpha _{\rho }(sk)\) w.r.t. language \(\mathcal {L}_{\rho } \in \mathscr {L}\), the projection key \(\alpha _{\rho _0}(sk)\) w.r.t. language \(\mathcal {L}_{\rho _0} \in \mathscr {L}_0\) can be switched to \(\alpha _{\rho _0}(sk')\) for an independent key \(sk'\).
The PKE in [20] makes use of three QA-HPS schemes, one for masking the message and the other two for proving the well-formedness of ciphertext. As far as we understand, it is hard to prove the tight security of their PKE under adaptive corruptions, since their proof strategy that increases the entropy in secret keys gradually does not work in the presence of corruptions.
To support corruptions in the tight security, (1) we define new properties for QA-HPS, (2) we use another approach: QA-HPS with new properties to mask the message and QA-NIZK to prove the well-formedness of ciphertext, and (3) we develop a new proof strategy to achieve tight \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security.
QA-HPS with New Properties. We define two new properties for QA-HPS.
-
Multi-language multi-fold SMP. This new type of SMP asks the computational indistinguishability of
 and
and  , where \(\mathcal {L}_\rho \in \mathscr {L}\), and \(\mathcal {L}_{\rho _0^{(1)}}, ..., \mathcal {L}_{\rho _0^{(n)}} \in \mathscr {L}_0\) are n independent languages chosen from \(\mathscr {L}_0\). Jumping ahead, this new SMP enables us to switch the language \(\mathcal {L}_{\rho }\) to different languages \(\{ \mathcal {L}_{\rho _0^{(i)}} \}_{i \in [n]}\) for different users in our tight proof.
, where \(\mathcal {L}_\rho \in \mathscr {L}\), and \(\mathcal {L}_{\rho _0^{(1)}}, ..., \mathcal {L}_{\rho _0^{(n)}} \in \mathscr {L}_0\) are n independent languages chosen from \(\mathscr {L}_0\). Jumping ahead, this new SMP enables us to switch the language \(\mathcal {L}_{\rho }\) to different languages \(\{ \mathcal {L}_{\rho _0^{(i)}} \}_{i \in [n]}\) for different users in our tight proof. -
\(\mathscr {L}_0\)-Multi-key multi-extracting. It demands the pseudorandomness of multiple hash values \(\{ \varLambda _{sk_i}(x_j) \}_{i \in [n], j \in [Q]}\) of multiple instances \(x_1, ..., x_Q \in \mathcal {L}_{\rho _0}\) under uniformly and independently chosen keys \(sk_1, ..., sk_n\).
Our PKE from QA-HPS with New Properties and QA-NIZK. The secret and public keys of PKE are just the secret key \(sk\) and projection key \(pk=\alpha _{\rho }(sk)\) of QA-HPS for language \(\mathcal {L}_{\rho }\). The ciphertext for plaintext m is

The decryption of \(c=(x, d, \pi )\) checks whether \(\textsf{Vrfy}_{\textsf{NIZK}}( \textsf{crs}, \tau , x, \pi ) = 1\) and recovers \(m:=d-\textsf{Priv}(sk, x)\) after a successful check.
It is interesting to note that our PKE shares a similar design with our SIG. However, their tight proofs are quite different.
In the \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security model, adversary \(\mathcal {A}\) adaptively issues encryption queries \((i^*, m_0, m_1)\) to encryption oracle and obtains challenge ciphertexts \(c^*=(x^*, d^*, \pi ^*)\) that encrypts \(m_\beta \) under \(pk_{i^*}\), where  is the challenge bit. It can issue corruption queries and get the corresponding secret keys, and issue decryption queries \((i, c= (x,d,\pi ))\) and obtain the decryption of \(c\) under \(sk_i\). Finally \(\mathcal {A}\) outputs a guessing bit \(\beta '\) and wins if \(\beta '=\beta \).
is the challenge bit. It can issue corruption queries and get the corresponding secret keys, and issue decryption queries \((i, c= (x,d,\pi ))\) and obtain the decryption of \(c\) under \(sk_i\). Finally \(\mathcal {A}\) outputs a guessing bit \(\beta '\) and wins if \(\beta '=\beta \).
Our tight \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security proof goes with five steps. See also Fig. 2 for a graphical high-level overview.
-
Step 1. Switch language from \(\mathcal {L}_{\rho }\) to \(\{ \mathcal {L}_{\rho _0^{(i^*)}} \}_{i^* \in [n]}\) for encryption queries. Through encryption queries \((i^*, m_0, m_1)\), \(\mathcal {A}\) obtains multiple challenge ciphertexts \(c^*=(x^*, d^*,\pi ^*)\).
-
According to the perfect zero-knowledge of \(\textsf{QANIZK}\), the computation of \(\pi ^*\) by \(\textsf{Prove}\) can be replaced by \(\textsf{Sim}\) without any witness of \(x^* \in \mathcal {L}_{\rho }\).
-
By the correctness of \(\textsf{QAHPS}\), the computation of \(d^*\) by \(\textsf{Pub}\) can be replaced by \(d^*:=\textsf{Priv}(sk_{i^*}, x^*)+m_\beta \), without any witness of \(x^* \in \mathcal {L}_{\rho }\).
-
By the new multi-language multi-fold SMP, for each user \(i^*\), the samplings of all \(x^*\) can be changed from
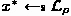 to
to  .
. -
For each user \(i^*\), since \(x^* \in \mathcal {L}_{\rho _0^{(i^*)}}\) with witness \(w^*\), we have \(d^*:=\textsf{Priv}(sk_{i^*}, x^*)+m_\beta =\textsf{Pub}(\alpha _{\rho _0^{(i^*)}}(sk_{i^*}), x^*, w^*)+m_\beta \). Hence

Now \(\{ \alpha _{\rho _0^{(i^*)}}(sk_{i^*}) \}_{i^* \in [n]}\) (out of whole \(\{ sk_{i^*} \}_{i^* \in [n]}\)) suffices for generating \(c^*\).
-
-
Step 2. Restrict language from \(\mathcal {X}\) to \(\mathcal {L}_{\rho }\) for decryption queries. For query \((i, c= (x,d,\pi ))\), \(\mathcal {A}\) obtains \(m:=d-\textsf{Priv}(sk_i, x)\) if \(\textsf{Vrfy}_{\textsf{NIZK}}( \textsf{crs}, \tau , x, \pi ) = 1\).
-
The USS property of \(\textsf{QANIZK}\) makes sure that \(\mathcal {A}\) obtains m only if \(x \in \mathcal {L}_{\rho }\) in the decryption query, except with a negligible probability.
Hence \(\mathcal {A}\) learns only \(\{ \alpha _{\rho }(sk_i) \}_{i \in [n]}\) (out of \(\{ sk_i \}_{i \in [n]}\)) from decryption queries.
-
-
Step 3. Switch \(\{ sk_{i^*} \}_{i^* \in [n]}\) to new keys \(\{ sk'_{i^*} \}_{i^* \in [n]}\) for encryption queries. Note that to avoid trivial attacks, \(\mathcal {A}\) is not allowed to corrupt those users \(i^*\) for which \(\mathcal {A}\) issues encryption queries. Thus for such users \(i^*\), after the first two steps, \(\mathcal {A}\)’s information about \(sk_{i^*}\) can be summarized by \(\alpha _{\rho }(sk_{i^*})\) (involved in public keys and decryption oracle) and \(\alpha _{\rho _0^{(i^*)}}(sk_{i^*})\) (involved in encryption oracle).
-
According to the \(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching property of \(\textsf{QAHPS}\), \(\alpha _{\rho _0^{(i^*)}}(sk_{i^*})\) can be switched to \(\alpha _{\rho _0^{(i^*)}}(sk_{i^*}')\) to compute \(d^*\) for encryption queries, with \(sk_{i^*}'\) uniformly and independently chosen.
Though there are n switches, it does not lead to a loose security reduction, since key-switching is a statistical property of \(\textsf{QAHPS}\). As a result, new independent secret keys \(\{ sk'_{i^*} \}_{i^* \in [n]}\) are split from the original \(\{ sk_{i^*} \}_{i^* \in [n]}\), and are only used for answering encryption queries.
-
-
Step 4. Switch languages \(\{ \mathcal {L}_{\rho _0^{(i^*)}} \}_{i^* \in [n]}\) to \(\mathcal {L}_{\rho _0}\) for encryption queries. The argument is similar to step 1. As a result, the computation of \(d^* := \textsf{Pub}(\alpha _{\rho _0^{(i^*)}}(sk'_{i^*}), x^*, w^*)+m_\beta \) is changed to \(d^* := \textsf{Pub}(\alpha _{\rho _0}(sk'_{i^*}), x^*, w^*)+m_\beta \), which is equivalent to \(d^* := \varLambda _{sk'_{i^*}}(x^*) +m_\beta \).
-
Step 5. Plaintexts \(m_\beta \) are perfectly hidden due to the \(\mathscr {L}_0\)-multi-key-multi-extracting property. Note that the new keys \(\{ sk'_{i^*} \}_{i^* \in [n]}\) are uniform and only used for computing \(d^* := \varLambda _{sk'_{i^*}}(x^*) +m_\beta \).
-
By the \(\mathscr {L}_0\)-multi-key-multi-extracting of \(\textsf{QAHPS}\), the hash values \(\varLambda _{sk'_{i^*}}(x^*)\) are pseudorandom, so all the \(d^*\)’s can be replaced by random elements.
Hence \(d^*\) perfectly hides \(m_\beta \), and \(\mathcal {A}\) has no advantage in guessing \(\beta \).
-
-
Strategy for corruptions in reductions. Similar to the security reductions for SIG, the reduction algorithms in steps 1, 2, 4, 5 can handle \(\mathcal {A}\)’s adaptive corruption queries by choosing all users’ secret keys themselves. In particular, in step 5, new keys \(\{sk'_{i^*}\}_{i^* \in [n]}\) (for answering encryption queries) have been split from \(\{sk_{i^*}\}_{i^* \in [n]}\) (for answering adaptive corruptions, decryption queries and generation of public keys). Thus the reduction algorithm to the \(\mathscr {L}_0\)-multi-key-multi-extracting property of \(\textsf{QAHPS}\) is able to implicitly set \(\{sk'_{i^*}\}_{i^* \in [n]}\) as the keys chosen by its own challenger, but choose \(\{sk_{i^*}\}_{i^* \in [n]}\) itself to deal with \(\mathcal {A}\)’s adaptive corruption queries.
How We Circumvent the Seemingly Paradoxical Technical Problem. Now we conclude how we circumvent the paradoxical technical problem for achieving tight \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security of PKE: our proof goes with a constant number of computationally indistinguishable changes, as well as n statistical changes, to arrive at a final game where the challenge ciphertexts are no longer generated by the users’ real secret keys.
-
(1)
All the reduction algorithms to computational properties or problems possess the secret keys of all users to handle adaptive corruption queries.
-
(2)
With n statistical changes (\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching), new and independent secret keys (for generating challenge ciphertexts) have been split from real secret keys (for corruption and other queries), ready for the final game.
-
(3)
In the final game, the reduction algorithm (for \(\mathscr {L}_0\)-multi-key-multi-extracting) can embed its challenge instances in the new secret keys to randomize challenge ciphertexts, and sample the real secret keys itself to handle adaptive corruption queries from the adversary.
How We Circumvent the Existing Impossibility Results. Recall that the impossibility results apply to a PKE scheme when the relation between the public key and the secret key is “unique” or “re-randomizable” [5]. For reasons similar to our SIG (as shown in Subsect. 2.1), we can show that the relation between the public key \(pk= \alpha _\rho (sk)\) and the secret key \(sk\) of our PKE is neither “unique” nor “re-randomizable”, by the new properties we defined for QA-HPS.
2.3 Our SC, MAC and AE: Technical Overview
Our SC. There are a variety of constructions for building SignCryption (SC) from SIG and PKE, encompassing “Encrypt-then-Sign”, “Sign-then-Encrypt”, “Encrypt-and-Sign”, etc. [3, 9]. However, there is no SC available with tight \({\textsf{MUMC}^{\textsf{c}}}\)-\( \textsf{Priv}{\small { \& }}\textsf{Auth}\) (multi-user multi-challenge CCA privacy and authenticity under corruptions) in the standard model. As far as we see, this is mainly due to the missing of tightly strongly \({\textsf{MU}^{\textsf{c}}}\) secure SIG and tightly \({\textsf{MU}^{\textsf{c}}}\) secure PKE.
Our SIG and PKE constructions fill the blank and immediately lead to tightly \( {\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) secure SC.
Moreover, we can optimize the SC construction by taking advantage of the similar structures and compatible underlying building blocks of our SIG and PKE. In our optimized construction of SC, we integrate the ciphertext of PKE and signature of SIG in a more efficient way of reusing the instance \(x\in \mathcal {L}_\rho \) and the proof \(\pi \) of \(\textsf{QANIZK}\), and the signcryption of message \(m\) is now given by

where \(\tau := H(\widetilde{vk}_s,pk_r, d, \widetilde{d})\), \(pk_r\) is receiver’s public (encryption) key and \(\widetilde{sk}_s\) sender’s secret (signing) key. The tight \( {\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) security of our SC can be proved similar to the tight \({\textsf{MU}^{\textsf{c}}}\) security of PKE and SIG.
Our MAC and AE. A SIG scheme is itself a MAC scheme and a SC scheme is an AE scheme, when taking the secret key as the symmetric key. Therefore, our SIG and SC constructions immediately lead to a strongly \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) secure MAC and \( {\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) secure AE. However, we can do more about MAC since it does not need public verification. We provide a more efficient MAC following our SIG construction but replacing the building block \(\textsf{PVQAHPS}\) by \(\textsf{QAHPS}\) with new properties. Furthermore, the security of MAC can also be improved to an even stronger notion, namely strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMVA}\) security, which considers chosen verification attacks as well [13] in addition to strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\).
2.4 Instantiations from MDDH Assumptions and Leakage Resilience
Instantiations. We instantiate PV-QA-HPS and QA-HPS with new properties from the MDDH assumptions. The associated language collections \(\mathscr {L}\) and \(\mathscr {L}_0\) are independently generated linear subspaces [25]. The instantiations stem from the DDH-based HPS proposed by Cramer and Shoup [11], and rely on pairing groups to accomplish public verifiability of PV-QA-HPS, inspired by [25]. We provide tight security proofs for the properties of PV-QA-HPS and QA-HPS based on MDDH. Below we give a high-level overview of our PV-QA-HPS instantiation. We rely on an asymmetric pairing group \((\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, e)\) of prime order p with \(e: \mathbb {G}_1\times \mathbb {G}_2\longrightarrow \mathbb {G}_T\). We use implicit representation of group elements [14], namely, using \([\cdot ]_1, [\cdot ]_2, [\cdot ]_T\) to denote component-wise exponentiations in respective groups \(\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T\).
-
\(\bullet \) Let us start with the Cramer-Shoup HPS [11]. We describe the MDDH-based generalized version with \(k \ge 1\) the MDDH parameter (\(k = 1\) corresponds to the original DDH-based version). The hashing key is \(sk= \textbf{K} \in \mathbb {Z}_{p}^{(k+1) \times (2k+1)}\) and the projection key is \(pk= [\textbf{KA} ]_1\) on a linear subspace language \(\mathcal {L}_\rho = {\textsf{Span}( [\textbf{A}]_1 )} = \big \{[\textbf{c}]_1 \big |\exists ~\textbf{w} \in \mathbb {Z}_{p}^{k}, \text {~s.t.~} [\textbf{c}]_1 = [\textbf{A} \textbf{w}]_1 \big \}\) with \(\rho = [\textbf{A}]_1 \in \mathbb {G}_1^{(2k+1) \times k}\). For an instance \([\textbf{c}]_1 = [\textbf{Aw}]_1 \in \mathcal {L}_\rho \), the HPS hash value is given by \([\boldsymbol{hv}]_1 =\)

-
\(\bullet \) To support public verification, we resort to pairing technique, inspired by the Kiltz-Wee QA-NIZK [25]. We use \(vk= [\textbf{K}^\top \textbf{B}]_2\) as the verification key with matrix \([\textbf{B}]_2 \in \mathbb {G}_2^{(k+1) \times k}\) defined by the MDDH assumption. Then, the correctness of hash value \([\boldsymbol{hv}]_1 {\mathop {=}\limits ^{?}} [\textbf{Kc}]_1\) can be verified publicly via pairing:
$$\begin{aligned} e([\boldsymbol{hv}^\top ]_1, [\textbf{B}]_2) {\mathop {=}\limits ^{?}} e([\textbf{c}^\top ]_1, [\textbf{K}^\top \textbf{B}]_2) ~~~(= [(\textbf{Kc})^\top \textbf{B}]_T). \end{aligned}$$ -
Verification soundness. This is tightly implied by the Kernal Matrix DH (KerMDH) assumption [31], which in turn is implied by the MDDH assumption [31]. If the adversary is able to produce an incorrect hash value \([\boldsymbol{hv}]_1 \ne [\textbf{Kc}]_1\) but passes the public verification \(e([\boldsymbol{hv}^\top ]_1, [\textbf{B}]_2) = e([\textbf{c}^\top ]_1, [\textbf{K}^\top \textbf{B}]_2)\), then \([\boldsymbol{hv} - \textbf{Kc}]_1\) is a non-zero element such that \(e([(\boldsymbol{hv} - \textbf{Kc})^\top ]_1, [\textbf{B}]_2) = [\textbf{0}]_T\), resulting in a solution to the KerMDH problem defined by \([\textbf{B}]_2\).
-
\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting. This holds information-theoretically, where \(\mathcal {L}_{\rho _0} = {\textsf{Span}( [\textbf{A}_0]_1 )} \in \mathscr {L}_0\) and \(\mathcal {L}_\rho = {\textsf{Span}( [\textbf{A}]_1 )} \in \mathscr {L}\) with \(\rho _0 = [\textbf{A}_0]_1 \in \mathbb {G}_1^{(2k+1) \times k}\) chosen independently of \(\rho = [\textbf{A}]_1\). Note that \(\textbf{A}_0\) is \((2k+1)\) by k, \(\textbf{B}\) is \((k+1)\) by k, and \(sk=\textbf{K}\) is \((k+1)\) by \((2k+1)\) matrices. Given the projection key \(pk_{\rho _0} = [\textbf{K} \textbf{A}_0]_1\) w.r.t. \(\mathcal {L}_{\rho _0}\) and \(vk= [\textbf{K}^\top \textbf{B}]_2\), the hashing key \(sk=\textbf{K}\) reserves entropy in its projection on the kernel of \(\textbf{A}_0\) and \(\textbf{B}\). Then for any (non-zero) instance \([\textbf{c}]_1 \in \mathcal {L}_\rho = {\textsf{Span}( [\textbf{A}]_1 )}\), \([\textbf{c}]_1\) is outside \(\mathcal {L}_{\rho _0} = {\textsf{Span}( [\textbf{A}_0]_1 )}\), thus the reserved entropy of \(sk=\textbf{K}\) is transmitted to the hash value \([\textbf{Kc}]_1\) so that the adversary can hardly guess \([\textbf{Kc}]_1\) correctly. This holds even if some extra (bounded) information of \(sk=\textbf{K}\) is leaked to the adversary.
The instantiation of tag-based QA-NIZK can be adapted from the QA-NIZK scheme proposed by Abe et al. [1], which has tight USS based on MDDH.
According to our generic constructions, the instantiations of PV-QA-HPS, QA-HPS and tag-based QA-NIZK result in concrete SIG, PKE, SC, MAC, AE schemes with tight \({\textsf{MU}^{\textsf{c}}}\) security from MDDH in the standard model.
Leakage Resilience. Note that HPS is intrinsically leakage resilient [32]. The leakage resilience can naturally extend to QA-HPS [20], and also to PV-QA-HPS. More precisely, we define leakage-resilient-\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting property for PV-QA-HPS (cf. Sect. 4) and adopt the leakage-resilient-\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching for QA-HPS defined in [20], which are met by our MDDH-based instantiations. This shows that all our SIG, PKE, SC, MAC, AE schemes not only have tight \({\textsf{MU}^{\textsf{c}}}\) security but also support key leakage, thus achieving tight \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security.
The tight \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security protects our schemes from key leakages on the uncorrupted users besides adaptive corruptions. When used in the construction of more advanced protocols, the applications of our tightly \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) secure primitives may also improve the security of the protocols to be leakage resilient ones. For instance, we can always make a drop-in replacement of the tightly \({\textsf{MU}^{\textsf{c}}}\) secure SIG with our tightly \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) secure SIG in the construction of tightly secure authenticated key exchange (AKE) protocols [4, 18, 29] where the signing key of SIG serves as the long-term secret key of AKE, and the resulting AKEs readily augment their tight security with leakage-resilience.
Moreover, our tightly \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) secure PKE scheme has essential improvements in terms of leakage resilience beyond corruptions, compared with the tightly leakage-resilient CCA-secure PKE scheme in [20]. See Table 2. Concretely, (1) our leakage rate is \(\frac{1}{3}-o(1)\) while theirs is \(\frac{1}{18}-o(1)\); (2) our multi-user leakage model is stronger than theirs, since their model [20, Appendix A.1] does not allow any leakage queries to any user after the very first encryption query to any user, while our model allows leakage queries for any particular user until the first encryption query to that user (cf. Definition 16 in Subsect. 6.1). Informally speaking, our PKE achieves the stronger multi-user leakage resilience mainly due to the introduction of multi-language multi-fold SMP, which helps to switch \(\mathcal {L}_{\rho }\) to different and independently chosen languages \(\{ \mathcal {L}_{\rho _0^{(i)}} \}\) for different users, thus the leakages w.r.t. different users can be handled independently.
2.5 Comparison with Existing Techniques for Tight \({\textsf{MU}^{\textsf{c}}}\) Security
Most existing works on tight \({\textsf{MU}^{\textsf{c}}}\) security [4, 12, 17, 27] designed their schemes in a “double encryption/signing” fashion (the only exception is [18]), and the secret key of their schemes consists of only one key (say \(sk_0\)) out of two possible keys (say \(sk_0, sk_1\)). For example, in [4, 27], their PKE encrypts plaintext by running a “sub-encryption procedure” twice (possibly in a correlated way), resulting in a ciphertext containing two “sub-ciphertexts” of the plaintext, and there are two decryption ways according to which possible key (\(sk_0\) or \(sk_1\)) is used. In their tight \({\textsf{MU}^{\textsf{c}}}\) security proofs, the reduction algorithms always possess the real secret keys (\(sk_0\)) of all users, while embed the challenges in the other possible keys (\(sk_1\)). With this strategy, their reductions can handle adaptive corruptions.
In contrast, all our constructions are different from the “double encryption/signing” design. For example, it is hard to split the ciphertext of our PKE to two “sub-ciphertexts”. So the proof strategy in [4, 12, 17, 27] does not apply.
We develop two different novel proof strategies for tight strong \({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\) security of SIG and tight \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) security of PKE (cf. Fig. 1 and Fig. 2), respectively. At a high level, we do not “double” the secret key by construction, but “split” the key during our tight proofs, which can be summarized as first “switch the languages for different oracles” then “apply quasi-adaptive properties” (such as \(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting, \(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-Key-switching, \(\mathscr {L}_0\)-Multi-key multi-extracting).
3 Preliminaries
Notations. Let \(\lambda \in \mathbb {N}\) denote the security parameter throughout the paper, and all algorithms, distributions, functions and adversaries take \(1^\lambda \) as an implicit input. Let \(\emptyset \) denote the empty set. If x is defined by y or the value of y is assigned to x, we write \(x:=y\). For \(n \in \mathbb {N}\), define \([n]:=\{1,2,...,n\}\). For a set \(\mathcal {X}\), denote by  the procedure of sampling x from \(\mathcal {X}\) uniformly at random. If \(\mathcal {D}\) is distribution,
the procedure of sampling x from \(\mathcal {X}\) uniformly at random. If \(\mathcal {D}\) is distribution,  means that x is sampled according to \(\mathcal {D}\). All our algorithms are probabilistic unless stated otherwise. We use
means that x is sampled according to \(\mathcal {D}\). All our algorithms are probabilistic unless stated otherwise. We use  to define the random variable y obtained by executing algorithm \(\mathcal {A}\) on input x. We use \(y \in \mathcal {A}(x)\) to indicate that y lies in the support of \(\mathcal {A}(x)\). If \(\mathcal {A}\) is deterministic we write \(y \leftarrow \mathcal {A}(x)\). We also use \(y \leftarrow \mathcal {A}(x; r)\) to make explicit the random coins r used in the probabilistic computation. Denote by \(\textbf{T}(\mathcal {A})\) the running time of \(\mathcal {A}\). “PPT” abbreviates probabilistic polynomial-time. Denote by \(\textsf{poly}\) some polynomial function and \(\textsf{negl}\) some negligible function.
to define the random variable y obtained by executing algorithm \(\mathcal {A}\) on input x. We use \(y \in \mathcal {A}(x)\) to indicate that y lies in the support of \(\mathcal {A}(x)\). If \(\mathcal {A}\) is deterministic we write \(y \leftarrow \mathcal {A}(x)\). We also use \(y \leftarrow \mathcal {A}(x; r)\) to make explicit the random coins r used in the probabilistic computation. Denote by \(\textbf{T}(\mathcal {A})\) the running time of \(\mathcal {A}\). “PPT” abbreviates probabilistic polynomial-time. Denote by \(\textsf{poly}\) some polynomial function and \(\textsf{negl}\) some negligible function.
The syntax of signature (SIG), public-key encryption (PKE) and the definition of collision-resistant hash functions are presented in the full version [19].
3.1 Language Distribution
We formalize a collection of NP-languages as a language distribution.
Definition 1
(Language Distribution). A language distribution \(\mathscr {L}\) is a probability distribution that outputs a language parameter \(\rho \) as well as a trapdoor \(td\) in polynomial time. The language parameter \(\rho \) publicly defines an NP-language \(\mathcal {L}_{\rho } \subseteq \mathcal {X}_{\rho }\). For simplicity, we assume that the universe \(\mathcal {X}_{\rho }\) is the same for all parameters \(\rho \) output by all distributions \(\mathscr {L}\), and denoted by \(\mathcal {X}\). The trapdoor \(td\) is required to contain enough information for efficiently deciding whether an instance \(x \in \mathcal {X}\) is in \(\mathcal {L}_{\rho }\). We require that there are PPT algorithms for sampling  uniformly together with a witness w and sampling
uniformly together with a witness w and sampling  uniformly.
uniformly.
A language distribution is associated with a subset membership problem (SMP), which asks whether an element is uniformly chosen from \(\mathcal {L}_\rho \) or \(\mathcal {X}\). SMP can be extended to multi-fold SMP by considering multiple elements.
Definition 2
(SMP). The subset membership problem (SMP) related to a language distribution \(\mathscr {L}\) is hard, if for any PPT adversary \(\mathcal {A}\), it holds that \({\textsf{Adv}_{\mathscr {L}, \mathcal {A}}^{\textsf{smp}}(\lambda )} := | \Pr [ \mathcal {A}(\rho , x) = 1 ] - \Pr [ \mathcal {A}(\rho , x') = 1 ] | \le \textsf{negl}(\lambda ),\) where the probability is over  ,
,  and
and  .
.
Definition 3
(Multi-fold SMP). The multi-fold SMP related to a language distribution \(\mathscr {L}\) is hard, if for any PPT adversary \(\mathcal {A}\) and any polynomial \(Q = \textsf{poly}(\lambda )\), it holds that \({\textsf{Adv}_{\mathscr {L}, \mathcal {A}, Q}^{\textsf{msmp}}(\lambda )} := | \Pr [ \mathcal {A}(\rho , \{x_j\}_{j \in [Q]}) = 1 ] - \Pr [ \mathcal {A}(\rho , \{x'_j\}_{j \in [Q]})\) \(= 1 ] | \le \textsf{negl}(\lambda ),\) where  ,
,  and
and  .
.
3.2 Quasi-Adaptive Hash Proof System
Hash proof system (HPS) was proposed by Cramer and Shoup [11], and turned out to be a powerful tool in a wide range of applications. Han et al. [20] generalized HPS in a quasi-adaptive setting, termed as Quasi-Adaptive HPS (QA-HPS), by allowing the projection key to depend on the specific language \(\mathcal {L}_\rho \) for which hash values are computed. We give the definition of QA-HPS according to [20].
Definition 4
(QA-HPS). A quasi-adaptive hash proof system (QA-HPS) scheme \(\textsf{QAHPS}= (\textsf{Setup}_{\textsf{HPS}}, \alpha _{(\cdot )}, \textsf{Pub}, \textsf{Priv})\) for a language distribution \(\mathscr {L}\) consists of four PPT algorithms:
-
 : The setup algorithm outputs a public parameter \(\textsf{pp}_{\textsf{HPS}}\), which implicitly defines a hashing key space \(\mathcal{S}\mathcal{K}\), a hash value space \(\mathcal{H}\mathcal{V}\), and a family of hash functions \(\varLambda _{(\cdot )}: \mathcal {X}\longrightarrow \mathcal{H}\mathcal{V}\) indexed by hashing keys \(sk\in \mathcal{S}\mathcal{K}\), where \(\mathcal {X}\) is the universe for languages output by \(\mathscr {L}\).
: The setup algorithm outputs a public parameter \(\textsf{pp}_{\textsf{HPS}}\), which implicitly defines a hashing key space \(\mathcal{S}\mathcal{K}\), a hash value space \(\mathcal{H}\mathcal{V}\), and a family of hash functions \(\varLambda _{(\cdot )}: \mathcal {X}\longrightarrow \mathcal{H}\mathcal{V}\) indexed by hashing keys \(sk\in \mathcal{S}\mathcal{K}\), where \(\mathcal {X}\) is the universe for languages output by \(\mathscr {L}\).We require that \(\varLambda _{(\cdot )}\) is efficiently computable and there are PPT algorithms for sampling
 uniformly and sampling
uniformly and sampling  uniformly. We require \(\textsf{pp}_{\textsf{HPS}}\) to be an implicit input of other algorithms.
uniformly. We require \(\textsf{pp}_{\textsf{HPS}}\) to be an implicit input of other algorithms. -
\(pk_\rho \leftarrow \alpha _\rho (sk)\): Taking as input a hashing key \(sk\in \mathcal{S}\mathcal{K}\), the projection algorithm indexed by language parameter \(\rho \) outputs a projection key \(pk_\rho \).
-
\(hv\leftarrow \textsf{Pub}(pk_\rho , x, w)\): Taking as input a projection key \(pk_\rho = \alpha _\rho (sk)\) specified by \(\rho \), an instance \(x \in \mathcal {L}_\rho \) and a witness w for \(x \in \mathcal {L}_\rho \), the public evaluation algorithm outputs a hash value \(hv= \varLambda _{sk}(x) \in \mathcal{H}\mathcal{V}\).
-
\(hv\leftarrow \textsf{Priv}(sk, x)\): Taking as input a hashing key \(sk\) and an instance \(x \in \mathcal {X}\), the private evaluation algorithm outputs a hash value \(hv= \varLambda _{sk}(x) \in \mathcal{H}\mathcal{V}\).
Correctness requires that for all \((\rho , td) \in \mathscr {L}\), \(\textsf{pp}_{\textsf{HPS}}\in \textsf{Setup}_{\textsf{HPS}}\), \(sk\in \mathcal{S}\mathcal{K}\), \(x \in \mathcal {L}_\rho \) with witness w, \(pk_\rho := \alpha _\rho (sk)\), it holds that \(\textsf{Pub}(pk_\rho , x, w) =\varLambda _{sk}(x) =\textsf{Priv}(sk, x).\)
We can naturally define QA-HPS for two language distributions \(\mathscr {L}\) and \(\mathscr {L}_0\), by requiring correctness to hold not only for language parameters \(\rho \) output by \(\mathscr {L}\), but also for language parameters \(\rho _0\) output by \(\mathscr {L}_0\).
We recall a statistical property of QA-HPS from [20], parameterized by \(\kappa \in \mathbb {N}\) and two language distributions \(\mathscr {L}\), \(\mathscr {L}_0\), called \(\kappa \)-leakage-resilient(LR)-\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching. Informally speaking, it stipulates that in the presence of a projection key \(\alpha _{\rho }(sk)\) w.r.t. a language parameter \(\rho \) output by \(\mathscr {L}\) and given \(\kappa \) bits leakage information about \(sk\), the projection key \(\alpha _{\rho _0}(sk)\) w.r.t. another language parameter \(\rho _0\) output by \(\mathscr {L}_0\) can be switched to \(\alpha _{\rho _0}(sk')\) for an independent \(sk'\).
Definition 5
( \(\kappa \)-LR-\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-Key-Switching of QA-HPS). Let \(\kappa = \kappa (\lambda ) \in \mathbb {N}\), and let \(\mathscr {L}\) and \(\mathscr {L}_0\) be a pair of language distributions. A QA-HPS scheme \(\textsf{QAHPS}\) for \(\mathscr {L}\) supports \(\kappa \)-LR-\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching, if for any (possibly unbounded) adversary \(\mathcal {A}\), it holds that \({\boldsymbol{\epsilon }_{\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{}, \mathscr {L}_{0}\rangle \text {-}\textsf{ks}}(\lambda )}:= \big | \Pr [ {\textsf{Exp}_{\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{}, \mathscr {L}_{0}\rangle \text {-}\textsf{ks}}} \Rightarrow 1] -\frac{1}{2} \big | \le \textsf{negl}(\lambda ),\) where the experiment \({\textsf{Exp}_{\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{}, \mathscr {L}_{0}\rangle \text {-}\textsf{ks}}}\) is specified in Fig. 3.
3.3 Tag-Based Quasi-Adaptive Non-Interactive Zero-Knowledge
Quasi-Adaptive Non-Interactive Zero-Knowledge argument (QA-NIZK) was proposed by Jutla and Roy [24], where the common reference string (CRS) may depend on the specific language \(\mathcal {L}_{\rho }\) for which proofs are generated. We present the formal definition of QA-NIZK in its tag-based variant following [25].
Definition 6
(Tag-based QA-NIZK). A tag-based quasi-adaptive non-interactive zero-knowledge scheme \(\textsf{QANIZK}= (\textsf{Setup}_{\textsf{NIZK}}, \textsf{CRSGen}, \textsf{Prove},\) \( \textsf{Vrfy}_{\textsf{NIZK}}, \textsf{Sim})\) for a language distribution \(\mathscr {L}\) with tag space \(\mathcal {T}\) consists of five PPT algorithms:
-
 : The setup algorithm outputs a public parameter \(\textsf{pp}_{\textsf{NIZK}}\), which serves as an implicit input of other algorithms.
: The setup algorithm outputs a public parameter \(\textsf{pp}_{\textsf{NIZK}}\), which serves as an implicit input of other algorithms. -
 : Taking as input a language parameter \(\rho \), the CRS generation algorithm outputs a common reference string (CRS) \(\textsf{crs}\) and a simulation trapdoor \(\textsf{td}_{\textsf{crs}}\).
: Taking as input a language parameter \(\rho \), the CRS generation algorithm outputs a common reference string (CRS) \(\textsf{crs}\) and a simulation trapdoor \(\textsf{td}_{\textsf{crs}}\). -
 : Taking as input \(\textsf{crs}\), a tag \(\tau \in \mathcal {T}\), \(x \in \mathcal {L}_\rho \) and a witness w for \(x \in \mathcal {L}_\rho \), the proof generation algorithm outputs a proof \(\pi \).
: Taking as input \(\textsf{crs}\), a tag \(\tau \in \mathcal {T}\), \(x \in \mathcal {L}_\rho \) and a witness w for \(x \in \mathcal {L}_\rho \), the proof generation algorithm outputs a proof \(\pi \). -
\(0/1 \leftarrow \textsf{Vrfy}_{\textsf{NIZK}}(\textsf{crs}, \tau , x, \pi )\): Taking as input \(\textsf{crs}\), a tag \(\tau \in \mathcal {T}\), \(x \in \mathcal {X}\) and a proof \(\pi \), the deterministic verification algorithm outputs a bit indicating whether \(\pi \) is a valid proof.
-
 : Taking as input \(\textsf{crs}\), a simulation trapdoor \(\textsf{td}_{\textsf{crs}}\), a tag \(\tau \in \mathcal {T}\) and \(x \in \mathcal {X}\), the simulation algorithm outputs a simulated proof \(\pi \).
: Taking as input \(\textsf{crs}\), a simulation trapdoor \(\textsf{td}_{\textsf{crs}}\), a tag \(\tau \in \mathcal {T}\) and \(x \in \mathcal {X}\), the simulation algorithm outputs a simulated proof \(\pi \).
Perfect completeness requires that for all \((\rho , td) \in \mathscr {L}\), \(\textsf{pp}_{\textsf{NIZK}}\in \textsf{Setup}_{\textsf{NIZK}}\), \((\textsf{crs}, \textsf{td}_{\textsf{crs}}) \in \textsf{CRSGen}(\rho )\), \(\tau \in \mathcal {T}\), \(x \in \mathcal {L}_\rho \) with witness w, \(\pi \in \textsf{Prove}(\textsf{crs}, \tau , x, w)\), it holds that \(\textsf{Vrfy}_{\textsf{NIZK}}(\textsf{crs}, \tau , x, \pi ) = 1.\)
Perfect zero-knowledge requires that for all \((\rho , td) \in \mathscr {L}\), \(\textsf{pp}_{\textsf{NIZK}}\in \textsf{Setup}_{\textsf{NIZK}}\), \((\textsf{crs}, \textsf{td}_{\textsf{crs}}) \in \textsf{CRSGen}(\rho )\), \(\tau \in \mathcal {T}\), \(x \in \mathcal {L}_\rho \) with witness w, the outputs of \(\textsf{Prove}(\textsf{crs},\) \(\tau , x, w)\) and \(\textsf{Sim}(\textsf{crs}, \textsf{td}_{\textsf{crs}}, \tau , x)\) are identically distributed, where the probability is over the inner coin tosses of \(\textsf{Prove}\) and \(\textsf{Sim}\).
Below we define Unbounded Simulation-Soundness (USS) according to [1, 22].
Definition 7
(USS of Tag-based QA-NIZK). A tag-based QA-NIZK scheme \(\textsf{QANIZK}\) for \(\mathscr {L}\) has unbounded simulation-soundness (USS), if for any PPT adversary \(\mathcal {A}\), it holds that \({\textsf{Adv}_{\textsf{QANIZK},\mathcal {A}}^{\textsf{uss}}(\lambda )} := \Pr [ {\textsf{Exp}_{\textsf{QANIZK},\mathcal {A}}^{\textsf{uss}}} \Rightarrow 1 ] \le \textsf{negl}(\lambda )\), where the experiment \({\textsf{Exp}_{\textsf{QANIZK},\mathcal {A}}^{\textsf{uss}}}\) is defined in Fig. 4.
We note that the above USS definition for tag-based QA-NIZK is stronger than the usual one in [15, 25] in two aspects.
-
Firstly, \(\mathcal {A}\) is given the trapdoor \(td\) of the language parameter \(\rho \). Recall that \(td\) contains enough information for efficiently deciding whether or not an instance x is in \(\mathcal {L}_{\rho }\). This is stronger than the usual USS, but weaker than the USS for witness-sampleable distributions defined in [1, 22], where \(\mathcal {A}\) essentially samples \((\rho , td)\) itself and provides \((\rho , td)\) to the experiment.
-
Secondly, \(\mathcal {A}\) is allowed to output a forgery with a reused tag.
In [1], Abe et al. proposed a QA-NIZK scheme with tight USS for witness-sampleable distributions based on the MDDH assumptions. As noted in [1, Subsect. 3.2], their scheme can be easily extended to a tag-based QA-NIZK scheme with tight USS, by using collision-resistant hash functions.
4 Publicly-Verifiable QA-HPS and New Properties
In this section, we propose a new variant of QA-HPS, called Publicly-Verifiable QA-HPS (PV-QA-HPS), which additionally enables public verification of hash values with an extra verification key. Then we formalize a set of computational and statistical properties for PV-QA-HPS and QA-HPS serving different applications in subsequent sections.
-
For PV-QA-HPS, we define a computational verification soundness and statistical properties including leakage-resilient one-time-extracting (LR-OT-extracting) and verification key diversity (VK-diversity). PV-QA-HPS will be an important building block for SIG in Sect. 5 and these properties help SIG to achieve tight multi-user security under corruptions and leakages.
-
For QA-HPS, we define a computational multi-key-multi-extracting and a statistical projection key diversity (PK-diversity). We also define a multi-language multi-fold SMP for language distributions. QA-HPS will be an important building block for PKE in Sect. 6, and these new properties help PKE to achieve tight multi-user security under corruptions and leakages.
Jumping ahead, we will give instantiations of PV-QA-HPS and QA-HPS based on the matrix DDH (MDDH) assumptions in Sect. 7 and the full version [19].
Firstly, we present the syntax of PV-QA-HPS.
Definition 8
(PV-QA-HPS). A publicly-verifiable QA-HPS (PV-QA-HPS) scheme \(\textsf{PVQAHPS}= (\textsf{Setup}_{\textsf{HPS}}, \alpha _{(\cdot )}, \nu , \textsf{Pub}, \textsf{Priv}, \textsf{Vrfy}_{\textsf{HPS}})\) for a language distribution \(\mathscr {L}\) consists of six PPT algorithms:
-
\((\textsf{Setup}_{\textsf{HPS}}, \alpha _{(\cdot )}, \textsf{Pub}, \textsf{Priv})\) is a QA-HPS scheme for \(\mathscr {L}\) as per Definition 4.
-
 : It outputs a public parameter \(\textsf{pp}_{\textsf{HPS}}\), which also defines a verification key space \(\mathcal{V}\mathcal{K}\) besides \((\mathcal{S}\mathcal{K},\mathcal{H}\mathcal{V}, \varLambda _{(\cdot )})\) as per Definition 4.
: It outputs a public parameter \(\textsf{pp}_{\textsf{HPS}}\), which also defines a verification key space \(\mathcal{V}\mathcal{K}\) besides \((\mathcal{S}\mathcal{K},\mathcal{H}\mathcal{V}, \varLambda _{(\cdot )})\) as per Definition 4. -
\(vk\leftarrow \nu (sk)\): Taking as input a hashing key \(sk\in \mathcal{S}\mathcal{K}\), the verification key generation algorithm outputs a verification key \(vk\in \mathcal{V}\mathcal{K}\).
-
\(0/1 \leftarrow \textsf{Vrfy}_{\textsf{HPS}}(vk, x, hv)\): Taking as input a verification key \(vk= \nu (sk) \in \mathcal{V}\mathcal{K}\), an instance \(x \in \mathcal {X}\) and a hash value \(hv\in \mathcal{H}\mathcal{V}\), the deterministic verification algorithm outputs a bit indicating whether \(hv= \varLambda _{sk}(x)\) or not.
Verification completeness requires that for all \((\rho , td) \in \mathscr {L}\), \(\textsf{pp}_{\textsf{HPS}}\in \textsf{Setup}_{\textsf{HPS}}\), \(sk\in \mathcal{S}\mathcal{K}\), \(x \in \mathcal {X}\), \(vk:= \nu (sk)\) and \(hv:= \varLambda _{sk}(x)\), it holds \(\textsf{Vrfy}_{\textsf{HPS}}(vk, x, hv) = 1\).
Remark 1
(Relations between PV-QA-HPS and QA-NIZK). PV-QA-HPS can be viewed as a special kind of Designated-Prover (DP) QA-NIZK [1], but with different properties. The \(pk_\rho \) of PV-QA-HPS can be viewed as the proving key of DP-QA-NIZK, \(sk\) as the simulation trapdoor and \(vk\) as the common reference string (used for verification). With \(pk_\rho \), the prover can prove \(x \in \mathcal {L}_{\rho }\) with the help of a witness w via \(hv\leftarrow \textsf{Pub}(pk_\rho , x, w)\), where the hash value \(hv\) can be viewed as a proof for \(x \in \mathcal {L}_{\rho }\) . With \(vk\), the verifier can check whether \(hv\) is a valid proof for \(x \in \mathcal {L}_{\rho }\) via \(\textsf{Vrfy}_{\textsf{HPS}}(vk, x, hv)\). Moreover, with \(sk\), the simulator can generate a proof for x without knowing a witness via \(hv\leftarrow \textsf{Priv}(sk, x)\).
Verification completeness of PV-QA-HPS corresponds to the perfect completeness of DP-QA-NIZK. Correctness of (PV-)QA-HPS guarantees \(\textsf{Pub}(pk_\rho , x,\) \(w) = \textsf{Priv}(sk, x)\) for all \(x \in \mathcal {L}_{\rho }\) with witness w, thus corresponding to the perfect zero-knowledge of DP-QA-NIZK.
On the other hand, PV-QA-HPS has its own features. Firstly, it has a projection function \(\alpha _\rho (\cdot )\) (which is inherent to HPS) and a verification key generation function \(\nu (\cdot )\). Secondly, a set of properties of PV-QA-HPS and QA-HPS are built upon functions \(\alpha _\rho (\cdot )\) and/or \(\nu (\cdot )\). For instance, the \(\kappa \)-LR-\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-Key-Switching (cf. Definition 5 in Subsect. 3.2) is closely associated with \(\alpha _\rho (\cdot )\).
Next we define a computational verification soundness for PV-QA-HPS in the setting of multiple keys. Intuitively, it requires that for any \((sk, vk)\) among the multiple key pairs, a PPT adversary cannot find a tuple \((x^* \in \mathcal {X}, hv^*)\) such that \(hv^* \ne \varLambda _{ sk}(x^*)\) but \(\textsf{Vrfy}_{\textsf{HPS}}(vk, x^*, hv^*)=1\), even given all the key pairs.
Definition 9
(Verification Soundness of PV-QA-HPS). A PV-QA-HPS scheme \(\textsf{PVQAHPS}\) for \(\mathscr {L}\) has verification soundness, if for any PPT adversary \(\mathcal {A}\) and any polynomial \(n= \textsf{poly}(\lambda )\), it holds that \({\textsf{Adv}_{\textsf{PVQAHPS},\mathcal {A},n}^{\textsf{vrfy}\text {-}\textsf{snd}}(\lambda )} := \Pr [ {\textsf{Exp}_{\textsf{PVQAHPS},\mathcal {A},n}^{\textsf{vrfy}\text {-}\textsf{snd}}}\) \(\Rightarrow 1 ] \le \textsf{negl}(\lambda )\), where \({\textsf{Exp}_{\textsf{PVQAHPS},\mathcal {A},n}^{\textsf{vrfy}\text {-}\textsf{snd}}}\) is defined in Fig. 5.
We formalize a statistical extracting property for (PV-)QA-HPS, parameterized by \(\kappa \in \mathbb {N}\) and two language distributions \(\mathscr {L}_0\), \(\mathscr {L}\), called \(\kappa \)-leakage-resilient(LR)-\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-one-time(OT)-extracting. Informally speaking, it demands high min-entropy of \(\varLambda _{sk}(x)\) for any \(x \in \mathcal {L}_{\rho }\) with \(\rho \) output by \(\mathscr {L}\), when \(sk\) is uniformly chosen from \(\mathcal{S}\mathcal{K}\), even in the presence of a projection key \(\alpha _{\rho _0}(sk)\) w.r.t. \(\rho _0\) output by \(\mathscr {L}_0\) and given \(\kappa \) bits leakage information about \(sk\). For PV-QA-HPS, it requires the property to hold even in the presence of the verification key \(\nu (sk)\).
Definition 10
(\(\kappa \)-LR-\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-Extracting of QA-HPS and PV-QA-HPS). Let \(\kappa = \kappa (\lambda ) \in \mathbb {N}\), and let \(\mathscr {L}_0\) and \(\mathscr {L}\) be a pair of language distributions. A (PV-)QA-HPS scheme (\(\textsf{PV}\))\(\textsf{QAHPS}\) for \(\mathscr {L}\) supports \(\kappa \)-LR-\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting, if for any (unbounded) adversary \(\mathcal {A}\), it holds that \({\boldsymbol{\epsilon }_{(\textsf{PV})\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{0}, \mathscr {L}_{}\rangle \text {-}\textsf{otext}}(\lambda )}:= \Pr [ {\textsf{Exp}_{(\textsf{PV})\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{0}, \mathscr {L}_{}\rangle \text {-}\textsf{otext}}} \Rightarrow 1] \le \textsf{negl}(\lambda ),\) where \({\textsf{Exp}_{(\textsf{PV})\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{0}, \mathscr {L}_{}\rangle \text {-}\textsf{otext}}}\) is defined in Fig. 6.
The \(\kappa \)-LR-\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-Extracting experiment \({\textsf{Exp}_{(\textsf{PV})\textsf{QAHPS},\mathcal {A},\kappa }^{\textsf{lr}\text {-}\langle \mathscr {L}_{0}, \mathscr {L}_{}\rangle \text {-}\textsf{otext}}}\) for \(\textsf{QAHPS}\) (without gray part) and Publicly-Verifiable \(\textsf{PVQAHPS}\) (with gray part).
Han et al. [20] proposed a computational property for QA-HPS, called \(\mathscr {L}_0\)-multi-extracting, which demands the pseudorandomness of \(\varLambda _{sk}(x_j)\) for multiple instances \(x_j \in \mathcal {L}_{\rho _0}\) (\(j \in [Q]\)) with \(\rho _0\) output by \(\mathscr {L}_0\), when \(sk\) is uniformly chosen from \(\mathcal{S}\mathcal{K}\). We extend this property in the multi-key setting as follows.
Definition 11
(\(\mathscr {L}_0\)-Multi-Key-Multi-Extracting of QA-HPS). A QA-HPS scheme \(\textsf{QAHPS}\) for \(\mathscr {L}\) supports \(\mathscr {L}_0\)-multi-key-multi-extracting, if for any PPT \(\mathcal {A}\), any polynomial \(n = \textsf{poly}(\lambda )\) and any polynomial \(Q = \textsf{poly}(\lambda )\), it holds

where  ,
,  ,
,  ,
,  and
and  .
.
We formalize two statistical properties, called projection key diversity (PK-diversity) and verification key diversity (VK-diversity), for QA-HPS and PV-QA-HPS respectively. Intuitively, PK-diversity (resp. VK-diversity) expresses statistical collision resistance of projection keys (resp. verification keys) under different hashing keys.
Definition 12
(PK-Diversity of QA-HPS). A QA-HPS scheme \(\textsf{QAHPS}\) for \(\mathscr {L}\) has projection key diversity (PK-diversity), if \({\boldsymbol{\epsilon }_{\textsf{QAHPS}}^{\textsf{pk}\text {-}\textsf{div}}(\lambda )}:= \Pr [ \alpha _\rho (sk) = \alpha _\rho (sk') ] \le \textsf{negl}(\lambda ),\) where  ,
,  and
and  .
.
Definition 13
(VK-Diversity of PV-QA-HPS). A PV-QA-HPS scheme \(\textsf{PVQAHPS}\) for \(\mathscr {L}\) has verification key diversity (VK-diversity), if \({\boldsymbol{\epsilon }_{\textsf{PVQAHPS}}^{\textsf{vk}\text {-}\textsf{div}}(\lambda )}:= \Pr [ \nu (sk) = \nu (sk') ] \le \textsf{negl}(\lambda ),\) where  \(\textsf{Setup}_{\textsf{HPS}}\) and
\(\textsf{Setup}_{\textsf{HPS}}\) and  .
.
Finally, we define a multi-language multi-fold SMP for language distributions.
Definition 14
(Multi-Language Multi-fold SMP). The multi-language multi-fold SMP related to \(\mathscr {L}\) is hard, if for any PPT adversary \(\mathcal {A}\), any polynomial \(n = \textsf{poly}(\lambda )\) and any polynomial \(Q = \textsf{poly}(\lambda )\), it holds that \({\textsf{Adv}_{\mathscr {L}, \mathcal {A}, n,Q}^{\textsf{ml}\text {-}\textsf{msmp}}(\lambda )} := | \Pr [ \mathcal {A}( \{\rho ^{(i)}, \{x_j^{(i)} \}_{j \in [Q]} \}_{i \in [n]} ) = 1 ] - \Pr [ \mathcal {A}( \{\rho ^{(i)}, \{x_j'^{(i)} \}_{j \in [Q]} \}_{i \in [n]} ) = 1 ] | \le \textsf{negl}(\lambda ),\) where for each \(i \in [n]\),  ,
,  ,
,  .
.
Multi-language multi-fold SMP can generally be reduced to SMP with a security loss of nQ with n the number of languages and Q the number of folds per language. For some language distributions, such as those for linear subspaces based on the MDDH assumptions (cf. the full version [19]), the hardness of multi-language multi-fold SMP can be tightly reduced to that of SMP.
5 SIG with Tight Strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) Security
In this section, we present digital signature (SIG) schemes with tight strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) security, by using Publicly-Verifiable QA-HPS (PV-QA-NIZK) formalized in Sect. 4 as a central building block.
In Subsect. 5.1, we define the strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) security of SIG. Then in Subsect. 5.2, we present our generic construction of SIG.
5.1 Definition of Strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) Security
In [4], Bader et al. defined existential unforgeability for digital signatures under chosen-message attacks (CMA) in a Multi-User setting with adaptive corruptions of secret keys (\({\textsf{MU}^{\textsf{c}}}\text {-}\textsf{CMA}\)). Here we extend it to \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\), which considers existential unforgeability under not only chosen-message attacks and adaptive corruptions but also key leakages in the multi-user setting. Moreover, strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) requires that the adversary cannot even forge a new signature for a message that it has ever queried. Below we present the definition of strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) and the non-strong version can be easily adapted accordingly.
Definition 15
(Strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) Security for SIG). Let \(\kappa = \kappa (\lambda ) \in \mathbb {N}\). A signature scheme \(\textsf{SIG}=(\textsf{Setup}_{\textsf{SIG}},\textsf{Gen},\textsf{Sign}, \textsf{Vrfy}_{\textsf{SIG}})\) is strongly \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) secure under \(\kappa \) bits leakage per user, if for any PPT adversary \(\mathcal {A}\) and any polynomial \(n\), it holds that \( {\textsf{Adv}_{\textsf{SIG},\mathcal {A},n,\kappa }^{\textsf{s}\text {-}\textsf{cma}\text {-}\textsf{c}{\tiny { \& }}\textsf{l}}(\lambda )}:=\Pr [ {\textsf{Exp}_{\textsf{SIG},\mathcal {A},n,\kappa }^{\textsf{s}\text {-}\textsf{cma}\text {-}\textsf{c}{\tiny { \& }}\textsf{l}}} \Rightarrow 1] \le \textsf{negl}(\lambda )\), where the experiment \( {\textsf{Exp}_{\textsf{SIG},\mathcal {A},n,\kappa }^{\textsf{s}\text {-}\textsf{cma}\text {-}\textsf{c}{\tiny { \& }}\textsf{l}}}\) is defined in Fig. 7.
5.2 Generic Construction of SIG from PV-QA-HPS and QA-NIZK
We present a generic construction of strongly \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) secure SIG. Let \(\mathcal {M}\) be an arbitrary message space. The underlying building blocks are as follows.
-
Two language distributions \(\mathscr {L}\) and \(\mathscr {L}_0\), both of which have hard SMPs.
-
A publicly-verifiable \(\textsf{PVQAHPS}= (\textsf{Setup}_{\textsf{HPS}}, \alpha _{(\cdot )}, \nu , \textsf{Pub}, \textsf{Priv}, \textsf{Vrfy}_{\textsf{HPS}})\) for both \(\mathscr {L}\) and \(\mathscr {L}_0\), with hashing key space \(\mathcal{S}\mathcal{K}\) and verification key space \(\mathcal{V}\mathcal{K}\).
-
A tag-based \(\textsf{QANIZK}= (\textsf{Setup}_{\textsf{NIZK}}, \textsf{CRSGen}, \textsf{Prove}, \textsf{Vrfy}_{\textsf{NIZK}}, \textsf{Sim})\) for \(\mathscr {L}\), whose tag space is \(\mathcal {T}\).
-
A family of collision-resistant hash functions \(\mathcal {H}= \{ H: \mathcal{V}\mathcal{K}\times \mathcal {M}\longrightarrow \mathcal {T}\}\).
Our generic construction of \(\textsf{SIG}=(\textsf{Setup}_{\textsf{SIG}},\textsf{Gen},\textsf{Sign},\textsf{Vrfy}_{\textsf{SIG}})\) is shown in Fig. 8.
Correctness of \(\textsf{SIG}\) follows directly from the verification completeness of \(\textsf{PVQAHPS}\) and the perfect completeness of \(\textsf{QANIZK}\).
Next, we show its strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) security. We stress that the projection key \(pk_\rho = \alpha _\rho (sk)\) is not published as part of \(\textsf{SIG}\)’s verification key, and this is crucial to the security of \(\textsf{SIG}\) since otherwise one can publicly generate valid signatures for any message via the \(\textsf{Pub}\) algorithm of \(\textsf{PVQAHPS}\) by using \(pk_\rho \).
Theorem 1
(Strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) Security of \(\textsf{SIG}\)). Assume that (i) \(\mathscr {L}\) and \(\mathscr {L}_0\) have hard SMPs, (ii) \(\textsf{PVQAHPS}\) is a publicly-verifiable QA-HPS for both \(\mathscr {L}\) and \(\mathscr {L}_0\), having verification soundness, VK-diversity, and supporting \(\kappa \)-LR-\(\langle \mathscr {L}_0, \mathscr {L}\rangle \)-OT-extracting, (iii) \(\textsf{QANIZK}\) is a tag-based QA-NIZK for \(\mathscr {L}\), satisfying both perfect zero-knowledge and unbounded simulation-soundness, (iv) \(\mathcal {H}\) is collision-resistant. Then the proposed \(\textsf{SIG}\) scheme in Fig. 8 is strongly \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) secure under \(\kappa \) bits leakage per user.
Concretely, for any number \(n\) of users and any adversary \(\mathcal {A}\) who makes at most \(Q_s\) times of \({\mathcal {O}_{\textsc {Sign}}}\) queries, there exist adversaries \(\mathcal {B}_1, \cdots , \mathcal {B}_6\), such that \(\textbf{T}(\mathcal {B}_1) \approx \cdots \approx \textbf{T}(\mathcal {B}_5) \approx \textbf{T}(\mathcal {A}) + (n+Q_s) \cdot \textsf{poly}(\lambda )\), with \(\textsf{poly}(\lambda )\) independent of \(\textbf{T}(\mathcal {A})\), and
We refer to Subsect. 2.1 and Fig. 1 therein for an overview of the proof. Due to space limitations, we postpone the formal proof to the full version [19].
6 PKE with Tight \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) Security
In this section, we present public-key encryption (PKE) schemes with tight \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) security, by using QA-HPS with new properties formalized in Sect. 4 as a central building block.
In Subsect. 6.1, we define the \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) security of PKE. Then in Subsect. 6.2, we present our generic construction of PKE.
6.1 Definition of \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) Security
In [27], Lee et al. defined indistinguishability for PKE schemes under chosen-ciphertext attacks (CCA) in a Multi-User Multi-Challenge setting with adaptive corruptions of secret keys (which was originally called MUC\(^{+}\) in [27] and is denoted by \({\textsf{MUMC}^{\textsf{c}}}\text {-}\textsf{CCA}\) in this paper). Here we extend it to \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\), which also takes key leakages into account. Below we present the formal definition.
Definition 16
(\( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) Security for PKE). Let \(\kappa = \kappa (\lambda ) \in \mathbb {N}\). A PKE scheme \(\textsf{PKE}= (\textsf{Setup}_{\textsf{PKE}}, \textsf{Gen}, \textsf{Enc}, \textsf{Dec})\) is \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) secure under \(\kappa \) bits leakage per user, if for any PPT adversary \(\mathcal {A}\) and any polynomial \(n\), it holds that \( {\textsf{Adv}_{\textsf{PKE},\mathcal {A},n,\kappa }^{\textsf{cca}\text {-}\textsf{c}{\tiny { \& }}\textsf{l}}(\lambda )}:= \big | \Pr [ {\textsf{Exp}_{\textsf{PKE},\mathcal {A},n,\kappa }^{\textsf{cca}\text {-}\textsf{c}{\tiny { \& }}\textsf{l}}} \Rightarrow 1] -\frac{1}{2} \big | \le \textsf{negl}(\lambda )\), where the experiment \( {\textsf{Exp}_{\textsf{PKE},\mathcal {A},n,\kappa }^{\textsf{cca}\text {-}\textsf{c}{\tiny { \& }}\textsf{l}}}\) is defined in Fig. 9.
6.2 Generic Construction of PKE from QA-HPS and QA-NIZK
In this subsection, we present a generic construction of \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) secure PKE. The underlying building blocks are as follows.
-
Two language distributions \(\mathscr {L}\) and \(\mathscr {L}_0\), both of which have hard SMPs.
-
A \(\textsf{QAHPS}= (\textsf{Setup}_{\textsf{HPS}}, \alpha _{(\cdot )}, \textsf{Pub}, \textsf{Priv})\) for both \(\mathscr {L}\) and \(\mathscr {L}_0\), whose hashing key space is \(\mathcal{S}\mathcal{K}\), projection key space is \(\mathcal{P}\mathcal{K}\) and hash value space is \(\mathcal{H}\mathcal{V}\). We require \(\mathcal{H}\mathcal{V}\) to be an (additive) group. We stress that \(\textsf{QAHPS}\) is not required to be publicly-verifiable.
-
A tag-based \(\textsf{QANIZK}= (\textsf{Setup}_{\textsf{NIZK}}, \textsf{CRSGen}, \textsf{Prove}, \textsf{Vrfy}_{\textsf{NIZK}}, \textsf{Sim})\) for \(\mathscr {L}\), whose tag space is \(\mathcal {T}\).
-
A family of collision-resistant hash functions \(\mathcal {H}= \{ H: \mathcal{P}\mathcal{K}\times \mathcal{H}\mathcal{V}\longrightarrow \mathcal {T}\}\).
Our generic construction of \(\textsf{PKE}= (\textsf{Setup}_{\textsf{PKE}}, \textsf{Gen}, \textsf{Enc}, \textsf{Dec})\) is shown in Fig. 10.
Correctness of \(\textsf{PKE}\) follows directly from the correctness of \(\textsf{QAHPS}\) and the perfect completeness of \(\textsf{QANIZK}\). Next, we show its \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) security.
Theorem 2
(\( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) Security of \(\textsf{PKE}\)). Assume that (i) \(\mathscr {L}\) and \(\mathscr {L}_0\) have hard SMPs, (ii) \(\textsf{QAHPS}\) is a QA-HPS for both \(\mathscr {L}\) and \(\mathscr {L}_0\), having PK-diversity, and supporting both \(\kappa \)-LR-\(\langle \mathscr {L}, \mathscr {L}_0 \rangle \)-key-switching and \(\mathscr {L}_0\)-multi-key-multi-extracting, (iii) \(\textsf{QANIZK}\) is a tag-based QA-NIZK for \(\mathscr {L}\), satisfying both perfect zero-knowledge and unbounded simulation-soundness, (iv) \(\mathcal {H}\) is collision-resistant. Then the proposed \(\textsf{PKE}\) scheme in Fig. 10 is \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) secure under \(\kappa \) bits leakage per user.
Concretely, for any number \(n\) of users and any adversary \(\mathcal {A}\) who makes at most \(Q_e\) times of \({\mathcal {O}_{\textsc {Enc}}}\) queries and \(Q_d\) times of \({\mathcal {O}_{\textsc {Dec}}}\) queries, there exist adversaries \(\mathcal {B}_1, \cdots , \mathcal {B}_7\), such that \(\textbf{T}(\mathcal {B}_1) \approx \cdots \approx \textbf{T}(\mathcal {B}_6) \approx \textbf{T}(\mathcal {A}) + (n+ Q_e+ Q_d) \cdot \textsf{poly}(\lambda )\), with \(\textsf{poly}(\lambda )\) independent of \(\textbf{T}(\mathcal {A})\), and
We refer to Subsect. 2.2 and Fig. 2 therein for an overview of the proof. Due to space limitations, we postpone the formal proof to the full version [19].
7 More Primitives and Instantiations from MDDH
Tightly \( {MU^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) Secure SC, MAC and AE. Our SIG and PKE immediately lead to direct constructions of tightly \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{Priv}{\small { \& }}\textsf{Auth}\) secure SC [3, 9]. By fully exploiting the similar and composable components of our SIG and PKE, we can obtain a more efficient SC construction, which is shown in the full version [19]. Since SIG naturally implies MAC and SC implies AE, we can also obtain the constructions of tightly secure MAC and AE. We also give optimized MAC and AE constructions in the full version [19], where \(\textsf{PVQAHPS}\) is replaced with \(\textsf{QAHPS}\). Our MAC achieves tight strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMVA}\) security, which also considers chosen verification attacks [13] in addition to strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\).
Instantiations from MDDH. We give instantiations of SIG and PKE from the matrix DDH (MDDH) assumptions over asymmetric pairing groups. Our SC, MAC and AE can be similarly instantiated.
Firstly, we instantiate the building blocks needed in our generic constructions (cf. the full version [19]). More precisely, we give concrete instantiations of Publicly-Verifiable QA-HPS (with an overview in Subsect. 2.4) and QA-HPS, built upon the MDDH-based QA-HPS schemes proposed in [20], which are in turn generalizations of the well-known DDH-based HPS scheme proposed by Cramer and Shoup in [11]. Then we instantiate tag-based QA-NIZK with a tag-base variant of the QA-NIZK scheme proposed in [1] that has tight USS based on MDDH, which is recalled in the full version [19] for completeness.
Next we instantiate the generic SIG construction in Sect. 5 with the above building blocks. Let \(x \cdot \mathbb {G}\) denote x elements in \(\mathbb {G}\). Under MDDH parameters \(\ell ,k \in \mathbb {N}\) where \(\ell \ge 2k+1\), the MDDH-based SIG scheme \(\textsf{SIG}_{\textsf{MDDH}}\) has public parameter \(\textsf{pp}_{\textsf{SIG}}: (5 k^2 + 3k + \ell k) \cdot \mathbb {G}_1+ (5 k^2 + 4k + 1 + 2\ell k) \cdot \mathbb {G}_2\), verification key \(vk: (\ell k) \cdot \mathbb {G}_2\), signing key \(sk: \ell (k+1) \cdot \mathbb {Z}_{p}\), and signature \(\sigma : (4 k^2 + 4k + 2 + \ell ) \cdot \mathbb {G}_1+ (2 k^2 + 3k + 1) \cdot \mathbb {G}_2\). By plugging the theorems regarding the tight security of the MDDH-based PV-QA-HPS and QA-NIZK schemes (cf. the full version [19]) into Theorem 1, we have the following corollary showing the tight strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) security of \(\textsf{SIG}_{\textsf{MDDH}}\) based on the MDDH assumptions (as well as the collision-resistance of hash functions).
Corollary 1
(Tight Strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) Security of \(\textsf{SIG}_{\textsf{MDDH}}\)). Let \(\ell \ge 2k+1\) and \(\kappa \le \log p-\varOmega (\lambda )\). For any number \(n\) of users and any adversary \(\mathcal {A}\) who makes at most \(Q_s\) times of \({\mathcal {O}_{\textsc {Sign}}}\) queries, there exist adversaries \(\mathcal {B}_1, \mathcal {B}_2\) and \(\mathcal {B}_3\), such that \(\textbf{T}(\mathcal {B}_1) \approx \textbf{T}(\mathcal {B}_2) \approx \textbf{T}(\mathcal {B}_3) \approx \textbf{T}(\mathcal {A}) + (n+Q_s) \cdot \textsf{poly}(\lambda )\), with \(\textsf{poly}(\lambda )\) independent of \(\textbf{T}(\mathcal {A})\), and
Since \(Q_s= \textsf{poly}(\lambda )\) for PPT adversaries, the security loss is in fact \(O(\log Q_s) =O(\log \lambda )\), which is lower than \(O(\lambda )\). For \(k = 1\) and \(\ell = 3\), we get a fully compact SIG scheme with \(\textsf{pp}_{\textsf{SIG}}: 11 \cdot \mathbb {G}_1+ 16 \cdot \mathbb {G}_2\), \(vk: 3 \cdot \mathbb {G}_2\), \(sk: 6 \cdot \mathbb {Z}_{p}\) and \(\sigma : 13 \cdot \mathbb {G}_1+ 6 \cdot \mathbb {G}_2\). The resulting SIG scheme has tight strong \( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CMA}\) security based on the SXDH assumption (which requires the DDH assumption to hold both in \(\mathbb {G}_1\) and \(\mathbb {G}_2\)), and supports \(\kappa = \log p - \varOmega (\lambda )\) bits leakage per user. The leakage rate (i.e., \(\kappa /\) bit-length of \(sk\)) is \(\frac{\log p - \varOmega (\lambda )}{6\log p} = \frac{1}{6} - o(1)\) asymptotically as p grows.
We also instantiate the generic PKE construction in Sect. 6. Under MDDH parameters \(\ell ,k \in \mathbb {N}\) where \(\ell \ge 2k+1\), the MDDH-based PKE scheme \(\textsf{PKE}_{\textsf{MDDH}}\) has public parameter \(\textsf{pp}_{\textsf{PKE}}: (5 k^2 + 3k + \ell k) \cdot \mathbb {G}_1+ (4 k^2 + 3k + 1 + 2\ell k) \cdot \mathbb {G}_2\), public key \(pk: k \cdot \mathbb {G}_1\), secret key \(sk: \ell \cdot \mathbb {Z}_{p}\), and ciphertext \(c: (4 k^2 + 3k + 2 + \ell ) \cdot \mathbb {G}_1+ (2 k^2 + 3k + 1) \cdot \mathbb {G}_2\). By plugging the theorems regarding the tight security of the MDDH-based QA-HPS and QA-NIZK schemes (cf. the full version [19]) into Theorem 2, we have the following corollary showing the tight \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) security of \(\textsf{PKE}_{\textsf{MDDH}}\) based on the MDDH assumptions (as well as the collision-resistance of hash functions).
Corollary 2
(Tight \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) Security of \(\textsf{PKE}_{\textsf{MDDH}}\)). Let \(\ell \ge 2k+1\) and \(\kappa \le \log p-\varOmega (\lambda )\). For any number \(n\) of users and any adversary \(\mathcal {A}\) who makes at most \(Q_e\) times of \({\mathcal {O}_{\textsc {Enc}}}\) queries and \(Q_d\) times of \({\mathcal {O}_{\textsc {Dec}}}\) queries, there exist adversaries \(\mathcal {B}_1, \mathcal {B}_2\) and \(\mathcal {B}_3\), such that \(\textbf{T}(\mathcal {B}_1) \approx \textbf{T}(\mathcal {B}_2) \approx \textbf{T}(\mathcal {B}_3) \approx \textbf{T}(\mathcal {A}) + (n+Q_e+Q_d) \cdot \textsf{poly}(\lambda )\), with \(\textsf{poly}(\lambda )\) independent of \(\textbf{T}(\mathcal {A})\), and
For \(k = 1\) and \(\ell = 3\), we get a fully compact PKE scheme with \(\textsf{pp}_{\textsf{PKE}}: 11 \cdot \mathbb {G}_1+ 14 \cdot \mathbb {G}_2\), \(pk: 1 \cdot \mathbb {G}_1\), \(sk: 3 \cdot \mathbb {Z}_{p}\) and \(c: 12 \cdot \mathbb {G}_1+ 6 \cdot \mathbb {G}_2\). The resulting PKE scheme has tight \( {\textsf{MUMC}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\text {-}\textsf{CCA}\) security based on the SXDH assumption, and supports \(\kappa = \log p - \varOmega (\lambda )\) bits leakage per user. The leakage rate is \(\frac{\log p - \varOmega (\lambda )}{3\log p} = \frac{1}{3} - o(1)\) asymptotically as p grows.
For an overview, we refer to Table 1 and Table 2 in the introduction.
On Tightness of our MDDH-Based Schemes. Our MDDH-based schemes are the first ones achieving almost tight \({\textsf{MU}^{\textsf{c}}}\)/\( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security in the standard model, and the security loss factor is \(O(\log \lambda )\).
We stress that all our generic constructions are fully tightness-preserving, i.e., the \({\textsf{MU}^{\textsf{c}}}\)/\( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) securities of the resulting SIG, PKE, SC, MAC, AE schemes are tightly reduced to the security properties of the building blocks PV-QA-HPS, QA-HPS and tag-based QA-NIZK, with constant security loss factors. Moreover, our instantiations of PV-QA-HPS and QA-HPS have fully tight securities, and only the tag-based QA-NIZK instantiation has security loss factor \(O(\log \lambda )\). Therefore, our fully tightness-preserving generic constructions leave spaces for even tighter (fully tight) \({\textsf{MU}^{\textsf{c}}}\)/\( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security, as long as we can find instantiations of tag-based QA-NIZK with tighter security.
On Efficiency of Our MDDH-Based Schemes. Note that all our schemes enjoy full compactness (i.e., all the parameters, keys, signatures and ciphertexts consist of only a constant number of group elements). We believe our fully compact schemes are good starts for almost tight \({\textsf{MU}^{\textsf{c}}}\)/\( {\textsf{MU}^{\textsf{c}{\tiny { \& }}\textsf{l}}}\) security in the standard model and follow-up work might improve efficiency even further.
Notes
- 1.
Strictly speaking, the loss factor is defined as \(\ell := (\epsilon _{\mathcal {A}}/\epsilon _{\mathcal {B}}) \cdot (\textbf{T}(\mathcal {B})/\textbf{T}(\mathcal {A}))\), where \(\textbf{T}(\mathcal {A})\) and \(\textbf{T}(\mathcal {B})\) denote the running time of \(\mathcal {A}\) and \(\mathcal {B}\), respectively. For reductions where \(\textbf{T}(\mathcal {A})\) and \(\textbf{T}(\mathcal {B})\) are approximately the same (as in many related works and also in this work), the loss factor can be simplified to \(\epsilon _{\mathcal {A}}/\epsilon _{\mathcal {B}}\).
- 2.
For primitives like PKE, SC, AE, we also consider Multi-User Multi-Challenge security under corruptions to capture multiple challenge ciphertexts, denoted by \({\textsf{MUMC}^{\textsf{c}}}\).
- 3.
This means that \(\textsf{PVQAHPS}\) works correctly both for \(x \in \mathcal {L}_\rho \) with \(pk= \alpha _\rho (sk)\) and \(x \in \mathcal {L}_{\rho _0}\) with \(pk= \alpha _{\rho _0}(sk)\).
- 4.
Here \(\rho \) is part of the public parameters of SIG and is chosen from the language collection \(\mathscr {L}\) by the setup algorithm of SIG, while w is a witness for \(x \in \mathcal {L}_\rho \) and is picked along with
 by the signing algorithm of SIG.
by the signing algorithm of SIG.
References
Abe, M., Jutla, C.S., Ohkubo, M., Pan, J., Roy, A., Wang, Y.: Shorter QA-NIZK and SPS with tighter security. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019. LNCS, vol. 11923, pp. 669–699. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34618-8_23
Akavia, A., Goldwasser, S., Vaikuntanathan, V.: Simultaneous hardcore bits and cryptography against memory attacks. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 474–495. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_28
An, J.H., Dodis, Y., Rabin, T.: On the security of joint signature and encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 83–107. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_6
Bader, C., Hofheinz, D., Jager, T., Kiltz, E., Li, Y.: Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_26
Bader, C., Jager, T., Li, Y., Schäge, S.: On the impossibility of tight cryptographic reductions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 273–304. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_10
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_41
Bellare, M., Rogaway, P.: Entity authentication and key distribution. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 232–249. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_21
Bellare, M., Stepanovs, I.: Security under message-derived keys: signcryption in iMessage. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 507–537. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_17
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Diemert, D., Gellert, K., Jager, T., Lyu, L.: More efficient digital signatures with tight multi-user security. In: Garay, J.A. (ed.) PKC 2021. LNCS, vol. 12711, pp. 1–31. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-75248-4_1
Dodis, Y., Kiltz, E., Pietrzak, K., Wichs, D.: Message authentication, revisited. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 355–374. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_22
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_1
Gay, R., Hofheinz, D., Kohl, L.: Kurosawa-Desmedt meets tight security. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 133–160. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_5
Gjøsteen, K., Jager, T.: Practical and tightly-secure digital signatures and authenticated key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 95–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_4
Han, S., et al.: Authenticated key exchange and signatures with tight security in the standard model. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12828, pp. 670–700. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84259-8_23
Han, S., Liu, S., Gu, D.: Almost tight multi-user security under adaptive corruptions & leakages in the standard model. Cryptology ePrint Archive, Report 2023/153. https://eprint.iacr.org/2023/153
Han, S., Liu, S., Lyu, L., Gu, D.: Tight leakage-resilient CCA-security from quasi-adaptive hash proof system. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 417–447. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_15. https://eprint.iacr.org/2019/512
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Hofheinz, D., Jia, D., Pan, J.: Identity-based encryption tightly secure under chosen-ciphertext attacks. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11273, pp. 190–220. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_7
Jager, T., Stam, M., Stanley-Oakes, R., Warinschi, B.: Multi-key authenticated encryption with corruptions: reductions are lossy. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 409–441. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_14
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_1
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_4
Langrehr, R., Pan, J.: Tightly secure hierarchical identity-based encryption. In: Lin, D., Sako, K. (eds.) PKC 2019. LNCS, vol. 11442, pp. 436–465. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17253-4_15
Lee, Y., Lee, D.H., Park, J.H.: Tightly CCA-secure encryption scheme in a multi-user setting with corruptions. Des. Codes Crypt. 88(11), 2433–2452 (2020). https://doi.org/10.1007/s10623-020-00794-z
Liu, X., Liu, S., Gu, D.: Tightly secure chameleon hash functions in the multi-user setting and their applications. In: Liu, J.K., Cui, H. (eds.) ACISP 2020. LNCS, vol. 12248, pp. 664–673. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-55304-3_36. https://eprint.iacr.org/2022/1258
Liu, X., Liu, S., Gu, D., Weng, J.: Two-pass authenticated key exchange with explicit authentication and tight security. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12492, pp. 785–814. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64834-3_27
Morgan, A., Pass, R., Shi, E.: On the adaptive security of MACs and PRFs. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12491, pp. 724–753. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64837-4_24
Morillo, P., Ràfols, C., Villar, J.L.: The kernel matrix Diffie-Hellman assumption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 729–758. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_27
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 18–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_2
Pan, J., Wagner, B.: Lattice-based signatures with tight adaptive corruptions and more. In: Hanaoka, G., Shikata, J., Watanabe, Y. (eds.) PKC 2022. LNCS, vol. 13178, pp. 347–378. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-97131-1_12
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: FOCS 1999, pp. 543–553 (1999)
Steinfeld, R., Pieprzyk, J., Wang, H.: How to strengthen any weakly unforgeable signature into a strongly unforgeable signature. In: Abe, M. (ed.) CT-RSA 2007. LNCS, vol. 4377, pp. 357–371. Springer, Heidelberg (2006). https://doi.org/10.1007/11967668_23
Acknowledgment
We would like to thank the reviewers for their helpful comments and valuable suggestions. Shuai Han and Shengli Liu were partially supported by National Natural Science Foundation of China (Grant Nos. 62002223, 61925207), Guangdong Major Project of Basic and Applied Basic Research (2019B030302008), the National Key R &D Program of China under Grant 2022YFB2701500, Shanghai Sailing Program (20YF1421100), Young Elite Scientists Sponsorship Program by China Association for Science and Technology (YESS20200185), and Ant Group through CCF-Ant Research Fund (CCF-AFSG RF20220224). Dawu Gu was partially supported by the National Key R &D Program of China under Grant 2020YFA0712302.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Han, S., Liu, S., Gu, D. (2023). Almost Tight Multi-user Security Under Adaptive Corruptions & Leakages in the Standard Model. In: Hazay, C., Stam, M. (eds) Advances in Cryptology – EUROCRYPT 2023. EUROCRYPT 2023. Lecture Notes in Computer Science, vol 14006. Springer, Cham. https://doi.org/10.1007/978-3-031-30620-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-30620-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30619-8
Online ISBN: 978-3-031-30620-4
eBook Packages: Computer ScienceComputer Science (R0)





 to
to  .
.
 and
and  , where
, where 
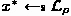 to
to  .
.

 : The setup algorithm outputs a public parameter
: The setup algorithm outputs a public parameter  uniformly and sampling
uniformly and sampling  uniformly. We require
uniformly. We require  : The setup algorithm outputs a public parameter
: The setup algorithm outputs a public parameter  : Taking as input a language parameter
: Taking as input a language parameter  : Taking as input
: Taking as input  : Taking as input
: Taking as input 

 : It outputs a public parameter
: It outputs a public parameter 





 by the signing algorithm of SIG.
by the signing algorithm of SIG.