Keywords

1 Introduction

Otto Fischer is the inventor of 3-D human gait analysis, for which he developed theory in the late 19th century [2, 4]. His method of principal vectors allows to analyze the dynamics of a system of rigid bodies in an insightful way and, especially important at that time, by hand calculations as computers were yet to be invented [1]. After recording the movements of (parts of) a person in motion, e.g. by photographs at multiple time steps, with the principal vectors he could graphically derive the motion of the common center of mass (CoM) and the motions of body segments relative to the common CoM. Subsequently from the kinetic energy and the equations of motion, both written in a special insightful form due to the principal vectors, he could calculate the acting forces onto and within the system separately. With this inverse dynamical analysis he was able to ultimately derive the individual muscle forces responsible for the motions.

His theory has not found much application in gait analysis by others, perhaps since it is still cumbersome to apply and computers took over or since it is written in a challenging way in older German. However for machine design the method of principal vectors has turned out especially interesting for shaking force balancing as a clear graphical tool for both analysis and synthesis [5]. The principal vectors are at the basis of the synthesis method of inherent balancing [7].

Fischer applied his theory mainly in its planar form for which the approach to project 3-D gait motions onto the three orthogonal planes for individual analysis turned out an accurate approximation for 3-D gait analysis, keeping the calculations relatively simple. However to study general human motions apart from gait analysis such as motions of the arms about the shoulders, he considered the spatial theory to be necessary, which he presented for a serial two-link chain in [3, 4] but unfortunately never applied.

This paper presents Fischer’s spatial theory of principal vectors for dynamical analysis in a modern and understandable way. Fischer’s challenging original texts and explanations in older German in [3] have been transformed into a modern presentation that can be readily used for application. This can be of significant interest for general system dynamics [6] and in specific for spatial balancing. First the kinematics of a serial chain of two links are presented, followed by the kinetic energy equations, the reduced mass models, and the equations of motion at the end for both an unconstrained motion and motion about a fixed base joint.

2 The Kinematics

Fig. 1.
figure 1

(a) Spatially moving chain of two links connected with a spherical joint in \(A_1\) and its geometry of principal vectors describing the location of the common CoM in S; (b) Spatial pantograph geometry with the principal points \(P_1\) and \(P_2\) and the principal dimensions \(a_1\) and \(a_2\).

Full size image

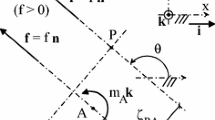
Fischer explained his spatial theory by use of a serial chain of two links [3] (pg. 305) as shown in a new way in Fig. 1a with two rectangular bars connected with a spherical joint in \(A_1\). The origin of the fixed reference frame \(x_0y_0z_0\) is located in the extremity of link 1 \(A_0\) and each link i has a center of mass (CoM) in point \(S_i\), which is on the longitudinal axis of each link. The common CoM of the two links is located in S and is geometrically found by a parallelogram based on the principal vectors. Figure 1b shows this geometry which is a spatially moving pantograph of which \(P_1\) and \(P_2\) are the principal points which define a parallelogram in the plane through S, \(P_1\), \(A_1\), and \(P_2\) with principal dimensions \(a_1\) and \(a_2\). The conditions for which the common CoM of \(S_1\) and \(S_2\) is in S for all motions can be found as \(m_1p_1=m_2a_1\) and \(m_2p_2=m_1a_2\).

The spatial orientations of each link in Fig. 1a, each having a body fixed reference frame \(x_iy_iz_i\) with origin in \(P_i\), are defined with angles \(\theta _i\), \(\varphi _i\), and \(\psi _i\) as illustrated, which are all defined positively in the negative rotational direction. Angles \(\theta _i\) and \(\varphi _i\) define the orientation of the longitudinal axis of each link relative to the \(z_0\)-axis and the \(y_0\)-axis, respectively, where \(\varphi _i\) defines the rotation of the vertical planes and and \(\theta _i\) defines the orientation of the links within each of the two planes. The line of intersection of these two planes intersects with the joint in \(A_1\) and plane also intersects with the \(z_0\)-axis. Angle \(\psi _i\) defines the rotation of each link about its longitudinal axis relative to the illustrated line that is normal to the longitudinal link axis and lays within the respective plane or . The spatial orientation of the plane of parallelogram \(SP_1A_1P_2\) depends on all the six angles.

This spatial two-link chain with a ball joint connection can be considered the most general two-link model with maximal mobility, which might be reduced for applications that require lower mobility. For the kinetic energy equations and the equations of motion Fischer considered two cases of this model: (1) the case that the two-link chain is moving freely in space and (2) the case that point \(A_0\) is a spherical base joint and the motion of the two-link chain is constrained. The second case would represent for instance the motion of the upper and lower arm with the shoulder joint in a fixed point.

The positions of the link CoMs can be written in a special way relative to the common CoM in S as the sum of the principal vectors from the common CoM to each link CoM as

$$\begin{aligned} \overline{r}_1= & {} \overline{SP_1}+\overline{P_1S_1}=-a_2\left[ \begin{array}{c} \sin \theta _2\sin \varphi _2 \\ \sin \theta _2\cos \varphi _2 \\ \cos \theta _2 \end{array}\right] -p_1\left[ \begin{array}{c} \sin \theta _1\sin \varphi _1 \\ \sin \theta _1\cos \varphi _1 \\ \cos \theta _1 \end{array}\right] \end{aligned}$$
(1)
$$\begin{aligned} \overline{r}_2= & {} \overline{SP_2}+\overline{P_2S_2}=a_1\left[ \begin{array}{c} \sin \theta _1\sin \varphi _1 \\ \sin \theta _1\cos \varphi _1 \\ \cos \theta _1 \end{array}\right] +p_2\left[ \begin{array}{c} \sin \theta _2\sin \varphi _2 \\ \sin \theta _2\cos \varphi _2 \\ \cos \theta _2 \end{array}\right] \end{aligned}$$
(2)

from which the velocities of \(S_1\) and \(S_2\) relative to the common CoM in S can be derived as

$$\begin{aligned} \upsilon _1= & {} \dot{\overline{r}}_1=-a_2\left[ \begin{array}{c} c\theta _2\dot{\theta }_2s\varphi _2+s\theta _2c\varphi _2\dot{\varphi }_2 \\ c\theta _2\dot{\theta }_2c\varphi _2-s\theta _2s\varphi _2\dot{\varphi }_2 \\ -s\theta _2\dot{\theta }_2 \end{array}\right] - p_1\left[ \begin{array}{c} c\theta _1\dot{\theta }_1s\varphi _1+s\theta _1c\varphi _1\dot{\varphi }_1 \\ c\theta _1\dot{\theta }_1c\varphi _1-s\theta _1s\varphi _1\dot{\varphi }_1 \\ -s\theta _1\dot{\theta }_1 \end{array}\right] \end{aligned}$$
(3)
$$\begin{aligned} \upsilon _2= & {} \dot{\overline{r}}_2=a_1\left[ \begin{array}{c} c\theta _1\dot{\theta }_1s\varphi _1+s\theta _1c\varphi _1\dot{\varphi }_1 \\ c\theta _1\dot{\theta }_1c\varphi _1-s\theta _1s\varphi _1\dot{\varphi }_1 \\ -s\theta _1\dot{\theta }_1 \end{array}\right] + p_2\left[ \begin{array}{c} c\theta _2\dot{\theta }_2s\varphi _2+s\theta _2c\varphi _2\dot{\varphi }_2 \\ c\theta _2\dot{\theta }_2c\varphi _2-s\theta _2s\varphi _2\dot{\varphi }_2 \\ -s\theta _2\dot{\theta }_2 \end{array}\right] \end{aligned}$$
(4)

with s and c representing the \(\sin \) and \(\cos \), respectively.

Fig. 2.
figure 2

Angular velocities of each link, all defined positively in the negative directions.

Full size image

Figure 2 shows the angular velocities \(\omega _{ix}\), \(\omega _{iy}\), and \(\omega _{iz}\) of each link about the principal inertial axes \(x^\prime _i\), \(y^\prime _i\), and \(z^\prime _i\), which are equal to the link rotations about the body fixed reference frame \(x_iy_iz_i\) located in the principal point \(P_i\) since both reference frames are parallel. The angular velocities can be obtained as

$$\begin{aligned} \left[ \begin{array}{c} \omega _{ix} \\ \omega _{iy} \\ \omega _{iz} \end{array}\right] =\left[ \begin{array}{ccc} \cos \psi _i&{} \sin \psi _i &{} 0\\ \sin \psi _i&{} -\cos \psi _i &{} 0\\ 0 &{}0 &{} 1 \end{array}\right] \left[ \begin{array}{ccc} 1&{} 0 &{} 0\\ 0&{} \sin \theta _i &{} 0\\ 0 &{}\cos \theta _i &{} 1 \end{array}\right] \left[ \begin{array}{c} \dot{\theta }_i \\ \dot{\varphi }_i \\ \dot{\psi }_i \end{array}\right] \end{aligned}$$
(5)

This is a mapping of the absolute link rotations to the relative rotations of the links which can be rewritten for each link as

$$\begin{aligned} \omega _{1x}= & {} \dot{\theta }_1\cos \psi _1+\dot{\varphi }_1\sin \theta _1\sin \psi _1 \quad \omega _{2x}=\dot{\theta }_2\cos \psi _2+\dot{\varphi }_2\sin \theta _2\sin \psi _2\nonumber \\ \omega _{1y}= & {} \dot{\theta }_1\sin \psi _1-\dot{\varphi }_1\sin \theta _1\cos \psi _1 \quad \omega _{2y}=\dot{\theta }_2\sin \psi _2-\dot{\varphi }_2\sin \theta _2\cos \psi _2 \\ \omega _{1z}= & {} \dot{\varphi }_1\cos \theta _1+\dot{\psi }_1 \qquad \quad \quad \quad \quad \omega _{2z}=\dot{\varphi }_2\cos \theta _2+\dot{\psi }_2 \nonumber \end{aligned}$$
(6)

3 The Kinetic Energy

The kinetic energy T of the two-link chain can be written as

$$\begin{aligned} T= & {} T_S+T_{rel}+T_{rot} \end{aligned}$$
(7)

where \(T_S\) is the kinetic energy of the two-link chain translating as a single rigid body in space, \(T_{rel}\) is the kinetic energy of the link masses in \(S_1\) and \(S_2\) moving relative to the common CoM in S, and \(T_{rot}\) is the kinetic energy of the rotations of the two links. As compared to \(T_{rot}\), \(T_S+T_{rel}=T_{trans}\) can be regarded the translational kinetic energy with the absolute and the relative kinetic energy separately calculated as, respectively,

$$\begin{aligned} T_S= & {} \frac{m_{tot}}{2}\upsilon _S^2, \quad T_{rel}=\frac{m_1}{2}\upsilon _1^2+\frac{m_2}{2}\upsilon _2^2 \end{aligned}$$
(8)

with the total mass \(m_{tot}=m_1+m_2\). The rotational kinetic energy can be obtained as

$$\begin{aligned} T_{rot}=\frac{1}{2}(I_{1x}\omega _{1x}^2+I_{1y}\omega _{1y}^2+I_{1z}\omega _{1z}^2)+\frac{1}{2}(I_{2x}\omega _{2x}^2+I_{2y}\omega _{2y}^2+I_{2z}\omega _{2z}^2) \end{aligned}$$
(9)

with the inertia tensor \(I_i=[I_{ix}, I_{iy}, I_{iz}]\) of each link about its CoM in \(S_i\).

For \(T_{rel}\) the squared velocities of the link masses are calculated as \(\upsilon _i^2=\upsilon _{ix}^2+\upsilon _{iy}^2+\upsilon _{iz}^2\) which from (3) and (4) can be derived as

$$\begin{aligned} \upsilon _1^2= & {} p_1^2\dot{\theta }_1^2+p_1^2\sin ^2\theta _1\dot{\varphi }_1^2+a_2^2\dot{\theta }_2^2+a_2^2\sin ^2\theta _2\dot{\varphi }_2^2+\\{} & {} 2a_2p_1(\sin \theta _1\sin \theta _2+\cos \theta _1\cos \theta _2\cos (\varphi _2-\varphi _1))\dot{\theta }_1\dot{\theta }_2-\nonumber \\{} & {} 2a_2p_1\cos \theta _1\sin \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_1\dot{\varphi }_2+\nonumber \\{} & {} 2a_2p_1\sin \theta _1\cos \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_2\dot{\varphi }_1+\nonumber \\{} & {} 2a_2p_1\sin \theta _1\sin \theta _2\cos (\varphi _2-\varphi _1)\dot{\varphi }_1\dot{\varphi }_2\nonumber \end{aligned}$$
(10)
$$\begin{aligned} \upsilon _2^2= & {} p_2^2\dot{\theta }_2^2+p_2^2\sin ^2\theta _2\dot{\varphi }_2^2+a_1^2\dot{\theta }_1^2+a_1^2\sin ^2\theta _1\dot{\varphi }_1^2+\\{} & {} 2a_1p_2(\sin \theta _1\sin \theta _2+\cos \theta _1\cos \theta _2\cos (\varphi _2-\varphi _1))\dot{\theta }_1\dot{\theta }_2-\nonumber \\{} & {} 2a_1p_2\cos \theta _1\sin \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_1\dot{\varphi }_2+\nonumber \\{} & {} 2a_1p_2\sin \theta _1\cos \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_2\dot{\varphi }_1+\nonumber \\{} & {} 2a_1p_2\sin \theta _1\sin \theta _2\cos (\varphi _2-\varphi _1)\dot{\varphi }_1\dot{\varphi }_2\nonumber \end{aligned}$$
(11)

These terms are very similar with only all the indices 1 and 2 reversed. Combining both terms and substituting also the balance conditions \(m_1p_1=m_2a_1\) and \(m_2p_2=m_1a_2\) for \(m_1p_1\) and \(m_2p_2\), \(T_{rel}\) can be rewritten as

$$\begin{aligned} T_{rel}= & {} (\frac{m_1}{2}p_1^2+\frac{m_2}{2}a_1^2)\dot{\theta }_1^2+(\frac{m_1}{2}a_2^2+\frac{m_2}{2}p_2^2)\dot{\theta }_2^2+\\{} & {} (\frac{m_1}{2}p_1^2+\frac{m_2}{2}a_1^2)\sin ^2\theta _1\dot{\varphi }_1^2+(\frac{m_1}{2}a_2^2+\frac{m_2}{2}p_2^2)\sin ^2\theta _2\dot{\varphi }_2^2+\nonumber \\{} & {} m_{tot}a_1a_2(\sin \theta _1\sin \theta _2+\cos \theta _1\cos \theta _2\cos (\varphi _2-\varphi _1))\dot{\theta }_1\dot{\theta }_2-\nonumber \\{} & {} m_{tot}a_1a_2\cos \theta _1\sin \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_1\dot{\varphi }_2+\nonumber \\{} & {} m_{tot}a_1a_2\sin \theta _1\cos \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_2\dot{\varphi }_1+\nonumber \\{} & {} m_{tot}a_1a_2\sin \theta _1\sin \theta _2\cos (\varphi _2-\varphi _1)\dot{\varphi }_1\dot{\varphi }_2\nonumber \end{aligned}$$
(12)

For the rotational kinetic energy the squared rotational velocities of each link i are obtained from (6) as

$$\begin{aligned} \omega _{ix}^2= & {} \cos ^2\psi _i\dot{\theta }_i^2+\sin ^2\theta _i\sin ^2\psi _i\dot{\varphi }_i^2+2\cos \psi _i\sin \theta _i\sin \psi _i\dot{\theta }_i\dot{\varphi }_i\\ \omega _{iy}^2= & {} \sin ^2\psi _i\dot{\theta }_i^2+\sin ^2\theta _i\cos ^2\psi _i\dot{\varphi }_i^2-2\sin \psi _i\sin \theta _i\cos \psi _i\dot{\theta }_i\dot{\varphi }_i\\ \omega _{iz}^2= & {} \cos ^2\theta _i\dot{\varphi }_i^2+\dot{\psi }_i^2+2\cos \theta _i\dot{\varphi }_i\dot{\psi }_i \end{aligned}$$

with which the rotational kinetic energy can be derived and written as

$$\begin{aligned} T_{rot}= & {} \frac{1}{2}(I_{1x}\cos ^2\psi _1+I_{1y}\sin ^2\psi _1)\dot{\theta }_1^2+\frac{1}{2}(I_{2x}\cos ^2\psi _2+I_{2y}\sin ^2\psi _2)\dot{\theta }_2^2+\\{} & {} \frac{1}{2}(I_{1x}\sin ^2\theta _1\sin ^2\psi _1+I_{1y}\sin ^2\theta _1\cos ^2\psi _1+I_{1z}\cos ^2\theta _1)\dot{\varphi }_1^2+\nonumber \\ {}{} & {} \frac{1}{2}(I_{2x}\sin ^2\theta _2\sin ^2\psi _2+I_{2y}\sin ^2\theta _2\cos ^2\psi _2+I_{2z}\cos ^2\theta _2)\dot{\varphi }_2^2+\nonumber \\{} & {} \frac{1}{2}I_{1z}\dot{\psi }_1^2+\frac{1}{2}I_{2z}\dot{\psi }_2^2+\nonumber \\{} & {} (I_{1x}-I_{1y})\sin \theta _1\sin \psi _1\cos \psi _1\dot{\theta }_1\dot{\varphi }_1+\nonumber \\{} & {} (I_{2x}-I_{2y})\sin \theta _2\sin \psi _2\cos \psi _2\dot{\theta }_2\dot{\varphi }_2+\nonumber \\{} & {} I_{1z}\cos \theta _1\dot{\varphi }_1\dot{\psi }_1+I_{2z}\cos \theta _2\dot{\varphi }_2\dot{\psi }_2\nonumber \end{aligned}$$
(13)

When summed together, the complete kinetic energy of the two-link chain (7) can now be written as

$$\begin{aligned} T= & {} \frac{m_{tot}}{2}\upsilon _S^2+\frac{1}{2}(I_{1x}\cos ^2\psi _1+I_{1y}\sin ^2\psi _1+m_1p_1^2+m_2a_1^2)\dot{\theta }_1^2+\\ {}{} & {} \frac{1}{2}(I_{2x}\cos ^2\psi _2+I_{2y}\sin ^2\psi _2+m_1a_2^2+m_2p_2^2)\dot{\theta }_2^2+\nonumber \\{} & {} \frac{1}{2}(I_{1x}\sin ^2\theta _1\sin ^2\psi _1+I_{1y}\sin ^2\theta _1\cos ^2\psi _1+I_{1z}\cos ^2\theta _1+(m_1p_1^2+m_2a_1^2)\sin ^2\theta _1)\dot{\varphi }_1^2+\nonumber \\ {}{} & {} \frac{1}{2}(I_{2x}\sin ^2\theta _2\sin ^2\psi _2+I_{2y}\sin ^2\theta _2\cos ^2\psi _2+I_{2z}\cos ^2\theta _2+(m_1a_2^2+m_2p_2^2)\sin ^2\theta _2)\dot{\varphi }_2^2+\nonumber \\{} & {} \frac{1}{2}I_{1z}\dot{\psi }_1^2+\frac{1}{2}I_{2z}\dot{\psi }_2^2+\nonumber \\{} & {} (I_{1x}-I_{1y})\sin \theta _1\sin \psi _1\cos \psi _1\dot{\theta }_1\dot{\varphi }_1+\nonumber \\{} & {} (I_{2x}-I_{2y})\sin \theta _2\sin \psi _2\cos \psi _2\dot{\theta }_2\dot{\varphi }_2+\nonumber \\{} & {} I_{1z}\cos \theta _1\dot{\varphi }_1\dot{\psi }_1+I_{2z}\cos \theta _2\dot{\varphi }_2\dot{\psi }_2+\nonumber \\{} & {} m_{tot}a_1a_2(\sin \theta _1\sin \theta _2+\cos \theta _1\cos \theta _2\cos (\varphi _2-\varphi _1))\dot{\theta }_1\dot{\theta }_2-\nonumber \\{} & {} m_{tot}a_1a_2\cos \theta _1\sin \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_1\dot{\varphi }_2+\nonumber \\{} & {} m_{tot}a_1a_2\sin \theta _1\cos \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_2\dot{\varphi }_1+\nonumber \\{} & {} m_{tot}a_1a_2\sin \theta _1\sin \theta _2\cos (\varphi _2-\varphi _1)\dot{\varphi }_1\dot{\varphi }_2\nonumber \end{aligned}$$
(14)

This formulation can be significantly simplified in a particular way when the expressions before \(\dot{\theta }_i^2\) are rewritten as

$$\begin{aligned}{} & {} I_{1x}\cos ^2\psi _1+I_{1y}\sin ^2\psi _1+m_1p_1^2+m_2a_1^2=m_{tot}(\chi _{1x}^2\cos ^2\psi _1+\chi _{1y}^2\sin ^2\psi _1)\\ {}{} & {} I_{2x}\cos ^2\psi _2+I_{2y}\sin ^2\psi _2+m_1a_2^2+m_2p_2^2=m_{tot}(\chi _{2x}^2\cos ^2\psi _2+\chi _{2y}^2\sin ^2\psi _2) \end{aligned}$$

with the reduced inertias \(I_{Ri}\) formulated as

$$\begin{aligned} m_{tot}\chi _{1x}^2= & {} I_{1x}+m_1p_1^2+m_2a_1^2=I_{R1x} \quad m_{tot}\chi _{2x}^2=I_{2x}+m_1a_2^2+m_2p_2^2=I_{R2x}\nonumber \\ m_{tot}\chi _{1y}^2= & {} I_{1y}+m_1p_1^2+m_2a_1^2=I_{R1y} \quad m_{tot}\chi _{2y}^2=I_{2y}+m_1a_2^2+m_2p_2^2=I_{R2y}\nonumber \\ m_{tot}\chi _{1z}^2= & {} I_{1z}=I_{R1z} \qquad \qquad \quad \quad \qquad m_{tot}\chi _{2z}^2=I_{2z}=I_{R2z} \end{aligned}$$
(15)

These reduced inertias can be explained geometrically as the inertias of the reduced mass models shown in Fig. 3. In the model of link 1 the principal point \(P_1\) is the common CoM of mass \(m_1\) in \(S_1\) and mass \(m_2\) projected in joint \(A_1\), while in the model of link 2 the principal point \(P_2\) is the common CoM of mass \(m_2\) in \(S_2\) and mass \(m_1\) projected in joint \(A_1\). The inertias of these models about \(P_i\), consisting of the inertia of the two masses \(m_1\) and \(m_2\) at their distance from \(P_i\) and the inertia tensors of the links, then result in the reduced inertia terms. The coefficients \(\chi _{i}\) can be regarded as the radii of gyration of these reduced mass models.

Fig. 3.
figure 3

Reduced mass model of (a) link 2 and (b) link 1 of which the common CoM is in the principal point \(P_i\). The inertias of these models about the principal point result in the reduced inertias terms.

Full size image

Also the expressions before \(\dot{\varphi }_i^2\) can be simplified and rewritten as

$$\begin{aligned}{} & {} I_{1x}\sin ^2\theta _1\sin ^2\psi _1+I_{1y}\sin ^2\theta _1\cos ^2\psi _1+I_{1z}\cos ^2\theta _1+(m_1p_1^2+m_2a_1^2)\sin ^2\theta _1=\\{} & {} \qquad m_{tot}((\chi _{1x}^2\sin ^2\psi _1+\chi _{1y}^2\cos ^2\psi _1)\sin ^2\theta _1+\chi _{1z}^2\cos ^2\theta _1)\\ {}{} & {} I_{2x}\sin ^2\theta _2\sin ^2\psi _2+I_{2y}\sin ^2\theta _2\cos ^2\psi _2+I_{2z}\cos ^2\theta _2+(m_1a_2^2+m_2p_2^2)\sin ^2\theta _2=\\ {}{} & {} \qquad m_{tot}((\chi _{2x}^2\sin ^2\psi _2+\chi _{2y}^2\cos ^2\psi _2)\sin ^2\theta _2+\chi _{2z}^2\cos ^2\theta _2) \end{aligned}$$

and

$$\begin{aligned} I_{1x}-I_{1y}= & {} m_{tot}(\chi _{1x}^2-\chi _{1y}^2) \quad I_{2x}-I_{2y}=m_{tot}(\chi _{2x}^2-\chi _{2y}^2) \end{aligned}$$
(16)

With the reduced inertias substituted, the kinetic energy of the two-link chain moving freely in space can be written in its final form as

$$\begin{aligned} T= & {} \frac{m_{tot}}{2}\upsilon _S^2+\frac{m_{tot}}{2}(\chi _{1x}^2\cos ^2\psi _1+\chi _{1y}^2\sin ^2\psi _1)\dot{\theta }_1^2+\\ {}{} & {} \frac{m_{tot}}{2}(\chi _{2x}^2\cos ^2\psi _2+\chi _{2y}^2\sin ^2\psi _2)\dot{\theta }_2^2+\nonumber \\{} & {} \frac{m_{tot}}{2}((\chi _{1x}^2\sin ^2\psi _1+\chi _{1y}^2\cos ^2\psi _1)\sin ^2\theta _1+\chi _{1z}^2\cos ^2\theta _1)\dot{\varphi }_1^2+\nonumber \\ {}{} & {} \frac{m_{tot}}{2}((\chi _{2x}^2\sin ^2\psi _2+\chi _{2y}^2\cos ^2\psi _2)\sin ^2\theta _2+\chi _{2z}^2\cos ^2\theta _2)\dot{\varphi }_2^2+\nonumber \\{} & {} \frac{m_{tot}}{2}\chi _{1z}^2\dot{\psi }_1^2+\frac{m_{tot}}{2}\chi _{2z}^2\dot{\psi }_2^2+\nonumber \\{} & {} m_{tot}(\chi _{1x}^2-\chi _{1y}^2)\sin \theta _1\sin \psi _1\cos \psi _1\dot{\theta }_1\dot{\varphi }_1+\nonumber \\{} & {} m_{tot}(\chi _{2x}^2-\chi _{2y}^2)\sin \theta _2\sin \psi _2\cos \psi _2\dot{\theta }_2\dot{\varphi }_2+\nonumber \\{} & {} m_{tot}\chi _{1z}^2\cos \theta _1\dot{\varphi }_1\dot{\psi }_1+m_{tot}\chi _{2z}^2\cos \theta _2\dot{\varphi }_2\dot{\psi }_2+\nonumber \\{} & {} m_{tot}a_1a_2(\sin \theta _1\sin \theta _2+\cos \theta _1\cos \theta _2\cos (\varphi _2-\varphi _1))\dot{\theta }_1\dot{\theta }_2-\nonumber \\{} & {} m_{tot}a_1a_2\cos \theta _1\sin \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_1\dot{\varphi }_2+\nonumber \\{} & {} m_{tot}a_1a_2\sin \theta _1\cos \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_2\dot{\varphi }_1+\nonumber \\{} & {} m_{tot}a_1a_2\sin \theta _1\sin \theta _2\cos (\varphi _2-\varphi _1)\dot{\varphi }_1\dot{\varphi }_2\nonumber \end{aligned}$$
(17)

It is remarkable that this formulation is solely based on the total mass, the two principal dimensions, and the reduced inertias, in an elegant and compact form.

The kinetic energy of the two-link chain for the second case when it would have a spherical base joint in \(A_0\), for which \(A_0\) has no translational motions, can be easily derived from the kinetic energy of the free moving system. The only differences are a modification of the reduced inertias according

$$\begin{aligned} \chi _{1x,o}^2= & {} \chi _{1x}^2+a_1^{\prime 2} \qquad \quad \chi _{2x,o}^2=\chi _{2x}^2+a_2^2\nonumber \\ \chi _{1y,o}^2= & {} \chi _{1y}^2+a_1^{\prime 2} \qquad \quad \chi _{2y,o}^2=\chi _{2y}^2+a_2^2 \\ \chi _{1z,o}^2= & {} \chi _{1z}^2 \qquad \qquad \quad \quad \chi _{2z,o}^2=\chi _{2z}^2\nonumber \end{aligned}$$
(18)

with \(a^\prime _1\) the distance between \(P_1\) and \(A_0\) as illustrated in Fig. 1b and with \(a_1\) substituted with \(l_1=a_1+a^\prime _1\) which is the length of link 1. This means that the reduced inertia of the reduced mass model of the first link in Fig. 3b is calculated about joint \(A_0\) and that the reduced inertia of the reduced mass model of the second link is calculated about joint \(A_1\). With these changes the kinetic energy of the two links rotating about \(A_0\) is written as

$$\begin{aligned} T_{A_0}= & {} \frac{m_{tot}}{2}(\chi _{1x,o}^2\cos ^2\psi _1+\chi _{1y,o}^2\sin ^2\psi _1)\dot{\theta }_1^2+\\ {}{} & {} \frac{m_{tot}}{2}(\chi _{2x,o}^2\cos ^2\psi _2+\chi _{2y,o}^2\sin ^2\psi _2)\dot{\theta }_2^2+\nonumber \\{} & {} \frac{m_{tot}}{2}((\chi _{1x,o}^2\sin ^2\psi _1+\chi _{1y,o}^2\cos ^2\psi _1)\sin ^2\theta _1+\chi _{1z,o}^2\cos ^2\theta _1)\dot{\varphi }_1^2+\nonumber \\ {}{} & {} \frac{m_{tot}}{2}((\chi _{2x,o}^2\sin ^2\psi _2+\chi _{2y,o}^2\cos ^2\psi _2)\sin ^2\theta _2+\chi _{2z,o}^2\cos ^2\theta _2)\dot{\varphi }_2^2+\nonumber \\{} & {} \frac{m_{tot}}{2}\chi _{1z,o}^2\dot{\psi }_1^2+\frac{m_{tot}}{2}\chi _{2z,o}^2\dot{\psi }_2^2+\nonumber \\{} & {} m_{tot}(\chi _{1x,o}^2-\chi _{1y,o}^2)\sin \theta _1\sin \psi _1\cos \psi _1\dot{\theta }_1\dot{\varphi }_1+\nonumber \\{} & {} m_{tot}(\chi _{2x,o}^2-\chi _{2y,o}^2)\sin \theta _2\sin \psi _2\cos \psi _2\dot{\theta }_2\dot{\varphi }_2+\nonumber \\{} & {} m_{tot}\chi _{1z,o}^2\cos \theta _1\dot{\varphi }_1\dot{\psi }_1+m_{tot}\chi _{2z,o}^2\cos \theta _2\dot{\varphi }_2\dot{\psi }_2+\nonumber \\{} & {} m_{tot}l_1a_2(\sin \theta _1\sin \theta _2+\cos \theta _1\cos \theta _2\cos (\varphi _2-\varphi _1))\dot{\theta }_1\dot{\theta }_2-\nonumber \\{} & {} m_{tot}l_1a_2\cos \theta _1\sin \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_1\dot{\varphi }_2+\nonumber \\{} & {} m_{tot}l_1a_2\sin \theta _1\cos \theta _2\sin (\varphi _2-\varphi _1)\dot{\theta }_2\dot{\varphi }_1+\nonumber \\{} & {} m_{tot}l_1a_2\sin \theta _1\sin \theta _2\cos (\varphi _2-\varphi _1)\dot{\varphi }_1\dot{\varphi }_2\nonumber \end{aligned}$$
(19)

From this equation the kinetic energy of a planar two-link chain or double pendulum rotating about a revolute base joint in \(A_0\) can be derived too by substituting \(\varphi _i=\psi _i=0\) and \(\dot{\varphi }_i=\dot{\psi }_i=0\) for planar 2-DoF motion with \(\theta _1\) and \(\theta _2\) as

$$\begin{aligned} T_{A_0}^{planar}= & {} \frac{m_{tot}}{2}(\chi _{1x,o}^2\dot{\theta }_1^2+\chi _{2x,o}^2\dot{\theta }_2^2)+ m_{tot}l_1a_2\cos (\theta _1-\theta _2)\dot{\theta }_1\dot{\theta }_2 \end{aligned}$$
(20)

4 Equations of Motion

The Euler-Lagrange equations of motion can be derived from the kinetic energy. For the two-link chain moving in free space this leads to 9 differential equations, for which this paper leaves no space unfortunately to show the derivations. The first three equations of motion are related to the absolute translational motions of the complete linkage in space as if it is a single rigid body and write

$$\begin{aligned} m_{tot}\ddot{x}_S= & {} \varSigma X \qquad m_{tot}\ddot{y}_S=\varSigma Y \qquad m_{tot}\ddot{z}_S=\varSigma Z\ \end{aligned}$$
(21)

in which \(\varSigma X\), \(\varSigma Y\), and \(\varSigma Z\) represent the sums of all externally applied forces anywhere to the two-link chain. The other six equations of motion are related to the relative motions of the links with respect to the common CoM in S. Here Fischer made the assumption that the links are symmetric about their longitudinal axes for which \(\chi _{1y}=\chi _{1x}\) and \(\chi _{2y}=\chi _{2x}\), which he considered realistic for biomechanics where the links represent arms or legs. With this assumption the three equations of motion for link 1 result in

$$\begin{aligned}{} & {} m_{tot}\chi _{1x}^2\ddot{\theta }_1-m_{tot}(\chi _{1x}^2-\chi _{1z}^2)\sin \theta _1\cos \theta _1\dot{\varphi }_1^2+m_{tot}\chi _{1z}^2\sin \theta _1\dot{\varphi }_1\dot{\psi }_1 =D_{\theta _1}\nonumber \\{} & {} m_{tot}(\chi _{1x}^2\sin ^2\theta _1+\chi _{1z}^2\cos ^2\theta _1)\ddot{\varphi }_1+m_{tot}\chi _{1z}^2\cos \theta _1\ddot{\psi }_1+\nonumber \\{} & {} \quad 2m_{tot}(\chi _{1x}^2-\chi _{1z}^2)\sin \theta _1\cos \theta _1\dot{\theta }_1\dot{\varphi }_1-m_{tot}\chi _{1z}^2\sin \theta _1\dot{\theta }_1\dot{\psi }_1=D_{\varphi _1} \\{} & {} m_{tot}\chi _{1z}^2\ddot{\psi }_1+m_{tot}\chi _{1z}^2\cos \theta _1\ddot{\varphi }_1-m_{tot}\chi _{1z}^2\sin \theta _1\dot{\theta }_1\dot{\varphi }_1=D_{\psi _1}\nonumber \end{aligned}$$
(22)

Remarkable here is that these equations are elegantly and compactly written solely in terms of the total mass and the reduced inertias. Also particular are the terms \(D_{\theta _1}\), \(D_{\varphi _1}\), and \(D_{\psi _1}\) which are the principal moments, i.e. the resultant moments in the reduced model of the link about the principal point due to all the applied internal and external forces and moments. From these principal moments Fischer could derive the individual muscle forces causing these moments and responsible for the recorded motions. Since with the reduced mass models each link can be investigated individually with the dynamics of a single rigid body, it allows a simple investigation of different situations, e.g. different combinations of internally and externally applied forces and moments, for which the equations remain the same and do not need to be derived again. The three equations of motion for link 2 are identical with index 1 changed into 2.

For the constrained two-link chain with spherical base joint in \(A_0\) there are just 6 equations of motion, 3 for each link which are equal to (22) but with the reduced inertias of (18) replacing the reduced inertias of the free moving system.

By rewriting (22), the principal moments of each link i can also be expressed in terms of the reduced inertias as

$$\begin{aligned} D_{\theta _i}= & {} I_{Rix}(\ddot{\theta }_i-\sin \theta _i\cos \theta _i\dot{\varphi }_i^2)+I_{Riz}(\sin \theta _i\cos \theta _i\dot{\varphi }_i^2+\sin \theta _i\dot{\varphi }_i\dot{\psi }_i) \nonumber \\ D_{\varphi _i}= & {} I_{Rix}(\sin ^2\theta _i\ddot{\varphi }_i+2\sin \theta _i\cos \theta _i\dot{\theta }_i\dot{\varphi }_i)+\nonumber \\{} & {} \quad I_{Riz}(\cos ^2\theta _i\ddot{\varphi }_i+\cos \theta _i\ddot{\psi }_i-2\sin \theta _i\cos \theta _i\dot{\theta }_i\dot{\varphi }_i-\sin \theta _i\dot{\theta }_i\dot{\psi }_i) \\ D_{\psi _i}= & {} I_{Riz}(\ddot{\psi }_i+\cos \theta _i\ddot{\varphi }_i-\sin \theta _i\dot{\theta }_i\dot{\varphi }_i) \nonumber \end{aligned}$$
(23)

5 Conclusion

This paper presented in a modern and understandable way the kinetic energy, the reduced mass models, the equations of motion, and the principal moments of an unconstrained spatial two-link chain with spherical joint by means of principal vectors as originally published by Fischer in 1905. The formulations have a specific simple form with full geometric meaning and depend solely only the total mass, the reduced inertias and the principal dimensions. The characteristics of the spatial form therefore are equal to the planar form.

From the unconstrained case the equations for a variety of constrained spatial two-link chains with lower mobility can be derived easily, as was shown for a spatial two-link chain with a spherical base joint. Although presented for a two-link chain, extending the spatial theory to serial chains with more than two links will be, as the planar theory already showed, straightforward with similar results. The theory is expected to be especially useful as a simpler and insightful way to analyze the dynamics of a system of rigid bodies since with the reduced mass models system dynamics can be investigated at a single body level. This is to be investigated further.