Keywords

20.1 Introduction

The field of rigid body dynamics was initiated and established by Euler in the eighteenth century. Nowadays rigid body dynamics is an integral part of the design process in engineering. This field is covered in every course on engineering mechanics. However, the theoretical aspects are often not discussed in detail. In particular, this applies to the analysis of rotations. A possible reason for this is given in the textbook of Taylor [14, p. 336]: “A detailed study of rotations is actually surprisingly complicated. Fortunately, we do not need many of the details, and some of the properties that are quite hard to prove are reasonably plausible and can be stated without proof.”

Rotations are present in many dynamical systems, e.g., classical problems such as the pendulum or advanced applications ranging from aircraft dynamics [8], to motion capturing techniques [12]. In order to characterize the rotational movement of a rigid body, three degrees of freedom are introduced. Commonly used concepts are Euler angles, Tait–Bryant angles, Euler parameters and quaternions. The first two angle approaches divide the rotation of the body into three successive rotations around specified axes and hence introduce three corresponding axes. The Euler parameters and quaternions, however, describe a rotation with one axis and a rotation angle, see [15].

In the following representations of rotations in terms of three successive rotations with specified axes and its consequences regarding the kinematics are discussed. While the presentation and discussion of these rotations is rather uniform in the literature, difference arise when the angular velocities are introduced. These differences are due to inaccuracies related to the term angular velocity. Often this term is confused with rotational velocities. However, as will be shown in Sect. 20.4, the angular velocity and the rotational velocity are not the same in general. Moreover, additional confusion arises, because the angular velocity due to multiple successive rotation is (surprisingly) given by the sum of the corresponding elementary rotational velocities. Sometimes this result is referred to as the “addition theorem of angular velocities.” The validity of this theorem makes it hard to distinguish the concept of the angular velocity from the rotational velocity. Furthermore, this fact renders the distinction of these concepts obsolete if only the final result is considered. In order to clarify the relations, this paper reconsiders the successive rotations and their angular velocities in a rational manner.

This paper starts with a brief introduction to the representations of rotations using an abstract tensor notation. Then, the angular velocity is introduced based on a tensor-based approach as in [3, 17]. Subsequently, successive rotations are investigated and relations for the corresponding angular velocities are derived and the addition theorem is proved. Furthermore, the terms rotational velocity, elementary angular velocity and angular velocity are precisely defined and explained. Based on this framework, a literature review is given on rotations in rigid body dynamics.

20.2 Rotation and Change of Base

In the following, the concept of tensor rotations is introduced by using orthogonal transformations. Let \(\varvec{Q}\) be a proper orthogonal tensor such that

$$\begin{aligned} \varvec{Q} \cdot \varvec{Q}^\mathrm {T} = \varvec{Q}^\mathrm {T} \cdot \varvec{Q} = \varvec{1} \ , \quad \det (\varvec{Q}) = 1 \ , \end{aligned}$$
(20.1)

where \(\varvec{Q}^\mathrm {T}\) denotes the transpose of \(\varvec{Q}\). Consider two orthonormal bases with proper orientation \(\{\varvec{e}_i'\}\) and \(\{\varvec{e}_i^0\}\). They are connected by the following transformation

$$\begin{aligned} \varvec{e}_i' = \varvec{Q} \cdot \varvec{e}_i^0 \ , \end{aligned}$$
(20.2)

which is the rotation of \(\varvec{e}_i^0\) onto \(\varvec{e}_i'\). Therefore, the tensor \(\varvec{Q}\) is also referred to as rotation tensor. Based on the identity tensor, \(\varvec{1} = \varvec{e}_i' \otimes \varvec{e}_i' = \varvec{e}_i^0 \otimes \varvec{e}_i^0\), one can derive a mixed representation of the rotation tensor

$$\begin{aligned} \varvec{Q} = \varvec{e}_i' \otimes \varvec{e}_i^0 \ , \end{aligned}$$
(20.3)

where the Einstein summation convention is applied. The component matrices \(Q'\) and \(Q^0\) corresponding to the non-mixed base representations,

$$\begin{aligned} \varvec{Q} = Q_{ij}' \varvec{e}_i' \otimes \varvec{e}_j' = Q_{ij}^0 \varvec{e}_i^0 \otimes \varvec{e}_j^0 \ , \end{aligned}$$
(20.4)

can be found via the projections:

$$\begin{aligned} Q_{ij}' = \varvec{e}_i' \cdot \varvec{Q} \cdot \varvec{e}_j' = \varvec{e}_i^0 \cdot \varvec{e}_j' \ , \quad Q_{ij}^0 = \varvec{e}_i^0 \cdot \varvec{Q} \cdot \varvec{e}_j^0 = \varvec{e}_i^0 \cdot \varvec{e}_j' \ . \end{aligned}$$
(20.5)

Note that the result \(Q = Q' = Q_0\) is remarkable and inherent to the rotation tensor.

20.2.1 Rotations of Tensors

After agreeing on the rotation of base vectors, the rotation of a vector \(\varvec{a}\) is given by

$$\begin{aligned} \varvec{b} = \varvec{Q} \cdot \varvec{a} \ . \end{aligned}$$
(20.6)

In order to emphasize that \(\varvec{b}\) is a new vector, we refrain from using \(\varvec{a}'\) and instead introduce \(\varvec{b}\) as the result. Both vectors can be represented in both bases \(\{\varvec{e}_i^0\}\) and \(\{\varvec{e}_i'\}\), respectively:

$$\begin{aligned} \varvec{a} = a_i^0 \varvec{e}_i^0 = a_i' \varvec{e}_i' \ , \quad \varvec{b} = b_i^0 \varvec{e}_i^0 = b_i' \varvec{e}_i' \ , \end{aligned}$$
(20.7)

and the following transformation rules for the components arise

$$\begin{aligned} a_i^0 = Q_{ij} a_j' \ , \quad b_i^0 = Q_{ij} b_j' \ . \end{aligned}$$
(20.8)

It is essential to note that the transformations in Eq. (20.8) do not correspond to real tensor rotations as introduced in Eq. (20.6). The components \(a_i^0\) and \(a_i'\) are nothing but different representations of the same object, \(\varvec{a}\). Bearing in mind the nomenclature of Eq. (20.7), the rotation in Eq. (20.6) may be represented in various forms:

$$\begin{aligned} b_i^0 = Q_{ij}a_j^0 = Q_{ik} Q_{kj} a_j' \ , \quad b_i' = a_i^0 = Q_{ij} a_j' \ . \end{aligned}$$
(20.9)

Note that the difference between a tensor rotation as in Eq. (20.6) cannot be distinguished from a change of base as in Eq. (20.7) if only the component equations are considered, cf., Eqs. (20.8) and (20.9). For example, the transformation of the components for the rotation \(\varvec{b} = \varvec{Q} \cdot \varvec{a}\) looks exactly the same as the component equation for the change of base of \(\varvec{a}\), i.e., Eq. (20.8)\(_1\) is equal to Eq. (20.9)\(_2\). However, the underlying interpretation is rather different.

Furthermore note that, from a mathematical point of view, one could conclude that it does not matter whether a change of the base or a vector rotation is considered. However, from a physical point of view the difference could be significant, e.g., if a change of observer is considered. Note that this is not considered in this article. The interested reader is referred to [7].

If rotations of higher order tensors are considered, the Rayleigh product “\(*\)” is used conveniently. It is a non-commutative product between a tensor of second rank and a tensor of rank n, see [3],

$$\begin{aligned} \varvec{Q} * \overset{{\langle n\rangle }}{\varvec{C}} = \varvec{Q} * (C_{i_1 \ldots i_n} \varvec{e}_{i_1} \otimes \cdots \otimes \varvec{e}_{i_n}) := C_{i_1 \ldots i_n} \varvec{Q} \cdot \varvec{e}_{i_1} \otimes \cdots \otimes \varvec{Q} \cdot \varvec{e}_{i_n} \ . \end{aligned}$$
(20.10)

Hence, the tensor of second rank is applied to every base vector of the second tensor. If \(\varvec{Q}\) is a proper orthogonal tensor, its application with the Rayleigh product rotates any tensor. In particular, one has

$$\begin{aligned} \varvec{Q} * \varvec{a} = \varvec{Q} \cdot \varvec{a} \ , \quad \varvec{Q} * \varvec{A} = \varvec{Q} \cdot \varvec{A} \cdot \varvec{Q}^\mathrm {T} \ . \end{aligned}$$
(20.11)

20.2.2 Representation of the Rotation Tensor

In order to construct the rotation tensor in terms of orientation parameters, the Rodrigues formula is used,

$$\begin{aligned} \varvec{Q} = \hat{\varvec{Q}}(\psi , \varvec{q}) = \varvec{1} + \sin (\psi ) \varvec{D} + \big (1-\cos (\psi )\big ) \varvec{D}^2 \ , \end{aligned}$$
(20.12)

where

$$\begin{aligned} \varvec{D} = \varvec{q} \times \varvec{1} = - \varvec{q} \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \quad \left| \left| \varvec{q} \right| \right| = 1 \ . \end{aligned}$$
(20.13)

Therein, the vector \(\varvec{q}\) is parallel to the axis of rotation, \(\psi \) is the angle of rotation and \(\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\) is the Levi-Civita tensor, see Appendix 20.7. The simple contraction of the tensor \(\varvec{D}\) with a vector, \(\varvec{x}\), yields

$$\begin{aligned} \varvec{D} \cdot \varvec{x} = \varvec{q} \times \varvec{x} \quad \Rightarrow \quad \varvec{D}^2 \cdot \varvec{x} = \varvec{D} \cdot (\varvec{q} \times \varvec{x}) = \varvec{q} \times (\varvec{q} \times \varvec{x}) \ . \end{aligned}$$
(20.14)

Hence, the action of a rotation tensor in the form (20.12) on a vector, \(\varvec{x}\), reads

$$\begin{aligned} \varvec{Q} \cdot \varvec{x} = \varvec{x} + \sin (\psi ) \varvec{q} \times \varvec{x} + \big (1-\cos (\psi )\big ) \varvec{q} \times (\varvec{q} \times \varvec{x}) \ . \end{aligned}$$
(20.15)

Another useful representation is given by

$$\begin{aligned} \varvec{Q}=\cos (\psi )\varvec{1}+\big (1-\cos (\psi )\big )\varvec{q}\otimes \varvec{q}-\sin (\psi )\varvec{q}\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ . \end{aligned}$$
(20.16)

20.3 Time Derivatives in Rotating Systems

In the preceding sections, tensors were treated as invariant regarding their representation. However, if time derivatives are concerned one has to clarify in which system the temporal change is measured. In the following, the notation \(\dot{\varvec{a}}\) denotes the time derivative in an inertial system. Consider a body-fixed system \(\mathcal {B} = \{\varvec{b}_i\}\) that differs from an intertial system \(\mathcal {I} = \{\varvec{e}_i^0\}\) by a rotation

$$\begin{aligned} \varvec{b}_i(t) = \varvec{Q} \cdot \varvec{e}_i^0 \ , \end{aligned}$$
(20.17)

where \(\varvec{Q} = \hat{\varvec{Q}}(t)\) is a proper orthogonal tensor. Then, if a vector \(\varvec{a}\) is represented in the \(\mathcal {B}\)-base, one finds from the product rule:

$$\begin{aligned} \dot{\varvec{a}} := \frac{\mathrm {d} ^\mathcal {I}\varvec{a}}{\mathrm {d} t} = \frac{\mathrm {d} ^\mathcal {B}\varvec{a}}{\mathrm {d} t} + a_i \frac{\mathrm {d} ^\mathcal {I}\varvec{b}_i}{\mathrm {d} t} \ , \qquad \frac{\mathrm {d} ^\mathcal {B}\varvec{a}}{\mathrm {d} t} := \frac{\mathrm {d} ^\mathcal {I}a_i}{\mathrm {d} t} \varvec{b}_i\ . \end{aligned}$$
(20.18)

Therein, the time derivative with respect to \(\mathcal {B}\), \(\nicefrac {\mathrm {d}^\mathcal {B}}{\mathrm {d}t}\), can be interpreted as the measurement of the temporal change in the body-fixed system.

In order to further analyze \(\dot{\varvec{b}}_i\), the temporal change of the rotation tensor \(\dot{\varvec{Q}}\) is investigated and the angular velocity tensor is introduced as

$$\begin{aligned} \varvec{\varOmega }:= \dot{\varvec{Q}} \cdot \varvec{Q}^\mathrm {T} \quad \text {with} \quad \varvec{\varOmega }= -\varvec{\varOmega }^\mathrm {T} \ . \end{aligned}$$
(20.19)

Therefore, the time derivative of \(\varvec{b}_i\) can be written as

$$\begin{aligned} \frac{\mathrm {d} ^\mathcal {I}\varvec{b}_i}{\mathrm {d} t} = \dot{\varvec{Q}} \cdot \varvec{e}_i^0 = \varvec{\varOmega }\cdot \varvec{Q} \cdot \varvec{e}_i^0 = \varvec{\varOmega }\cdot \varvec{b}_i \ . \end{aligned}$$
(20.20)

Since the angular velocity tensor is skew-symmetric, a corresponding axial vector, the angular velocity \(\varvec{\omega }\), is the solution of the axial equation for all \(\varvec{x} \ne \varvec{0}\):

$$\begin{aligned} \varvec{\varOmega }\cdot \varvec{x} = \varvec{\omega }\times \varvec{x} \quad \Rightarrow \quad \varvec{\varOmega }= - \varvec{\omega }\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\quad \Rightarrow \quad \varvec{\omega }= - \tfrac{1}{2} \varvec{\varOmega }\, {\cdot }{\cdot }\,\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \end{aligned}$$
(20.21)

where the double contraction is defined as \(\varvec{A} \, {\cdot }{\cdot }\,\varvec{B} = A_{ij}B_{ij}\). Note that sometimes the so-called Poisson relation is stated as follows

$$\begin{aligned} \dot{\varvec{Q}} = \varvec{\varOmega }\cdot \varvec{Q} = \varvec{\omega }\times \varvec{Q} \end{aligned}$$
(20.22)

for the “left angular velocity” and one might introduce a “right angular velocity,” which is shown in, e.g., [7, 17] but will not be used in the following. Note that in this paper \(\varvec{\varOmega }\) is the angular velocity tensor and not the right angular velocity vector as in [7]. Furthermore, note that the inverse problem of determining the rotation tensor from a given angular velocity vector is also called Darboux problem.

With the angular velocity \(\varvec{\omega }\), the time derivative in Eq. (20.18) can be simplified:

$$\begin{aligned} \dot{\varvec{a}} = \frac{\mathrm {d} ^\mathcal {B}\varvec{a}}{\mathrm {d} t} + \varvec{\omega }\times \varvec{a} \ . \end{aligned}$$
(20.23)

Note that although only bold symbols are used this equation, it is system dependent because a system-dependent time derivative is involved.

It is worthwhile mentioning that the angular velocity is not a velocity in the usual sense, i.e., it is not a time derivative of some position or orientation. In order to see this, the angular velocity is computed in terms of the rotation angle and axis from Rodrigues’ formula. Since this computation is lengthy, it is detailed in Appendix 20.8. The angular velocity tensor as well as its axial vector are given by:

$$\begin{aligned} \begin{aligned} \varvec{\varOmega }&= \big (1-\cos (\psi )\big )\big [\dot{\varvec{q}} \otimes \varvec{q}- \varvec{q}\otimes \dot{\varvec{q}}\big ] - \big (\dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}}\big ) \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \\ \varvec{\omega }&= \dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}}+\big (1-\cos (\psi )\big )\varvec{q}\times \dot{\varvec{q}} \ . \end{aligned} \end{aligned}$$
(20.24)

This result shows that the angular velocity is only coaxial to the current axis of rotation, i.e., the vector \(\varvec{q}\), if this axis is fixed in space, viz., \(\dot{\varvec{q}}= \varvec{0}\). This is for example the case for two-dimensional settings in which the axis of rotation is always perpendicular to the plane under consideration and thus constant.

Consider a body-fixed axis of rotation \(\varvec{q}\) with constant components in the \(\mathcal {B}\) system. From Eq. (20.23), it follows that \(\dot{\varvec{q}} = \varvec{\omega }\times \varvec{q}\). Bearing in mind Eq. (20.15), the insertion of this relation into Eq. (20.24)\(_2\) yields:

$$\begin{aligned} \varvec{\omega }= \dot{\psi }\varvec{q}+\sin (\psi )\varvec{\omega }\times \varvec{q} +\big (1-\cos (\psi )\big )\varvec{q}\times (\varvec{\omega }\times \varvec{q}) \quad \Rightarrow \quad \varvec{Q} \cdot \varvec{\omega }= \dot{\psi } \varvec{q} \ . \end{aligned}$$
(20.25)

There is another representation of the angular velocity that arises from Eq. (20.21)\(_3\) if the representation from Eq. (20.3) is inserted:

$$\begin{aligned} \varvec{\omega }= - \tfrac{1}{2} \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\, {\cdot }{\cdot }\,(\dot{\varvec{Q}} \cdot \varvec{Q}^\mathrm {T}) = - \tfrac{1}{2} \dot{\varvec{b}}_i \times \varvec{b}_i = \tfrac{1}{2} \varepsilon _{ijk}(\dot{\varvec{b}}_j \cdot \varvec{b}_k) \varvec{b}_i \ . \end{aligned}$$
(20.26)

However, since the base \(\mathcal {B}\) is orthonormal, the time derivative applied to the condition \(\varvec{b}_i \cdot \varvec{b}_j = \delta _{ij}\) reveals (no summation w.r.t. \(\alpha \))

$$\begin{aligned} \dot{\varvec{b}}_\alpha \cdot \varvec{b}_\alpha = 0 \ , \quad \dot{\varvec{b}}_1 \cdot \varvec{b}_2 = - \varvec{b}_1 \cdot \dot{\varvec{b}}_2 \ , \quad \dot{\varvec{b}}_1 \cdot \varvec{b}_3 = - \varvec{b}_1 \cdot \dot{\varvec{b}}_3 \ , \quad \dot{\varvec{b}}_2 \cdot \varvec{b}_3 = - \varvec{b}_2 \cdot \dot{\varvec{b}}_3 \ . \end{aligned}$$
(20.27)

Hence, the angular velocity can be written as

$$\begin{aligned} \varvec{\omega }= (\dot{\varvec{b}}_2 \cdot \varvec{b}_3) \varvec{b}_1 + (\dot{\varvec{b}}_3 \cdot \varvec{b}_1) \varvec{b}_2 + (\dot{\varvec{b}}_1 \cdot \varvec{b}_2) \varvec{b}_3 \ . \end{aligned}$$
(20.28)

20.4 Analysis of Sequential Rotations

Hitherto a single rotation was considered. However, for (say) the Euler angle approach the total rotation is composed of three successive rotations. These rotations are referred to as elementary rotations \(\varvec{Q}_\alpha \). Then, the total rotation tensor is given by

$$\begin{aligned} \varvec{Q} = \varvec{Q}_3 \cdot \varvec{Q}_2 \cdot \varvec{Q}_1 \ , \end{aligned}$$
(20.29)

with the respective elementary rotation tensors and elementary angular velocity tensors according to Eqs. (20.16) and (20.24)\(_1\):

$$\begin{aligned} \begin{aligned} \varvec{Q}_\alpha&= \cos (\psi _\alpha )\varvec{1}+\big (1-\cos (\psi _\alpha )\big )\varvec{q}_\alpha \otimes \varvec{q}_\alpha -\sin (\psi _\alpha )\varvec{q}_\alpha \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \\ \varvec{\varOmega }_\alpha&= \big (1-\cos (\psi _\alpha )\big )\big [\dot{\varvec{q}}_\alpha \otimes \varvec{q}_\alpha - \varvec{q}_\alpha \otimes \dot{\varvec{q}}_\alpha \big ] - \big (\dot{\psi }_\alpha \varvec{q}_\alpha +\sin (\psi _\alpha )\dot{\varvec{q}}_\alpha \big ) \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \end{aligned} \end{aligned}$$
(20.30)

where the Einstein summation convection does not apply to Greek indices. Then, the total angular velocity tensor follows as

$$\begin{aligned} \begin{aligned} \varvec{\varOmega }&=\dot{\varvec{Q}} \cdot \varvec{Q}^\mathrm {T} \\&= \dot{\varvec{Q}}_3 \cdot \varvec{Q}_3^\mathrm {T} + \varvec{Q}_3 \cdot \dot{\varvec{Q}}_2 \cdot \varvec{Q}_2^\mathrm {T} \cdot \varvec{Q}_3^\mathrm {T} + \varvec{Q}_3 \cdot \varvec{Q}_2 \cdot \dot{\varvec{Q}_1} \cdot \varvec{Q}_1^\mathrm {T} \cdot \varvec{Q}_2^\mathrm {T} \cdot \varvec{Q}_3^\mathrm {T} \\&= \varvec{\varOmega }_3 + \varvec{Q}_3 * \varvec{\varOmega }_2 + (\varvec{Q}_3 \cdot \varvec{Q}_2) * \varvec{\varOmega }_1 \ . \end{aligned} \end{aligned}$$
(20.31)

In the Appendix, it is shown that the Levi-Civita tensor is invariant under rotations, i.e., \(\varvec{Q} * \overset{{\langle 3\rangle }}{\varvec{\epsilon }}= \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\) for all proper orthogonal tensors \(\varvec{Q}\), see Eq. (20.51). Hence, the rotation of \(\varvec{\varOmega }_2\) can be simplified:

$$\begin{aligned} \begin{aligned} \varvec{Q}_3 * \varvec{\varOmega }_2&= - \varvec{Q}_3 * (\varvec{\omega }_2 \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}) = - \varvec{Q}_3 * (\varvec{\omega }_2 \cdot \varvec{Q}_3^\mathrm {T} \cdot \varvec{Q}_3 \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}) \\&= - \varvec{\omega }_2 \cdot \varvec{Q}_3^\mathrm {T} \cdot (\varvec{Q}_3 * \overset{{\langle 3\rangle }}{\varvec{\epsilon }}) = - \varvec{\omega }_2 \cdot \varvec{Q}_3^\mathrm {T} \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}= - \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{Q}_3 \cdot \varvec{\omega }_2 \ . \end{aligned} \end{aligned}$$
(20.32)

The term \((\varvec{Q}_3 \cdot \varvec{Q}_2) * \varvec{\varOmega }_1 \) in Eq. (20.31) is treated analogously such that

$$\begin{aligned} \varvec{\varOmega }= \varvec{\varOmega }_3 - \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{Q}_3 \cdot \varvec{\omega }_2 - \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{Q}_3 \cdot \varvec{Q}_2 \cdot \varvec{\omega }_1 \ . \end{aligned}$$
(20.33)

Hence, the total angular velocity vector is then obtained via double contraction with the Levi-Civita tensor \(\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\),

$$\begin{aligned} \varvec{\omega }= \varvec{\omega }_3 + \varvec{Q}_3 \cdot \varvec{\omega }_{2} + (\varvec{Q}_3 \cdot \varvec{Q}_2) \cdot \varvec{\omega }_1 \ , \end{aligned}$$
(20.34)

where the elementary angular velocities are given according to Eq. (20.24)\(_2\),

$$\begin{aligned} \varvec{\omega }_\alpha = \dot{\psi }_\alpha \varvec{q}_\alpha +\sin (\psi _\alpha )\dot{\varvec{q}}_\alpha +\big (1-\cos (\psi _\alpha )\big )\varvec{q}_\alpha \times \dot{\varvec{q}}_\alpha \ . \end{aligned}$$
(20.35)

It is interesting to note that the total angular velocity is not given by the sum of the elementary angular velocities.

The formulas in Eqs. (20.24) and (20.34) are useful to solve the Darboux problem. Note that in some cases even closed-form analytical solutions can be derived. Examples are presented, among others, in [1] and [16]. In literature, the concept of a skew-symmetric spin tensor is commonly introduced, which corresponds to the angular velocity tensor \(\varvec{\varOmega }\) in this paper. However, the angular velocity vector, instead of the “spin tensor,” and representations as in Eq. (20.34) can be very useful not only in rigid body mechanics but also in continuum mechanics. Indeed, some simple and transparent relationships for different angular velocity vectors, e.g., vorticity vector, rotation of principal directions of tensors and logarithmic strain can be derived, see [10, Sect. 4.1.3].

20.4.1 Simplification for Attached Axes

Commonly used descriptions of rotations, e.g., by the Euler angles, are based on fixed elementary axes of rotation, where the term “fixed” needs further explanation. Since the rotation is divided into three successive rotations, two intermediate systems, \(\mathcal {B}_1\) and \(\mathcal {B}_2\), are generated before the inertial system is transformed into the body-fixed system:

$$\begin{aligned} \mathcal {I} \;\rightarrow \; \mathcal {B}_1 \;\rightarrow \; \mathcal {B}_2 \;\rightarrow \; \mathcal {B} \ . \end{aligned}$$

The first elementary axis of rotation is usually spatially fixed and the second and third elementary axes are attached to the intermediate systems \(\mathcal {B}_1\) and \(\mathcal {B}_2\), respectively. Hence, the time derivatives of these elementary axes are given by

$$\begin{aligned} \dot{\varvec{q}}_1 = \varvec{0} \ , \quad \dot{\varvec{q}}_2 = \varvec{\omega }_1 \times \varvec{q}_2 \ , \quad \dot{\varvec{q}}_3 = (\varvec{\omega }_2 + \varvec{Q}_2 \cdot \varvec{\omega }_1) \times \varvec{q}_3 \ . \end{aligned}$$
(20.36)

These axes are therefore called “attached” rather than fixed. If these results are plugged into the angular velocities in Eq. (20.35), similar to the result in Eq. (20.25), one obtains

$$\begin{aligned} \begin{aligned} \varvec{\omega }_1&= \dot{\psi }_1 \varvec{q}_1 \ , \quad \varvec{\omega }_2 = \dot{\psi }_2 \varvec{q}_2 + \big [\varvec{1} - \varvec{Q}_2\big ] \cdot \varvec{\omega }_1 \ , \\ \varvec{\omega }_3&= \dot{\psi }_3 \varvec{q}_3 + \big [\varvec{1} - \varvec{Q}_3\big ] \cdot (\varvec{\omega }_2 + \varvec{Q}_2 \cdot \varvec{\omega }_1) \ . \end{aligned} \end{aligned}$$
(20.37)

With these relations, the expression for the total angular velocity vector in Eq. (20.34) can be simplified such that all rotation tensors \(\varvec{Q}_\alpha \) cancel:

$$\begin{aligned} \varvec{\omega }= \dot{\psi }_1 \varvec{q}_1 + \dot{\psi }_2 \varvec{q}_2 + \dot{\psi }_3 \varvec{q}_3 \ . \end{aligned}$$
(20.38)

This final representation of the total angular velocity vector is much simpler than the first one in Eq. (20.34), but it is only obtained if the elementary axes of rotation are “attached” to the intermediate systems. Note that the products \(\psi _\alpha \varvec{q}_\alpha \) are not necessarily angular velocities in the sense of the definition introduced above. The fact that for attached axes the simple addition rule holds was pointed out in [16] without detailed proof.

20.4.2 Summary for Sequential Rotations

The results of the foregoing analysis are summarized in the following. First the universal results read:

For a rotation tensor \(\varvec{Q}\) expressed in terms of a rotation axis \(\varvec{q}\) and a rotation angle \(\psi \),

$$\begin{aligned} \varvec{Q} = \cos (\psi )\varvec{1}+\big (1-\cos (\psi )\big )\varvec{q}\otimes \varvec{q}-\sin (\psi )\varvec{q}\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \end{aligned}$$
(20.39)

where \(\left| \left| \varvec{q} \right| \right| = 1\), the angular velocity tensor and the corresponding angular velocity vector are given by:

$$\begin{aligned} \begin{aligned} \varvec{\varOmega }&= \dot{\varvec{Q}} \cdot \varvec{Q}^\mathrm {T} = \big (1-\cos (\psi )\big )\big [\dot{\varvec{q}} \otimes \varvec{q}- \varvec{q}\otimes \dot{\varvec{q}}\big ] - \big (\dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}}\big ) \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \\ \varvec{\omega }&= -\tfrac{1}{2} \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\, {\cdot }{\cdot }\,\varvec{\varOmega }=\dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}}+\big (1-\cos (\psi )\big )\varvec{q}\times \dot{\varvec{q}} \ . \end{aligned} \end{aligned}$$
(20.40)

If three successive rotations are considered, i.e., \(\varvec{Q} = \varvec{Q}_3 \cdot \varvec{Q}_2 \cdot \varvec{Q}_1\), with their respective elementary axes and angles of rotation, then the following composition rule holds for the total angular velocity

$$\begin{aligned} \varvec{\omega }= \varvec{\omega }_3 + \varvec{Q}_3 \cdot \varvec{\omega }_2 + \varvec{Q}_3 \cdot \varvec{Q}_2 \cdot \varvec{\omega }_1 \ . \end{aligned}$$
(20.41)

Therein, each elementary angular velocity \(\varvec{\omega }_\alpha \) is constructed by the formulae from Eq. (20.40)\(_2\).

For commonly used descriptions of sequential rotations, e.g., the Euler angles, the following simplifications are possible:

If all axes are “attached,” i.e., have constant components in their intermediate bases,

$$\begin{aligned} \varvec{q}_3 = q^3_i \varvec{Q}_2 \cdot \varvec{Q}_1 \cdot \varvec{e}_i^0 \ , \quad \varvec{q}_2 = q^2_i \varvec{Q}_1 \cdot \varvec{e}_i^0 \ , \quad \varvec{q}_1 = q^1_i \varvec{e}_i^0 \ , \qquad \dot{q}^\alpha _i = 0 \ , \end{aligned}$$
(20.42)

for all \(\alpha \in \{1, 2, 3\}\), where \(\{\varvec{e}_i^0\}\) is an inertial base, then the total angular velocity vector is given by

$$\begin{aligned} \varvec{\omega }= \dot{\psi }_1 \varvec{q}_1 + \dot{\psi }_2 \varvec{q}_2 + \dot{\psi }_3 \varvec{q}_3 \ . \end{aligned}$$
(20.43)

Following [11, p. 29], the products \(\dot{\psi }_\alpha \varvec{q}_\alpha \) (no summation) are referred to as elementary rotational velocity vectors. Hence, the addition theorem for the angular velocity vector of successive rotations can be restated as:

The angular velocity vector is given by the sum of the elementary rotational velocity vectors.

However, note that if one chooses to use three spatially fixed axes, all their time derivatives vanish and the associated angular velocities of the elementary rotations are simply given by

$$\begin{aligned} \varvec{\omega }_1 = \dot{\psi }_1 \varvec{q}_1 \ , \quad \varvec{\omega }_2 = \dot{\psi }_2 \varvec{q}_2 \ , \quad \varvec{\omega }_3 = \dot{\psi }_3 \varvec{q}_3 \ . \end{aligned}$$
(20.44)

In this case, the elementary angular velocity vectors are equal to the elementary rotational velocity vectors. However, according to the composition rule in Eq. (20.41) [in contrast to Eq. (20.43)] the following total angular velocity results

$$\begin{aligned} \varvec{\omega }= \dot{\psi }_3 \varvec{q}_3 + \dot{\psi }_2 \varvec{Q}_3 \cdot \varvec{q}_2 + \dot{\psi }_1 \varvec{Q}_3 \cdot \varvec{Q}_2 \cdot \varvec{q}_1 \ , \end{aligned}$$
(20.45)

which is not the sum of the elementary rotational velocity vectors. Finally, note that spatially fixed axes are rarely used.

20.5 Treatment of Successive Rotations in the Literature

In this section, a review of several classical textbooks, which cover rigid body dynamics and successive rotations, is presented. In particular, the approaches of the different authors to the problem of successive rotations are discussed. Note that the given list is by far not complete and for this short review limited to the essentials.

First, one can note that most of the authors rely mostly on matrix calculus, e.g., [4, 6, 9, 11, 13, 15] in contrast to the ones using an abstract tensor notation, e.g., [3, 8, 14, 17]. Recalling the discussion in Sect. 20.2, it is therefore not certain if authors, who rely on a matrix-based approach, regard their equations in terms of a change of bases or in terms of a rotation of a vector. This requires a detailed investigation of each equation in terms of the meaning intended by the author.

Second, several authors do not introduce a precise definition of the angular velocity vector \(\varvec{\omega }\). If sequential rotations are considered a profound definition of \(\varvec{\omega }\) is required because otherwise confusion may arise. This confusion manifests itself in a mix of terms. For example, the rotational velocities are referred to as Euler angular velocities, angular, or elementary angular velocities in several sources. As outlined in Sect. 20.4 some of the terminology used in the literature is at least partially inconsistent, see [6, p. 176], [14, p. 402] and [15, Sect. 2.3]. In some of the exemplary literature cited in this paper, products of angle velocities, \(\dot{\psi }_\alpha \), and corresponding axes of rotation, \(\varvec{q}_\alpha \), are called “angular velocities.” In the classical book of Taylor [14, p. 337], the angular velocity is even introduced as \(\varvec{\omega }= \psi \varvec{q}\), which gives the impression of this statement being true in general. However, on the same page a comment is given on the possible time dependence of the axis of rotation and in the subsequent analysis the more general statement \(\dot{\varvec{e}} = \varvec{\omega }\times \varvec{e}\) for a body-fixed vector \(\varvec{e}\) is used by Taylor.

In [11, p. 29] the products \(\dot{\psi }_\alpha \varvec{q}_\alpha \) are also introduced without any further comment, but they are called “elementary rotational velocities.” This nomenclature is precise and is recommended to be used. Furthermore Schiehlen and Eberhard present a formula similar to Eq. (20.41), which is rarely seen in any textbook. However, they use a matrix notation and do not give a derivation. In [2, pp. 12–14], which is an introductory book for the same topic, several definitions for the angular velocity are given of the form \(\dot{\psi } \varvec{q}\), but ultimately on page 15 the author writes for a body-fixed vector, \(\varvec{r}\), a defining equation for the angular velocity, \(\dot{\varvec{r}} = \varvec{\omega }\times \varvec{r}\). All references have this definition in common. However, this definition is mentioned as a side note in [4, p. 23], which is a book for numerical applications of rigid body dynamics. It is curious that no definition on the angular velocity is given in [4].

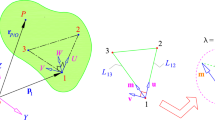
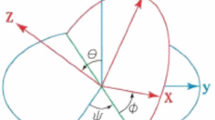
Third, a rational proof of the addition theorem for the angular velocity vector of successive rotations is rarely presented in the literature considered in this review. The theorem is discussed mostly in context with specific examples like, for example, the Euler angles and it is established by determining the elementary components from a figure similar to the one in Fig. 20.1. While some authors present a derivation of the theorem for infinitesimal successive rotations, the requirements and restrictions related the addition theorem are often not specified. This is annoying, because for the Euler angles, for example, one could infer that the successive elementary axes of rotation need to be orthogonal since \(\varvec{i}_3\perp \varvec{j}_1\) and \(\varvec{j}_1\perp \varvec{k}_3\), see Fig. 20.1. In order to avoid such a misleading conclusion, the presentation of a derivation, which clearly states all assumptions, is didactically beneficial to the reader.

Fig. 20.1
figure 1

Illustration of the rotations related the Euler angles \(\psi \), \(\theta \) and \(\varphi \). The sequence of the elementary axes of rotation is given by \(\varvec{i}_3\), \(\varvec{j}_1\) and \(\varvec{k}_3\). The \(\{\varvec{i}_i\}\)-system is the inertial system and the \(\{\varvec{e}_i\}\)-system the body-fixed one

Full size image

However, there is at least one example in the given literature list [8, p. 16], in which the angular velocity is defined formally in terms of a representation in a body-fixed base. Also Kane and Levinson distinguish between a general angular velocity and a simple one, namely \(\dot{\psi } \varvec{q}\). In contrast to some other authors, the authors always specify the angular velocity \({^A}\varvec{\omega }^B\) as a quantity that conveys between two systems A and B. Hence, the time derivatives associated with \({}^A\varvec{\omega }^B\) are measured with respect to A, even if A is a rotating system from an inertial point of view. Hence, for every vector \(\varvec{a}\) fixed in B one can write

$$\begin{aligned} \frac{\mathrm {d} ^A \varvec{a}}{\mathrm {d} t} = {}^A\varvec{\omega }^B \times \varvec{a} \ . \end{aligned}$$
(20.46)

Therefore, with this different notion of the angular velocity, intermediate angular velocities for a gyroscope consisting of rotor and gimbal rings are introduced, see [8, p. 22]. These intermediate angular velocities are simple ones for a gimbal suspension, as two intermediate systems always share one common vector. Finally, the textbook [8, Sect. 2.4] is the only one from the given reference list, in which the addition theorem of angular velocities is stated, analyzed and proved. Bearing in mind the notion of an angular velocity that conveys between two “frames,” intermediate frames \(A_i\) are introduced such that

$$\begin{aligned} {}^A\varvec{\omega }^B = {}^A\varvec{\omega }^{A_1} + {}^{A_1}\varvec{\omega }^{A_2} + \cdots + {}^{A_n}\varvec{\omega }^B \ , \end{aligned}$$
(20.47)

where the intermediate quantities \({}^{A_i}\varvec{\omega }^{A_{i+1}}\) do not necessarily need to be simple. One should note that with the term frame a set of basis vectors is meant and not a frame of an observer as in [7]. Furthermore, it is correctly stated that: “Indeed, Eq. (20.1) represents precisely such a resolution of \({}^A\varvec{\omega }^B\) into components. In no case, however, are these components themselves angular velocities of B in A, for there exists at any one instant only one angular velocity of B in A.” Together with Eq. (20.46) the addition rule in Eq. (20.47) is equivalent to our composition rule. Finally note that the quantity \(\varvec{\omega }\) in our paper conveys from an inertial system to the moving one and the angular velocities \(\varvec{\omega }_\alpha \) are the intermediate quantities \({}^{A_i}\varvec{\omega }^{A_{i+1}}\) from [8], but measured only from an inertial system. Therefore, the definitions in [8] are more general, allow for less constrained terminology and may even be more useful for practical applications.

20.6 Conclusion

This paper revisited the description of rotations in general. Successive rotations, which commonly occur in engineering applications of rigid body dynamics, were considered in detail. The mathematical description of a single rotation by Rodrigues’ formula was recalled and the related representations of the angular velocity tensor and the angular velocity vector were derived using an invariant notation.

The analysis of successive rotations focused on the addition theorem for the angular velocity vector, which was proved in a rational manner. Requirements and restrictions on the successive rotations related to the addition theorem were discussed. Moreover, the vectors of rotational velocity, elementary angular velocity and total angular velocity were defined and labeled clearly. Finally, a short literature review was presented and the treatment of successive rotations by several authors was put in context with the rational approach presented in this study. The literature review revealed that the addition theorem is rarely proved in classical textbooks covering the subject.

20.7 The Levi-Civita Tensor

This section briefly presents important properties of the Levi-Civita tensor \(\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\), which is given by

$$\begin{aligned} \overset{{\langle 3\rangle }}{\varvec{\epsilon }}=\epsilon _{ijk}\varvec{e}_i\otimes \varvec{e}_j\otimes \varvec{e}_k=\tilde{\epsilon }_{ijk}\tilde{\varvec{e}}_i\otimes \tilde{\varvec{e}}_j\otimes \tilde{\varvec{e}}_k\ . \end{aligned}$$
(20.48)

In this equation, the components w.r.t. the \(\varvec{e}_i\)-base are given by the permutation symbol \(\epsilon _{ijk}\), which has the properties as introduced, for example, in [5]. The components w.r.t. the \(\tilde{\varvec{e}}\)-base are denoted by \(\tilde{\epsilon }_{ijk}\). These base vectors are connected to the ones of the \(\varvec{e}_i\)-base by a proper rotation,

$$\begin{aligned} \tilde{\varvec{Q}} \cdot \tilde{\varvec{e}}_i = \varvec{e}_i \quad \Rightarrow \quad \tilde{\varvec{Q}} = \varvec{e}_i \otimes \tilde{\varvec{e}}_i = \tilde{Q}_{ij} \varvec{e}_i \otimes \varvec{e}_i \ , \quad \tilde{Q}_{ij} = \tilde{\varvec{e}}_i \cdot \varvec{e}_j \ . \end{aligned}$$
(20.49)

In order to obtain a relation between these components, Eq. (20.48) is contracted with the triad \(\tilde{\varvec{e}}_i\otimes \tilde{\varvec{e}}_j\otimes \tilde{\varvec{e}}_k\) and scalar products of the different base vectors are replaced by the components of the orthogonal tensor. The resulting relation reads:

$$\begin{aligned} \tilde{\epsilon }_{ijk}=\epsilon _{lmn}\tilde{Q}_{il}\tilde{Q}_{jm}\tilde{Q}_{kn}=\det (\tilde{Q})\epsilon _{ijk}\,, \end{aligned}$$
(20.50)

where the connection of the permutation symbol to the determinant was used in the second step, see [5, p. 184]. This equation implies that the components of the Levi-Civita tensor w.r.t. the \(\varvec{e}\)-base are the same as the ones of the \(\tilde{\varvec{e}}\)-base if the tensor \(\tilde{\varvec{Q}}\) is a proper orthogonal tensor, i.e., \(\epsilon _{ijk}=\tilde{\epsilon }_{ijk}\) if \(\det (\tilde{Q})=1\).

Note that some authors tend to call the tensor \(\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\) a tensor density due to the component transformation rule in Eq. (20.50). The transformation rule for the components has the consequence that a Rayleigh product of the Levi-Civita tensor with a proper orthogonal tensor is equal to the Levi-Civita tensor, i.e., it is invariant under a rotation. This may be shown by the following calculation:

$$\begin{aligned} \tilde{\varvec{Q}}*\overset{{\langle 3\rangle }}{\varvec{\epsilon }}=\tilde{\epsilon }_{ijk}(\tilde{\varvec{Q}}\cdot \tilde{\varvec{e}}_i)\otimes (\tilde{\varvec{Q}}\cdot \tilde{\varvec{e}}_j)\otimes (\tilde{\varvec{Q}}\cdot \tilde{\varvec{e}}_k)=\tilde{\epsilon }_{ijk}\varvec{e}_i\otimes \varvec{e}_j\otimes \varvec{e}_k=\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\,, \end{aligned}$$
(20.51)

where \(\det (\tilde{\varvec{Q}})=\det (\tilde{Q})=1\) must hold true in order to substitute \(\tilde{\epsilon }_{ijk}\) by \(\epsilon _{ijk}\) in the last step.

20.8 Angular Velocity in Terms of Orientation Parameters

In this section, an expression of the angular velocity vector \(\varvec{\omega }\) in terms of the Rodrigues parameters \(\psi \) and \(\varvec{q}\) shall be derived. In order to do so, the time derivative of the tensor \(\varvec{Q}\) in Eq. (20.16) is computed as

$$\begin{aligned} \begin{aligned} \dot{\varvec{Q}}=-\sin (\psi )\dot{\psi }(\varvec{1}-\varvec{q}\otimes \varvec{q})+\big (1-&\cos (\psi )\big )(\varvec{q}\otimes \dot{\varvec{q}}+\dot{\varvec{q}}\otimes \varvec{q}) \\&-(\cos (\psi )\dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}})\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ . \end{aligned} \end{aligned}$$
(20.52)

Furthermore, it is convenient to compute the products of \(\dot{\varvec{Q}}\) with the tensors on the right-hand side of Eq. (20.16), i.e., with \(\varvec{q}\otimes \varvec{q}\) and \(\varvec{q}\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\). In order to simplify the resulting expression, the following identities related to Levi-Civita tensor are required

$$\begin{aligned} \tfrac{1}{2}\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\, {\cdot }{\cdot }\,\overset{{\langle 3\rangle }}{\varvec{\epsilon }}&=\varvec{1} \ , \quad \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}=\overset{{\langle 4\rangle }}{\varvec{1}}-\overset{{\langle 4\rangle }}{\varvec{T}}\ , \end{aligned}$$
(20.53a)
$$\begin{aligned} \overset{{\langle 4\rangle }}{\varvec{1}}&= \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_i \otimes \varvec{e}_j \ , \quad \overset{{\langle 4\rangle }}{\varvec{T}}= \varvec{e}_i \otimes \varvec{1} \otimes \varvec{e}_i \ , \end{aligned}$$
(20.53b)
$$\begin{aligned} \overset{{\langle 4\rangle }}{\varvec{1}}\, {\cdot }{\cdot }\,\varvec{A}&= \varvec{A} \ , \quad \overset{{\langle 4\rangle }}{\varvec{T}}\, {\cdot }{\cdot }\,\varvec{A} = \varvec{A}^\mathrm {T} \ , \end{aligned}$$
(20.53c)
$$\begin{aligned} \big (\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{a}\big )\cdot \big (\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{b}\big )&=\varvec{a}\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{b}=\varvec{b}\otimes \varvec{a}-(\varvec{a}\cdot \varvec{b})\varvec{1}\, ,\end{aligned}$$
(20.53d)
$$\begin{aligned} \varvec{a} \times \varvec{b}&= - \varvec{a} \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{b} = \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\, {\cdot }{\cdot }\,(\varvec{a} \otimes \varvec{b}) . \end{aligned}$$
(20.53e)

Note that the tensor \(\overset{{\langle 4\rangle }}{\varvec{1}}\) is referred as the identity tensor of rank four and that the tensor \(\overset{{\langle 4\rangle }}{\varvec{T}}\) is the “transposer,” i.e., a tensor of rank four representing to the transposition of a tensor of rank two. In addition, the Grassmann identities for the double cross product will be used in the following and may be expressed in terms of the Levi-Civita tensor

$$\begin{aligned} \varvec{a}\times (\varvec{b}\times \varvec{c})=\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\, {\cdot }{\cdot }\,(\varvec{a}\otimes (\varvec{b}\times \varvec{c}))=\varvec{a}\cdot (\varvec{c}\otimes \varvec{b}-\varvec{b}\otimes \varvec{c})\, ,\end{aligned}$$
(20.53f)
$$\begin{aligned} (\varvec{a}\times \varvec{b})\times \varvec{c}=\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\, {\cdot }{\cdot }\,((\varvec{a}\times \varvec{b})\otimes \varvec{c})=\varvec{c}\cdot (\varvec{a}\otimes \varvec{b}-\varvec{b}\otimes \varvec{a}). \end{aligned}$$
(20.53g)

After same algebraic manipulations, the product of \(\dot{\varvec{Q}}\) with the tensor \(\varvec{q}\otimes \varvec{q}\) is given by

$$\begin{aligned} \dot{\varvec{Q}}\cdot \varvec{q}\otimes \varvec{q}=\big (1-\cos (\psi )\big )\dot{\varvec{q}}\otimes \varvec{q}+\sin (\psi )(\dot{\varvec{q}}\times \varvec{q})\otimes \varvec{q}. \end{aligned}$$
(20.54)

The final expression for the product with the tensor \(\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{q}\) reads

$$\begin{aligned} \begin{aligned} \dot{\varvec{Q}}\cdot \big (\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{q}\big )=-\sin (\psi )\dot{\psi }\overset{{\langle 3\rangle }}{\varvec{\epsilon }}\cdot \varvec{q}-\big (1-&\cos (\psi )\big )\varvec{q}\otimes (\dot{\varvec{q}}\times \varvec{q})\\ +\cos (\psi )\dot{\psi }[\varvec{1}&-\varvec{q}\otimes \varvec{q}]-\sin (\psi )\varvec{q}\otimes \dot{\varvec{q}}. \end{aligned} \end{aligned}$$
(20.55)

Using the two previous relations, the angular velocity tensor \(\varvec{\Omega }\) can be expressed as

$$\begin{aligned} \varvec{\varOmega }=\sin (\psi )\big (&\!1-\cos (\psi )\big )[(\dot{\varvec{q}}\times \varvec{q})\otimes \varvec{q}-\varvec{q}\otimes (\dot{\varvec{q}}\times \varvec{q})]-{}\nonumber \\&-[\dot{\psi }\varvec{q}+\sin (\psi )\cos (\psi )\dot{\varvec{q}}]\cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}+\big (1-\cos (\psi )\big )[\dot{\varvec{q}}\otimes \varvec{q}-\varvec{q}\otimes \dot{\varvec{q}}]\ . \end{aligned}$$
(20.56)

From this expression, the angular velocity vector \(\varvec{\omega }\) is obtained by computing the axial vector of \(\varvec{\Omega }\) according to Eq. (20.21),

$$\begin{aligned} \varvec{\omega }=\dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}}+\big (1-\cos (\psi )\big )\varvec{q}\times \dot{\varvec{q}}\ . \end{aligned}$$
(20.57)

By means of Eq. (20.21), the angular velocity tensor can be recomputed from Eq. (20.57)

$$\begin{aligned} \varvec{\varOmega }= \big (1-\cos (\psi )\big )\big [\dot{\varvec{q}} \otimes \varvec{q}- \varvec{q}\otimes \dot{\varvec{q}}\big ] - \big (\dot{\psi }\varvec{q}+\sin (\psi )\dot{\varvec{q}}\big ) \cdot \overset{{\langle 3\rangle }}{\varvec{\epsilon }}\ , \end{aligned}$$
(20.58)

which is a simpler expression than the one in Eq. (20.56).