A Sustainable Approach for Determining Compromise Ranking Based on Intuitonistic Fuzzy Score Functions

Abstract

Many real-world decision-making problems require some degree of uncertainty to be taken into account. For purpose of representing such problems, intuitionistic fuzzy sets are used, however, most well-known multi-criteria decision-making methods operate in a crisp environment. In this paper, we present an assessment of score functions that are used to convert fuzzy numbers into crisp ones. Five score functions were selected to assess their usefulness and effectiveness. Those functions were used to transform the theoretical fuzzy decision matrix problems into a crisp environment for evaluating alternatives using the Measurement Alternatives and Ranking according to COmpromise Solution (MARCOS) method. In addition, the compromise between score functions is presented and compared with the other results. The research showed that score functions are useful tools when dealing with problems in an uncertain environment and might prove helpful for decision-makers.

1 Introduction

Multi-criteria decision-making problems consider problems that are represented either by crisp values, or ones that consist of some type of uncertainty. There are many studies devoted to providing a way of modeling uncertain data based on classical arithmetic methods [1]. Most real-world problems are presented with some kind of uncertainty, thus such an approach is crucial to model problems as precisely as possible to reflect uncertain knowledge flexibly. Uncertainty modeling is often used in multi-criteria decision-making problems due to its high reliability [15].

Throughout the years, numerous ways of representing uncertain knowledge emerged. Among the classical approaches are fuzzy sets (FS), based on the idea related to partial membership [10]. Over the years, fuzzy sets have seen many developments: Hesitant Fuzzy Sets (HFS) [24], Fermatean Fuzzy Sets (FFS) [22], or Intuitionistic Fuzzy Sets (IFS) [11]. Indeed, the main advantage of the generalization of fuzzy sets is a new approach to uncertainty modeling that considers new degrees of membership, which gives the expert the ability to adapt to the characteristics of the problem.

The Intuitionistic Fuzzy Sets are one of the most popular fuzzy approaches, as it introduces the possibility of determining the degree of membership and non-membership, which provides its usefulness in many areas e.g. sustainable supplier selection [18], medical diagnosis [9] or investment selection [31]. The wide use of Intuitionistic Fuzzy Sets has led to many studies which improved their usability and significance in multi-criteria decision-making environments.

Many multi-criteria decision-making methods were extended to enable problem-solving in an uncertain environment. However, most of the highly developed methods are designed to solve problems where the values are crisp [2]. This has given rise to a number of methods for converting fuzzy values to sharp values, and one approach is the use of the score functions which was originally proposed by Chen and Tan [6]. The consequence of the appearance of such a solution was a trend in which various score functions were proposed. This emerged a new problem, as their use within the same problem may be characterized by obtaining different results. It creates a research gap that needs to be filled and determines which score function to select so that the results are satisfactory.

In this study, five different score functions were chosen to carry out the analysis. The score functions provide a way to convert fuzzy numbers into crisp ones which then can be used with the Measurement Alternatives and Ranking according to COmpromise Solution (MARCOS) method to assess alternatives of the decision matrix. The decision problems were generated to ensure that solution would not depend on a specific problem. The theoretical problems were then assessed using the previously mentioned approach to provide rankings that can be compared with selected correlation coefficients. Additionally, the compromise solution of all score function preferences is proposed. The main purpose of this study is to emphasize the differences in utilizing different score functions regarding their influence on the final rankings of multi-criteria decision problems.

The rest of the paper is organized as follows. Section 2 presents a literature review providing a view of current trends in fuzzy problem-solving and the score functions used in them. In Sect. 3 the preliminaries of the IFS, the scores functions, the MARCOS method, and selected similarity coefficients are presented. In Sect. 4, the study case is shown, where the theoretical problem of the functioning of the different scores function is raised. Section 5 includes a description of the results obtained from the examined research. Finally, in Sect. 6, the summary is presented, and the conclusions are drawn.

2 Literature Review

The utility of score functions has been demonstrated in a number of researches that solve real-world problems that are based on intuitionistic fuzzy data.

G. Büyüközkan and F. Göçer [4] showed the usefulness of score functions in the problem of supplier selection, where five alternatives were considered. They proposed a new approach consisting of IF-AHP, IFAD, and score functions which they compared to IF-TOPSIS. C. Zhang et al. [32] presented a similar approach to solving MCDA problems, as they have as well utilized the MCDA method with score functions, but the method they chose was MULTIMOORA. In their work, they have created the assessment of the energy storage technologies, where fourteen alternatives described by eleven criteria were considered. A different approach was presented by Y. Chen [8] in his work, where for the evaluation of physical education teachers he proposed an evaluation solely based on intuitionistic fuzzy information. Jian Lin et al. [17] presented a new MCDA method based on a score function which they called Preference Attitude-Based. Moreover, they presented its usage in a real problem, which considered renewable energy source selection, where four different alternatives were considered. D. Tripathi et al. [25] presented an improved CoCoSo method that incorporated intuitionistic fuzzy parametric divergence measures and score function. The usage of this method was presented as a medical decision-maker support system where treatment options for patients were evaluated. S. Zeng et al. [30] and JH Park et al. [20], both presented their approach to modifying the VIKOR method that incorporated the score functions, however, S. Zeng et al. presented its usage in the subject of supply chain management, on the other hand, JH Park et al. problem at hand was evaluating university faculty. Moreover, the usage of score functions was adopted for interval-valued intuitionistic fuzzy problems. Their usage was presented for example by Jin Han Park [21] in his work where he proposed an extended TOPSIS method that incorporated the score function for IVIFNs, which usage was shown through the evaluation of five air-conditioning systems should be installed in a library. Additionally, Liangping Wu et al. [27] provided a way of using the score function with the VIKOR method for financing risk assessment of rural tourism projects under interval-valued intuitionistic fuzzy circumstances. Aside from the practical presentations of usage, the score functions utility is researched through many angles, which is presented in Table 1. The literature review shows how crucial the score functions are in the MCDM problems, but not enough analysis was carried out. This research tries to provide a comprehensive view of how the usage of different score functions alters the final results and advises the most favourable score function depending on the problem at hand.

Table 1. Applications of score functions in MCDA

3 Research Methodology

3.1 Intuitionistic Fuzzy Sets

Definition 1

An Intuitionistic Fuzzy Set (IFS) A in a universe X is defined as an object of the following form:

$$\begin{aligned} A=\left\{ \left\langle x_{j}, \mu _{j}, \nu _{j}\right\rangle \mid x_{j} \in X\right\} \end{aligned}$$

(1)

where $\mu : X \rightarrow [0, 1]$ and $\nu : X \rightarrow [0,1]$ such that $0 \leqslant \mu _{j}+\nu _{j} \leqslant 1$ for all $x_j \in X$. The values of $\mu _j$ and $\nu _j$ represent the degrees of membership and non-membership of $x_j \in X$ in A respectively [7].

For every $A \in IFS(X)$ (the class of IFSs in the universe X), the value of

$$\begin{aligned} \pi _{j}=1-\mu _{j}-\nu _{j} \end{aligned}$$

(2)

represents the degree of hesitation (or uncertainty) associated with the membership of element $x_j \in X$ in IFS A, where $0 \leqslant \pi _{j} \leqslant 1$.

3.2 IFS Score Functions

The purpose of the score function is to convert the uncertain data representation to a crisp value. Different approaches to performing such an action obtain diverse values as a final output. Selected score functions and the formulas for their calculations are presented below [7, 9, 15].

$$\begin{aligned} S_{\textrm{I}}\left( X_{i j}\right) =\mu _{i j}-v_{i j} \end{aligned}$$

(3)

$$\begin{aligned} S_{\textrm{II}}\left( X_{i j}\right) =\mu _{i j}-v_{i j} \cdot \pi _{i j} \end{aligned}$$

(4)

$$\begin{aligned} S_{\textrm{III}}\left( X_{i j}\right) =\mu _{i j}-\left( \frac{v_{i j}+\pi _{i j}}{2}\right) \end{aligned}$$

(5)

$$\begin{aligned} S_{\textrm{IV}}\left( X_{i j}\right) =\left( \frac{\mu _{i j}+v_{i j}}{2}\right) -\pi _{i j} \end{aligned}$$

(6)

$$\begin{aligned} S_{\textrm{V}}\left( X_{i j}\right) =\gamma \cdot \mu _{i j}+(1-\gamma ) \cdot \left( 1-v_{i j}\right) , \quad \gamma \in [0,1] \end{aligned}$$

(7)

where $S_I(X_{ij}),S_{II}(X_{ij}),S_V(X_{ij}) \in [-1,1]$, $S_{III}(X_{ij}) \in [-0.5,1]$, and $S_{IV}(X_{ij}) \in [-1, 0.5]$.

3.3 MARCOS Method

The Measurement Alternatives and Ranking according to COmpromise Solution (MARCOS) method was introduced by Željko Stević in 2020 [23] as a new multi-criteria decision-making method, which was presented in the study case of sustainable supplier selection in healthcare industries. This method provides a new approach to solving decision problems, as it considers an anti-ideal and an ideal solution at the initial steps of consideration of the problem. Moreover, it proposes a new way to determine utility functions and their further aggregation, while maintaining stability in the problems requiring a large set of alternatives and criteria.

Step 1. The initial step requires to define set of n criteria and m alternatives to create decision matrix.

Step 2. Next, the extended initial matrix X should be formed by defining ideal (AI) and anti-ideal (AAI) solution.

$$\begin{aligned} X=\begin{gathered} AII \\ A_{1} \\ A_{2} \\ \cdots \\ A_{m} \\ A I \end{gathered}\left[ \begin{array}{cccc} x_{a a 1} &{} x_{a a 2} &{} \ldots &{} x_{a a n} \\ x_{11} &{} x_{12} &{} \cdots &{} x_{1 n} \\ x_{21} &{} x_{22} &{} \ldots &{} x_{2 n} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ x_{m 1} &{} x_{22} &{} \cdots &{} x_{m n} \\ x_{a i 1} &{} x_{a i 2} &{} \cdots &{} x_{a i n} \end{array}\right] \end{aligned}$$

(8)

The anti-ideal solution (AAI) which is the worst alternative is defined by Eq. (9), whereas the ideal solution (AI) is the best alternative in the problem at hand defined by Eq. (10).

$$\begin{aligned} A A I=\min _{i} x_{i j} \quad \text{ if } j \in B \text{ and } \max _{i} x_{i j} \quad \text{ if } j \in C \end{aligned}$$

(9)

$$\begin{aligned} A I=\max _{i} x_{i j} \quad \text{ if } j \in B \text{ and } \min _{i} x_{i j} \quad \text{ if } j \in C \end{aligned}$$

(10)

where B is a benefit group of criteria and C is a group of cost criteria.

Step 3. After defining anti-ideal and ideal solutions, the extended initial matrix X needs to be normalized, by applying Eqs. (11) and (12) creating normalized matrix N.

$$\begin{aligned} n_{i j}=\frac{x_{a i}}{x_{i j}} \quad \text{ if } j \in C \end{aligned}$$

(11)

$$\begin{aligned} n_{i j}=\frac{x_{i j}}{x_{a i}} \quad \text{ if } j \in B \end{aligned}$$

(12)

Step 4. The weight for each criterion needs to be defined to present its importance in accordance with others. The weighted matrix V needs to be calculated by multiplying the normalized matrix N with the weight vector through Eq. (13).

$$\begin{aligned} v_{i j}=n_{i j} \times w_{j} \end{aligned}$$

(13)

Step 5. Next, the utility degree K of alternatives in relation to the anti-ideal and ideal solutions needs to be calculated by using Eqs. (14) and (15).

$$\begin{aligned} K_{i}^{-}=\frac{\sum _{i=1}^{n} v_{i j}}{\sum _{i=1}^{n} v_{a a i}} \end{aligned}$$

(14)

$$\begin{aligned} K_{i}^{+}=\frac{\sum _{i=1}^{n} v_{i j}}{\sum _{i=1}^{n} v_{a i}} \end{aligned}$$

(15)

Step 6. The utility function f of alternatives, which is the compromise of the observed alternative in relation to the ideal and anti-ideal solution, needs to be determined. Its done using Eq. (16).

$$\begin{aligned} f\left( K_{i}\right) =\frac{K_{i}^{+}+K_{i}^{-}}{1+\frac{1-f\left( K_{i}^{+}\right) }{f\left( K_{i}^{+}\right) }+\frac{1-f\left( K_{i}^{-}\right) }{f\left( K_{i}^{-}\right) }} \end{aligned}$$

(16)

where $f\left( K_{i}^{-}\right)$ represents the utility function in relation to the anti-ideal solution and $f\left( K_{i}^{+}\right)$ represents the utility function in relation to the ideal solution.

Utility functions in relation to the ideal and anti-ideal solution are determined by applying Eqs. (17) and (18).

$$\begin{aligned} f\left( K_{i}^{-}\right) =\frac{K_{i}^{+}}{K_{i}^{+}+K_{i}^{-}} \end{aligned}$$

(17)

$$\begin{aligned} f\left( K_{i}^{+}\right) =\frac{K_{i}^{-}}{K_{i}^{+}+K_{i}^{-}} \end{aligned}$$

(18)

Step 7. Finally, rank alternatives accordingly to the values of the utility functions. The higher the value the better an alternative is.

3.4 Rank Similarity Coefficients

In order to compare the performance of the score functions, it would be useful to compare the rankings obtained after evaluating the values calculated using these functions. For this purpose, one can use rank similarity coefficients, which are often used in the literature to compare the resulting rankings. In the case of our study, we decided to use the weighted Spearman’s correlation coefficient, which allows comparing rankings considering alternatives rated the best as more significant, and the WS ranking similarity coefficient, which the main assumption that the positions of top of the rankings have a more significant influence on similarity. The formulas for the calculation of both coefficients are presented below in Eq. (19) for weighted Spearman’s correlation and Eq. (20) for WS rank similarity coefficient.

$$\begin{aligned} r_{w}=1-\frac{6 \cdot \sum _{i=1}^{n}\left( x_{i}-y_{i}\right) ^{2}\left( \left( n-x_{i}+1\right) +\left( n-y_{i}+1\right) \right) }{n \cdot \left( n^{3}+n^{2}-n-1\right) } \end{aligned}$$

(19)

$$\begin{aligned} W S=1-\sum _{i=1}^{n}\left( 2^{-x_{i}} \frac{\left| x_{i}-y_{i}\right| }{\max \left\{ \left| x_{i}-1\right| ,\left| x_{i}-n\right| \right\} }\right) \end{aligned}$$

(20)

where $x_i$ means position in the reference ranking, $y_i$ is the position in the second ranking and n is a number of ranked elements.

4 Research Findings

With the increasing popularity of multi-criteria decision-making, the need has arisen to reflect real-world problems as accurately as possible. However, in many real-world problems, it is impossible to give crisp values, as uncertainties arise that can significantly alter the results. For the purposes of mapping expert knowledge as accurately as possible and providing sufficient flexibility, fuzzy sets have been proposed as one of the solutions. The intuitionistic fuzzy sets are a type of fuzzy set that represents decisiveness and indecisiveness for a given alternative. However, many multi-criteria decision-making methods have been developed that base their operation on crisp values, rendering them unsuitable for use with IFS problems.

In order to ensure that existing methods can be used for fuzzy problems, score functions were proposed to convert crisp to fuzzy values. However, as a number of score functions were developed, it presented a need of comparing those functions. For this purpose, we present two examples, one with a small decision matrix and the second with a big one. The matrices were generated to provide an objective view of the results, as the field of the problems is no concern in this matter. Moreover, the compromise ranking was calculated, by creating a matrix from the preferences acquired by score functions and executing the MARCOS method for such a decision matrix.

4.1 Small Example

The small example was generated for six alternatives and four criteria and is presented in Table 2. Such matrix dimensions should represent most of the problems considered, as small problems are the most prevailing in the literature. In the matrix, the first value indicates the value of decisiveness, while the second determines the degree of indecisiveness.

Table 2. Small decision matrix represented by intuitionistic fuzzy sets.

4.2 Big Example

The second example taken into consideration is supposed to represent problems with a large number of alternatives. For this purpose, the matrix of twenty alternatives and six criteria was generated. Problems with such dimensionality are less frequently used in literature, however, in real-world problems, one often encounters even more alternatives and it is usually even more difficult for the decision-maker to make the right choice, which makes it an important case to check with every MCDA solution. The generated values for the decision matrix are presented in Table 3 for criteria one to three and in Table 4 for criteria four to six.

Table 3. Big decision matrix represented by intuitionistic fuzzy sets $C_{1}-C_{3}$.

Table 4. Big decision matrix represented by intuitionistic fuzzy sets $C_{4}-C_{6}$.

5 Discussion of Findings

5.1 Small Example

The crisp values of criteria for each alternative calculated by the score function are presented by corresponding Tables. Table 5 presents the values for the $S_{I}$ score function. This function operates in the range $[-1, 1]$ and the spread of its values is around 1.624, which shows that the range is used effectively, and values should differ greatly from each other.

Table 5. Crisp small decision matrix calculated with $S_{I}$ score function.

Table 6 presents values calculated using $S_{II}$ score function. This function is defined as the degree of membership minus the product of the non-membership and hesitation degrees. This function operates in the same range as the $S_{I}$ functions, which is $[-1, 1]$. However, in its case, the spread of the values is around 0.9937 which is significantly lower than the one for the $S_{I}$ function. Which might be crucial in terms of highlighting the differences between alternatives.

Table 6. Crisp small decision matrix calculated with $S_{II}$ score function.

The values acquired by execution of $S_{III}$ function are presented in Table 7. This function subtracts the arithmetic mean of the non-membership and hesitation degrees and operates in the range of $[-0.5, 1]$. Considering this and the fact that the spread of the values is around 1.1396 it presents high differentiation of the individual IFS values from the initial decision matrix.

Table 7. Crisp small decision matrix calculated with $S_{III}$ score function.

Score function $S_{IV}$ operates in a similar range as the $S_{III}$ function, but the exact values are different, namely, the range of this function is $[-1, 0.5]$. This function is defined as the arithmetic mean of the membership and non-membership degrees minus the hesitation degree and the values calculated using it, are presented in Table 8. The spread of calculated values is around 1.1713, which suggests that this function is used to a similar extent as the $S_{III}$ function, making visible differences between original IFS values.

Table 8. Crisp small decision matrix calculated with $S_{IV}$ score function.

In Table 9, the values calculated using the function $S_{V}$ are presented. This function operates in exactly the same range as the $S_{I}$ and $S_{II}$ functions, however, the spread of the values is the smallest, being around 0.812. This function differentiates the original values the least and even though it may not be suitable for all decision-makers, this function may prove to be more suitable for use with decision-making methods.

Table 9. Crisp small decision matrix calculated with $S_{V}$ score function.

Each of the matrices acquired with the usage of score functions was used to execute the MARCOS method to calculate the preference of considered alternatives. The preferences for specific score functions are shown in Table 10. Those results provide us with a better view of how those functions differ in terms of the final results of conducting a multi-criteria decision analysis. Functions $S_{I}$ and $S_{IV}$ provide values, that might be hard to distinguish by the decision maker as most of them are on the second decimal place and the spread of the values is 0.0301 and 0.0403 respectively. The function $S_{III}$ is somewhat in the middle presenting relatively easy-to-distinguish differences between preferences with a spread of 0.2547. While functions $S_{II}$ and $S_{V}$ allowed to obtain values that are easy to distinguish and their spread is 0.6069 and 0.3739 respectively.

Table 10. Preferences for small decision matrix computed with MARCOS method for $S_{I}$-$S_{V}$ score functions.

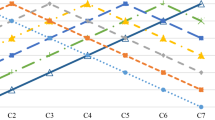
In order to better reflect the differences in the obtained rankings, two similarity coefficients were used. The first one, Weighted Spearman’s correlation coefficient is shown on the heatmap in Fig. 1. In this specific example, we can see that rankings provided by the function $S_{II}$ and $S_{III}$ are identical. Considering this, the score function $S_{II}$ might be preferred by decision-makers as it provided more distinctive values of preference. Those two rankings are highly similar to the one provided by the function $S_{V}$ which was the second function with the highest spread in terms of preference values. However, the compromise ranking showed the highest similarity with the one acquired using the function $S_{IV}$. This is an interesting case and should be taken into account when choosing the score function, because even though the score function $S_{IV}$ provided values with low spread, the consensus of all score functions is the closest to provided by this exact function.

The second coefficient, namely the WS coefficient is presented in Fig. 1. In the case of this coefficient, the situation is very similar, which only confirms the previous conclusions. The use of this coefficient is important not only to confirm but also to see how the podium changes, as this coefficient is asymmetric. As can be seen from the presented heatmap, it is not very significant in the case under consideration.

Fig. 1.

Weighted Spearman’s correlation and WS coefficient of rankings for small decision matrix.

5.2 Big Example

Table 11 presents values calculated using $S_{I}$ function. Similarly to the small problem in this case the function managed to utilize almost the whole range considering that it operates in the range $[-1, 1]$, and provided values which spread is around 1.9379 (Table 11).

Table 11. Crisp big decision matrix calculated with $S_{I}$ score function.

The second function, namely the $S_{II}$ function yielded values presented in Table 12. Their spread is about 1.1971, which is higher than in the case of the small example, but there may be a tendency for more alternatives to result in more spread-out values.

Table 12. Crisp big decision matrix calculated with $S_{II}$ score function.

The values acquired using the function $S_{III}$ are presented in Table 13. This function operates in the range of $[-0.5, 1]$ and its spread is around 1.4427, which shows that it yielded values almost across the whole range similar to function $S_{I}$.

Table 13. Crisp big decision matrix calculated with $S_{III}$ score function.

The function $S_{IV}$ similar to function $S_{III}$ used up almost the whole range of values, as its spread is 1.4 and presented values are easily distinguishable from each other. Once again the spread is even higher than in the small example, which is preferable considering that such differences should be more prominent to the decision maker making it suitable for problems where a high number of alternatives is considered.

Table 14. Crisp big decision matrix calculated with $S_{IV}$ score function.

The last function, namely function $S_{V}$ yielded values presented in Table 15. This function operates in the same range as functions $S_{I}$ and $S_{II}$, however, the spread of its values which is around 0.9689 is the smallest out of all presented functions. The same characteristics are present as in the small problem, where function $S_{V}$ provides the smallest spread of values, which might be less preferable by a decision maker, as the perceived differences are not so apparent. However, in some of the decision-making methods, such an approach might be preferable.

Table 15. Crisp big decision matrix calculated with $S_{V}$ score function.

Each of the score functions provided matrices of crisp values, which then were used in the MARCOS method. The calculated preferences of considered alternatives are presented in Table 16. Similar to the small problem, using score function $S_{I}$ the calculated preferences are hard to distinguish as almost all values have zeros on the first two decimal places. This function provided preferences with a spread of 0.0026, which might be perceived by decision-makers that this function does not differentiate the values enough. Functions $S_{III}$, $S_{IV}$ and $S_{V}$ provide preferences whose spread is respectively 0.2851, 0.2291 and 0.2961. The function $S_{II}$ once again provided the highest spread of preference values, as its spread is 0.4665, which might be highly preferable by decision-makers.

Table 16. Preferences for big decision matrix computed with MARCOS method for $S_{I}$-$S_{V}$ score functions.

Figure 2 presents a heatmap of the values of correlation calculated using Weighted Spearman’s correlation coefficient for resulting rankings. Once again rankings acquired using functions $S_{II}$ and $S_{III}$ present high similarity equal to 0.96. Additionally, those two functions are highly similar to rankings provided by the function $S_{V}$. The compromise ranking shows the highest similarity of 0.78 with rankings yielded using the function $S_{IV}$, but it is worth mentioning that functions $S_{II}$ and $S_{III}$ have significant similarity as well. Contrary to the small example, the function $S_{IV}$ did not provide a similar ranking to the compromise one.

WS similarity coefficient presented in Fig. 2 allows us to draw similar conclusions as in the case of Weighted Spearman’s correlation coefficient. However, this coefficient shows a higher similarity of compromise ranking with rankings provided by functions $S_{II}$ and $S_{III}$, which means that more important alternatives, namely the one closer to the podium are more alike than the end of the ranking. Additionally, the similarity of ranking of the function $S_{IV}$ shows asymmetrical similarity to compromise ranking.

Fig. 2.

Weighted Spearman’s correlation and WS coefficient of rankings for big decision matrix.

6 Conclusion

The multitude of decision-making problems in the real world requires a constant search for new solutions in this area. Often the problems considered are problems in which there is a degree of uncertainty that renders a large proportion of the already-known solutions useless and unusable. This creates a great need to find ways of defuzzification of problems, so as not to be limited to methods that only solve a specific type of problem.

In this study, defuzzification of the intuitionistic fuzzy sets was taken into consideration. For this purpose, five different score functions were compared in terms of what values they return and ultimately how this affects the ranking obtained using the MARCOS method. From the results obtained, it can be concluded that the $S_{I}$ function uses most of the range in which it operates, and yet the preference values that are obtained using this function differ from each other at the third decimal place, making the values unreadable to the decision-maker. The function $S_{III}$ shows similar characteristics to the $S_{I}$ function. On the other hand, functions $S_{II}$, $S_{III}$ and $S_{V}$ provide highly distinguishable preference values and moreover, the rankings acquired by using those functions are highly similar to the compromise ranking. Additionally, the decision maker could calculate the problem using all of the score functions and conduct additional MARCOS method assessment as the ranking yielded by such compromise showed to be a viable option.

In future studies, practical examples might be presented to encourage the use of score functions in real-world problems and present their reliability in practical settings. Moreover, the technique for compromise of score functions should be further studied, as it might prove to be even more reliable in decision-making problems than any of the considered score functions on its own.