Abstract
Visibly Pushdown Automata (VPAs) are a subclass of pushdown automata, which can be well applied as specification formalism for verification and the model for XML streams process. The input alphabet is partitioned into three disjoint sets: call, internal and return symbols, which can determine a push, pop or no stack operation taken by VPAs respectively. Hence, the matchings of push (call) and pop (return) make languages with matching nested relations accepted. Nevertheless, it is limited to one-to-one matching. In this paper, we extend the model of VPAs over multi-matching nested relations. By a subdivision for call and return symbols, inner-calls and inner-returns are obatined to discriminate a one-to-n or n-to-one matching relation. Then, Multi-matching Visibly Pushdown Automata (MVPA) are formally defined whose stack behavior is achieved by setting a guard in the stack, which can guarantee whether a one-to-n or n-to-one matching nested relation is read without confusion. Each nondeterministic multi-matching visibly pushdown automaton is demonstrated to be transformed into a deterministic one. Moreover, the symbolic version of multi-matching visibly pushdown automata is proposed when the input alphabet is given by a Boolean algebra where there is an infinite domain.
This research is supported by the NSFC Grant Nos. 62202371 and 61902312.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A model of nested words is proposed for describing the data with a dual linear-hierarchical structure [1]. A nested word consists of a linear sequence of positions, calls, internals and returns, augmented with matching relations connecting from calls to returns. Visibly Pushdown Automata (VPAs) are proposed over nested words by Alur in [2] as a subclass of Pushdown Automata (PDAs) [3]. VPAs are well applied as the automaton model for processing XML streams [4, 5] and specification formalism for verification [6, 7]. The key character is that the alphabet in VPAs is partitioned into three disjoint sets of call, internal, and return symbols. Based on the partition, VPAs can push symbols into the stack by reading a call, pop the top of the stack by a return, and via an internal, VPAs only modify the state with the stack unchanged. Hence, this setting makes the stack behavior visible. In classical automata theory, there are two basic assumptions: a finite state space and a finite alphabet. The concept of automata with predicates instead of concrete symbols was first mentioned in [8] and was first discussed in [9] in the context of natural language processing. Accordingly, Symbolic Visibly Pushdown Automata (SVPAs) are proposed as an executable model for nested words over infinite alphabets [10], which are further applied in XML processing and program trace analysis [11].
Nevertheless, the models above are limited to describe only one-to-one matching structures. If a call (resp. return) is matched with multiple returns (resp. calls), a one-to-n (resp. n-to-one) multi-matching nested relation is obtained. By introducing a tagged alphabet, multi-matching nested words are defined where symbols can be calls, inner-calls, internals, inner-returns and returns. Multi-matching Nested Traceable Automata (MNTAs) are proposed to describe the languages of multi-matching nested words [12,13,14], which is an variant of Traceable Automata (TAs) and VPAs. In a MNTA, both of states and input symbols, which are recorded in the stack, are utilized to determine the subsequent transitions together. For a call, the current input symbol and state are pushed into the stack, while for a return they are popped. Note that the automaton traces back to the state which is popped then. As for inner-calls and inner-returns, the top stack is updated besides state transfer.
However, natural nondeterminization exists in MNTAs if there are several calls at a state. Suppose two calls \({^<\negmedspace a}\) and \({^<\negmedspace b}\) can be read at a state q, one cannot construct a MNTA such that \({^<\negmedspace a}\) is certain to read indeed ahead of \({^<\negmedspace b}\). In addition, the characteristic that a state is pushed at a call and finally traced back upon a return makes MNTAs accept languages always beyond a single multi-matching nested relation. With this motivation, we loosen the restriction on stack behavior of MNTAs by eliminating the record of states from the stack. Only symbols are recorded as a guard during transitions. Accordingly, Multi-matching Visibly Pushdown Automata (MVPAs) are proposed as a new model for describing multi-matching nested words. And nondeterministic MVPAs are as expressive as deterministic ones. In addition, if the input alphabet is given by a Boolean algebra where there is an infinite domain, symbolic version of multi-matching visibly pushdown automata is formally proposed.
The rest of paper is organized as follows. In Sect. 2, we revisit the definitions of multi-matching nested relations and its linear word encoding. Section 3 extends visibly pushdown automata over multi-matching relations. Multi-matching visibly pushdown automata are formally defined. Besides, a deterministic MVPA can be constructed for a nondeterministic one. When the input alphabet is given by a Boolean algebra where there is an infinite domain, symbolic version of multi-matching visibly pushdown automata is proposed in Sect. 4. Finally, conclusions are drawn in Sect. 5.
2 Preliminaries
In this section, we first recall the concept of multi-matching nested relations. By linear word encodings, multi-matching nested languages can be obtained.
2.1 Multi-matching Nested Relation
Given a linear sequence, the positions are divided into calls, internals and returns. To realize n-to-one and one-to-n matchings, inner-call and inner-return are introduced. Hence, n-to-one matching relation can be achieved by a call, multiple inner-calls and a return, while one-to-n by a call, multiple inner-returns and a return. Suppose pending edges are indicated by edges starting at \(-\infty \) and edges ending at \(+\infty \). Assume that \(-\infty< i,j < +\infty \) for integers i and j.
Definition 1 (Multi-matching Nested Relation)
A multi-matching nested relation \(\dot{\leadsto }\) of length m, \(m \ge 0\), is a subset of \(\{-\infty , 1, 2, \cdots , m\} \times \{1, 2, \cdots , m, +\infty \}\) such that for any \(i \dot{\leadsto } j\), \(i' \dot{\leadsto } j'\), (i) nesting edges go only forward(\(i<j\)); (ii) nesting edges do not cross(\(i<i' \le j<j'\) does not hold); (iii) only one end of a nesting edge can be shared with others.
For \(i \dot{\leadsto } j\), i, j are denoted as a call and a return respectively. Specifically, if \(j=+\infty \), i is called a pending call while j is denoted a pending return if \(i=-\infty \). Suppose there are n different nesting edges sharing the same call i, namely \(i \dot{\leadsto } j_k\), where \(1 \le k \le n\) and \(1 \le i<j_1<j_2< \cdots <j_n \le m\). Among them, \(i \dot{\leadsto } j_n\) is the outermost nesting edge. By contrast, for each inner nesting edge, \(j_h\) is identified as an inner-return where \(1 \le h<n\). Similarly, for n different nesting edges sharing the same return j, namely \(i_k \dot{\leadsto } j\), where \(1 \le i_1<i_2< \cdots<i_n<j \le m\), each \(i_h\), \(1<h \le n\), is identified as an inner-return. A position is an internal if it is neither a call (resp. inner-call) nor a return (resp. inner-return). A multi-matching nested relation is well-matched if there is no pending call or pending return.
2.2 Word Encoding
Given a multi-matching nested relation, a word can be obtained by assigning each position with a symbol. To distinguish different position categories, a tagged alphabet \(\hat{\varSigma }=\varSigma _c \cup \dot{\varSigma _c} \cup \varSigma _i \cup \dot{\varSigma _r} \cup \varSigma _r\) is introduced, where \(\varSigma _c=\{^<\negmedspace a_1 | a_1 \in \varSigma \}\), \(\dot{\varSigma _c}=\{^<\negmedspace \dot{a_2} | a_2 \in \varSigma \}\), \(\varSigma _i=\varSigma \), \(\dot{\varSigma _r}=\{\dot{a_3} \negmedspace ^> | a_3 \in \varSigma \}\) and \(\varSigma _r=\{a_4 \negmedspace ^> | a_4 \in \varSigma \}\) are the symbols of call, inner-call, internal, inner-return and return, respectively. \(\varSigma \) is a normal alphabet. Note that \(^<\negmedspace a_1\), \({^<\negmedspace \dot{a_2}}\), \({\dot{a_3} \negmedspace ^>}\) and \({a_4\negmedspace ^>}\) are indicated to be matched if and only if \(a_1=a_2=a_3=a_4\).
The set of all multi-matching nested words over \(\hat{\varSigma }\) are denoted as \(\textit{MNW}(\hat{\varSigma })\). Note that due to the requirement of symbol matching, it can be obtained \(\textit{MNW}(\hat{\varSigma })\) \(\subset \hat{\varSigma }^*\).
3 Multi-matching Visibly Pushdown Automata
3.1 Model
Definition 2 (Multi-matching Visibly Pushdown Automata, MVPA)
A multi-matching visibly pushdown automaton is a tuple \(M=(Q, Q_0, F, \hat{\varSigma }, \varGamma , \delta )\), where
-
Q, \(Q_0 \subseteq Q\), \(F\subseteq Q\) are finite sets of states, initial states, final states respectively;
-
\(\hat{\varSigma }=\varSigma _c \cup \dot{\varSigma _c} \cup \varSigma _i \cup \dot{\varSigma _r} \cup \varSigma _r\) is a finite set of input symbols, where \(\varSigma _c\), \(\dot{\varSigma _c}\), \(\varSigma _i\), \(\dot{\varSigma _r}\) and \(\varSigma _r\) denote call, inner-call, internal, inner-return and return symbols, respectively;
-
\(\varGamma \subseteq (\varSigma _c \cup \dot{\varSigma _c} \cup \dot{\varSigma _r}) \times \varXi \cup \{\bot \}\) is a finite set of stack elements including a special bottom-of-stack symbol \(\bot \), where \(\varXi \) is a finite alphabet; and
-
\(\delta \) is a finite set of transitions consisting of the following four parts:
$$\begin{aligned} \delta _c \subseteq&~Q \times \varSigma _c \times Q \times (\varSigma _c \times \varXi )\\ \delta _i \subseteq&~Q \times \varSigma _i \times Q\\ \delta _u \subseteq&~Q \times \varGamma \times (\dot{\varSigma _c} \cup \dot{\varSigma _r}) \times Q \times \varGamma \\ \delta _r \subseteq&~Q \times \varGamma \times \varSigma _r \times Q \end{aligned}$$
The transitions in M can be classified into four categories. Let \(q, q' \in Q\), \(\gamma , \gamma ' \in \varGamma \), \({^<\negmedspace a} \in \varSigma _c\), \({^<\negmedspace \dot{a}} \in \dot{\varSigma _c}\), \(i \in \varSigma _i\), \({\dot{a} \negmedspace ^>} \in \dot{\varSigma _r}\) and \({a \negmedspace ^>} \in \varSigma _r\). For convenience, we use notation a/b to denote a or b.
-
1.
call transition (push transition): \((q, {^<\negmedspace a}, q', {^<\negmedspace a}\xi ) \in \delta _c\) When reading a call \({^<\negmedspace a}\) at state q, M turns to state \(q'\), meanwhile both the call \({^<\negmedspace a}\) and the symbol \(\xi \in \varXi \) are pushed into the stack.
-
2.
internal transition: \((q, i, q') \in \delta _i\)
For an internal i, the operation is similar to the usual finite automata, M only updates the state from q to \(q'\) without the stack modified.
-
3.
update transition: \((q, \gamma , x, q', \gamma ') \in \delta _u\)
-
(a)
Upon an inner-call \(x={^<\negmedspace \dot{a}}\), it is noteworthy that the symbol of the top stack must be \({^<\negmedspace a}\) or \({^<\negmedspace \dot{a}}\) stating that it is the same as or matched with the input symbol. Then, the state is updated to \(q'\) and the top of the stack modifies from \(\gamma ={^<\negmedspace a}\xi / {^<\negmedspace \dot{a}}\xi \) to \(\gamma '={^<\negmedspace \dot{a}}\xi '\) where \(\xi ,\xi ' \in \varXi \). Hence, this transition is denoted as a call update one.
-
(b)
As for an inner-return \(x={\dot{a} \negmedspace ^>}\), it is similar to the case of inner-calls. Besides M turns to \(q'\), the top of the stack is modified from \(\gamma _1={^<\negmedspace a}\xi / {\dot{a} \negmedspace ^>}\xi \) to \(\gamma _2={\dot{a} \negmedspace ^>}\xi '\) where \(\xi ,\xi ' \in \varXi \).
-
(a)
-
4.
return transition (pop transition): \((q, \gamma , {a \negmedspace ^>}, q') \in \delta _r\)
-
(a)
In a return transition with the input return \({a \negmedspace ^>}\), suppose that the top of the stack is \(\gamma =x\xi \). Symbol x can only be one of \({^<\negmedspace a}\), \({^<\negmedspace \dot{a}}\) or \({\dot{a} \negmedspace ^>}\), since x must be matched with \({a \negmedspace ^>}\). Then M turns to \(q'\) and \(\gamma \) is popped.
-
(b)
In particularly, when the stack is empty, i.e. \(\gamma =\bot \), only the state is updated and the stack remains unchanged.
-
(a)
Formally, a stack \(\sigma \) is a finite word over the set \(\varGamma \). All stacks constitute the set \(St=(\varGamma \backslash \{\bot \})^* \cdot \{\bot \}\). Let \(|\sigma |\) stand for the length of \(\sigma \). Especially, when \(\sigma =\bot \), \(|\sigma |=0\); otherwise \(|\sigma |>0\).
A configuration of M is a pair \((q, \sigma )\) where \(q \in Q\) and \(\sigma \in St\). Given a word \(w=w_1 w_2 \cdots w_n\) with multi-matching nest relations, w can be accepted by M if there exists a run of M on w. A run \(\rho \) is defined as a non-empty sequence of configurations, i.e. \(\rho =(q_0, \sigma _0) {\mathop {}\limits ^{\underrightarrow{w_1}}} (q_1, \sigma _1) {\mathop {}\limits ^{\underrightarrow{w_2}}} \cdots {\mathop {}\limits ^{\underrightarrow{w_n}}} (q_n, \sigma _n)\), where \(q_0 \in Q_0\) is an initial state and \(\sigma _0=\bot \). \(\rho \) is accepted by M if \(q_n \in F\) is a final state and \(\sigma _n \in (\varSigma _c \times \varXi )^* \cdot \{\bot \}\). In another word, when M terminates, no inner-call or inner-return symbols are allowed to exist in the stack, since only well-matched or pending calls/returns are considered. The case of a call and multiple inner-calls without a return (or multiple inner-returns and a return without a call) is illegal. The set of multi-matching nested words that are accepted by M constitutes the language L(M).
3.2 Determinization
Given a multi-matching visibly pushdown automaton \(M=(Q, q_0, F, \hat{\varSigma }, \varGamma , \delta )\), M is called to be deterministic if \(q_0\) is the unique initial state in M. Besides, for each transition \(q \in Q\), \(\gamma \in \varGamma \) and \(x \in \hat{\varSigma }\), there is at most one transition for \(\delta (q, \gamma , x)\).
As shown in [2], the main idea of transformation from a nondeterministic MVPA to an equivalent deterministic one is the subset construction with call transitions postponed handling. To do this, two components S and R are introduced, where S is a set of summary edges that keeps track of what transitions are possible from a call transition to a matched return one, and R is a set of reachable states by using the summary information. However, in MVPAs, update transitions require special treatments.
Let \(w=w_1 {^<\negmedspace a} w_2 x w_3\) accepted by a MVPA M, where \(w_1\), \(w_2\) and \(w_3\) are well-matched words where there are no pending calls or returns. One can construct an equivalent deterministic MVPA. After reading call \({^<\negmedspace a}\), the stack of M is now \(({^<\negmedspace a} \lceil S_1,R_1 \rfloor ) \bot \) and M turns to state \(\lceil S,R \rfloor \). All possible pairs \((q,q')\) are included in \(S_1\) such that M can get on \(w_1\) from q with empty stack \(\bot \) to \(q'\) with empty stack \(\bot \). \(R_1\) contains all reachable states by M from any initial state on \(w_1\). Then, several situations are taken into consideration.
-
1.
If \(x \in \varSigma _c\) is a new call, the stack then is \((x \lceil S_2,R_2 \rfloor ) ({^<\negmedspace a} \lceil S_1,\) \(R_1 \rfloor ) \bot \). \(S_2\) contains all pairs such that the stack of M updates from \({^<\negmedspace a}\xi \bot \) to \({^<\negmedspace a}\xi \bot \). \(R_2\) records reachable states by M on \(w_2\).
-
2.
When \(x={^<\negmedspace \dot{a}} \in \dot{\varSigma _c}\) is an inner-call, the stack is updated to \(({^<\negmedspace \dot{a}} \lceil S'_1,R_1 \rfloor ) \bot \). Then \(S'_1=S_1 \cup \{q,q'\}\) where \((q,q')\) records the summary such that M can get from q with \({^<\negmedspace a}\xi \bot \) to \(q'\) with \({^<\negmedspace \dot{a}}\xi \bot \).
-
3.
On the basis of the second case, suppose the inner symbol x is read for the second time, namely \(w=w_1 {^<\negmedspace a} w_2 x w_3 x\). Similarly, the new updated stack is \(({^<\negmedspace \dot{a}} \lceil S''_1, R_1 \rfloor ) \bot \). \(S''_1=S'_1 \cup \{q,q'\}\) where \((q,q')\) records the summary such that M can get \(w_2\) from q with \({^<\negmedspace \dot{a}}\xi \bot \) to \(q'\) with \({^<\negmedspace \dot{a}}\xi \bot \).
-
4.
When the matched return \({a \negmedspace ^>}\) is read with x be inner-call \({^<\negmedspace \dot{a}}\), that means the word is \(w=w_1 {^<\negmedspace a} w_2 {^<\negmedspace \dot{a}} w_3 {a \negmedspace ^>}\). \({^<\negmedspace \dot{a}} \lceil S''_1, R_1 \rfloor \) is popped. And state is updated by using the current summaries \(S''_1\) and S along with a call transition on \({^<\negmedspace a}\), a call update transition on \({^<\negmedspace \dot{a}}\) and a return transition on \({a \negmedspace ^>}\).
Note that the treatment for an inner-return is similar to the analysis above for an inner-call. Accordingly, we present the determinization procedure in detail as below.
Theorem 1
Given a multi-matching visibly pushdown automaton M, an equivalent deterministic one \(M_D\) can be constructed such that they can accept the same language, i.e. \(L(M)=L(M_D)\).
Proof
For a multi-matching visibly pushdown automaton \(M=(Q, Q_0, F, \hat{\varSigma }, \varGamma , \delta )\), one can acquire an equivalent deterministic one \(M_D=(Q', Q_0', F', \hat{\varSigma }, \varGamma ', \delta ')\) according to the following constructions.
First, the set of states in \(M_D\) is expanded as the set \(Q'=2^{Q \times Q} \times 2^Q\). The set \(2^{Q \times Q}\), denoted by S, records the summary edges within a multi-matching nested relation accepted by M, i.e. from a call to an inner-call/inner-return/return or from an inner-call (resp. inner-return) to an inner-call/return (resp. inner-return/return), while a reachable state set can be calculated by \(2^Q\), called R. For convenience and clarity, we denote \(Q'=\lceil S,R\rfloor \).
Let \(Id_X\) indicate the set \(\{(q,q) | q \in X\}\). Then, the set of initial states can be obtained as \(Q_0'=\{\lceil Id_Q, Q_0 \rfloor \}\). A state \(\lceil S,R \rfloor \) is a final one if \(q_f \in R\) where \(q_f \in F\). Hence, \(F'=\{\lceil S,R \rfloor | R \cap F \ne \emptyset \}\).
For the set of stack elements, let \(\varGamma '=\{\varSigma _c \cup \dot{\varSigma _c} \cup \dot{\varSigma _r}\} \times S \times R\) where \(\varXi =S \times R\).
For each symbol \(x \in \hat{\varSigma }\), the top of stack \(\gamma ' \in \varGamma '\) and state \(\lceil S,R \rfloor \in Q'\), the set of transitions \(\delta '\) is constructed as follows:
-
Call. When \(x={^<\negmedspace a} \in \varSigma _c\) is a call, one can construct a call transition \((\lceil S,R \rfloor , {^<\negmedspace a},\) \(\lceil Id_{R'}, R' \rfloor , {^<\negmedspace a} \lceil S,R \rfloor ) \in \delta '_c\) where
$$\begin{aligned} R'=\{q'~|~\exists q \in R, \xi \in \varXi , \text{ s.t. } (q, {^<\negmedspace a}, q', {^<\negmedspace a}\xi ) \in \delta _c\}. \end{aligned}$$ -
Internal. For an internal \(x=i \in \varSigma _i\), there is a transition \((\lceil S,R \rfloor , i, \lceil , S',R' \rfloor ) \in \delta '_i\) where
$$\begin{aligned} S'&=\{(q,q')~|~\exists q'' \text{ s.t. } (q, q'') \in S \text{ and } (q'', i, q') \in \delta _i\},\\ R'&=\{q'~|~\exists q \in R \text{ s.t. } (q, i, q') \in \delta _i\}. \end{aligned}$$ -
Update. There are two cases for inner symbols.
-
Call Update. With regard to an inner-call \(x={^<\negmedspace \dot{a}} \in \dot{\varSigma _c}\), one can construct \((\lceil S,R \rfloor , {^<\negmedspace a} \lceil S_1,R_1 \rfloor / {^<\negmedspace \dot{a}} \lceil S_1,R_1 \rfloor , {^<\negmedspace \dot{a}}, \lceil Id_{R'},R' \rfloor , {^<\negmedspace \dot{a}} \lceil S_2,R_2 \rfloor ) \in \delta '_u\) where
$$\begin{aligned} R'&=\{q'~|~\exists q \in R, \xi ,\xi ' \in \varXi , \text{ s.t. } (q, {^<\negmedspace a}\xi / {^<\negmedspace \dot{a}}\xi , q',{^<\negmedspace \dot{a}}\xi ') \in \delta _u\},\\ S_2&=S_1 \cup S,\\ R_2&=R_1. \end{aligned}$$The pair \((q, q') \in S\) records the summary such that M can get after a call or call update transition, in which the state is updated to state q with stack \(\gamma ={^<\negmedspace a}\xi / {^<\negmedspace \dot{a}}\xi \), to a call update transition from \(q'\) with stack \(\gamma '={^<\negmedspace \dot{a}}\xi '\).
-
Return Update. Similarly, when \(x={\dot{a} \negmedspace ^>} \in \dot{\varSigma _r}\), \((\lceil S,R \rfloor , {^<\negmedspace a} \lceil S'',R'' \rfloor / {\dot{a} \negmedspace ^>} \lceil S'',\) \(R'' \rfloor , {\dot{a} \negmedspace ^>}, \lceil Id_{R'}, R' \rfloor , {\dot{a} \negmedspace ^>} \lceil S'',R'' \rfloor ) \in \delta '_u\) can be constructed, where
$$\begin{aligned} R'&=\{q'~|~ \exists q \in R, \xi ,\xi ' \in \varXi , \text{ s.t. } (q, {^<\negmedspace a}\xi / {\dot{a} \negmedspace ^>}\xi , q',{\dot{a} \negmedspace ^>}\xi ') \in \delta _u\},\\ S_2&=S_1 \cup S,\\ R_2&=R_1. \end{aligned}$$
-
-
Return. When a return \(x={a \negmedspace ^>}\) is read, any type of call, inner-call, inner-return or return symbol can be met at the top of the stack since they are all matched with x. Especially, the stack can also be empty. Hence, four cases are taken into consideration as follows. Suppose the return transition is constructed as \((\lceil S,R \rfloor , y \lceil S'',R'' \rfloor , {a \negmedspace ^>}, \lceil S',R' \rfloor ) \in \delta '_r\). Update is a set of state pairs in S.
-
If \(y={^<\negmedspace a}\), let
$$\begin{aligned} \textit{Update}=\{(q,q') ~|&~ \exists q_1,q_2 \in Q, \xi \in \varXi \text{ s.t. } (q, {^<\negmedspace a}, q_1, {^<\negmedspace a}\xi ) \in \delta _c, (q_1, q_2) \in S\\&\text{ and } (q_2, {^<\negmedspace a}\xi , {a \negmedspace ^>}, q') \in \delta _r\}. \end{aligned}$$Then the two components of the state \((S',R')\) satisfy conditions
$$\begin{aligned} S'&=\{(q,q') ~|~ \exists p \text{ s.t. } (q,p) \in S'' \text{ and } (p, q') \in \textit{Update})\}\\ R'&=\{q'~|~\exists q \text{ s.t. } q \in R'' \text{ and } (q,q') \in \textit{Update}\}. \end{aligned}$$In this case, the matching nested relation has only a one-to-one matching structure.
-
When \(y={^<\negmedspace \dot{a}}\), it indicates that an n-to-one matching relation is currently read. The set Update is defined as:
$$\begin{aligned} \textit{Update}&=\{(q_0,q) ~|~ \exists q \in Q, (q_i,q'_i) \in S'', (q_S, q'_S) \in S, \xi ,\xi ' \in \varXi , 0 \le i \le n, \\&\qquad \qquad \quad ~ n \ge 1, \text{ s.t. } (q'_0, {^<\negmedspace a}, q_1, {^<\negmedspace a}\xi ) \in \delta _c (i=0),\\&\qquad \qquad \quad ~ (q'_i, {^<\negmedspace a}\xi / {^<\negmedspace \dot{a}}\xi , {^<\negmedspace \dot{a}}, q_{i+1}, {^<\negmedspace \dot{a}}\xi ') \in \delta _u (0<i<n),\\&\qquad \qquad \quad ~ (q'_n, {^<\negmedspace \dot{a}}\xi , {^<\negmedspace \dot{a}}, q_S, {^<\negmedspace a}\xi ') \in \delta _u,\\&\qquad \qquad \quad ~ (q'_S, {^<\negmedspace \dot{a}}\xi , {a \negmedspace ^>}, q) \in \delta _r\}. \end{aligned}$$The value of n needs to be larger than 1, since in this case, there is at least one call update transition in the run from a call transition to a return transition. Based on Update, the state \((S',R')\) is calculated by:
$$\begin{aligned} S'&=\{(q,q') ~|~ \exists p \text{ s.t. } (q,p) \in S'' \text{ and } (p, q') \in \textit{Update})\\ R'&=\{q'~|~\exists q \text{ s.t. } q \in R'' \text{ and } (q,q') \in \textit{Update}\}\} \end{aligned}$$ -
For \(y={\dot{a} \negmedspace ^>}\), it is similar to the case of a call update transition. One can easily acquire each component by
$$\begin{aligned} \textit{Update}&=\{(q_0,q) ~|~ \exists q \in Q, (q_i,q'_i) \in S'', (q_S, q'_S) \in S, \xi ,\xi ' \in \varXi , 0 \le i \le n, \\&\qquad \qquad \quad ~ n \ge 1, \text{ s.t. } (q'_0, {^<\negmedspace a}, q_1, {^<\negmedspace a}\xi ) \in \delta _c (i=0),\\&\qquad \qquad \quad ~ (q'_i, {^<\negmedspace a}\xi / {\dot{a} \negmedspace ^>}\xi , {^<\negmedspace \dot{a}}, q_{i+1}, {\dot{a} \negmedspace ^>}\xi ') \in \delta _u (0<i<n),\\&\qquad \qquad \quad ~ (q'_n, {\dot{a} \negmedspace ^>}\xi , {\dot{a} \negmedspace ^>}, q_S, {\dot{a} \negmedspace ^>}\xi ') \in \delta _u,\\&\qquad \qquad \quad ~ (q'_S, {\dot{a} \negmedspace ^>}\xi , {a \negmedspace ^>}, q) \in \delta _r\},\\ S'&=\{(q,q') ~|~ \exists p \text{ s.t. } (q,p) \in S'' \text{ and } (p, q') \in \textit{Update})\\ R'&=\{q'~|~\exists q \text{ s.t. } q \in R'' \text{ and } (q,q') \in \textit{Update}\}\} \end{aligned}$$ -
If the stack is empty, then \((\lceil S,R \rfloor , \bot , {a \negmedspace ^>}, \lceil S',R' \rfloor ) \in \delta '_r\) where
$$\begin{aligned} S'&=\{(q,q') ~| \exists q'' \text{ s.t. } (q'', \bot , {a \negmedspace ^>}, q') \in \delta _r\}\\ R'&=\{q'~|~\exists q \in R \text{ s.t. } (q, \bot , {a \negmedspace ^>}, q') \in \delta _r\}. \end{aligned}$$
-
4 Symbolic Multi-matching Visibly Pushdown Automata
In this section, the definitions of symbolic alphabets are presented first. Then symbolic multi-matching visibly pushdown automata are formally defined.
4.1 Notations
The conventional notations of symbolic visibly pushdown automata is used in [10, 11]. First, let symbol \(\varPsi \) be a label theory including a recursively enumerable set of formulas. \(\varPsi \) is closed under Boolean operations. Notation \(\mathbb {P}_x(\varPsi )\) represents the set of unary predicates in \(\varPsi \) where the subscript x is set as the unique free variable in \(\mathbb {P}_x(\varPsi )\). Similarly, \(\mathbb {P}_{x,y}(\varPsi )\) signifies the set of binary predicates where there are only two free variables x and y. For two predicates \(\varphi _1\) and \(\varphi _2\), we can obtain that:
-
1.
if \(\varphi _1, \varphi _2 \in \mathbb {P}_x(\varPsi )\), \(\varphi _1 \wedge \varphi _2\) and \(\lnot \varphi _1 \in \mathbb {P}_x(\varPsi )\) are also both unary predicates;
-
2.
if \(\varphi _1 \in \mathbb {P}_x(\varPsi ) \cup \mathbb {P}_{x,y}(\varPsi )\) and \(\varphi _2 \in \mathbb {P}_{x,y}(\varPsi )\), \(\varphi _1 \wedge \varphi _2\) and \(\lnot \varphi _2 \in \mathbb {P}_{x,y}(\varPsi )\) are both binary predicates.
We define IsSat(\(\varphi \)) as the satisfiability of the predicate \(\varphi \in \mathbb {P}_x(\varPsi )\). \(\varphi \) is satisfiable, if there exists a witness a such that \(\varphi \) is true when variable x is substituted by a, i.e.  =true. Similarly, when \(\varphi \in \mathbb {P}_{x,y}(\varPsi )\),
=true. Similarly, when \(\varphi \in \mathbb {P}_{x,y}(\varPsi )\),  =true when x and y are substituted by a and b respectively. If for each predicate \(\varphi \in \varPsi \), it is decidable to check whether IsSat(\(\varphi \)) is true or not, then we say the label theory \(\varPsi \) is decidable.
=true when x and y are substituted by a and b respectively. If for each predicate \(\varphi \in \varPsi \), it is decidable to check whether IsSat(\(\varphi \)) is true or not, then we say the label theory \(\varPsi \) is decidable.
4.2 Model
Next we propose the model of symbolic multi-matching visibly pushdown automata which is defined as follows.
Definition 3 (Symbolic Multi-matching Visibly Pushdown Automata, SMVPA)
A symbolic multi-matching visibly pushdown automaton is a tuple \(\mathbb {M}=(Q, Q_0, F, \hat{\varSigma }, \varGamma , \varPsi , \delta )\), where
-
1.
Q is a finite set of states;
-
2.
\(Q_0 \subseteq Q\) is the set of initial states;
-
3.
\(F\subseteq Q\) is the set of final states;
-
4.
\(\hat{\varSigma }=\varSigma _c \cup \dot{\varSigma _c} \cup \varSigma _i \cup \dot{\varSigma _r} \cup \varSigma _r\) is a finite set of input symbols;
-
5.
\(\varGamma \subseteq (\varSigma _c \cup \dot{\varSigma _c} \cup \dot{\varSigma _r}) \times \varXi \cup \{\bot \}\) is a finite set of stack elements including a special bottom-of-stack symbol \(\bot \);
-
6.
\(\varPsi \) is a label theory; and
-
7.
\(\delta =\delta _c \cup \delta _i \cup \delta _u \cup \delta _r\) is the set of transitions consisting of four parts:
$$\begin{aligned} \delta _c \subseteq&~Q \times \mathbb {P}_x \times Q \times \varGamma \\ \delta _i \subseteq&~Q \times \mathbb {P}_x \times Q\\ \delta _u \subseteq&~Q \times \varGamma \times \mathbb {P}_{x,y} \times Q \times \varGamma \\ \delta _r \subseteq&~Q \times \varGamma \times \mathbb {P}_{x,y} \times Q \end{aligned}$$
A configuration of \(\mathbb {M}\) is a pair \((q, \sigma )\) where \(q \in Q\) and \(\sigma \in St\). Given a word \(w=w_1 w_2 \cdots w_n\) with multi-matching nest relations, w can be accepted by \(\mathbb {M}\) if there exists a run of \(\mathbb {M}\) on w. A run \(\rho \) is defined as a non-empty sequence of configurations, i.e. \(\rho =(q_0, \sigma _0) \xrightarrow [\varphi _1]{w_1} (q_1, \sigma _1) \xrightarrow [\varphi _2]{w_2} \cdots \xrightarrow [\varphi _n]{w_n} (q_n, \sigma _n)\), where \(q_0 \in Q_0\) is an initial state and \(\gamma _0=\bot \). For \(0<i\le n\), each configuration \((q_i, \sigma _i)\), where \(q_i \in Q\) and \(\gamma _i \in \varGamma \), satisfies one of the following cases:
-
1.
call if \(w_i={^<\negmedspace a}\) is a call, there is \((q_{i-1}, \varphi _i, q_i, w_i \xi ) \in \delta _c\) where
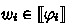 , \(\varphi _i \in \mathbb {P}_x\) and \(\sigma _i=w_i \xi \cdot \sigma _{i-1}\);
, \(\varphi _i \in \mathbb {P}_x\) and \(\sigma _i=w_i \xi \cdot \sigma _{i-1}\); -
2.
internal if \(w_i=i\) is an internal, there is \((q_{i-1}, \varphi _i, q_i) \in \delta _i\) where
 , \(\varphi _i \in \mathbb {P}_x\) and \(\sigma _i=\sigma _{i-1}\);
, \(\varphi _i \in \mathbb {P}_x\) and \(\sigma _i=\sigma _{i-1}\); -
3.
update
-
(a)
if \(w_i={^<\negmedspace \dot{a}}\) is an inner-call, there is \((q_{i-1}, \gamma _{i-1}, \varphi _i, q_i, \gamma _i) \in \delta _u\) where
 , \(\varphi _i \in \mathbb {P}_{x,y}\), \(\sigma _{i-1}={^<\negmedspace a}\xi \sigma ' / {^<\negmedspace \dot{a}}\xi \sigma '\), \(\sigma _i={^<\negmedspace \dot{a}}\xi \sigma '\) and \(\sigma ' \in St\);
, \(\varphi _i \in \mathbb {P}_{x,y}\), \(\sigma _{i-1}={^<\negmedspace a}\xi \sigma ' / {^<\negmedspace \dot{a}}\xi \sigma '\), \(\sigma _i={^<\negmedspace \dot{a}}\xi \sigma '\) and \(\sigma ' \in St\); -
(b)
it is similar for an inner-return \(w_i={\dot{a} \negmedspace ^>}\). The difference is that \(\sigma _{i-1}={^<\negmedspace a}\xi \sigma ' / {\dot{a} \negmedspace ^>}\xi \sigma '\) and \(\sigma _i={\dot{a} \negmedspace ^>}\xi \sigma '\);
-
(a)
-
4.
return
-
(a)
with regarding to a return \(w_i={a \negmedspace ^>}\), there is \((q_{i-1}, \gamma _{i-1}, \varphi _i, q_i) \in \delta _r\) where
 , \(\varphi _i \in \mathbb {P}_{x,y}\) \(\sigma _{i-1}={^<\negmedspace a}\xi \sigma ' / {^<\negmedspace \dot{a}}\xi \sigma '\) and \(\sigma _i={^<\negmedspace \dot{a}}\xi \sigma '\);
, \(\varphi _i \in \mathbb {P}_{x,y}\) \(\sigma _{i-1}={^<\negmedspace a}\xi \sigma ' / {^<\negmedspace \dot{a}}\xi \sigma '\) and \(\sigma _i={^<\negmedspace \dot{a}}\xi \sigma '\); -
(b)
specifically, when the stack is empty, i.e. \((q_{i-1}, \bot , \varphi _i, q_i) \in \delta _r\), there is \(\sigma _{i-1}=\sigma _i=\bot \),
 , and \(\varphi _i \in \mathbb {P}_x\).
, and \(\varphi _i \in \mathbb {P}_x\).
-
(a)
A run \(\rho =(q_0, \sigma _0) \xrightarrow [\varphi _1]{w_1} (q_1, \sigma _1) \xrightarrow [\varphi _2]{w_2} \cdots \xrightarrow [\varphi _n]{w_n} (q_n, \sigma _n)\) is accepted by \(\mathbb {M}\) if \(q_n \in F\) is a final state and \(\sigma _n \in (\varSigma _c \times \varXi )^* \cdot \{\bot \}\).
Given a symbolic multi-matching visibly pushdown automaton \(\mathbb {M}\), \(\mathbb {M}\) is called to be deterministic if \(q_0\) is the unique initial state in \(\mathbb {M}\), besides, the transition set \(\delta \) satisfies the following conditions:
-
1.
for any two call transitions \((q_1, \varphi _1, q'_1, \gamma _1) \in \delta _c\) and \((q_2, \varphi _2, q'_2, \gamma _2) \in \delta _c\): if \(q_1=q_2\) and IsSat(\(\varphi _1 \wedge \varphi _2\)), there is \(q'_1=q'_2\) and \(\gamma _1=\gamma _2\);
-
2.
for any two internal transitions \((q_1, \varphi _1, q'_1) \in \delta _i\) and \((q_2, \varphi _2, q'_2) \in \delta _i\): if \(q_1=q_2\) and IsSat(\(\varphi _1 \wedge \varphi _2\)), there is \(q'_1=q'_2\);
-
3.
for any two call/return update transitions \((q_1, \gamma _1, \varphi _1, q'_1, \gamma '_1) \in \delta _u\) and \((q_2, \gamma _2,\) \(\varphi _2, q'_2, \gamma '_2) \in \delta _u\): if \(q_1=q_2\), \(\gamma _1=\gamma _2\) and IsSat(\(\varphi _1 \wedge \varphi _2\)), \(q'_1=q'_2\) and \(\gamma '_1=\gamma '_2\) hold;
-
4.
for any two return transitions \((q_1, \gamma _1, \varphi _1, q'_1) \in \delta _u\) and \((q_2, \gamma _2, \varphi _2, q'_2) \in \delta _u\): if \(q_1=q_2\), \(\gamma _1=\gamma _2\) and IsSat(\(\varphi _1 \wedge \varphi _2\)), there is \(q'_1=q'_2\); especially, if the stack is empty, the difference from the former case is that \(\gamma _1=\gamma _2=\bot \).
5 Conclusion
In this paper, we extend the model of visibly pushdown automata over multi-matching nested relations. Different categories of transitions are determined according to a fixed partition of input tagged alphabet. Then, languages with one-to-one, one-to-n and n-to-one relations can be described. Besides, each nondeterministic multi-matching visibly pushdown automaton is demonstrated to be transformed into a deterministic one. In addition, if the input alphabet is given by a Boolean algebra where there is an infinite domain, symbolic version of multi-matching visibly pushdown automata is formally proposed. In the future, we will further investigate the closure properties and decision problems of multi-matching visibly pushdown automata and the symbolic version. Moreover, how visibly pushdown automata over multi-matching nested relations can be well applied in more fields are further explored.
References
Alur, R., Madhusudan, P.: Adding nesting structure to words. J. ACM (JACM) 56(3), 1–43 (2009)
Alur, R., Madhusudan, P.: Visibly pushdown languages. In: Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing, pp. 202–211 (2004)
Hopcroft, J.E., Motwani, R., Ullman, J.D.: Introduction to Automata Theory, Languages, and Computation, 2nd edn. Pearson Education, London (2000). ISBN 0-201-44124-1
Kumar, V., Madhusudan, P., Viswanathan, M.: Visibly pushdown automata for streaming XML. In: Proceedings of the 16th International Conference on World Wide Web (WWW 2007), 1053C1062 (2007)
Debarbieux, D., Gauwin, O., Niehren, J., et al.: Early nested word automata for XPath query answering on XML streams. Theor. Comput. Sci. 578, 100–125 (2015)
Chaudhuri, S., Alur, R.: Instrumenting C programs with nested word monitors. In: International SPIN Workshop on Model Checking of Software, pp. 279–283 (2007)
Driscoll, E., Thakur, A., Reps, T.: OpenNWA: a nested-word automaton library. In: International Conference on Computer Aided Verification, pp. 665–671 (2012)
Watson, B.W.: Implementing and using finite automata toolkits. In: Extended Finite State Models of Language, pp. 19–36. Cambridge University Press, New York (1999)
van Noord, G., Gerdemann, D.: Finite state transducers with predicates and identities. Grammars 4(3), 263–286 (2001)
D’Antoni, L., Alur, R.: Symbolic visibly pushdown automata. In: International Conference on Computer Aided Verification (CAV 2014), pp. 209–225 (2014)
Margus, V., Pieter, H., Benjamin, L., et al.: Symbolic finite state transducers: algorithms and applications. In: Proceedings of the 39th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL 2012), pp. 137–150 (2012)
Liu, J.. Duan, Z., Tian, C.: Transforming multi-matching nested traceable automata to multi-matching nested expressions. In: Proceedings of the 14th International Conference on Combinatorial Optimization and Applications (COCOA 2020), pp. 320–333 (2020)
Liu, J., Duan, Z., Tian, C.: Multi-matching nested relations. Theor. Comput. Sci. 854, 77–93 (2021)
Liu, J., Duan, Z., Tian, C.: Multi-matching nested languages. Chin. J. Electron. 31(1), 137–145 (2022)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Liu, J., Xiao, Y., Wang, H., Wang, W. (2023). Extending Visibly Pushdown Automata over Multi-matching Nested Relations. In: Liu, S., Duan, Z., Liu, A. (eds) Structured Object-Oriented Formal Language and Method. SOFL+MSVL 2022. Lecture Notes in Computer Science, vol 13854. Springer, Cham. https://doi.org/10.1007/978-3-031-29476-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-29476-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-29475-4
Online ISBN: 978-3-031-29476-1
eBook Packages: Computer ScienceComputer Science (R0)





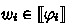 ,
,  ,
,  ,
,  ,
,  , and
, and