Abstract
The aim of this chapter is to study the regularity and the stability in the α-norm for neutral partial functional differential equations in fading memory spaces. We assume that a linear part is densely defined and generates an analytic semigroup. The delayed part is assumed to be Lipschitzian. For illustration, we provide an example for some reaction–diffusion equation involving infinite delay.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Analytic semigroup
- Neutral partial functional differential equations
- α-norm
- Stability
- Fading memory space
8.1 Introduction
Let \((X, \left |.\right |)\) be a Banach space, \((\mathscr {L}(X), \left |.\right |{ }_{\mathscr {L}})\) be the space of bounded linear operators on X, and α be a constant such that 0 < α < 1. The aim of this chapter is to study the stability results of the following class of neutral partial functional differential equations in the α-norm in fading memory spaces
where \(f:\mathcal {B}_\alpha \rightarrow X\) is a continuous function and \(A: D(A)\subseteq X\rightarrow X\) is a linear operator such that (−A) generates an analytic semigroup \(\left (T(t)\right )_{t\geq 0}\) on the Banach space X. D(A) is the domain of the operator A. We also denote R(A) the range of the operator A. For 0 < α < 1, Aα denotes the fractional power of A, and the space Xα will be defined later. The initial function ϕ belongs to a Banach space \(\mathcal {B}_\alpha \) of functions mapping (−∞, 0] into Xα and satisfying some axioms to be introduced later. \(\mathcal {D}\) is a bounded linear operator defined on \(\mathcal {B}_\alpha \) with values in X as follows:
where \(\mathcal {D}_0\) is also a bounded linear operator defined on \(\mathcal {B}_\alpha \) with values in X.
We denote by ut for \(t\in \mathbb {R}^+\) the historic function defined on (−∞, 0] by
where u is a function from \(\mathbb {R}\) into Xα.
The existence results of neutral partial functional differential equations with delay are an important subject studied by many authors (see [1, 3, 5, 6, 8, 11, 20] and the references therein). One of the qualitative behaviours of solutions of neutral partial functional differential equations with delay developed in many works is the stability (see [2, 4, 7, 9, 10, 15, 21, 22] and the references therein).
One of the most important qualitative results of the functional partial differential equations is the stability, extensively studied by many authors. A mechanical or an electrical device can be constructed to a level of perfect accuracy that is restricted by technical, economic, or environmental constraints. What happens to the expected result if the construction is a little off specifications? Does output remain near design values? How sensitive is the design to variations in fabrication parameters? Stability theory gives some answers to these and similar questions.
Adimy and Ezzinbi in [4] established the stability results in the α-norm for the problem of neutral type of the form
where \(f:\mathbb {R}\times \mathcal {C}_\alpha \rightarrow X\) is a continuous function and \(A: D(A)\subseteq X\rightarrow X\) is a linear operator;
ut for \(t\in \mathbb {R}\) is the historic function defined on [−r, 0] with r > 0 by ut(θ) = u(t + θ) for θ ∈ [−r, 0], where u is a continuous function from \(\mathbb {R}\) into Xα; \(\mathcal {C}_{\alpha }=C([-r,0];D(A^{\alpha }))\) is the space of continuous functions from [−r, 0] into D(Aα) provided with the uniform norm topology, \(\mathcal {D}\) is a bounded linear operator from C = C([−r, 0];X) into X defined by
where the operator \(\mathcal {D}_0\) is given by
and \(\eta : [-r,0]\rightarrow \mathscr {L}(X)\) is of bounded variation and non-atomic at zero, that is, there exists a continuous nondecreasing function \(\delta : [0,r]\rightarrow [0,+\infty )\) such that δ(0) = 0 and
In our work, we study the stability results of Eq. (8.1) following the results obtained in [2, 4, 7, 9, 10, 21].
To get some stability results in the uniform fading memory spaces, we make use of the spectral theory of linear operators, the fractional power operators, and the linear semigroup theory (see [13, 19]).
The organization of this chapter is as follows: In Sect. 8.2, we introduce some preliminary results on analytic semigroups, fractional powers of operator, and axiomatic phase space adapted to the fractional norm space for infinite delay. In Sect. 8.3, the existence and uniqueness of strict solutions is established. In Sect. 8.4, we are concerned with the smoothness results of the solutions. In Sect. 8.5, we investigate the stability near an equilibrium by using the linearized principle. In the last section, an example is provided to illustrate the applications of the main results of this chapter.
8.2 Analytic Semigroup, Fractional Power of Its Generator, and Partial Functional Differential Equations
Throughout this chapter, we assume the following:
- (H1 ):
-
(−A) is the infinitesimal generator of an analytic semigroup of linear operators \(\left \{T(t)\right \}_{t\geq 0}\) on a Banach space X. Without loss of generality, we suppose that 0 ∈ ρ(A); otherwise, instead of A, we take A − δI, where δ is chosen such that 0 ∈ ρ(A − δI) and where ρ(A) is the resolvent set of A.
It is well-known that |T(t)x|≤ Meωt|x| for all t ≥ 0, x ∈ X, where M ≥ 1 and \(\omega \in \mathbb {R}\).
For all 0 < α < 1, we define (see [19]) the operator A−α by
where Γ(α) denotes the well-known gamma function at the point α. The operator A−α is bijective, and the operator Aα is defined by
We denote by D(Aα) the domain of the operator Aα. Then, D(Aα) endowed with the norm |x|α = |Aαx| for all x ∈ D(Aα) is a Banach space [19]. We denote it by Xα. Moreover, we recall the following known results.
Theorem 8.2.1 ([19], p.69–75)
Let 0 < α < 1, and assume that (H1) holds. Then:
-
(a)
\(T(t):X\rightarrow D(A^{\alpha })\) for each t > 0 and α ≥ 0.
-
(b)
For all x ∈ D(Aα), T(t)Aαx = AαT(t)x.
-
(c)
For each t > 0, the linear operator AαT(t) is bounded and |AαT(t)x|≤ Mαt−αeωt|x|, where Mα is a positive real constant.
-
(d)
For 0 < α ≤ 1 and x ∈ D(Aα), |T(t)x − x|≤ Nαtα|Aαx|, for t > 0, where Nα is a positive real constant.
-
(e)
For 0 < α < β < 1, Xβ↪Xα.
From now on, we use an axiomatic definition of the phase space \(\mathcal {B}\) that was first introduced by Hale and Kato in [16]. We assume that \(\mathcal {B}\) is the normed space of functions mapping (−∞, 0] into X and satisfying the following axioms:
-
(A)
There exist a positive constant N, a locally bounded continuous function M(.) on [0, +∞), and a continuous function K(.) on [0, +∞), such that if \(u: (-\infty ,a]\rightarrow X\) is continuous on [ξ, a] with \(u_\xi \in \mathcal {B}\) for some ξ < a where 0 < a, then for all t ∈ [ξ, a]:
-
(i)
\(u_t\in \mathcal {B}\).
-
(ii)
\(t\rightarrow u_t\) is continuous on [ξ, a].
-
(iii)
\(\displaystyle N|u(t)|\leq |u_t|{ }_{\mathcal {B}}\leq K(t-\xi )\sup _{\xi \leq s\leq t}|u(s)|+M(t-\xi )|u_\xi |{ }_{\mathcal {B}}\).
-
(i)
-
(B)
\(\mathcal {B}\) is a Banach space.
Lemma 8.2.1 ([7])
Let C00 be the space of continuous functions mapping (−∞, 0] into X with compact supports and \(C_{00}^{a}\) be the subspace of functions in C00 with supports included in [−a, 0] endowed with the uniform norm topology. Then \(C_{00}^{a}\hookrightarrow \mathcal {B}\). □
Let
and provide \(\mathcal {B}_\alpha \) with the following norm:
We also assume that
- (H2 ):
-
\(A^{-\alpha }\phi \in \mathcal {B}\) for all \(\phi \in \mathcal {B}\), where the function A−αϕ is defined by
$$\displaystyle \begin{aligned} (A^{-\alpha}\phi)(\theta)=A^{-\alpha}(\phi(\theta))\,\,\,\text{for}\,\,\theta\leq 0 \end{aligned}$$
and
- (H3 ):
-
\(K(0)|\mathcal {D}_0|<1\).
Lemma 8.2.2 ([7])
Assume that (H1) and (H2) hold. Then, \(\mathcal {B}_\alpha \) is a Banach space and satisfies the axiom (A). □
For regularity results in the Banach space X, consider the following problem:
Definition 8.2.1
Let \(\phi \in \mathcal {B}\). A function \(u:(-\infty ,a]\rightarrow X\) is called a mild solution of Eq. (8.3) associated to ϕ if
Definition 8.2.2
Let \(\phi \in \mathcal {B}\). A function \(u:(-\infty ,a]\rightarrow X\) is called a strict solution of Eq. (8.3) associated to ϕ if
We have the following important result.
Theorem 8.2.2
Let u0 = ϕ, \(\mathcal {D}(\phi )\in D(A)\), and f ∈ C1([0, a];X). The existence of a mild solution u of (8.3) on [0, a] implies the existence of a strict solution of (8.3) on [0, a]. □
Proof
Let u be a mild solution of (8.3). Then,
Show that \(t\mapsto \mathcal {D}(u_t)\) is continuously differentiable. We need to only examine the second term of the right-hand side of (8.4), which will be denoted by v(t). It is well-known that \(T(t-s)=-\frac {\partial }{\partial s}(T(t-s))(-A)^{-1}\) since (−A) generates the analytic semigroup (T(t))t≥0. Hence,
Since \(\displaystyle \lim _{h\rightarrow 0}\left [\int _{0}^{t}\!\frac {T(t+h-s)-T(t{-}s)}{h}(-A)^{-1}\!f^{\prime }(s)ds+\frac {1}{h}\int _{t}^{t+h}\!T(t{-}s)(-A)^{-1}\right .\\ \left .f^{\prime }(s)ds\right ] =(-A)^{-1}f^{\prime }(t)+\int _{0}^{t}T(t-s)f^{\prime }(s)ds\), it is easy to see that
Using Eq. (8.5) and the fact that f ∈ C1([0, a];X) and the semigroup (T(t))t≥0 is analytic, then \(t\mapsto \frac {d}{dt}v(t)\) is continuous. Consequently, \(t\mapsto \mathcal {D}(u_t)\) is continuously differentiable on t ∈ [0, a].
Now, let us show that \(\mathcal {D}(u_t)\in D(A)\). Since \(T(t)\mathcal {D}(\phi )\in D(A)\), it remains to prove that v(t) ∈ D(A). We use the relation (8.5) in order to obtain
Thus, \(\displaystyle Av(t)=-\frac {d}{dt}v(t)+f(t)\) exists and v(t) ∈ D(A).
To finish, let us prove that u verifies (8.3). Using (8.4), one can write
□
8.3 Existence and Uniqueness of Strict Solutions
Now, we give the notions of solutions that will be studied in our work.
Definition 8.3.1
Let \(\phi \in \mathcal {B}_{\alpha }\). A function \(u:(-\infty ,+\infty )\rightarrow X_\alpha \) is called a mild solution of Eq. (8.1) associated to ϕ if:
-
(i)
\(\displaystyle \mathcal {D}(u_t)=T(t)\mathcal {D}(\phi )+\int _{0}^{t}T(t-s)f(u_s)ds\,\,\,\text{for}\,\,t\geq 0.\)
-
(ii)
u0 = ϕ.
□
Definition 8.3.2
Let \(\phi \in \mathcal {B}_{\alpha }\). A function \(u:(-\infty ,+\infty )\rightarrow X_\alpha \) is called a strict solution of Eq. (8.1) associated to ϕ if:
-
(i)
\(t\longmapsto \mathcal {D}(u_t)\) is continuously differentiable on [0, +∞).
-
(ii)
\(\mathcal {D}(u_t)\in D(A)\) for t ≥ 0.
-
(iii)
u(t) satisfies the system (8.1) for t ≥ 0.
□
Often in this chapter, ut(., ϕ) and ut(ϕ) denote the mild solution associated to the initial data ϕ, and we simply denote it by ut if there is no confusion.
We assume that there exists k > 0 such that
- (H4 ):
-
\(|f(\phi _1)-f(\phi _2)|\leq k|\phi _1-\phi _2|{ }_{\mathcal {B}_\alpha }\) for all ϕ1, \(\phi _2\in \mathcal {B}_\alpha \).
Theorem 8.3.1 ([14])
Assume that (H1), (H2), (H3), and (H4) hold. Then, for each \(\phi \in \mathcal {B}_{\alpha }\), there exists a unique mild solution of Eq.(8.1) that is defined for t ≥ 0.
Lemma 8.3.1
Assume that (H1), (H2), and (H3) hold. Let \(\phi \in \mathcal {B}_\alpha \) and \(h\in \mathcal {C}(\mathbb {R}^{+};X_\alpha )\) such that \(\mathcal {D}(\phi )=h(0)\). Then, there exists a unique continuous function x on \(\mathbb {R}^+\) that solves the following problem:
Moreover, there exist two functions a and b in \(L_{loc}^{\infty }(\mathbb {R}^+;\mathbb {R}^+)\) such that
Proof
We define for p > 0 the space
endowed with the uniform norm topology. For x ∈ W, we define its extension \(\tilde {x}\) on \(\mathbb {R}^{-}\) by
Using axiom (A), one can see that \(t\mapsto \tilde {x}_t\) is continuous from [0, p] to \(\mathcal {B}_{\alpha }\). Let us define the function \(\mathcal {K}\) on W by
One must show that \(\mathcal {K}\) has a unique fixed point on W. Since \(h\in \mathcal {C}(\mathbb {R}^{+};X_\alpha )\), then \(h\in \mathcal {C}([0,p];X_\alpha )\). Moreover, \(h(0)=\mathcal {D}(\phi )=\phi (0)-\mathcal {D}_0(\phi )\). It follows that
We can also write for x, y ∈ W with their respective extensions \(\tilde {x}\) and \(\tilde {y}\) associated to ϕ
Choosing p > 0 small enough, one obtains that \(\mathcal {K}\) is a strict contraction. Consequently, (8.6) has a unique solution x on (−∞, p].
It follows for s ∈ [0, p] that
where Kp =sups ∈ [0,p]K(s) and Mp =sups ∈ [0,p]M(s).
Therefore,
Thus, for p > 0 small enough and using (H3), one can write for t ∈ [0, p],
As a consequence, we have the existence of \(a,b\in L_{loc}^{\infty }([0,p];\mathbb {R}^+)\) such that
Now, to extend the solution x on [p, 2p], we consider the space
endowed with the uniform norm topology and the following problem:
We define the function \(\mathcal {K}_1\) on W1 by
Using the same arguments as above, we show that \(\mathcal {K}_1\) is a strict contraction on W1. That leads to the existence of a unique solution u of (8.6) on (−∞, 2p], and u is the extension of x on (−∞, 2p].
Also, we have to extend a, b on [p, 2p]. Therefore, let s ∈ [p, 2p]. Then, one can write
Therefore, for each t ∈ [p, 2p] such that s ≤ t, we have
Thus, for t ∈ [p, 2p],
Since p ∈ [0, p], one can write
Consequently,
Thus, for all t ∈ [p, 2p],
where a1 can be seen as the extension of a on [0, 2p] and b1 the extension of b on [0, 2p]. It is exactly to say there exist \(a,b\in L_{loc}^{\infty }([0,2p];\mathbb {R}^+)\) such that
Inductively, one can show the existence of an extension u of x on [np, (n + 1)p] and the extension anp of a, bnp of b on [np, (n + 1)p]. Finally, the solution x is unique and continuous defined on \(\mathbb {R}^+\). Also, the functions \(a\in L_{loc}^{\infty }(\mathbb {R}^+;\mathbb {R}^+) \) and \(b\in L_{loc}^{\infty }(\mathbb {R}^+;\mathbb {R}^+)\) are well-defined. □
We have the following result.
Theorem 8.3.2 ([14])
Assume that (H1), (H2), (H3), and (H4) hold. Let u and v be two mild solutions of Eq.(8.1) on \(\mathbb {R}\), respectively, associated to the initial data ϕ and ψ. Then, for any a > 0, there exists l(a) > 0 such that
For the regularity of the mild solution, we suppose that \(\mathcal {B}\) satisfies the following axiom:
- (B1 ):
-
If (ϕn)n≥0 is a Cauchy sequence in \(\mathcal {B}\) and converges compactly to ϕ in (−∞, 0], then \(\phi \in \mathcal {B}\) and \(|\phi _n-\phi |{ }_{\mathcal {B}}\rightarrow 0\) as \(n\rightarrow +\infty \).
Now, we can claim the existence and uniqueness of strict solution for Eq. (8.1).
Theorem 8.3.3
Assume that (H1), (H2), (H3), and (H4) hold. Furthermore, assume that \(\mathcal {B}\) satisfies axiom: (B1) \(f:\mathcal {B}_{\alpha }\rightarrow X\) is continuously differentiable with f′ locally Lipschitz continuous. Let \(\phi \in \mathcal {B}_{\alpha }\) be such that
Then, the mild solution u of the problem (8.1) is a strict solution of the problem (8.1). □
Proof
Let p > 0 and u be the mild solution of the problem (8.1) associated to ϕ. We consider the following problem:
and z ∈ C((−∞, p];Xα) defined by
Then (8.9) has a unique mild and continuous solution w on (−∞, p]. Also, one can recall the following lemma that plays an important role in the proof of this current theorem.
Lemma 8.3.2 ([7])
The function z defined above verifies
Note that our objective is to show that u = z on [0, p]. Using (8.9), we get
For t ∈ [0, p], we have
Consequently,
Using Eq. (8.11), it follows that
Using Eq. (8.14), we have
Therefore,
By Fubini’s theorem, we get that
Then, we put for t ∈ [0, p],
to obtain for some positive constants k and C1,
One can write for ω > 0
Therefore,
Moreover, since for all θ ∈ (−∞, 0], u(θ) = z(θ), then one has for all s ∈ [0, t],
Thus,
Using Lemma 8.3.1, one obtains
One can choose p > 0 small enough such that
It follows that u = z in (−∞, p] and that leads to u continuously differentiable on [0, p] with respect to the α-norm. In order to extend the solution to [p, 2p], we consider the following problems:
and \(\tilde {z}\in C((-\infty ,2p];X_\alpha )\) defined by
Using the same technique, one obtains that \(u=\tilde {z}\) on (−∞, 2p]. Proceeding inductively, solution u is uniquely extended to [np, (n + 1)p] for all \(n\in \mathbb {N}^{*}\) with respect to the α-norm. Since Xα↪X, one obtains that u ∈ C1([0, +∞);X). Finally, using Theorem 8.2.2 , u is the strict solution defined on \(\mathbb {R}\). □
8.4 Smoothness Results of the Operator Solution
Let \(K:D(K)\subseteq Y\rightarrow Y\) be a closed linear operator with dense domain D(K) in a Banach space Y . We denote by σ(K) the spectrum of K.
Definition 8.4.1
The essential spectrum σess(K) of K is the set of all \(\lambda \in \mathbb {C}\) such that at least one of the following relations holds:
-
(i)
The range Im(λI − K) is not closed.
-
(ii)
The generalized eigenspace Mλ(K) =⋃ n≥0ker(λI − K)n of λ is infinite-dimensional.
-
(iii)
λ is a limit of σ(K), that is, \(\lambda \in \overline {\sigma (K)-\left \{\lambda \right \}}\).
□
The essential radius denoted by ress(K) is given by
Definition 8.4.2
The spectral bound s(A) of the linear operator A is defined as
Definition 8.4.3
The type of the linear operator (T(t))t≥0 is defined by
In the sequel, we recall the χ measure of noncompactness, which will be used in the next to analyse the spectral properties of semigroup solution. The χ measure of noncompactness for a bounded set H of a Banach space Y with the norm |.|Y is defined by
The following results are some basic properties of the χ measure of noncompactness.
Lemma 8.4.1 ([17])
Let A 1 and A 2 be bounded sets of a Banach space Y . Then:
-
(i)
χ(A1) ≤ dia(A1), where \(\displaystyle dia(A_1)=\sup _{x,y\in A_1}|x-y|\).
-
(ii)
χ(A1) = 0 if and only if A1 is relatively compact in Y .
-
(iii)
\(\chi (A_1\bigcup A_2)=max\left \{\chi (A_1), \chi (A_2)\right \}\).
-
(iv)
χ(λA1) = |λ|χ(A1), \(\lambda \in \mathbb {R}\), where \(\lambda A_1=\left \{\lambda x:\,\,x\in A_1\right \}\).
-
(v)
χ(A1 + A2) ≤ χ(A1) + χ(A2), where \(A_1+A_2=\left \{x+y:\,\,x\in A_1,\,y\in A_2\right \}\).
-
(vi)
χ(A1) ≤ χ(A2) if A1 ⊆ A2.
Definition 8.4.4
The essential norm of a bounded linear operator K on Y is defined by
Let \(V=\left (V(t)\right )_{t\geq 0}\) be a c0-semigroup on a Banach space Y .
Definition 8.4.5
The essential growth ωess(V ) of \(\left (V(t)\right )_{t\geq 0}\) is defined by
Theorem 8.4.1 ([7])
The essential growth bound of \(\left (V(t)\right )_{t\geq 0}\) is given by
Moreover,
Assume now that:
- (H5 ):
-
The semigroup \(\left (T(t)\right )_{t\geq 0}\) is compact for t > 0.
Theorem 8.4.2
Assume that (H1), (H2), (H3), (H4), and (H5) hold. Then, the solution u(., ϕ) of Eq.(8.1) is decomposed as follows:
where \(\mathscr {W}(t)\) is a compact operator on \(\mathcal {B}_\alpha \), for each t > 0, and \(\mathscr {U}(t)\) is the semigroup solution of the following equation:
Proof
Let \(\mathscr {U}(t)\) be defined by
where v is a unique solution of the problem
We can write \(\mathscr {W}(t)\phi =w_t(.,\phi )=u_t(.,\phi )-\mathscr {U}(t)\phi =u_t(.,\phi )-v_t(.,\phi )\). Then,
Consequently,
Let \(\left \{\phi _k\right \}_{k\geq 0}\) be a bounded sequence in \(\mathcal {B}_\alpha \). We will show that the family {h(., ϕk) : k ≥ 0} is equicontinuous and bounded on \(\mathcal {C}([0,\sigma ];X_\alpha )\), for any σ > 0 fixed. For all 0 < α < β < 1, there exists a positive constant C such that
for every k ≥ 0.
Using the compactness of the operator \(A^{-\beta }: X\rightarrow X_\alpha \), we get that the set {h(t, ϕk) : k ≥ 0} is relatively compact in Xα for each t ≥ 0. Now, let us prove the equicontinuity of the family {h(., ϕk) : k ≥ 0} in the α-norm. For this purpose, let t > t0 ≥ 0. Then,
We obtain that
Moreover, since \(\displaystyle \{A^{\alpha }\int _{0}^{t_0}T(t_0-s)f(u_s(.,\phi _k))ds:\,\,\,k\geq 0\}\) is relatively compact in X, then there is a compact set Γ in X such that
It is well-known by the Banach–Steinhaus theorem that
Thus,
Using the same argument, we also obtain for t0 > t,
Therefore, the family {h(., ϕk) : k ≥ 0} is relatively compact on \(\mathcal {C}([0,\sigma ];X_\alpha )\) for each σ > 0. Then, there exists a subsequence {ϕk : k ≥ 0} such that h(t, ϕk) converges as \(k\rightarrow +\infty \) uniformly on [0, σ] to some function h(t) with respect to the α-norm. Let \(w_{t}^{k}\) be the solution of problem (8.23) with the initial data ϕ = ϕk. Then,
Using Lemma 8.3.1, we obtain
which implies that \(\{w_{t}^{k}\}_{k\geq 0}=\{w_{t}(.,\phi _{k})\}_{k\geq 0}\) is a Cauchy sequence in \(\mathcal {B}_{\alpha }\). Therefore, \(\mathscr {W}(t)\) is compact in \(\mathcal {B}_{\alpha }\). □
Definition 8.4.6
\(\mathcal {D}\) is said to be stable if the zero solution of the difference system
is exponentially stable. □
Now, we give the definitions of fading memory spaces that will be used later on. For \(\phi \in \mathcal {B}\), t ≥ 0 and θ ≤ 0, we define the following:
Then, {S(t)}t≥0 is a strongly continuous semigroup on \(\mathcal {B}\). We set
Definition 8.4.7
[7] We say that \(\mathcal {B}\) is a uniform fading memory space if the following conditions hold:
-
(i)
If a uniformly bounded sequence \((\phi _n)_{n\in \mathbb {N}}\) in C00 converges to a function ϕ compactly on (−∞, 0], then ϕ is in \(\mathcal {B}\) and \(|\phi _n-\phi |{ }_{\mathcal {B}}\rightarrow 0\) as \(n\rightarrow +\infty \).
-
(ii)
\(|S_0(t)|{ }_{\mathcal {B}}\rightarrow 0\) as \(t\rightarrow +\infty \). □
Lemma 8.4.2 ([7])
If \(\mathcal {B}\) is a uniform fading memory space, then K and M can be chosen such that K is bounded on \(\mathbb {R}^+\) and \(M(t)\rightarrow 0\) as \(t\rightarrow +\infty \). □
Lemma 8.4.3
If \(\mathcal {B}\) is a uniform fading memory space, then \(\mathcal {B}_{\alpha }\) is a uniform fading memory space. □
Proof
Let \((\phi _n)_{n\in \mathbb {N}}\) in C00 be a uniformly bounded sequence that converges to a function ϕ compactly on (−∞, 0]. Then ϕ is in \(\mathcal {B}\) and \(|\phi _n-\phi |{ }_{\mathcal {B}}\rightarrow 0\) as \(n\rightarrow +\infty \) since \(\mathcal {B}\) is a uniform fading memory space. Using (H2), one can write \(A^{-\alpha }\phi \in \mathcal {B}\) since \(\phi \in \mathcal {B}\). \(A^{-\alpha }\phi \in \mathcal {B}\) leads to the existence of A−αϕ(θ). We know that R(A−α) = D(Aα). For this reason, \(\left |A^{-\alpha }\phi (\theta )\right |{ }_\alpha \) is well-defined. The fact that A−α is bounded linear operator implies \(\left |\phi (\theta )\right |{ }_\alpha \) exists. Therefore, ϕ(θ) ∈ D(Aα) for all θ ≤ 0. Also,
Using again the boundedness of A−α, one obtains the existence of \(\left |A^{\alpha }\phi \right |{ }_{\mathcal {B}}\). Thus, \(A^{\alpha }\phi \in \mathcal {B}\). Hence, we establish that \(\phi \in \mathcal {B}_\alpha \). Moreover,
Since A−α is a bounded linear operator, one obtains
Consequently, the condition (i) of Definition 8.4.7 is satisfied.
Now, we have to show that the condition (ii) of Definition 8.4.7 is verified. In order to do this, we use the fact that A−α is a bounded linear operator and \(\mathcal {B}\) is a uniform fading memory space to write
and
Hence, the condition (ii) is satisfied. Finally, \(\mathcal {B}_{\alpha }\) is a uniform fading memory space. □
Now, we have to prove that \(\mathscr {U}(t)\) is exponentially stable. It is known that \(\mathscr {U}(t)\) in Theorem 8.4.2 is defined by
where v is a unique solution for the same initial data ϕ of the following problem:
Using the superposition principle of solutions of linear systems, we have
where
and
Now, let K∞ =sups≥0K(s). We have the following result.
Theorem 8.4.3
Assume that (H1), (H2), and (H3) hold. Moreover, suppose that \(\mathcal {B}_\alpha \) is a uniform fading memory space, \(\mathcal {D}\) is stable, the semigroup {T(t)}t≥0 is exponentially stable, and \(K_{\infty }|\mathcal {D}_0|<1\). Then, the semigroup solution \(\{\mathscr {U}(t)\}_{t\geq 0}\) defined in Theorem 8.4.2 is exponentially stable. □
Proof
Since y verifies problem (8.26) and \(\mathcal {B}_\alpha \) is a uniform fading memory space, then, using Axiom (A)-(iii), one can write for t ≥ s ≥ 𝜖 > 0
Therefore, taking 𝜖 > 0 such that s − 𝜖 ≥ t − 2𝜖 ≥ 0, then
Now, one can write
Since \(M(\epsilon )\rightarrow 0\) as \(\epsilon \rightarrow +\infty \), then we choose 𝜖 big enough such that \(0<1-K_\infty |\mathcal {D}_0|-M(\epsilon )\). We obtain that
Since {T(t)}t≥0 is exponentially stable, then there exist positive constants α′ and β′ such that \(|y_t|{ }_{\mathcal {B}_\alpha }\leq \beta 'e^{-\alpha ' t}\) for all t ≥ 0.
Since \(\mathcal {D}\) is stable, then \(x_t(\phi )\rightarrow 0\) as \(t\rightarrow +\infty \). On the other hand, we have
Then, it follows that \(\mathscr {U}(t)\rightarrow 0\) as \(t\rightarrow 0\) and \(\{\mathscr {U}(t)\}_{t\geq 0}\) is exponentially stable. □
In the sequel, we give the following.
Theorem 8.4.4
Assume that there exists r > 0 such that the elements \(\phi \in \mathcal {B}_\alpha \) are continuous from [−r, 0] to Xα. If \(\mathcal {D}(\phi )=\phi (0)-q\phi (-r)\) for all \(\phi \in \mathcal {B}_\alpha \) with 0 < q < 1 and \(\mathcal {B}_\alpha \) a uniform fading memory space, then \(\mathcal {D}\) is stable. □
Proof
Since \(\mathcal {D}(x_t)=0\) and x0 = ϕ, then for all t ∈ [0, r], we have x(t) = qx(t − r). Therefore,
Also, for all t ∈ [r, 2r],
Inductively, for all t ∈ [(n − 1)r, nr], we have
since t ∈ [(n − 1)r, nr], then t − nr ∈ [−r, 0]. Furthermore, \(\mathcal {B}_{\alpha }\) is assumed to be the space of functions from (−∞, 0] to Xα that are continuous on [−r, 0]. Thus, for all t ∈ [(n − 1)r, nr],
for all \(\phi \in \mathcal {B}_{\alpha }\).
Thus, there exist \(\alpha =-\frac {\ln (q)}{r}>0\) and C > 0 such that
Hence, for all \(\phi \in \mathcal {B}_{\alpha }\),
Now, let \(\phi \in \mathcal {B}_\alpha \) such that \(|\phi |{ }_{\mathcal {B}_\alpha }\leq 1\).
Using again Axiom (A)-(iii) and the fact that \(\mathcal {B}_{\alpha }\) is a uniform fading memory space, we have for t ≥ s ≥ 𝜖 > 0
Choosing 𝜖 > 0 such that s − 𝜖 ≥ t − 2𝜖 ≥ 0, we have
Thus,
Since \(M(\epsilon )\rightarrow 0\) as \(\epsilon \rightarrow +\infty \), then we can choose 𝜖 big enough such that 0 < 1 − M(𝜖). Therefore,
Thus, \(x_t(.,\phi )\rightarrow 0\) as \(t\rightarrow +\infty \) whenever \(\phi \in \mathcal {B}_{\alpha }\) and \(|\phi |{ }_{\mathcal {B}_\alpha }\leq 1\). Hence, \(\mathcal {D}\) is stable. □
Example 8.4.1
Let γ be a real number, 1 ≤ p < +∞, and r > 0. We define the space \( \mathcal {C}_r\times L_{\gamma }^{p}\) that consists of measurable functions \(\varphi :(-\infty ,0]\rightarrow X\) that are continuous on [−r, 0] such that eγθ|φ(θ)|p is measurable on (−∞, −r]. Let us provide the space \( \mathcal {C}_r\times L_{\gamma }^{p}\) with the following norm:
\(( \mathcal {C}_r\times L_{\gamma }^{p}, |.|{ }_{\mathcal {B}})\) is a normed linear space satisfying Axioms (A) and (B).
Corollary 8.4.1
Suppose that assumptions (H1), (H2), and (H3) hold, and there exists a positive constant r such that all \(\phi \in \mathcal {B}_\alpha \) imply that ϕ is continuous on [−r, 0] with values in Xα. Moreover, suppose that \(\mathcal {B}_\alpha \) is a uniform fading memory space, \(\mathcal {D}(\phi )=\phi (0)-q\phi (-r)\) for all \(\phi \in \mathcal {B}_\alpha \), the semigroup {T(t)}t≥0 is exponentially stable, and \(K_{\infty }|\mathcal {D}_0|<1\). Then, the semigroup solution \(\{\mathscr {U}(t)\}_{t\geq 0}\) defined in Theorem 8.4.2 is exponentially stable. □
8.5 Linearized Stability of Solutions
Coming back to the operator U(t) for t ≥ 0 defined on \(\mathcal {B}_\alpha \) by
where ut(., ϕ) is the unique mild solution of the problem (8.1) for the initial condition \(\phi \in \mathcal {B}_\alpha \), it is proved that the following result holds.
Proposition 8.5.1 ([4])
The family (U(t))t≥0 is a nonlinear strongly continuous semigroup on \(\mathcal {B}_\alpha \), that is:
-
(i)
U(0) = I.
-
(ii)
U(t + s) = U(t)U(s), for t, s ≥ 0.
-
(iii)
For all \(\phi \in \mathcal {B}_\alpha \), U(t)(ϕ) is a continuous function of t ≥ 0 with values in \(\mathcal {B}_\alpha \).
-
(iv)
For t ≥ 0, U(t) is continuous from \(\mathcal {B}_\alpha \) to \(\mathcal {B}_\alpha \).
-
(v)
(U(t))t≥0 satisfies the following translation property, for t ≥ 0 and θ ≤ 0:
$$\displaystyle \begin{aligned} \displaystyle (U(t))(\theta)=\left \{\begin{array}{ll}(U(t+\theta)(\phi))(0), \,\,\quad \mathit{\text{if}}\,\,\,t+\theta\geq 0,\\\\ \phi(t+\theta)\,\,\,\quad \mathit{\text{if}}\,\,\,t+\theta\leq 0.\end{array}\right. \end{aligned} $$(8.27)
It is now interesting to investigate the stability results of the equilibriums of the problem (8.1). Recalling that equilibrium means a constant solution u∗ of the problem (8.1). To preserve the generality, we can suppose that u∗ = 0.
Now, let us assume that:
- (H6 ):
-
\(f:\mathcal {B}_\alpha \rightarrow X\) is differentiable at zero.
It is well-known that the linearized problem associated to problem (8.1) is given by
with L = f′(0).
Let (V (t))t≥0 be the semigroup solution on \(\mathcal {B}_\alpha \) associated to the problem (8.28).
Theorem 8.5.1
Assume that (H1), (H2),(H3), (H4), and (H6) hold. Then, for every t > 0, the derivative of U(t) is V (t). □
Proof
Let t ≥ 0 be fixed and \(\phi \in \mathcal {B}_\alpha \). One has
Let us set
and
Then, we can write
Using Lemma 8.3.1, we obtain
Moreover,
Using the fact that f is differentiable at zero with differential L at zero, we can state that for all 𝜖 > 0, there exists η > 0 such that
Note that w0 = 0, so we can write
Therefore, for t ∈ [0, T],
We can choose T > 0 small enough such that \(\displaystyle kM_\alpha b(T)\Big (\int _{0}^{T}\frac {e^{\omega s}}{s^{\alpha }}ds\Big )<1\).
Consequently, for all \(|\phi |{ }_{\mathcal {B}_\alpha }<\eta \),
Thus, U(t) is differentiable at zero for all t ∈ [0, T] with dϕU(t)(0) = V (t). Proceeding by steps, one can prove that dϕU(t)(0) = V (t), for all t > 0. □
Theorem 8.5.2
Assume that (H1), (H2), (H3), (H4), and (H6) hold. If the zero equilibrium of (V (t))t≥0 is exponentially stable, then the zero equilibrium of (U(t))t≥0 is locally exponentially stable, which means that there exist η > 0, β > 0, and C ≥ 1 such that for t ≥ 0,
Moreover, if \(\mathcal {B}_\alpha \) can be decomposed as \(\mathcal {B}_\alpha =\mathcal {B}_{\alpha }^{1}\oplus \mathcal {B}_{\alpha }^{2}\) , where \(\mathcal {B}_{\alpha }^{i}\) are V -invariant subspaces of \(\mathcal {B}_\alpha \) and \(\mathcal {B}_{\alpha }^{1}\) a finite-dimensional with
and
then the zero equilibrium of (U(t))t≥0 is not stable, in the sense that there exist 𝜖 > 0, a sequence \((\phi _n)_{n\in \mathbb {N}}\) converging to 0, and a sequence \((t_n)_{n\in \mathbb {N}}\) of positive real numbers such that |U(tn)ϕn|α > 𝜖. □
The proof of this theorem is based on the Theorem 8.5.1 and the following theorem.
Theorem 8.5.3 ([12])
Let (W(t))t≥0 be a nonlinear strongly continuous semigroup on the subset Ω of a Banach space (X;||.||). Assume that x0 ∈ Ω is an equilibrium of (W(t))t≥0 such that W(t) is differentiable at x0 for each t ≥ 0 with Z(t) the derivative of W(t) at x0. Then, (Z(t)t≥0 is a strongly nonlinear continuous semigroup of bounded linear operators on X, and if the zero equilibrium of (Z(t))t≥0 is exponentially stable, then the equilibrium x0 of (W(t))t≥0 is locally exponentially stable. Moreover, if X can be decomposed as X = X1 ⊕ X2, where Xi are Z-invariant subspaces of X, X1 a finite-dimensional with
and
then the zero equilibrium of (W(t))t≥0 is not stable, in the sense that there exist 𝜖 > 0, a sequence \((\phi _n)_{n\in \mathbb {N}}\) converging to 0, and a sequence \((t_n)_{n\in \mathbb {N}}\) of positive real numbers such that
Lemma 8.5.1 ([19], Corollary 1.2, page 43)
Let Θ be a continuous and right differentiable function on [a, b). If the right derivative function d+ Θ is continuous on [a, b), then Θ is continuously differentiable on [a, b). □
Now, we make some sufficient conditions on \(\mathcal {B}\) in order to determine (AV, D(AV)), the generator of the semigroup (V (t))t≥0. So, we assume the following axiom:
-
(C):
Let (ϕn)n≥0 be a sequence in \(\mathcal {B}\) such that \(\phi _n\rightarrow 0\) as \(n\rightarrow +\infty \) in \(\mathcal {B}\); then, \(\phi _n(\theta )\rightarrow 0\) as \(n\rightarrow +\infty \) for all θ ≤ 0.
We can state the following result.
Theorem 8.5.4
Assume that (H1), (H2), (H3), (H4), and (H6) hold. Moreover, suppose that \(\mathcal {B}\) satisfies axioms (A), (B), and (C). If \(\mathcal {B}\) is a subspace of the space of continuous functions from (−∞, 0] into X, then (AV, D(AV)) is given by
Proof
Let B be the infinitesimal generator of the semigroup (V (t))t≥0 on \(\mathcal {B}_\alpha \) and ϕ ∈ D(B). Then, one can write
Using axiom (C), one obtains
It follows that the right derivative d+ϕ exists on (−∞, 0) and is equal to ψ. The fact that each function in \(\mathcal {B}_\alpha \) is continuous on (−∞, 0] leads to d+ϕ continuous on (−∞, 0).
Using Lemma 8.5.1, we deduce that the function ϕ is continuously differentiable and ϕ′ = ψ on (−∞, 0). Moreover,
which implies that the function ϕ is continuously differentiable from (−∞, 0] to Xα and ϕ′ = ψ on (−∞, 0].
We have
It is well-known that
in X-norm and
in α-norm. The fact that Xα↪X implies
in X-norm. Consequently,
in X-norm. It follows that
Conversely, let \(\phi \in \mathcal {B}_{\alpha }\) be such that
Since \(t\rightarrow T(t)\phi \) is continuously differentiable from \(\mathbb {R}^{+}\) to Xα, then ϕ ∈ D(B). □
Now, let us study the spectral of the linear equation. We assume that \(\mathcal {B}_\alpha \) satisfies the following axiom:
-
(D)
There exists a constant \(\nu \in \mathbb {R}\) such that for every x ∈ X and \(\lambda \in \mathbb {C}\) with \(\Re (\lambda )>\nu \), one has
$$\displaystyle \begin{aligned} \epsilon_\lambda\otimes x\in\mathcal{B}_\alpha\,\quad \text{and}\quad \sup_{|x|\leq 1}|\epsilon_\lambda\otimes x|<\infty, \end{aligned}$$where (𝜖λ ⊗ x)(θ) = eλθx for θ ≤ 0.
For \(\lambda \in \mathbb {C}\) such that \(\Re (\lambda )>\nu \), we define the linear operator Δ(λ) by
Let (AV, D(AV)) be the infinitesimal generator of the semigroup (V (t))t≥0 and σp(AV) be the point spectrum of AV.
Theorem 8.5.5
Assume that (H1), (H2), (H3), (H4), and (H6) hold. Assume furthermore that the axioms (A), (B), (C), and (D) are satisfied. Let \(\lambda \in \mathbb {C}\) with \(\Re (\lambda )>\nu \). If \(\mathcal {B}_\alpha \) is a uniform fading memory space and \(\mathcal {D}\) is stable, then the following are equivalent:
-
(i)
λ ∈ σp(AV).
-
(ii)
ker Δ(λ) ≠ {0}.
□
Proof
Let λ ∈ σp(AV) with \(\Re (\lambda )>\nu \). Then, there exists ϕ ∈ D(AV), ϕ ≠ 0, with AVϕ = λϕ. That leads to
and
Since for all t > 0,
then letting t goes to 0, and one obtains
Moreover, using the spectral mapping (Theorem 2.4 in [18]), we have
Letting t > 0 and θ ≤ 0 such that t + θ ≥ 0, the translation property of the semigroup solution leads to
Thus, ϕ(θ) = eλθϕ(0) for θ ≥ 0. Since ϕ ≠ 0, using (8.29), it follows that \(\mathcal {D}(\phi (0))\in ker\Delta (\lambda )\).
Conversely, if ϕ verifies all conditions of Theorem 8.3.3, then AVϕ = ϕ′. Taking x ∈ D(A) such that x ≠ 0 and Δ(λ)x = 0, then the function 𝜖λ ⊗ x satisfies all conditions of Theorem 8.3.3, and we deduce that
□
Now, let
Lemma 8.5.2 ([18])
If \(\mathcal {B}\) is a uniform fading memory space, then ν0 < 0. □
Definition 8.5.1
\(\lambda \in \mathbb {C}\) is a characteristic value of Eq. (8.28) if
Let
It is well-known that σ(AV) − σess(AV) contains a finite number of eigenvalues of AV. Consequently, the stability of (V (t))t≥0 is completely determined by s′(AV).
Theorem 8.5.6
Assume that (H1), (H2), (H3), (H4), (H5), and (H6) hold. Furthermore, assume that the axioms (A), (B), (C), and (D) are satisfied. If \(\mathcal {B}\) is a uniform fading memory space and \(\mathcal {D}\) is stable, then the following holds:
-
(i)
If s′(AV) < 0, then (V (t))t≥0 is exponentially stable.
-
(ii)
If s′(AV) = 0, then there exists \(\phi \in \mathcal {B}_\alpha \) such that \(|V(t)\phi |{ }_{\mathcal {B}_\alpha }=|\phi |{ }_{\mathcal {B}_\alpha }\).
-
(iii)
If s′(AV) > 0, then there exists \(\phi \in \mathcal {B}_\alpha \) such that \(\displaystyle \lim _{t\rightarrow +\infty }|V(t)\phi |{ }_{\mathcal {B}_\alpha }=+\infty \).
□
We deduce the following stability result in the nonlinear case, from Theorem 8.5.2.
Theorem 8.5.7
Assume that (H1), (H2), (H3), (H4), (H5), and (H6) hold. Furthermore, assume that the axioms (A), (B), (C), and (D) are satisfied. If \(\mathcal {B}\) is a uniform fading memory space and \(\mathcal {D}\) is stable, then the following holds:
-
(i)
If s′(AV) < 0, then the zero equilibrium of (U(t))t≥0 is locally exponentially stable.
-
(ii)
If s′(AV) > 0, then the zero equilibrium of (U(t))t≥0 is unstable.
□
8.6 Application
To apply the theoretical results of this chapter, we consider the following nonlinear system with infinite delay:

where \(g:(-\infty ,0]\times \mathbb {R}\rightarrow \mathbb {R}\) is a function and \(c\in \mathbb {R}_{+}^{*}\), \(b\in \mathbb {R}\). q is a positive constant such that |q| < 1. \(H:\mathbb {R}^2\rightarrow \mathbb {R}\) is a Lipschitz continuous with H(0, 0) = 0. The initial data ψ will be precised in the next.
In order to write system (8.30) in an abstract form, we introduce the space \(X=L^2((0,\pi );\mathbb {R})\). Let A be the operator defined on X by
Then, (−A) generates an analytic semigroup (T(t))t≥0 on X. Moreover, T(t) is compact on X for every t > 0. The spectrum σ(−A) is equal to the point spectrum Pσ(−A) and is given by \(\sigma (-A)=\left \{-n^2:\,\,n\geq 1\right \}\), and the associated eigenfunctions (ϕn)n≥1 are given by \(\phi _n=\sqrt {\frac {2}{\pi }}\sin {}(nx)\) for x ∈ [0, π]; the associated analytic semigroup is explicitly given by
where \(\left (. ,.\right )\) is an inner product on X.
Lemma 8.6.1 ([21])
If \(\alpha =\frac {1}{2}\) , then
and
There exists M ≥ 1 (see [21]) such that for t ≥ 0, |T(t)|≤ Meωt for some − 1 < ω < 0.
Then, the semigroup {T(t)}t≥0 is exponentially stable.
Note also that (see [21]) there exists \(M_{\frac {1}{2}}\geq 0\) such that
Therefore, hypotheses (H1) and (H5) are satisfied.
Lemma 8.6.2 ([7])
If \(m\in D(A^{\frac {1}{2}})\) , then m is absolutely continuous, \(\frac {\partial }{\partial x}m\in X\) . Moreover, there exist positive constants N 0 and M 0 such that
Let γ > 0. We consider the following phase space
provided with the following norm:
According to [7], \(\mathcal {B}\) satisfies Axioms (A), (B) and is a uniform fading memory space. Moreover, it is well-known that K(t) = 1 for every \(t\in \mathbb {R}^+\) and M(t) = e−γt for \(t\in \mathbb {R}^+\). Therefore, the norm in \(\mathcal {B}_{\frac {1}{2}}\) is given (see [7]) by
One can write ( see, [21], p.144)
Next, we assume the following.
- (H7 ):
-
For θ ≤ 0 and \(\zeta _1,\zeta _2\in \mathbb {R}\), |g(θ, ζ1) − g(θ, ζ2)|≤ s(θ)|ζ1 − ζ2|, g(θ, 0) = 0, \(\frac {\partial }{\partial \zeta }g(\theta ,0)\neq 0\), where s is some nonnegative function that verifies
$$\displaystyle \begin{aligned} \int_{-\infty}^{0}e^{-2\gamma\theta}s(\theta)<\infty. \end{aligned}$$
Let f1, f2, and f be defined on \(\mathcal {B}_{\frac {1}{2}}\) by
and
Proposition 8.6.1
For each \(\phi \in \mathcal {B}_{\frac {1}{2}}\), \(f(\phi )\in L^{2}((0,\pi );\mathbb {R})\), and f is continuous on \(\mathcal {B}_{\frac {1}{2}}\). □
Proof
Let \(\phi \in \mathcal {B}_{\frac {1}{2}}\). Since for all ξ ∈ [0, π] and for all θ ∈ (−∞, 0], we have
then for all ξ ∈ [0, π],
Let us set
Using H\(\ddot {\mbox{o}}\)lder inequality, one can write
Then, using the above inequality and the inequality (8.31),
Also, we refer to Minkowski inequality to obtain
We conclude that \(f(\phi )=(f_1+f_2)(\phi )\in L^2([0,\pi ];\mathbb {R})\) for all \(\phi \in \mathcal {B}_{\frac {1}{2}}\).
Let us show that f is continuous. For this purpose, let \((\phi _n)_{n\in \mathbb {N}}\) be a sequence in \(\mathcal {B}_{\frac {1}{2}}\) and \(\phi \in \mathcal {B}_{\frac {1}{2}}\) such that \(\phi _n\rightarrow \phi \) in \(\mathcal {B}_{\frac {1}{2}}\) as \(n\rightarrow +\infty \). Then
and we obtain that
Let us set for all ξ ∈ [0, π],
Then
which leads to
Since \(\phi _n\rightarrow \phi \) in \(\mathcal {B}_{\frac {1}{2}}\), then \(\displaystyle \int _{0}^{\pi }|J_n(\xi )|{ }^2d\xi \rightarrow 0\) as \(n\rightarrow +\infty \). Therefore, f1 is continuous. Moreover,
Using the fact that \(\phi _n\rightarrow \phi \) in \(\mathcal {B}_{\frac {1}{2}}\) as \(n\rightarrow +\infty \), we obtain that \(\displaystyle \int _{0}^{\pi }\Big |f_2\Big (\phi _n(\xi )-\phi (\xi )\Big )\Big |{ }^2d\xi \rightarrow 0\) when \(n\rightarrow +\infty \).
Hence, \(f(\phi _n)\rightarrow f(\phi )\) in \(L^{2}([0,\pi ];\mathbb {R})\) as \(n\rightarrow +\infty \) and the proof is complete. □
Let

We need the following result to prove that (H3) is satisfied.
Proposition 8.6.2
Assume that (H7) holds. Then, f is Lipschitzian.
Proof
We have to show that f1 and f2 are Lipschitz functions. So, let ϕ and ψ be in \(\mathcal {B}_{\frac {1}{2}}\). Then, for ξ ∈ [0, π], one has
Note that using H\(\ddot {\mbox{o}}\)lder inequality, one can write
Therefore,
for which we deduce that
Finally, we obtain that
where
Moreover,
Therefore, f is Lipschitzian and (H4) is satisfied. □
Let us define the operators \(\mathcal {D}\) and \(\mathcal {D}_0\) on \(\mathcal {B}_{\frac {1}{2}}\) by
and
Then, \(\mathcal {D}(\phi )=\phi (0)-\mathcal {D}_0(\phi )\).
Proposition 8.6.3
\(\mathcal {D}\in \mathcal {L}(\mathcal {B}_{\frac {1}{2}};X)\). □
Proof
Let \(\phi \in \mathcal {B}_{\frac {1}{2}}\). Then, \(\mathcal {D}_0(\phi )(\xi )=q\phi (-r)(\xi )\) for all ξ ∈ [0, π]. We can write
Hence, \(\mathcal {D}_0\in \mathcal {L}(\mathcal {B}_{\frac {1}{2}};X)\). It is obvious that \(\phi (0)\in \mathcal {L}(\mathcal {B}_{\frac {1}{2}};X)\). Therefore, we can conclude that \(\mathcal {D}\in \mathcal {L}(\mathcal {B}_{\frac {1}{2}};X)\) and the proof is complete. □
Since 0 < q < 1, then \(\mathcal {D}\) is stable and \(|\mathcal {D}_0|<1\). Thus, hypothesis (H3) is satisfied.
Now, let φ be defined by φ(θ)(ξ) = ψ(θ, ξ) for all θ ∈ (−∞, 0] and ξ ∈ [0, π]. We make the following additional assumption.
- (H8 ):
-
\(\varphi (\theta )\in D(A^{\frac {1}{2}})\) for all θ ≤ 0, with
$$\displaystyle \begin{aligned} \sup_{\theta\leq 0}e^{\gamma\theta}\sqrt{\int_{0}^{\pi}\left(\frac{\partial}{\partial \xi}\psi(\theta,\xi)\right)^2d\xi}<\infty \end{aligned}$$and
$$\displaystyle \begin{aligned} \lim_{\theta\rightarrow\theta_0}\int_{0}^{\pi}\left(\frac{\partial}{\partial \xi}\psi(\theta,\xi)-\frac{\partial}{\partial \xi}\psi(\theta_0,\xi)\right)^2d\xi=0\,\,\,\text{for}\,\,\text{all}\,\,\theta_0\leq 0. \end{aligned}$$Remark that (H8) implies \(\varphi \in \mathcal {B}_{\frac {1}{2}}\). Then, Eq. (8.30) can be written as follows:
$$\displaystyle \begin{aligned}\left \{\begin{array}{ll}\displaystyle\frac{d}{dt}\mathcal{D}(u_t)=-A\mathcal{D}(u_t)+f(u_t)\,\,\text{for}\,\,t\geq 0,\\\\ u_0=\varphi.\end{array}\right. \end{aligned} $$(8.32)
Consequently, we obtain the existence and uniqueness of a mild solution of problem (8.32). Furthermore, it is clear that f1 and f2 are continuously differentiable and their differential functions are given for \(\phi ,\psi \in \mathcal {B}_{\frac {1}{2}}\) and ξ ∈ [0, π] by
and
Let \(v_0=\psi \in \mathcal {B}_{\frac {1}{2}}\) such that:
-
(a)
\(v_0(0,.)-qv_0(-r,.)\in H^2(0,\pi )\cap H_{0}^{1}(0,\pi )\) and \(\frac {\partial v_0}{\partial \theta }\in \mathcal {B}_{\frac {1}{2}}\).
-
(b)
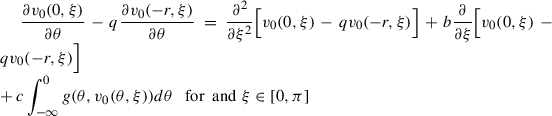 ).
).
We deduce that
Then, problem (8.32) has a unique strict solution for every \(\phi \in \mathcal {B}_{\frac {1}{2}}\).
Now, we can see that f = f1 + f2 is continuously differentiable, and zero is a solution of (8.30), ,i.e., f(0) = 0. The differential of f in 0 is given for \(\phi ,\psi \in \mathcal {B}_{\frac {1}{2}}\) and ξ ∈ [0, π] by
Consequently, the linearized equation of (8.30) can be written as follows:

where \(p=\frac {\partial }{\partial \zeta }g(.,0):(-\infty ,0]\rightarrow \mathbb {R}\) is a continuous and measurable function.
We state the main result of the stability of the solutions.
Theorem 8.6.1
Assume that (H7) and (H8) hold. Furthermore, suppose that
Then, the semigroup solution of (8.33) is exponentially stable. □
The proof of Theorem 8.6.1 makes use of this following lemma.
Lemma 8.6.3 ([4])
The spectrum \(\sigma (\tilde {A})\) of the operator \(\tilde {A}=\displaystyle \frac {\partial ^2}{\partial \xi ^2}+b\frac {\partial }{\partial \xi }\) is equal to the point spectrum \(P\displaystyle \sigma (\tilde {A})=\{-n^2-\frac {b^2}{4}:\,\,\,n\in \mathbb {N}^{*}\}\). □
Proof of Theorem 8.6.1
The exponential stability of (8.33) is obtained when \(s^{\prime }(\tilde {A})<0\), which is true only if
Moreover, the characteristic equation is given by
which leads to
Since
then the characteristic equation (8.35) becomes
Let \(\displaystyle k_n=n+\frac {b^2}{4}\). Then, using (8.36), we obtain that
Therefore,
We have also
and
It follows that
Now, assume that \(\Re (\lambda _n)\geq 0\). Then,
Consequently,
Finally, since \((1-q)\Re (\lambda _n)\), we obtain
Taking n = 1, we obtain a contraction with condition (8.34). That leads to \(\Re (\lambda )<0\). □
References
M. Adimy, K. Ezzinbi, A class of linear partial neutral functional differential equations with nondense domains. J. Differ. Equ., 147, 285–332 (1998)
M. Adimy, K. Ezzinbi, Existence and linearized stability for partial neutral functional differential equations with nondense domains. Differ. Equ. Dyn. Syst. 7, 371–417 (1999)
M. Adimy, K. Ezzinbi, Strict solutions of nonlinear hyperbolic neutral differential equations. Appl. Math. Lett. 12, 107–112 (1999)
M. Adimy, K. Ezzinbi, Existence and stability in the α-norm for some partial functional differential equations of neutral type. Ann. Mate. Pura ed Appl. 185(3), 437–460 (2006)
M. Adimy, H. Bouzahir, K. Ezzinbi, Local existence for a class of partial neutral functional differential equations with infinite delay. Differ. Equ. Dyn. Syst. 12(3–4), 353–370 (2004)
C. Avramescu, A fixed point theorem for multivalued mappings. Electron. J. Qual. Theory Differ. Equ. 2004(17), 1–10 (2004)
R. Benkhalti, K. Ezzinbi, Existence and stability in the α-norm for some partial functional differential equations with infinite delay. Differ. Integral Equ. 19(5), 545–572 (2006)
H. Bouzahir, On neutral functional differential equations with infinite delay. Fixed Point Theory 6(1), 11–24 (2005)
T. Burton, Stability and Periodic Solutions of Ordinary Differential Equations and Functional Differential Equations (Academic Press, San Diego, 1985), pp. 197–308
M.A. Cruz, J.K. Hale, Stability of functional differential equations of neutral type. J. Differ. Equ. 7, 334–355 (1970)
R. Datko, Linear autonomous neutral differential equations in a Banach space. J. Differ. Equ. 25, 258–274 (1977)
W. Desch, W. Schappacher, Linearized stability for nonlinear semigroup, in Differential Equations in Banach Spaces, ed. by A. Favini, E. Obrecht. Lecture Notes, vol. 1223 (Springer, Berlin, 1986)
K. Engel, R. Nagel, One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194 (Springer, Berlin, 2001)
K. Ezzinbi, B.A. Kyelem, S. Ouaro, Periodicity in α-Norm for partial functional differential equations in fading memory spaces. Nonlinear Anal. Theory Methods Appl. 97, 30–54 (2014)
J.K. Hale, Asymptotic Behavior of Dissipative Systems (American Mathematical Society, Providence, 1988)
J. Hale, J. Kato, Phase space for retarded equations with infinite delay. Funkcial. Ekvac. 21, 11–41 (1978)
V. Lakshmikantham, S. Leela, Differential and Integral Inequalities, vol. 1 (Academic, New York, 1969)
T. Naito, J.S. Shin, S. Murakami, The generator of the solution semigroup for the general linear functional differential equation. Bull. Univ. Electro-Commun. 11(1), 29–36 (1998)
A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations (Springer, New-York, 1993)
C.C. Travis, G.F. Webb, Partial differential equations with deviating arguments in the time variable. J. Math. Anal. Appl. 56, 397–409 (1976)
C.C. Travis, G.F. Webb, Existence, stability and compactness in α-norm for partial functional differential equations. Trans. Am. Math. Soc. 240, 129–143 (1978)
J. Wu, H. Xia, Self-sustained oscillations in a ring array of coupled lossless transmission lines. J. Differ. Equ. 124, 247–278 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Ezzinbi, K., Kyelem, B.A., Ouaro, S. (2023). Existence, Regularity, and Stability in the α-Norm for Some Neutral Partial Functional Differential Equations in Fading Memory Spaces. In: Diagana, T., Ezzinbi, K., Ouaro, S. (eds) Partial Differential Equations and Applications. Springer Proceedings in Mathematics & Statistics, vol 420. Springer, Cham. https://doi.org/10.1007/978-3-031-27661-3_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-27661-3_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-27660-6
Online ISBN: 978-3-031-27661-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



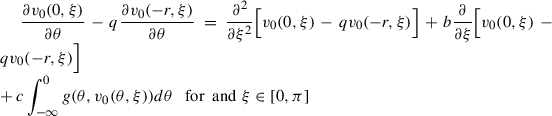 ).
).