Abstract
This work leverages an original dependency analysis to parallelize loops regardless of their form in imperative programs. Our algorithm distributes a loop into multiple parallelizable loops, resulting in gains in execution time comparable to state-of-the-art automatic source-to-source code transformers when both are applicable. Our graph-based algorithm is intuitive, language-agnostic, proven correct, and applicable to all types of loops. Importantly, it can be applied even if the loop iteration space is unknown statically or at compile time, or more generally if the loop is not in canonical form or contains loop-carried dependency. As contributions we deliver the computational technique, proof of its preservation of semantic correctness, and experimental results to quantify the expected performance gains. We also show that many comparable tools cannot distribute the loops we optimize, and that our technique can be seamlessly integrated into compiler passes or other automatic parallelization suites.
This research is supported by the Transatlantic Research Partnership of the Embassy of France in the United States and the FACE Foundation. Th. Rubiano and Th. Seiller are also supported by the Île-de-France region through the DIM RFSI project “CoHOp”. N. Rusch is supported in part by the Augusta University Provost’s office, and the Translational Research Program of the Department of Medicine, Medical College of Georgia at Augusta University.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Program transformation
- Automatic parallelization
- Loop optimization
- Abstract interpretation
- Program analysis
- Dependency analysis
1 Original Approaches to Automatic Parallelization

1.1 The Challenge of Unknown Iteration Space
Loop fission (a.k.a. loop distribution) is an optimization technique that breaks loops into multiple loops, with the same condition or index range, each taking only a part of the original loop’s body. Such transformation creates opportunity for parallelization and reduces program’s running time. For instance, the loop

under this transformation. In the transformed program, variable
 is substituted with two copies,
is substituted with two copies,
 and
and
 , and we obtain two
, and we obtain two
 loops that can be executed in parallelFootnote 1 . The gain, in terms of time, results from the fact that the original loop could only be executed sequentially, while the transformed loops can each be assigned to one core. If we consider similarly structured loops that perform resource-intensive computation or that can be distributed in e.g., 8 loops running on 8 cores, it becomes intuitive how this technique can yield measurable performance gain.
loops that can be executed in parallelFootnote 1 . The gain, in terms of time, results from the fact that the original loop could only be executed sequentially, while the transformed loops can each be assigned to one core. If we consider similarly structured loops that perform resource-intensive computation or that can be distributed in e.g., 8 loops running on 8 cores, it becomes intuitive how this technique can yield measurable performance gain.
This example straightforwardly captures the idea behind loop fission. Of course, as a loop with a short body, it misses the richness and complexities of realistic software. It is therefore very surprising that all the existing loop fission approaches fail at transforming such an elementary program! The challenge comes from the kind of loop presented. Applying loop fission to “canonical” (Definition 15) loops or loops whose number of iterations can be pre-determined is an established convention. But our example of a non-canonical loop with a (potentially) unknown iteration space cannot be handled by those approaches (Sect. 4).
In this paper we present a loop fission technique that can resolve this limitation, because it can be applied to all kinds of a loopsFootnote 2. The technique is applicable to any programming language in the imperative paradigm, lightweight and proven correct. The loop fission technique derives these capabilities from a graph-based dependency analysis, first introduced in our previous work [33]. Now we refine this dependency analysis and explain how it can be leveraged to obtain loop-level parallelism: a form of parallelism concerned with extracting parallel tasks from loops. We substantiate our claim of running time improvement by benchmarking our technique in Sect. 5. The results show, in cases where iteration space is unknown, that we obtain gain up to the number of parallelizable loops, and that in other cases the speedup is comparable to alternative techniques.
1.2 Motivations for Correct, Universal and Automatic Parallelization
The increasing need to discover and introduce parallelization potential in programs fuels the demand for loop fission. To leverage the potential speedup available on modern multicore hardware, all programs—including legacy software—should instruct the hardware to take advantage of its available processors.
Existing parallel programming APIs, such as OpenMP [25], PPL [32], and oneTBB [22], facilitate this progression, but several issues remain. For example, classic algorithms are written sequentially without parallelization in mind and require reformatting to fit the parallel paradigm. Suitable sequential programs with opportunity for parallelization must be modified, often manually, by carefully inserting parallelization directives. The state explosion resulting from parallelization makes it impossible to exhaustively test the code running on parallel architectures [12]. These challenges create demand for correct automatic parallelization approaches, to transform large bodies of software to semantically equivalent parallel programs.
Compilers offer an ideal integration point for many program analyses and optimizations. Automatic parallelization is already a standard feature in developing industry compilers, optimizing compilers, and specialty source-to-source compilers. Tools that perform local transformations, generally on loops, are frequently conceived as compiler passes. How those passes are intertwined with sequential code optimizations can however be problematic [14]. As an example, OpenMP directives are by default applied early in the compilation and hence the parallelized source code cannot benefit from sequential optimizations such as unrolling. Furthermore, compilers tend to make conservative choices and miss opportunities to parallelize [14, 21].
The loop fission technique presented in this paper offers an incremental improvement in this direction. It enables discovery of parallelization potential in previously uncovered cases. In addition, the flexibility of the system makes it suitable to integration and pipelining with existing parallelization tools at various stages of compilation, as discussed in Sect. 6.
1.3 Our Technique: Properties, Benefits and Limitations
Our technique possesses four notable properties, compared to existing techniques:
-
Suitable to loops with unknown iteration spaces—our method does not require knowing loop iteration space statically nor at compile time, making it applicable to loops which are often ignored.
-
Loop-agnostic—our method requires practically no structure from the loops: they can be
 or
or
 loops, have arbitrarily complex update and termination conditions, loop-carried dependencies, and arbitrarily deep loop nests.
loops, have arbitrarily complex update and termination conditions, loop-carried dependencies, and arbitrarily deep loop nests. -
Language-agnostic—our method can be used on any imperative language, and without manual annotations, making it flexible and suitable for application and integration with tools and languages ranging from high-level to intermediate representations.
-
Correct—our method is easy to prove correct and intuitive, largely because it does not apply to loop bodies with pointers or complex function calls.
All the approaches we know of fail in at least one respect. For instance, polyhedral optimizations cannot transform loops with unknown iteration spaces, since they work on static control parts of programs, where all control flow and memory accesses are known at compile time [20, p. 36]. More importantly, all the “popular” [35] automatic tools fail to optimize
 loops, and require
loops, and require
 and
and
 loops to have canonical forms, that generally require the trip count to be known at compilation time. We discuss these alternative approaches in detail in Sect. 4.
loops to have canonical forms, that generally require the trip count to be known at compilation time. We discuss these alternative approaches in detail in Sect. 4.
The main limitation of our approach is with function calls and memory accesses. Although we can treat loops with pure function calls, we exclude treatment of loops that contain explicit pointer manipulation, pointer arithmetic or certain function calls. We reserve the introduction of these enhancements as future extensions of our technique. In the meantime, and with these limitations in mind, we believe our approach to be a good complement to existing approaches. Polyhedral models [24]—that are also pushing to remove some restrictions [13]—, advanced dependency analyses, or tools developed for very precise cases (such as loop tiling [14]), should be used in conjunction with our technique, as their use cases diverge (Sect. 6).
1.4 Contributions: From Theory to Benchmarks
We deliver a complete perspective on the design and expected real-time efficiency of our loop fission technique, from its theoretical foundations to concrete measurements. We present three main contributions:
-
1.
The loop fission transformation algorithm—Sect. 3.1—that analyzes dependencies of loop condition and body variables, establishes cliques between statements, and splits independent cliques into multiple loops.
-
2.
The correctness proof—Sect. 3.2—that guarantees the semantic preservation of loop transformation.
-
3.
Experimental results [8]—Sect. 5—that evaluate the potential gain of the proposed technique, including loops with unknown iteration spaces, and demonstrates its integrability with existing parallelization frameworks.
But first, we present and illustrate the dependency analysis that enables our loop fission technique.
2 Background: Language and Dependency Analysis
2.1 A Simple While Imperative Language with Parallel Capacities
We use a simple imperative
 language, with semantics similar to C, extended with a
language, with semantics similar to C, extended with a
 command, similar to e.g., OpenMP’s directives [25], allowing to execute its arguments in parallelFootnote 3. Our language supports arrays but not pointers, and we let
command, similar to e.g., OpenMP’s directives [25], allowing to execute its arguments in parallelFootnote 3. Our language supports arrays but not pointers, and we let
 and
and
 loops be represented using
loops be represented using
 loops. It is easy to map to fragments of C, Java, or any other imperative programming language with parallel support.
loops. It is easy to map to fragments of C, Java, or any other imperative programming language with parallel support.
The grammar is given Fig. 1. A variable represents either an undetermined “primitive” datatype, e.g., not a reference variable, or an array, whose indices are given by an expression. We generally use \(\texttt{s}\) and \(\texttt{t}\) for arrays. An expression is either a variable, a value (e.g., integer literal) or the application to expressions of some operator op, which can be e.g., relational (==, \(\texttt {<}\), etc. ) or arithmetic (+, -, etc. ). We let \(\texttt{V}\) (resp. \(\texttt{e}\), \(\texttt{C}\)) ranges over variables (resp. expression, command) and \(\texttt{W}\) range over
 loops. We also use combined assignment operators and write e.g.,
loops. We also use combined assignment operators and write e.g.,
 for
for
 . We assume commands to be correct, e.g., with operators correctly applied to expressions, no out-of-bounds errors, etc.
. We assume commands to be correct, e.g., with operators correctly applied to expressions, no out-of-bounds errors, etc.
A program is thus a sequence of statements, each statement being either an assignment, a conditional, a while loop, a function callFootnote 4 or a skip. Statements are abstracted into commands, which can be a statement, a sequence of commands, or multiple commands to be run in parallel. The semantics of
 is the following: variables appearing in the arguments are considered local, and the value of a given variable
is the following: variables appearing in the arguments are considered local, and the value of a given variable
 after execution of the
after execution of the
 command is the value of the last modified local variable \(\texttt{x}\). This implies possible race conditions, but our transformation (detailed in Sect. 3) is robust to those: it assumes given
command is the value of the last modified local variable \(\texttt{x}\). This implies possible race conditions, but our transformation (detailed in Sect. 3) is robust to those: it assumes given
 -free programs, and introduces
-free programs, and introduces
 commands that either uniformly update the (copy of the) variables across commands, or update them in only one command. The rest of this section assumes
commands that either uniformly update the (copy of the) variables across commands, or update them in only one command. The rest of this section assumes
 -free programs, that will be given as input to our transformation explained in Sect. 3.1.
-free programs, that will be given as input to our transformation explained in Sect. 3.1.
For convenience we define the following sets of variables.
Definition 1
Given an expression
 , we define the variables occurring in
, we define the variables occurring in
 by:
by:

Definition 2
Let \(\texttt{C}\) be a command, we let \({{\,\textrm{Out}\,}}(\texttt{C})\) (resp. \({{\,\textrm{In}\,}}(\texttt{C})\), \({{\,\textrm{Occ}\,}}(\texttt{C})\)) be the set of variables modified by (resp. used by, occurring in) \(\texttt{C}\) as defined in Table 1. In the
 (
(
 ) case, \(\texttt{f}\) is a fresh variable introduced for this command.
) case, \(\texttt{f}\) is a fresh variable introduced for this command.
Our treatment of arrays is an over-approximation: we consider the array as a single entity, and that changing one value in it changes it completely. This is however satisfactory: since we do not split loop “vertically” (e.g., distributing the iteration space between threads) but “horizontally” (e.g., distributing the tasks between threads), we want each thread in the
 command to have control of the array it modifies, and not to have to synchronize its writes with other commands.
command to have control of the array it modifies, and not to have to synchronize its writes with other commands.
2.2 Data-Flow Graphs for Loop Dependency Analysis
The loop transformation algorithm relies fundamentally on its ability to analyze data-flow dependencies between loop condition and variables in the loop body, to identify opportunities for loop fission. In this section we define the principles of this dependency analysis, founded on the theory of data-flow graphs, and how it maps to the presented
 language. This dependency analysis was influenced by a large body of works related to static analysis [1, 26, 29], semantics [27, 38] and optimization [33]; but is presented here in self-contained and compact manner.
language. This dependency analysis was influenced by a large body of works related to static analysis [1, 26, 29], semantics [27, 38] and optimization [33]; but is presented here in self-contained and compact manner.
We assume the reader is familiar with semi-rings, standard operations on matrices (multiplication and addition), and on graphs (union and inclusion).
Definition of Data-Flow Graphs. A data-flow graph for a given command \(\texttt{C}\) is a weighted relation on the set \({{\,\textrm{Occ}\,}}(\texttt{C})\). Formally, this is represented as a matrix over a semi-ring, with the implicit choice of a denumeration of \({{\,\textrm{Occ}\,}}(\texttt{C})\)Footnote 5.
Definition 3
(dfg). A data-flow graph (dfg) for a command \(\texttt{C}\) is a \(|{{\,\textrm{Occ}\,}}(\texttt{C})|\,\times \,|{{\,\textrm{Occ}\,}}(\texttt{C})|\) matrix over a fixed semi-ring \((\mathcal {S},+,\times )\), with \(|{{\,\textrm{Occ}\,}}(\texttt{C})|\) the cardinal of \({{\,\textrm{Occ}\,}}(\texttt{C})\). We write \(\mathbb {M}(\texttt{C})\) the dfg of \(\texttt{C}\) and
 for the coefficient in \(\mathbb {M}(\texttt{C})\) at the row corresponding to \(\texttt{x}\) and column corresponding to \(\texttt{y}\).
for the coefficient in \(\mathbb {M}(\texttt{C})\) at the row corresponding to \(\texttt{x}\) and column corresponding to \(\texttt{y}\).
How a data-flow graph is constructed, by induction over the command, is explained in Sect. 2.3. To avoid resizing matrices whenever additional variables are considered, we identify \(\mathbb {M}(\texttt{C})\) with its embedding in a larger matrix, i.e., we abusively call the dfg of \(\texttt{C}\) any matrix containing \(\mathbb {M}(\texttt{C})\) and the multiplication identity element on the other diagonal coefficients, implicitly viewing the additional rows/columns as variables not in \({{\,\textrm{Occ}\,}}(\texttt{C})\).
2.3 Constructing Data-Flow Graphs
The data-flow graph (dfg) of a command is constructed by induction on the structure of the command. In the remainder of this paper, we use the semi-ring \((\{0,1,\infty \},\max ,\times )\) to represent dependencies: \(\infty \) represents dependence, 1 represents propagation, and 0 represents reinitialization.
Base Cases (assignment, Skip, Use). The dfg for an assignment \(\texttt{C}\) is computed using \({{\,\textrm{In}\,}}(\texttt{C})\) and \({{\,\textrm{Out}\,}}(\texttt{C})\):
Definition 4
(Assignment). Given an assignment \(\texttt{C}\), its dfg is given by:

We illustrate in Fig. 2 some basic cases and introduce the graphical conventions of using weighted relations, or weighted bi-partite graphs, to illustrate the matrices. Note that in the case of dependencies, \({{\,\textrm{In}\,}}(\texttt{C})\) is exactly the set of variables that are source of a dependence arrow, while \({{\,\textrm{Out}\,}}(\texttt{C})\) is the set of variables that either are targets of dependence arrows or were reinitialized.
Note that we over-approximate arrays in two ways: the dependencies of the value at one index are the dependencies of the whole array, and the index at which the value is assigned is a dependence of the whole array (cf. the solid arrow from \(\texttt{i}\) to \(\texttt{t}\) in the last example of Fig. 2). This is however enough for our purpose, and simplify our treatment of arrays.
The dfg for
 is simply the empty matrix, but the dfg of
is simply the empty matrix, but the dfg of
 function calls requires a fresh “e
function calls requires a fresh “e
 fect” variable to anchor the dependencies.
fect” variable to anchor the dependencies.
Definition 5
(
 ). We let \(\mathbb {M}(\mathtt {\texttt{skip}})\) be the matrix with 0 rows and columnsFootnote 6.
). We let \(\mathbb {M}(\mathtt {\texttt{skip}})\) be the matrix with 0 rows and columnsFootnote 6.
Definition 6
(
 ). We let
). We let
 be the matrix with coefficients from each
be the matrix with coefficients from each
 to \(\texttt{f}\), and from \(\texttt{f}\) to \(\texttt{f}\) equal to \(\infty \), and 0 coefficients otherwise, for \(\texttt{f}\) a freshly introduced variable. Graphically, we get:
to \(\texttt{f}\), and from \(\texttt{f}\) to \(\texttt{f}\) equal to \(\infty \), and 0 coefficients otherwise, for \(\texttt{f}\) a freshly introduced variable. Graphically, we get:

Composition and Multipaths. The definition of dfg for a (sequential) composition of commands is an abstraction that allows treating a block of statements as one command with its own dfg.
Definition 7
(Composition). We let \(\mathbb {M}(\mathtt {\mathtt {C_{1}};\dots ;\mathtt {C_{n}}})\) be \(\mathbb {M}(\mathtt {C_{1}}) \times \cdots \times \mathbb {M}(\mathtt {C_{n}})\).
For two graphs, the product of their matrices of weights is represented in a standard way, as a graph of length 2 paths; as illustrated in Fig. 3—where \(\mathtt {C_1}\) and \(\mathtt {C_2}\) are themselves already the result of compositions of assignments involving disjoint variables, and hence straightforward to compute.
Correction. Conditionals and loops both requires a correction to compute their dfgs. Indeed, the dfgs of
 \(\texttt{e}\)
\(\texttt{e}\)
 \(\mathtt {C_{1}}\)
\(\mathtt {C_{1}}\)
 \(\mathtt {C_{2}}\) and
\(\mathtt {C_{2}}\) and
 \(\texttt{e}\)
\(\texttt{e}\)
 \(\texttt{C}\) require more than the dfg of its body. The reason for this is that all the modified variables in \(\mathtt {C_1}\) and \(\mathtt {C_2}\) or \(\texttt{C}\) (e.g., \({{\,\textrm{Out}\,}}(\mathtt {C_1}) \cup {{\,\textrm{Out}\,}}(\mathtt {C_2})\) or \({{\,\textrm{Out}\,}}(\texttt{C})\)) depend on the variables occurring in \(\texttt{e}\) (e.g., in \({{\,\textrm{Occ}\,}}(\texttt{e})\)). To reflect this, a correction is needed:
\(\texttt{C}\) require more than the dfg of its body. The reason for this is that all the modified variables in \(\mathtt {C_1}\) and \(\mathtt {C_2}\) or \(\texttt{C}\) (e.g., \({{\,\textrm{Out}\,}}(\mathtt {C_1}) \cup {{\,\textrm{Out}\,}}(\mathtt {C_2})\) or \({{\,\textrm{Out}\,}}(\texttt{C})\)) depend on the variables occurring in \(\texttt{e}\) (e.g., in \({{\,\textrm{Occ}\,}}(\texttt{e})\)). To reflect this, a correction is needed:
Definition 8
(Correction). For \(\texttt{e}\) an expression and \(\texttt{C}\) a command, we define \(\texttt{e}\)’s correction for \(\texttt{C}\), \(\textrm{Corr}(\texttt{e})_{\texttt{C}}\), to be \(E^t \times O\), for
-
\(E^t\) the (column) vector with coefficient equal to \(\infty \) for the variables in \({{\,\textrm{Occ}\,}}(\texttt{e})\) and \(0\) for all the other variables,
-
\(O\) the (row) vector with coefficient equal to \(\infty \) for the variables in \({{\,\textrm{Out}\,}}(\texttt{C})\) and \(0\) for all the other variables.
As an example, let us re-use the programs \(\mathtt {C_1}\) and \(\mathtt {C_2}\) from Fig. 3, to construct \(\mathtt {w>x}\)’s correction for \(\mathtt {C_1; C_2}\), that we write \(\textrm{Corr}(\mathtt {w>x})_{\mathtt {C_1; C_2}}\):

This last matrix represents the fact that \(\texttt{w}\) and \(\texttt{x}\), through the expression
 , control the values of \(\texttt{w}\), \(\texttt{x}\) and \(\texttt{z}\) if \(\mathtt {C_1}\) and \(\mathtt {C_2}\)’s execution depend of it.
, control the values of \(\texttt{w}\), \(\texttt{x}\) and \(\texttt{z}\) if \(\mathtt {C_1}\) and \(\mathtt {C_2}\)’s execution depend of it.
Conditionals. To construct the dfg of
 \(\texttt{e}\)
\(\texttt{e}\)
 \(\mathtt {C_{1}}\)
\(\mathtt {C_{1}}\)
 \(\mathtt {C_{2}}\), there are two aspects to consider:
\(\mathtt {C_{2}}\), there are two aspects to consider:
-
1.
First, our analysis does not seek to evaluate whether \(\mathtt {C_{1}}\) or \(\mathtt {C_{2}}\) will get executed. Instead, it will overapproximate and assume that both will get executed, hence using \(\mathbb {M}(\mathtt {C_{1}})+\mathbb {M}(\mathtt {C_{2}})\).
-
2.
Second, all the variables assigned in \(\mathtt {C_1}\) and \(\mathtt {C_2}\) (e.g., \({{\,\textrm{Out}\,}}(\mathtt {C_1}) \cup {{\,\textrm{Out}\,}}(\mathtt {C_2})\)) depends on the variables occurring in \(\texttt{e}\). For this reason, \(\textrm{Corr}(\texttt{e})_{\mathtt {C_1; C_2}}\) needs to be added to the previous matrix.
Putting it together, we obtain:
Definition 9
(
 ). We let
). We let
 be \(\mathbb {M}(\mathtt {C_{1}})+\mathbb {M}(\mathtt {C_{2}})+ \textrm{Corr}(\texttt{e})_{\mathtt {C_1; C_2}}\).
be \(\mathbb {M}(\mathtt {C_{1}})+\mathbb {M}(\mathtt {C_{2}})+ \textrm{Corr}(\texttt{e})_{\mathtt {C_1; C_2}}\).
Re-using the programs \(\mathtt {C_1}\) and \(\mathtt {C_2}\) from Fig. 3 and \(\textrm{Corr}(\mathtt {w>x})_{\mathtt {C_1; C_2}}\), we obtain:

The boxed value represents the impact of \(\texttt{x}\) on itself: \(\mathtt {C_1}\) has the value 1, since \(\texttt{x}\) is not assigned in it. On the other hand, \(\mathtt {C_2}\) has 0 for coefficient, since the value of \(\texttt{x}\) is reinitialized in it. The correction, however, has a \(\infty \), to represent the fact that the value of \(\texttt{x}\) controls the values assigned in the body of \(\mathtt {C_1}\) and \(\mathtt {C_2}\)—and \(\texttt{x}\) itself is one of them. As a result, we have again the value \(\infty \) in the matrix summing them three, since \(\texttt{x}\) controls the value it gets assigned to itself—as it controls which branch ends up being executed. On the other hand, the circled value at
 is a 0 since \(\texttt{y}\)’s value is not controlled by \(\texttt{w}\), since neither \(\mathtt {C_1}\) nor \(\mathtt {C_2}\) assign \(\texttt{y}\): regardless of
is a 0 since \(\texttt{y}\)’s value is not controlled by \(\texttt{w}\), since neither \(\mathtt {C_1}\) nor \(\mathtt {C_2}\) assign \(\texttt{y}\): regardless of
 ’s truth value,
’s truth value,
 ’s value will remain the same.
’s value will remain the same.
While Loops. To define the dfg of a command
 \(\texttt{e}\)
\(\texttt{e}\)
 \(\texttt{C}\) from \(\mathbb {M}(\texttt{C})\), we need, as for conditionals, the correction \(\textrm{Corr}(\texttt{e})_{\texttt{C}}\), to account for the fact that all the modified variables in \(\texttt{C}\) depend on the variables used in \(\texttt{e}\):
\(\texttt{C}\) from \(\mathbb {M}(\texttt{C})\), we need, as for conditionals, the correction \(\textrm{Corr}(\texttt{e})_{\texttt{C}}\), to account for the fact that all the modified variables in \(\texttt{C}\) depend on the variables used in \(\texttt{e}\):
Definition 10
(
 ). We let
). We let
 be \(\mathbb {M}(\texttt{C}) + \textrm{Corr}(\texttt{e})_{\texttt{C}}\)Footnote 7.
be \(\mathbb {M}(\texttt{C}) + \textrm{Corr}(\texttt{e})_{\texttt{C}}\)Footnote 7.
As an example, we let the reader convince themselves that the dfg of

 . Intuitively, one can note that the rows for
. Intuitively, one can note that the rows for
 and
and
 are filled with 0s, since those variables do not control any other variable and are assigned in the body of the loop. On the other hand,
are filled with 0s, since those variables do not control any other variable and are assigned in the body of the loop. On the other hand,
 and
and
 all three control the values of
all three control the values of
 and
and
 , since they determine if the body of the loop will execute. The variables
, since they determine if the body of the loop will execute. The variables
 and
and
 are the only one whose value is propagated (e.g., with a 1 on their diagonal), since they are not assigned in this short example. The command
are the only one whose value is propagated (e.g., with a 1 on their diagonal), since they are not assigned in this short example. The command
 is the only command that has the potential to impact the loop’s condition. We call it an update command:
is the only command that has the potential to impact the loop’s condition. We call it an update command:
Definition 11
(Update command). Given a loop
 , the update commands \(\mathtt {C_u}\) are the commands in \(\texttt{C}\) such that
, the update commands \(\mathtt {C_u}\) are the commands in \(\texttt{C}\) such that
 for
for
 and
and
 .
.
3 Loop Fission Algorithm
We now present our loop transformation technique and prove its correctness.
3.1 Algorithm, Presentation and Intuition
Our algorithm, presented in Algorithm 1, requires essentially to
-
1.
Pick a loop at top level,
-
2.
Compute its condensation graph (Definition 13)—this requires first the dependence graph (Definition 12), which itself uses the dfg,
-
3.
Compute a covering (Definition 14) of the condensation graph,
-
4.
Create a loop per element of the covering.
Even if our technique could distribute nested loops, it would require adjustments that we prefer to omit to simplify our presentation. None of our examples in this paper require to distribute nested loops. Note, however, that our algorithm handles loops containing themselves loops.
Definition 12
(Dependence graph). The dependence graph of the loop
 is the graph whose vertices is the set of commands \(\{\mathtt {C_1}; \cdots ; \mathtt {C_n}\}\), and there exists a directed edge from \(\texttt{C}_i\) to \(\texttt{C}_j\) if and only if there exists variables
is the graph whose vertices is the set of commands \(\{\mathtt {C_1}; \cdots ; \mathtt {C_n}\}\), and there exists a directed edge from \(\texttt{C}_i\) to \(\texttt{C}_j\) if and only if there exists variables
 and
and
 such that
such that
 .
.
The last example of Sect. 2.3 gives

Note that all the commands in the body of the loop are the sources of dependence edges whose target is the update commands: for our example, this means that every command will be the source of an arrow whose target is
 . This comes from the correction, even if the condition does not explicitly appear in the dependence graph.
. This comes from the correction, even if the condition does not explicitly appear in the dependence graph.
The remainder of the loop transforming principle is simple: once the graph representing the dependencies between commands is obtained, it remains to determine the cliques in the graph and forms strongly connected components (sccs); and then to separate the sccs into subgraphs to produce the final parallelizable loops that contain a copy of the loop header and update commands.
Definition 13
(Graph helpers). Given the dependence graph of a loop \(\texttt{W}\),
-
its strongly connected components (sccs) are its strongly connected subgraphs,
-
its condensation graph
 is the graph whose vertices are sccs and edges are the edges whose source and target belong to distinct sccs.
is the graph whose vertices are sccs and edges are the edges whose source and target belong to distinct sccs.
In our example, the sccs are the nodes themselves, and the condensation graph is

Excluding the update command
 , there are now two nodes in the condensation graph, and we can construct the parallel loops by 1. inserting a
, there are now two nodes in the condensation graph, and we can construct the parallel loops by 1. inserting a
 command, 2. duplicating the loop header and update command, 3. inserting the command in the remaining nodes of the condensation graph in each loop. For our example, we obtain, as expected,
command, 2. duplicating the loop header and update command, 3. inserting the command in the remaining nodes of the condensation graph in each loop. For our example, we obtain, as expected,

Formally, what we just did was to split the saturated covering.
Definition 14
(Coverings [16]). A covering of a graph G is a collection of subgraphs \(G_1, G_2,\dots ,G_j\) such that \(G=\cup _{i=1}^j G_i\).
A saturated covering of G is a covering \(G_1, G_2,\dots ,G_k\) such that for all edge in G with source in \(G_i\), its target belongs to \(G_i\) as well. It is proper if none of the subgraph is a subgraph of another.
The algorithm then simply consists in finding a proper saturated covering of the loop’s condensation graph, and to split the loop accordingly. In our example, the only proper saturated covering is

If the covering was not proper, then the
 node on its own would be in it, leading to create a useless loop that performs nothing but updating its own condition.
node on its own would be in it, leading to create a useless loop that performs nothing but updating its own condition.

Sometimes, duplicating commands that are not update commands is needed to split the loop. We illustrate this principle with a more complex example that involve function call and multiple update commands in Fig. 4.
3.2 Correctness of the Algorithm
We now need to prove that the semantics of the initial loop \(\texttt{W}\) is equal to the semantics of \(\mathtt {\tilde{W}}\) given by Algorithm 1. This is done by showing that for any variable \(\texttt{x}\) appearing in \(\texttt{W}\), its final value after running \(\texttt{W}\) is equal to its final value after running \(\mathtt {\tilde{W}}\). We first prove that the loops in \(\mathtt {\tilde{W}}\) has the same iteration space as \(\texttt{W}\):
Lemma 1
The loops in \(\mathtt {\tilde{W}}\) have the same number of iterations as \(\texttt{W}\).
Proof
Let \(\texttt{W}_i\) be a loop in \(\mathtt {\tilde{W}}\). By property of the saturated covering, the update commands are in the body of \(\texttt{W}_i\): there is always an edge from any command to the update commands due to the loop correction, and hence the update commands are part of all the subgraphs in the saturated covering. Furthermore, if there exists a command \(\texttt{C}\) that is the target of an edge whose source is an update command \(\mathtt {C_u}\), then \(\texttt{C}\) and \(\mathtt {C_u}\) are always both present in any subgraph of the saturated covering. Indeed, since there are edges from \(\mathtt {C_u}\) to \(\texttt{C}\) and from \(\texttt{C}\) to \(\mathtt {C_u}\), they are part of the same node in the condensation graph.
Since the condition of \(\texttt{W}_i\) is the same as the condition of \(\texttt{W}\), and since all the instructions that impact (directly or indirectly) the variables occurring in that condition are present in \(\texttt{W}_i\), we conclude that the number of iterations of \(\texttt{W}_i\) and \(\texttt{W}\) are equal. \(\square \)
Theorem 1
The transformation \(\texttt{W}\rightsquigarrow \mathtt {\tilde{W}}\) given in Algorithm 1 preserves the semantic.
Proof
(sketch). We show that for every variable \(\texttt{x}\), the value of \(\texttt{x}\) after the execution of \(\texttt{W}\) is equal to the value of \(\texttt{x}\) after the execution of \(\mathtt {\tilde{W}}\). Variables are considered local to each loop \(\texttt{W}_i\) in \(\mathtt {\tilde{W}}\), so we need to avoid race condition. To do so, we prove the following more precise result: for each variable \(\texttt{x}\) and each loop \(\texttt{W}_i\) in \(\mathtt {\tilde{W}}\) in which the value of \(\texttt{x}\) is modified, the value of \(\texttt{x}\) after executing \(\texttt{W}\) is equal to the value of \(\texttt{x}\) after executing \(\texttt{W}_i\).
The previous claim is then straightforward to prove, based on the property of the covering. One shows by induction on the number of iterations k that for all the variables \(\mathtt {x_1},\dots ,\mathtt {x_h}\) appearing in \(\texttt{W}_i\), the values of \(\texttt{x}_1,\dots ,\mathtt {x_h}\) after k loop iterations of \(\texttt{W}_i\) are equal to the values of \(\mathtt {x_1},\dots ,\mathtt {x_h}\) after k loop iterations of \(\texttt{W}\). Note some other variables may be affected by the latter but the variables \(\texttt{x}_1,\dots ,\mathtt {x_h}\) do not depend on them (otherwise, they would also appear in \(\texttt{W}_i\) by definition of the dependence graph and the covering). Since the number of iteration match (Lemma 1), the claim is proven. \(\square \)
4 Limitations of Existing Alternative Approaches
In the beginning of this paper, we made the bold claim that other loop fission approaches do not handle unknown iteration spaces, which makes our loop-agnostic technique interesting. In this section we discuss these alternative approaches, their capabilities, and provide evidence to support this claim. We also give justification for the need to introduce our loop analysis into this landscape.
4.1 Comparing Dependency Analyses
Since its first inception, loop fission [2] has been implemented using different techniques and dependency mechanisms. Program dependence graph (PDG) [18] can be used to identify when a loop can be distributed [3, p. 844], but other—sometimes simpler—mechanisms are often used in practice. For instance, a patch integrating loop fission into LLVM [28] tuned the simpler data dependence graph (DDG) to obtain a Loop Fission Interference Graph (FIG) [30]. GCC, on the other hand, build a partition dependence graph (PG) based on the data dependency given by a reduced dependence graph (RG) to perform the same task [19]. In this paper, we introduce another loop dependency analysis, not to further obfuscate the landscape, but because it allows us to express our algorithm simply and—more importantly—to verify it mathematicallyFootnote 8.
We assume that the more complex mechanisms listed above (PDG, DDG or PG) could be leveraged to implement our transformation, but found it more natural to express ourselves in this language. We further believe that the way we compute the data dependencies is among the lightest, and with a very low memory footprint, as it requires only one pass on the source code to construct a matrix whose size is the number of variables in the program.
4.2 Assessment of Existing Automated Loop Transformation and Parallelization Tools
While we conjecture that other mechanisms could, in theory, treat loops of any kind like we do, we now substantiate our claim that none of them do: in short, any loop with non-basic condition or update statement is excluded from the optimizations we now discuss. We limit this consideration to tools that support C language transformations, because it is our choice implementation language for experimental evaluation in Sect. 5. We also focus on presenting the kinds of loops that other “popular” [35] automatic loop transformation frameworks do not distribute, but that our algorithm can distribute. In particular, we do not discuss loops containing control-flow modifiers (such as
 or
or
 ): neither our algorithm nor OpenMP nor the underlying dependency mechanisms of the discussed tools—to the best of our knowledge—can accommodate those.
): neither our algorithm nor OpenMP nor the underlying dependency mechanisms of the discussed tools—to the best of our knowledge—can accommodate those.
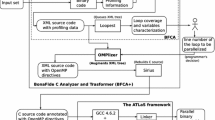
Tools that fit the above specification include Cetus, a compiler infrastructure for the source-to-source transformation; Clava, a C/C++ source-to-source tool based on Clang; Par4All, an automatic parallelizing and optimizing compiler; Pluto, an automatic parallelizer and locality optimizer for affine loop nests; ROSE, a compiler-based infrastructure for building source-to-source program transformations and analysis tools; Intel’s C++ compiler (icc), and TRACO, an automatic parallelizing and optimizing compiler, based on the transitive closure of dependence graphs. While these tools perform various automatic transformations and optimizations, only ROSE and icc perform loop fission [35, Section 3.1].
Based on our assessment, most of these tools process only canonical loops:
Definition 15
(Canonical Loop [25], 4.4.1 Canonical Loop Nest Form). A canonical loop is a loop of the form

for
 a (single) increment or decrement by a constant or a variable, and
a (single) increment or decrement by a constant or a variable, and
 a single comparison between a variable and a variable or a constant.
a single comparison between a variable and a variable or a constant.
Additional constraints on loop dependences are sometimes needed, e.g., the absence of loop-carried dependency for Cetus. It seems further that some tools cannot parallelize loops whose body contains e.g.,
 or
or
 statements [35, p. 18], but we have not investigated this claim further. However, our algorithm can handle
statements [35, p. 18], but we have not investigated this claim further. However, our algorithm can handle
 —and
—and
 too, if it was part of our syntax—present in the body of the loop seamlessly.
too, if it was part of our syntax—present in the body of the loop seamlessly.
It is always hard to infer the absence of support, but we evaluated the lack of formal discussion or example of e.g.,
 loop to be sufficient to determine that the tool cannot process
loop to be sufficient to determine that the tool cannot process
 loops, unless of course they can trivially be transformed into
loops, unless of course they can trivially be transformed into
 loops of the required form [39, p. 236]. We refer to a recent study [35, Section 2] for more detail on those notions and on the limitations of some of the tools discussed in Table 2.
loops of the required form [39, p. 236]. We refer to a recent study [35, Section 2] for more detail on those notions and on the limitations of some of the tools discussed in Table 2.
5 Evaluation
We performed an experimental evaluation of our loop fission technique on a suite of parallel benchmarks. Taking the sequential baseline, we applied the loop fission transformation and parallelization. We compared the result of our technique to the baseline and to an alternative loop fission method implemented in ROSE.
We conducted this experiment in C programming language because it naturally maps to the syntax of the imperative
 language presented in Sect. 2. We implement the parallel command as OpenMP directives. For instance, the sequential baseline program on the left of Fig. 5 becomes the parallel version on rightFootnote 9, after applying our loop fission transformation and parallelization.
language presented in Sect. 2. We implement the parallel command as OpenMP directives. For instance, the sequential baseline program on the left of Fig. 5 becomes the parallel version on rightFootnote 9, after applying our loop fission transformation and parallelization.
The evaluation experimentally substantiated two claims about our technique:
-
1.
It can parallelize loops that are completely ignored by other automatic loop transformation tools, and results in appreciable gain, upper-bounded by the number of parallelizable loops produced by loop fission.
-
2.
Concerning loops that other automatic loop transformation tools can distribute, it yields comparable results in speedup potential. We also demonstrate how insertion of parallel directives can be automated, which supports the practicality of our method.
These results combined confirm that our loop fission technique can easily be integrated into existing tools to improve the performances of the resulting code.
5.1 Benchmarks
Special consideration was necessary to prepare an appropriate benchmark suite for evaluation. We wanted to test our technique on a range of standard problems, across different domains and data sizes, and to include problems containing
 loops. Because our technique is specifically designed for loop fission, we also needed to identify problems that offered potential to apply this transformation. Finding a suite to fit these parameters is challenging, because standard parallel programming benchmark suites offer mixed opportunity for various program optimizations and focus on loops in canonical form.
loops. Because our technique is specifically designed for loop fission, we also needed to identify problems that offered potential to apply this transformation. Finding a suite to fit these parameters is challenging, because standard parallel programming benchmark suites offer mixed opportunity for various program optimizations and focus on loops in canonical form.
We resolved this challenge by preparing a curated set, pooling from three standard parallel programming benchmark suites. PolyBench/C is a polyhedral benchmark suite, representing e.g., linear algebra, data mining and stencils; and commonly used for measuring various loop optimizations. NAS Parallel Benchmarks are designed for performance evaluation of parallel supercomputers, derived from computational fluid dynamics applications. MiBench is an embedded benchmark suite, with everyday programming applications e.g., image-processing libraries, telecommunication, security and office equipment routines. From these suites, we extracted problems that offered potential for loop fission, or already assumed expected form, resulting in 12 benchmarks. We detail these benchmarks in Table 4. Because these three suites are not mutually compatible, we leveraged the timing utilities from PolyBench/C to establish a common and comparable measurement strategy. To assess performance of other kinds of loops that our algorithm can distribute, but which do not occur prevalently in these benchmarks, we converted a portion of problems to use
 loops.
loops.
Comparison Target. We compared our approach to ROSE Compiler. It is a rich compiler architecture that offers various program transformations and automatic parallelization, and supports multiple compilation targets. ROSE’s built-in LoopProcessor tool supports loop fission for C-to-C programs. This input/output specification was necessary to allow observation of the transformation results and fit with the measurement strategy we defined previously. To our knowledge, ROSE is the only tool that satisfies these evaluation requirements.
Experimental Setup. We ran the benchmarks using a Linux 5.10.0-18-amd64 #1 SMP Debian 5.10.140-1 (2022-09-02) x86_64 GNU/Linux machine, with 4 Intel(R) Core(TM) i5-6300U CPU @ 2.40GHz processors, and gcc compiler version 7.5.0. The evaluation was performed in a containerized environment on Docker version 20.10.18, build b40c2f6. For each benchmark, we recorded the clock time 5 times, excluded min and max, and averaged the remaining 3 times to obtain the result. We constrained variance between recorded times not to exceed 5%. We ran experiments on 5 input data sizes, as defined in PolyBench/C: MINI, SMALL, MEDIUM, LARGE and EXTRALARGE (abbr. XS, S, M, L, XL). We also tested 4 gcc compiler optimization levels -O0 through -O3. Speedup is the ratio of sequential and parallel executions, \(S = T_{\text {Seq}}/T_{\text {Par}}\), where a value greater than 1 indicates parallel is outperforming the sequential execution. In presentation of these results, the sequential benchmarks are always considered the baseline, and speedup is reported in relation to the transformed versions. Our open source benchmarks, and instructions for reproducing the results, are available online [8]. It should be noted that some results may be sensitive to the particular setup on which those experiments are run.
5.2 Results
In analyzing the results, we distinguish two cases: distributing and parallelizing loops with potentially unknown iterations, and loops with pre-determined iterations (typically
 and
and
 loops, respectively). The difficulty of parallelizing the former arises from the need to synchronize evaluation of the loop recurrence and termination condition. Improper synchronization results in overshooting the iterations [37], rendering such loops effectively sequential.
loops, respectively). The difficulty of parallelizing the former arises from the need to synchronize evaluation of the loop recurrence and termination condition. Improper synchronization results in overshooting the iterations [37], rendering such loops effectively sequential.
Loop fission addresses this challenge by recognizing independence between statements and producing parallelizable loops. Special care is needed when inserting parallelization directives for such loops. This remains a limitation of automated tools and is not natively supported by OpenMP. We resolved this issue by using the OpenMP single directive, to prevent overshooting the loop termination condition and need for synchronization between threads, enabling parallel execution by multiple threads on individual loop statements. The strategy is simple, implementable, and we show it to be effective. However, it is also upper-bounded in speedup potential by the number of parallelizable loops produced by the transformation. This is a syntactic constraint, rather than one based on number of available cores.
The results, presented in Table 3, show that our approach, paired with the described parallelization strategy, yields a gain relative to the number of independent parallelizable loops in the transformed benchmark. We observe this e.g., for benchmarks bicg, gesummv, and mvt, as presented in Fig. 6. We also confirm that ROSE’s approach did not transform these loops, and report no gain for the alternative approach.
Speedup of selected benchmarks implemented using
 loops. Note the influence of various compiler optimization levels, -O0 to -O3 on each problem, and how parallelization overhead tends to decrease as input data size grows from MINI to EXTRALARGE. The gain is lower for mvt because it assumes fissioned form in the original benchmark. bicg and gesummv obtain higher gain from applied loop distribution.
loops. Note the influence of various compiler optimization levels, -O0 to -O3 on each problem, and how parallelization overhead tends to decrease as input data size grows from MINI to EXTRALARGE. The gain is lower for mvt because it assumes fissioned form in the original benchmark. bicg and gesummv obtain higher gain from applied loop distribution.
 loop (in bold) are not transformed by ROSE and therefore report no gain. The other results vary depending on parallelization strategy, but as noted with e.g., problems conjgrad and tblshft, we obtain similar speedup for both fission strategies when automatic parallelization yields optimal OpenMP directives.
loop (in bold) are not transformed by ROSE and therefore report no gain. The other results vary depending on parallelization strategy, but as noted with e.g., problems conjgrad and tblshft, we obtain similar speedup for both fission strategies when automatic parallelization yields optimal OpenMP directives.Comparison with ROSE. The remaining benchmarks, with known iteration spaces, can be transformed by both evaluated loop fission techniques: ours and ROSE’s LoopProcessor. In terms of transformation results, we observed relatively similar results for both techniques. We discovered one interesting transformation difference, with benchmark gemm, which ROSE handles differently from our technique.
After transformation, the program must be parallelized by inserting OpenMP directives. This parallelization step can be fully automatic and performed with e.g., ROSE or Clava, demonstrating that pipelining the transformed programs is feasible. For evaluations, we used manual parallelization for our technique and automatic approach for ROSE. However, we also noted that the automatic insertion of parallelization directives yielded, in some cases, suboptimal choices, such as parallelization of loop nests. This added unnecessary overhead to execution time, and negatively impacted the results obtained for ROSE, e.g., for benchmarks fdtd-2d and gemm, as observable in the results. It is possible this issue could be mitigated by providing annotations and more detailed instructions for applying the parallelization directives. In other experiments with alternative parallelization tools [7, Sect. 4.3], we have been successful at finding optimal parallelization directives automatically, and therefore conclude it is achievable. We again refer to Table 3 for a detailed presentation of the experimental evaluation results.
6 Conclusion
This work is only the first step in a very exciting direction. “Ordinary code”, and not only code that was specifically written for e.g., scientific calculation or other resource-demanding operations, should be executed in parallel to leverage our modern architectures. As a consequence, the much larger codebase concerned with parallelization is much less predictable and offers more diverse loop structures. Focusing on resource-demanding programs led previous efforts not only to focus on predictable loop structures, but to completely ignore other non-canonical loops. Our effort, based on an original dependency analysis, leads to re-integrate such loops in the realm of parallel optimization. This alone, in our opinion, justifies further investigation in integrating our algorithm into specialized tools.
As presented in Fig. 6, our experimental results offer some variability, but they need to be put in context: loop distribution is often only the first step in the optimization pipeline. Loops that have been split can then be vectorized, blocked, unrolled, etc. , providing additional gain in terms of speed. Exactly as for loop fusion [31], a more global treatment of loops is needed to strike the right balance and find the optimum code transformation. Such a journey will be demanding and complex, but we believe this work enables it by reintegrating all loops in the realm of parallel optimization.
Notes
- 1.
In practice, private copies of
 are automatically created by e.g., the standard parallel programming API for C, OpenMP. Its
are automatically created by e.g., the standard parallel programming API for C, OpenMP. Its
 directives are illustrated in Fig. 5.
directives are illustrated in Fig. 5. - 2.
We focus on
 loops, but other kinds of loops (
loops, but other kinds of loops (
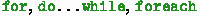 ) can always be translated into
) can always be translated into
 and general applicability follows.
and general applicability follows. - 3.
OpenMP’s
 directive is illustrated in Sect. 5.
directive is illustrated in Sect. 5. - 4.
The use command represents any command which does not modify its variables but use them and should not be moved around carelessly (e.g., a
 ). In practice, we currently treat all function calls as use, even if the function is pure.
). In practice, we currently treat all function calls as use, even if the function is pure. - 5.
We will use the order in which the variables occur in the program as their implicit order most of the time.
- 6.
Identifying the dfg with its embeddings, it is hence the identity matrix of any size.
- 7.
This is different from our previous treatment of
 loop [33, Definition 6], that required to compute the transitive closure of \(\mathbb {M}(\texttt{C})\): for the transformation we present in Sect. 3, this is not needed, as all the relevant dependencies are obtained immediately—this also guarantees that our analysis can distribute loop-carried dependencies.
loop [33, Definition 6], that required to compute the transitive closure of \(\mathbb {M}(\texttt{C})\): for the transformation we present in Sect. 3, this is not needed, as all the relevant dependencies are obtained immediately—this also guarantees that our analysis can distribute loop-carried dependencies. - 8.
- 9.
This example is inspired by benchmark bicg from PolyBench/C and presented in our artifact.
References
Abel, A., Altenkirch, T.: A predicative analysis of structural recursion. J. Funct. Program. 12(1), 1–41 (2002). https://doi.org/10.1017/S0956796801004191
Abu-Sufah, W., Kuck, D.J., Lawrie, D.H.: On the performance enhancement of paging systems through program analysis and transformations. IEE Trans. Comput. 30(5), 341–356 (1981). https://doi.org/10.1109/TC.1981.1675792
Aho, A.V., Lam, M.S., Sethi, R., Ullman, J.D.: Compilers: Principles, Techniques, and Tools, 2nd edn. Addison Wesley, Boston (2006)
Amini, M.: Source-to-source automatic program transformations for GPU-like hardware accelerators. Theses, Ecole Nationale Supérieure des Mines de Paris, December 2012. https://pastel.archives-ouvertes.fr/pastel-00958033
Amini, M., et al.: Par4All: from convex array regions to heterogeneous computing. In: IMPACT 2012 : Second International Workshop on Polyhedral Compilation Techniques HiPEAC 2012. Paris, France, January 2012. https://hal-mines-paristech.archives-ouvertes.fr/hal- 00744733
Arabnejad, H., Bispo, J., Cardoso, J.M.P., Barbosa, J.G.: Source-to-source compilation targeting OpenMP-based automatic parallelization of C applications. J. Supercomput. 76(9), 6753–6785 (2019). https://doi.org/10.1007/s11227-019-03109-9
Aubert, C., Rubiano, T., Rusch, N., Seiller, T.: A novel loop fission technique inspired by implicit computational complexity, May 2022. https://hal.archives-ouvertes.fr/hal-03669387v1. draft
Aubert, C., Rubiano, T., Rusch, N., Seiller, T.: Loop fission benchmarks (2022). https://doi.org/10.5281/zenodo.7080145. https://github.com/statycc/loop-fission
Aubert, C., Rubiano, T., Rusch, N., Seiller, T.: MWP-analysis improvement and implementation: realizing implicit computational complexity. In: Felty, A.P. (ed.) 7th International Conference on Formal Structures for Computation and Deduction (FSCD 2022). Leibniz International Proceedings in Informatics, vol. 228, pp. 26:1–26:23. Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2022). https://doi.org/10.4230/LIPIcs.FSCD.2022.26
Aubert, C., Rubiano, T., Rusch, N., Seiller, T.: pymwp: MWP analysis in Python, September 2022. https://github.com/statycc/pymwp/
Bae, H., et al.: The Cetus source-to-source compiler infrastructure: overview and evaluation. Int. J. Parallel Program. 41(6), 753–767 (2013). https://doi.org/10.1007/s10766-012-0211-z
Baier, C., Katoen, J., Larsen, K.: Principles of Model Checking. MIT Press, Cambridge (2008)
Benabderrahmane, M.-W., Pouchet, L.-N., Cohen, A., Bastoul, C.: The polyhedral model is more widely applicable than you think. In: Gupta, R. (ed.) CC 2010. LNCS, vol. 6011, pp. 283–303. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11970-5_16
Bertolacci, I., Strout, M.M., de Supinski, B.R., Scogland, T.R.W., Davis, E.C., Olschanowsky, C.: Extending OpenMP to facilitate loop optimization. In: de Supinski, B.R., Valero-Lara, P., Martorell, X., Mateo Bellido, S., Labarta, J. (eds.) IWOMP 2018. LNCS, vol. 11128, pp. 53–65. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98521-3_4
Bondhugula, U., Hartono, A., Ramanujam, J., Sadayappan, P.: A practical automatic polyhedral Parallelizer and locality optimizer. SIGPLAN Not. 43(6), 101–113 (2008). https://doi.org/10.1145/1379022.1375595
Chung, F.R.K.: On the coverings of graphs. Discret. Math. 30(2), 89–93 (1980). https://doi.org/10.1016/0012-365X(80)90109-0
Dave, C., Bae, H., Min, S., Lee, S., Eigenmann, R., Midkiff, S.P.: Cetus: a source-to-source compiler infrastructure for multicores. Computer 42(11), 36–42 (2009). https://doi.org/10.1109/MC.2009.385
Ferrante, J., Ottenstein, K.J., Warren, J.D.: The program dependence graph and its use in optimization. ACM Trans. Programm. Lang. Syst. 9(3), 319–349 (1987). https://doi.org/10.1145/24039.24041
gcc.gnu.org git - gcc.git/blob - gcc/tree-loop-distribution.c. https://gcc.gnu.org/git/?p=gcc.git;a=blob;f=gcc/tree-loop- distribution.c;h=65aa1df4abae2c6acf40299f710bc62ee6bacc07;hb=HEAD#l39
Grosser, T.: Enabling Polyhedral Optimizations in LLVM. Master’s thesis, Universität Passau, April 2011. https://polly.llvm.org/publications/grosser-diploma- thesis.pdf
Holewinski, J., et al.: Dynamic trace-based analysis of vectorization potential of applications. In: Proceedings of the 33rd ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2012, pp. 371–382. Association for Computing Machinery, New York (2012). https://doi.org/10.1145/2254064.2254108
Intel: oneTBB documentation (2022). https://oneapi-src.github.io/oneTBB/
Intel Corporation: Intel C++ Compiler Classic Developer Guide and Reference. https://www.intel.com/content/dam/develop/external/us/en/ documents/cpp_compiler_classic.pdf
Karp, R.M., Miller, R.E., Winograd, S.: The organization of computations for uniform recurrence equations. J. ACM 14(3), 563–590 (1967). https://doi.org/10.1145/321406.321418
Klemm, M., de Supinski, B.R. (eds.): OpenMP application programming interface specification version 5.2. OpenMP Architecture Review Board, November 2021. https://www.openmp.org/wp-content/uploads/OpenMP-API- Specification-5-2.pdf
Kristiansen, L., Jones, N.D.: The flow of data and the complexity of algorithms. In: Cooper, S.B., Löwe, B., Torenvliet, L. (eds.) CiE 2005. LNCS, vol. 3526, pp. 263–274. Springer, Heidelberg (2005). https://doi.org/10.1007/11494645_33
Laird, J., Manzonetto, G., McCusker, G., Pagani, M.: Weighted relational models of typed lambda-calculi. In: LICS, pp. 301–310. IEEE Computer Society (2013). https://doi.org/10.1109/LICS.2013.36
Lattner, C., Adve, V.S.: LLVM: a compilation framework for lifelong program analysis & transformation. In: 2nd IEEE / ACM International Symposium on Code Generation and Optimization (CGO 2004), 20–24 March 2004, San Jose, CA, USA, pp. 75–88. IEEE Computer Society (2004). https://doi.org/10.1109/CGO.2004.1281665, https://ieeexplore.ieee.org/xpl/conhome/9012/proceeding
Lee, C.S., Jones, N.D., Ben-Amram, A.M.: The size-change principle for program termination. In: Hankin, C., Schmidt, D. (eds.) Conference Record of POPL 2001: The 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, London, UK, 17–19 January 2001, pp. 81–92. ACM (2001). https://doi.org/10.1145/360204.360210
[loopfission]: Loop fission interference graph (fig). https://reviews.llvm.org/D73801
Mehta, S., Lin, P., Yew, P.: Revisiting loop fusion in the polyhedral framework. In: Moreira, J.E., Larus, J.R. (eds.) ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2014, Orlando, FL, USA, 15–19 February 2014, pp. 233–246. ACM (2014). https://doi.org/10.1145/2555243.2555250
Microsoft: Parallel patterns library (PPL) (2021). https://docs.microsoft.com/en-us/cpp/parallel/concrt/ parallel-patterns-library-ppl?view=msvc-170
Moyen, J.-Y., Rubiano, T., Seiller, T.: Loop quasi-invariant chunk detection. In: D’Souza, D., Narayan Kumar, K. (eds.) ATVA 2017. LNCS, vol. 10482, pp. 91–108. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68167-2_7
Palkowski, M., Klimek, T., Bielecki, W.: TRACO: an automatic loop nest parallelizer for numerical applications. In: Ganzha, M., Maciaszek, L.A., Paprzycki, M. (eds.) 2015 Federated Conference on Computer Science and Information Systems, FedCSIS 2015, Lódz, Poland, 13–16 September 2015. Annals of Computer Science and Information Systems, vol. 5, pp. 681–686. IEEE (2015). https://doi.org/10.15439/2015F34
Prema, S., Nasre, R., Jehadeesan, R., Panigrahi, B.: A study on popular auto-parallelization frameworks. Concurr. Comput. Pract. Exp. 31(17), e5168 (2019). https://doi.org/10.1002/cpe.5168
Quinlan, D., et al.: Rose user manual: a tool for building source-to-source translators draft user manual (version 0.9.11.115). https://rosecompiler.org/uploads/ROSE-UserManual.pdf
Rauchwerger, L., Padua, D.A.: Parallelizing while loops for multiprocessor systems. In: Proceedings of the 9th International Symposium on Parallel Processing, IPPS 1995, pp. 347–356. IEEE Computer Society (1995)
Seiller, T.: Interaction graphs: full linear logic. In: Grohe, M., Koskinen, E., Shankar, N. (eds.) Proceedings of the 31st Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2016, New York, NY, USA, 5–8 July 2016, pp. 427–436. ACM (2016). https://doi.org/10.1145/2933575.2934568
Vitorović, A., Tomašević, M.V., Milutinović, V.M.: Manual parallelization versus state-of-the-art parallelization techniques. In: Hurson, A. (ed.) Advances in Computers, vol. 92, pp. 203–251. Elsevier (2014). https://doi.org/10.1016/B978-0-12-420232-0.00005-2
Acknowledgments
The authors wish to express their gratitude to João Bispo for explaining how to integrate AutoPar-Clava in the first version of their benchmark, to Assya Sellak for her contribution to the first steps of this work, and to the reviewers for their insightful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Aubert, C., Rubiano, T., Rusch, N., Seiller, T. (2023). Distributing and Parallelizing Non-canonical Loops. In: Dragoi, C., Emmi, M., Wang, J. (eds) Verification, Model Checking, and Abstract Interpretation. VMCAI 2023. Lecture Notes in Computer Science, vol 13881. Springer, Cham. https://doi.org/10.1007/978-3-031-24950-1_1
Download citation
DOI: https://doi.org/10.1007/978-3-031-24950-1_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-24949-5
Online ISBN: 978-3-031-24950-1
eBook Packages: Computer ScienceComputer Science (R0)




 or
or
 loops, have arbitrarily complex update and termination conditions, loop-carried dependencies, and arbitrarily deep loop nests.
loops, have arbitrarily complex update and termination conditions, loop-carried dependencies, and arbitrarily deep loop nests.
 language
language

 is the graph whose vertices are
is the graph whose vertices are 
 loop
loop

 are automatically created by e.g., the standard parallel programming API for
are automatically created by e.g., the standard parallel programming API for  directives are illustrated in Fig.
directives are illustrated in Fig.  loops, but other kinds of loops (
loops, but other kinds of loops (
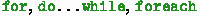 ) can always be translated into
) can always be translated into
 and general applicability follows.
and general applicability follows. directive is illustrated in Sect.
directive is illustrated in Sect.  ). In practice, we currently treat all function calls as
). In practice, we currently treat all function calls as  loop [
loop [