Learning to Solve a Stochastic Orienteering Problem with Time Windows

Abstract

Reinforcement learning (RL) has seen increasing success at solving a variety of combinatorial optimization problems. These techniques have generally been applied to deterministic optimization problems with few side constraints, such as the traveling salesperson problem (TSP) or capacitated vehicle routing problem (CVRP). With this in mind, the recent IJCAI AI for TSP competition challenged participants to apply RL to a difficult routing problem involving optimization under uncertainty and time windows. We present the winning submission to the challenge, which uses the policy optimization with multiple optima (POMO) approach combined with efficient active search and Monte Carlo roll-outs. We present experimental results showing that our proposed approach outperforms the second place approach by 1.7%. Furthermore, our computational results suggest that solving more realistic routing problems may not be as difficult as previously thought.

1 Introduction

Deep reinforcement learning (DRL) approaches represent an exciting new research avenue in artificial intelligence (AI) and operations research (OR) for automatically creating heuristics to solve combinatorial optimization (CO) problems. These approaches are attractive as they can solve CO problems with little domain knowledge by iteratively building a solution through a construction process. A central goal of these approaches is to make optimization technology more accessible to audiences without expertise in operations research and perhaps even limited problem domain knowledge. Since the approach “learns” a heuristic on its own, the overall process of solving the CO problem is transformed to a data science task, rather than an OR task.

RL has seen particular success in solving deterministic routing problems with few side constraints [18], even if concerns about generalization to very large problem sizes remain [15]. The recent IJCAI AI for TSP competition [4] aimed to expand the horizon of RL techniques in CO to stochastic problems with side constraints. The competition posed a stochastic orienteering problem with time windows to be solved with RL, thus presenting a difficult problem with novel components not yet solved with RL techniques in the literature. Given a set of customers, each providing a reward if they are visited, and a time window in which they can be visited, the objective of the time-dependent orienteering problem with stochastic weights and time windows (TDOP¹) is to construct a tour from a depot through a subset of the customers that maximizes the total rewards and returns to the depot before a maximum time is reached. A penalty is incurred for tours that exceed the maximum time, or that arrive at customer nodes after their time windows have closed. Travel times are subject to uncertainty, while the stay duration at customers is instant, provided the tour arrives after the start of the time window. However, tours that arrive at a customer before the time window are forced to wait until the start of the window.

The competition posed two tracks: supervised learning and reinforcement learning. In the supervised learning track, a complete solution to an instance of the TDOP is provided before the tour is traveled, meaning no recourse actions can be taken if delays are incurred while carrying out the tour. In the reinforcement learning track, the goal is to learn a policy for picking the next node to visit on a TDOP tour. Recourse is allowed, thus at each node visited in the solution, the future nodes to be visited can be adjusted according to how much time is left in the time horizon.

We propose a solution procedure using the policy optimization with multiple optima (POMO) method [19] and efficient active search (EAS) [12] that won first place in the reinforcement learning track². POMO is a DRL approach that exploits symmetries in the solution space of CO problems. EAS is an RL-based search method originally designed for deterministic problems.

POMO and EAS have been successfully applied to deterministic problems. In contrast to problems considered in earlier work, the TDOP is a stochastic problem in which the travel times between customers are only revealed during solution construction. This means that a solution needs to be generated online (taking into account the already realized travel times at each decision step) rather than offline. Furthermore, the TDOP is heavily constrained and there are no obvious symmetries in the solution space that POMO can exploit. Our contribution is as follows. (1) We adapt POMO to stochastic problems without symmetries in the solution space. (2) We use EAS as a method for fine-tuning a given RL policy, and further extend EAS to use entropy regularization to improve exploration. (3) We use Monte Carlo rollouts for the final online solution generation. We discuss our entry into the competition and show how the addition of EAS and Monte Carlo rollouts yields a novel, competition-winning technique.

2 Related Work

Models for automatically learning to solve routing problems have advanced significantly since [10] solved small TSP instances with a Hopfield network. The pointer network architecture [23] in particular has allowed deep networks to make high-quality recommendations for choosing the next step in a construction process. Further insights, such as using actor-critic RL [2], attention [18], multiple rollouts [19], and simulation-guided beam search [7], have further closed the gap to state-of-the-art, handcrafted routing algorithms.

While learned models are good at generating solutions to routing problems, search is still required to find high quality solutions comparable to those found with handcrafted heuristics. The neural network’s output distribution is sampled in [18], while [16] use a beam search with guidance from the neural network. The work of [13] proposes an improvement method that integrates a neural network into the repair operator of a large neighborhood search. Other iterative improvement methods for routing problems are proposed in [6, 8, 20, 26]. Generative machine learning models can also be used to create a searchable latent space as in [11], in which a generated latent space is searched with an unconstrained continuous optimizer for good solutions. The DPDP approach from [17] uses a dynamic programming algorithm that is guided by a “heatmap” of suggestions generated by the neural network from [16]. In NeuroLKH [27] a neural network is integrated into the well-known LKH algorithm [9], thus relying on LKH to perform its search. Finally, [12] introduces EAS to adjust a subset of (model) parameters at test time to better solve a given problem instance.

In contrast to deterministic routing problems, stochastic routing problems have seen little attention in the ML literature. DRL is used in [14] to solve a dynamic vehicle routing problem with stochastic customers and time-windows. In this VRP variant, new customers (requests) can arise at any time during the solution execution, resulting in already planned routes to be adjusted online. A similar VRP variant with stochastic customers is solved by [21] via DRL, but this variant also considers vehicles with limited capacity. A multiagent RL approach is proposed in [5] to solve the dynamic CVRP with stochastic travel times and stochastic customers with time windows. Finally, [1] consider the problem of routing a single electric vehicle with a reliable charge, taking into account stochastic energy consumption and dynamic customer requests. They propose an RL method that learns a policy aiming to minimize the risk of battery depletion by planning charging stops.

3 Background

We provide background information modeling routing problems using RL. As our approach uses a transformer architecture, we focus on this in the following. We note, however, that a number of options exist for RL for routing and combinatorial optimization problems in general (see [3]). We begin with a general description of modeling routing problems in a sequential decision process, followed by the POMO method and, finally, how to apply EAS.

Fig. 1.

POMO solution construction, from [12].

Solving Routing Problems with RL. Most ML-based approaches for solving routing problems formulate the solution construction as a sequential decision making problem. Starting from a start node, an actor decides, at each decision step $t \in \{0,...,T\}$, which node should be visited next. The actor $p_{\theta }$ is usually a deep neural network with weights $\theta$ that outputs a probability value for each possible action in the given state. The starting state $s_0$ describes the given problem instance (e.g., the positions of the customers and the depot) and the state $s_{t+1}$ is obtained by applying the action $a_t$ chosen at step t to the state $s_t$. Once a complete solution $\pi = (a_0,...,a_T)$ that satisfies all constraints of the problem is constructed, the objective function value of the solution can be computed (e.g., the tour length for the TSP). For the training of the network, most existing approaches use the REINFORCE algorithm [24] which adjusts the network weights based on the objective function value of the complete solution.

POMO. One state-of-the-art RL approach for sequential solution construction is the POMO approach [19]. POMO is an end-to-end approach that exploits symmetries in the solution space of combinatorial optimization problems to enforce exploration during the training phase. POMO uses a transformer-based network $p_\theta$ [22] that consists of an encoder and decoder. The encoder learns to generate an internal representation $\omega$ of a given problem instance (i.e., an embedding) and the decoder $q_{\phi }$ learns to construct a solution based on this embedding sequentially. Note that the weights $\phi$ of the decoder are a subset of all model weights $\theta$. Figure 1 shows the embedding generation and the autoregressive solution construction for a TSP instance. At each decoding step, an action is sampled according to the output distribution by the decoder.

Note, that once an instance embedding has been generated by the encoder, the decoder can be used to generate multiple solutions for that instance. POMO exploits this fact by sampling multiple solutions for each problem instance. Furthermore, POMO uses symmetries in the solution space to enforce exploration. For example, for the TSP with n cities, POMO constructs n solutions $\{\pi ^1,...,\pi ^n\}$ from the same embeddings. By starting each solution construction process from a different starting city, POMO ensures that each of the solutions is unique.

During training, POMO uses gradient ascent to update the neural network weights based on a set of sampled solutions $\{\pi ^1,...,\pi ^n\}$ with the objective to maximize the expected reward

$$\begin{aligned} \nabla _{\theta } J(\theta ) \approx \dfrac{1}{n} \sum _{i=1}^n ( R(\pi ^i) - b) \nabla _{\theta } \log p_{\theta }(\pi ^i \mid s_0^i) \end{aligned}$$

(1)

where $p_{\theta }(\pi ^i \mid s_0^i) \equiv \prod _{t=0}^{T} p_{\theta } (a_t^i \mid s_t^i)$, b is the baseline, and $R(\pi ^i)$ is the reward of the i-th solution. The baseline b is given by the average reward of all n solutions. The baseline stabilizes training by preventing the fluctuating reward between different instances and multiple solutions of single instances from overly influencing training.

EAS. Given a model trained as described above, we now focus on the search phase in which we are given an instance we have never seen before and need to solve it. Active search [2] performs an extensive search for high-quality solutions to a single test instance by iteratively solving the instance and adjusting the model parameters at the end of each iteration. In other words, active search performs a search for solutions by fine-tuning a given model towards a single instance using reinforcement learning. Over the course of the search/training, the model performance on the single test usually improves, and high-quality solutions are found. The best found solution at the end of the search/training is returned as the final solution. After solving the instance, the adjusted parameters are discarded and the model is returned to its original state, as they likely will not generalize to any other instances. While active search finds high-quality solutions, it is very slow because all instances have to be solved sequentially and a full update of the model parameters must be performed.

A recent extension to active search, called EAS [12], only updates a subset of (model) parameters during the search This significantly reduces the runtime and GPU memory requirements, since most model parameters are not updated and many model operations can hence be performed on a batch of test instances in parallel. For example, an extra layer can be added for each instance and only the parameters of this layer are updated during search. In this work, we use an EAS variant that adjusts the embeddings generated by the encoder, since both this and the extra layer versions of EAS show similar performance in [12].

4 The TDOP

In the TDOP, we are given a graph, $G = (V, E)$, with nodes V representing customers and a single depot, and edges E between all nodes. Each node i is assigned a location $(x_i,y_i)$ in a Euclidean plane, a time window $(\underline{w}_i,\bar{w}_i)$, as well as a reward $r_i$. The goal of the problem is to construct a tour starting and ending at the depot that maximizes the reward earned by visiting customers (nodes). If a node is visited, it must be visited during its time window. If a node is visited early, the model is forced to wait until the beginning of the time window. If a node is visited late, a penalty p is incurred. The travel time between nodes, $\hat{t}_{ij}$, is stochastic, but bounded above by the euclidean distance between each pair of nodes. The visit duration at each node is instantaneous. The maximum travel time is given by D, and the penalty $p \vert V \vert$ is added to the objective function if it is exceeded. Note that in this version of the orienteering problem, no costs are incurred traveling between nodes. Thus, given a variable $x_i \in \{0,1\}$ that is set to 1 iff the route visits node $i \in V$, and a variable $\delta _i \in \{0,1\}$ that is equal to 1 iff the time window at node $i \in V$ is violated, the objective function can be formulated as $\max \sum _{i \in V} \left( r_i x_i - p'_i \delta _i \right) ,$ with $p'_i$ defined as the penalty p for all nodes i that are not the depot, and $p\vert {}V\vert$ for the depot.

Figure 2 shows a TDOP instance with time windows for each node. For the purpose of illustration, assume the reward at every node is one. One possible solution is given by the black, solid line; assume the stochastic travel times between nodes are realized such that none of the time windows visited along the tour are violated. The tour thus incurs no penalty. The blue, dashed line shows an alternative end of the tour that would earn an extra reward. If we arrive at node 4 early enough, visiting node 5 may still be viable within its time window. This decision would be made on the fly as the tour is carried out. The red, dotted line, however, shows an alternative solution that is guaranteed to suffer a penalty regardless of the realization of the travel times, as the time window ends before the previous node’s time window begins.

Fig. 2.

An instance and solution (black, solid line) to the TDOP with time windows shown in square brackets. Alternate solutions are given by the red, dotted line and blue, dashed line. (Color figure online)

5 Solving the TDOP

Our solution approach for the TDOP consists of three steps. First, we use the POMO approach to learn a problem size-specific policy. To this end, we slightly adjust the POMO model to TDOP, e.g., by changing the structure of the input that the model accepts. In the next step, we use EAS to enhance the learned policy. EAS has been originally proposed as a search method for non-stochastic problems. We adjust EAS to the stochastic search setting and deploy it with the objective to find a fine-tuned policy to a given test instance. In the third step, we use Monte Carlo rollouts to construct the final solutions using the policies fine-tuned via EAS. In the following, we describe each of these three steps in more detail.

5.1 POMO for the TDOP

Modeling the TDOP .

The model of TDOP within POMO is straightforward and only requires a few adjustments to the CVRP model presented by [19] to output decent solutions.

POMO Rollouts. The core idea of POMO is to create n diverse solutions for each instance during training. The average reward of the n solutions for one instance can then be used as a baseline. POMO uses problem-specific mechanisms to enforce diversity among the solution rollouts for each instance. For the TSP, POMO starts each of the rollouts from a different starting city. For the CVRP, POMO visits a different customer first for each rollout. For both problems, the quality of the different rollouts for an instance can be directly compared, since the diversity enforcing mechanism only marginally (or not at all) influences the quality of the solutions that can be found. For the TDOP it is not possible to use a similar diversity enforcing mechanism, because the solution quality heavily depends on the selected start node. Instead, we leverage the stochastic nature of the TDOP and sample the travel times independent for each rollout. This encourages diversity among the different rollouts and hence increases exploration. We still use the average reward of all rollouts as the shared baseline. Future work could investigate if an individual baseline for each rollout taking into account the sampled travel times can improve performance.

Model Input. POMO accepts a vector representing each node of the problem instance. For example, for the TSP, POMO is given a vector consisting of the x and y-coordinates of each node. For the TDOP, we provide the vector $(x_i, y_i, r_i, \underline{w}_i,\bar{w}_i)$ for each node i. Note that we scale $\underline{w}_i$ and $\bar{w}_i$ based on the maximum travel time D.

Decoder Context. During decoding, POMO constructs a solution autoregressively. Starting from an empty solution it sequentially decides which customer should be visited next. To choose a customer, the POMO model has to consider the context of the decision (e.g., the currently visited customer). This context is provided to the model in the form of a vector. For example, for the TSP the POMO model is given the embedding of the current node, the embedding of the start node and the global graph embedding as context. For the TDOP, we additionally provide the decoder with the current time at which the last node in the partial solution is visited as input. Note that we scale current time based on the maximum travel time D.

Masking Schema. The output space of POMO potentially includes actions that are infeasible, such as visiting a previously visited node, in addition to actions that are clearly bad, such as visiting a node with a clearly violated time window. A simple mechanism for avoiding such actions is masking, which sets the probability of an undesired action in the output space to 0. We apply masking in both the train and test phases. Masking the previously visited nodes is sufficient to ensure that the solution created is always feasible.

We also use masking in the context of the time windows. Each state $s_t$ is associated with the current time at which the last node in the partial solution is visited. We mask any node with an end time window $\bar{w}_i$ that is less than the current time, as these nodes can clearly no longer be visited without incurring a large penalty³. It is still possible to get hit with a penalty due to the stochastic travel times, but we let the model choose its own risk/reward trade-off. Furthermore, we forbid actions that correspond to traveling to a node i where $\underline{w}_i > D$ and actions that involve traveling to a customer that has already been visited.

5.2 EAS for Stochastic Problems

EAS has originally been proposed as a search method for deterministic problems. In that setting, EAS fine-tunes a given model to a single test instance via reinforcement learning. The best solution observed during this fine-tuning process is returned as the final solution. In the stochastic setting considered in this work, we can not generate multiple solutions and pick the best one, because the solution quality depends on the realized travel times, and these are not known in advance. Hence, we do not use EAS to search for a solution, but as a tool to generate a fine-tuned, robust policy for each test instance. These instance-specific policies can then be used to generate the final solutions at test time.

In [12], three different variants of EAS are proposed. In this work, we use the EAS-Emb variant that updates the embeddings generated by the POMO encoder throughout the search. Note that we consider these instance embeddings a part of the policy. The overall EAS process then works as follows. For each single test instance, we first use the POMO encoder to generate a corresponding embedding $\omega$. We then fine-tune $\omega$ in an iterative process by repeatedly sampling a set of solutions $\{\pi ^1,...,\pi ^n\}$ using the POMO decoder $q_{\phi }(\pi \mid \omega )$ and adjusting the embeddings $\omega$ via gradient ascent using the gradient

$$\begin{aligned} \nabla _{\omega } \mathcal {J}_1(\omega ) \approx \dfrac{1}{n} \sum _{i=1}^n \big [( R(\pi ^i) - b) \nabla _{\hat{\omega }} \log q_{\phi }(\pi ^i \mid \omega ) \big ] \end{aligned}$$

(2)

where $q_{\phi }(\pi ^i \mid \omega ) \equiv \prod _{t=0}^T q_{\phi } (a_t^i \mid s^i_t, \omega )$, and b is the POMO baseline. Note that in contrast to (1), here we adjust the embedding $\omega$ rather than the model parameters $\theta$.

Entropy Regularization. As previously discussed, we are not able to force diverse rollouts as POMO does on the TSP and VRP, and instead sample n solutions independently. This hampers the exploration during the search, and we noticed that EAS often quickly converges towards a single solution. We propose to use entropy regularization [25] to increase the exploration during the search. Entropy regularization aims to increase the entropy of the model output (i.e., the distribution over all possible actions) and penalizes assigning a very high probability values to a single action. We use entropy regularization by considering a second gradient during the search that is defined as

$$\begin{aligned} \nabla _{\omega } \mathcal {J}_H(\omega ) \approx - \dfrac{1}{n} \sum _{i=1}^n \sum _{t=0}^T \sum _{a \in A(s^i_t)} \big [ \nabla _{\hat{\omega }} q_{\phi }(a \mid s^i_t, \omega ) \log q_{\phi }(a \mid s^i_t, \omega ) \big ] \end{aligned}$$

(3)

where $A(s^i_t)$ is the set of all actions that can be applied to the state $s^i_t$.

The gradient of the overall objective $\mathcal {J}_2$ is defined as

$$\begin{aligned} \nabla _{\hat{\omega }} \mathcal {J}_2(\omega ) = \nabla _{\omega } \mathcal {J}_1(\omega ) + \beta \cdot \nabla _{\omega } \mathcal {J}_H(\omega ) \end{aligned}$$

(4)

where $\beta$ is a hyperparameter that defines the regularization strength.

Since choosing a value for $\beta$ is not trivial, we perform EAS with m different values (see Sect. 6 for details). To do this, we create m copies of the initial embedding $\omega$ prior to the EAS search and then fine-tune each embedding completely separately (but in parallel) using different $\beta$ values. This allows us to effectively fill the available GPU memory. After the search, we evaluate each of the m fine-tuned embeddings on a separate validation set, and we discard all but the best performing embedding. We note that $\beta$ could also be tuned in a hyperparameter tuning phase.

5.3 Solution Construction Using Monte Carlo Rollouts

For the final solution construction, we use the fine-tuned policies and Monte Carlo rollouts to determine each node to visit. We solve the instances one at a time, but exploit the batching capability of the GPU in our method. Since we reveal the true travel time of each arc as we solve a TDOP instance, we can only solve it for “real” a single time. Once we commit to a move, the move is performed and the real travel time is revealed.

Monte Carlo Rollouts. Monte Carlo rollouts are a well-known mechanism for examining the quality of an action in a sequential decision process. In our case, we could of course just rely on the argmax action of the EAS-trained policy, but this is akin to assuming our model never makes mistakes. Naturally, our model is not always correct. We thus roll out, or complete, the solution from the top five model-recommended nodes using a simulation. The expected value of each of the top actions is then computed and we select the one with the highest expected value. Thus, the Monte Carlo rollouts are a recourse mechanism. If the decision maker is risk averse, one could also use an alternative criteria to the expected value, such as the conditional value-at-risk. However, the penalty in the competition is so high that our learned policy avoids risk as much as possible.

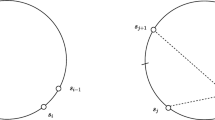
Figure 3 shows an example application of the Monte Carlo rollouts. From the depot, POMO is queried and provides a probability distribution over all unmasked nodes. As discussed, the Monte Carlo rollouts are only computed for the top actions, in this case the top 5 ranked descending. We thus receive an expected value for each action and see that b has the best value, even though the network ranked it below a. We select b, realize the stochastic travel time, and query POMO again, yielding the second set of nodes. While some are the same as in the first iteration, some are new, which corresponds to the fact that we are now at a different node and some actions may no longer be feasible or could be too risky to carry out. The rollouts are again performed on the top nodes and c is selected. The process continues until the route is complete.

Fig. 3.

Illustration of the POMO Monte Carlo procedure.

6 Computational Results

We evaluate our approach using the competition environment. We answer the following research questions:

• (RQ1) How does our approach perform on the competition test set? Can EAS and Monte Carlo rollouts improve the performance?

• (RQ2) Does entropy regularization improve the performance of EAS and what is the search trajectory of EAS?

• (RQ3) How often do the actions selected by the Monte Carlo rollouts diverge from greedy action selection, and in what cases?

Dataset. We use the competition dataset to evaluate our approach. The dataset consists of four different sizes of instances, with 25, 50, 100 and 200 nodes each, respectively. Each size category contains 250 instances. Nodes are assigned x, y coordinates in a Euclidean plane according to a uniform distribution. Time windows are generated according to a nearest neighbor procedure described in [4] in more detail. The rewards at the nodes are generated according to their Euclidean distance to the depot at (0, 0). The penalty p for missing a time window is 1. The instance generator is available at the competition’s GitHub page: https://github.com/paulorocosta/ai-for-tsp-competition.

Setup. For POMO, we train 4 separate models to solve instances with 20, 50, 100, and 200 nodes, respectively. During training, we generate training instances on the fly using the competition instance generator. We train until we achieve full convergence on a single Nvidia V100 GPU. This takes between five hours (for the 20 node model) up to a full day (for the 100 and 200 node model). For EAS, we perform 1500 iterations per instance with $m=120$ and set $\beta$ to values in the range [0, 3]. For the Monte Carlo rollouts, we perform 600 rollouts for each possible action at each decision step. On average, the EAS and MC computation takes between 7 min for 20 node instances and 48 min for 200 node instances.

6.1 RQ1: Test Set Performance

We evaluate our approach on the competition dataset and report results after each step in Table 1. Across all different instance sizes, EAS can improve the performance of POMO by 2.3% and the Monte Carlo rollouts (MCR) improve the performance of POMO and EAS by an additional 0.9%. The relative improvement of EAS is significantly higher on larger instances (e.g., 1.7% on instances of size 20 and 3.0% on instances of size 200). In contrast, for Monte Carlo rollouts the offered improvement is only slightly higher on larger instances (e.g., 0.8% on instances of size 20 and 1.1% on instances of size 200).

Table 1. Final performance on the test set instances

In Table 2 we report the final results for the reinforcement learning track of the competition. Our approach significantly outperforms the second best approach (by 1.75%) and the third best approach (by 3.66%). We note that we do not know the computational costs associated with the approaches of the other competition participants. However, our approach would have also won the competition without the expensive Monte Carlo rollout phase.

Table 2. Final leaderboard of the competition (top 3).

6.2 RQ2: EAS

EAS is examined in [12] for deterministic problems. There is no guarantee that using EAS on a stochastic problem like the TDOP will result in good performance. Thus, we examine how the reward improves with each iteration of EAS. Furthermore, we evaluate if entropy regularization is able to improve the quality of the solutions seen during EAS.

Figure 4 shows the average best reward in each EAS iteration for the four different problem sizes. That is, we report the average over the best reward of each instance at each iteration of EAS. We show results for EAS with and without entropy regularization. Note that although the total percentage improvement is not that high, for the class of TDOP investigated, it is rather significant since most of the rewards are earned from a few nodes. Thus, the challenge is to maximize the reward of the remaining route. In all problem sizes, EAS quickly increases the performance, with the average best reward at iteration 250 already near the quality achieved after 1500 iterations. Also note that on size 200 instances, EAS has not converged by iteration 1500, although the remaining performance improvement is likely rather small.

We now briefly examine entropy regularization. As can be seen, it provides a small boost in the average best reward on all sizes of instances. The additional exploration provided by entropy regularization is beneficial to the overall search, although we note that on size $n=200$ instances the default performance catches up given enough time. It is possible that a higher weight must be given to entropy regularization on this size of instance or that a reactive mechanism is necessary to properly balance the loss functions.

Fig. 4.

Average of the best reward at each EAS iteration over all instances.

6.3 RQ3: Monte Carlo Rollouts

While Monte Carlo rollouts are computationally expensive, they significantly improve the performance over greedy action selection on the test dataset. If enough rollouts are performed for each action, we get an accurate estimate of the expected total reward for each action. Consequently, the actions selected by the Monte Carlo rollouts should almost always be at least as good as those selected greedily. We hence use the Monte Carlo rollouts mechanism in this experiment to analyze in which cases the POMO model, using EAS enhanced policies and greedy action selection, makes mistakes. We thus track the decisions that were made based on the Monte Carlo rollouts and the decisions that would have been made based on greedy action selection for all test set instances.

Fig. 5.

Average of the best reward seen at each EAS iteration over all instances.

Each plot in Fig. 5 shows for each decision step t on how many instances (in %) the action selected greedily diverges from the action selected by the Monte Carlo rollouts. Furthermore, the percentage of solutions that are not yet complete are reported for each step t.

We note that the divergence is the average across those instances that are not yet fully solved. Hence, the divergence becomes unstable for high values of t when only a few incomplete solutions remain. Nonetheless, the divergence is lower towards the beginning of the solution construction process and higher towards the end. Upon closer investigation, we noticed that greedy action selection often results in returning to the depot earlier than Monte Carlo rollouts.

In general, the divergence is equally low for all instance sizes, with values staying below 5% for the majority of the solution construction process in all cases. This is especially surprising for instances with 100 and 200 nodes where the number of possible (unmasked) actions is much higher at each decision step than for instances with fewer nodes.

7 Conclusion

We presented an RL approach for solving the TDOP that won first place in the RL track of the IJCAI AI4TSP competition in 2021. Our approach modifies the POMO method and extends it with EAS and Monte Carlo rollouts. First, we enable the POMO method to handle stochastic problems without symmetries in the solution space. Then we use EAS with entropy regularization to fine-tune POMO’s learned policies. Finally, we use Monte Carlo rollouts to assist in solution construction. We show experimentally that each of these steps contributes towards the good performance of our method, and that entropy regularization can significantly improve the performance of EAS. In future work, we will examine the approach on different distributions of travel times and time windows.